数学答案_2024-2025高三（6-6月题库）_2024年09月试卷_0927云南省昆明市第一中学2025届高三第二次联考_云南省昆明市第一中学2024-2025学年高三上学期第二次联考数学

昆明市第一中学 2025 届高三年级第二次联考 数学参考答案 一、选择题 题号 1 2 3 4 5 6 7 8 答案 B D A C D C B B 1. 解析：由 得 ，所以 在复平面内对应的点为 ，在第二象限，选B. 2. 解析：若 是假命题，则 是真命题，即 恒成立，则 ， .所以 ，选D. 3. 解析：由 得 ，所以 ，所以 ，选A. 4. 解析：指标值 的样本频率是 ，所以指标值在区间 的产品约有 件，A选项正确；指标值的最大极差为 ，最小极差为 ，B选项正 确；由直方图可得出，从第一组至第七组的频率依次是 ，所以指 标值的第 百分位数在 内，小于 ，C选项不正确；抽取的产品的质量指标值的样本平均 数和样本方差分别为： ， ， D选项正确；综合以上分析，该样本统计量的叙述不正确的选项是C. 5. 解析：由双曲线 的渐近线方程是 得 ，即 ，所以离心率，选D . 6 ． 解 析 ： 当 时 ， ， ， 所 以 在区间 单调递增，即 ；当 时， 在 内单调递增，所 以 ，因为函数 的值域为 ，所以实数 的取值范围是 ，选C. 7. 解析：取 BC 的中点F，连接AF , FO ,因为 AB//CD ，所以直线 AO 与 CD 所 1 1 ⃗AO=⃗AF+⃗FO=⃗AB+ ⃗AD+ ⃗AA 成角即为 AO 与AB所成的角,所以 2 2 1 ,所以 ⃗AO2 =(⃗AB+ 1 ⃗AD+ 1 ⃗AA ) 2 =22 + 1 ×22 ×2+2×2×cos π + 1 ×2×2×cos π =9 2 2 1 4 3 2 3 ， | ⃗AO |=3 ⃗AO⋅⃗AB= ⃗AB2 + 1 ⃗AD⋅⃗AB+ 1 ⃗AB⋅⃗AA =5 即 ,又因为 2 2 1 ,所以 ⃗AO⋅ ⃗AB 5 5 cosθ= = = 5 | ⃗AO|⋅| ⃗AB| 3×2 6 ,所以直线 AO 与AB所成角的余弦值为6 ，选B. 8．解析：由 得 ，因为函数 满足 ， 所以 在 上单调递增，由 ，解得 ，即 ；因为 ， ，所以 ，当 时， 取的最小值为 ， 选B. 二、多选题 题号 9 10 11 答案 BC ACD ACD9. 解析：若 ，则 ，但 正负不确定，所以 与 大小不确定，A错误；若 ， 则 ，B正确；若 ，则 ，所以 ，C正确；由 ， ，知 ， ，所以 是 中的最大项，D错；选BC． 10. 解析：根据抛物线的定义， ，即 ，所以抛物线 的方程为 ，选项A正 确；当直线 的斜率不存在时， 的方程为 ，联立 得直线 与 有且仅有一个公共点 ，满足题意；当直线 的斜率存在时，设 的方程为 ，联立 得 ，由 得 或 ，此时直线 的方程为 或 ， 所以满足过定点 且与 有且仅有一个公共点的直线 共有 条，直线 的方程为 或 或 ，选项 B 错误；抛物线 的焦点 ，直线 的方程为： ，与抛物线方程 联立消去 化简得： ，设 ， ，则 ， ，所以 ，选项C正 确；由抛物线的定义知 , 所以满足 的点 就是满足 的点 ，由和 可得出线段 的中垂线方程是 ， 联立 消去 化简得方程： ，由于 ，此方程有 个不等根，即线段 的中垂线 与抛物线 有 个公共点，所以满足 的点 有且仅有 个，选项D正确；综合以上分析，选 ACD． 11．解析：因为 是奇函数，图象关于点 对称，所以 的图象关于点 对称，A正确；因为 ，由 解得 或 ， 解得 ，所以 在区间 单调递增， 单调递减， 单调递增，且 ， ， ，所以 有两个零点，B错误；又因为 ，所以 在区间 单调递减， 单调递增，即 只有一个极值点，C正确；设 ， ，由 解得 ， 解得 ，所以 在区间 单调递减， 单调递增， ，所以 ，因为 在区间 单调递增，所以由 ，得 ，D正确；选ACD. 三、填空题 12. 解析：因为 ， 所以 ． 13．解析：由 得 ，即 ，即，解得 或 ，因为 ，所以 14. 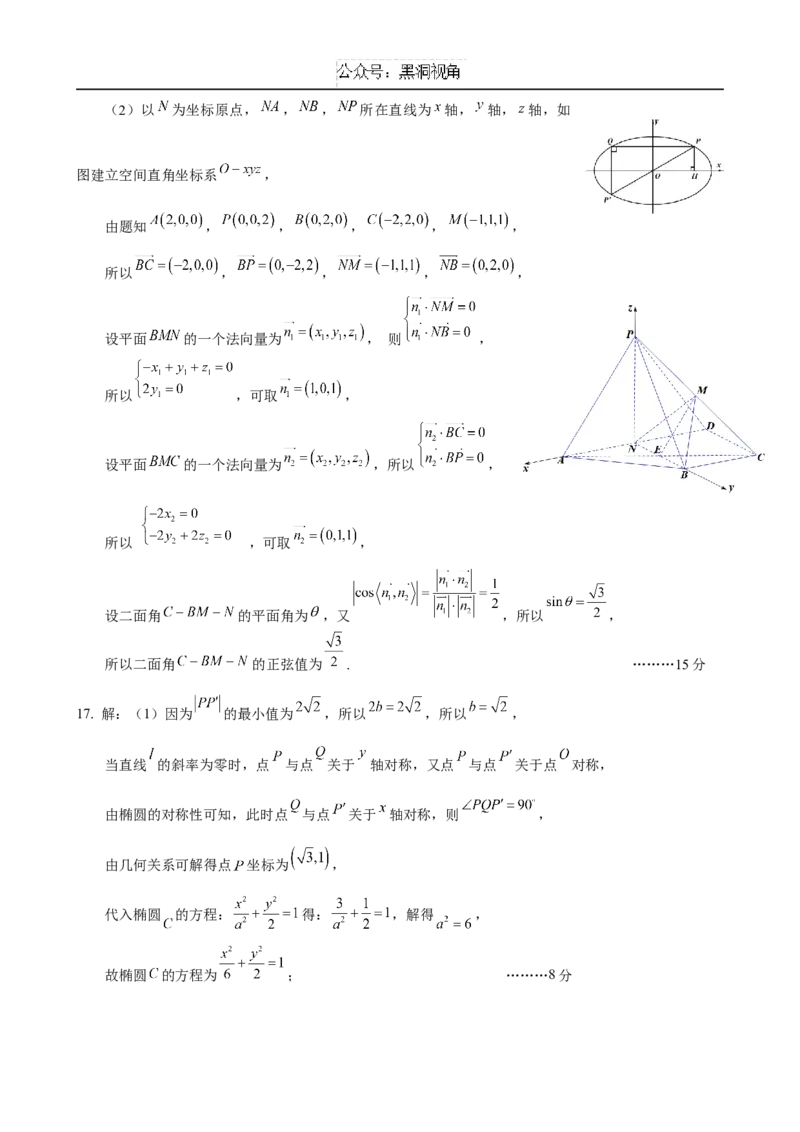解析：小张从 处出发选择最短路径前往 处，需要向右走 条街道和向上走 条街道，共走 条 街道．所以从 处出发选择最短路径到达 处一共有 种走法；同理，从 处到达 处有 种走法，从 处到达 处有 种走法， 所以根据分步计数原理，小张每天早上上班 途经街道 处的最短路径走法有 种． 四、解答题 15．解：（1） ， 因为 ，所以 ，所以 最大值为 ， 由 得 ． …………8分 （2）由 得 ， ， 所以函数 的单调递增区间为 ． …………13分 16．（1）证明：连接 ，设 交 于点 ，连接 ， 由 ，得 ， 又 ，所以△ ≌△ ，所以 是 的中点，又 是 的中点，所以 ， 因为 平面 ， 平面 ， 所以 平面 ； ………7分（2）以 为坐标原点， ， ， 所在直线为 轴， 轴， 轴，如 图建立空间直角坐标系 ， 由题知 ， ， ， ， ， 所以 ， ， ， ， 设平面 的一个法向量为 ， 则 ， 所以 ，可取 ， 设平面 的一个法向量为 ，所以 ， 所以 ，可取 ， 设二面角 的平面角为 ，又 ，所以 ， 所以二面角 的正弦值为 . 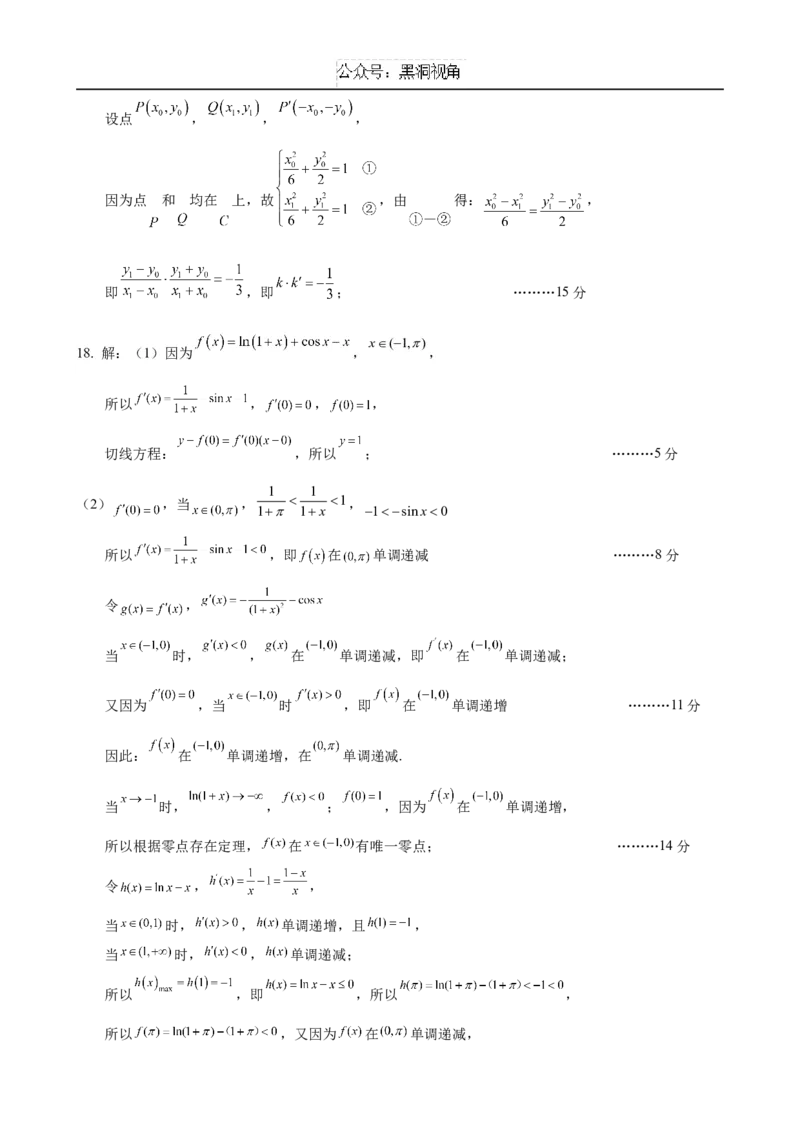………15分 17. 解：（1）因为 的最小值为 ，所以 ，所以 ， 当直线 的斜率为零时，点 与点 关于 轴对称，又点 与点 关于点 对称， 由椭圆的对称性可知，此时点 与点 关于 轴对称，则 ， 由几何关系可解得点 坐标为 ， 代入椭圆 的方程： 得： ，解得 ， 故椭圆 的方程为 ； ………8分设点 ， ， ， 因为点 和 均在 上，故 ，由 得： ， 即 ，即 ； ………15分 x(1,) 18. 解：（1）因为 ， ， 所以 ， ， ， 切线方程： ，所以 ； ………5分 1 1 （2） ，当 ，  1， 1 1x 1sinx0 所以 ，即 在 单调递减 ………8分 令 ， 当 时， ， 在 单调递减，即 在 单调递减； 又因为 ，当 时 ，即 在 单调递增 ………11分 因此： 在 单调递增，在 单调递减. 当 时， ， ； ，因为 在 单调递增， 所以根据零点存在定理， 在 有唯一零点； ………14分 令 ， ， 当 时， ， 单调递增，且 ， 当 时， ， 单调递减； 所以 ，即 ，所以 ， 所以 ，又因为 在 单调递减，根据零点存在定理 在 有唯一零点. 综上， 在 有2个零点. ………17分 19. 解：（1）记事件 为恰好答对一道判断题并且配对正确两道连线题， ； ………4分 （2）甲同学挑战成功有以下几种情况： ① “共答对四道”，即答对余下的判断题，答错两道连线题，则 ， ② “共答对五道”，即答错余下的判断题，答对余下的三道连线题， ， ③ “共答对六道”，即答对余下的四道问题， ， ，即甲同学挑战成功的概率为 ； ………10分 （3）设选择方式一､二的班级团队挑战成功的概率分别为 ． 当选择方式一时，因为两人都回答错误的概率为 ，则两人中至少有一人回答正确的概率为 ，所以 ， 当选择方式二时，因为一个小组闯关成功的概率为 ，则一个小组闯关不成功的概率为 ，所以 ，所以 ， 构造 ，则 ，因为 ，则 ，，可得 ，所以 ，即 ， 所以 单调递增，又因为 ， 且 ，所以 ，从而 ，即 ， 所以为使本班挑战成功的可能性更大，应选择方式一参赛． ………17分