数学答案_2024-2025高三（6-6月题库）_2024年09月试卷_0930山西省运城市2024-2025学年高三上学期9月摸底调研测试_山西省运城市2024-2025学年高三上学期9月摸底调研测试数学

9月运城市调研答案
一、1.D 2.B 3.D 4.A 5.B 6.C 7.A 8.C
二、9.AD 10.BC 11.ABD
x2 y2
   
三、13.2 14.  1 15. ,0  4,
2 8
四、答案：
sinC c
15. 解：（1）在ABC中，由正弦定理得，  ， ………………1分
sinB b
c2 sinC c2 c
因为  ，所以  ，
b2c2a2 sinB b2c2a2 b
………………3分
化简得，b2c2a2 bc，
b2c2a2 1
在ABC中，由余弦定理得，cosA  ， ………………5分
2bc 2
又因为0 Aπ，所以A
π ………………6分
3
1 3 3 3
（2）由S  bcsin A bc  ，得bc=6， ………………8分
ABC
2 4 2
由a2 b2c22bccosA，得7b2 c2 6，所以b2 c2 13. ………………10分
所以 bc 2 b2 c2 2bc 25，
所以b+c=5
………………12分
所以ABC的周长abc5 7
………………13分
16．解：（1）由题可得: f(x)ex a,
………………1分
当a0时， f(x)0， f(x)在R上单调递增. ………………3分
当a 0时，f(x)0可得xlna， ………………4分
若x(，lna)时，f(x)0, f(x)单调递减， ………………6分
若x(lna，)时，f(x)0, f(x)单调递增， ………………8分
综上可得：
当a0时 f(x)在R上单调递增.
当a 0时 f(x)在(，lna)单调递减，f(x)在(lna，)单调递增. ………………9分1 ex
（2）由f(x)2得ex ax，而x(0, )，a ………………11分
2 x
令g(x) ex ,g(x) ex(x1) 0， g(x)在（0， 1 ）上单调递减， …………13分
x x2 2
1
g(x) g( )2 e, …………14分
2
a2 e
. …………15分
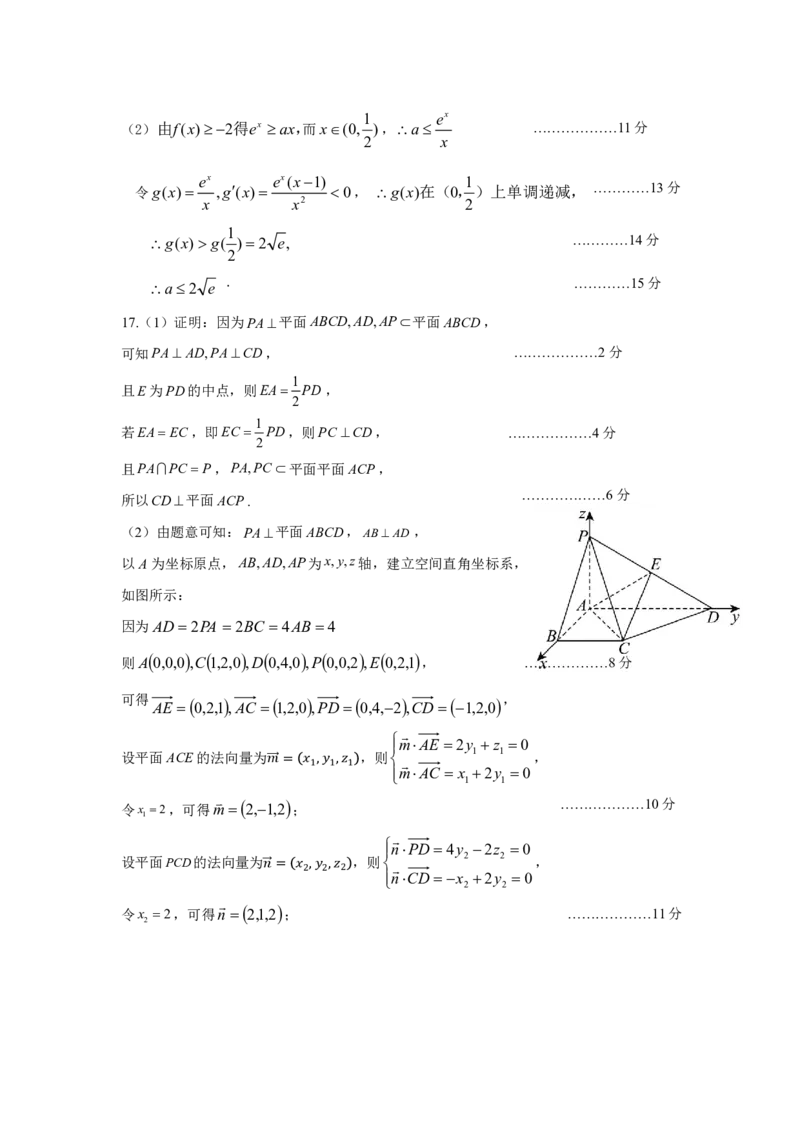
17.（1）证明：因为PA平面ABCD,AD,AP平面ABCD，
可知PA AD,PACD， ………………2分
1
且E为PD的中点，则EA PD ，
2
1
若EAEC，即EC  PD，则PC CD， ………………4分
2
且PAPC P，PA,PC平面平面ACP，
所以CD平面ACP.
………………6分
（2）由题意可知：PA平面ABCD，ABAD，
以A为坐标原点，AB,AD,AP为x,y,z轴，建立空间直角坐标系，
如图所示：
因为AD 2PA 2BC 4AB 4
则A  0,0,0  ,C  1,2,0  ,D  0,4,0  ,P  0,0,2  ,E  0,2,1  ， ………………8分
可得        ，
AE  0,2,1,AC  1,2,0 ,PD  0,4,2 ,CD  1,2,0

  mAE 2y z 0
设平面ACE的法向量为 ，则 1 1 ，

 mAC  x 2y 0
=  1,  1,  1 1 1
令x 2，可得m



2,1,2

；
………………10分
1

  nPD 4y 2z 0
设平面PCD的法向量为 ，则 2 2 ，

 nCD x 2y 0
  =  2,  2,  2 2 2
令x 2，可得n    2,1,2  ； ………………11分
2由题意可得：  
cos m

,n


m

n

………………12分
m  n
414 7
  ………………14分
414 414 9
………………15分
4 2
所以平面ACE和平面PCD所成二面角的正弦值为
9
18. 解：设摸球一次，“取到甲袋”为事件A ，“取到乙袋”为事件A ，“摸出白球”为事件B ，
1 2 1
“摸出红球”为事件B
2
（1）          
P B
1
 P A
1
P B
1
A
1
P A
2
P B
1
A
2
……………………3分
1 8 1 4 3
    
2 10 2 10 5
3
所以摸球一次就实验结束的概率为 ……………………6分
5
2
   
（2）①因为B ,B 是对立事件，P B 1P B  ， ……………………8分
1 2 2 1 5
1 6

 
  P A B 2 10 3
所以P A B  2 2  
2 2 P  B  2 4
2
5
3
所以选到的袋子为乙袋的概率为 ……………………10分
4
    3 1
②由①可知P A B 1P A B 1  ……………………11分
1 2 2 2 4 4
所以方案一种取到白球的概率为
        1 8 3 4 1
P  P A B P B A P A B P B A      ……………………13分
1 1 2 1 1 2 2 1 2 4 10 4 10 2
方案二种取到白球的概率为
        3 8 1 4 7
P  P A B P B A P A B P B A     
2 2 2 1 1 1 2 1 2 4 10 4 10 10
……………………15分
7 1
因为  ，
10 2
所以方案二中取到白球的概率更大，即选择方案二使得第二次摸球就实验结束的概率更大。
……………………17分
19．解（1）因为点P  t1,t  在抛物线C：x2 4y上，
1
则t12 4t，解得t 1. ………………3分（2）证明：由（1）可知：P  2,1  ，即x 2,y 1， ………………4分
1 1 1
方法一：因为点P x ,y 在抛物线C：x2 4y上，则 y  x n 2 ，且Q  x ,y  ，………………5分
n n n n 4 n1 n n
过P n1    x n1 , x n 4 1 2     ，且斜率为1的直线P n1 Q n1 : y x n 4 1 2   xx n1 ， ………………6分
 x 2
y n1   xx 
联立方程 4 n1 ，可得x2 4x4x x 2 0， ………………7分
n1 n1

x2 4y
解得x x 或xx 4，
n1 n1
所以x x 4，可得x x 4， ………………8分
n n1 n n1
 
另解：根据韦达定理可得x  x 4即：x x 4
n1 n n n1
所以数列

x

是以首项为2，公差为4的等差数列，
………………9分
n
所以x 24  n1  4n2， ………………10分
n
x 2  4n2 2
y  n    2n1 2. ………………11分
n 4 4
方法二：因为点P  x ,y  ，P x ,y ，Q  x ,y  在抛物线C：x2 4y上，
n1 n1 n1 n n n n1 n n
 x 2 4y
所以 n1 n1，两式相减得：  x x  x x  4  y  y  ………………5分
 x 2 4y n1 n n1 n n1 n
n n
y  y x x
所以：k  n1 n  n1 n 1 ………………6分
P n1 Q n x x 4
n1 n
可得x x 4，
………………8分
n n1
所以数列

x

是以首项为2，公差为4的等差数列，
………………9分
n
所以x 24  n1  4n2， ………………10分
n
x 2  4n2 2
y  n    2n1 2. ………………11分
n 4 4
     
（3）由（2）题意可知：P 4n2,  2n1 2 ,P 4n2,  2n1 2 ,P 4n6,  2n3 2 ， ………12分
n n1 n2方法一：梯形T PP T 的面积为：
n n n1 n1
y
S  1 TT  T P  P T 
TnPnPn1Tn1 2 n n1 n n n1 n1
1
 2n122n124n24n232n2， ………14分
 
2
即S 32n2，同理可得S 32n12，
TnPnPn1Tn1 Tn1Pn1Pn2Tn2
梯形T PP T 的面积为：S  1 TT  T P  P T 
n n n2 n2 TnPnPn2Tn2 2 n n2 n n n2 n2
1
 2n322n124n24n6162n12，
 
2
即S 162n12， ………15分
TnPnPn2Tn2
 
则PP P nN 的面积为： x
n n1 n2
S
PnPn1Pn2
S
TnPnPn1Tn1
S
Tn1Pn1Pn2Tn2
S
TnPnPn2Tn2
32n232n12162n12 16. ………17分
方法二：  
PP  4,  2n1 2   2n1 2   4,8n  ………………12分
n n1
 
P P  4,

2n3
2


2n1
2


4,8n8

………………14分
n1 n2
 
所以PP P nN 的面积为：
n n1 n2
1
 
S  4 8n8 48n 16 ………………17分
P n P n1 P n2 2