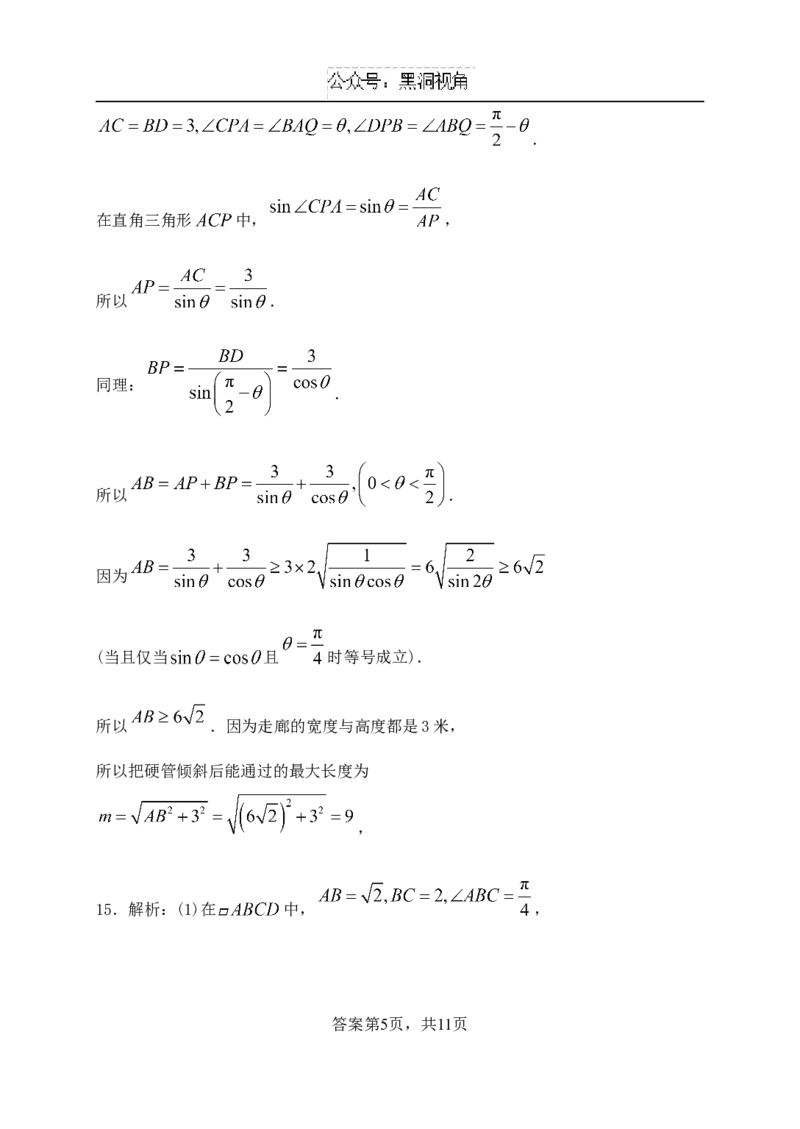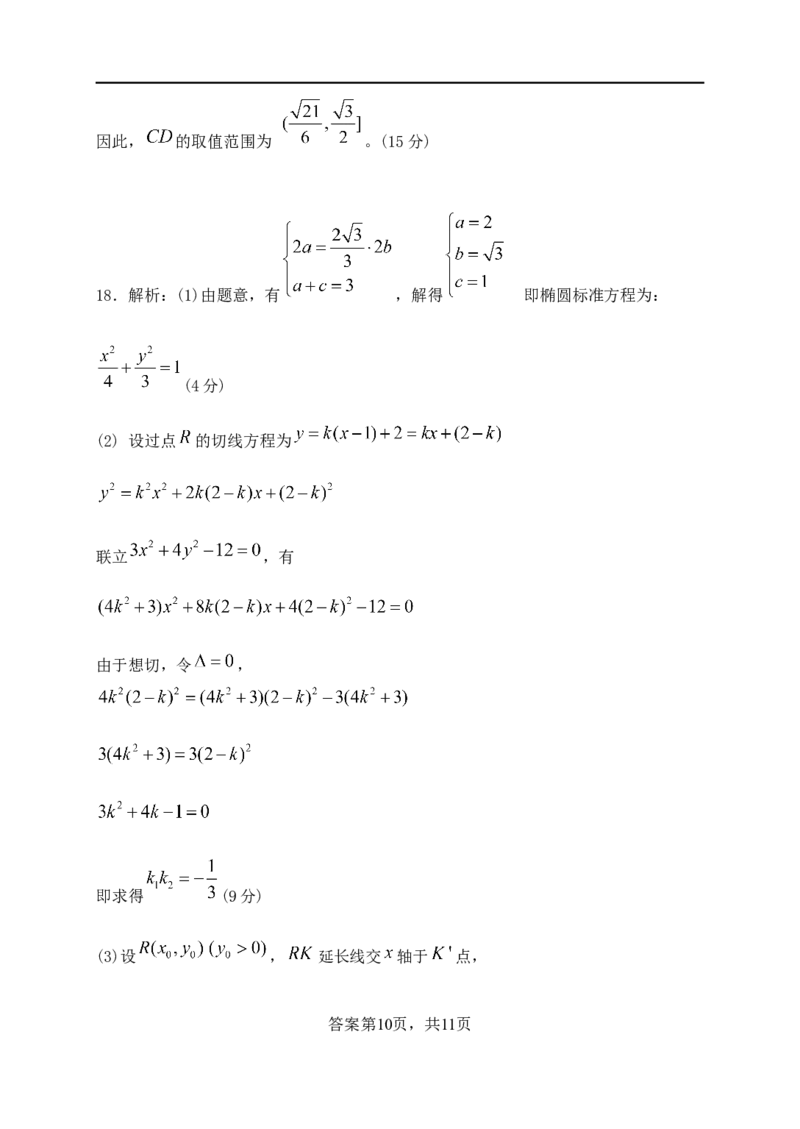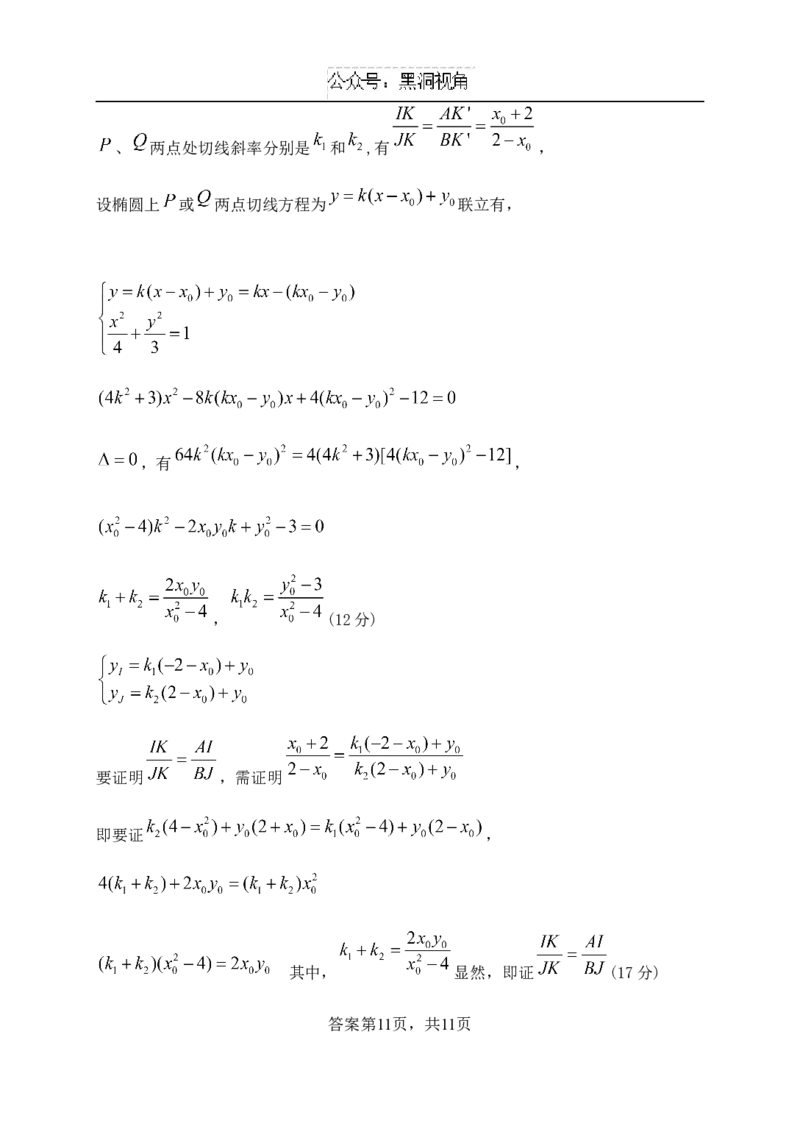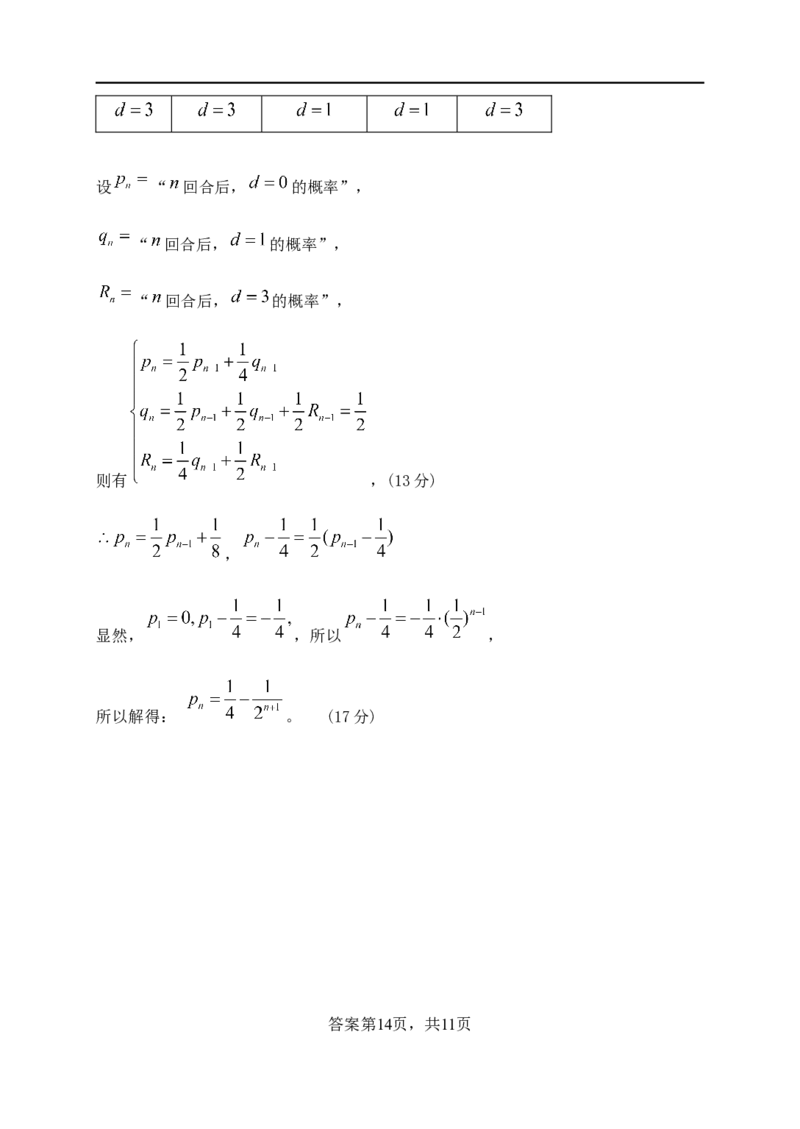文档内容
参考答案:
题号 1 2 3 4 5 6 7 8 9 10 11
答案 C A D A D A B B AB ABD AD
12. 13. 14.9
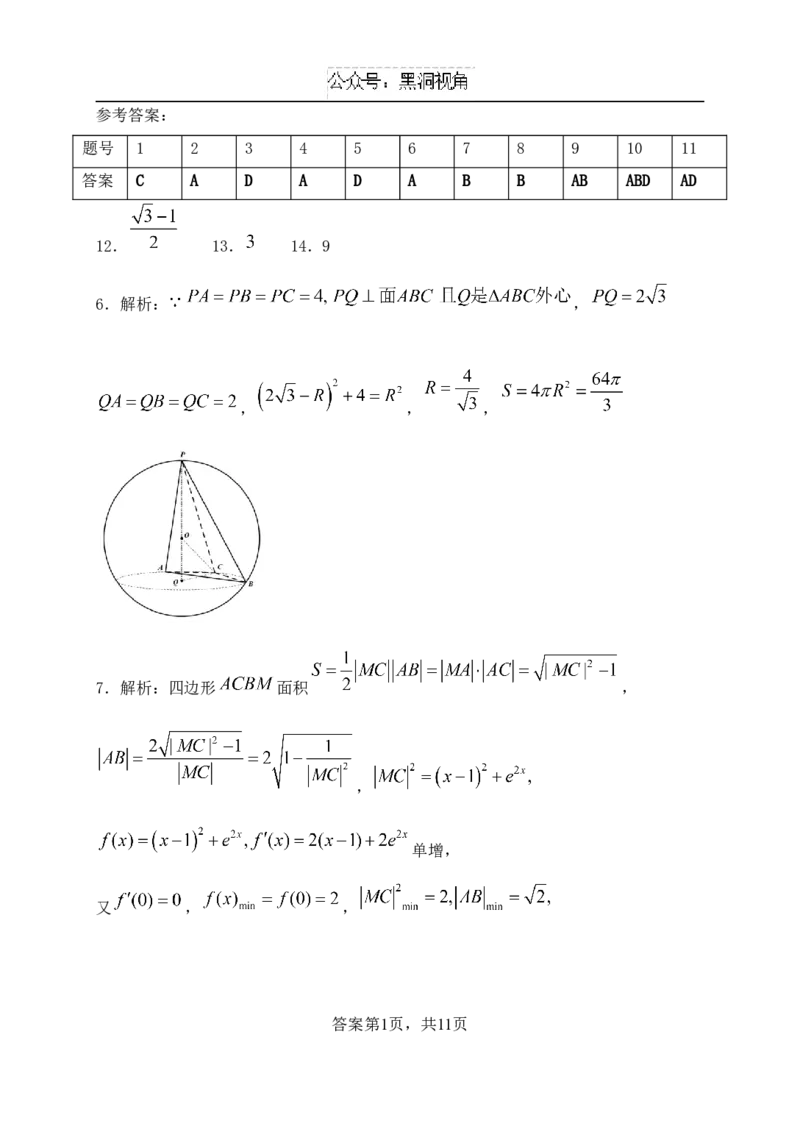
6.解析: ,
, , ,
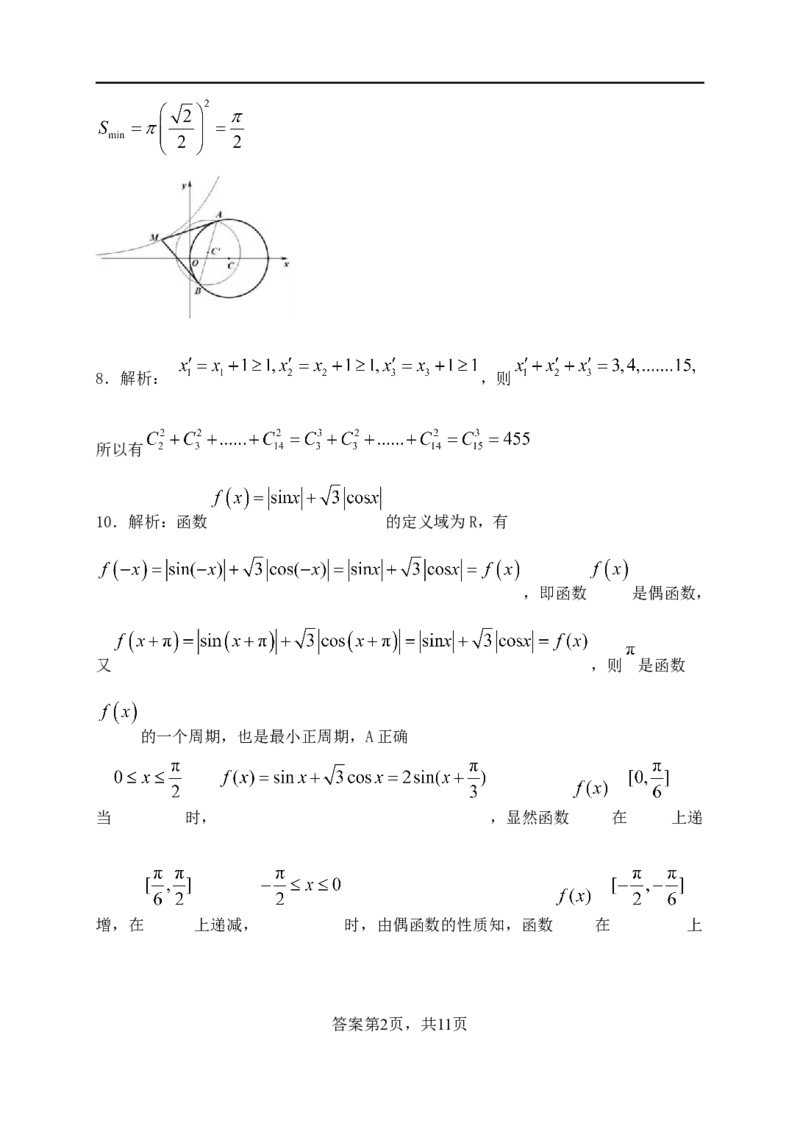
7.解析:四边形 面积 ,
,
单增,
又 , ,
答案第1页,共11页8.解析: ,则
所以有
10.解析:函数 的定义域为R,有
,即函数 是偶函数,
又 ,则 是函数
的一个周期,也是最小正周期,A正确
当 时, ,显然函数 在 上递
增,在 上递减, 时,由偶函数的性质知,函数 在 上
答案第2页,共11页递增,在 上递减,即当 时 ,
即函数 在 的取值集合为 ,
从而函数 在 的取值集合为 ,即在 上的值域为 ,因此
函数 在R上的值域为 ,B正确;
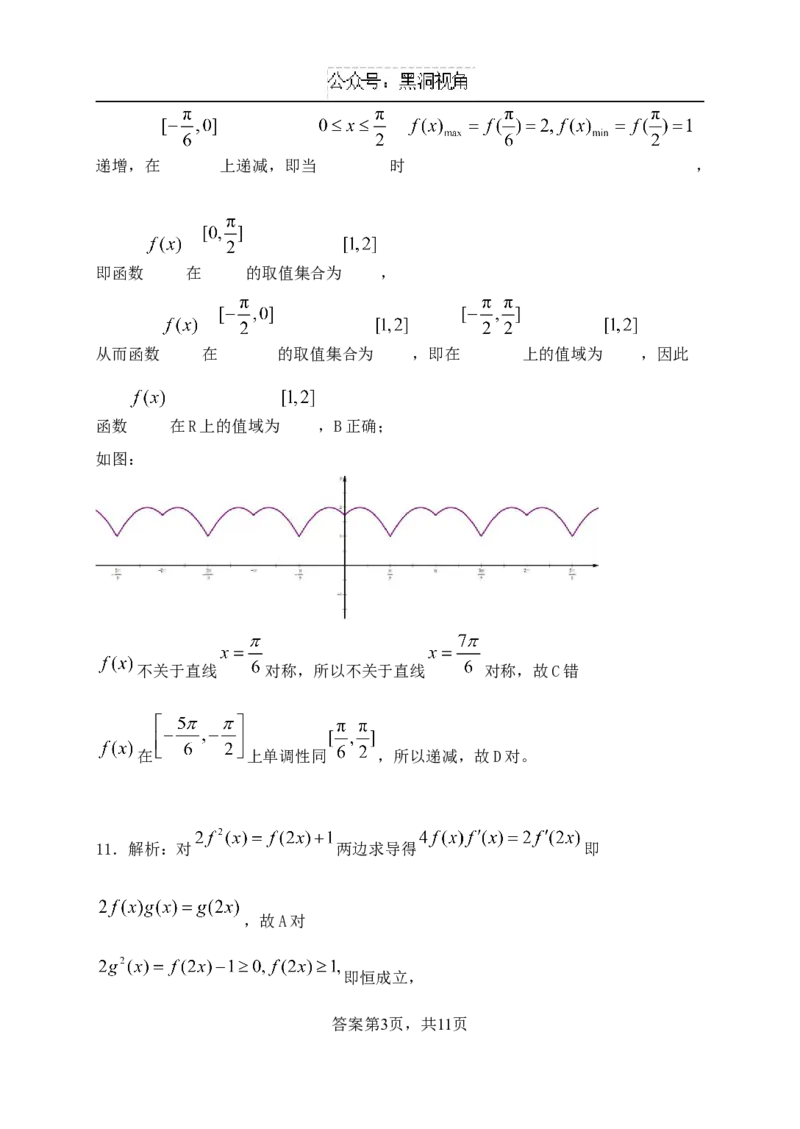
如图:
不关于直线 对称,所以不关于直线 对称,故C错
在 上单调性同 ,所以递减,故D对。
11.解析:对 两边求导得 即
,故A对
即恒成立,
答案第3页,共11页,故B错。
是奇函数, 是偶函数,
, 为增函数, 为增函数,
又 ,故C错。
,
,
为增函数,
,故D对。
14.解析:如图示,先求出硬管不倾斜,水平方向通过的最大长度AB.
设 ,则 .
过A作AC垂直内侧墙壁于C,B作BD垂直内侧墙壁于D,则
答案第4页,共11页.
在直角三角形 中, ,
所以 .
同理:
.
所以 .
因为
(当且仅当 且 时等号成立).
所以 .因为走廊的宽度与高度都是3米,
所以把硬管倾斜后能通过的最大长度为
,
15.解析:(1)在 中, ,
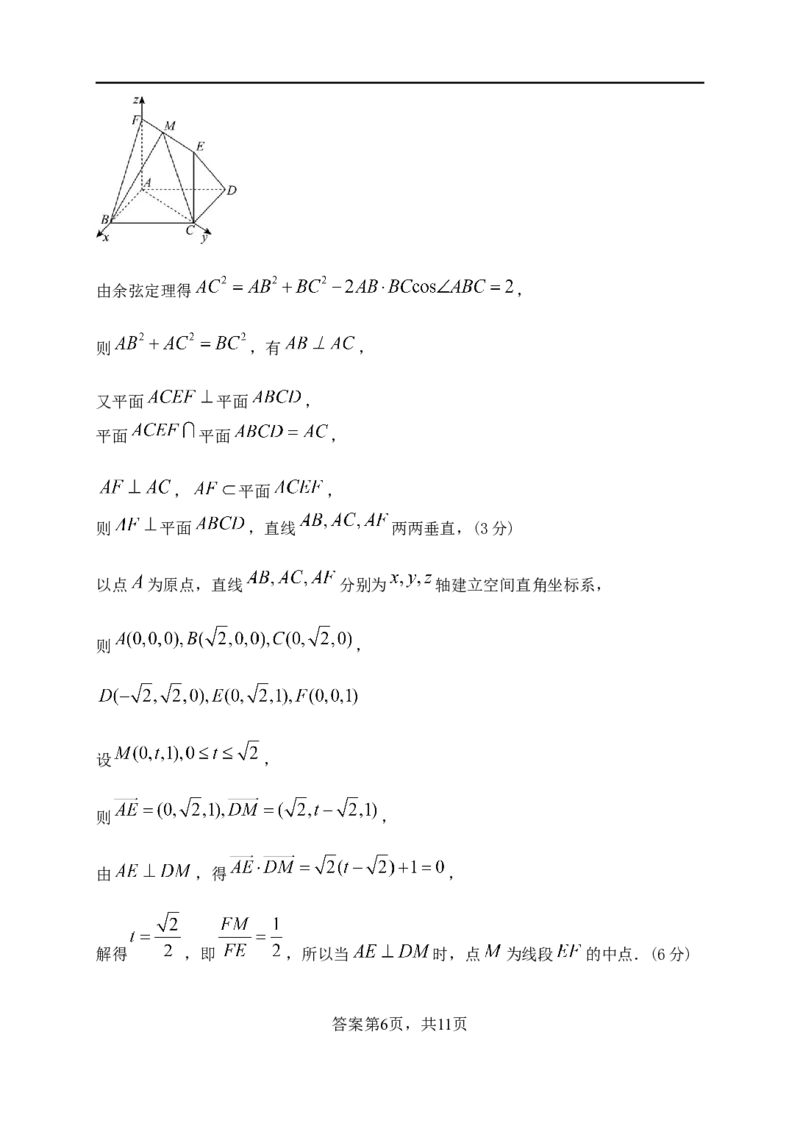
答案第5页,共11页由余弦定理得 ,
则 ,有 ,
又平面 平面 ,
平面 平面 ,
, 平面 ,
则 平面 ,直线 两两垂直,(3分)
以点 为原点,直线 分别为 轴建立空间直角坐标系,
则 ,
设 ,
则 ,
由 ,得 ,
解得 ,即 ,所以当 时,点 为线段 的中点.(6分)
答案第6页,共11页(2)由(1)可得 ,
设平面 的法向量为 ,
则 ,取 ,得 ,(9分)
平面 的法向量为 ,设平面 与平面 的夹角为 ,
则 ,
所以平面 与平面 的夹角的余弦值为 .(13分)
16.解析:(1)易知函数 ( )的定义域为 .所以 ,
(2分)当 时,由 ,得 ,由 ,得 .所以 的单调
增区间为 ,单调减区间为 ;(4分) 当 时,由 ,得 ,
由 ,得 .所以 的单调增区间为 ,单调减区间为 .
(6分)
(2) 即 在 上恒成立,(7分)令
答案第7页,共11页,易知函数 的定义域为 .所以
.(9分)当 时,
,故 ;(11分)当 时, ,故
.(13分)所以 在 上单调递增,在 上单调递减,所以
时, 在 上取得最大值 .所以 ,所以实数 的取值
范围是 .(15分)
17.解析:(1)由 可得, ,由正弦定理该式
化为 ,整理得: ,即: ,
即 ,因为 为三角形的内角,所以 。(5分)
(2)令 ,由题意: ,平方得: ,(7分)又
答案第8页,共11页由正弦定理
,
则: ,代入上式得:
(11分)
因为三角形是锐角三角形,所以
,
, ,即 ,
,
答案第9页,共11页因此, 的取值范围为 。(15分)
18.解析:(1)由题意,有 ,解得 即椭圆标准方程为:
(4分)
(2) 设过点 的切线方程为
联立 ,有
由于想切,令 ,
即求得 (9分)
(3)设 , 延长线交 轴于 点,
答案第10页,共11页、 两点处切线斜率分别是 和 ,有 ,
设椭圆上 或 两点切线方程为 联立有,
,有 ,
, (12分)
要证明 ,需证明
即要证 ,
其中, 显然,即证 (17分)
答案第11页,共11页19.(1)① , , (4分)
② 处于位置 时,得3分, ,
处于位置 时,得1分, ,
处于位置 时,得分1分, ,
所以最终得分的分布列为:
得分 的期望 。(9分)
(2)将棋盘按如图所示编号:
将棋子可以去的区域用箭头连接起来,如从3可以连接4或8,记做:4—3—8;从8
可以连接3或1,记做:3—8—1;然后将他们串联起来:4—3—8—1。依次类推,可
以串联出环状回路:-4—3—8—1—6—7—2—9—4-,如下图所示:
答案第12页,共11页3
4 8
9 1
2 6
7
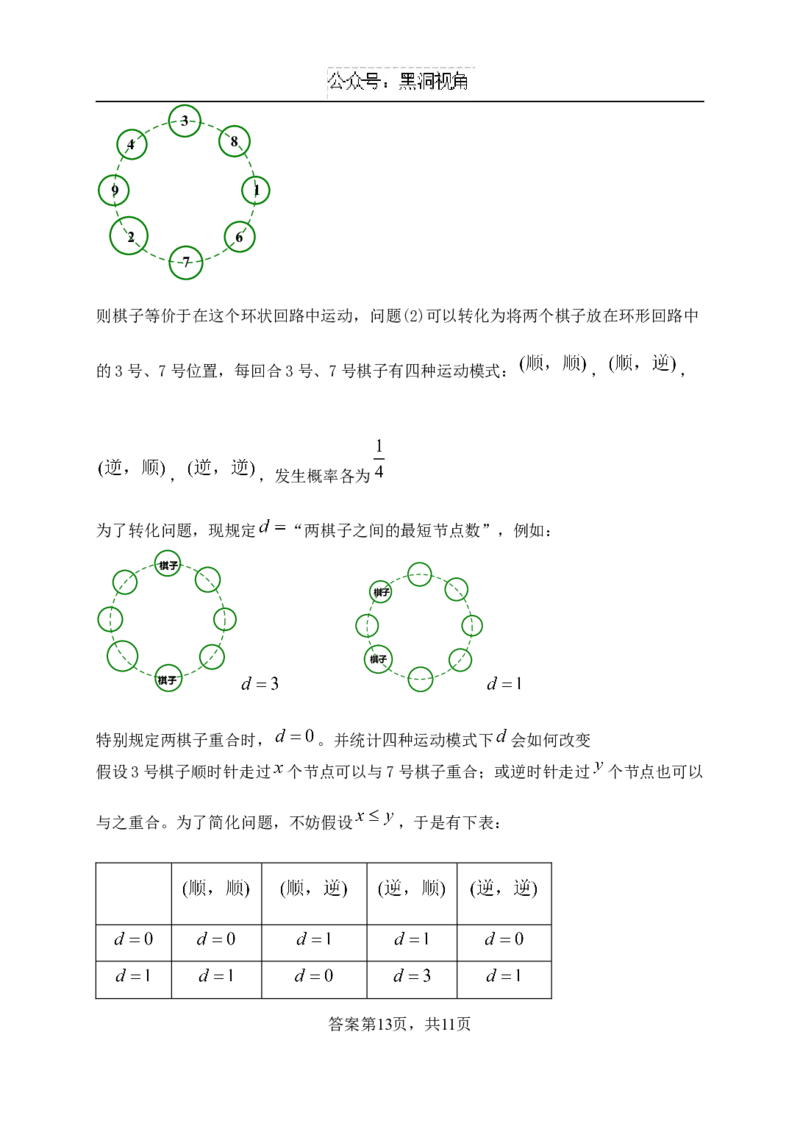
则棋子等价于在这个环状回路中运动,问题(2)可以转化为将两个棋子放在环形回路中
的3号、7号位置,每回合3号、7号棋子有四种运动模式: , ,
, ,发生概率各为
为了转化问题,现规定 “两棋子之间的最短节点数”,例如:
棋子
棋子
棋子
棋子
特别规定两棋子重合时, 。并统计四种运动模式下 会如何改变
假设3号棋子顺时针走过 个节点可以与7号棋子重合;或逆时针走过 个节点也可以
与之重合。为了简化问题,不妨假设 ,于是有下表:
答案第13页,共11页设 “ 回合后, 的概率”,
“ 回合后, 的概率”,
“ 回合后, 的概率”,
则有 ,(13分)
,
显然, ,所以 ,
所以解得: 。 (17分)
答案第14页,共11页