数学答案_2024-2025高三（6-6月题库）_2024年10月试卷_1010湖北省“腾·云”联盟2024-2025学年度上学期10月联考_2-数学

湖北省“腾·云”联盟2024-2025学年度上学期10月联考
数学参考答案
题号 1 2 3 4 5 6 7 8 9 10 11
答案 C A D A D A B B AB ABD AD
31
12． 13．3 14．9
2
6．解析： PAPB PC  4, PQ 面ABC 且Q是ABC外心，
 2 4 64
PQ 2 3 QAQBQC 2， 2 3R 4 R2，R ，S 4R2 
3 3
1
7．解析：四边形ACBM 面积S  MC AB  MA AC  |MC|2 1，
2
2 |MC|2 1 1
AB   2 1 ，
MC MC 2
MC 2  x1 2e2x, f(x) x1 2e2x, f (x)2(x1)2e2x 单增，
又 f(0)0， f(x)  f(0)2， MC 2 2, AB  2,
min min min
2
 2 
S   
min   2   2
答案第1页，共11页8．解析： x  x 11,x  x 11,x  x 11，则xx x 3,4,.......15,所
1 1 2 2 3 3 1 2 3
以有C2 C2 ......C2 C3 C2 ......C2 C3 455
2 3 14 3 3 14 15
10．解析：函数 f  x  sinx  3 cosx 的定义域为R，有
f x  sin(x)  3 cos(x)  sinx  3 cosx  f  x ，即函数 f  x 是偶函数，
又 f  xπ  sin  xπ   3 cos  xπ   sinx  3 cosx  f(x)，则π是函数
f

x
的一个周期，也是最小正周期，A正确
π π π
当0 x 时， f(x)sinx 3cosx2sin(x )，显然函数 f(x)在[0, ]上递
2 3 6
π π π π π
增，在[ , ]上递减，  x0时，由偶函数的性质知，函数 f(x)在[ , ]上
6 2 2 2 6
π π π π
递增，在[ ,0]上递减，即当0 x 时 f(x)  f( )2, f(x)  f( )1，
6 2 max 6 min 2
π
即函数 f(x)在[0, ]的取值集合为[1,2]，
2
π π π
从而函数 f(x)在[ ,0]的取值集合为[1,2]，即在[ , ]上的值域为[1,2]，因此函
2 2 2
数 f(x)在R上的值域为[1,2]，B正确；
如图：
答案第2页，共11页 7
f(x)不关于直线x  对称，所以不关于直线x  对称，故C错
6 6
 5  π π
f(x)在  , 上单调性同[ , ]，所以递减，故D对。
 
 6 2 6 2
11．解析：对2f 2(x) f(2x)1两边求导得4f(x)f(x)2f(2x)即
2f(x)g(x) g(2x) ，故A对
2g2(x) f(2x)10, f(2x)1,即恒成立，
1
2f 2(0) f(0)1, f(0)1, f(0) （舍），故B错。
2
g(x)是奇函数， f(x)是偶函数，
f(x)1,g(x)1，g(x)为增函数， f(x)为增函数，
又 f(0)0，故C错。
x3
F(x) g(x)( x) ，
6
x2 x2
F(x) g(x)( 1) f(x)( 1) ，
2 2
F(x) f(x)x g(x)x为增函数，
F(x) F(0)0,F(x) F(0)0,F(x) F(0)0，故D对。
14．解析：如图示，先求出硬管不倾斜，水平方向通过的最大长度AB．
答案第3页，共11页 π π
设BAQ,0

，则ABQ ．
 2 2
过A作AC垂直内侧墙壁于C，B作BD垂直内侧墙壁于D，则
π
AC  BD3,CPABAQ,DPBABQ ．
2
AC
在直角三角形ACP中，sinCPAsin ，
AP
AC 3
所以AP   ．
sin sin
BD 3
同理： BP  
π  cos．
sin  
2 
3 3  π
所以AB  APBP   ,0

．
sin cos  2
3 3 1 2
因为 AB   32  6  6 2
sin cos sincos sin2
π
(当且仅当sincos且 时等号成立)．
4
所以 ．因为走廊的宽度与高度都是3米，
AB6 2
所以把硬管倾斜后能通过的最大长度为
m AB232   6 2 2 32 9 ，
π
15．解析：(1)在 ABCD中，AB 2,BC 2,ABC  ，
4
答案第4页，共11页由余弦定理得AC2  AB2 BC2 2ABBCcosABC  2，
则AB2  AC2  BC2，有ABAC，
又平面ACEF 平面ABCD，
平面ACEF 平面ABCD  AC，
AF  AC ，AF 平面ACEF ，
则AF 平面ABCD，直线AB,AC,AF 两两垂直，(3分)
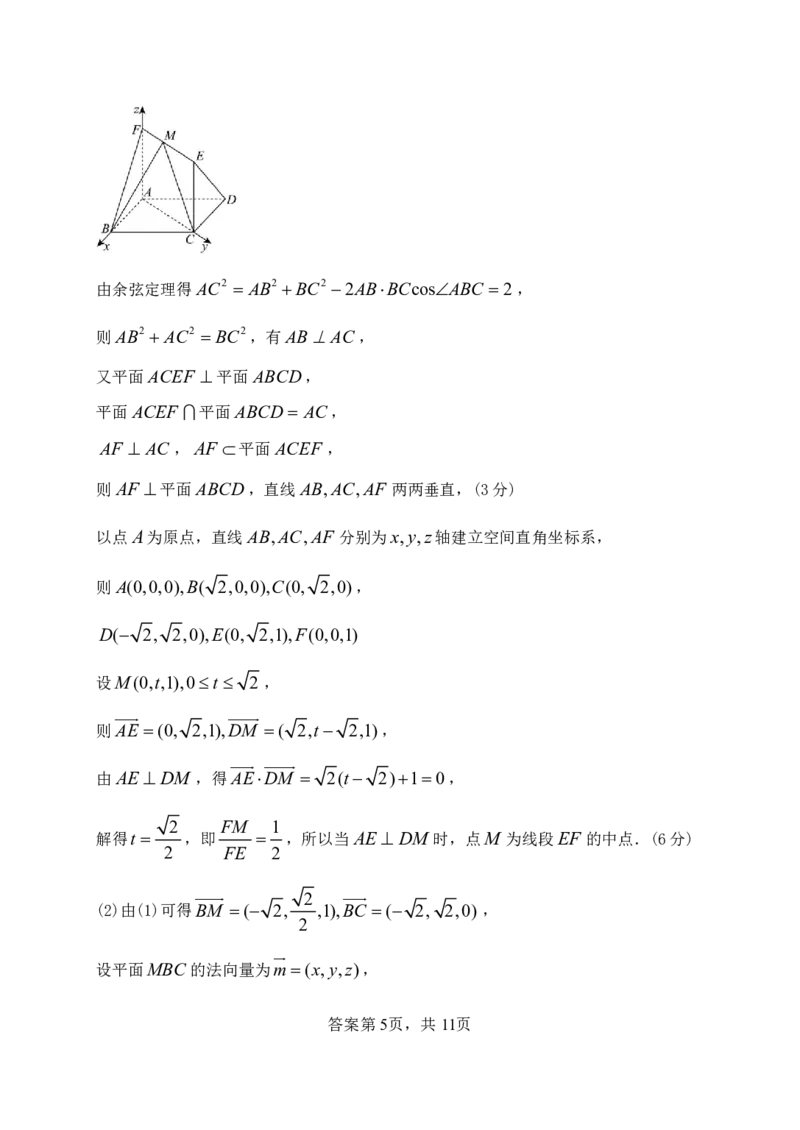
以点A为原点，直线AB,AC,AF 分别为x,y,z轴建立空间直角坐标系，
则A(0,0,0),B( 2,0,0),C(0, 2,0)，
D( 2, 2,0),E(0, 2,1),F(0,0,1)
设M(0,t,1),0t  2 ，
 
则AE (0, 2,1),DM ( 2,t 2,1)，
 
由AE  DM ，得AEDM  2(t 2)10，
2 FM 1
解得t  ，即  ，所以当AE  DM 时，点M 为线段EF 的中点．(6分)
2 FE 2
 2 
(2)由(1)可得BM ( 2, ,1),BC ( 2, 2,0) ，
2

设平面MBC的法向量为m(x,y,z)，
答案第5页，共11页   2
mBM  2x yz 0 
则 2 ，取 y 2，得m(2,2, 2)，(9分)


mBC  2x 2y 0

平面ECD的法向量为n(0,1,0)，设平面MBC与平面ECD的夹角为，
 
  |mn| 2 10
则cos|cosm,n|     ，
|m||n| 442 5
10
所以平面MBC与平面ECD的夹角的余弦值为 ．(13分)
5
ax a(1x)
16．解析：(1)易知函数 f  x  (a 0)的定义域为R．所以 f(x) ，(2
ex ex
分)当a 0时，由 f(x)0，得x1，由 f(x)0，得x1．所以 f(x)的单调增
区间为(,1)，单调减区间为(1,)；(4分) 当a<0时，由 f(x)0，得x1，由
f(x)0，得x1．所以 f(x)的单调增区间为(1,)，单调减区间为(,1)．(6
分)
3x 1 lnx
(2)xf(x)lnx1mx即m   在x(0,)上恒成立，(7分)令
ex x x
3x 1 lnx
h(x)   ，易知函数h(x)的定义域为(0,)．所以
ex x x
3ex 3xex 1 1lnx 3(1x) lnx
h  (x)     ．(9分)当0 x1时，
e2x x2 x2 ex x2
3(1x) lnx 3(1x) lnx
0, 0，故h(x)0；(11分)当x1时， 0, 0，故
ex x2 ex x2
h(x)0．(13分)所以h(x)在(0,1)上单调递增，在(1,)上单调递减，所以x1时，
3 3
h(x)在(0,)上取得最大值h(1) 1．所以m 1，所以实数m的取值范围是
e e
3 

1,

．(15分)
e 
答案第6页，共11页 
17．解析：(1)由mn可得，(ba)sin A(bc)(sinBsinC) ，由正弦定理该式化
b2 a2 c2 1
为(ba)a (bc)(bc)，整理得：b2 a2 c2 ab，即：  ，即
2ab 2
1 
cosC  ，因为C为三角形的内角，所以C  。(5分)
2 3
   
(2)令|CD| x，由题意：2CDCACB，平方得：4x2 b2 a2 ab，(7分)又
由正弦定理
a b C 2 3
   ，
sin A sinB sinC 3
2 3 2 3
则：a  sinA, b sinB，代入上式得：
3 3
4 4 4
4x2  sin2 B sin2 A sinAsinB
3 3 3
4 2 4 4 2
 sin2( A) sin2 A sinAsin( A)
3 3 3 3 3
4
1cos( 2A)
4 3 4 1cos2A 4 2
     sin Asin(  A)
3 2 3 2 3 3
4 2 5
= cos(2A ) (11分)
3 3 3
因为三角形是锐角三角形，所以
 
0 A

 2    2 
   A   2A  ，
2  6 2 3 3 3

0  A
 3 2
2 1 4 2 5 7 7
cos(2A )( ,1]， cos(2A ) ( ,3]，即4x2( ,3]，
3 2 3 3 3 3 3
21 3
x( , ]，
6 2
答案第7页，共11页21 3
因此，CD的取值范围为 ( , ]。(15分)
6 2
 2 3 a 2
2a  2b 
18．解析：(1)由题意，有 3 ，解得b 3 即椭圆标准方程为：
 
ac3 c1

x2 y2
 1(4分)
4 3
(2) 设过点R的切线方程为 y k(x1)2kx(2k)
y2 k2x2 2k(2k)x(2k)2
联立3x2 4y2 120，有
(4k2 3)x2 8k(2k)x4(2k)2 120
由于想切，令 0，
4k2(2k)2 (4k2 3)(2k)2 3(4k2 3)
3(4k2 3)3(2k)2
3k2 4k 10
1
即求得k k  (9分)
1 2 3
(3)设R(x ,y ) (y 0)，RK 延长线交x轴于K'点，
0 0 0
IK AK' x 2
P、Q两点处切线斜率分别是k 和k ,有   0 ，
1 2 JK BK' 2x
0
设椭圆上P或Q两点切线方程为y k(xx ) y 联立有，
0 0
答案第8页，共11页y k(xx ) y kx(kx  y )
 0 0 0 0
x2 y2

 1
 4 3
(4k2 3)x2 8k(kx  y )x4(kx  y )2 120
0 0 0 0
 0，有64k2(kx  y )2 4(4k2 3)[4(kx  y )2 12]，
0 0 0 0
(x2 4)k2 2x y k y2 30
0 0 0 0
2x y y2 3
k k  0 0 ，kk  0 (12分)
1 2 x2 4 1 2 x2 4
0 0
y k (2x ) y
I 1 0 0

y k (2x ) y
J 2 0 0
IK AI x 2 k (2x ) y
要证明  ，需证明 0  1 0 0
JK BJ 2x k (2x ) y
0 2 0 0
即要证k (4x2) y (2x )k (x2 4) y (2x )，
2 0 0 0 1 0 0 0
4(k k )2x y (k k )x2
1 2 0 0 1 2 0
2x y IK AI
(k k )(x2 4)2x y 其中，k k  0 0 显然，即证  (17分)
1 2 0 0 0 1 2 x2 4 JK BJ
0
19．(1)① (a,1)，(c,1)，(c,3) (4分)
1 1
② 处于位置(c,3)时，得3分，( )2  ，
2 4
1 1
处于位置(a,1)时，得1分，( )2  ，
2 4
X 1 3
1 1
处于位置(c,1)时，得分1分，2( )2  ，
3 1
2 2 P
4 4
所以最终得分的分布列为：
3 1 3
得分X 的期望E(X)1 3  1.5。(9分)
4 4 2
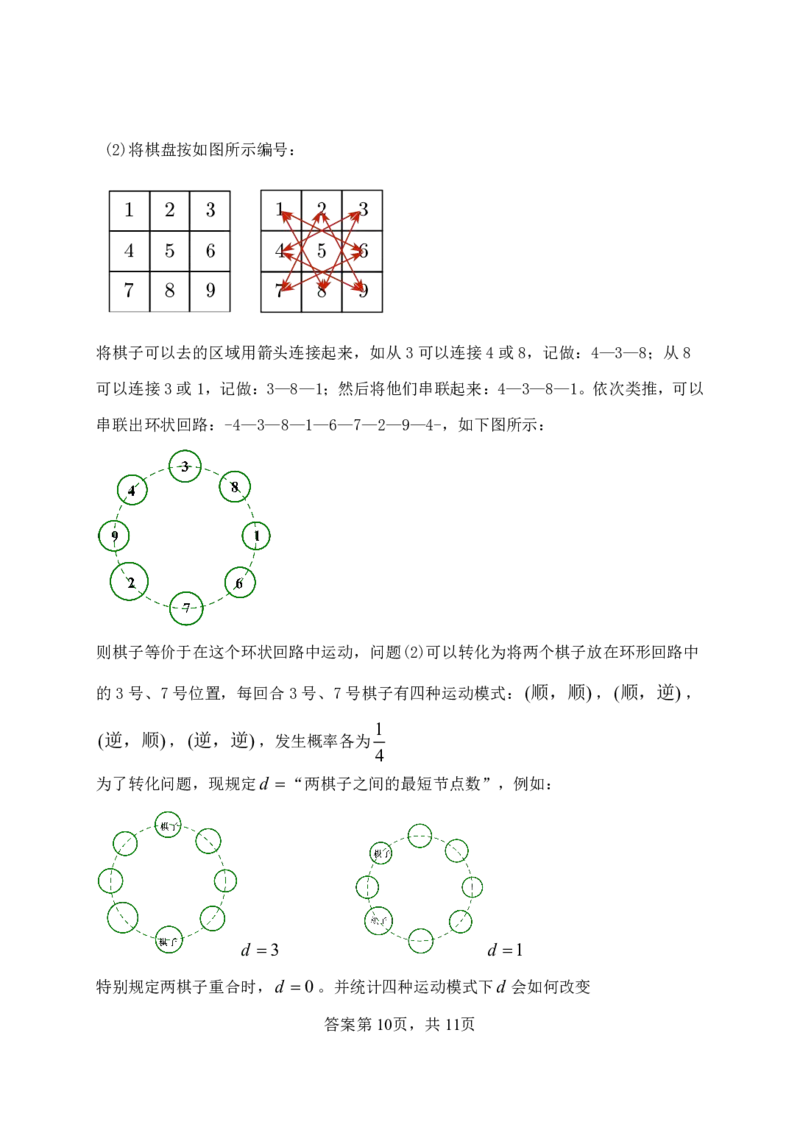
答案第9页，共11页(2)将棋盘按如图所示编号：
将棋子可以去的区域用箭头连接起来，如从3可以连接4或8，记做：4—3—8；从8
可以连接3或1，记做：3—8—1；然后将他们串联起来：4—3—8—1。依次类推，可以
串联出环状回路：-4—3—8—1—6—7—2—9—4-，如下图所示：
则棋子等价于在这个环状回路中运动，问题(2)可以转化为将两个棋子放在环形回路中
的3号、7号位置，每回合3号、7号棋子有四种运动模式：(顺，顺)，(顺，逆)，
1
(逆，顺)，(逆，逆)，发生概率各为
4
为了转化问题，现规定d “两棋子之间的最短节点数”，例如：
d 3 d 1
特别规定两棋子重合时，d 0。并统计四种运动模式下d 会如何改变
答案第10页，共11页假设3号棋子顺时针走过x个节点可以与7号棋子重合；或逆时针走过y个节点也可以
与之重合。为了简化问题，不妨假设x y，于是有下表：
(顺，顺) (顺，逆) (逆，顺) (逆，逆)
d 0 d 0 d 1 d 1 d 0
d 1 d 1 d 0 d 3 d 1
d 3 d 3 d 1 d 1 d 3
设 p “n回合后，d 0的概率”，
n
q “n回合后，d 1的概率”，
n
R “n回合后，d 3的概率”，
n
 1 1
p  p  q
 n 2 n1 4 n1

 1 1 1 1
则有q  p  q  R  ，(13分)
n 2 n1 2 n1 2 n1 2

 1 1
R  q  R
  n 4 n1 2 n1
1 1 1 1 1
p  p  ， p   (p  )
n 2 n1 8 n 4 2 n1 4
1 1 1 1 1
显然， p 0, p   ,，所以 p   ( )n1，
1 1 4 4 n 4 4 2
1 1
所以解得： p   。 (17分)
n 4 2n1
答案第11页，共11页