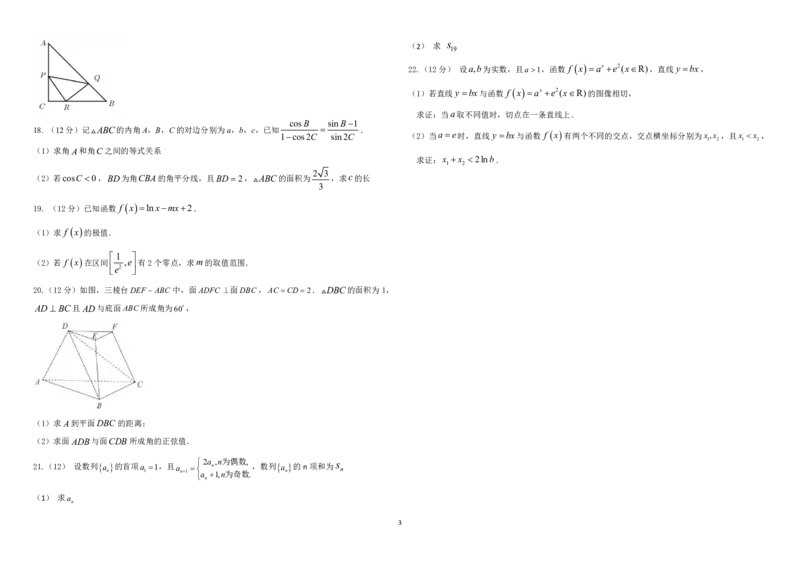高三数学试题(1)_2023年11月_0211月合集_2024届山东省高三年级适应性联考（一）_山东省2024届高三年级适应性联考（一）数学

山东省高三年级适应性联考（一） 2 4 8 A. B. C. 2 D. 3 3 3 数学试题  1  4. 已知sin( ) ，则sin(2 )（ ） 本试卷共 3 页，22 题.全卷满分 150 分.考试时间 120 分钟. 6 3 6 注意事项： 2 2 7 7 A.  B. C.  D. 1.答题前,先将自己的姓名、准考证号填写在答题卡上,并将准考证号条形码粘贴在 9 9 9 9 答题卡上的指定位置。 2.选择题的作答:每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂    1 2 5. 已知ABC，点D在线段BC上（不包括端点），向量AD xAB yAC，  的最小值为（ ） x y 黑。写在试题卷、草稿纸和答题卡上的非答题区域均无效。 3.非选择题的作答，用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、 A. 2 2 B. 2 22 C. 2 23 D. 2 32 草稿纸和答题卡上的非答题区域均无效。 4.考试结束后请将本试题卷和答题卡一并上交。 a 6. 设函数 f  x log (x )在区间  1, 上单调递减，则a的取值范围是（ ） 1 x 2 一、选择题：本题共8小题，每小题5 分，共 40分.在每小题给出的四个选项中，只有一 A. ,1  B.  0，1  项是符合题目要求的. C. 1，1  D.  1, 1. 已知集合M 3,2,1,0,1,2,3  ，N   x lnx1  ，则M N （ ） 2x2 2 2xy y2 A. 2,1,0,1，2  B.  0,1,2  C.  1，2  D.  2  7. 设x0,y0，m ，则m有（ ） x2  y2 2．若a0，则“a2 b2”是 “ab”的（ ） A. 最小值3 B. 最大值3 A．充分不必要条件 B．必要不充分条件 3 3 C. 最小值  2 D. 最大值  2 2 2 C．充分必要条件 D．既不充分也不必要条件 3. 阳马和鳖臑是我国古代对一些特殊锥体的称谓，取一长方体，按下图斜割一分为二，得两个一模一 1 3 1 样的三棱柱，称为堑堵，再沿堑堵的一顶点与相对棱剖开得一四棱锥和一三棱锥，以矩形为底，另有 8. 已知asin ,bln ,c ，则（ ） 2 2 3 一棱与底面垂直的四棱锥，称为阳马，余下的三棱锥称为鳖臑。（注：图4由左依次是堑堵、阳马、鳖臑） A. a bc B. bc a C. ba c D. c a b 二、选择题：本题共4 小题，每小题 5分，共 20分．在每小题给出的选项中，有多项符 合题目要求．全部选对的得 5分，部分选对的得 2 分，有选错的得 0 分. 上图中长方体为正方体，由该正方体得图4中阳马和鳖臑，已知鳖臑的外接球的体积为4 3，则鳖 9. 设等差数列  a  的前n项和为s ，公差为d ， a 0，a a 0，a a 0，下列结论正确 n n 1 6 7 6 7 臑体积为（ ） 1的是（ ） A. 平面D AM 截四棱柱ABCDABCD 的截面为直角梯形 1 1 1 1 1 A. d 0 B. CB 面D AM 1 1 B. 当 s  0时，n的最大值为13 n C. 平面BBCC内存在点P，使得DP AM 1 1 s  C. 数列 n为等差数列，且和数列  a  的首项、公差均相同 D. V :V 2:3 n  n A1 AD1M CAD1M 三、填空题：本题共 4 小题，每小题 5 分，共20分． s  D. 数列 n前n项和为T ，T 最大         1     n  n 12 13. 已知a，b为非零向量，且 a  ab 1，向量a在向量ab上的投影向量为 （ab），则 2ab 2 10.摩天轮是一种大型转轮状的机械建筑设施，游客坐在摩天轮的座舱里慢慢地往上转，可以从高处 的模为______． 俯瞰四周景色。某摩天轮最高点距离地面高度为60米，转盘直径为50 米，设置有24个座舱，摩天 14. 对于数列  a  ,由b a a 作通项得到的数列  b  ,称  b  为数列  a  的差分数列， n n n1 n n n n 轮开启前，距地面最近的座舱标为0号，距地面最远的座舱为12号，座舱逆时针排列且均匀分布，游       已知数列 b 为数列 a 的差分数列，且 b 是以1为首项以2为公差的等差数列， n n n 客甲坐2号舱位，乙坐6号舱位，开启后按逆时针方向匀速旋转，开启后的第8分钟游客这一时刻， 则a a ______． 甲和乙首次距离地面高度相同，游客甲在摩天轮转动过程中距离地面的高度为H米， 10 5   A. H关于t的函数解析式为 H 25sin( t )35 15. 已知矩形ABCD，AB1，BC  2，E是边BC的中点．AE和BD交于点M ，将ABE沿AE折 12 6 起，在翻折过程中当AB与MD垂直时．异面直线BA和CD所成角的余弦值为______． B. 开启后第20分钟这一时刻游客甲和乙第二次距离地面高度相同 C. 开启后第10分钟游客乙距离地面47.5米 16. 已知函数 f (x)及其导函数 f(x)的定义域均为R，记g(x) f(x)，若 f  12x 4x为偶函 1 5 D. 开启后第10分钟至第18分钟游客甲和乙运动方向相同（上升或下降） 数，g(x2) g(x1)g(x)，且g( )0，则g( )g(4)______． 2 2 11.已知函数 f(x)(x2 axb)ex，下列结论正确的是（ ） 四、解答题：本题共 6 小题，共70 分．解答应写出文字说明、证明过程或演算步骤． A. 若函数 f(x)无极值点，则 f(x)没有零点 17. （10分）如图等腰直角PQR的三个顶点分别在等腰直角ABC的三条边上，角PRQ和角C为 直角，BC 1，设PR x，PRC  B. 若函数 f(x)无零点，则 f(x)没有极值点 （1）求RB 的长（用x，表示）． C. 若函数 f(x)恰有一个零点，则 f(x)可能恰有一个极值点 （2）求PQR面积的最小值． D. 若函数 f(x)有二个零点，则 f(x)一定有二个极值点 12. 直四棱柱ABCDABCD ，所有棱长都相等，且DAB60，M 为BB 的中点，P为四边形 1 1 1 1 1 BBCC内一点（包括边界），下列结论正确的是（ ） 1 1 2（2） 求 s 19 22.（12分） 设a,b为实数，且a1，函数 f  x ax e2(xR)，直线y bx， （1）若直线 y bx与函数 f  x ax e2(xR)的图像相切， 求证：当a取不同值时，切点在一条直线上． cosB sinB1 18. （12分）记ABC的内角A，B，C的对边分别为a，b，c，已知 1cos2C  sin2C ． （2）当ae时，直线 y bx与函数 f  x  有两个不同的交点，交点横坐标分别为x,x ，且x x ， 1 2 1 2 （1）求角A和角C之间的等式关系 求证：x x  2lnb． 1 2 2 3 （2）若cosC 0，BD为角CBA的角平分线，且BD2，ABC的面积为 ，求c的长 3 19. （12分）已知函数 f  x lnxmx2．   （1）求 f x 的极值．  1  （2）若 f  x  在区间 ,e 有2个零点，求m的取值范围．   e2  20.（12分）如图，三棱台DEFABC中，面ADFC⊥面DBC，AC CD2．DBC的面积为1， ADBC且AD与底面ABC所成角为60， （1）求A到平面DBC 的距离； （2）求面ADB与面CDB所成角的正弦值． 21.（12） 设数列a n 的首项a 1 1，且 a n1    a 2a  n 1 ,n ,n 为 为 偶 奇 数 数 , . ，数列a n 的n项和为s n n （1） 求a n 3