文档内容
2024-2025 学年浙江省杭州市 S9 联盟高二下学期期中联考
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合 , ,则 ( )
2 2
A. ={ ∈ | B−. 9<0} ={ ∈C .| = −1, ∈ }D. ∩ =
2.在{0复,1,平2}面内,复数 {1,2} 对应的[−点1位,3于) ( ) (−3,3)
A.第一象限 =(B2.−第5二 )象(−限1−2 ) C.第三象限 D.第四象限
3.已知 , , ,则过点 且与线段 平行的直线方程为( )
A. (3,1) (1,−2)B. (1,1) C. D.
4.设3 +2 ,−则5“=0 ”是“2 −3 ”+的1(=0) 3 −2 −1=0 2 +3 −5=0
2
A.充 分∈不 必要条件 >1 > B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.函数 的单调递增区间是( )
A. ( )=( −2) B. C. D.
(−∞,2) (2,+∞) (−∞,1) (1,+∞)
6.椭圆 的两个焦点分别为 、 ,以 、 为边作正三角形,若椭圆恰好平分三角
2 2
形的另两 2 边+, 2 则=椭1(圆 >的离 >心0率) 为( ) 1 2 1 2
A. B. C. D.
3+1 3+2
7.正方2 体 中3,−直1线 与平面 4(2−所成3角) 的正弦值为4( )
− 1 1 1 1 1 1
A. B. C. D.
2 2 6 3
8.定4理:如果函数 及 3满足:①图像在闭区3间 上连续不断;2②在开区间 内可导;③对
( ) ( ) [ , ] ( , ) ∀ ∈
, ′ ,那么在 内至少存在一点 ,满足 成立,该定理称为柯西中值定理.请
( )− ( ) ′ ( )
( , ) ( )≠ 0 ( , ) ( )− ( )= ′ ( )
利用该定理解决下面问题:已知 ,若存在正数 , ,满足 ,则实数
2 −
的取值范围是( ) ( )= ( < ) ( )= ln + ( )
A. B. C. D.
32 1 8 2 4 1 4 2
二、 − 多 4 选 , 题 :本题共3小题, − 共 4 1 , 8 分。在每小题给 − 出 4 的 , 选项中,有多项 − 符 4 合 , 题目要求。
9.已知等差数列 的前 项和为 ,公差 , , 是 与 的等比中项,则下列选项正确的
是 { } ≠0 11 =110 7 3 9
第 页,共 页
1 7A. B.
C. 1有2 =最 大 值3+ 9 =20 D. 当=−2 时, 的最大值为
>0 21
10.已知函数 则下列结论正确的有( )
A. 的最小
(
正
)
周
=
期
s
为
in 2 +3 .
B. ( )是 的最大值
2 ( )
C.把函数 的图像上所有点向左平移 个单位长度,可得到函数 的图像
=sin2 6 = ( )
D.将函数 的图像向右平移 个单位长度,所得图像关于原点对称,则 的最小值为
11.如图所 示 = , 在 ( 棱 ) 长为 的正方体 ( >0) 中, , 分别为棱 , 的中 点,则以下四6个结论
正确的是( ) 1 − 1 1 1 1
A.棱 上存在一点 ,使得 平面
B.直线 1 1 到平面 的距离 为 / / 1
2
1 1 1 3
C.过 且与面 平行的平面截正方体所得截面面积为
9
1 1 1 8
D.过 的平面截正方体的外接球所得截面面积的最小值为
3
三、填 空题:本题共3小题,每小题5分,共15分。 8
12.甲射手击中靶心的概率为 ,乙射手击中靶心的概率为 ,甲、乙两人各射击一次,那么甲、乙不全击中
1 1
靶心的概率为________. 3 2
13.已知向量 与 的夹角为 , , ,则 .
14.已知斜率�为 � � � 的直线与抛60物° 线|� �|= 2 交|� � 于|=,1 两点|� �,+若2� �|= 的外心为 为坐标原点 ,则当
2 | |
最大时, 1 ________. =4 △ ( ) | |
四、解答题| :|本=题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15. 本小题 分
在 ( 中,13角 )、 、 的对边分别为 、 、 , , .
△ =2 = 3
第 页,共 页
2 7若 ,求 ;
(1) 若 = 4 的面 积 ,求 , .
(126). 本△小 题 分 = 3
( 15 )
已知数列 的前 项和 ,数列 是正项等比数列,满足 , .
2
+ ∗
求 {, } 的 通项公 式= 2 ( ∈ ) { } 1 = 2 3 = 8
(1) { } { } ;
设 ,记数列 的前 项和为 ,求 .
,( =2 −1) ∗
(2) = ( ∈ ) { } 99
17. 本小题 ,( 分 =2 )
已知(函数 15 ) ,
若 存( 在)=极 小值−, 且−极1小 值( 为)= ,ln求 .
(1)若 ( ) ,求 的取值范围.−1 ;
(128). 本 小( )题≥ (分 )
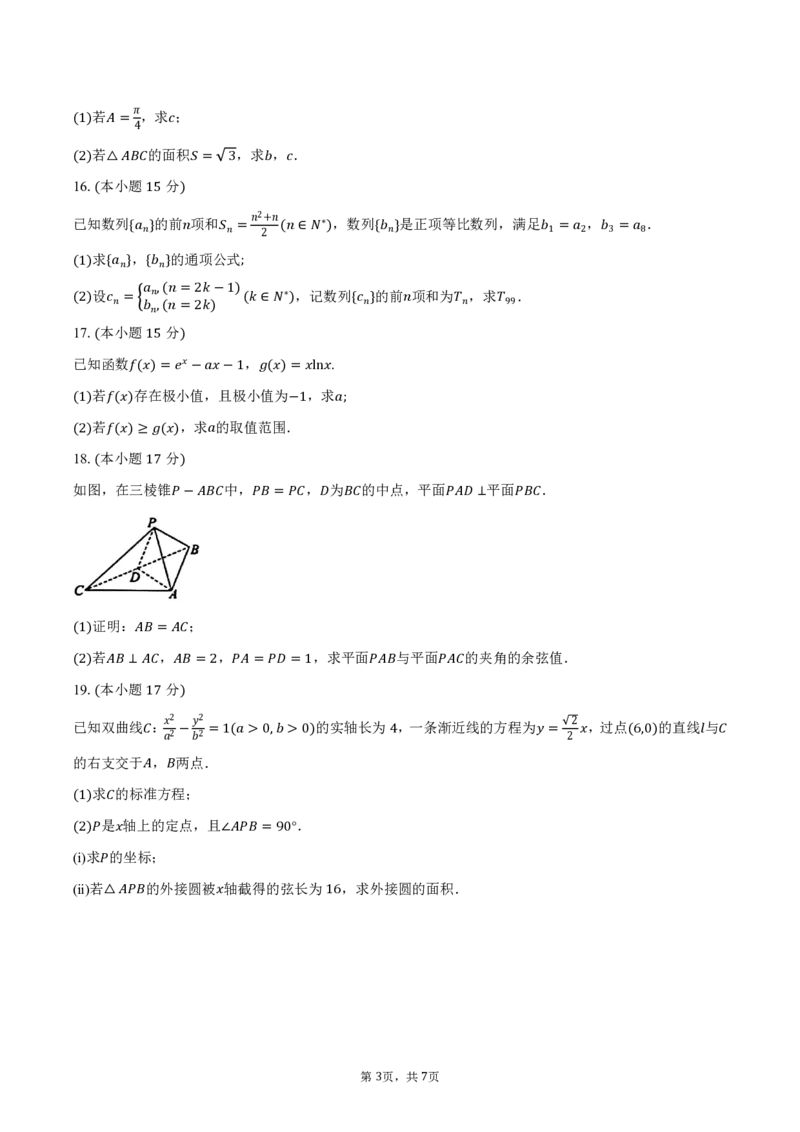
如图(,在三棱17锥 ) 中, , 为 的中点,平面 平面 .
− = ⊥
证明: ;
(1)若 =, , ,求平面 与平面 的夹角的余弦值.
(129). 本 小 题⊥ 分 =2 = =1
( 17 )
已知双曲线 : 的实轴长为 ,一条渐近线的方程为 ,过点 的直线 与
2 2
2
的右支交于 , 2 两−点 2 .=1( >0, >0) 4 = 2 (6,0)
求 的标准 方 程;
(1) 是 轴上的定点,且 .
((ⅰ2)求) 的 坐标; ∠ =90°
(ⅱ)若 的外接圆被 轴截得的弦长为 ,求外接圆的面积.
△ 16
第 页,共 页
3 7参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10 .
11.
12.
5
13.6
14.2 3
15.4解:10 由 ,
(1) sinA=sinC
得 .
3
2×2
= = 2 = 6
2
,
1
(2) =2
即 ,得 ,
1 3
又2×2 , × 2 = , 3 =2
故 =2 为 等 = 边3三角形,
所以△ .
=2
16.解: 当 时, ,
2 2
+ ( −1) +( −1)
又 (时1), ≥2 , =符合 − −1 ,=故2 − , 2 , =
∗
=1 1 = 1 =1 = = ∈
设等比数列 的公比为 ,则
1 = 2 =2
( >0) ,
解得 3 = 8 =8
=2
,
1 =2
第 页,共 页
4 7, ;
−1 ∗
∴ = 1 =2 ∈
, =2 −1 ∗
(2)∵ = ( ∈N ),
, =2
,
50×(1+99)
∴ 1+ 3+ 5+⋯⋯+ 99 = 1+ 3+ 5+⋯⋯+ 99 = 2 =2500
,
49 50
4(1−4 ) 4 −4
2+ 4+ 6+⋯⋯+ 98 = 2+ 4+ 6+⋯⋯+ 98 = 1−4 = 3
所以 .
50 50
4 −4 4 +7496
17.解 : 99 = 求3导 +′2500= 3,令 ′ ,则 ,
因为 (1存)在极 小值( ,)且=极 小−值 为 ,( )=0 =
所以 ( ) −,1所以 ,
ln
经检验 ( , )= 符合−题 意 ;−1=−1 =
由 = 可得 ,
(2) ( )≥ ( ) − −1≥ ln
因为 中 的定义域为 ,移项可得 在 上恒成立,
− l n −1
>0(ln >0) ⩽ (0,+∞)
设 ,则 ,
− ln −1
ℎ( )= ( >0) ⩽ℎ( )min
求导 ′ ,
( −1)+1− ( −1)( −1)
ℎ ( )= 2 = 2
令 ′ ,即 ,
( −1)( −1)
因为ℎ ( )=,0 2 =时0 ,所以 ,解得 ,
2
当 >0 时,−1>0( >,0 ) , 则−1′=0 , 所=以1 在 上单调递减,
当0< 时<,1 −1,<0 −1,>则0 ′ℎ ( ),<所0以 在ℎ( ) (0,1上) 单调递增,
>1 −1>0 −1>0 ℎ ( )>0 ℎ( ) (1,+∞)
由单调性可知 在 处取得最小值, ,
1
−1×ln1−1
所以 的取值范ℎ围( )是 =1 . ℎ(1)= 1 = −1
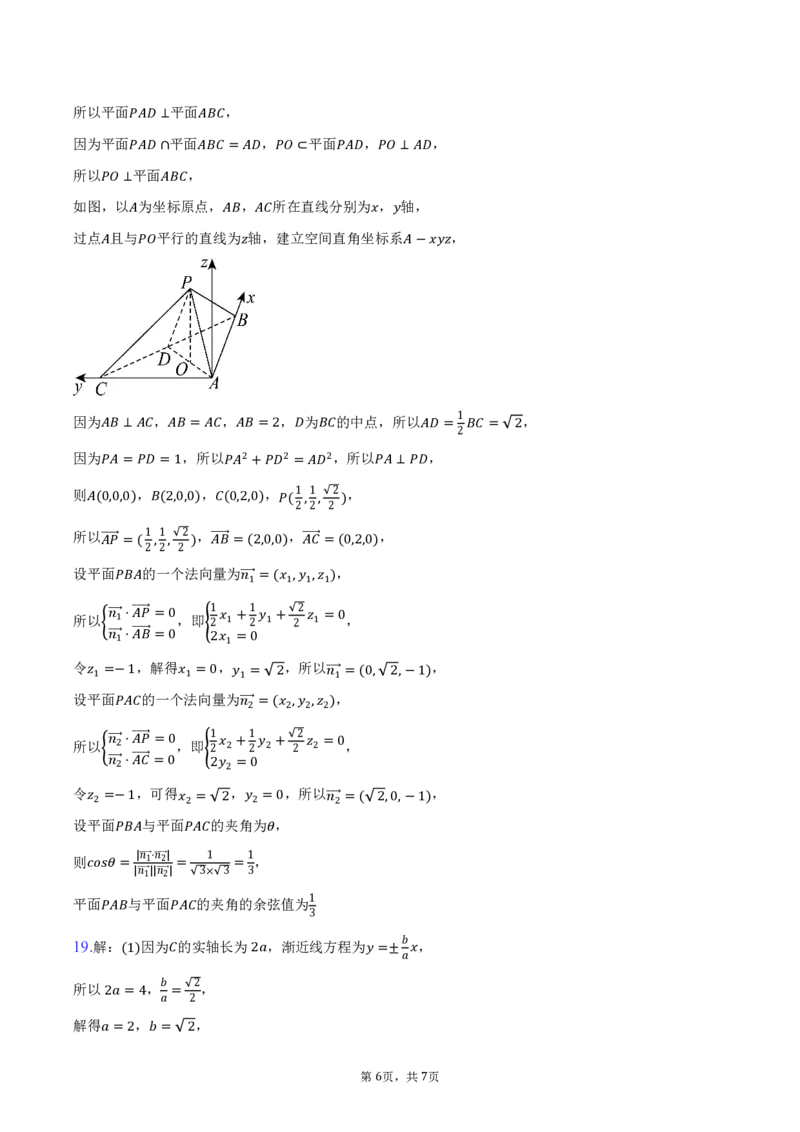
18. 证明:因为 为(−∞的, 中−点1], ,所以 ,
因为(1平)面 平 面 ,平面 =平 面 ⊥, 平面 ,
所以 平 面 ⊥ , ∩ = ⊂
又因为 ⊥ 平 面 ,所以 ,
因为 为 ⊂的中点 , 所以 ⊥ ;
解 :如 图,取 的中点 ,=连 接 ,
(因2)为 ,所 以 ,
由 = 平 面 , ⊥ 平 面 ,
(1) ⊥ ⊂
第 页,共 页
5 7所以平面 平面 ,
因为平面 ⊥平面 , 平面 , ,
所以 平 面 ∩ , = ⊂ ⊥
如图, 以⊥ 为坐 标 原点, , 所在直线分别为 , 轴,
过点 且与 平行的直线 为 轴 , 建立空间直角坐 标系 ,
−
因为 , , , 为 的中点,所以 ,
1
因为 ⊥ , = 所 以 =2 ,所以 , =2 = 2
2 2 2
则 = , =1 , +, = , ⊥
1 1 2
(0,0,0) (2,0,0) (0,2,0) (2,2, 2 )
所以 , , ,
1 1 2
设平面 ��� ��=(的2,一2,个2法)向 � 量 �� �� 为=(2,0,0) ��� �=,(0,2,0)
���1�=( 1, 1, 1)
所以 ,即 ,
1 1 2
���1�⋅ ��� ��=0 2 1+2 1+ 2 1 =0
令 ���1�⋅ � , �� �� 解=得0 2, 1 =0 ,所以 ,
设平 1面=−1 的一个 法1 =向0量为 1 = 2 ���1,�=(0, 2,−1)
���2�=( 2, 2, 2)
所以 ,即 ,
1 1 2
���2�⋅ ��� ��=0 2 2+2 2+ 2 2 =0
令 ���2�⋅ � , �� � 可=得0 2 2,=0 ,所以 ,
设平 2面=−1 与平面 2 = 的2夹角 2为=,0 ���2�=( 2,0,−1)
则 ,
| ���1�⋅ ���2�| 1 1
=| ���1�|| ���2�|= 3× 3=3
平面 与平面 的夹角的余弦值为
1
3
19.解: 因为 的实轴长为 ,渐近线方程为 ,
(1) 2 =±
所以 , ,
2
解得2 =,4 = 2,
=2 = 2
第 页,共 页
6 7所以 的标准方程为 ;
2 2
是 轴上的定点,4 且− 2 =1 ,
∘
(故2)直 线斜 率不为 ,设直∠线 的 方=程90为 ,
设 , 两点坐标0为 , ,= +6
( 1, 1) ( 2, 2)
联立 ,化简得, ,
= +6
2 2 2 2
( −2) +12 +32=0
4 − 2 =1
则 2 ,解得 ,
−2≠0
2 2
= 12 −4×32× −2 >0
− 2< < 2
32
1 2 = 2 −2<0
所以 , .
12 32
设 1+ , 2 则 =2− 2 1 2 = , 2 −2 ,
所以 ( ,0) ��� ��=( 1− , 1) ��� ��=( 2− , 2)
��� ��⋅ ��� ��=( 1− )( 2− )+ 1 2 =( 1+6− )( 2+6− )+ 1 2
2 2
=( +1) 1 2+(6− ) ( 1+ 2)+(6− )
,
2 2
32( +1) 12 (6− ) 2
=得 2 −2 − 2 −2 +(6− ) =0 ,
2 2 2 2
32( +1)+12( −6) +(6− ) ( −2)=,0
2 2 2
[ 所 (6 以 − ) +12( −6)+32] +32−2( −6) =0
2
(6− ) +12( −6)+32=0
2 ,
解得 ,所以 的坐标为
32−2( −6) =0
因 为=2 , 所以 (2,0外);接圆是以 为直径的圆,记为圆 ,
(因3)为 ⊥外 接 圆被 轴△截 得 的弦长为 , 且 ,
所以圆△ 交 轴于另一 点 , 16 (2,0)
所以圆心 在直线 (上18,,0显) 然 ,
=10 ≠0
联立 ,得 ,
4
= +6
=
所以 =10的外接圆圆心 ,即为 中点,
4
△ (10, )
所以 ,即 ,
4 1+ 2 6 2 4
= 2 =2− 2 =5
所以圆 半径的平方 ,
2 2 2 4 2
所以 外接圆的 面 = 积 | 为 | = . 10−2 +( −0) =84
△ 84
第 页,共 页
7 7