江苏省盐城市五校联考2024-2025学年高三上学期10月月考数学试题_2024-2025高三（6-6月题库）_2024年10月试卷_1017江苏省盐城市五校联考2024-2025学年高三上学期10月月考

2024/2025学年度第一学期
联盟校第一次学情调研检测高三年级数学试题
（总分150分 考试时间120 分钟）
注意事项：
1.本试卷中所有试题必须作答在答题纸上规定的位置 ，否则不给分．
2.答题前 ，务必将自己的姓名、准考证号用 0．5 毫米黑色墨水签字笔填写在试
卷及答题纸上．
3.作答非选择题时必须用黑色字迹 0.5 毫米签字笔书写在答题纸的指定位置上 ，
作答选择题必须用 2B 铅笔在答题纸上将对应题目的选项涂黑 。如需改动 ，请用橡皮
擦干净后 ，再选涂其它答案 ，请保持答题纸清洁 ，不折叠、不破损 。
一、选择题（本题共8小题，每小题 5分，共 40分，在每小题给出的四个选项
中，只有一项是符合题目要求的）
1. 已知集合A  x x23x40  ，B   xN 2x  0  ，则AB （ ）
A. {3,4} B. {0,1} C.
1,0,1 
D. {2,3,4}
2. 半径为2的圆上长度为4的圆弧所对的圆心角是（ ）
A.1 B.2 C.4 D.8
3已知x0，y 0，则（ ）
.
A 7lnxlny 7lnx 7lny B. 7lnxy 7lnx7lny
.
C. 7lnxlny 7lnx 7lny D. 7lnxy 7lnx7lny
4. 若正数x,y满足x2 2xy20，则x y的最小值是（ ）
6
A. 6 B. C. 2 2 D.2
2
1
5.已知sin  ，tan3tan，则sin （ ）
3
1 1 1 2
A. B. C. D.
6 3 2 3
 a1  x2,x1
6. 若函数f（x）= 是在R上的减函数，则a的取值范围是（ ）
 52lgx,x1
A.
6，1 
B.
，1 
C.
6，1 
D.
，6 
{#{QQABDQaAggiIAJAAAAhCUwUYCkMQkAGAASgOAEAEIAIACBFABCA=}#} π
7. 已知函数 f  x sin x  cosx 0 在 0,π 内有且仅有3个零点，则ω的取
 6
值范围是（ ）
8 11 8 11 10 13 10 13
A．  ,  B． ,  C． ,  D．  , 
3 3  3 3   3 3   3 3 
8. 已知a 1,b1.设甲：aeb bea，乙：ab ba，则（ ）
A.甲是乙的必要条件但不是充分条件
B.甲是乙的充分条件但不是必要条件
C. 甲是乙的充要条件
D. 甲既不是乙的充分条件也不是乙的必要条件
二、选择题（本题共 3小题，每小题 6分，共 18分．在每小题给出的选项中，
有多项符合题目要求．全部选对的得 6分，部分选对的得部分分，有选错的得0
分）
9．下列导数运算正确的是（ ）
1 1 1 1
A．( )'  B．(ex)' ex C．(tanx)'  D．(lgx)' 
x x2 cos2 x xln10
1
10. 已知函数 f  x tanπx，将函数 y  f  x  的图象向左平移 个单位长度，然后纵坐
3
 
标不变，横坐标伸长为原来的2倍，得到函数g x 的图象，则下列描述中正确的是（ ）．
 2 
A. 函数g  x  的图象关于点  ,0成中心对称 B. 函数g  x  的最小正周期为2
 3 
 5 1 
C. 函数g  x  的单调增区间为  k, k，kZ D. 函数g  x  的图象没有对称轴
 3 3 
11. 已知实数a，b是方程x2  k 3  xk 0的两个根，且a 1，b1，则（ ）
A.ab的最小值为9 B. a2 b2的最小值为18
3 1
C.  的最小值为 3 D. a4b的最小值为12
a1 b1
三、填空题（本题共 3小题，每小题 5分，共 15分）
12. 命题“x2024,lgx x ”的否定为__________.
a
13. 若过点  0,0  的直线是曲线 y  x2 1x 0和曲线 ylnx a的公切线，则
x1
{#{QQABDQaAggiIAJAAAAhCUwUYCkMQkAGAASgOAEAEIAIACBFABCA=}#}a  ________．
4051
14.已知函数 y  f  x2 1为定义在R上的奇函数，则  f  i2024 ______．
i1
四、解答题（本题共5小题，共 77分，解答应写出文字说明、证明过程或演算
步骤）
15. （本题13分）已知函数 f(x)cos4 x2sinxcosxsin4 x．
（1）求 f  x 的最小正周期；
 
（2）当x

0,

时，求 f  x 的最小值以及取得最小值时x的集合．
 2
2xa
16. （本题15分）已知定义在R上的奇函数 f x ，其中a0.
2x1
(1)求函数 f x的值域；
2
(2)解不等式：2f x
f x1
3
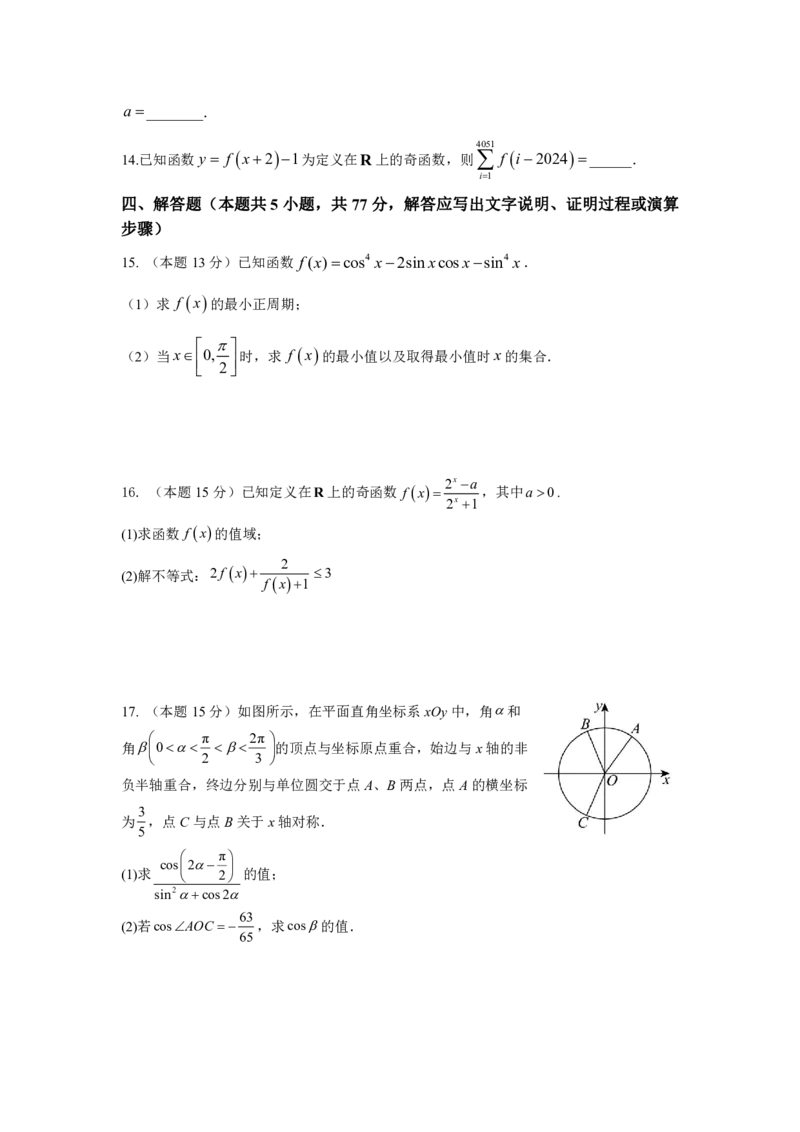
17. （本题15分）如图所示，在平面直角坐标系xOy中，角和
 π 2π 
角0  的顶点与坐标原点重合，始边与x轴的非
 2 3 
负半轴重合，终边分别与单位圆交于点A、B两点，点A的横坐标
3
为 ，点C与点B关于x轴对称．
5
 π
cos2 
(1)求  2 的值；
sin2cos2
63
(2)若cosAOC  ，求cos的值．
65
{#{QQABDQaAggiIAJAAAAhCUwUYCkMQkAGAASgOAEAEIAIACBFABCA=}#}18. （本题17分） 已知函数 f x2lnx 1 ，g  x ax．
x
（1）求 f (x)的单调区间；
（2）当x[1,)时，gx f x，求实数a的取值范围；
19. （本题17分） 设集合A为非空数集，定义
A {x|xab,a,bA},A {x x ab|,a,bA}.
(1)若集合A1,1 ,直接写出集合 A及A；
(2)若集合Ax,x ,x ,x,x  x  x  x且A  A，求证x x  x x ；
1 2 3 4 1 2 3 4 1 4 2 3
(3)若集合A{x|0x2024,xN}且AA ，求A中元素个数的最大值.
{#{QQABDQaAggiIAJAAAAhCUwUYCkMQkAGAASgOAEAEIAIACBFABCA=}#}