文档内容
义 务 教 育 教 科 书
数数 学学
六年级 上册
孙丽谷 王 林 主编
班级
姓名一一 长方体和正方体 !!!!!!!!!!!!!!! 1
表面涂色的正方体 !!!!!!!!!!!!! 26
二二 分数乘法 !!!!!!!!!!!!!!!!! 28
三三 分数除法 !!!!!!!!!!!!!!!!! 43
树叶中的比 !!!!!!!!!!!!!!!! 66
四四 解决问题的策略 !!!!!!!!!!!!!! 68
五五 分数四则混合运算 !!!!!!!!!!!!! 75
六六 百分数 !!!!!!!!!!!!!!!!!! 84
互联网的普及 !!!!!!!!!!!!!!! 110
七七 整理与复习 !!!!!!!!!!!!!!!! 112长方体和正方体
1
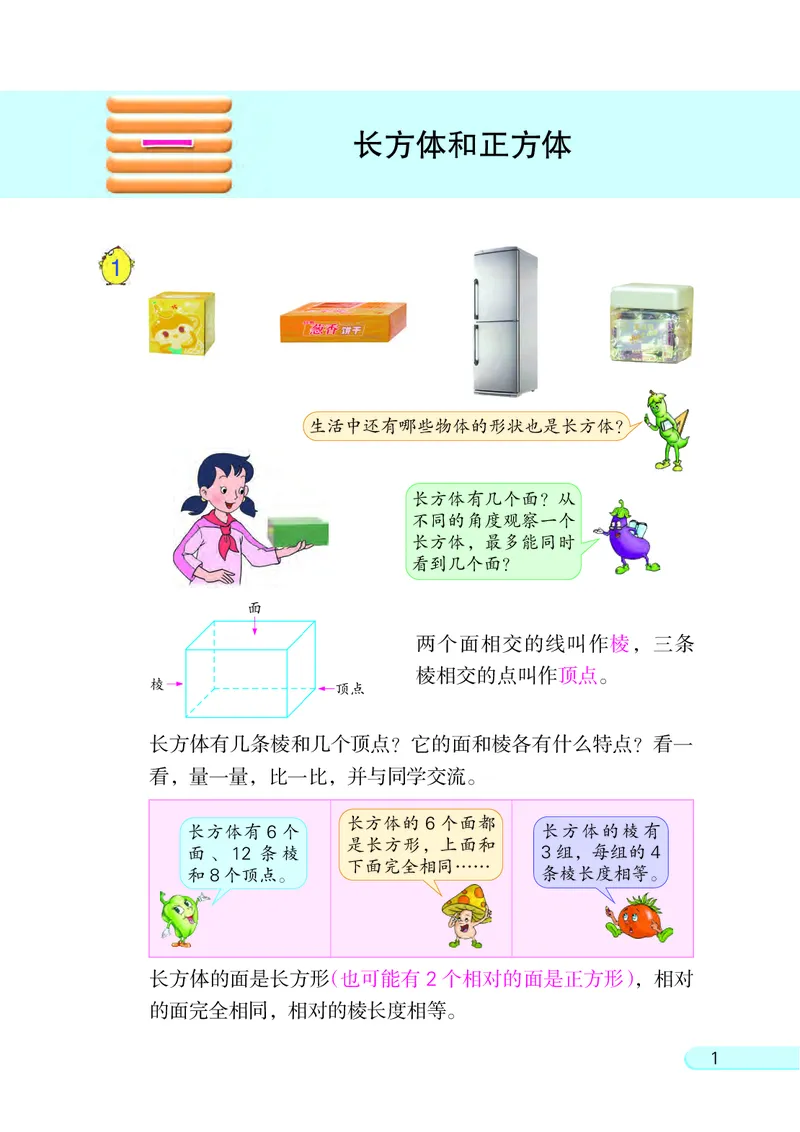
生活中还有哪些物体的形状也是长方体?
长方体有几个面? 从
不同的角度观察一个
长方体, 最多能同时
看到几个面?
面
两个面相交的线叫作棱, 三条
棱相交的点叫作顶点。
棱 顶点
长方体有几条棱和几个顶点? 它的面和棱各有什么特点? 看一
看, 量一量, 比一比, 并与同学交流。
长方体的 6 个面都
长方体有 6 个 长方体的棱有
是长方形, 上面和
面、 12 条棱 3 组, 每组的 4
下面完全相同……
和 8个顶点。 条棱长度相等。
长方体的面是长方形(也可能有 2 个相对的面是正方形), 相对
的面完全相同, 相对的棱长度相等。
1长方体和正方体
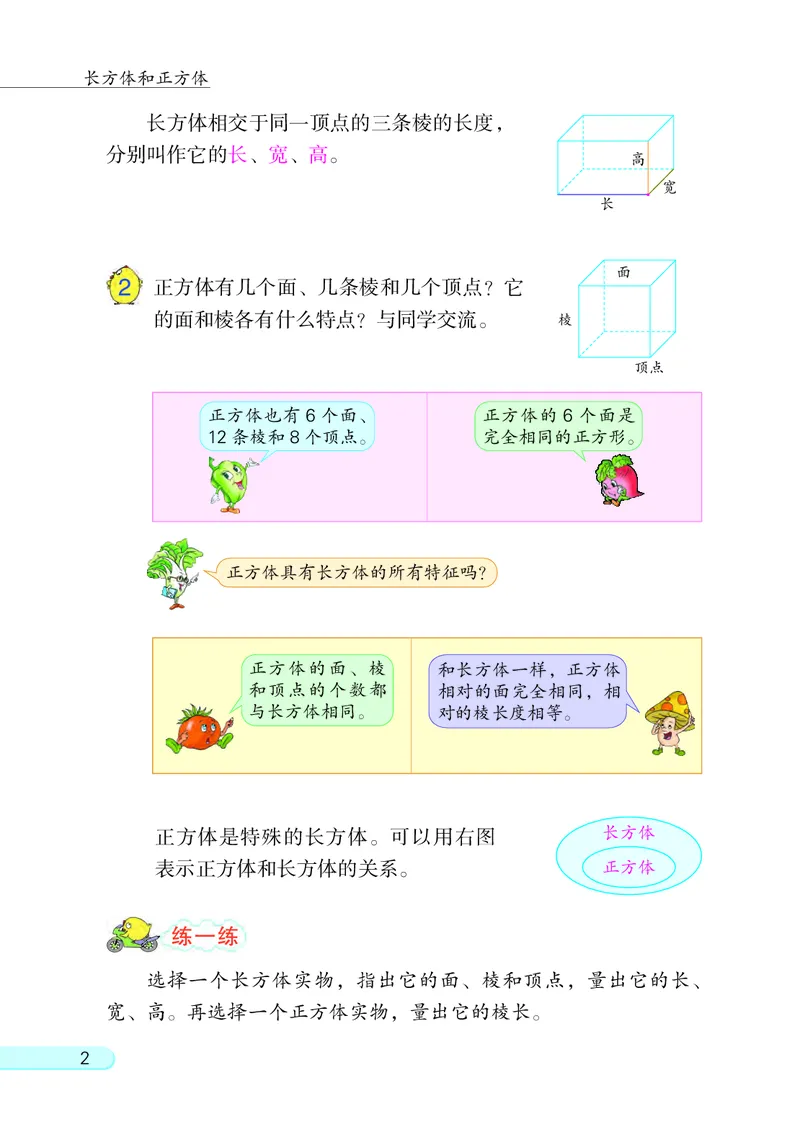
长方体相交于同一顶点的三条棱的长度,
分别叫作它的长、 宽、 高。
高
宽
长
面
2 正方体有几个面、 几条棱和几个顶点? 它
的面和棱各有什么特点? 与同学交流。 棱
顶点
正方体也有 6 个面、 正方体的 6 个面是
12条棱和8个顶点。 完全相同的正方形。
正方体具有长方体的所有特征吗?
正方体的面、 棱 和长方体一样, 正方体
和顶点的个数都 相对的面完全相同, 相
与长方体相同。 对的棱长度相等。
正方体是特殊的长方体。 可以用右图 长方体
表示正方体和长方体的关系。 正方体
练一练
选择一个长方体实物, 指出它的面、 棱和顶点, 量出它的长、
宽、 高。 再选择一个正方体实物, 量出它的棱长。
2长方体和正方体
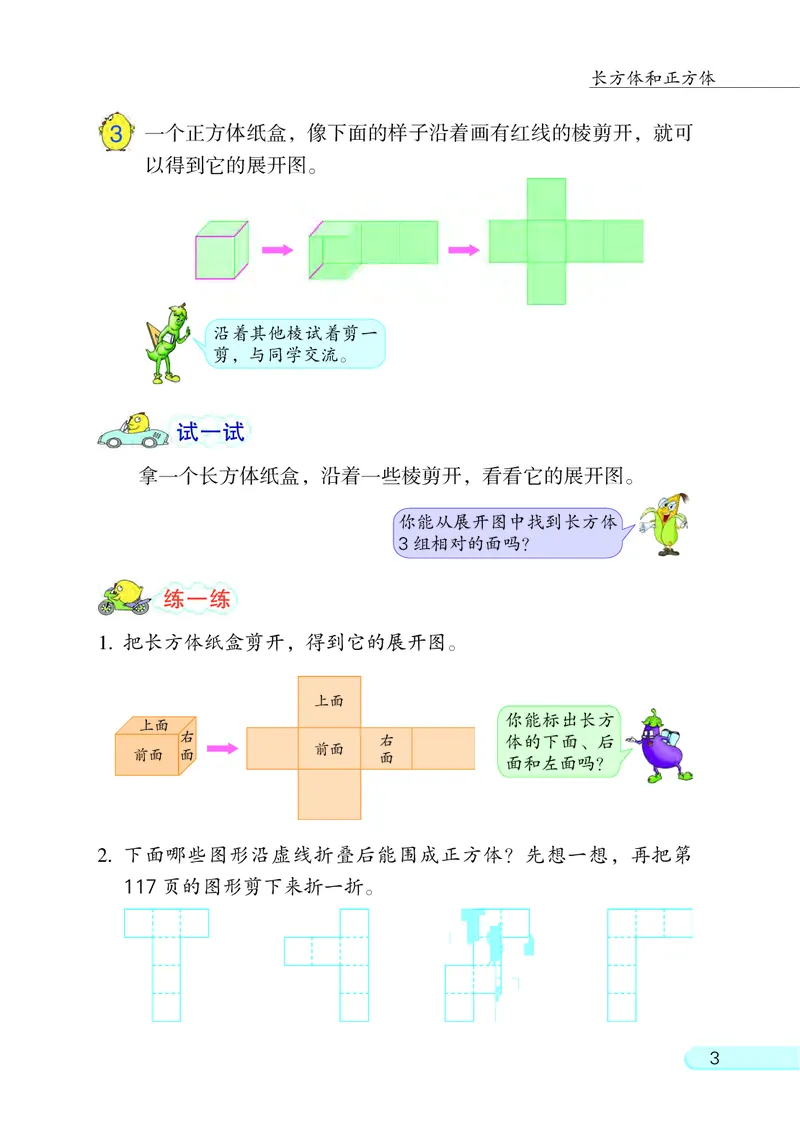
3 一个正方体纸盒, 像下面的样子沿着画有红线的棱剪开, 就可
以得到它的展开图。
沿着其他棱试着剪一
剪, 与同学交流。
试一试
拿一个长方体纸盒, 沿着一些棱剪开, 看看它的展开图。
你能从展开图中找到长方体
3组相对的面吗?
练一练
1. 把长方体纸盒剪开, 得到它的展开图。
上面
你能标出长方
上面
右 右 体的下面、 后
前面
前面 面 面 面和左面吗?
2. 下面哪些图形沿虚线折叠后能围成正方体? 先想一想, 再把第
117 页的图形剪下来折一折。
3md5
练 习 一
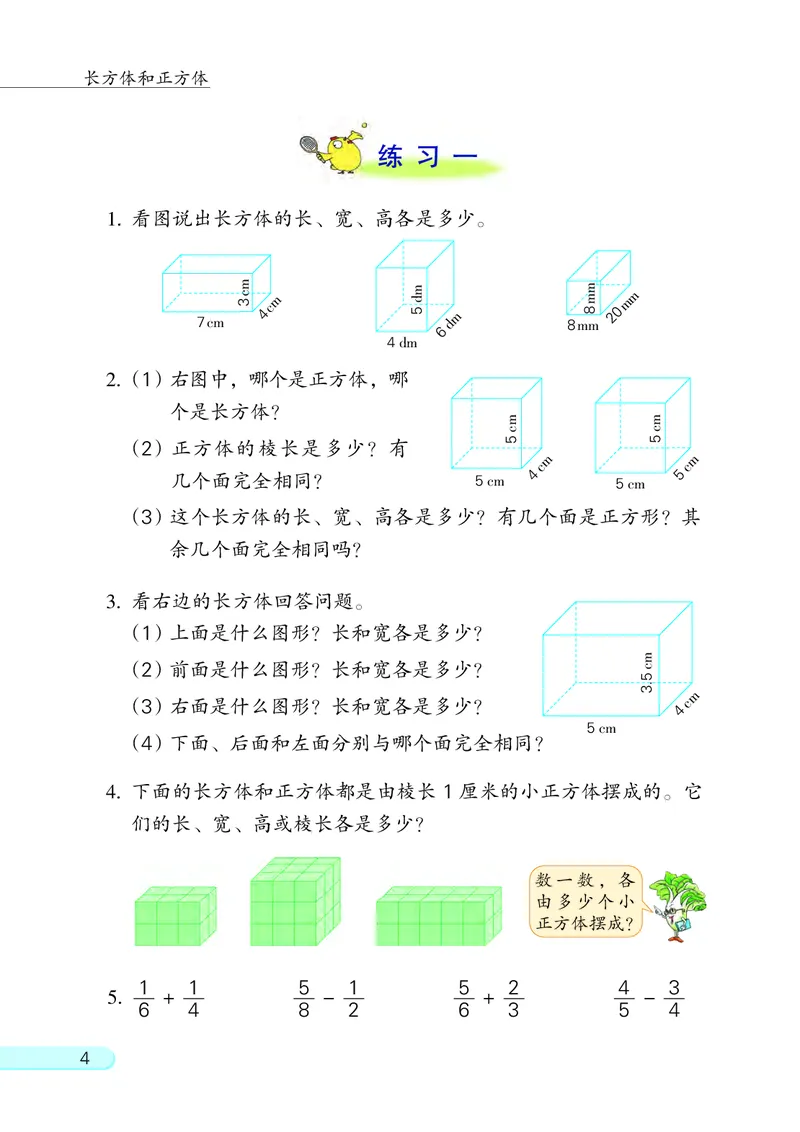
1. 看图说出长方体的长、 宽、 高各是多少。
m
c 4 m
d
6
4dm
mc3
3. 看右边的长方体回答问题。
(1)上面是什么图形? 长和宽各是多少?
(2)前面是什么图形? 长和宽各是多少?
m
(3)右面是什么图形? 长和宽各是多少? c
4
5cm
(4)下面、 后面和左面分别与哪个面完全相同?
mc5.3
7cm
2.(1)右图中, 哪个是正方体, 哪
个是长方体?
(2) 正方体的棱长是多少? 有
m
c
4
几个面完全相同? 5cm
(3)这个长方体的长、 宽、 高各是多少? 有几个面是正方形? 其
余几个面完全相同吗?
mc5
m
c
5
5cm
mc5
长方体和正方体
m
m
0 2
4. 下面的长方体和正方体都是由棱长 1 厘米的小正方体摆成的。 它
们的长、 宽、 高或棱长各是多少?
数一数, 各
由多少个小
正方体摆成?
1 1 5 1 5 2 4 3
5. + - + -
6 4 8 2 6 3 5 4
mm8
8mm
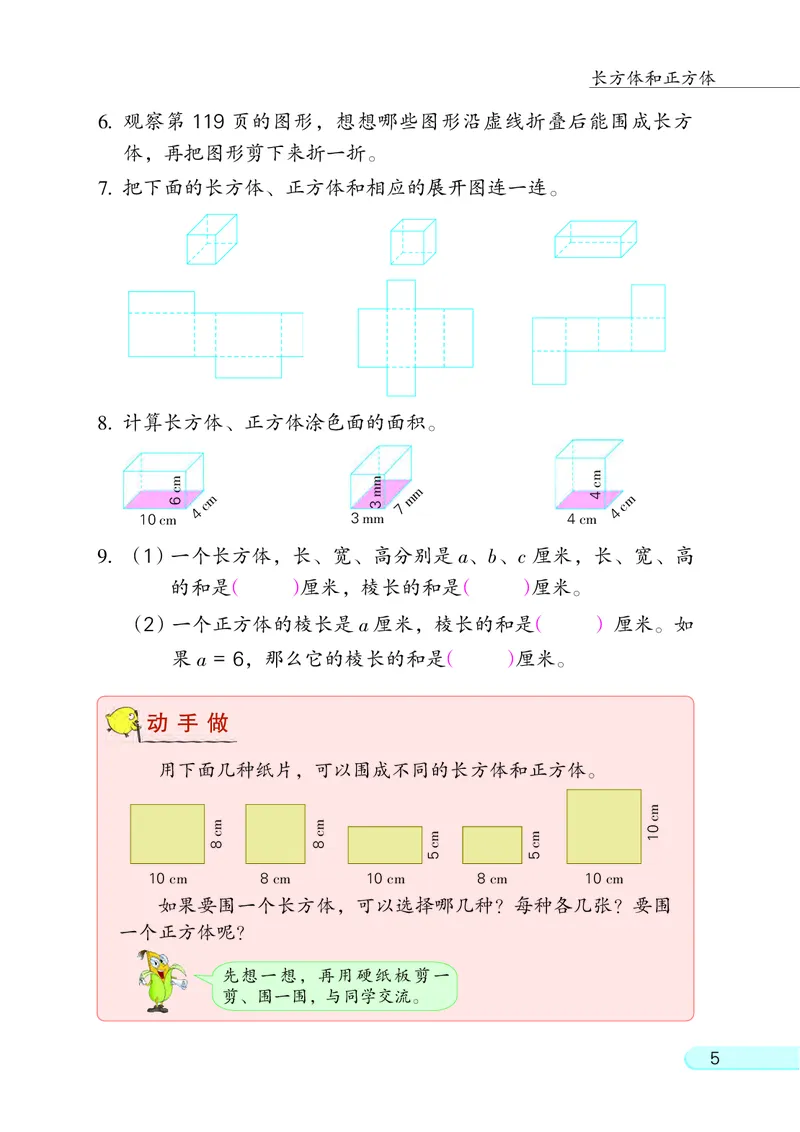
48. 计算长方体、 正方体涂色面的面积。
m
c 4
10cm
动 手 做
用下面几种纸片, 可以围成不同的长方体和正方体。
如果要围一个长方体, 可以选择哪几种? 每种各几张? 要围
一个正方体呢?
先想一想, 再用硬纸板剪一
剪、 围一围, 与同学交流。
mc6 mm3
7. 把下面的长方体、 正方体和相应的展开图连一连。
m
m m
7 c 4
3mm 4cm
9. (1)一个长方体, 长、 宽、 高分别是 a、 b、 c 厘米, 长、 宽、 高
的和是( )厘米, 棱长的和是( )厘米。
(2)一个正方体的棱长是 a 厘米, 棱长的和是( ) 厘米。 如
果 a = 6, 那么它的棱长的和是( )厘米。
mc4
长方体和正方体
10 cm
mc8
8 cm
mc8
10 cm
mc5
8 cm
mc5
10 cm
mc01
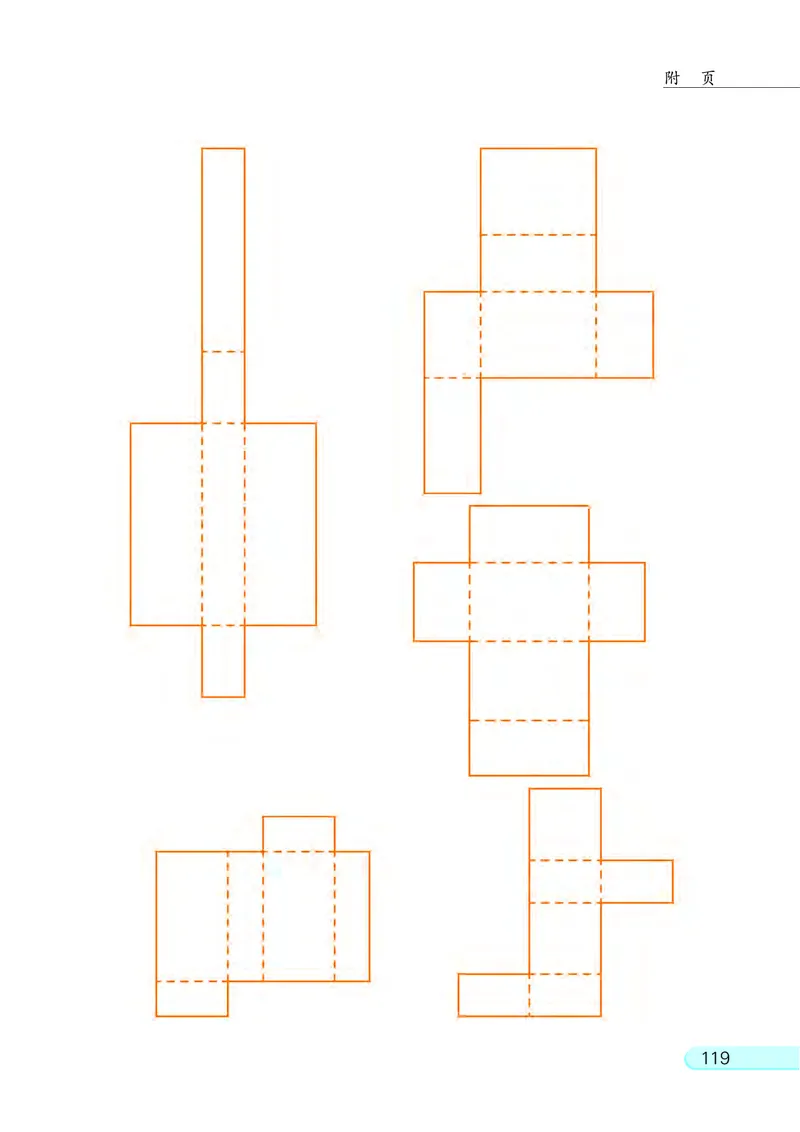
6. 观察第 119 页的图形, 想想哪些图形沿虚线折叠后能围成长方
体, 再把图形剪下来折一折。
5mc4
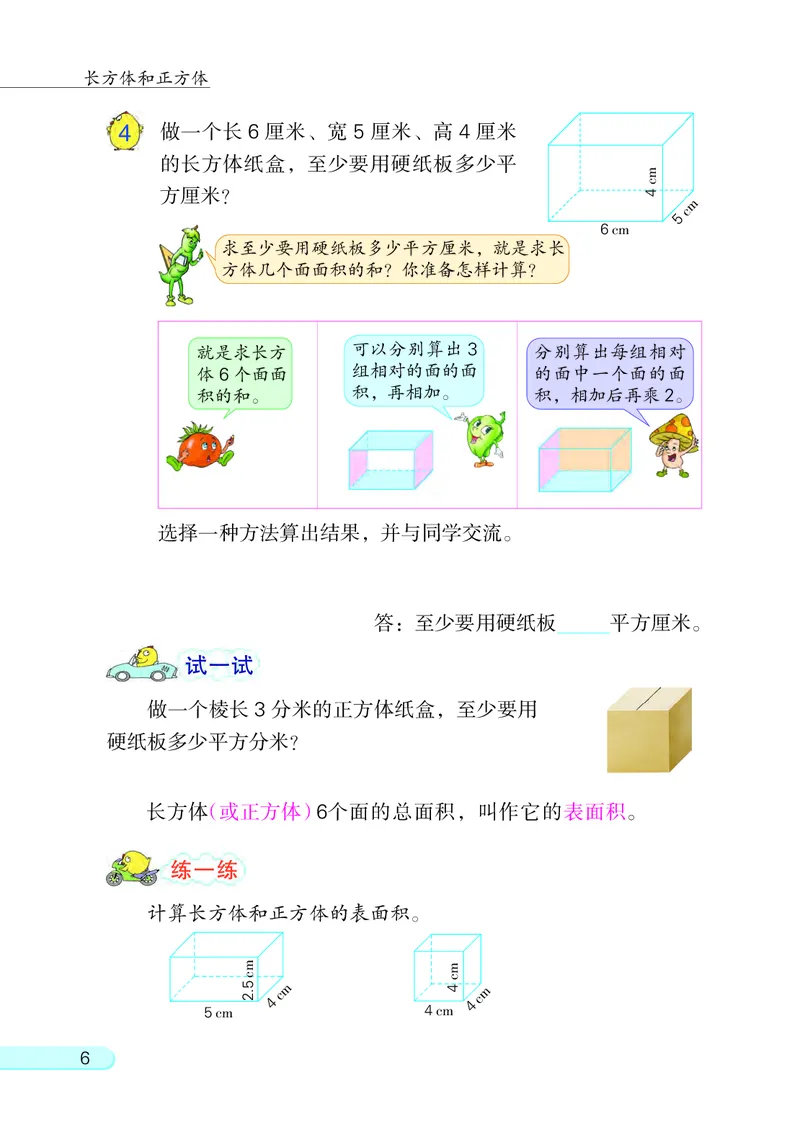
4 做一个长 6 厘米、 宽 5 厘米、 高 4 厘米
的长方体纸盒, 至少要用硬纸板多少平
方厘米?
答: 至少要用硬纸板 平方厘米。
试一试
做一个棱长 3 分米的正方体纸盒, 至少要用
硬纸板多少平方分米?
m m
4 c 4 c
5cm 4cm
mc5.2
长方体和正方体
m
c
5
6cm
求至少要用硬纸板多少平方厘米, 就是求长
方体几个面面积的和? 你准备怎样计算?
就是求长方 可以分别算出 3 分别算出每组相对
体6个面面 组相对的面的面 的面中一个面的面
积的和。 积, 再相加。 积, 相加后再乘2。
选择一种方法算出结果, 并与同学交流。
长方体(或正方体)6个面的总面积, 叫作它的表面积。
练一练
计算长方体和正方体的表面积。
mc4
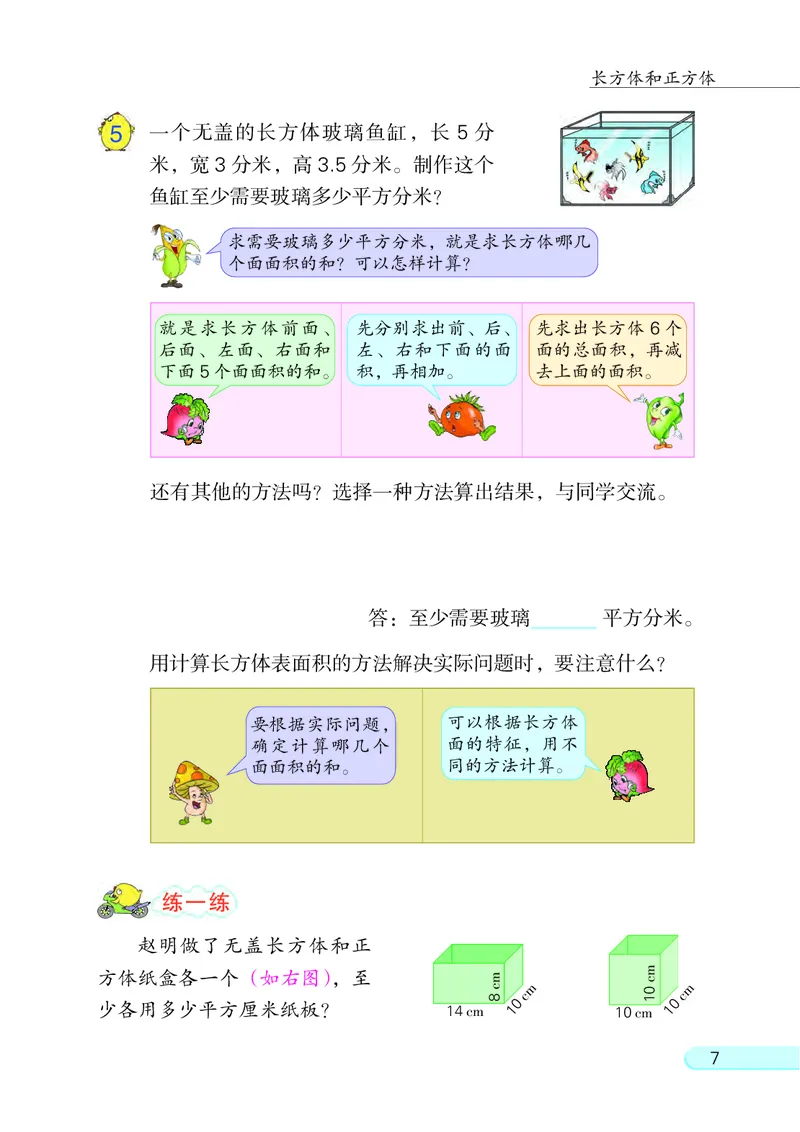
65 一个无盖的长方体玻璃鱼缸, 长 5 分
米, 宽 3 分米, 高 3.5 分米。 制作这个
鱼缸至少需要玻璃多少平方分米?
赵明做了无盖长方体和正
方体纸盒各一个(如右图), 至
少各用多少平方厘米纸板? 14cm
mc8
练一练
m
c
0
1 10cm
mc01
长方体和正方体
求需要玻璃多少平方分米, 就是求长方体哪几
个面面积的和? 可以怎样计算?
就是求长方体前面、 先分别求出前、 后、 先求出长方体 6 个
后面、 左面、 右面和 左、 右和下面的面 面的总面积, 再减
下面 5个面面积的和。 积, 再相加。 去上面的面积。
还有其他的方法吗? 选择一种方法算出结果, 与同学交流。
答: 至少需要玻璃 平方分米。
用计算长方体表面积的方法解决实际问题时, 要注意什么?
要根据实际问题, 可以根据长方体
确定计算哪几个 面的特征, 用不
面面积的和。 同的方法计算。
m
c
0
1
7练 习 二
1. 一个长方体如右图。
(1) 上、 下每个面的长是( )厘米, 宽是
( )厘米, 面积是( )平方厘米。
m
(2) 前、 后每个面的长是( )厘米, 宽是 3 c
4cm
( )厘米, 面积是( )平方厘米。
(3) 左、 右每个面的长是( )厘米, 宽是( )厘米, 面积是
( )平方厘米。
(4)这个长方体的表面积是( )平方厘米。
mc2
长方体和正方体
2. 右图是一个长方体。
(1) 它的上面、 前面、 右面 3 个面的面积
一共是多少?
(2)这个长方体的表面积是多少? 5dm
3. 一个长方体铁盒, 长 25 厘米, 宽 20 厘米, 高 15 厘米。 做这个
铁盒至少要用铁皮多少平方厘米?
4. 一个正方体纸盒, 棱长是 20 厘米。 做这个纸盒至少需要硬纸板
多少平方厘米?
5. 写出表中的物体是正方体还是长方体, 再计算表面积。
名 称 长/cm 宽/cm 高/cm 表面积/cm2
12 12 12
12 12 18
12 10 18
6. 一个长方体饼干盒, 长 17 厘米, 宽 11 厘米, 高
22 厘米。 如果在它的侧面贴满一圈包装纸(如右
图), 包装纸的面积至少有多少平方厘米?
md5.3
m
d
5
87. 一个用硬纸板做成的长方体影集封套
(如右图), 长 31 厘米, 宽 27 厘米, 高
2.5 厘米, 封套的左面不封口。 做这个
封套至少需要多少平方厘米硬纸板?
m
40cm 5 c
2
10.
下图表示用棱长 1 厘米的正方体摆成的物体。
(1) 从前面、 上面和右面看到的分别是什么形
状? 试着画一画。
(2)这个物体的表面积是多少平方厘米?
(3)如果添加同样的正方体, 把这个物体补成一
个大正方体, 表面积至少是多少平方厘米?
mc53
长方体和正方体
27cm
8. 学校生物小组做了一个昆虫箱(如下图)。 昆虫箱的上、 下、 左、
右面是木板, 前、 后两面装防蝇纱网。
制作这样一个昆虫箱, 至少需要
木板和纱网各多少平方厘米?
9. 我们的平顶教室长 8.5 米, 教室门窗和黑板的面
宽6米, 高 4.2米。 积一共有35.8平方米。
要粉刷教室的顶面和四面墙壁, 粉刷的面积有多少平方米?
找一个长方体火柴盒, 测量有关数据,
算出它的内盒和外盒至少各用硬纸多少
平方厘米。(接头处忽略不计)
9长方体和正方体
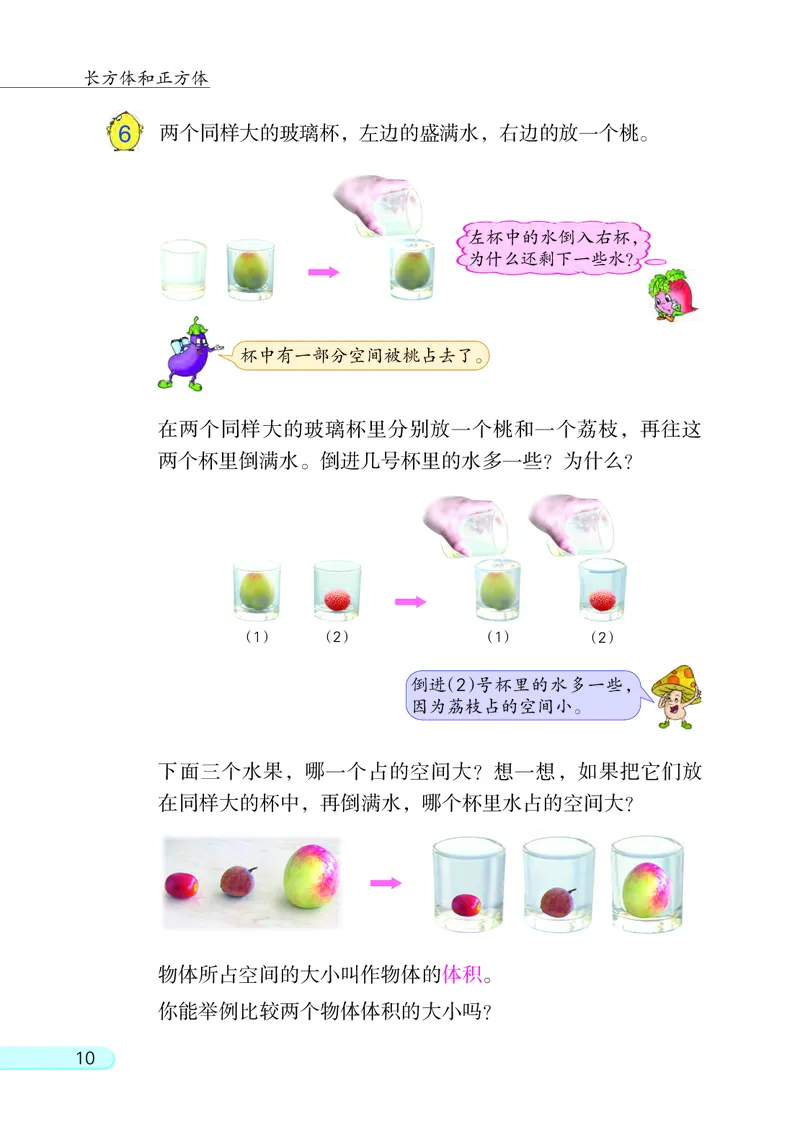
6 两个同样大的玻璃杯, 左边的盛满水, 右边的放一个桃。
左杯中的水倒入右杯,
为什么还剩下一些水?
杯中有一部分空间被桃占去了。
在两个同样大的玻璃杯里分别放一个桃和一个荔枝, 再往这
两个杯里倒满水。 倒进几号杯里的水多一些? 为什么?
(1) (2) (1) (2)
倒进(2)号杯里的水多一些,
因为荔枝占的空间小。
下面三个水果, 哪一个占的空间大? 想一想, 如果把它们放
在同样大的杯中, 再倒满水, 哪个杯里水占的空间大?
物体所占空间的大小叫作物体的体积。
你能举例比较两个物体体积的大小吗?
10长方体和正方体
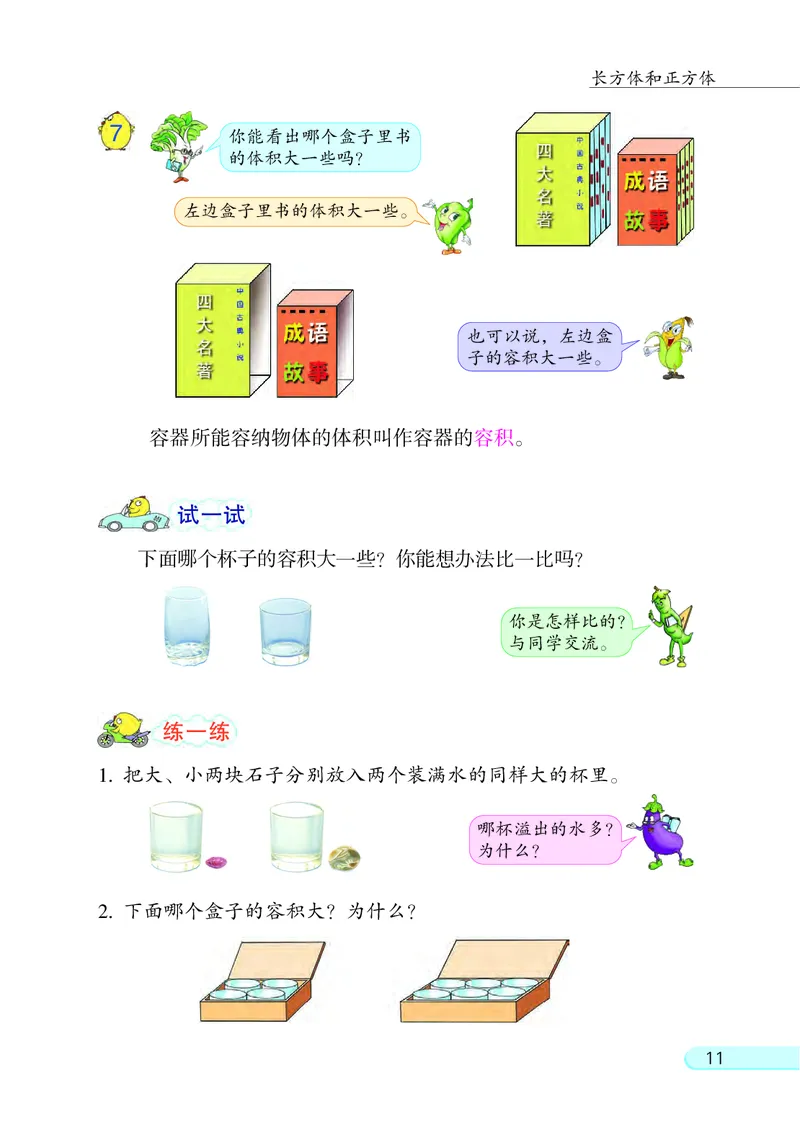
7
你能看出哪个盒子里书
的体积大一些吗?
左边盒子里书的体积大一些。
也可以说, 左边盒
子的容积大一些。
容器所能容纳物体的体积叫作容器的容积。
试一试
下面哪个杯子的容积大一些? 你能想办法比一比吗?
你是怎样比的?
与同学交流。
练一练
1. 把大、 小两块石子分别放入两个装满水的同样大的杯里。
哪杯溢出的水多?
为什么?
2. 下面哪个盒子的容积大? 为什么?
11长方体和正方体
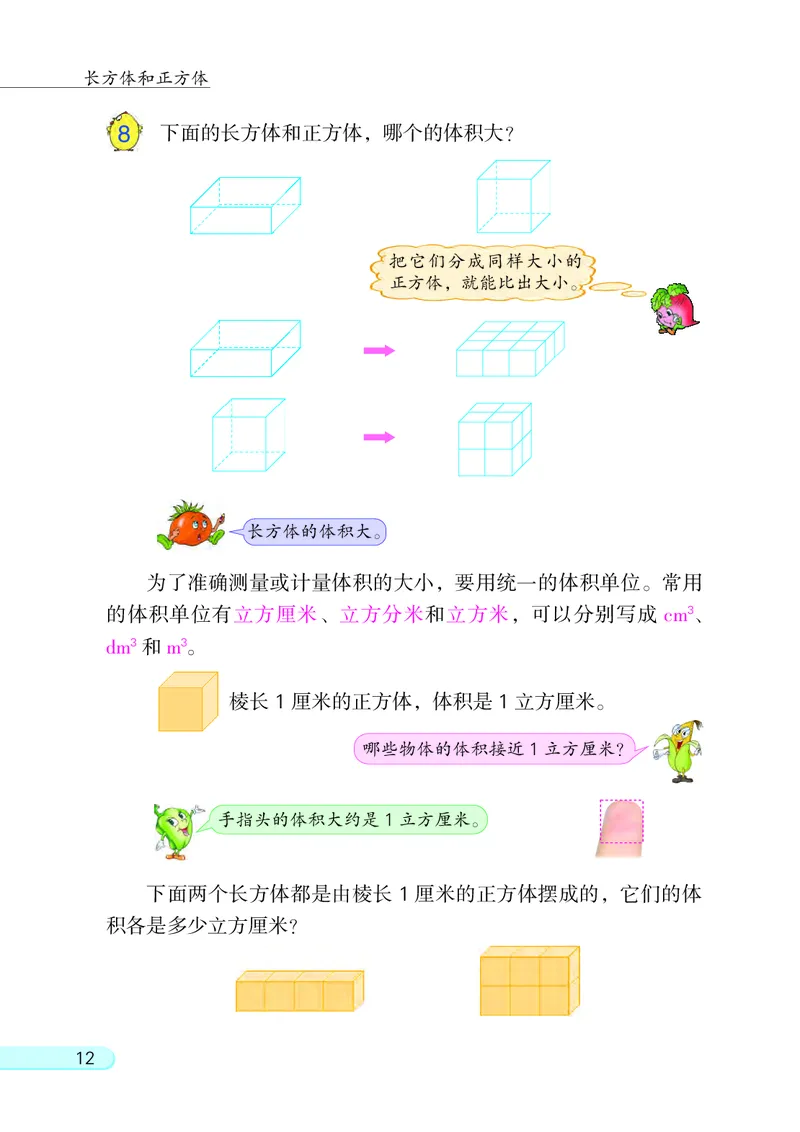
8 下面的长方体和正方体, 哪个的体积大?
把它们分成同样大小的
正方体, 就能比出大小。
长方体的体积大。
为了准确测量或计量体积的大小, 要用统一的体积单位。 常用
的体积单位有立方厘米、 立方分米和立方米, 可以分别写成 cm3、
dm3和 m3。
棱长 1 厘米的正方体, 体积是 1 立方厘米。
哪些物体的体积接近 1立方厘米?
手指头的体积大约是 1立方厘米。
下面两个长方体都是由棱长 1 厘米的正方体摆成的, 它们的体
积各是多少立方厘米?
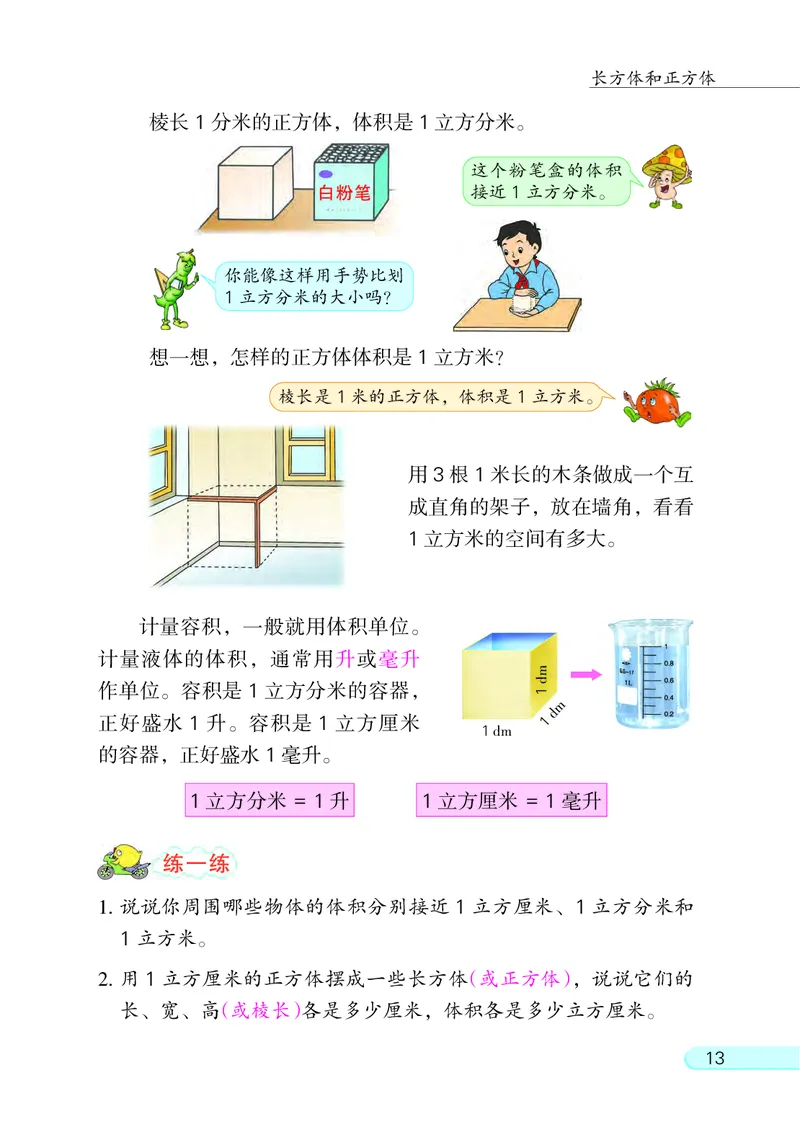
12计量容积, 一般就用体积单位。
计量液体的体积, 通常用升或毫升
作单位。 容积是 1 立方分米的容器,
正好盛水 1 升。 容积是 1 立方厘米
1dm
的容器, 正好盛水 1 毫升。
1 立方分米 = 1 升 1 立方厘米 = 1 毫升
md1
长方体和正方体
棱长 1 分米的正方体, 体积是 1 立方分米。
这个粉笔盒的体积
接近1立方分米。
你能像这样用手势比划
1立方分米的大小吗?
想一想, 怎样的正方体体积是 1 立方米?
棱长是 1米的正方体, 体积是 1立方米。
用 3 根 1 米长的木条做成一个互
成直角的架子, 放在墙角, 看看
1 立方米的空间有多大。
m
d
1
练一练
1. 说说你周围哪些物体的体积分别接近 1 立方厘米、 1 立方分米和
1 立方米。
2. 用 1 立方厘米的正方体摆成一些长方体(或正方体), 说说它们的
长、 宽、 高(或棱长)各是多少厘米, 体积各是多少立方厘米。
13长方体和正方体
练 习 三
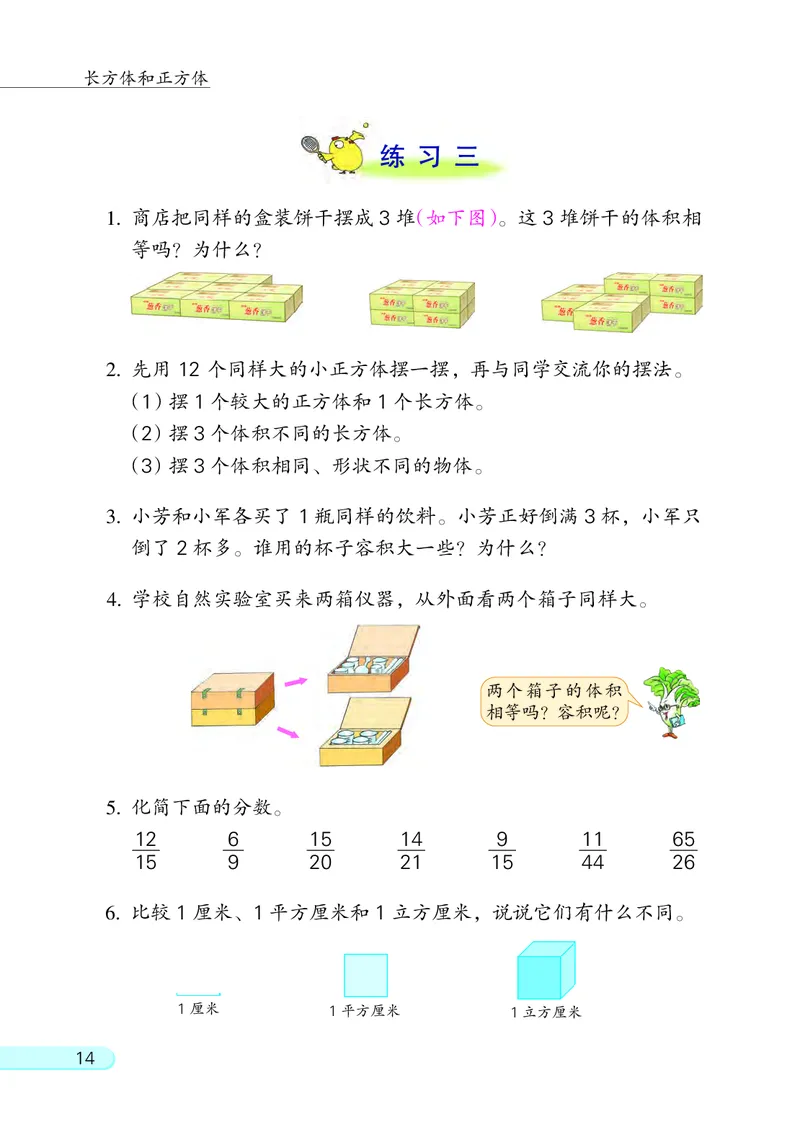
1. 商店把同样的盒装饼干摆成 3 堆(如下图)。 这 3 堆饼干的体积相
等吗? 为什么?
2. 先用 12 个同样大的小正方体摆一摆, 再与同学交流你的摆法。
(1)摆 1 个较大的正方体和 1 个长方体。
(2)摆 3 个体积不同的长方体。
(3)摆 3 个体积相同、 形状不同的物体。
3. 小芳和小军各买了 1 瓶同样的饮料。 小芳正好倒满 3 杯, 小军只
倒了 2 杯多。 谁用的杯子容积大一些? 为什么?
4. 学校自然实验室买来两箱仪器, 从外面看两个箱子同样大。
两个箱子的体积
相等吗? 容积呢?
5. 化简下面的分数。
12 6 15 14 9 11 65
15 9 20 21 15 44 26
6. 比较 1 厘米、 1 平方厘米和 1 立方厘米, 说说它们有什么不同。
1厘米 1平方厘米 1立方厘米
14长方体和正方体
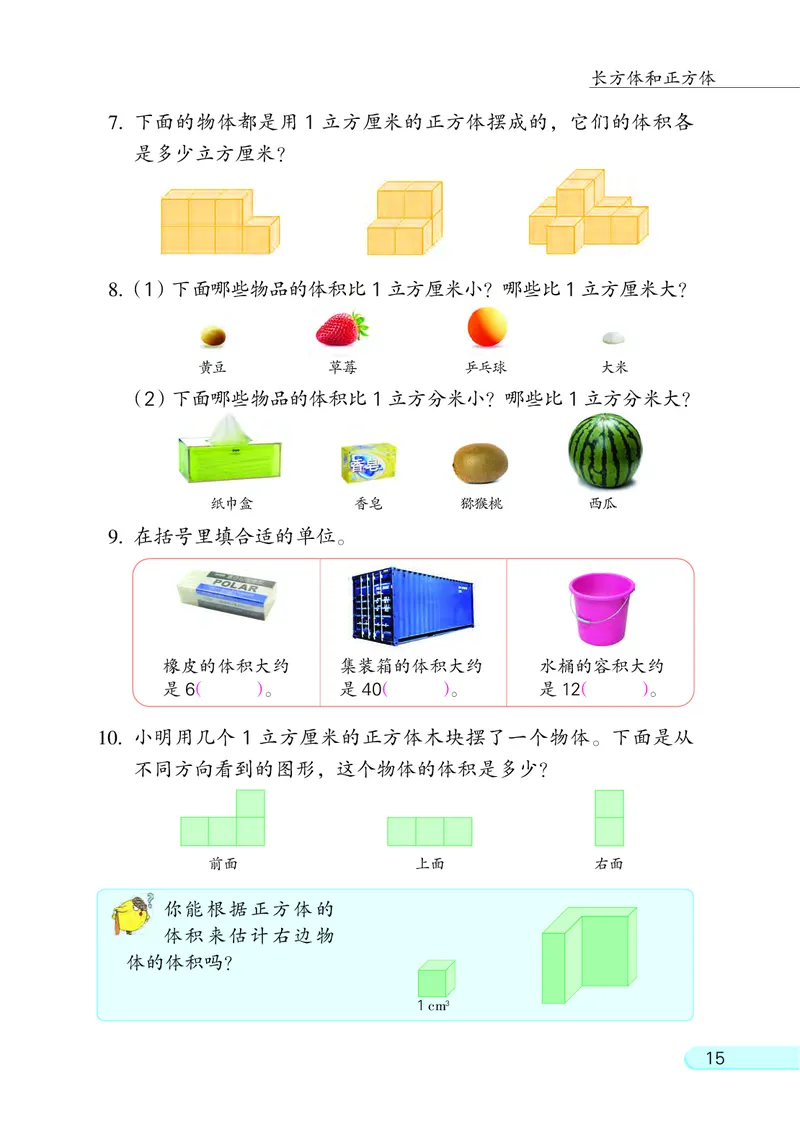
7. 下面的物体都是用 1 立方厘米的正方体摆成的, 它们的体积各
是多少立方厘米?
8.(1)下面哪些物品的体积比1立方厘米小? 哪些比1立方厘米大?
黄豆 草莓 乒乓球 大米
(2)下面哪些物品的体积比1立方分米小? 哪些比1立方分米大?
纸巾盒 香皂 猕猴桃 西瓜
9. 在括号里填合适的单位。
橡皮的体积大约 集装箱的体积大约 水桶的容积大约
是 6( )。 是40( )。 是12( )。
10. 小明用几个 1 立方厘米的正方体木块摆了一个物体。 下面是从
不同方向看到的图形, 这个物体的体积是多少?
前面 上面 右面
你能根据正方体的
体积来估计右边物
体的体积吗?
1cm3
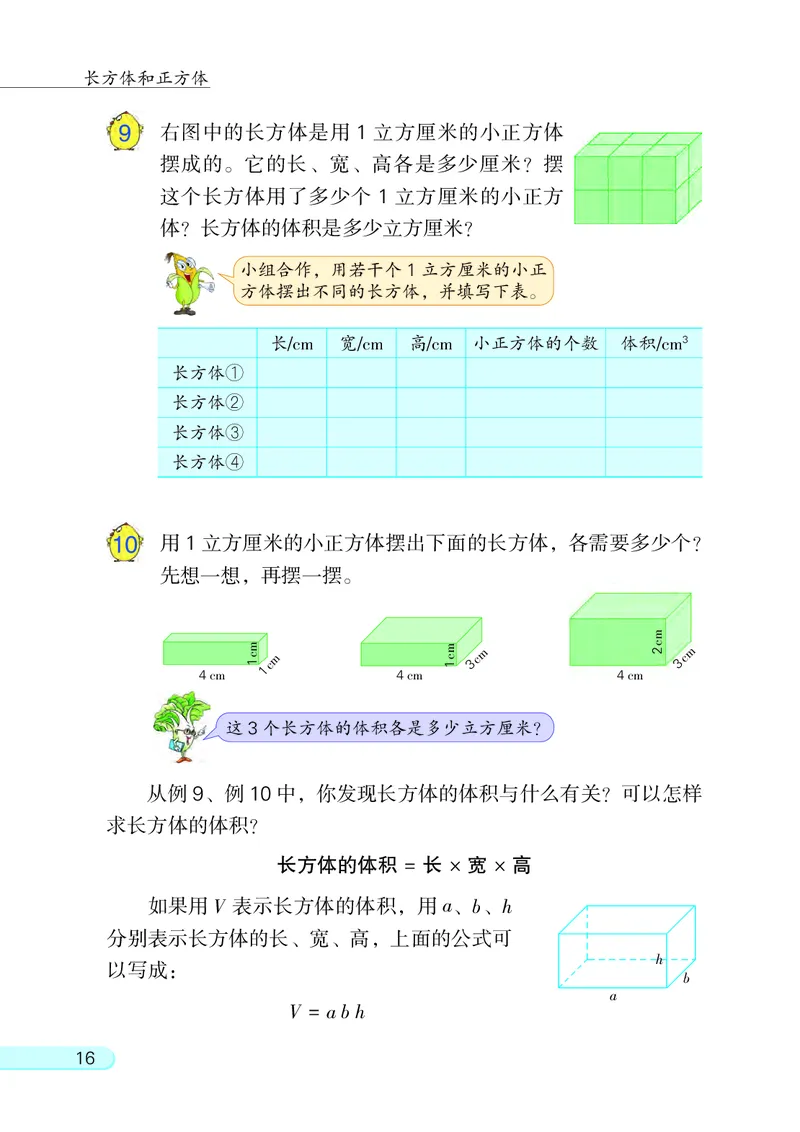
159 右图中的长方体是用 1 立方厘米的小正方体
摆成的。 它的长、 宽、 高各是多少厘米? 摆
这个长方体用了多少个 1 立方厘米的小正方
体? 长方体的体积是多少立方厘米?
长/cm 宽/cm 高/cm 小正方体的个数 体积/cm3
长方体①
长方体②
长方体③
长方体④
10
m
c 3
4cm
从例 9、 例 10 中, 你发现长方体的体积与什么有关? 可以怎样
求长方体的体积?
长方体的体积 = 长 × 宽 × 高
如果用 V 表示长方体的体积, 用 a、 b、 h
分别表示长方体的长、 宽、 高, 上面的公式可
h
以写成:
b
a
mc1
mc2
m
c 3
4cm
mc1
长方体和正方体
小组合作, 用若干个 1立方厘米的小正
方体摆出不同的长方体, 并填写下表。
用 1 立方厘米的小正方体摆出下面的长方体, 各需要多少个?
先想一想, 再摆一摆。
m c
1
4cm
这3个长方体的体积各是多少立方厘米?
V = a b h
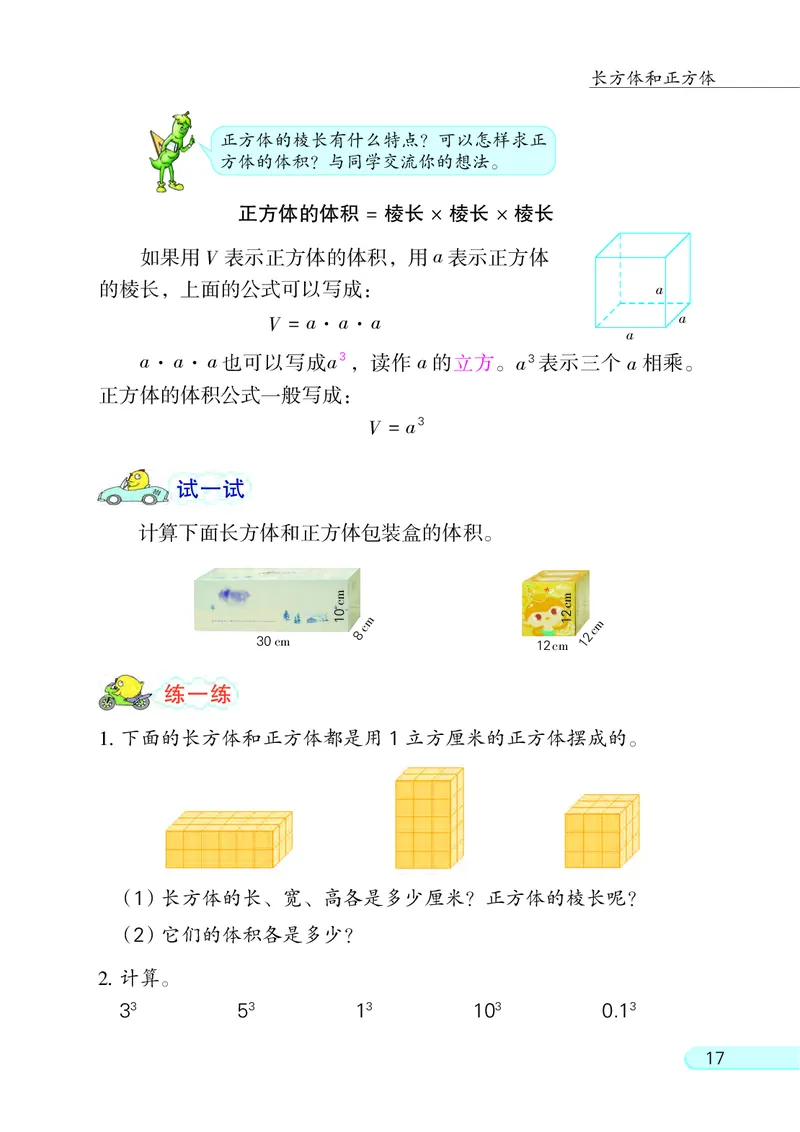
16正方体的体积 = 棱长 × 棱长 × 棱长
如果用 V 表示正方体的体积, 用 a 表示正方体
的棱长, 上面的公式可以写成: a
V = a·a·a a
a
a·a·a 也可以写成a3, 读作 a 的立方。 a3表示三个 a 相乘。
正方体的体积公式一般写成:
试一试
计算下面长方体和正方体包装盒的体积。
m c
2
12cm 1
练一练
1. 下面的长方体和正方体都是用 1 立方厘米的正方体摆成的。
mc21
m c
8
30cm
mc01
长方体和正方体
正方体的棱长有什么特点? 可以怎样求正
方体的体积? 与同学交流你的想法。
V = a3
(1)长方体的长、 宽、 高各是多少厘米? 正方体的棱长呢?
(2)它们的体积各是多少?
2. 计算。
33 53 13 103 0.13
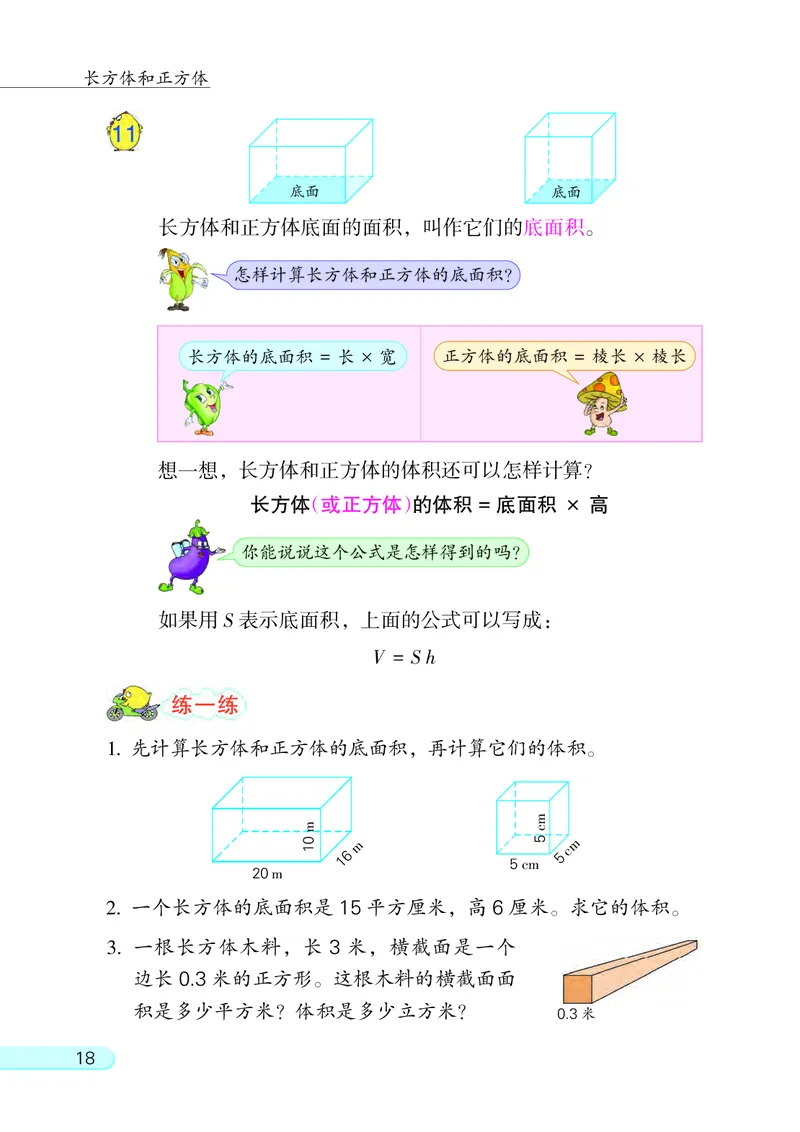
17底面 底面
长方体和正方体底面的面积, 叫作它们的底面积。
想一想, 长方体和正方体的体积还可以怎样计算?
长方体(或正方体)的体积 =�底面积 × 高
如果用 S 表示底面积, 上面的公式可以写成:
m
6 1
m01
m
c
5 5cm
20m
mc5
长方体和正方体
11
怎样计算长方体和正方体的底面积?
长方体的底面积 = 长 × 宽 正方体的底面积 = 棱长 × 棱长
你能说说这个公式是怎样得到的吗?
V = S h
练一练
1. 先计算长方体和正方体的底面积, 再计算它们的体积。
2. 一个长方体的底面积是 15 平方厘米, 高 6 厘米。 求它的体积。
3. 一根长方体木料, 长 3 米, 横截面是一个
边长 0.3 米的正方形。 这根木料的横截面面
积是多少平方米? 体积是多少立方米?
0.3米
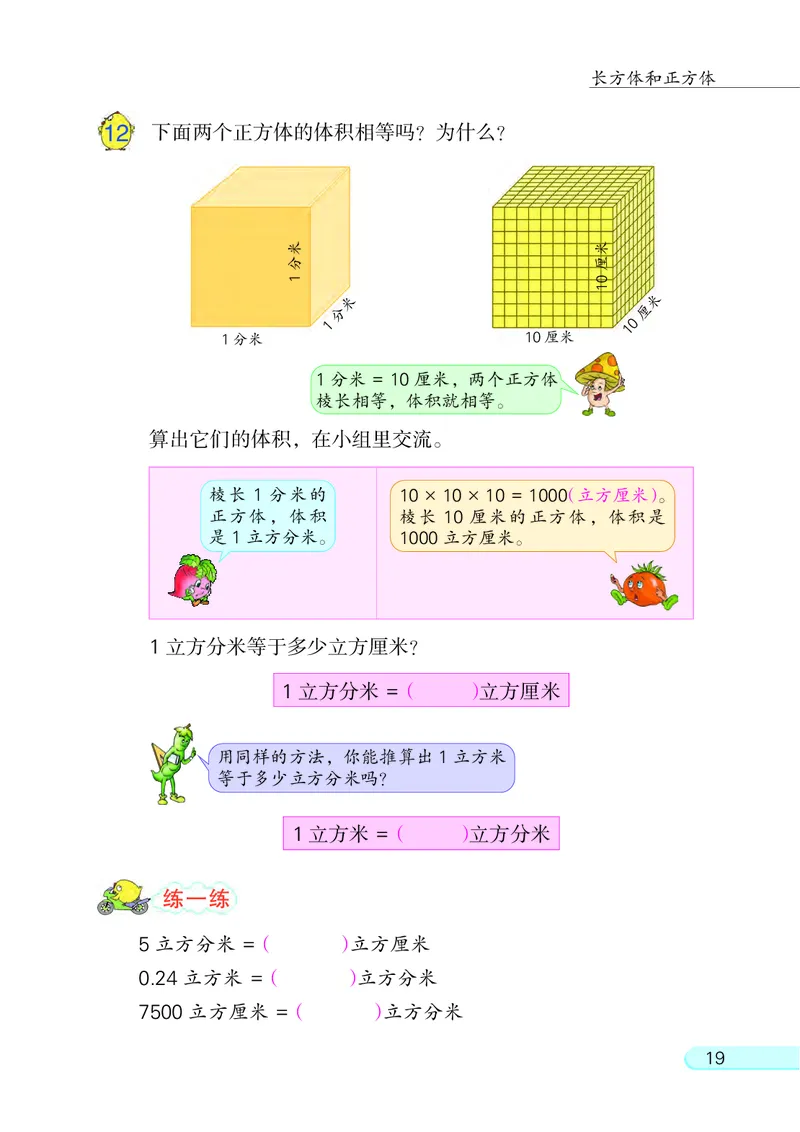
1812 下面两个正方体的体积相等吗? 为什么?
10厘米
算出它们的体积, 在小组里交流。
1 立方分米 =( )立方厘米
1 立方米 =( )立方分米
练一练
5 立方分米 =( )立方厘米
0.24 立方米 =( )立方分米
7500 立方厘米 =( )立方分米
米厘01
米
厘
0 1
1分米
米分1
长方体和正方体
米
分
1
1分米 = 10厘米, 两个正方体
棱长相等, 体积就相等。
棱长 1 分米的 10 × 10 × 10 = 1000(立方厘米)。
正方体, 体积 棱长 10 厘米的正方体, 体积是
是 1立方分米。 1000立方厘米。
1 立方分米等于多少立方厘米?
用同样的方法, 你能推算出 1 立方米
等于多少立方分米吗?
191. 计算下面长方体和正方体的体积。
m c
6
9cm
2. 一种冷藏车的车厢是长方体, 从里面量,
长 4 米, 宽 1.7 米, 高 1.8 米。 它的容积
是多少立方米?
mc5 md6
m d
6
6dm
3. 一块正方体石料, 棱长 8 分米。 这块石料的体积是多少立方分
米? 如果 1 立方分米的石料重 2.7 千克, 这块石料重多少千克?
5. 幼儿园有一排长方体的储物柜, 共占地 0.84 平方米, 储物柜高
0.75 米。 这排储物柜所占的空间是多少立方米?
米57.0
长方体和正方体
1 1 1 7 3 1 1 1 1
4. + - - + + +
4 2 3 8 4 2 3 2 6
6. 一辆运煤车的车厢是长方体。 从里面量, 底面积是 4.5 平方米,
装的煤高 0.6 米。 如果每立方米煤重 1.32 吨, 这辆运煤车大约
装煤多少吨?(得数保留一位小数)
7. 工人把 10.5 立方米黄沙铺在一个长 6 米、 宽 3.5 米的长方体沙
坑里, 可以铺多厚?(用方程解)
m8.0
练 习 四
m
5 2.
0.5m
8. 光明小学修筑一条长 60 米、 宽 12 米的直跑道。 先铺上 0.3 米厚
的三合土, 再铺上 0.03 米厚的塑胶。 需要三合土、 塑胶各多少
立方米?
20长方体和正方体
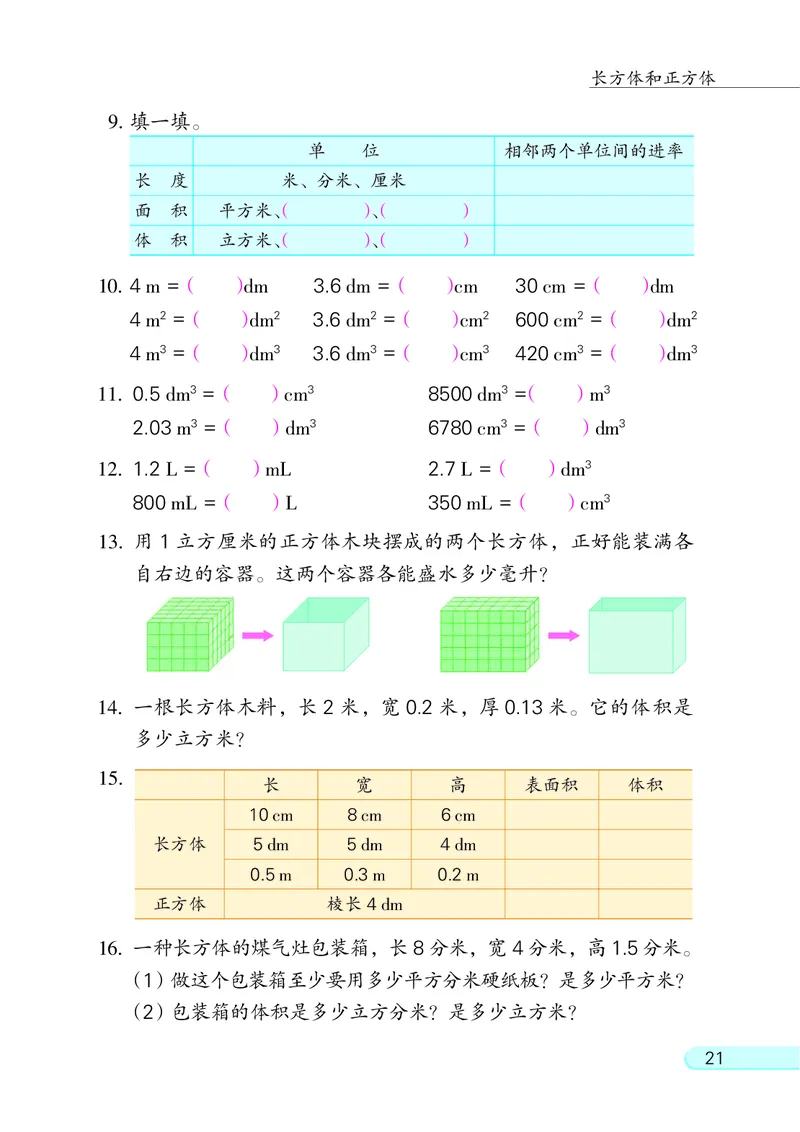
9. 填一填。
单 位 相邻两个单位间的进率
长 度 米、 分米、 厘米
面 积 平方米、( )、( )
体 积 立方米、( )、( )
10. 4 m =( )dm 3.6 dm =( )cm 30 cm =( )dm
4 m2 =( )dm2 3.6 dm2 =( )cm2 600 cm2 =( )dm2
4 m3 =( )dm3 3.6 dm3 =( )cm3 420 cm3 =( )dm3
11. 0.5 dm3 =( )cm3 8500 dm3 =( )m3
2.03 m3 =( )dm3 6780 cm3 =( )dm3
12. 1.2 L =( )mL 2.7 L =( )dm3
800 mL =( )L 350 mL =( )cm3
13. 用 1 立方厘米的正方体木块摆成的两个长方体, 正好能装满各
自右边的容器。 这两个容器各能盛水多少毫升?
14. 一根长方体木料, 长 2 米, 宽 0.2 米, 厚 0.13 米。 它的体积是
多少立方米?
15.
长 宽 高 表面积 体积
10cm 8cm 6cm
长方体 5dm 5dm 4dm
0.5m 0.3m 0.2m
正方体 棱长 4dm
16. 一种长方体的煤气灶包装箱, 长8分米, 宽 4分米, 高1.5分米。
(1)做这个包装箱至少要用多少平方分米硬纸板? 是多少平方米?
(2)包装箱的体积是多少立方分米? 是多少立方米?
21长方体和正方体
17. 一个无盖的长方体铁皮水槽, 长12分米, 宽 5分米, 高2分米。
(1)做这个水槽至少需要铁皮多少平方分米?
(2)这个水槽最多可以盛水多少升?
18. 一个花坛(如右图), 高 0.9 米, 底面是边
长 1.2 米的正方形, 四周用木条围成。
(1)这个花坛占地多少平方米?
(2)用泥土填满这个花坛,大约需要泥土多
少立方米?(木条的厚度忽略不计)
(3)做这样一个花坛, 四周大约需要木条多少平方米?
19. 一台冰柜, 从外面量, 长 1 米, 宽 0.6 米, 高 1.1 米; 从里面
量, 长9分米, 宽4.5分米, 深6分米。
(1)这台冰柜所占的空间有多大?
(2)这台冰柜的容积是多少?
一个长方体, 如果高增加 2 厘米, 就变成一个
正方体。 这时表面积比原来增加 56 平方厘米。
原来长方体的体积是多少立方厘米?
你知道吗
你注意过像右边包装箱上这样的连
乘式子吗? 它表示这个长方体包装箱的 包装尺寸:185×150×230mm
长、 宽、 高分别是 185 mm、 150 mm 和
230 mm。
你能根据左图中冰箱说明
书上的乘式, 估算出这台
冰箱的体积吗?
22回顾与整理
小组讨论:
1. 正方体和长方体各有哪些特征? 有什么联系?
2. 体积和容积的意义分别是什么? 常用的体积单位有哪些?
3. 怎样计算长方体、 正方体的表面积? 解决有关的实际问题时
要注意什么?
4. 你是怎样发现长方体(或正方体)体积公式的? 应用这些公式
能解决哪些实际问题?
练习与应用
1. 下面的图形表示的是正方体还是长方体? 先估计哪个体积最大,
再分别计算它们的体积和表面积。
m
c 4 6cm
2. 一个土豆浸没在盛有水的量杯
中, 这个土豆的体积是多少立方
厘米?
3. 7.02 dm3 =( )cm3 3.2 m3 =( )dm3
8020 dm3 =( )m3 4200 cm3 =( )dm3
4.5 L =( )mL =( )cm3 2300 mL =( )L
4. 长/cm 宽/cm 高/cm 底面积/cm2 表面积/cm2 体积/cm3
12 9 5
长方体
3.2 6.4 25.6
正方体 8
mc4
m
c 4cm 4
mc4
m
c 4 4cm
mc3
长方体和正方体
整理与练习
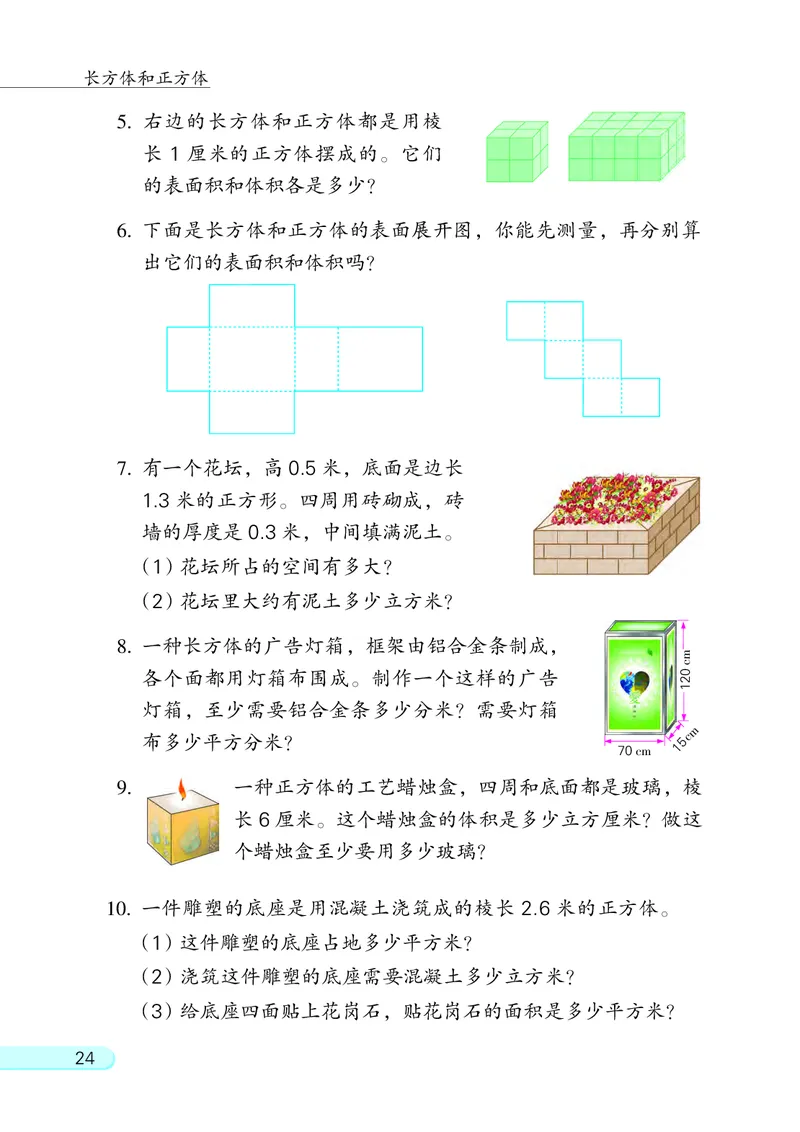
238. 一种长方体的广告灯箱, 框架由铝合金条制成,
各个面都用灯箱布围成。 制作一个这样的广告
灯箱, 至少需要铝合金条多少分米? 需要灯箱
m
布多少平方分米? 5 c
70cm 1
10. 一件雕塑的底座是用混凝土浇筑成的棱长 2.6 米的正方体。
(1)这件雕塑的底座占地多少平方米?
(2)浇筑这件雕塑的底座需要混凝土多少立方米?
(3)给底座四面贴上花岗石, 贴花岗石的面积是多少平方米?
mc021
长方体和正方体
5. 右边的长方体和正方体都是用棱
长 1 厘米的正方体摆成的。 它们
的表面积和体积各是多少?
6. 下面是长方体和正方体的表面展开图, 你能先测量, 再分别算
出它们的表面积和体积吗?
7. 有一个花坛, 高 0.5 米, 底面是边长
1.3 米的正方形。 四周用砖砌成, 砖
墙的厚度是 0.3 米, 中间填满泥土。
(1)花坛所占的空间有多大?
(2)花坛里大约有泥土多少立方米?
9. 一种正方体的工艺蜡烛盒, 四周和底面都是玻璃, 棱
长 6 厘米。 这个蜡烛盒的体积是多少立方厘米? 做这
个蜡烛盒至少要用多少玻璃?
24长方体和正方体
探索与实践
11. 用小棒和橡皮泥团, 可以做出不同的长方体和正方体框架。 小
组合作, 先填写选料单, 再做一做。
材 料
10cm 8cm 6cm 5cm
数 量 ( )团 ( )根 ( )根 ( )根 ( )根
12. 调查几种长方体形状家用电器长、 宽、 高的数据, 算出它们的
表面积和体积。
电器名称 长/cm 宽/cm 高/cm 表面积/cm2 体积/cm3
13. 你能求出一张纸的体积吗? 小组合作, 动手试一试。
右图中一共有多少个小正
方体? 你是怎样数的? 与
同学交流。
评价与反思
根据自己的学习表现, 能得几个★, 就把几个☆涂上颜色。
在认识长方体、 正方体的特征及体积、 容积的意
☆☆☆☆☆
义时, 能认真操作、 主动探索、 积极思考
在探索长方体、 正方体表面积和体积的计算方法
☆☆☆☆☆
时, 能主动尝试、 实践, 并进行简单的推理
能灵活运用体积和表面积的计算方法解决简单实
☆☆☆☆☆
际问题, 并对结果进行解释
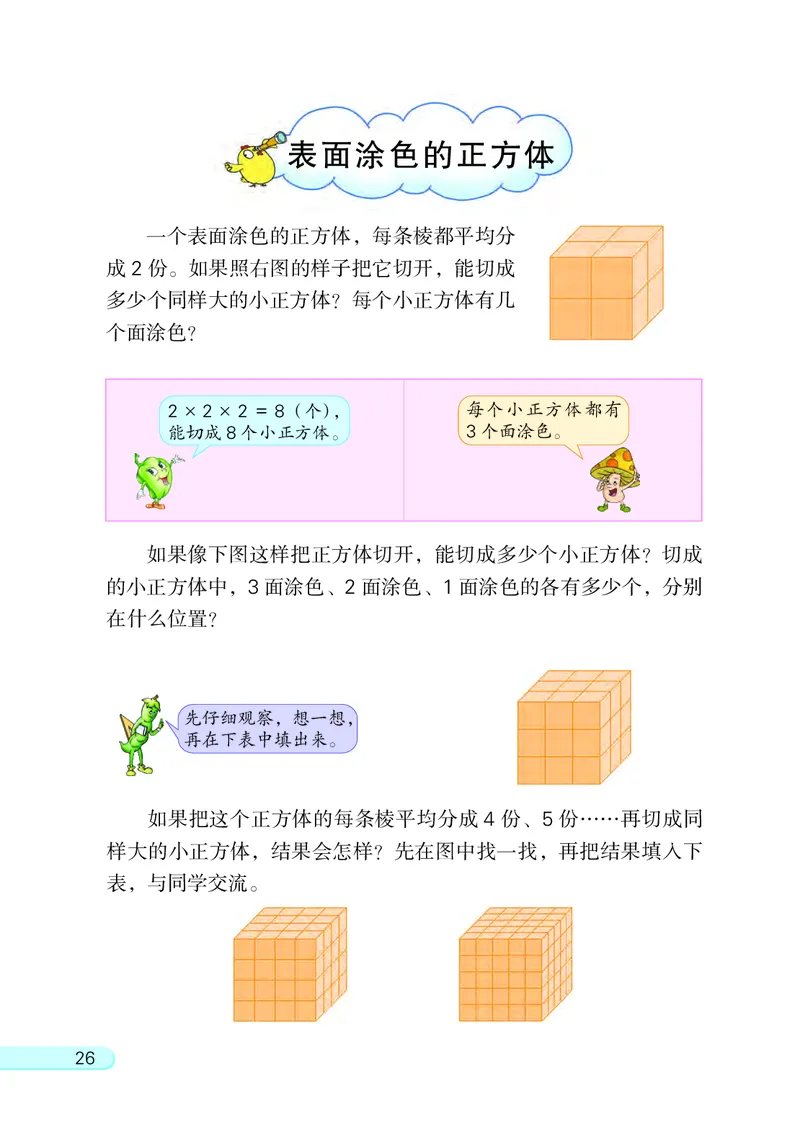
25表面涂色的正方体
一个表面涂色的正方体, 每条棱都平均分
成 2 份。 如果照右图的样子把它切开, 能切成
多少个同样大的小正方体? 每个小正方体有几
个面涂色?
2 × 2 × 2 = 8(个), 每个小正方体都有
能切成8个小正方体。 3个面涂色。
如果像下图这样把正方体切开, 能切成多少个小正方体? 切成
的小正方体中, 3 面涂色、 2 面涂色、 1 面涂色的各有多少个, 分别
在什么位置?
先仔细观察, 想一想,
再在下表中填出来。
如果把这个正方体的每条棱平均分成 4 份、 5 份……再切成同
样大的小正方体, 结果会怎样? 先在图中找一找, 再把结果填入下
表, 与同学交流。
26探索规律
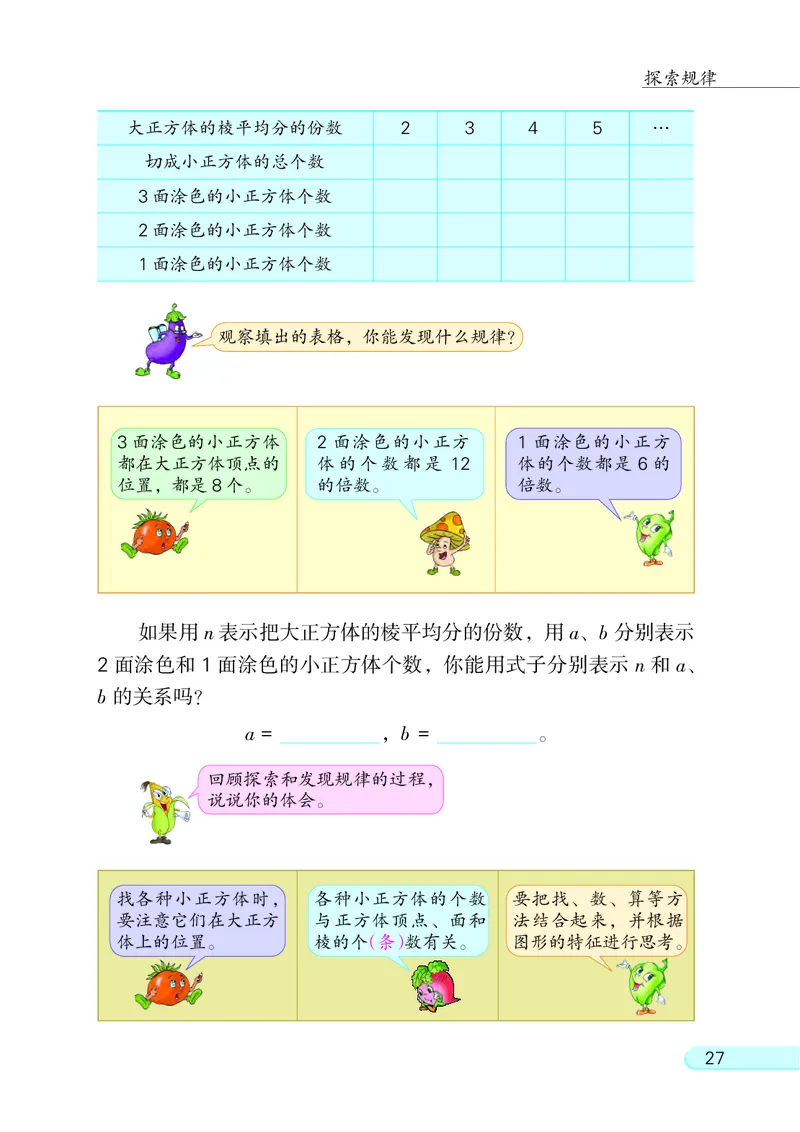
大正方体的棱平均分的份数 2 3 4 5 …
切成小正方体的总个数
3面涂色的小正方体个数
2面涂色的小正方体个数
1面涂色的小正方体个数
观察填出的表格, 你能发现什么规律?
3 面涂色的小正方体 2 面涂色的小正方 1 面涂色的小正方
都在大正方体顶点的 体的个数都是 12 体的个数都是 6 的
位置, 都是8个。 的倍数。 倍数。
如果用 n 表示把大正方体的棱平均分的份数, 用 a、 b 分别表示
2 面涂色和 1 面涂色的小正方体个数, 你能用式子分别表示 n 和 a、
b 的关系吗?
a = , b = 。
回顾探索和发现规律的过程,
说说你的体会。
找各种小正方体时, 各种小正方体的个数 要把找、 数、 算等方
要注意它们在大正方 与正方体顶点、 面和 法结合起来, 并根据
体上的位置。 棱的个(条)数有关。 图形的特征进行思考。
27分 数 乘 法
3
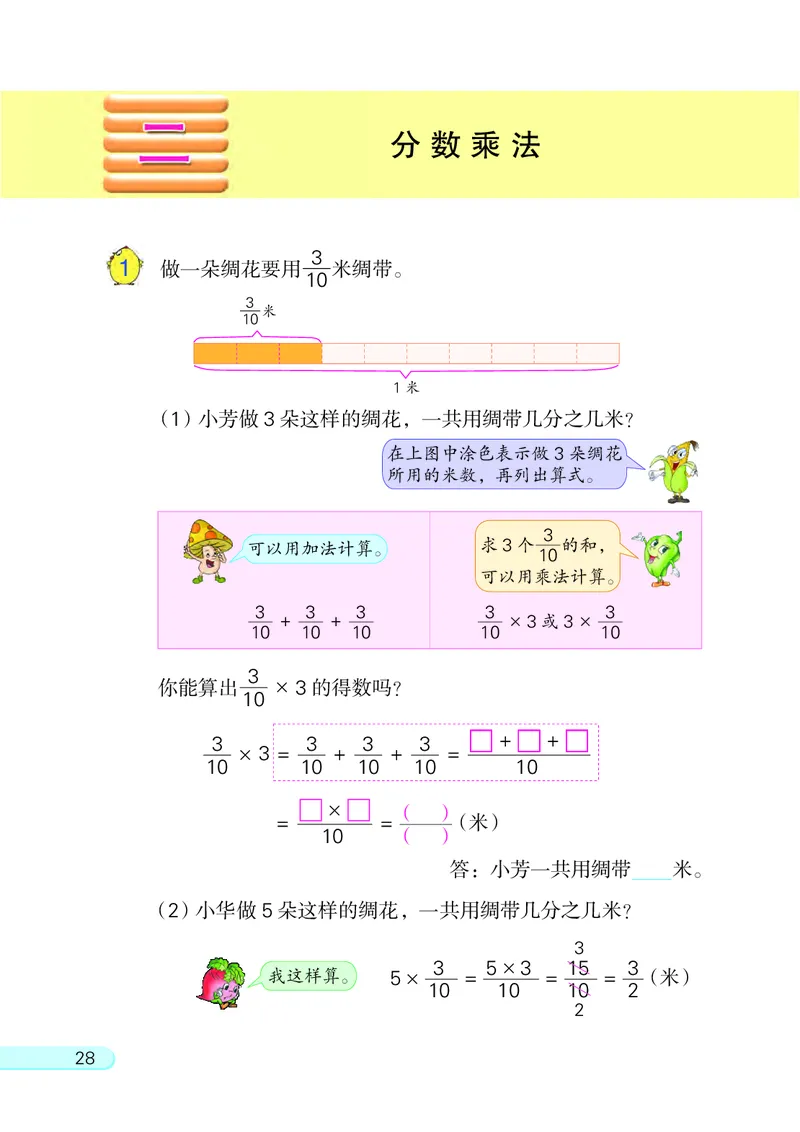
1 做一朵绸花要用 米绸带。
10
3
米
10
1米
(1)小芳做 3 朵这样的绸花, 一共用绸带几分之几米?
在上图中涂色表示做 3朵绸花
所用的米数, 再列出算式。
3
可以用加法计算。 求3个 的和,
10
可以用乘法计算。
3 3 3 3 3
+ + × 3或3 ×
10 10 10 10 10
3
你能算出 × 3 的得数吗?
10
3 3 3 3 �+ +
× 3 = + + =
10 10 10 10 10
�× ( )
= = (米)
10 ( )
答: 小芳一共用绸带 米。
(2)小华做 5 朵这样的绸花, 一共用绸带几分之几米?
3
3 5 × 3 15 3
我这样算。 5 × = = = (米)
10 10 10 2
2
28分数乘法
可以先约分, 再计算。
1
3 5 × 3 3
5 × = = (米)
10 10 2
2
答: 小华一共用绸带 米。
分数和整数相乘, 可以怎样计算?
练一练
3
1. 先在右边的长方形中涂出 4 个 , 再算出
16
涂色部分一共是这个长方形的几分之几。
2 5 7 5
2. × 3 4 × × 5 9 ×
7 6 10 12
1 2
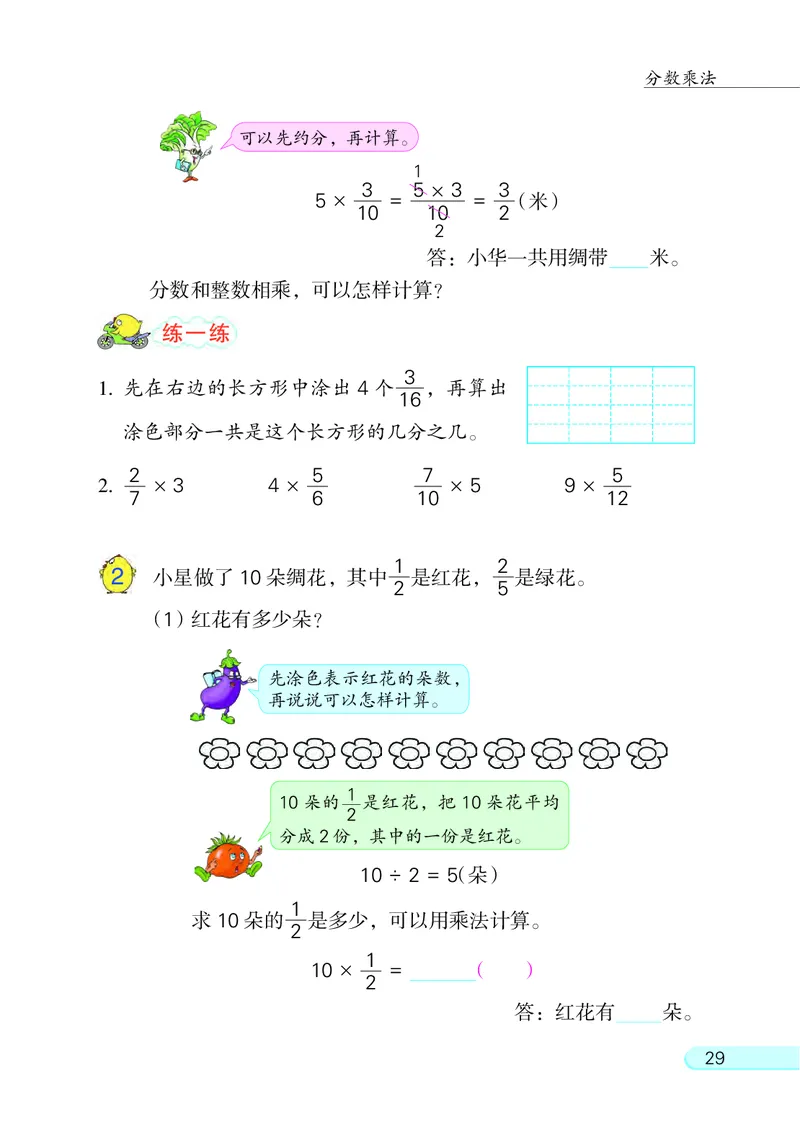
2 小星做了 10 朵绸花, 其中 是红花, 是绿花。
2 5
(1)红花有多少朵?
先涂色表示红花的朵数,
再说说可以怎样计算。
1
10 朵的 是红花, 把 10 朵花平均
2
分成 2份, 其中的一份是红花。
10 ÷ 2 = 5(朵)
1
求 10 朵的 是多少, 可以用乘法计算。
2
1
10 × = ( )
2
答: 红花有 朵。
29分数乘法
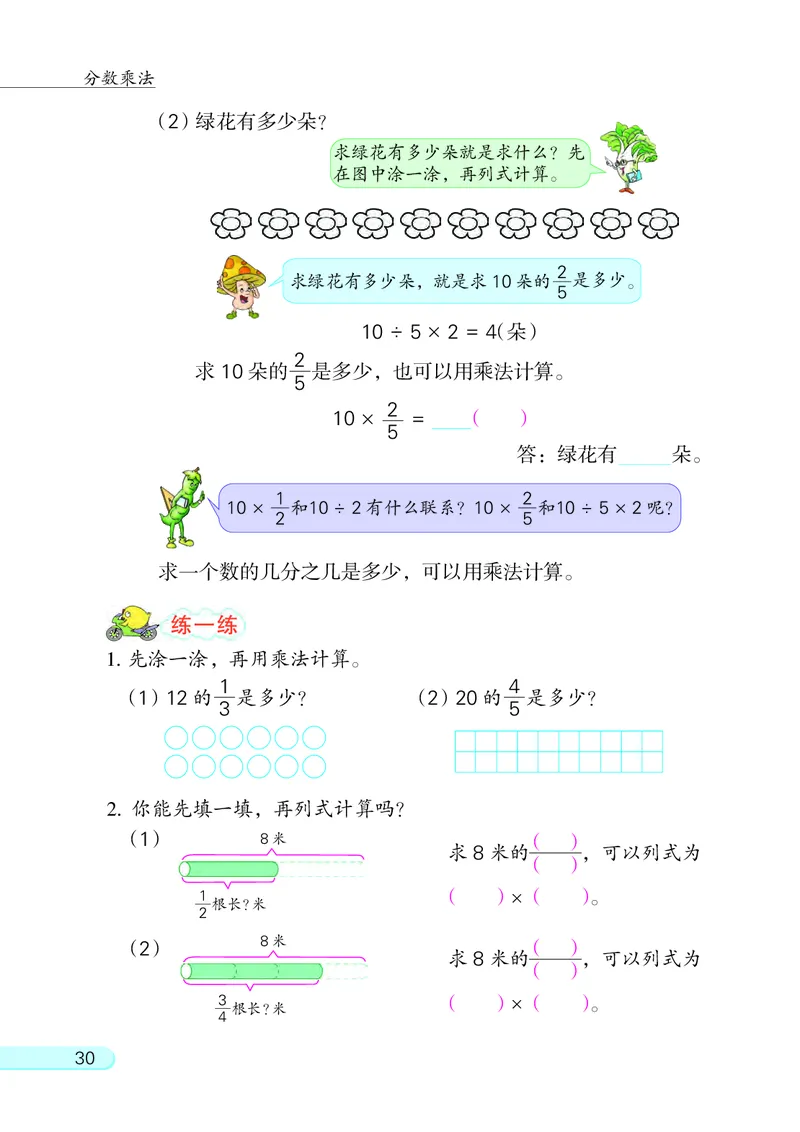
(2)绿花有多少朵?
求绿花有多少朵就是求什么? 先
在图中涂一涂, 再列式计算。
2
求绿花有多少朵, 就是求10朵的 是多少。
5
10 ÷ 5 × 2 = 4(朵)
2
求 10 朵的 是多少, 也可以用乘法计算。
5
2
10 × = ( )
5
答: 绿花有 朵。
1 2
10 × 和10 ÷ 2有什么联系? 10 × 和10 ÷ 5 × 2呢?
2 5
求一个数的几分之几是多少, 可以用乘法计算。
练一练
1. 先涂一涂, 再用乘法计算。
1 4
(1)12 的 是多少? (2)20 的 是多少?
3 5
2. 你能先填一填, 再列式计算吗?
(1) 8米 ( )
求 8 米的 , 可以列式为
( )
1 ( )×( )。
根长?米
2
8米
(2) ( )
求 8 米的 , 可以列式为
( )
3 ( )×( )。
根长?米
4
30分数乘法
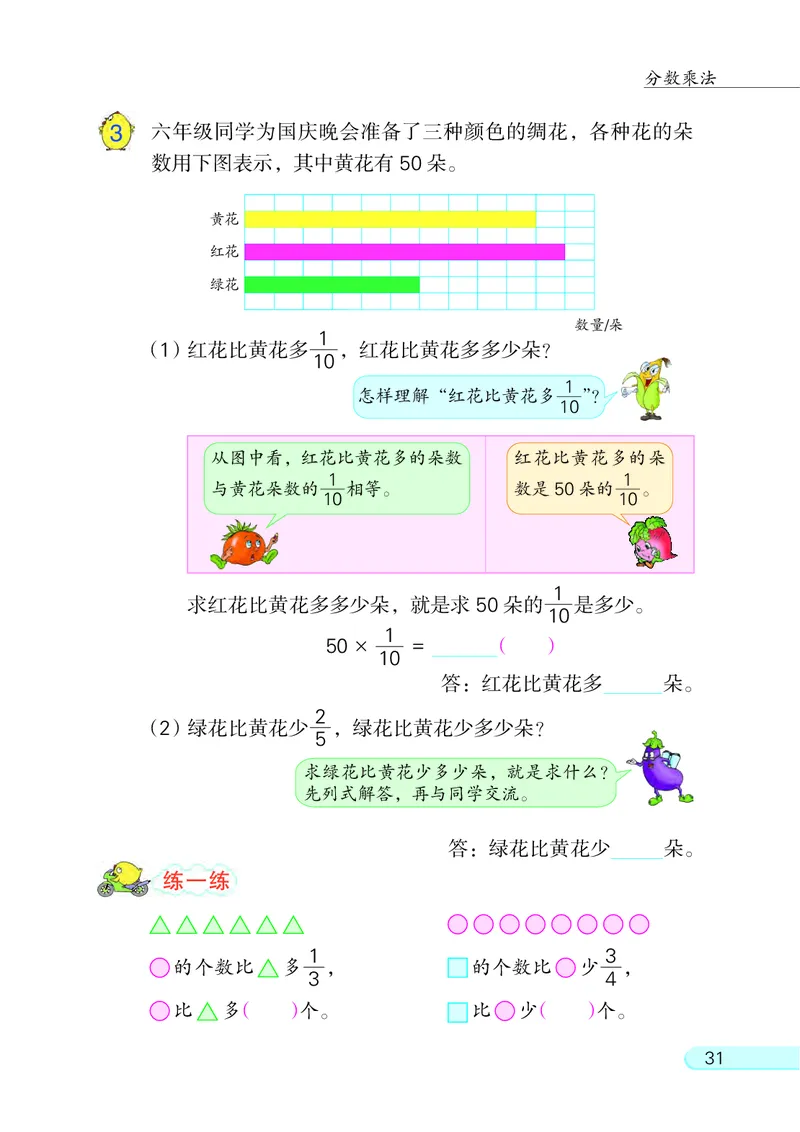
3 六年级同学为国庆晚会准备了三种颜色的绸花, 各种花的朵
数用下图表示, 其中黄花有 50 朵。
黄花
红花
绿花
数量/朵
1
(1)红花比黄花多 , 红花比黄花多多少朵?
10
1
怎样理解“红花比黄花多 ”?
10
从图中看, 红花比黄花多的朵数 红花比黄花多的朵
1 1
与黄花朵数的 相等。 数是50朵的 。
10 10
1
求红花比黄花多多少朵, 就是求 50 朵的 是多少。
10
1
50 × = ( )
10
答: 红花比黄花多 朵。
2
(2)绿花比黄花少 , 绿花比黄花少多少朵?
5
求绿花比黄花少多少朵, 就是求什么?
先列式解答, 再与同学交流。
答: 绿花比黄花少 朵。
练一练
1 3
的个数比 多 , 的个数比 少 ,
3 4
比 多( )个。 比 少( )个。
31分数乘法
练 习 五
1. 看图计算并填空。
3 3 3 ( )
× 2 可以表示( )个 。
7 7
7 ( )
3
× 2 =( )
7
?
4 1 2 5
2. × 3 × 6 × 9 6 ×
5 7 27 12
7 2 3 3
2 × 7 × × 8 × 15
10 3 40 5
3. 1
幼儿园有 36 个小朋友, 每个小朋友吃 块月饼,
2
一共吃多少块月饼?
4
4. 一个正方体的底面积是 平方米, 它的表面积是多少平方米?
9
1
5. 小力步行的速度是 千米/分, 15分钟步行多少千米? 1小时呢?
12
6. 每瓶饮料的净含量是 900 毫升。
(1)3 瓶有多少毫升?
1 3
(2) 瓶有多少毫升? 瓶有多少毫升?
3 5
1
(3)小明喝了这瓶饮料的 , 喝了多少毫升?
4
2 5
7. 150 厘米的 是多少厘米? 400 千克的 是多少千克?
3 8
1 2
8. 学校花坛里有 84 棵花, 其中 是月季, 是杜鹃。 这两种花各
6 3
有多少棵?
32分数乘法
9. 星河小学举行运动会, 参加长跑的有 24 人, 短跑的人数是长跑
5 9
的 1.5 倍, 跳高的人数是长跑的 , 跳远的人数是长跑的 。
6 8
先估计参加哪一项比赛的人数最多, 参加哪一项比赛的人数最
少, 再算出参加短跑、 跳高和跳远的各有多少人。
10. 先说说各个分数的意义, 再把数量关系式补充完整。
2
(1)皮球的个数比足球多 。
5
2
( )的个数 × =( )的个数
5
1
(2)实际用水量比原计划节约 。
9
1
( )的用水量 × =( )的用水量
9
2
11. 小军有 28 颗玻璃球, 小力的玻璃球比小军多 。 小力的玻璃球
7
比小军多多少颗?
12. 新湖乡去年种植黄豆 24 公顷, 今年黄豆的种植面积比去年增加
3
了 。 今年黄豆的种植面积比去年增加多少公顷?
8
13. 一种毛衣的原价是 56 元, 现在的售价比原来降低
2
。 现在的售价比原来降低多少元?
7
14. 东港小学买了 24 个排球。
1
(1)买的足球比排球多 , 买的足球比排球多多少个?
4
5
(2)买的足球是排球的 , 买了多少个足球?
4
2
15. 吴大伯家去年收白果 520 千克, 收的核桃比白果多 。 收的核
5
桃比白果多多少千克? 收核桃多少千克?
33分数乘法
1 1
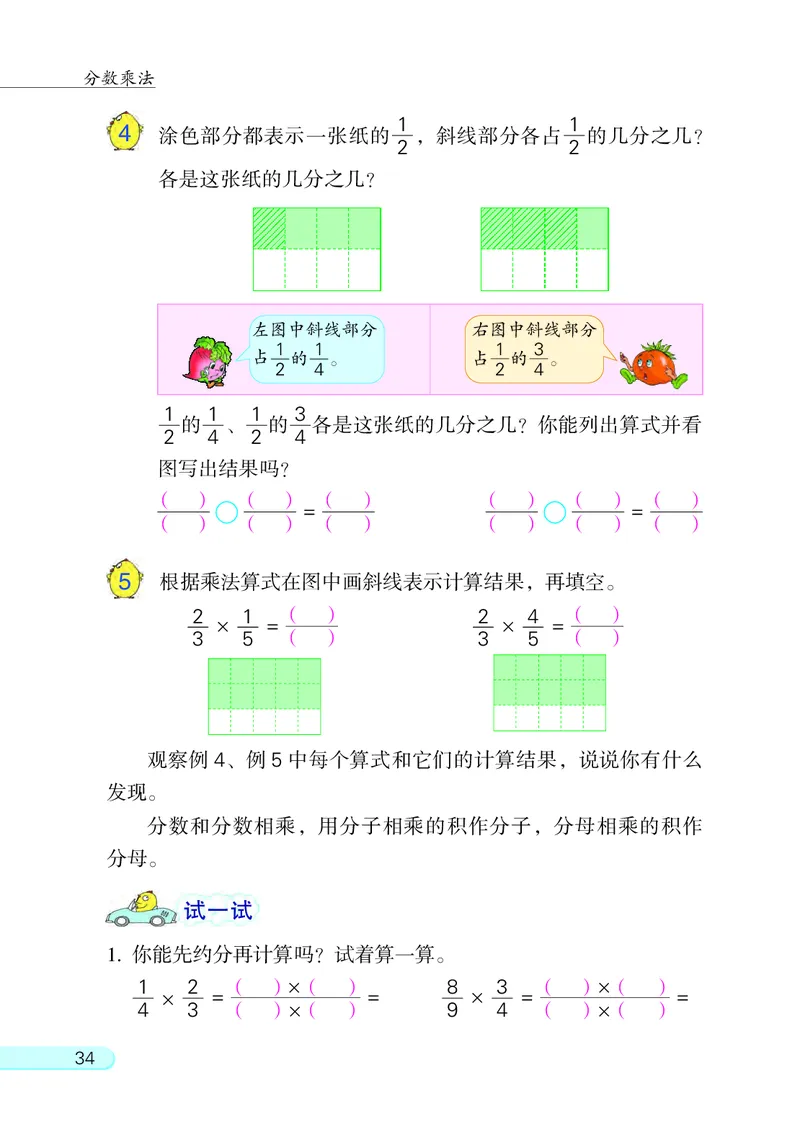
4 涂色部分都表示一张纸的 , 斜线部分各占 的几分之几?
2 2
各是这张纸的几分之几?
左图中斜线部分 右图中斜线部分
1 1 1 3
占 的 。 占 的 。
2 4 2 4
1 1 1 3
的 、 的 各是这张纸的几分之几? 你能列出算式并看
2 4 2 4
图写出结果吗?
( ) ( ) ( ) ( ) ( ) ( )
= �� � � �=
( ) ( ) ( ) ( ) ( ) ( )
5 根据乘法算式在图中画斜线表示计算结果, 再填空。
2 1 ( ) 2 4 ( )
× = × =
3 5 ( ) 3 5 ( )
观察例 4、 例 5 中每个算式和它们的计算结果, 说说你有什么
发现。
分数和分数相乘, 用分子相乘的积作分子, 分母相乘的积作
分母。
试一试
1. 你能先约分再计算吗? 试着算一算。
1 2 ( )×( ) 8 3 ( )×( )
× = = × = =
4 3 ( )×( ) 9 4 ( )×( )
34分数乘法
2. 你能用分数和分数相乘的方法计算下面各题吗?
2 ( )×( ) 5 ( )×( )
× 3 = = 4 × = =
11 ( )×( ) 6 ( )×( )
分数与分数相乘的方法适用于
分数与整数相乘吗? 为什么?
练一练
1 1 3 2
× = × =
3 4 4 5
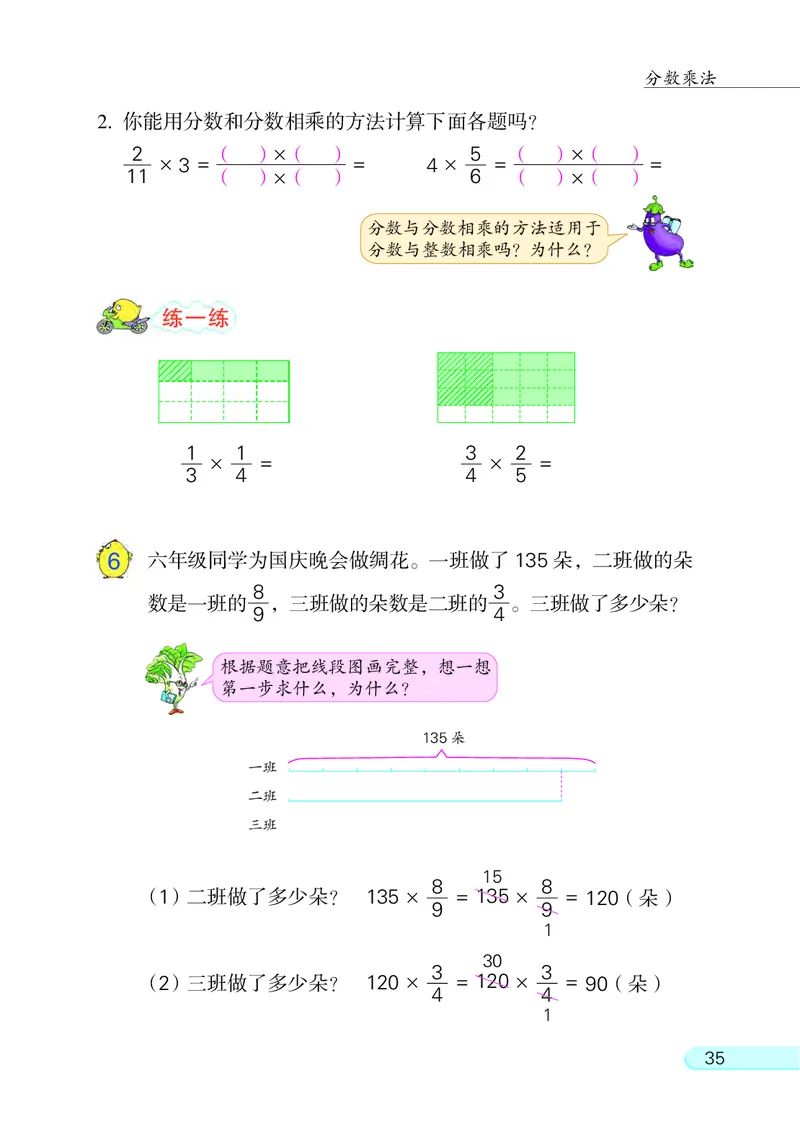
6 六年级同学为国庆晚会做绸花。 一班做了 135 朵, 二班做的朵
8 3
数是一班的 , 三班做的朵数是二班的 。 三班做了多少朵?
9 4
根据题意把线段图画完整, 想一想
第一步求什么, 为什么?
135朵
一班
二班
三班
15
8 8
(1)二班做了多少朵? 135 × = 135 × = 120(朵)
9 9
1
30
3 3
(2)三班做了多少朵? 120 × = 120 × = 90(朵)
4 4
1
35分数乘法
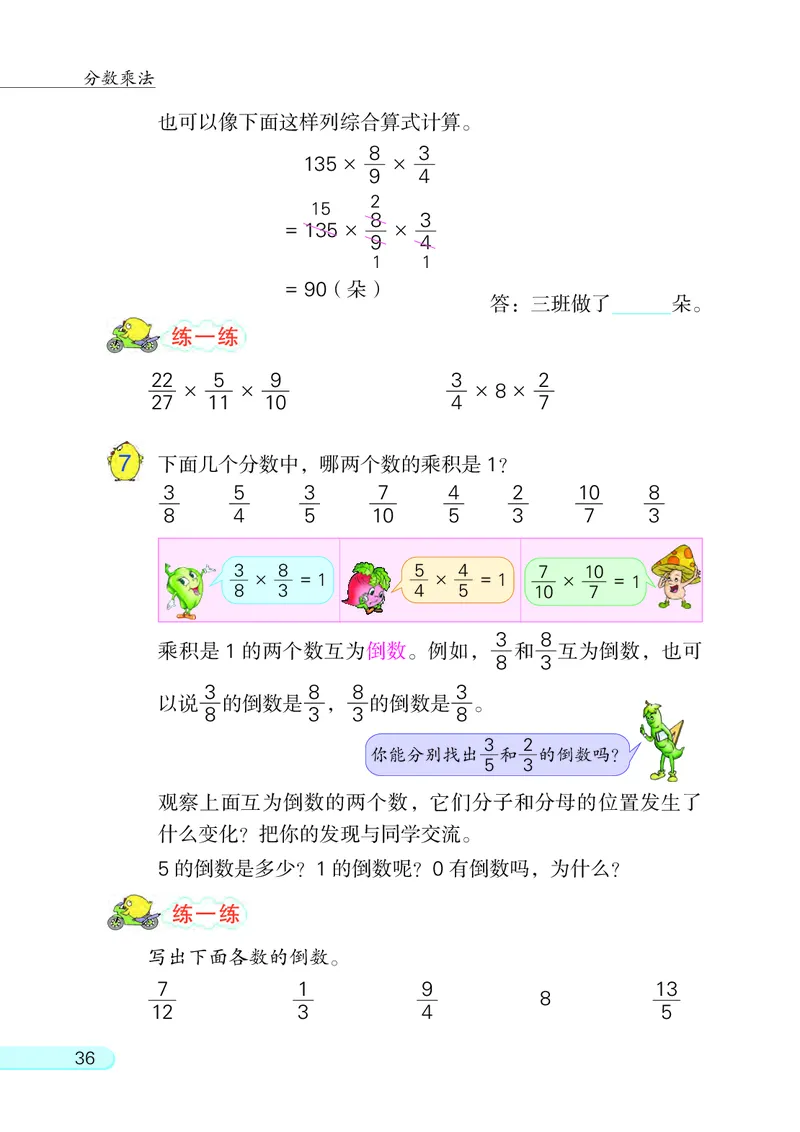
也可以像下面这样列综合算式计算。
8 3
135 × ×
9 4
2
15
8 3
= 135 × ×
9 4
1 1
= 90(朵)
答: 三班做了 朵。
练一练
22 5 9 3 2
× × × 8 ×
27 11 10 4 7
7 下面几个分数中, 哪两个数的乘积是 1?
3 5 3 7 4 2 10 8
8 4 5 10 5 3 7 3
3 8 5 4 7 10
× = 1 × = 1 × = 1
8 3 4 5 10 7
3 8
乘积是 1 的两个数互为倒数。 例如, 和 互为倒数, 也可
8 3
3 8 8 3
以说 的倒数是 , 的倒数是 。
8 3 3 8
3 2
你能分别找出 和 的倒数吗?
5 3
观察上面互为倒数的两个数, 它们分子和分母的位置发生了
什么变化? 把你的发现与同学交流。
5 的倒数是多少? 1 的倒数呢? 0 有倒数吗, 为什么?
练一练
写出下面各数的倒数。
7 1 9 13
8
12 3 4 5
36练 习 六
1 1
公顷 公顷
2 2
3 2 1 4 3 5 4 5
2. × × × ×
5 7 4 5 10 9 7 6
5 9 1 15 21 3
× × 4 × 16 ×
6 20 10 7 20 5
1 4
5. 一辆汽车行驶 1 千米耗油 升。 照这样计算, 行驶 千米耗油
12 5
多少升? 行驶 50 千米呢?
3 4 7 2 3 4 4 5
6. × × × 6 × × ×
10 7 9 3 8 5 7 12
16 3 5 2 7 1 5
× × 4 × × 3 × ×
9 4 9 7 10 5 7
{ {
分数乘法
1 1 2
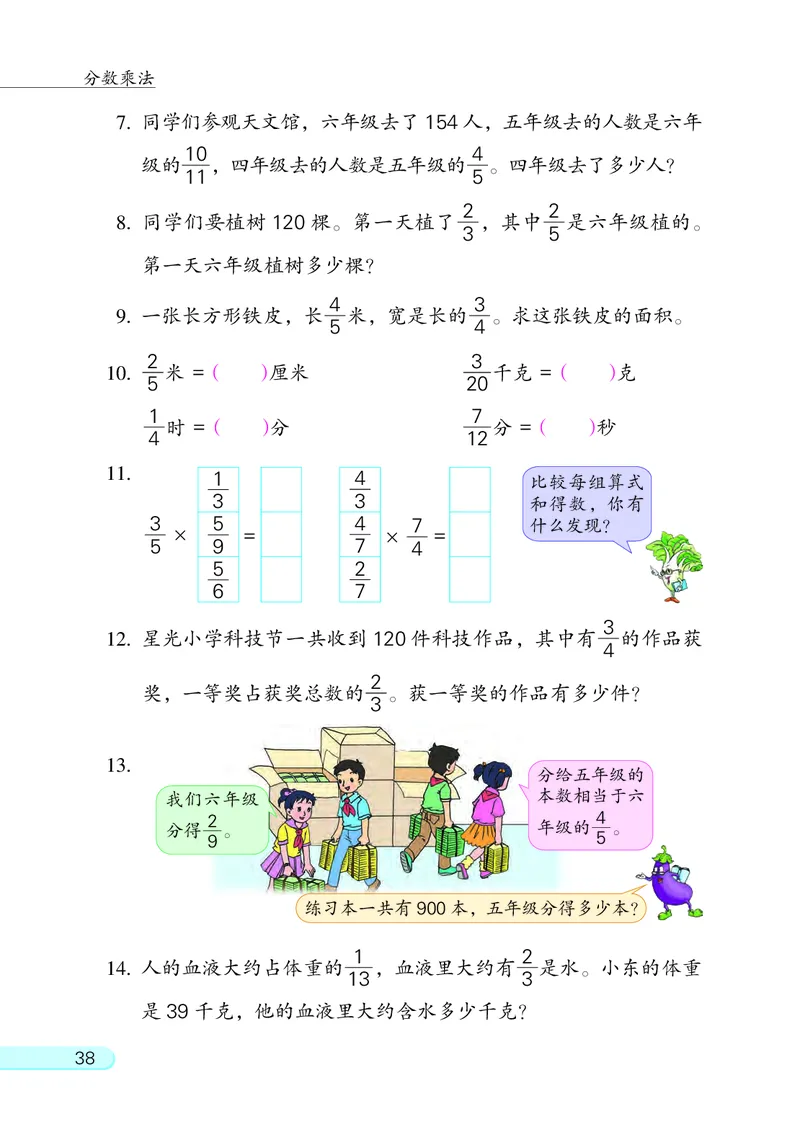
1. 一台拖拉机每小时耕地 公顷, 小时耕地多少公顷? 小时
2 3 3
呢? 先在图中表示出来, 再列式计算。
3.
下面的计算对吗? 把不对的改正。
1 1 1
1
5 5 1 8 7 8 7
(1)5 × = 5 × = (2) × = × = 9
6 6 6 21 24 21 24
3 3
4. 2 4 1 1 3 3
× 2 5 × × ×
7 5 2 2 4 4
2 4 1 1 3 3
× 7 4 × + +
7 5 2 2 4 4
37分数乘法
7. 同学们参观天文馆, 六年级去了 154 人, 五年级去的人数是六年
10 4
级的 , 四年级去的人数是五年级的 。 四年级去了多少人?
11 5
2 2
8. 同学们要植树 120 棵。 第一天植了 , 其中 是六年级植的。
3 5
第一天六年级植树多少棵?
4 3
9. 一张长方形铁皮, 长 米, 宽是长的 。 求这张铁皮的面积。
5 4
2 3
10. 米 =( )厘米 千克 =( )克
5 20
1 7
时 =( )分 分 =( )秒
4 12
11.
1 4
比较每组算式
3 3 和得数, 你有
3 5 4 7 什么发现?
× = × =
5 9 7 4
5 2
6 7
3
12. 星光小学科技节一共收到 120 件科技作品, 其中有 的作品获
4
2
奖, 一等奖占获奖总数的 。 获一等奖的作品有多少件?
3
13.
分给五年级的
我们六年级 本数相当于六
2 4
分得 。 年级的 。
9 5
练习本一共有 900本, 五年级分得多少本?
1 2
14. 人的血液大约占体重的 , 血液里大约有 是水。 小东的体重
13 3
是 39 千克, 他的血液里大约含水多少千克?
38分数乘法
4 1 1
15. 一个长方体的金鱼缸, 从里面量, 长 米, 宽 米, 高 米。
5 4 2
3
鱼缸里水深 米。 鱼缸里有水多少立方米?
10
3 ( ) ( ) 1 ( )
16. × =1 7× =1 × =1
4 ( ) ( ) 9 ( )
17. 说出下面哪两个数互为倒数。
1 1 3 11 7 6
4 6
4 6 7 6 3 11
1 1
18.(1) 的倒数是( ), 的倒数是( )。
8 11
9
(2) 9 的倒数是( ), 的倒数是( )。
2
7
(3) 的倒数是( ), 1 的倒数是( )。
4
19. 先找出每组中各数的倒数, 再看看能发现什么。
3 2 7 7 9 13
(1) (2)
4 5 9 2 5 6
1 1 1
(3) (4)3 9 15
2 10 12
3
20. 一个正方体的棱长是 米, 求这个正方体的表面积和体积。
10
3 2
21.(1)食堂有煤 吨, 用去一部分后还剩 。 还剩多少吨?
4 5
3 2
(2)食堂有煤 吨, 用去 吨, 还剩多少吨?
4 5
3 5 5 5 9 16 21
把 、 、 、 、 、 、 这
4 6 7 4 8 15 16
七个数填入右边的 里, 使每条线上 3
个数的乘积都是 1。
39分数乘法
整理与练习
回顾与整理
小组讨论:
1. 怎样计算分数乘法?
2. 怎样的两个数互为倒数? 怎样求一个数的倒数?
3. 举例说说你能用分数乘法解决哪些实际问题。
练习与应用
1. 先涂色, 再计算。
2 3 2
× 2 = × =
9 4 3
2. 直接写出得数。
4 3 5 7 3 5
× = ��3 × = ��� × 1 = × =
9 4 6 9 14 7
1 4 5 2 3
× 8 = �� × = ���0 × = 16 × =
12 5 8 13 5
4 9 2 8 11 9
3. × ���21 × ����� × 26 �� ×
15 8 35 13 36 22
4 21 2 3 2
× × × 15 ×
7 10 5 5 9
3 3
4. 吨 =( )千克 平方米 =( )平方分米
10 4
2 5
时 =( )分 分 =( )秒
5 12
1
5. 小军家有 5 口人, 早上每人喝一瓶 升的牛奶, 一共喝了多少
4
6
升? 每升牛奶大约含钙 克, 一瓶牛奶大约含钙多少克?
5
40分数乘法
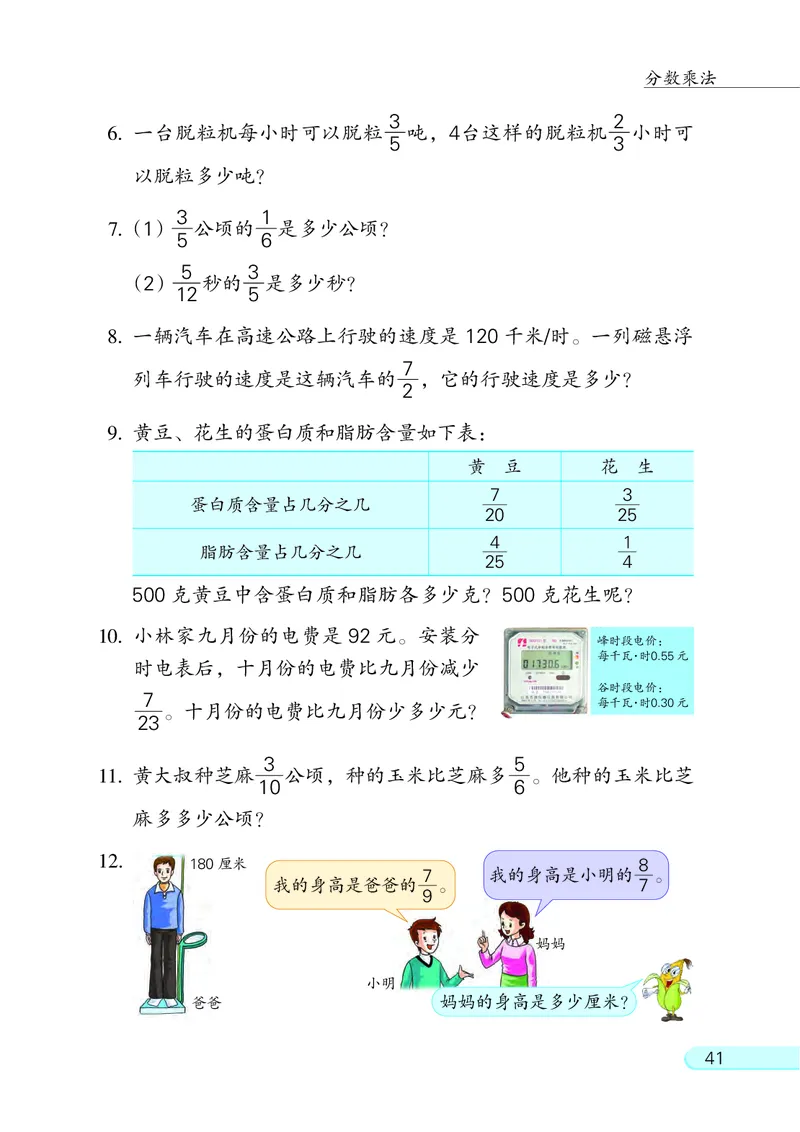
3 2
6. 一台脱粒机每小时可以脱粒 吨, 4台这样的脱粒机 小时可
5 3
以脱粒多少吨?
3 1
7.(1) 公顷的 是多少公顷?
5 6
5 3
(2) 秒的 是多少秒?
12 5
8. 一辆汽车在高速公路上行驶的速度是 120 千米/时。 一列磁悬浮
7
列车行驶的速度是这辆汽车的 , 它的行驶速度是多少?
2
9. 黄豆、 花生的蛋白质和脂肪含量如下表:
黄 豆 花 生
7 3
蛋白质含量占几分之几
20 25
4 1
脂肪含量占几分之几
25 4
500 克黄豆中含蛋白质和脂肪各多少克? 500 克花生呢?
10. 小林家九月份的电费是 92 元。 安装分
峰时段电价:
每千瓦·时0.55元
时电表后, 十月份的电费比九月份减少
谷时段电价:
7
每千瓦·时0.30元
。 十月份的电费比九月份少多少元?
23
3 5
11. 黄大叔种芝麻 公顷, 种的玉米比芝麻多 。 他种的玉米比芝
10 6
麻多多少公顷?
12.
180厘米 8
7 我的身高是小明的 。
我的身高是爸爸的 。 7
9
妈妈
小明
爸爸 妈妈的身高是多少厘米?
41分数乘法
13. 六年级一班举行 1 分钟跳绳比赛, 小芳跳了 126 下, 小华比小
2
芳多跳 。 小华比小芳多跳多少下? 小华跳了多少下?
9
探索与实践
14. 先找规律, 再填数。
4 2 1 1
(1) , , ,( ), ,( ),( )。
5 5 5 20
2 3 9
(2) , 1, , ,( ),( )。
3 2 4
2 4
15. 先把图中方格的 涂绿色, 涂黄色,
9 9
3
再把黄色方格的 画上斜线。
5
(1)绿色方格有多少个? 你是怎样计算的?
(2)你还能提出哪些用乘法计算的问题?
先计算, 再观察每组算式的得数, 能发现什么规律?
1 1 ( ) 1 1 ( )
(1) - = × =
2 3 ( ) 2 3 ( )
1 1 ( ) 1 1 ( )
(2) - = × =
4 5 ( ) 4 5 ( )
你能根据发现的规律再写几组这样的算式吗?
评价与反思
在学习分数乘法时, 能积极探索和归纳计算方法,
☆☆☆☆☆
正确进行计算
在解决有关分数乘法的实际问题时, 能主动思考,
☆☆☆☆☆
动手操作, 正确分析数量之间的关系, 有条理地
表述解决问题的过程
42分 数 除 法
4
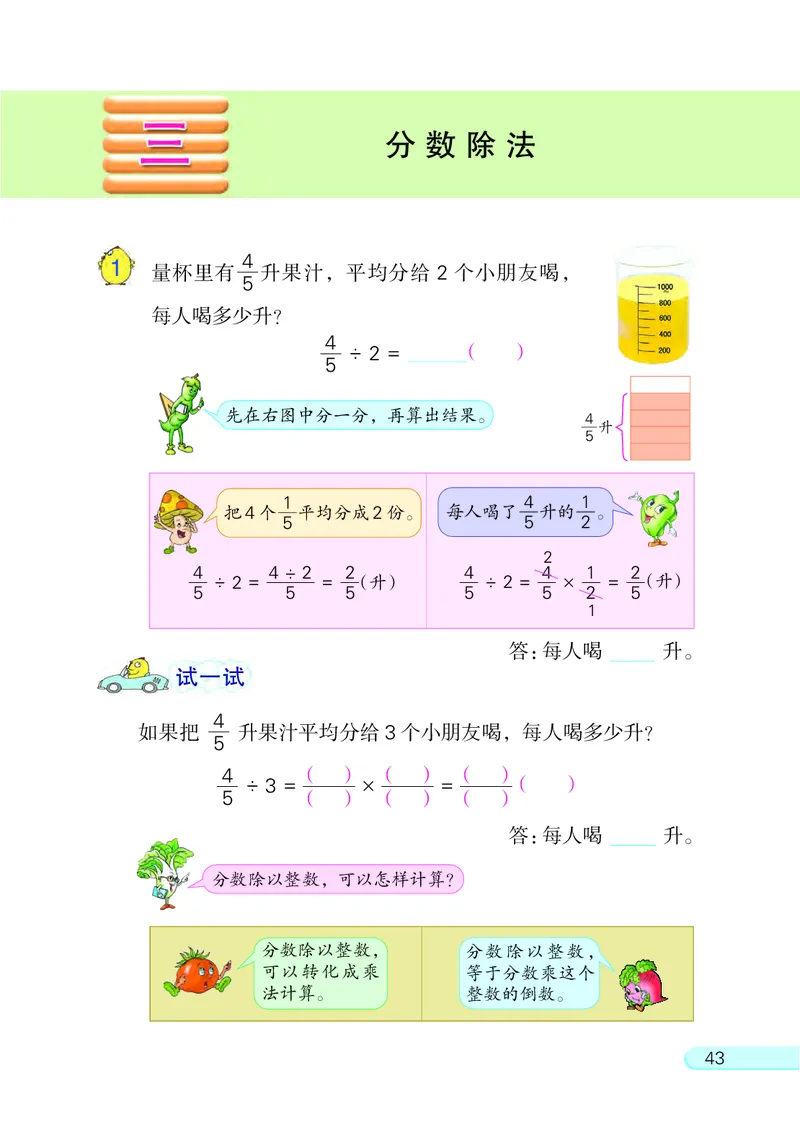
1
量杯里有 升果汁, 平均分给 2 个小朋友喝,
5
每人喝多少升?
4
÷ 2 = ( )
5
先在右图中分一分, 再算出结果。
4
升
5
1 4 1
把4个 平均分成2份。 每人喝了 升的 。
5 5 2
2
4 4 ÷ 2 2 4 4 1 2
÷ 2 = = (升) ÷ 2 = × = (升)
5 5 5 5 5 2 5
1
答:每人喝 升。
试一试
4
如果把 升果汁平均分给 3 个小朋友喝, 每人喝多少升?
5
4 ( ) ( ) ( )
÷ 3 = × = ( )
5 ( ) ( ) ( )
答:每人喝 升。
分数除以整数, 可以怎样计算?
分数除以整数, 分数除以整数,
可以转化成乘 等于分数乘这个
法计算。 整数的倒数。
43分数除法
练一练
6
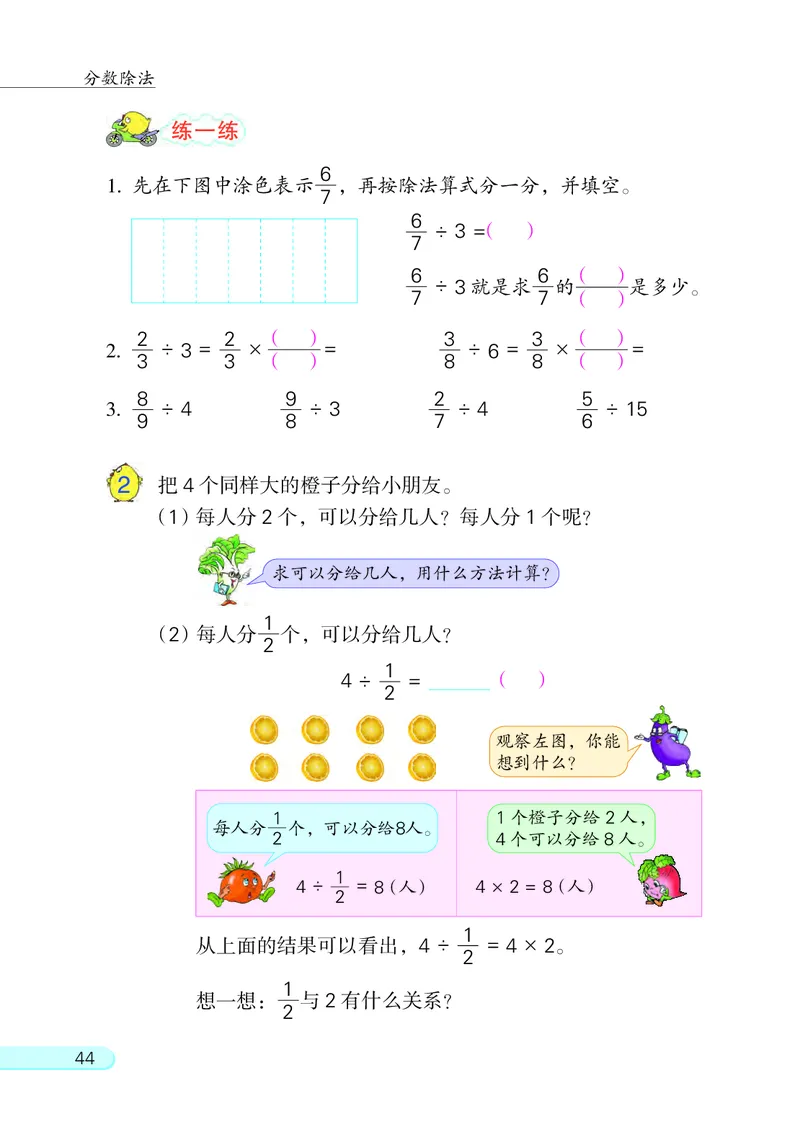
1. 先在下图中涂色表示 , 再按除法算式分一分, 并填空。
7
6
÷ 3 =( )
7
6 6 ( )
÷ 3 就是求 的 是多少。
7 7 ( )
2 2 ( ) 3 3 ( )
2. ÷ 3 = × = ÷ 6 = × =
3 3 ( ) 8 8 ( )
8 9 2 5
3. ÷ 4 ÷ 3 ÷ 4 ÷ 15
9 8 7 6
2 把 4 个同样大的橙子分给小朋友。
(1)每人分 2 个, 可以分给几人? 每人分 1 个呢?
求可以分给几人, 用什么方法计算?
1
(2)每人分 个, 可以分给几人?
2
1
4 ÷ = ( )
2
观察左图, 你能
想到什么?
1 1个橙子分给 2 人,
每人分 个, 可以分给8人。
2 4个可以分给 8人。
1
4 ÷ = 8(人) 4 × 2 = 8(人)
2
1
从上面的结果可以看出, 4 ÷ = 4 × 2。
2
1
想一想: 与 2 有什么关系?
2
44分数除法
1 1
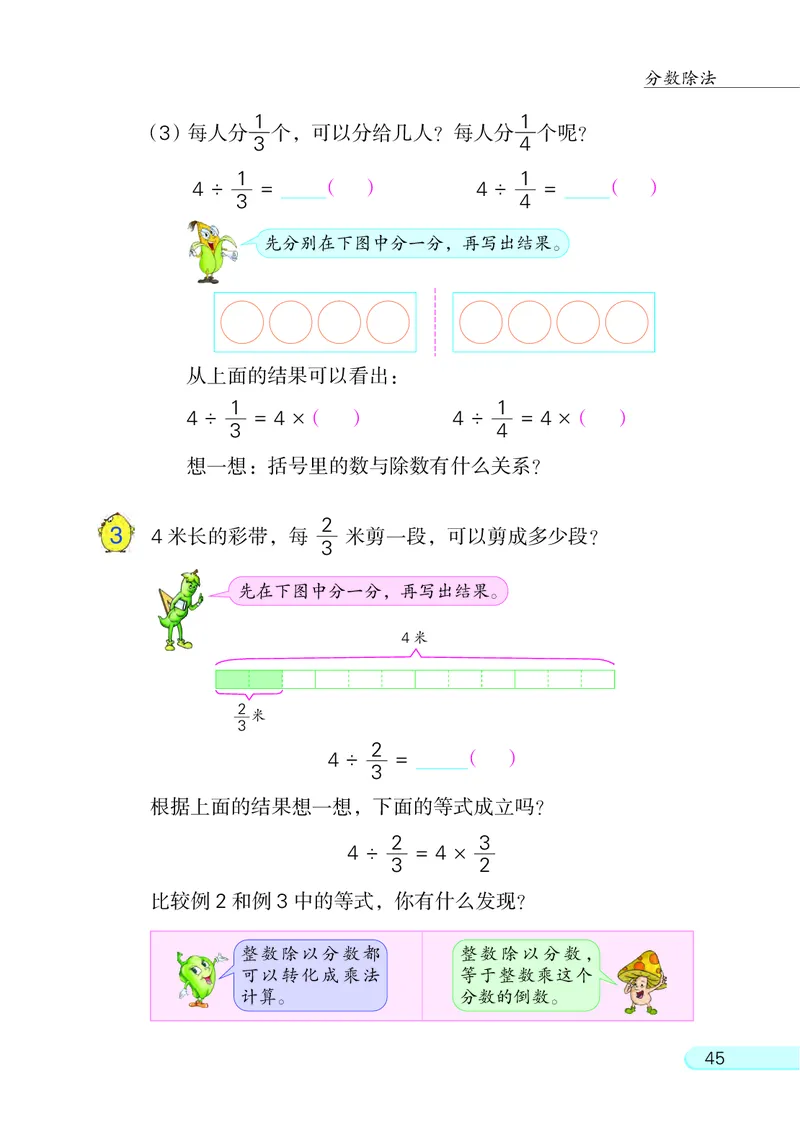
(3)每人分 个, 可以分给几人? 每人分 个呢?
3 4
1 1
4 ÷ = ( ) 4 ÷ = ( )
3 4
先分别在下图中分一分, 再写出结果。
从上面的结果可以看出:
1 1
4 ÷ = 4 ×( ) 4 ÷ = 4 ×( )
3 4
想一想: 括号里的数与除数有什么关系?
2
3 4 米长的彩带, 每 米剪一段, 可以剪成多少段?
3
先在下图中分一分, 再写出结果。
4米
2
米
3
2
4 ÷ = ( )
3
根据上面的结果想一想, 下面的等式成立吗?
2 3
4 ÷ = 4 ×
3 2
比较例 2 和例 3 中的等式, 你有什么发现?
整数除以分数都 整数除以分数,
可以转化成乘法 等于整数乘这个
计算。 分数的倒数。
45分数除法
练一练
2 ( ) 6 ( )
1. 12 ÷ = 12 × = 9 ÷ = 9 × =
3 ( ) 7 ( )
2 2 6 8
2. 10 ÷ 8 ÷ 3 ÷ 12 ÷
5 3 7 7
9 3
4 量杯里有 升果汁, 玻璃杯的容量是 升。 量杯里的果汁
10 10
倒入玻璃杯, 能倒满几杯?
9 3
÷ = ?
10 10
分数除以分数, 也可以用被除数乘除数的倒数来计算吗? 先
试着算一算, 再在图中分一分, 看结果是否相同。
9 3 9 ( )
÷ = × = ( )
9 升 10 10 10 ( )
10
答: 能倒满 杯。
联系前面学习的分数除以整数、 整数除以分数的计算, 你能说
一说怎样计算分数除法吗?
甲数除以乙数(0 除外), 等于甲数乘乙数的倒数。
练一练
3 3
先在右图中涂色表示 , 看看 里有几个
5 5
1 3
, 有几个 , 再计算。
5 10
3 1 3 ( ) 3 3 3 ( )
÷ = × = ÷ = × =
5 5 5 ( ) 5 10 5 ( )
46分数除法
练 习 七
9 4 6 3
1. ÷ 3 ÷ 4 ÷ 9 ÷ 1
10 7 13 10
1 5 3 12
÷ 3 ÷ 5 ÷ 6 ÷ 8
3 8 5 13
2. 1 3 1 5
÷ 2 � ÷ 12 �� × 3 � × 2
4 4 5 12
1 3 3 5
× 2 � × 12 �� ÷ 3 � ÷ 2
4 4 5 6
3
3. 6 个苹果重 千克, 平均每个苹果重多少千克?
5
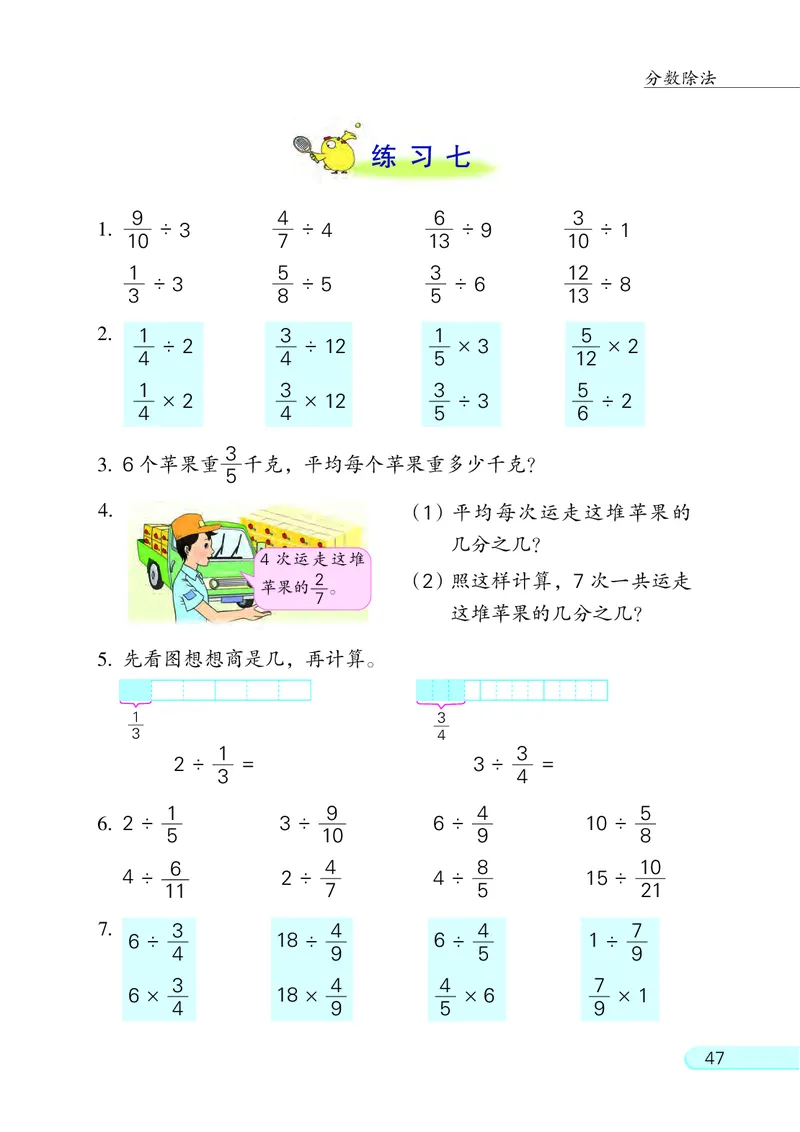
4. (1) 平均每次运走这堆苹果的
几分之几?
4 次运走这堆
2 (2)照这样计算, 7 次一共运走
苹果的 。
7
这堆苹果的几分之几?
5. 先看图想想商是几, 再计算。
1 3
3 4
1 3
2 ÷ = 3 ÷ =
3 4
1 9 4 5
6. 2 ÷ 3 ÷ 6 ÷ 10 ÷
5 10 9 8
6 4 8 10
4 ÷ 2 ÷ 4 ÷ 15 ÷
11 7 5 �21
7. 3 4 4 7
6 ÷ 18 ÷ 6 ÷ 1 ÷
4 9 5 9
3 4 4 7
6 × 18 × × 6 × 1
4 9 5 9
47分数除法
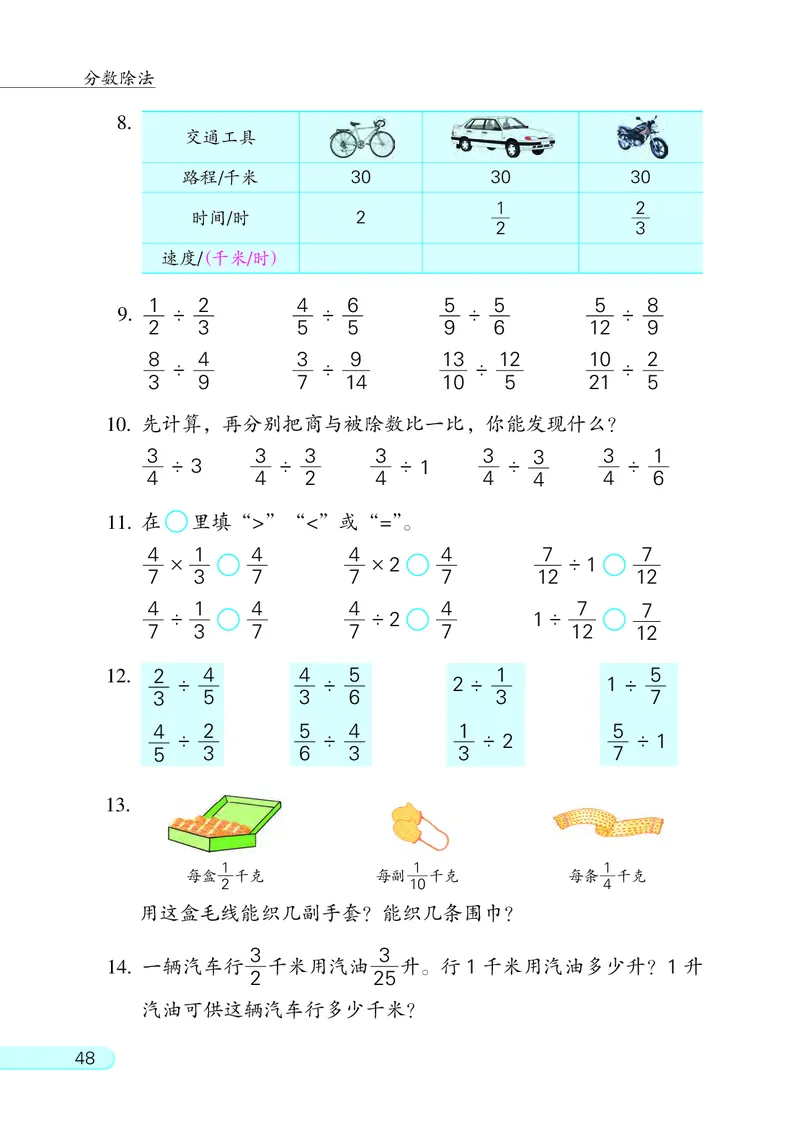
8.
交通工具
路程/千米 30 30 30
1 2
时间/时 2
2 3
速度/(千米/时)
1 2 4 6 5 5 5 8
9. ÷ ÷ ÷ ÷
2 3 5 5 9 6 12 9
8 4 3 9 13 12 10 2
÷ ÷ ÷ ÷
3 9 7 14 10 5 21 5
10. 先计算, 再分别把商与被除数比一比, 你能发现什么?
3 3 3 3 3 3 3 1
÷ 3 ÷ ÷ 1 ÷ ÷
4 4 2 4 4 4 4 6
11. 在 里填“>” “<” 或“=”。
4 1 4 4 4 7 7
× × 2 ÷ 1
7 3 7 7 7 12 12
4 1 4 4 4 7 7
÷ ÷ 2 1 ÷
7 3 7 7 7 12 12
12. 2 4 4 5 1 5
÷ ÷ 2 ÷ 1 ÷
3 5 3 6 3 7
4 2 5 4 1 5
÷ ÷ ÷ 2 ÷ 1
5 3 6 3 3 7
13.
1 1 1
每盒 千克 每副 千克 每条 千克
2 10 4
用这盒毛线能织几副手套? 能织几条围巾?
3 3
14. 一辆汽车行 千米用汽油 升。 行 1 千米用汽油多少升? 1 升
2 25
汽油可供这辆汽车行多少千米?
48分数除法
5
660000mmLL ?? mmLL
2
小瓶的果汁是大瓶的 。 一大瓶果汁有多少毫升?
3
大瓶和小瓶的果汁量有什么关系?
2
大瓶的果汁量 × = 小瓶的果汁量
3
解: 设一大瓶果汁有 x 毫升。
2
x = 600
3
2 3 3
x × = 600 ×
3 2 2
x =
答: 一大瓶果汁有 毫升。
试一试
1 2
李刚早上喝了一盒牛奶的 , 正好是 升。 这盒牛奶有多少
2 5
升?(先把数量关系式补充完整,再解答)
1
( )× =( )
2
练一练
5
1. 一种裤子的单价是 45 元/条, 是上衣单价的 。 求上衣的单价。
8
3
2. 西林果园有桃树 360 棵, 占果树总棵数的 。 西林果园有果树
5
多少棵?
49分数除法
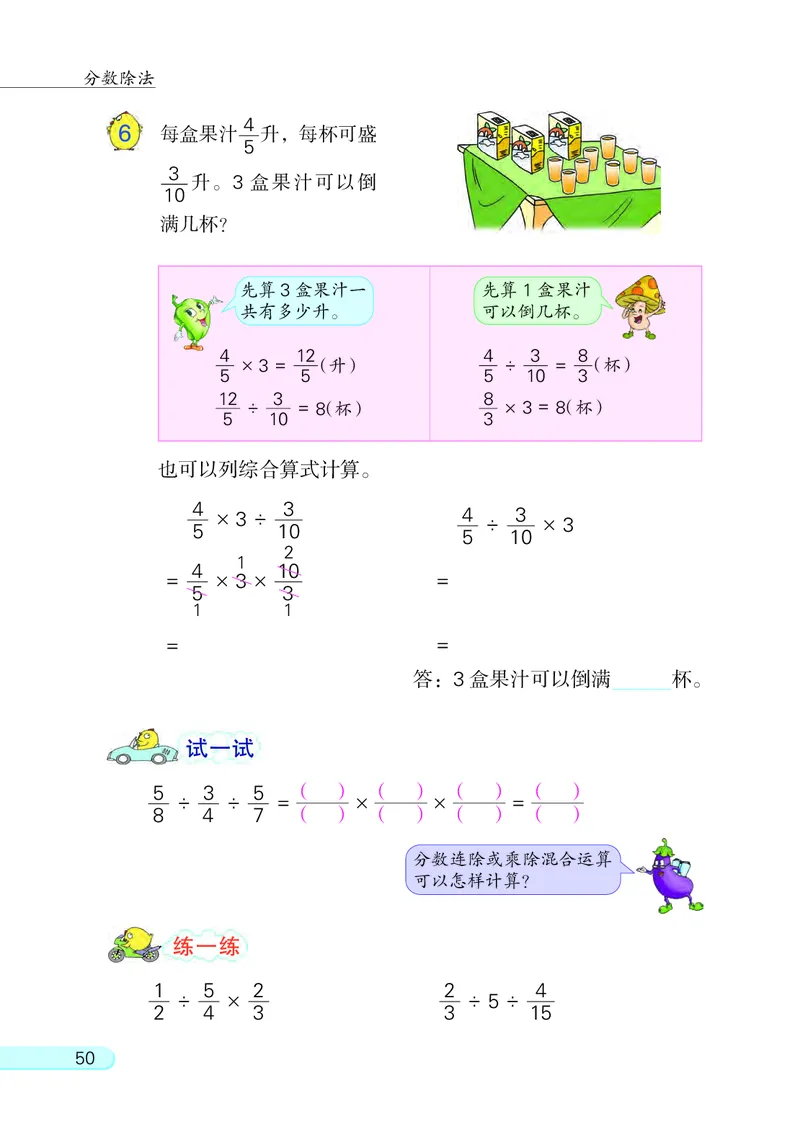
4
6 每盒果汁 升, 每杯可盛
5
3
升。 3 盒果汁可以倒
10
满几杯?
先算 3盒果汁一 先算 1 盒果汁
共有多少升。 可以倒几杯。
4 12 4 3 8
× 3 = (升) ÷ = (杯)
5 5 5 10 3
12 3 8
÷ = 8(杯) × 3 = 8(杯)
5 10 3
也可以列综合算式计算。
4 3
× 3 ÷ 4 3
÷ × 3
5 10
5 10
2
1
4 10
= × 3 × =
5 3
1 1
= =
答: 3 盒果汁可以倒满 杯。
试一试
5 3 5 ( ) ( ) ( ) ( )
÷ ÷ = × × =
8 4 7 ( ) ( ) ( ) ( )
分数连除或乘除混合运算
可以怎样计算?
练一练
1 5 2 2 4
÷ × ÷ 5 ÷
2 4 3 3 15
50分数除法
练 习 八
1. 解方程。
2 4 7 2 14 5
8 x = x = x = x = 10
3 5 10 3 15 9
2. 先把数量关系式补充完整, 再列方程解答。
3
(1)一桶油用去 , 正好用去 12 千克。 这桶油重多少千克?
5
3
( )的千克数 × =( )的千克数
5
2
(2) 学校饲养组养黑兔 12 只, 是白兔只数的 。 饲养组养白兔
3
多少只?
2
( )的只数 × =( )的只数
3
3
3. 小华看一本课外书, 已经看了全书的 , 正好是 75 页。 这本书
4
有多少页?
1
4. 一种轿车的最快速度是 140 千米/时, 相当于超音速飞机的 。
15
超音速飞机的速度是多少?
5. 解方程。
1 2 10 5 3
x = x = x = 48
3 3 21 7 8
6. 我国科学家培育的杂交水稻, 每公顷产量大约 12 吨, 相当于原
4
来水稻产量的 。 原来水稻产量大约是每公顷多少吨?
3
4 1
7. 一条扬子鳄的尾长 米, 是它身长的 。
3 2
这条扬子鳄身长多少米?
51分数除法
3
8.(1)冬冬家买来一袋 15 千克的面粉, 吃了 , 吃了多少千克?
5
3
(2) 冬冬家买来一袋面粉, 吃了 , 正好是 9 千克。 原来这袋
5
面粉重多少千克?
5
9. 李庄村玉米的种植面积相当于水稻的 。
8
水稻的种植面积 玉米的种植面积
是 24 公顷, 玉 是 15 公顷, 水
米有多少公顷? 稻有多少公顷?
9 3 1 4 1 3 8 5
10. ÷ ÷ ÷ × 7 × ×
10 8 5 7 5 4 15 6
9 3
11. 一块地有 公顷, 用 2 台拖拉机耕, 小时可以耕完。 平均每
10 4
台拖拉机每小时耕地多少公顷?
2 7 3
12. 永新面粉厂 小时可以加工面粉 吨。 照这样计算, 小时
5 10 4
可以加工面粉多少吨?
13. 世界上最小的洲是大洋洲, 面积大约是900万平方千米。 欧洲的面
10 5 6
积是大洋洲的 , 是北美洲的 。 北美洲的面积是亚洲的 , 是
9 12 11
12 3 3
南极洲的 。 南美洲的面积是北美洲的 , 是非洲的 。 分别
7 4 5
算出各个洲的面积, 并填入下表。
亚洲 非洲 北美洲 南美洲 南极洲 欧洲 大洋洲
面积/万平方千米
1
小明和小红都养了一些金鱼, 小明把自己金鱼条数的 送给
5
小红后, 两人的金鱼条数同样多。 已知小明原来的金鱼比小
红多 8 条, 小红和小明原来各有金鱼多少条?
52分数除法
7 妈妈早晨准备了 2 杯果汁和 3 杯牛奶。 果汁和牛奶的杯数之
间有什么关系?
2 3
2÷3= 3÷2=
3 2
2 3
果汁的杯数是牛奶的 。 牛奶的杯数是果汁的 。
3 2
两个数量之间的这种关系还可以说成:
果汁与牛奶杯数的比是 2 比 3;
牛奶与果汁杯数的比是 3 比 2。
2 比 3 记作 2: 3; 3 比 2 记作 3: 2。
“: ” 是比号, 比号前面的数叫作比的前项, 比号后面的数叫
作比的后项。
8 走一段 900 米长的山路, 小军用了 15 分钟, 小伟用了 20 分
钟。 你能分别算出他们的速度吗?
900÷15=60(米/分) 900÷20=45(米/分)
小军的速度是 60米/分。 小伟的速度是 45米/分。
速度=路程÷时间, 路程和时间的这种关系也可以用比来表示:
小军走的路程与时间的比是 900: 15;
小伟走的路程与时间的比是 900: 20。
53分数除法
从例 7、 例 8 中可以看出, 两个
数相除的关系可以怎样表示?
两个数相除的关系 两个数相除的关系可以
可以用分数表示。 用两个数的比来表示。
两个数相除又可以叫作两个数的比。 比的前项除以后项所得的
商叫作比值。
你能说出例 7、 例 8 中每个
比的比值各是多少吗?
( )
3: 5 =( )÷( )=
( )
填写上面的等式, 想一想: 比的前项、 后项和比值分别相当于
除法算式或分数中的什么?
比的后项可以是0吗?
2
两个数的比也可以写成分数形式。 例如: 2: 3 也可以写作 ,
3
仍读作 2 比 3。
练一练
1. 小华家养了 10 只鸡, 9 只鸭。
(1) 鸡和鸭只数的比是( ):( ), 比值是( )。
(2) 鸭和鸡只数的比是( ):( ), 比值是( )。
2. 张祥买 3 本笔记本用了 10.5 元, 笔记本的总价和数量的比是
( ):( ), 比值是( )。
( )
3. 11 ÷ 6 =( ):( )=
( )
54分数除法
9 求出下面每个比的比值, 并把比值相等的比填入等式。
4: 5 16: 20 50: 40 40: 50
( ):( )=( ):( )=( ):( )
观察上面的等式, 联系分数的基本
性质想一想, 比会有什么性质?
比的前项和后项同时乘或除以相同的数(0 除外), 比值不变。
这是比的基本性质。
上面三个相等的比, 哪个比的
前项和后项只有公因数1?
应用比的基本性质, 可以把一些比化成最简单的整数比。
10 把下面各比化成最简单的整数比。
5 3
(1)12: 18 (2) : (3)1.8: 0.09
6 4
为什么要同
(1)12: 18 =(12 ÷ 6):(18 ÷ 6)
时除以 6?
= 2: 3
5 3 5 3 为什么要同
(2) : =( × 12):( × 12)
6 4 6 4 时乘 12?
=( ):( )
为什么要同
(3)1.8: 0.09 =(1.8 × 100):(0.09 × 100)
时乘 100?
=( ):( )=( ):( )
练一练
1. 在括号里填合适的数。
0.3 ( )
8: 5=32:( ) 25: 15= ( ): 3 =
0.5 10
2. 把下面各比化成最简单的整数比。
5 4
21: 35 : 1.25: 2 6.3: 0.9
6 9
55分数除法
练 习 九
1. 看图填空。
(1)红色方格与白色方格个数的比是 ;
白色方格与红色方格个数的比是 。
(2)黄色部分与圆面积的比是 ;
绿色部分与圆面积的比是 。
2. 几种水果的总价和数量如下表:
品 种 总价/元 数量/千克 单价(/ 元/千克)
苹 果 15 3
橘 子 8 4
香 蕉 4.8 2
(1)苹果的总价与数量的比是 , 比值是 。
(2)橘子的总价与数量的比是 , 比值是 。
(3)香蕉的总价与数量的比是 , 比值是 。
3. 量出三角尺上 30°角所对的边和斜边的长,
写出它们长度的比, 并计算比值, 再与同学 边
斜
交流计算结果。
4. 在方格纸上画出两个大小不
同的长方形, 使每个长方形
长与宽的比都是 2: 1。
5. 把比值相等的比连一连。
15 18
6: 9 2: 0.8
36 12
5 2
3: 2 5: 12
2 3
56分数除法
6. 化简下面各比。
102
(1)20: 8 36: 2
68
1 4 3 5 4 4
(2) : : :
3 5 7 21 15 25
(3)0.32: 0.8 1: 0.25 1.35: 9.25
7.《中华人民共和国国旗法》规定, 国旗的通用规格有以下五种。
写出每种规格国旗长与宽的比, 并化简。
长/厘米 288 240 192 144 96
宽/厘米 192 160 128 96 64
8. 分别写出每组正方形边长的比和面积的比, 并化简。
(1) (2)
3cm 6cm 8m 12m
9. 化简下面各比, 并求出比值。
比 4: 16 5.6: 4.2 75: 25
化简后的比
比 值
10. 先估计, 再量一量、 填一填。
(1)红色部分的长度与彩条全长的比是 , 比值是 ;
(2)绿色部分的长度与彩条全长的比是 , 比值是 ;
(3)红色部分与绿色部分长度的比是 , 比值是 。
11. 把下面各比改写成后项是 100 的比。
(1) 小华做黄豆种子发芽试验, 发芽的种子数与试验种子总数
的比是18: 25。
(2)新光电视机厂九月份完成的产量与计划产量的比是214: 200。
5713. 搬运工人为了把油桶推上汽车, 用木板搭了两个斜面(如下图)。
分别写出每个斜面最高点的高度与木板长度的比, 并化简。
你知道吗
mc051
300cm mc051
分数除法
12. 在洗洁液中加入不同数量的水后, 可以清洗不同的衣物。 下图
表示几种洗洁液与水的比。 你能把下面的表格填写完整吗?
第一种 洗洁液
水
第二种
第三种
洗洁液与水的比 比 值 化成前项是 1的比
第一种
第二种
第三种
500cm
1
两个长方形重叠部分的面积相当于小长方形面积的 , 相当
4
1
于大长方形面积的 。 小长方形与
6
大长方形面积的比是多少?
你听说过“黄金比” 吗? 黄金比的比值约等于 0.618。 把黄金
比应用于造型艺术, 可以给人以最美的感觉。 因此, 黄金比在日常
生活中有着广泛的应用。
宽宽与与长长的的比比值值接接近近 00..661188 的的 一幅画的主体部分约占画面
长长方方形形,, 被被认认为为是是最最美美的的。。 的0.618, 令人赏心悦目。
58分数除法
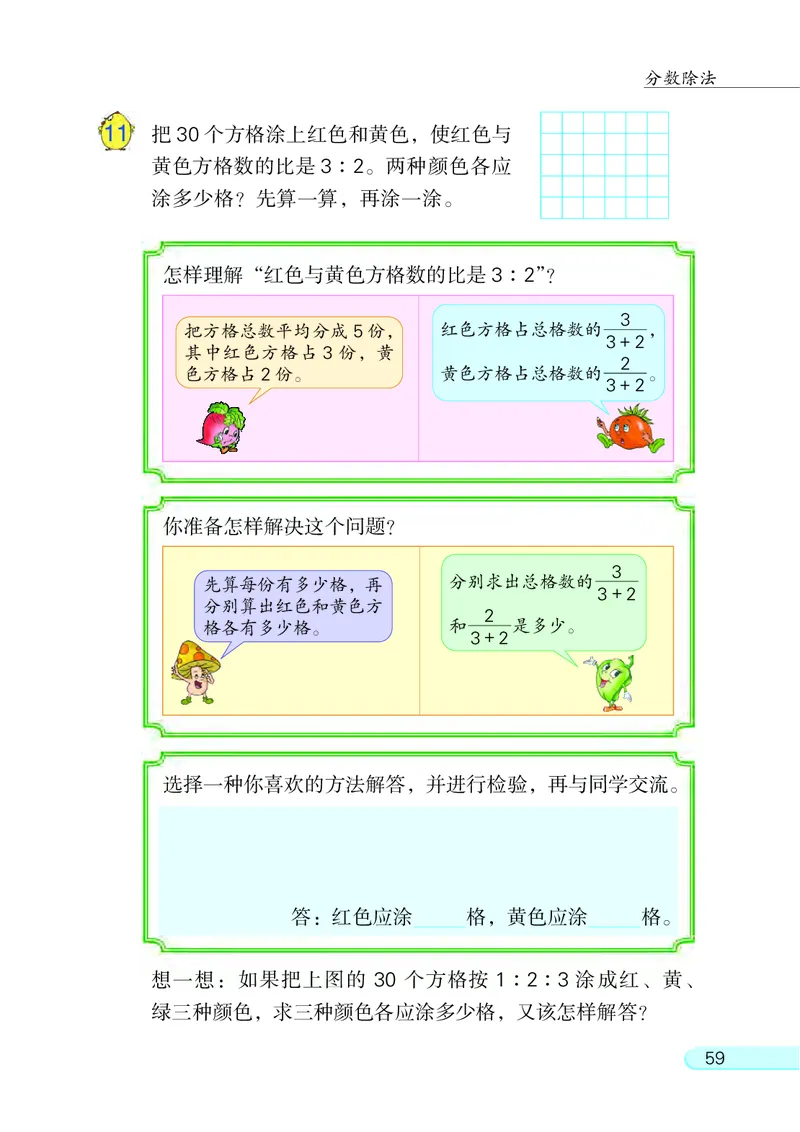
11 把 30 个方格涂上红色和黄色, 使红色与
黄色方格数的比是 3: 2。 两种颜色各应
涂多少格? 先算一算, 再涂一涂。
怎样理解“红色与黄色方格数的比是 3: 2”?
3
把方格总数平均分成 5 份, 红色方格占总格数的 ,
3+2
其中红色方格占 3 份, 黄
2
色方格占 2份。 黄色方格占总格数的 。
3+2
你准备怎样解决这个问题?
3
先算每份有多少格, 再 分别求出总格数的
3+2
分别算出红色和黄色方
2
格各有多少格。 和 是多少。
3+2
选择一种你喜欢的方法解答, 并进行检验, 再与同学交流。
答: 红色应涂 格, 黄色应涂 格。
想一想: 如果把上图的 30 个方格按 1: 2: 3 涂成红、 黄、
绿三种颜色, 求三种颜色各应涂多少格, 又该怎样解答?
59分数除法
试一试
三个小组去植树, 植树棵数按各小组人数的比分配。 每个小组
各应植树多少棵?
三组9人
二组7人
一组8人
72棵
怎样理解“植树棵数按
各小组人数的比分配”?
练一练
1. 学校合唱队有 48 人, 其中男生和女生人数的比是 1: 3。 男、 女
生各有多少人?
2. 蓓蕾幼儿园大班有 35 人, 中班有 31 人, 小班有 24 人。 张老师
准备把 180 块巧克力按班级人数的比分给 3 个班。 每班各应分得
多少块?
3. 妈妈用橙汁和水调制了几杯 300 毫升的饮料, 每杯饮料中橙汁与
水体积的比如下表:
橙汁和水的体积比 1: 5 1: 4 1: 1 2: 1
橙汁/毫升
水/毫升
你能很快算出每杯饮料中
橙汁和水各是多少毫升吗?
60分数除法
练 习 十
1. 一种足球的表面是由 32 块黑色五边形皮和白色六边
形皮围成的。 黑色皮和白色皮块数的比是 3: 5。
两种颜色的皮各有多少块?
2. 张斌、 李洪和马力三人合作投资兴办服装厂, 张斌投资 30 万元,
李洪投资 40 万元, 马力投资 50 万元。 服装厂去年的可分配利润
是 24 万元。 按投资额分配, 三人各应获得利润多少万元?
3. 进行一场足球比赛需要 90 分钟。 涂色的扇形表示
比赛已经进行的时间。 先估计已经比赛的时间与剩
余时间的比, 再算出这场比赛大约还剩多少分钟。
4. 根据已知条件回答问题。
(1)母鸡和公鸡只数的比是 4: 3。
① 母鸡的只数是公鸡的几分之几?
② 公鸡的只数是母鸡的几分之几?
(2)男生和全班人数的比是 5: 11。
① 男生和女生人数的比是几比几?
② 男生人数是女生的几分之几?
③ 女生人数是男生的几分之几?
5. 一个直角三角形两个锐角度数的比是 3: 2。
这两个锐角分别是多少度?
6. 配制一种药液, 药粉和水的质量比是 1: 40。
(1)400 克药粉需加水多少克?
(2)400 克水中应加药粉多少克?
61分数除法
7. 校园里玫瑰花和月季花棵数的比是 3: 5。
(1)如果玫瑰和月季一共有 120 棵, 这两种花各有多少棵?
(2)如果月季有 120 棵, 玫瑰有多少棵?
8. 下图表示配制一种混凝土所用材料的份数。
水泥
黄沙
石子
(1)这种混凝土的三种材料是按怎样的比配制的?
(2)要配制 120 吨这样的混凝土, 三种材料各需要多少吨?
(3) 如果这三种材料各有 18 吨, 配制这种混凝土, 当黄沙全部
用完时, 水泥还剩多少吨? 石子已经增加了多少吨?
把右边的三角形分成两部分, 使这两部分
面积的比是 1: 1, 你能分一分吗? 如果
要使两部分面积的比是 1: 2, 又该怎样分?
动 手 做
连接右边五边形的顶点, 画出一个“五角
星”。 在这个图形中找出不同的等腰三角形, 量
出每种等腰三角形的底和腰, 判断它们按角的特
点分类各是什么三角形, 填入下表。
编 号 底/mm 腰/mm 按角分是什么三角形
先算出每种锐角等腰三角形底与一条腰长度比的比值, 再算
出每种钝角等腰三角形一条腰与底长度比的比值。
观察这些比值, 你有什么发现?
62分数除法
整理与练习
回顾与整理
小组讨论:
1. 怎样计算分数除法?
2. 举例说明比的意义和比的基本性质, 以及比、 分数、 除法之
间的联系和区别。
3. 解决有关分数、 比的实际问题时, 应怎样分析数量关系? 举
例说一说。
练习与应用
1. 直接写出得数。
1 2 3 8 3 4
÷ = 6 ÷ = ÷ 2 = ÷ =
5 3 5 11 4 3
3 1 2 8 5 1 2
÷ = ÷ = 0 ÷ = × =
10 5 7 7 8 2 3
2 4 7 10 8 1
2. ÷ 35 ÷ ÷ 15 ÷
3 9 8 13 45 20
1 9 1 2 1 1 4 3
÷ ÷ ÷ × 3 × ÷
13 13 3 5 5 6 9 8
3. 六年级二班有男生 24 人, 女生 25 人; 三班有男生 26 人, 女生
24 人。 根据上面的条件, 你能写出哪些比?
( )
4. 3: 5 = =( )÷( )= 9 :( )=( ): 25
( )
5.
2
你能写出几个比值是 的比吗?
3
6. 先化简下面各比, 再求比值。
3 5
20: 8 : 1.25: 0.25 3.6: 0.16
5 8
63分数除法
2 5
7. 一辆摩托车的行驶速度是 千米/分, 一只燕子的飞行速度是
3 2
千米/分。 燕子的飞行速度是摩托车的几倍?
2 2
8.(1)王师傅 小时织 米长的毯子, 1小时织多少米?
3 5
2 2
(2)李师傅每小时织 米长的毯子, 小时织多少米?
5 3
2 2
(3)张师傅每小时织 米长的毯子, 织 米长的毯子需要几小时?
5 3
9. 解方程。
1 3 7 14 3 2
x = x = + x =
2 4 10 25 8 5
3 1
10. 花果林场有桃园 公顷, 占果园总面积的 。 果园的总面积有
8 4
多少公顷?
11. 常青湖小学修建一条塑胶跑道, 实际造价 27 万元, 是原计划的
9
。 原计划造价多少万元?
10
12. 我国的国土面积大约是 960 万平方千米, 其中林地面积大约占
1
, 林地面积大约是多少万平方千米? 林地面积大约是耕地面
4
25
积的 , 耕地面积大约是多少万平方千米?
13
13.(1)甲农场在一块 36 公顷的土地上种植大豆和玉米, 大豆和玉
米种植面积的比是 4: 5。 分别求大豆和玉米的种植面积。
(2)乙农场大豆的种植面积是 36 公顷, 大豆和玉米种植面积的
比是 4: 5。 求玉米的种植面积。
64分数除法
探索与实践
14. 你能用哪些方法来说明“甲数除以乙数(0 除外), 等于甲数乘
乙数的倒数”?
15. 小明、 小华和小军各用 4 元买一种水
每千克 每千克 每千克
6元 2.5元 5元
4
果。 小明买的水果重 千克, 是小华
5 每千克 每千克
3元 2元
2 3
所买水果的 , 是小军所买水果的 。
5 5
他们买的各是什么水果?
16. 下面每个方格的边长表示 1 厘米。
(1)画一个长方形, 面积是 24 平方厘米, 长与宽的比是 3: 2。
(2)画一个长方形, 周长是 16 厘米, 长与宽的比是 5: 3。
17. 你的身高是多少厘米? 脚长和头长呢? 你父母的身高、 脚长和
头长分别是多少厘米? 先量一量, 再分别算出脚长与身高、 头
长与身高的比(前项都化成 1, 后项保留一位小数), 看看有什么
发现。
评价与反思
学习分数除法计算时, 能积极探索和归纳计算方
☆☆☆☆☆
法, 正确进行计算
理解比的意义和基本性质时, 能联系生活实际和
☆☆☆☆☆
所学知识积极思考, 并加以应用
能联系学过的知识, 主动探索解决问题的方法, 有
☆☆☆☆☆
条理地说明解决问题的思考过程
65树 叶 中 的 比
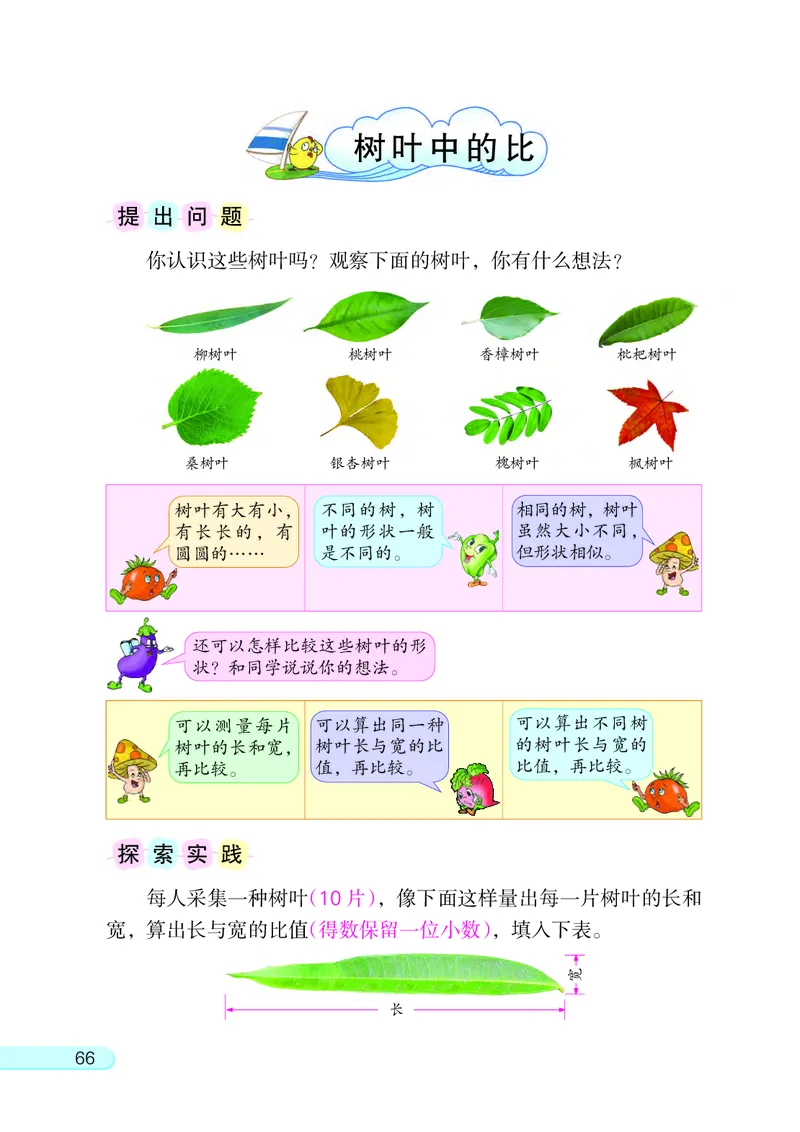
柳树叶 桃树叶 香樟树叶 枇杷树叶
桑树叶 银杏树叶 槐树叶 枫树叶
长
宽
提 出 问 题
你认识这些树叶吗? 观察下面的树叶, 你有什么想法?
树叶有大有小, 不同的树, 树 相同的树, 树叶
有长长的, 有 叶的形状一般 虽然大小不同,
圆圆的…… 是不同的。 但形状相似。
还可以怎样比较这些树叶的形
状? 和同学说说你的想法。
可以测量每片 可以算出同一种 可以算出不同树
树叶的长和宽, 树叶长与宽的比 的树叶长与宽的
再比较。 值, 再比较。 比值, 再比较。
探 索 实 践
每人采集一种树叶(10 片), 像下面这样量出每一片树叶的长和
宽, 算出长与宽的比值(得数保留一位小数), 填入下表。
66综合与实践
树叶的长与宽及比值
编 号 长/mm 宽/mm 比 值 编 号 长/mm 宽/mm 比 值
1 6
2 7
3 8
4 9
5 10
在小组里交流各自测量的 10 片树叶长与宽比值的平均数, 并
填写下表。
树叶名称
比值的平均数
将测量和计算的结果与树叶的
形状对照, 你还有什么发现?
树叶长与宽
同一种树叶, 比值接近的不
的 比 值 越
长与宽的比值 同树叶, 形状
大, 树叶就
都比较接近。 也相似。
越狭长。
回 顾 反 思
通过这次活动, 你有什么收获?
通过测量、 计算和比
善于观察和思考,
自然界中隐藏着很
较, 可以帮助我们分
才能发现和提出生
多有趣的规律。
析问题、 解决问题。
活中的数学问题。
67解决问题的策略
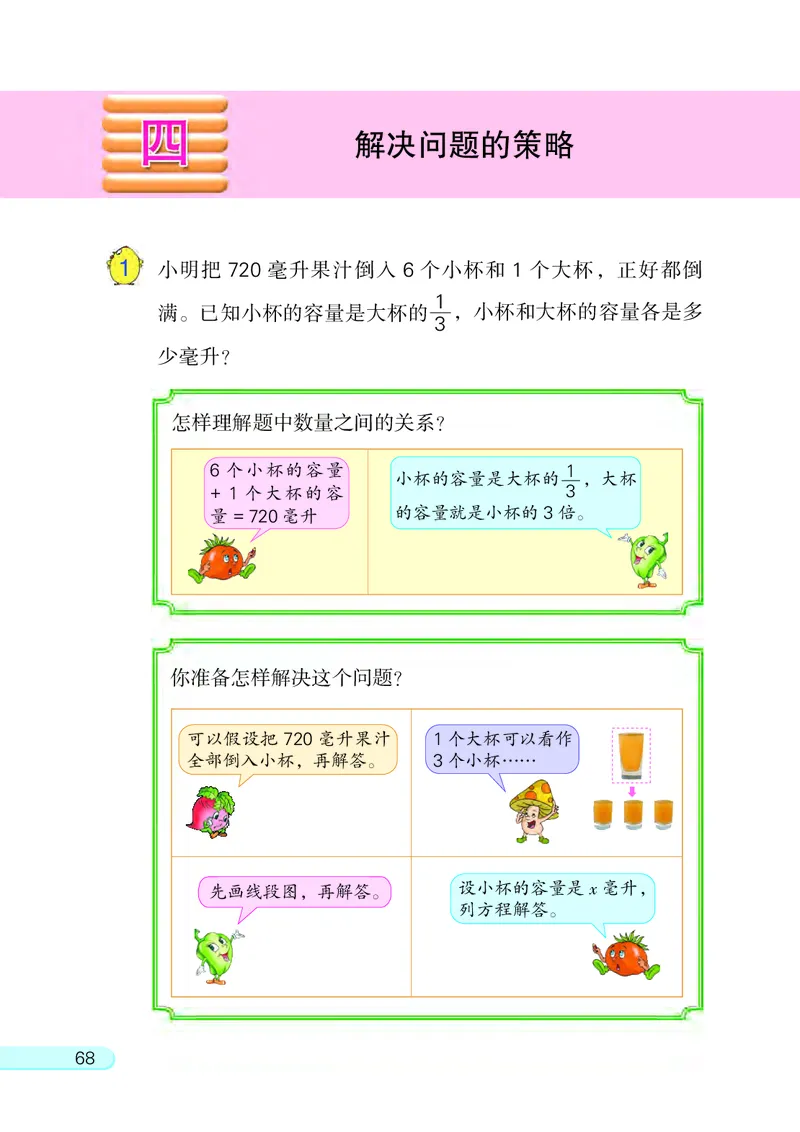
1 小明把 720 毫升果汁倒入 6 个小杯和 1 个大杯, 正好都倒
1
满。 已知小杯的容量是大杯的 , 小杯和大杯的容量各是多
3
少毫升?
怎样理解题中数量之间的关系?
6 个小杯的容量 1
小杯的容量是大杯的 , 大杯
+ 1 个大杯的容 3
量 =720毫升 的容量就是小杯的3倍。
你准备怎样解决这个问题?
可以假设把 720 毫升果汁 1个大杯可以看作
全部倒入小杯, 再解答。 3个小杯……
先画线段图, 再解答。 设小杯的容量是 x 毫升,
列方程解答。
68解决问题的策略
选择一种方法列式解答, 并进行检验。
答: 小杯的容量是 毫升, 大杯的容量是 毫升。
想一想: 假设把 720 毫升果汁全部倒入大杯, 可以倒满几个
大杯? 你能根据这样的假设算出结果吗?
回顾解决问题的过程, 你有什么体会?
通过假设可以转 假设时要弄清 假设时也可以用
化问题, 使数量 楚数量之间的 字母表示未知量,
关系变得简单。 关系。 列方程解答。
在以前的学习中, 我们曾经运用假设的策略解决过哪些问题?
把接近整百或整 已知两个数的和与
计算除数是两位数
十的数看作整百 差, 假设两个数同
的除法, 把除数当
或整十数, 估算 样多, 分别求出这
作整十数试商。
出大致的结果。 两个数。
练一练
1 张桌子和 4 把椅子的总价是 2700 元, 椅子的单价是桌子的
1
。 桌子和椅子的单价各是多少?
5
69解决问题的策略
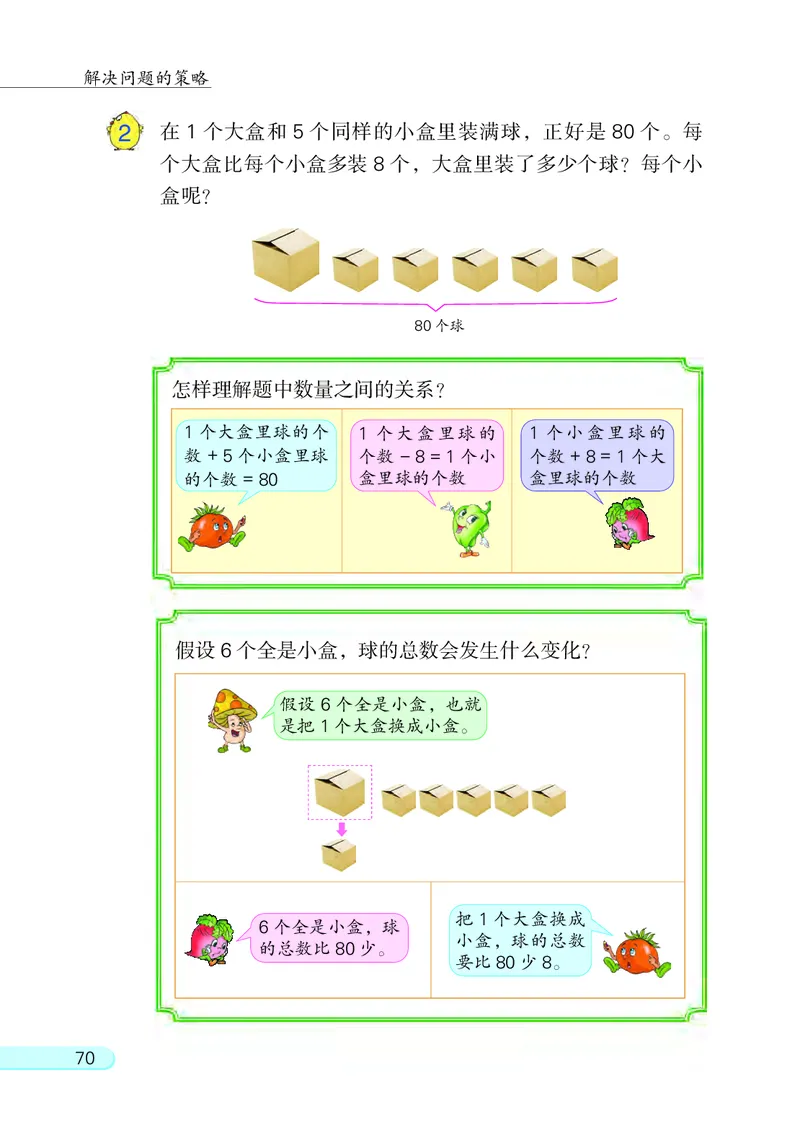
2 在 1 个大盒和 5 个同样的小盒里装满球, 正好是 80 个。 每
个大盒比每个小盒多装 8 个, 大盒里装了多少个球? 每个小
盒呢?
80个球
怎样理解题中数量之间的关系?
1 个大盒里球的个 1 个大盒里球的 1 个小盒里球的
数 + 5 个小盒里球 个数 - 8= 1 个小 个数 + 8= 1个大
的个数 =80 盒里球的个数 盒里球的个数
假设 6 个全是小盒, 球的总数会发生什么变化?
假设 6 个全是小盒, 也就
是把 1个大盒换成小盒。
把 1 个大盒换成
6 个全是小盒, 球
小盒, 球的总数
的总数比80少。
要比 80少 8。
70解决问题的策略
先根据假设后的数量关系列式解答, 再进行检验。
答: 大盒里装了 个, 每个小盒装了 个。
回顾例 1 和例 2 解决问题的过程, 你有什么体会?
都可以通过假设 要弄清假设前后的数 要在不同的假设
使数量关系变得 量关系, 注意假设前 方法中选择比较
简单。 后总量有没有变化。 简单的。
练一练
1.
250元
每件上衣比每条裤子贵 25 元, 求上衣和裤子的单价。
2. 星期天, 欢欢和爸爸、 妈妈一起去森林公园游玩。 买了 2 张成人
票和 1 张儿童票, 一共用去 78 元。 每张成人票比每张儿童票贵
12 元, 一张成人票多少元? 一张儿童票呢?
71解决问题的策略
练习十一
1. 填空。
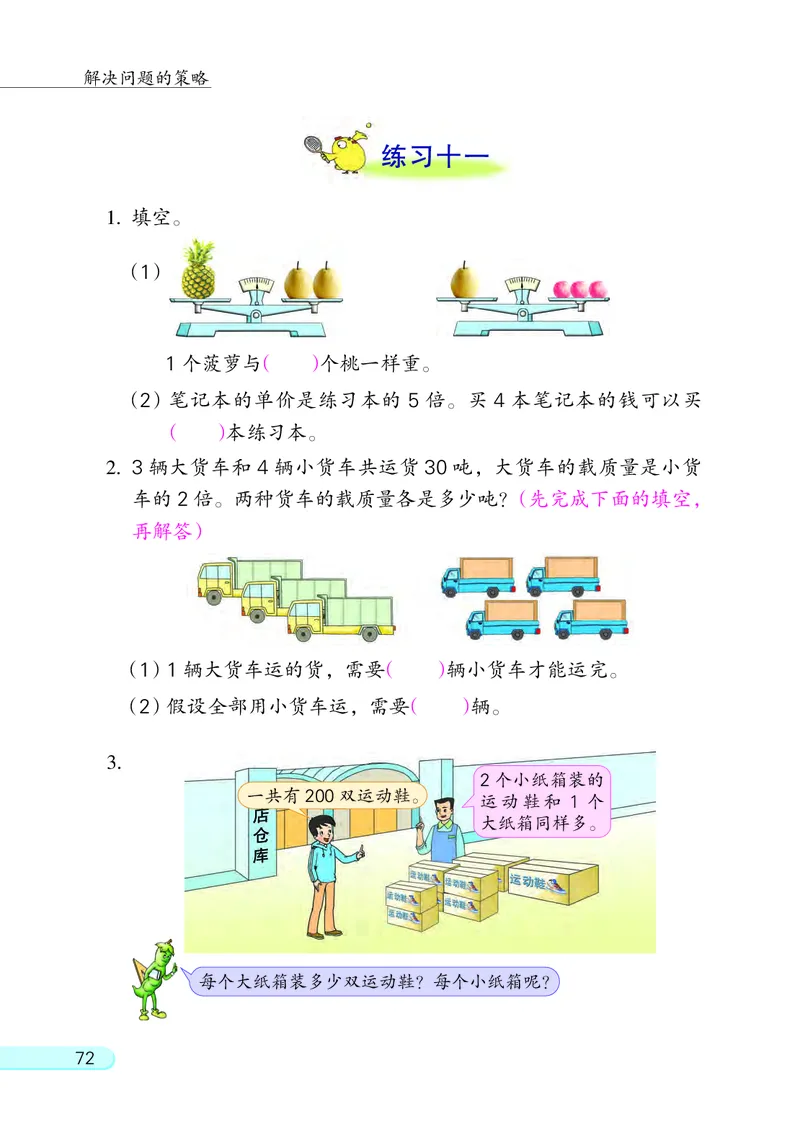
(1)
1 个菠萝与( )个桃一样重。
(2) 笔记本的单价是练习本的 5 倍。 买 4 本笔记本的钱可以买
( )本练习本。
2. 3 辆大货车和 4 辆小货车共运货 30 吨, 大货车的载质量是小货
车的 2 倍。 两种货车的载质量各是多少吨?(先完成下面的填空,
再解答)
(1)1 辆大货车运的货, 需要( )辆小货车才能运完。
(2)假设全部用小货车运, 需要( )辆。
3.
2 个小纸箱装的
一共有 200双运动鞋。
运动鞋和 1 个
大纸箱同样多。
每个大纸箱装多少双运动鞋? 每个小纸箱呢?
72解决问题的策略
4. 解方程。
2 3
x + x = 60 x - x = 120 4 x + 18 x = 132
3 5
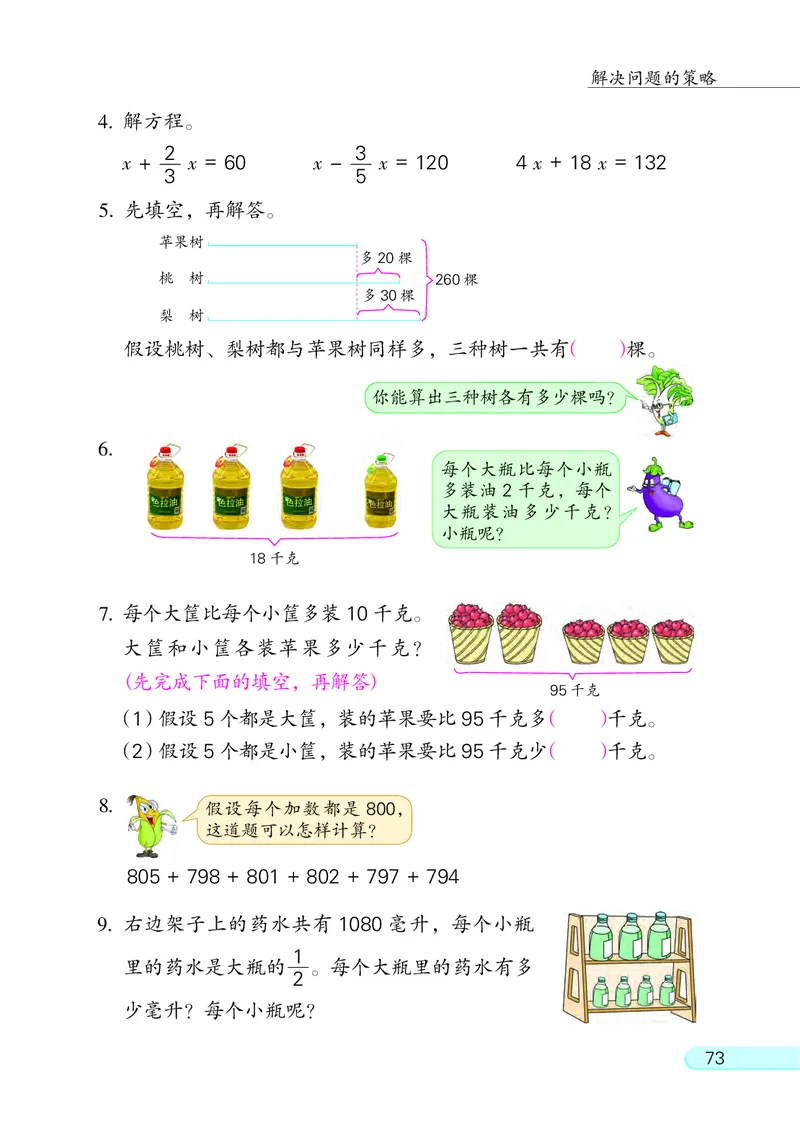
5. 先填空, 再解答。
苹果树
多20棵
桃 树 260棵
多30棵
梨 树
假设桃树、 梨树都与苹果树同样多, 三种树一共有( )棵。
你能算出三种树各有多少棵吗?
6.
每个大瓶比每个小瓶
多装油 2 千克, 每个
大瓶装油多少千克?
小瓶呢?
18千克
7. 每个大筐比每个小筐多装 10 千克。
大筐和小筐各装苹果多少千克?
(先完成下面的填空, 再解答)
95千克
(1)假设 5 个都是大筐, 装的苹果要比 95 千克多( )千克。
(2)假设 5 个都是小筐, 装的苹果要比 95 千克少( )千克。
8.
假设每个加数都是 800,
这道题可以怎样计算?
805 + 798 + 801 + 802 + 797 + 794
9. 右边架子上的药水共有 1080 毫升, 每个小瓶
1
里的药水是大瓶的 。 每个大瓶里的药水有多
2
少毫升? 每个小瓶呢?
73解决问题的策略
10.
钢笔的单价是铅笔的 6 倍, 钢笔
和铅笔的单价各是多少?
10.8元
11. 师徒两人一共做了 120 个零件, 师傅比徒弟多做 16 个, 两人各
做了多少个?
12.
海芙蓉 雀梅 榕树
王大伯买了上面的三盆盆景, 一共用去 405 元, 雀梅比海芙蓉
便宜 20 元, 榕树比海芙蓉便宜 49 元。 三种盆景的单价各是多
少?(先把下面的线段图补充完整, 再解答)
海芙蓉
雀 梅 405元
榕 树
13. 张宁和王晓星一共有画片 108 张。 张宁给王晓星 18 张后, 两人
画片的张数同样多。 两人原来各有多少张?(先画图表示题中的
数量关系, 再解答)
14. 梨花庄小学有 3 个同样大的花圃和 3 个同样大的苗圃, 一共是
180 平方米。 每个花圃比每个苗圃大 10 平方米, 每个花圃和苗
圃的面积各是多少平方米?
小华和小力出同样多的钱买一箱苹果, 结果小华拿了 8 千
克, 小力拿了 12 千克。 这样, 小力就要给小华 16 元。 苹
果的单价是多少元/千克?
74分数四则混合运算
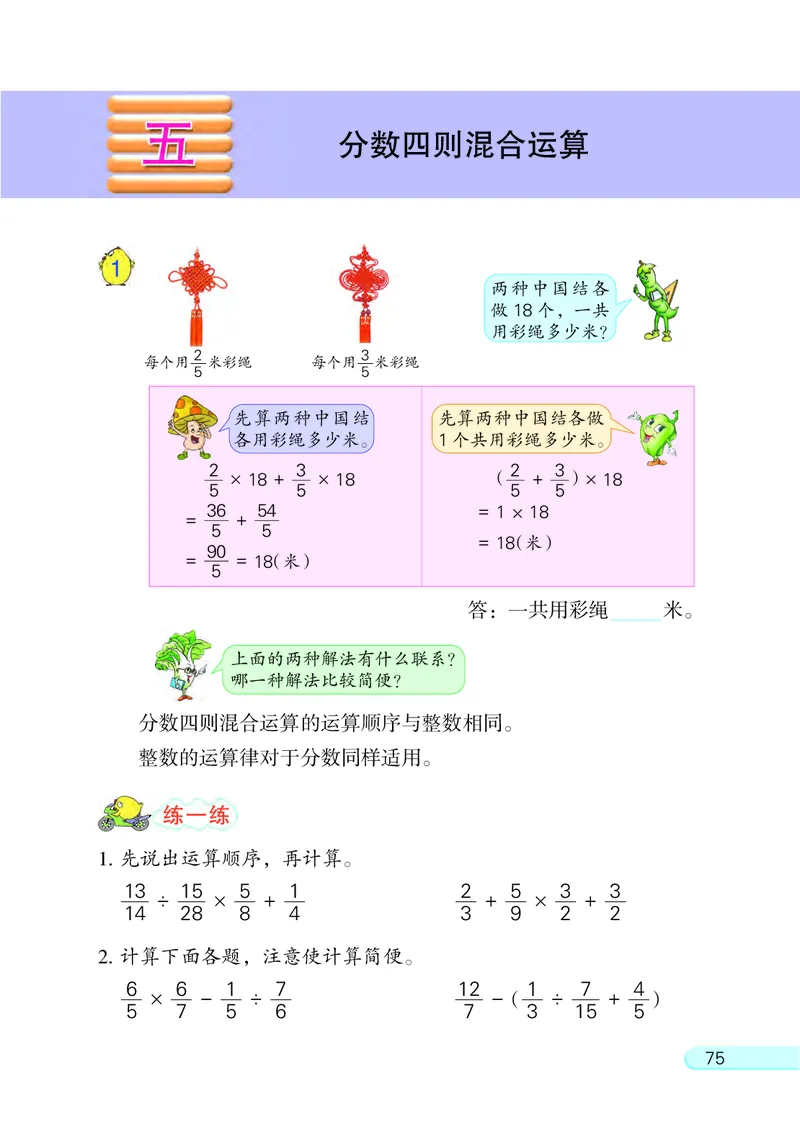
1
两种中国结各
做 18 个, 一共
用彩绳多少米?
2 3
每个用 米彩绳 每个用 米彩绳
5 5
先算两种中国结 先算两种中国结各做
各用彩绳多少米。 1个共用彩绳多少米。
2 3 2 3
× 18 + × 18 ( + )× 18
5 5 5 5
36 54 = 1 × 18
= +
5 5
= 18(米)
90
= = 18(米)
5
答: 一共用彩绳 米。
上面的两种解法有什么联系?
哪一种解法比较简便?
分数四则混合运算的运算顺序与整数相同。
整数的运算律对于分数同样适用。
练一练
1. 先说出运算顺序, 再计算。
13 15 5 1 2 5 3 3
÷ × + + × +
14 28 8 4 3 9 2 2
2. 计算下面各题, 注意使计算简便。
6 6 1 7 12 1 7 4
× - ÷ -( ÷ + )
5 7 5 6 7 3 15 5
75分数四则混合运算
练习十二
1. 直接写出得数。
5 5 3 1 4 3
÷ = 1 ÷ = × 2 = ÷ =
8 12 7 8 5 5
11 2 4 3 2 3
× = ÷ = 0 ÷ = 12 × =
4 11 9 5 3 8
1 3 5 1 9
2. ÷ - + 3 ÷
7 14 8 3 10
1 4 2 8 5 3
- ÷ 1 - ÷ ×
2 25 5 9 6 16
2 2 3 3 5 3
÷ (1 - ) ( - × )÷
3 3 4 4 6 2
3. 计算下面各题, 注意使用简便算法。
1 1 2 5 2 2
30 ×( + ) × + ×
5 3 3 7 3 7
3 1 1 6 3 3
× + ÷ 9 5 -( ÷ + )
4 9 4 7 14 16
2 3
4. 商店运来苹果 吨, 运来梨的吨数是苹果的 , 运来梨多少吨?
5 4
运来的苹果和梨一共有多少吨?
1
5. 把 1 升果汁先倒满 3 小瓶, 每小瓶 升。 剩下的平均倒进 2 个
4
杯里。
每个杯里倒进
果汁多少升?
6. 解方程。
2 3 1 3 9
x+ x= x- x= 2x+7x=
7 4 5 10 10
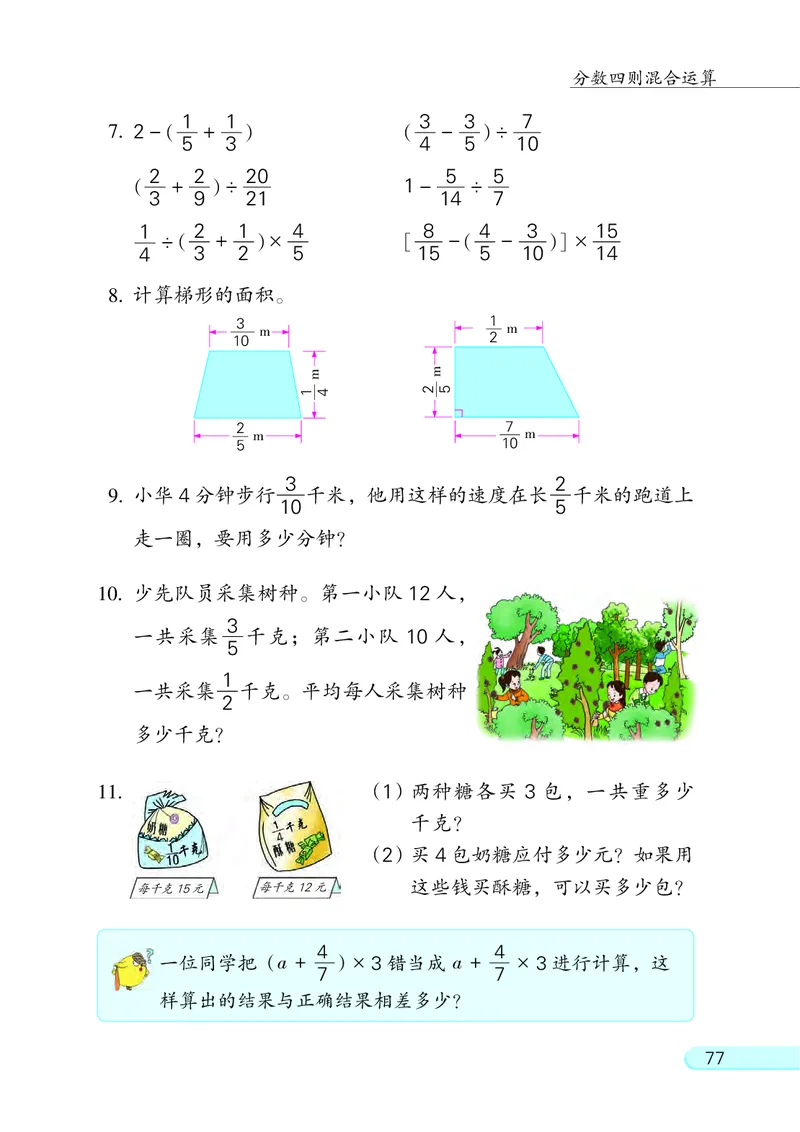
761 1 3 3 7
7. 2-( + ) ( - )÷
5 3 4 5 10
2 2 20 5 5
( + )÷ 1- ÷
3 9 21 14 7
1 2 1 4 8 4 3 15
÷( + )× [ -( - )]×
4 3 2 5 15 5 10 14
8. 计算梯形的面积。
3 2
9. 小华 4 分钟步行 千米, 他用这样的速度在长 千米的跑道上
10 5
走一圈, 要用多少分钟?
11. (1) 两种糖各买 3 包, 一共重多少
千克?
(2)买 4 包奶糖应付多少元? 如果用
每千克15元 每千克12元 这些钱买酥糖, 可以买多少包?
1
m
4
3 m
10
2
m
5
2
m
5
分数四则混合运算
1 m
2
7
m
10
10. 少先队员采集树种。 第一小队 12 人,
3
一共采集 千克; 第二小队 10 人,
5
1
一共采集 千克。 平均每人采集树种
2
多少千克?
4 4
一位同学把(a + )× 3 错当成 a + × 3 进行计算, 这
7 7
样算出的结果与正确结果相差多少?
77分数四则混合运算
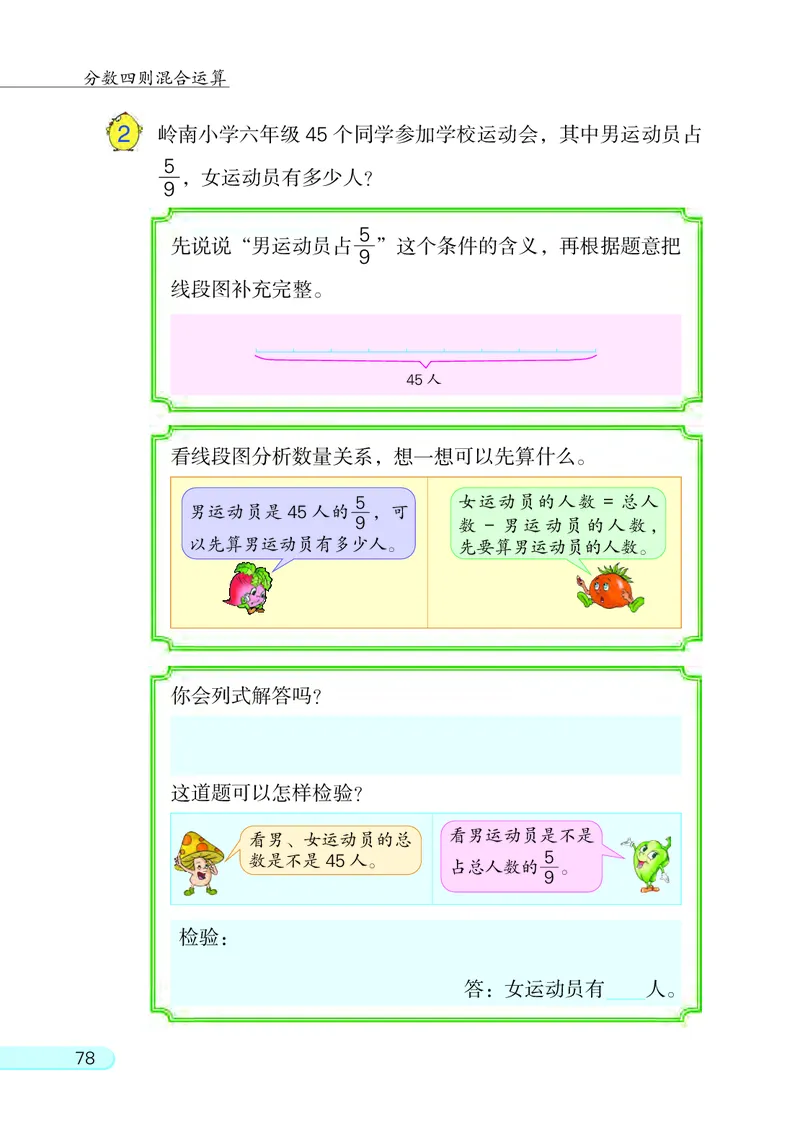
2 岭南小学六年级 45 个同学参加学校运动会, 其中男运动员占
5
, 女运动员有多少人?
9
5
先说说“男运动员占 ” 这个条件的含义, 再根据题意把
9
线段图补充完整。
45人
看线段图分析数量关系, 想一想可以先算什么。
5 女运动员的人数 = 总人
男运动员是 45 人的 , 可
9 数 - 男运动员的人数,
以先算男运动员有多少人。 先要算男运动员的人数。
你会列式解答吗?
这道题可以怎样检验?
看男、 女运动员的总 看男运动员是不是
数是不是 45人。 5
占总人数的 。
9
检验:
答: 女运动员有 人。
78分数四则混合运算
回顾解决问题的过程, 你有什么体会?
理解已知条件 画线段图可以清楚 解决分数实际问题
中分数的意义 地看出分数实际问 同样可以从条件想
非常重要。 题的数量关系。 起, 或从问题想起。
练一练
先说一说可以怎样想, 再解答。
2
1. 李林看一本 150 页的故事书, 已经看了全书的 , 还剩多少页
3
没有看?
3
2. 学校饲养组养白兔和黑兔一共 28 只, 其中白兔占 , 黑兔有
7
多少只?
4 3
3. 红光印刷厂两天用纸 吨, 其中 是第一天用的, 第二天用了
5 8
多少吨?
1
3
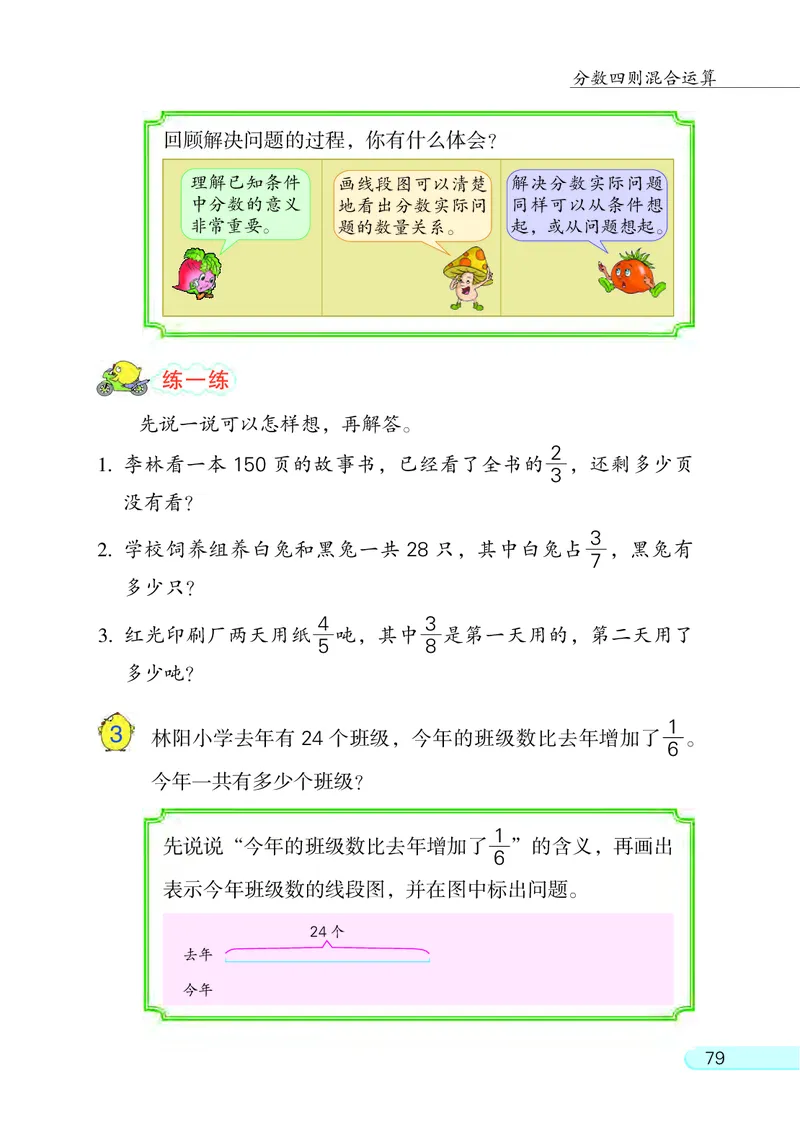
林阳小学去年有 24 个班级, 今年的班级数比去年增加了 。
6
今年一共有多少个班级?
1
先说说“今年的班级数比去年增加了 ” 的含义, 再画出
6
表示今年班级数的线段图, 并在图中标出问题。
24个
去年
今年
79分数四则混合运算
看线段图分析数量关系, 想一想可以先算什么。
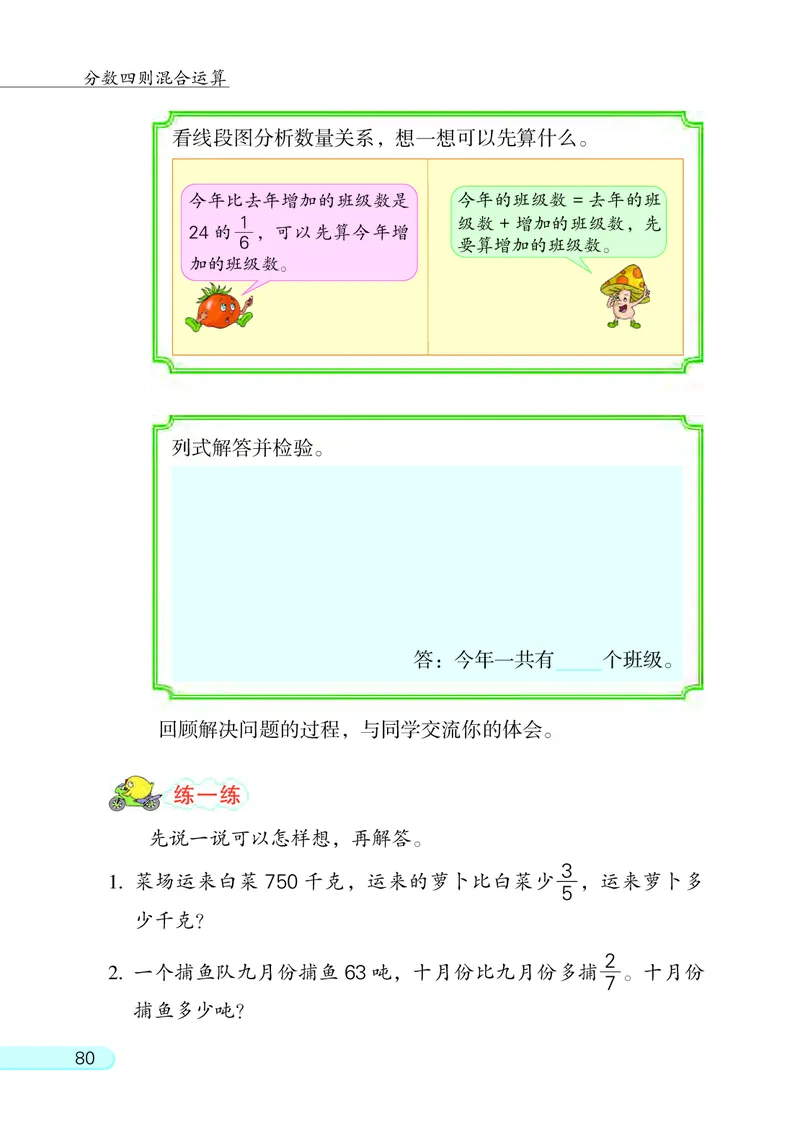
今年比去年增加的班级数是 今年的班级数 = 去年的班
1 级数 + 增加的班级数, 先
24 的 , 可以先算今年增
6 要算增加的班级数。
加的班级数。
列式解答并检验。
答: 今年一共有 个班级。
回顾解决问题的过程, 与同学交流你的体会。
练一练
先说一说可以怎样想, 再解答。
3
1. 菜场运来白菜 750 千克, 运来的萝卜比白菜少 , 运来萝卜多
5
少千克?
2
2. 一个捕鱼队九月份捕鱼 63 吨, 十月份比九月份多捕 。 十月份
7
捕鱼多少吨?
80分数四则混合运算
练习十三
5
1. 一桶油漆重 18 千克, 用去 , 还剩多少千克?
6
5
2. 陈征有 84 枚邮票, 其中 是中国邮票, 其余的是外国邮票。 陈
7
征有多少枚外国邮票?
1 1 3 2 1 1 1
3. × = 1 - = + = � ÷ =
2 3 10 15 5 2 4
3
4. 月星小学去年有 64 台计算机, 今年比去年增加 。 今年有多少
8
台计算机?
5. 从北京到上海原来乘火车大约需要 12 小时。 高速铁路开通后,
3
时间缩短了 。 从北京到上海乘坐高铁大约需要多少小时?
5
2 5 3 3 5 6 4 1
6. -( - )÷ ÷[ ×( + )]
3 6 4 8 14 7 9 6
3
7. 工人要在地下铺设 840 米电缆, 已经铺设了 。
5
(1)已经铺设了多少米?
(2)还要铺设多少米?
8. 10岁儿童平均每分钟心跳大约90次。
(1) 新生儿平均每分钟心跳的次数比
1
10 岁儿童多 。 新生儿平均每
2
分钟心跳大约多少次?
1
(2) 青少年平均每分钟心跳的次数比 10 岁儿童少 。 青少年平
5
均每分钟心跳大约多少次?
81分数四则混合运算
3
9. 一根 2 米长的木料锯成两段, 第一段占全长的 , 第二段长多
8
少米?
2 1
10. 春岭小学植树 90 棵, 其中六年级植了 , 五年级植了 。 五、
5 3
六年级一共植树多少棵?
5
11. 李大伯养鸡 160 只, 养鸭的只数是鸡的 。 养的鸡和鸭一共有
8
多少只? 鸡比鸭多多少只?
12. 计算下面各题, 注意使用简便算法。
5 9 5 5 4 6
×( + 18) ÷ + ×
9 5 9 6 9 5
4 4 7 2 7
4 ÷ - ÷ 4 ÷[ -(1 - )]
5 5 11 5 10
5 1
13.(1)一根钢条长 米, 用去 , 还剩多少米?
8 4
5 1
(2)一根钢条长 米, 用去一些后还剩 , 还剩多少米?
8 4
3
14.(1)海豚每小时游 50 千米, 蓝鲸的速度比海豚慢 。 蓝鲸每小
10
时游多少千米?
3
(2)蓝鲸每小时游 35 千米, 海豚的速度比蓝鲸快 。 海豚每小
7
时游多少千米?
4
15. 学校食堂计划十月份用煤 吨。
5
1
(1)实际用煤比计划节约了 , 实际用煤多少吨?
8
1
(2)实际用煤比计划节约了 吨, 实际用煤多少吨?
8
82分数四则混合运算
16. 同学们参加义务劳动, 六年级去了 60 人, 五年级去的人数是六
4
年级的 。 五年级比六年级少去了多少人?
5
2
17.(1)校园里有银杏 36 棵, 香樟比银杏少 。 香樟有多少棵?
9
(2) 校园里有香樟 28 棵, 香樟与银杏棵数的比是7: 9。 银杏有
多少棵?
5 2 3
18. 一个街心花园占地 公顷, 其中草坪占 , 花圃占 , 其余
8 5 10
是人行道。
(1)草坪和花圃的面积一共是多少公顷?
(2)草坪的面积比花圃大多少公顷?
(3)人行道的面积是多少公顷?
2 3
六年级一班有 48 人, 其中 喜欢跳舞, 喜欢唱歌, 没有
3 4
人既不喜欢跳舞又不喜欢唱歌。 既喜欢跳舞又喜欢唱歌的有
多少人?
动 手 做
在方格纸上画一个长 6 厘米、 宽 4 厘米的长方形, 再把这个
1
长方形的长和宽分别增加 。 算一算, 新长方形的面积是原来长
2
方形的几分之几。
1
任意画几个长方形, 把每个长方形的长和宽分别增加 。
2
先算出新长方形的长和宽, 再算出它的面积是原来长方形的几
分之几。
你能发现什么?
83百 分 数
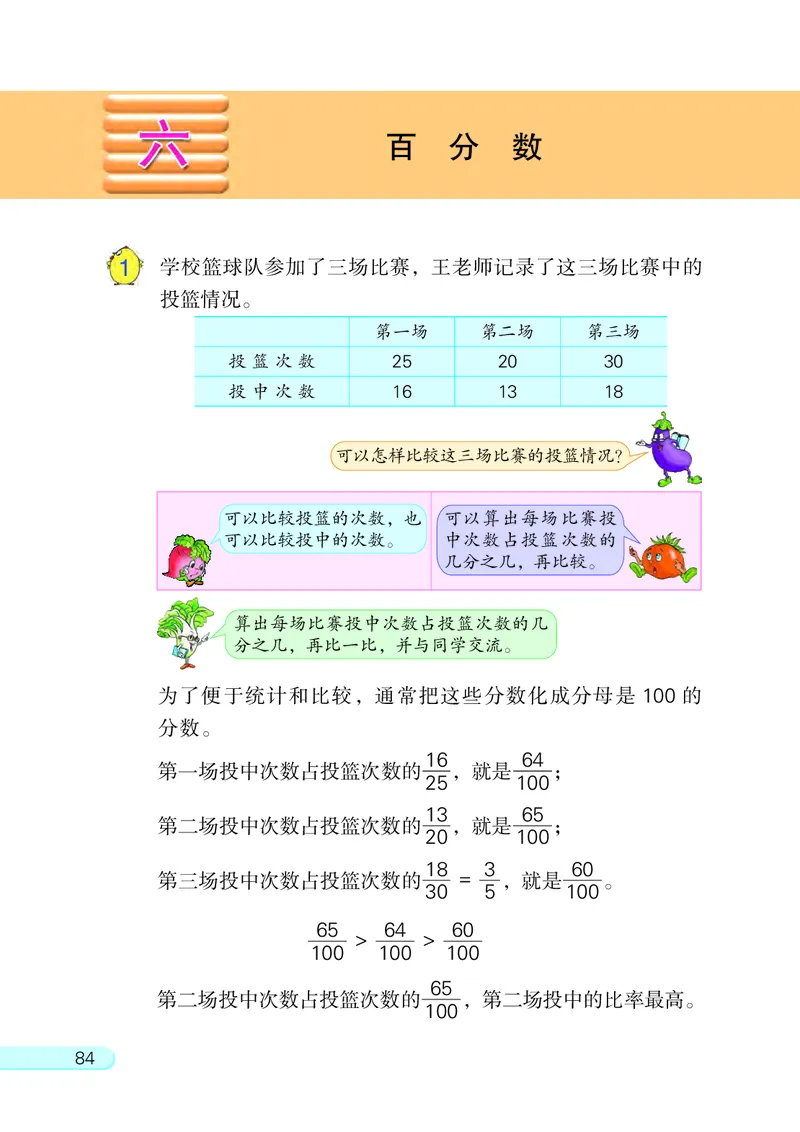
1 学校篮球队参加了三场比赛, 王老师记录了这三场比赛中的
投篮情况。
第一场 第二场 第三场
投 篮 次 数 25 20 30
投 中 次 数 16 13 18
可以怎样比较这三场比赛的投篮情况?
可以比较投篮的次数, 也 可以算出每场比赛投
可以比较投中的次数。 中次数占投篮次数的
几分之几, 再比较。
算出每场比赛投中次数占投篮次数的几
分之几, 再比一比, 并与同学交流。
为了便于统计和比较, 通常把这些分数化成分母是 100 的
分数。
16 64
第一场投中次数占投篮次数的 , 就是 ;
25 100
13 65
第二场投中次数占投篮次数的 , 就是 ;
20 100
18 3 60
第三场投中次数占投篮次数的 = , 就是 。
30 5 100
65 64 60
> >
100 100 100
65
第二场投中次数占投篮次数的 , 第二场投中的比率最高。
100
84百 分 数
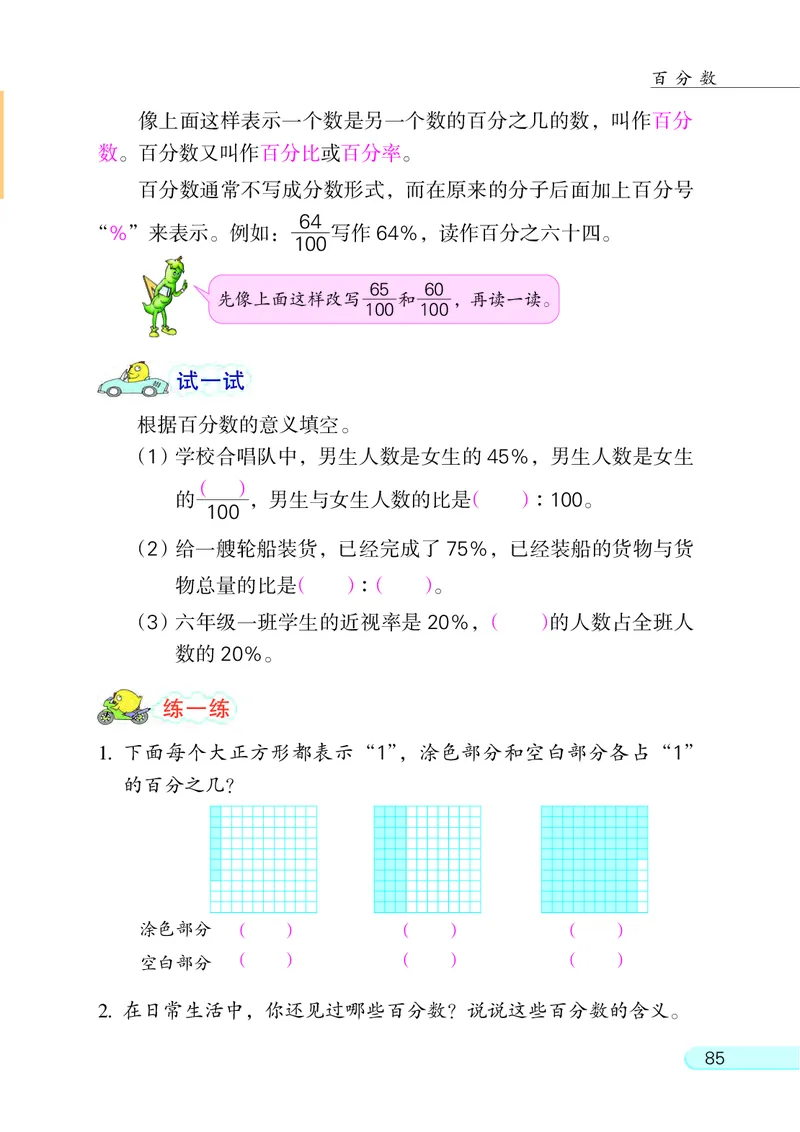
像上面这样表示一个数是另一个数的百分之几的数, 叫作百分
数。 百分数又叫作百分比或百分率。
百分数通常不写成分数形式, 而在原来的分子后面加上百分号
64
“%” 来表示。 例如: 写作 64%, 读作百分之六十四。
100
65 60
先像上面这样改写 和 , 再读一读。
100 100
试一试
根据百分数的意义填空。
(1)学校合唱队中, 男生人数是女生的 45%, 男生人数是女生
( )
的 , 男生与女生人数的比是( ): 100。
100
(2)给一艘轮船装货, 已经完成了 75%, 已经装船的货物与货
物总量的比是( ):( )。
(3) 六年级一班学生的近视率是 20%,( )的人数占全班人
数的 20%。
练一练
1. 下面每个大正方形都表示“1”, 涂色部分和空白部分各占“1”
的百分之几?
涂色部分 ( ) ( ) ( )
空白部分 ( ) ( ) ( )
2. 在日常生活中, 你还见过哪些百分数? 说说这些百分数的含义。
85百 分 数
2 学校田径队进行体能训练, 李老师要求队员用 5 分钟完成指
定个数的仰卧起坐练习。 结果王红完成了指定个数的 1.15
倍, 李芳完成了指定个数的 110%。 谁完成的个数多?
要知道谁完成的个数多, 可以比
较哪两个数的大小? 怎样比?
可以先把小数改写 可以先把百分数改
要知道谁完成的
成百分数, 再比较。 写成小数, 再比较。
个数多, 只要比
较 1.15 和 110%
哪个大。
115 110
1.15 = = 115% 110% = = 1.1
100 100
115% > 110% 1.15 > 1.1
…… ……
1.15 110%
答: 完成的个数多。
试一试
1. 把下面的小数改写成百分数, 并把百分号前面的数与原来的小数
比较, 你有什么发现?
( ) ( )
0.3 = = =( )%
10 100
( ) ( )
0.248 = = =( )%
1000 100
想一想, 怎样把小数直接改写成百分数?
怎样把百分数直接改写成小数?
2. 你能把下面的百分数直接改写成小数吗?
27% =( ) 150% =( ) 13.5% =( )
86百 分 数
练一练
1. 把 0.25、 0.08、 0.8、 1.7、 2 改写成百分数。
2. 把 43%、 131%、 16%、 1.6%、 0.4%改写成小数。
3 青阳小学六年级一班的体育委员调查了全班同学中会游泳和
会溜冰的人数, 得到如下结果:
会游泳的 会溜冰的 你会用百分
数表示表中
3 2
占全班人数的几分之几 的分数吗?
5 7
先把分数改写成小数,
再改写成百分数。
3
(1) = 3 ÷ 5 = 0.6 = 60%
5
2
(2) = 2 ÷ 7 ≈ 0.286* = 28.6%
7
试一试
把下面的百分数改写成分数。
( ) ( ) ( )
23% = 75% = =
100 100 ( )
( ) ( ) ( )
12.5% = = =
100 1000 ( )
想一想: 把分数改写成百分数时要
注意什么? 把百分数改写成分数呢?
练一练
1 1 3 1 5
1. 把 、 、 、 、 改写成百分数。
5 4 8 3 9
2. 把 27%、 40%、 65%、 145%、 2.6%改写成分数。
*计算中遇到除不尽时, 一般保留三位小数(即在百分号前面保留一位小数)。
87百 分 数
练习十四
1. 读出下面的百分数, 并说出每个百分数的含义。
我们班有40%
的同学会游泳。
50%苹果汁
40%葡萄汁
2. 写出下面横线上的百分数。
我国西部地区资源十分丰富, 其中
我国西部地区幅员辽阔, 土地面 煤炭储量大约占全国的百分之八
积大约占全国的百分之七十一, 十, 石油储量大约占百分之十七,
人口大约占全国的百分之二十九。 天然气储量大约占百分之七十八。
3. 下面哪些分数可以用百分数表示, 哪些不能? 为什么?
97 75
(1)一堆煤 吨, 运走了它的 。
100 100
23 46 50
(2) 米相当于 米的 。
100 100 100
4. 地球上陆地面积大约占29%, 海洋面积大约占71%。
(1)陆地面积与地球总面积的比大约是( ):( )。
(2)海洋面积与地球总面积的比大约是( ):( )。
5. 东方小学教学楼的占地面积与操场面积的比是27: 100, 艺术楼的
占地面积与操场面积的比是19: 100。
(1)教学楼的占地面积相当于操场面积的( )%。
(2)艺术楼的占地面积相当于操场面积的( )%。
88百 分 数
6. 目前我国的残疾人大约占全国总人口的6%, 残疾
儿童入学率已达到95%。 残疾人与全国总人口的
比大约是( ):( ), 残疾儿童入学的人数与
残疾儿童总人数的比是( ):( )。
7. 几种食物中蛋白质和脂肪的含量如下表:
鸡 蛋 鸡 肉 黄 豆 带 鱼 花 生
蛋白质 12.8% 19.3% 35.1% 17.7% 12.1%
脂 肪 11.1% 9.4% 16.0% 4.9% 25.4%
(1)在这几种食物中, 蛋白质含量最高的是哪一种? 最低的呢?
脂肪含量最高和最低的呢?
(2)100 克黄豆中大约含蛋白质和脂肪各多少克? 其他食物呢?
8. 小明从网上下载一份文件, 下图表示下载的进度。 图中的 65%
表示什么? 还有多少没有下载?
已完成65%
9. 下面是三家超市十月份的营业额示意图:
比佳美超市
多20% 比佳美超市 (1) 至诚超市十月份的营业额相当于
少15%
佳美超市的( )%。
(2) 大达超市十月份的营业额相当于
佳美超市的( )%。
至诚 佳美 大达
超市 超市 超市
10. 学校进行团体操表演, 男生人数占 40%。 如果有 100 人参加表
演, 男生有( )人; 如果有 200 人参加表演, 男生有( )人。
11. 我们学校的女生 我们学校的女生
人数占49%。 人数也占 49%。
这两个学校的女生人数一定相等吗? 为什么?
89百 分 数
1 2 2 3 3 1
12. ÷ = 1 ÷ = + = × 5 =
5 3 5 4 4 8
13. 把相等的两个数连起来。
1.05 2.13 0.09 1.5 0.13 0.009
150% 9% 13% 213% 0.9% 105%
14. 把 0.4、 0.752、 1.36、 0.018、 3.9 改写成百分数。
15. 把 80%、 8%、 56%、 200%、 0.7%改写成小数或整数。
16.
( )
(1)红色方格占方格总数的 , 也就是( )%。
( )
( )
(2)橘色方格相当于红色方格的 , 也就是( )%。
( )
7 3 5 4 9
17. 把 、 、 、 、 改写成百分数。
10 4 8 7 11
18. 把 45%、 18%、 125%、 4%、 0.6%改写成分数。
19. 下面每个大正方形都表示“1”, 分别用分数、 小数和百分数表
示图中的涂色部分。
分 数( ) 分 数( ) 分 数( )
小 数( ) 小 数( ) 小 数( )
百分数( ) 百分数( ) 百分数( )
20. 先求出下面各题的商, 再把它们改写成百分数。
3 ÷ 8 3.2 ÷ 8 20 ÷ 16 7 ÷ 9
90百 分 数
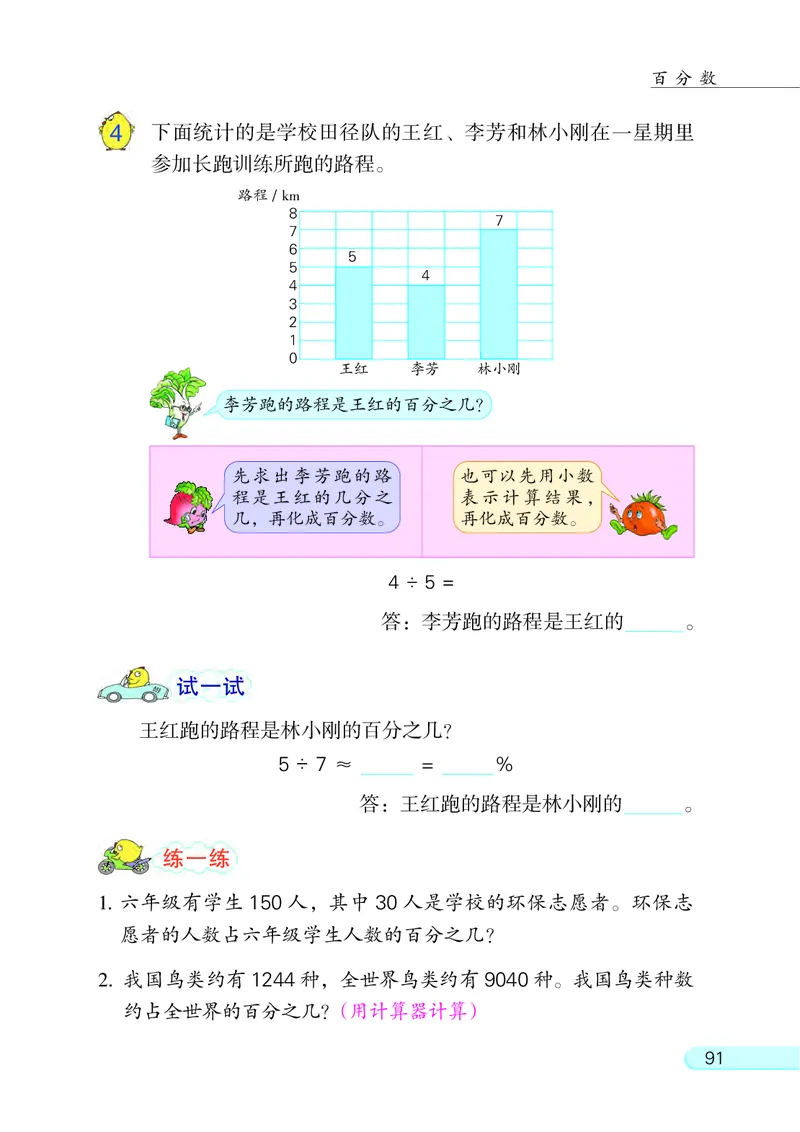
4 下面统计的是学校田径队的王红、 李芳和林小刚在一星期里
参加长跑训练所跑的路程。
路程 / km
8
7
7
6
5
5
4
4
3
2
1
0
王红 李芳 林小刚
李芳跑的路程是王红的百分之几?
先求出李芳跑的路 也可以先用小数
程是王红的几分之 表示计算结果,
几, 再化成百分数。 再化成百分数。
4 ÷ 5 =
答: 李芳跑的路程是王红的 。
试一试
王红跑的路程是林小刚的百分之几?
5 ÷ 7 ≈ = %
答: 王红跑的路程是林小刚的 。
练一练
1. 六年级有学生 150 人, 其中 30 人是学校的环保志愿者。 环保志
愿者的人数占六年级学生人数的百分之几?
2. 我国鸟类约有 1244 种, 全世界鸟类约有 9040 种。 我国鸟类种数
约占全世界的百分之几?(用计算器计算)
91百 分 数
5 学校田径队有 40 人, 下面是田径队某星期每天早晨参加训练
的人数统计。
星 期 一 二 三 四 五
出勤人数 39 38 40 40 38
田径队星期一的出勤率是多少?
出勤率表示实际出勤人数占应出勤人数的百分之几。
39 ÷ 40 = =
答: 星期一的出勤率是 。
从上表中再选择两天的数据,
分别算出相应的出勤率。
答: 星期 的出勤率是 , 星期 的出勤率是 。
练一练
1. 下面的百分率各表示什么含义?
2011 年我国小学学龄儿童入学 2011 年我国的森林覆盖率已达
率已达到 99.8%。 到 20.4%。
2. 学校今年春季植树 50 棵, 成活了 43 棵。 求这批树苗的成活率。
3. 举出生活中百分率的例子, 并说说怎样求出这些百分率。
92百 分 数
6 东山村去年原计划造林 16 公顷, 实际造林 20 公顷。 实际造
林面积比原计划多百分之几?
原计划造林
实际比原
16公顷 计划多的
实 际 造 林
20公顷
怎样理解“实际造林面积比
原计划多百分之几”?
“实际造林面积比原计划多百分之几” 就是实际比
原计划多造林的面积相当于原计划的百分之几。
这道题可以先算什么? 你能试着做一做吗?
先算实际造林是原计划
先算实际造林比原计划
的百分之几, 再算……
多多少公顷, 再算……
20 - 16 = 4(公顷) 20 ÷ 16 = 1.25 = 125%
4 ÷ 16 = 0.25 = 25% 125% - 100% = 25%
答: 实际造林面积比原计划多 。
如果把问题改成“原计划造林面积比实际少百分之几”, 应该
怎样解答?
答: 原计划造林面积比实际少 。
比较这两题的解法和计算结果, 你有什么发现? 与同学交流。
练一练
鸵鸟蛋的孵化期大约是 42 天, 鸽蛋的孵化期大约是 18 天。 鸽
蛋的孵化期比鸵鸟蛋短百分之几?
93百 分 数
练习十五
1. 校园里有杨树 80 棵, 柳树 50 棵。 柳树的棵数相当于杨树的百分
之几? 杨树的棵数相当于柳树的百分之几?
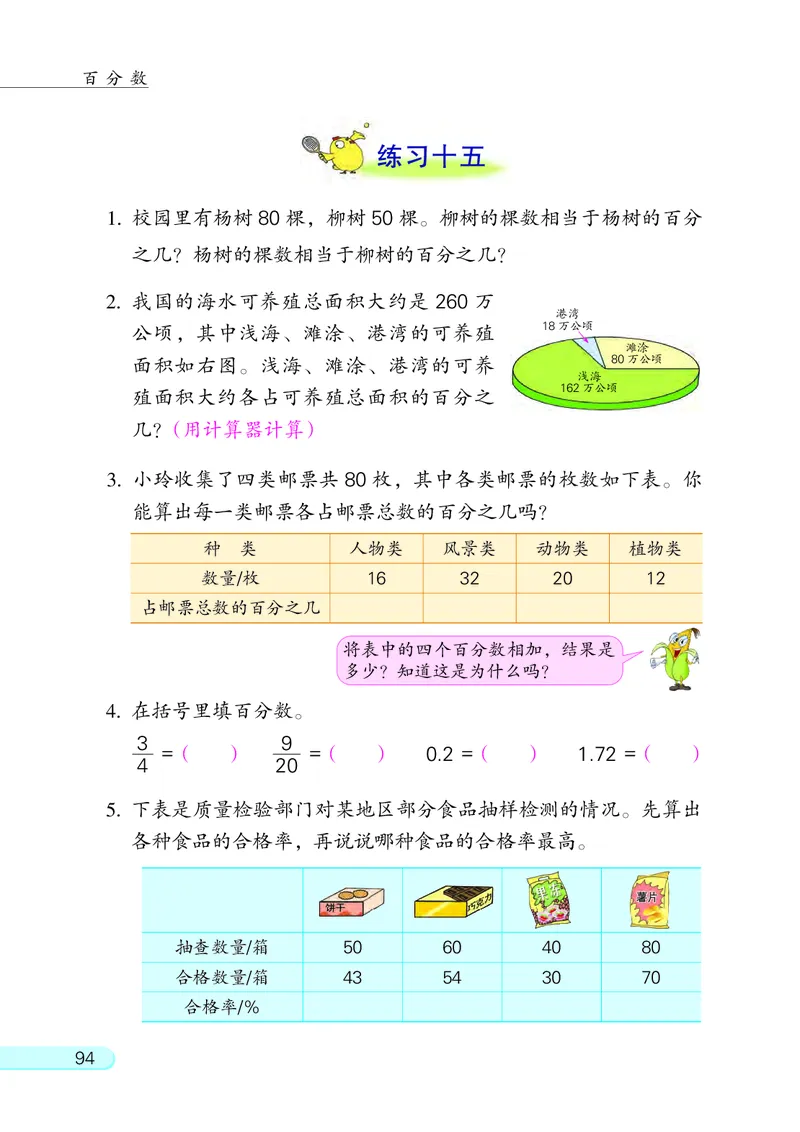
2. 我国的海水可养殖总面积大约是 260 万
港湾
公顷, 其中浅海、 滩涂、 港湾的可养殖 18万公顷
滩涂
面积如右图。 浅海、 滩涂、 港湾的可养 80万公顷
浅海
162万公顷
殖面积大约各占可养殖总面积的百分之
几?(用计算器计算)
3. 小玲收集了四类邮票共 80 枚, 其中各类邮票的枚数如下表。 你
能算出每一类邮票各占邮票总数的百分之几吗?
种 类 人物类 风景类 动物类 植物类
数量/枚 16 32 20 12
占邮票总数的百分之几
将表中的四个百分数相加, 结果是
多少? 知道这是为什么吗?
4. 在括号里填百分数。
3 9
=( ) =( ) 0.2 =( ) 1.72 =( )
4 20
5. 下表是质量检验部门对某地区部分食品抽样检测的情况。 先算出
各种食品的合格率, 再说说哪种食品的合格率最高。
抽查数量/箱 50 60 40 80
合格数量/箱 43 54 30 70
合格率/%
94百 分 数
6. 今年 8 月 12 日某市抽样调查了 800 名学生, 其中有 360 人观
看了市电视台的《快乐儿童》节目。 求《快乐儿童》节目的学生收
视率。
7. 学校生物小组用两种不同的大豆
种子做发芽试验, 结果如下表:
第一种 第二种
发芽率 92% 97%
(1)哪种大豆种子的发芽率高一些?
(2)第二种大豆种子发芽的粒数一定比第一种多吗? 为什么?
发芽率有可能超过 100%吗?
8. (1) 如果两个杯里都加入 40 克糖, 哪
杯糖水的含糖率高一些?
(2) 如果左杯加入 60 克糖, 右杯加入
45 克糖。 哪杯糖水会更甜一些?
300克 200克
9. 填空。
(1)2011 年我国国内生产总值是 2010 年的 117.8%, 2011年比
2010年增长( )%。
(2) 1990 年我国城镇居民人均可支配收入比 2011年少 93.8%,
1990年我国城镇居民人均可支配收入是2011年的( )%。
(3)2011 年我国的人均水资源量是 2010 年的 74.9%, 2011年
我国的人均水资源量比2010年下降了( )%。
10. 我国第一大岛台湾岛的面积大
约是 3.6 万平方千米, 第二大
岛海南岛的面积大约是 3.4 万
平方千米。 台湾岛的面积比海
台湾岛 海南岛
南岛大约大百分之几?
95百 分 数
11. 一条带鱼长 72 厘米, 重 450 克。 一条海鳗长 36 厘米, 重 820
克。 带鱼的体长比海鳗长百分之几? 体重比海鳗轻百分之几?
12. 直接写出得数。
4 1 1 2 3 1 10
× = + = - = ÷ 5 =
3 2 4 5 4 2 11
5 2 4 3 2 1 7 4
- = ÷ = + = × =
6 3 5 5 9 3 12 7
13. 六年级一班有 48 人, 其中 30 人会游泳。
(1)会游泳的占全班人数的百分之几?
(2)不会游泳的占全班人数的百分之几?
14. 车站运一批货物, 已经运走 65 吨, 还剩下 15 吨。 还剩下百分
之几没有运走?
15.(1) 小红身高 135 厘米, 小娟身高 150 厘米。 小娟的身高是小
红的百分之几?
(2) 小红身高 135 厘米, 小娟身高 150 厘米。 小娟比小红高百
分之几?
(3)小红身高 135 厘米, 小娟比小红高 15 厘米。 小娟的身高是
小红的百分之几?
16.
巧克力的单价比奶糖贵百分之几? 比水果糖和酥糖呢?
17. 用计算器算出我国铁路和公路客运量 2011 年比 2010 年增长
的百分数, 填入表中。
2010年 2011年 2011年比 2010年增长的百分数
铁路客运量/亿人次 16.76 18.62
公路客运量/亿人次 305.3 328.6
哪一种运输方式客运量的增长速度更快一些?
96百 分 数
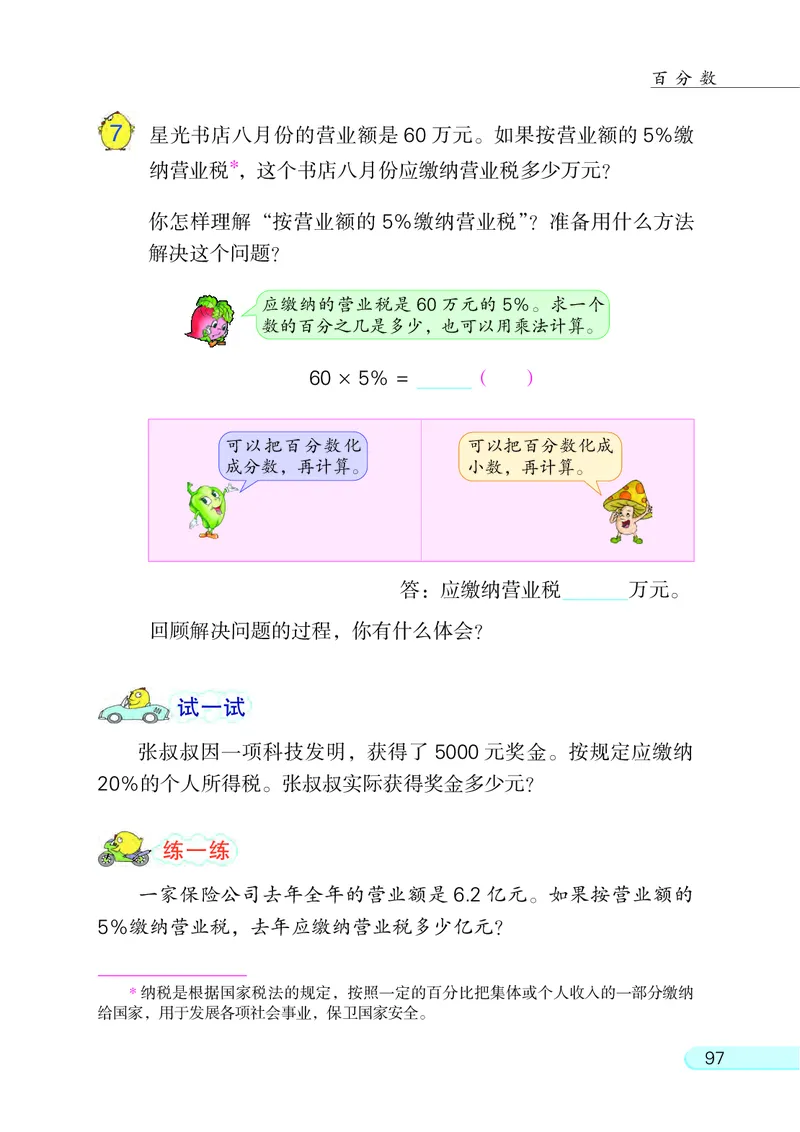
7 星光书店八月份的营业额是 60 万元。 如果按营业额的 5%缴
纳营业税*, 这个书店八月份应缴纳营业税多少万元?
你怎样理解“按营业额的 5%缴纳营业税”? 准备用什么方法
解决这个问题?
应缴纳的营业税是 60 万元的 5%。 求一个
数的百分之几是多少, 也可以用乘法计算。
60 × 5% = ( )
可以把百分数化 可以把百分数化成
成分数, 再计算。 小数, 再计算。
答: 应缴纳营业税 万元。
回顾解决问题的过程, 你有什么体会?
试一试
张叔叔因一项科技发明, 获得了 5000 元奖金。 按规定应缴纳
20%的个人所得税。 张叔叔实际获得奖金多少元?
练一练
一家保险公司去年全年的营业额是 6.2 亿元。 如果按营业额的
5%缴纳营业税, 去年应缴纳营业税多少亿元?
*纳税是根据国家税法的规定, 按照一定的百分比把集体或个人收入的一部分缴纳
给国家, 用于发展各项社会事业, 保卫国家安全。
97百 分 数
8 2012 年 10 月 8 日, 亮亮把 400 元按二年期整存整取存入银
行, 到期后应得利息*多少元?(当时银行公布的储蓄年利率如
下表)
存期(整存整取) 年利率
一 年 3.25%
二 年 3.75%
三 年 4.25%
五 年 4.75%
利息 = 本金 × 利率 × 时间
400 × 3.75% × 2 = ( )
答: 到期后应得利息 元。
试一试
2012 年 12 月 10 日, 丹丹把 500 元存入银行, 定期一年, 年
利率是 3.25%。 到期后应从银行取回多少元?
到期后应取回的钱包括哪两个
部分? 怎样解答上面的问题?
答: 到期后应从银行取回 元。
练一练
2012 年 11 月, 王大爷把 20000 元存入银行, 定期三年, 年利
率是 4.25%。 到期后, 应得利息多少元?
*储蓄主要有定期和活期两种。 存入银行的钱叫作本金。 取款时银行除还给本金
外, 另外付的钱叫作利息。 利息占本金的百分率叫作利率, 按年计算的叫作年利率。
银行存款利率有时会根据国家经济的发展变化而有所调整。
98百 分 数
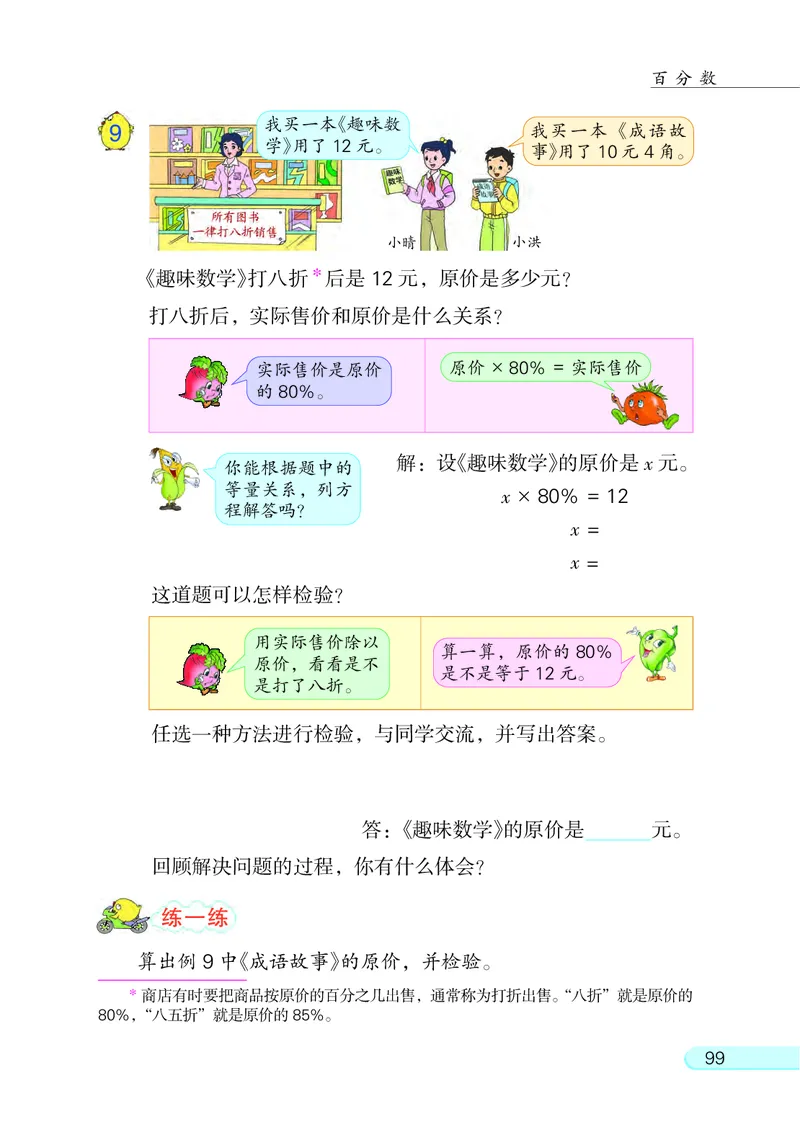
我买一本《趣味数
9 我买一本《成语故
学》用了12元。
事》用了10元 4角。
小晴 小洪
《趣味数学》打八折*后是 12 元, 原价是多少元?
打八折后, 实际售价和原价是什么关系?
实际售价是原价 原价 × 80% = 实际售价
的80%。
解: 设《趣味数学》的原价是 x 元。
你能根据题中的
等量关系, 列方
x × 80% = 12
程解答吗?
x =
x =
这道题可以怎样检验?
用实际售价除以
算一算, 原价的 80%
原价, 看看是不
是不是等于 12元。
是打了八折。
任选一种方法进行检验, 与同学交流, 并写出答案。
答:《趣味数学》的原价是 元。
回顾解决问题的过程, 你有什么体会?
练一练
算出例 9 中《成语故事》的原价, 并检验。
*商店有时要把商品按原价的百分之几出售, 通常称为打折出售。“八折” 就是原价的
80%,“八五折” 就是原价的85%。
99百 分 数
练习十六
1. 某旅游景区上个月共接待游客 12 万人次, 门票收入 360 万元。
按门票收入的 3%缴纳营业税, 上个月应缴纳营业税多少万元?
2. 某服装厂去年销售服装的收入总额是 840 万元。 按规定应缴纳
17%的增值税。 一共要缴纳增值税多少万元?
3. 朱晓刚给杂志社审稿, 获得审稿费 900 元。 他需要按照 3%缴
纳个人所得税, 纳税后, 他实际得到多少元?
( ) 3
4. 0.75 = =( )% =( )÷( )=( )%
( ) 5
5. 2012 年 8 月, 胡强把 5000 元存入银行, 定期五年, 年利率是
4.75%。 到期后, 应得利息多少元?
6. 2012 年 9 月, 冯明把 3000 元存入银行, 定期一年, 年利率是
3.25%。 到期后, 一共可以获得本息多少元?
7. 说一说下面各种商品是打几折出售的。
(1)一台电视机按原价的 70%出售。
(2)一架钢琴按原价的 95%出售。
(3)一件衣服按原价的 68%出售。
8.
你能算出右边商品
打折后的价钱吗?
原价68.00元/个 原价380.00元/台
九折出售 七五折出售
9. 王叔叔以八五折的优惠价买了一辆自行车, 实际付了 357 元。
这辆自行车的原价是多少元?
10. 一台取暖器原价 280 元, 现在的售价是 252 元。 这台取暖器是
打几折出售的?
100百 分 数
11. 解方程。
40%x = 144 x - 25%x = 3 x + 20%x = 180
12. 徐奶奶 2012 年 3 月把 3000 元存入银行, 定期三年, 年利率是
5.00%。 到期后, 她一共可取回多少元?
13. 某电影城去年的营业额是 600 万元。 预计今年的营业额将比去
年增加 20%, 今年的营业额将达到多少万元? 如果按营业额的
3%缴纳营业税, 预计今年要缴纳营业税多少万元?
14. (1) 这件夹克的实际售价
原价120元 原 价
80元
是多少元?
(2) 买这件西服比原来便
八五折 七八折
出售 出售
宜多少元?
15.(1) 张阿姨买一件羊毛衫用了 180
元, 这件羊毛衫原价多少元?
(2)一件西服原价 480 元, 现在售价
多少元? 使用商场贵宾卡, 可以
再打九五折。 李阿姨用贵宾卡买这件西服, 需要多少元?
16. 李小军按九折的优惠价格购买了 2 张足球赛门票, 一共用去 54
元。 每张门票的原价是多少元?
17. 孙华买了一辆 6400 元的摩托车。 按规定, 买摩托车要缴纳
10%的车辆购置税。 他买这辆摩托车一共要花多少元?
你知道吗
在农业生产中, 粮食、 棉花等农作物收成的变化情况, 常用
“成数” 来表示。“一成” 是十分之一, 改写成百分数是 10%;“三成
五” 是十分之三点五, 改写成百分数是 35%。“成数” 还用来表示各
行各业的发展变化情况。
101百 分 数
10
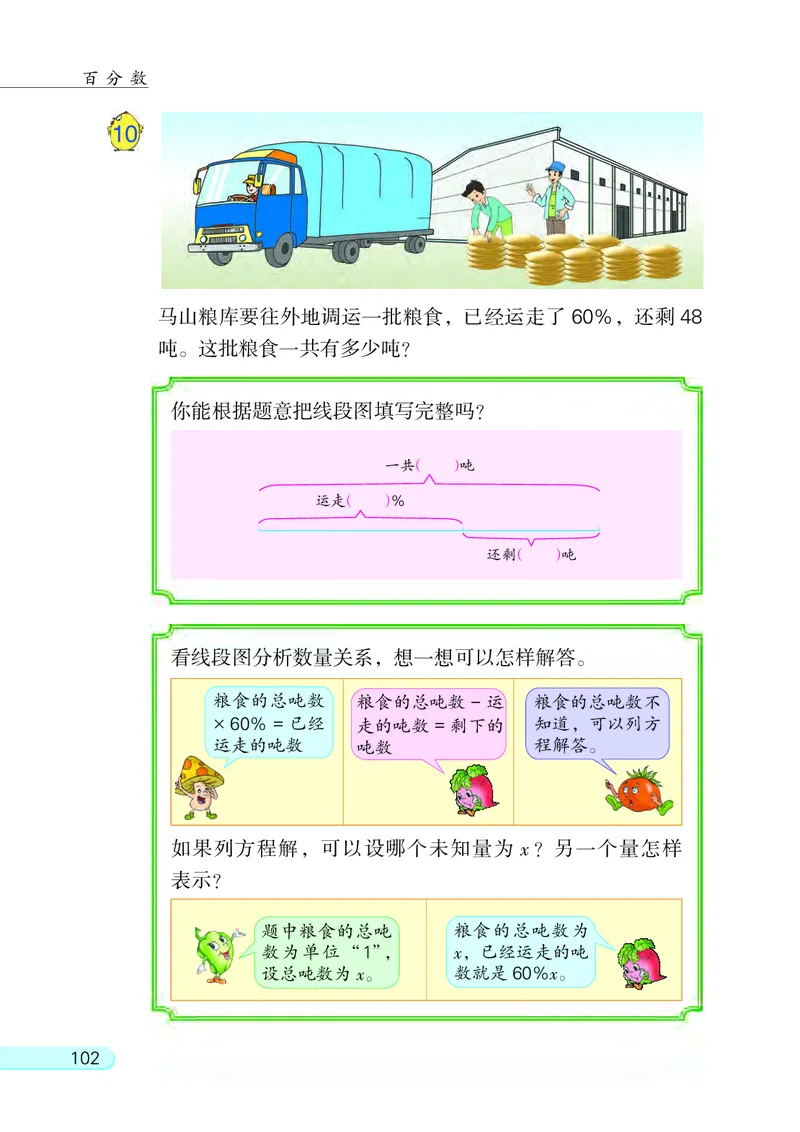
马山粮库要往外地调运一批粮食, 已经运走了 60%, 还剩 48
吨。 这批粮食一共有多少吨?
你能根据题意把线段图填写完整吗?
一共( )吨
运走( )%
还剩( )吨
看线段图分析数量关系, 想一想可以怎样解答。
粮食的总吨数 粮食的总吨数 - 运 粮食的总吨数不
× 60% = 已经 走的吨数 = 剩下的 知道, 可以列方
运走的吨数 吨数 程解答。
如果列方程解, 可以设哪个未知量为 x? 另一个量怎样
表示?
题中粮食的总吨 粮食的总吨数为
数为单位“1”, x, 已经运走的吨
设总吨数为 x。 数就是60%x。
102百 分 数
列方程并解答。
解: 设这批粮食一共有 x 吨。
x - 60% x = 48
你想怎样检验? 与同学交流。
答: 这批粮食一共有 吨。
回顾解决问题的过程, 你有什么体会?
要理解已知条件中 根据数量关系的特 列方程解答要选择
百分数的意义, 弄 点, 确定是否用方 一个合适的未知
清数量之间的关系。 程解答。 量, 把它设为 x。
练一练
1. 先把数量关系式填写完整, 再列方程解答。
(1) 某工程队铺一条地下电缆, 已经铺了 350 米, 还剩 75%没
有铺。 这条电缆长多少米?
( )米数 -( )米数 =( )米数
(2) 西林小学六年级有男生 94 人, 女生人数占全年级总人数的
53%。 六年级一共有多少人?
( )人数 -( )人数 =( )人数
2. 建筑工地要运进一批水泥, 已经运了 30%, 还剩下 56 吨没有
运。 这批水泥有多少吨?
103百 分 数
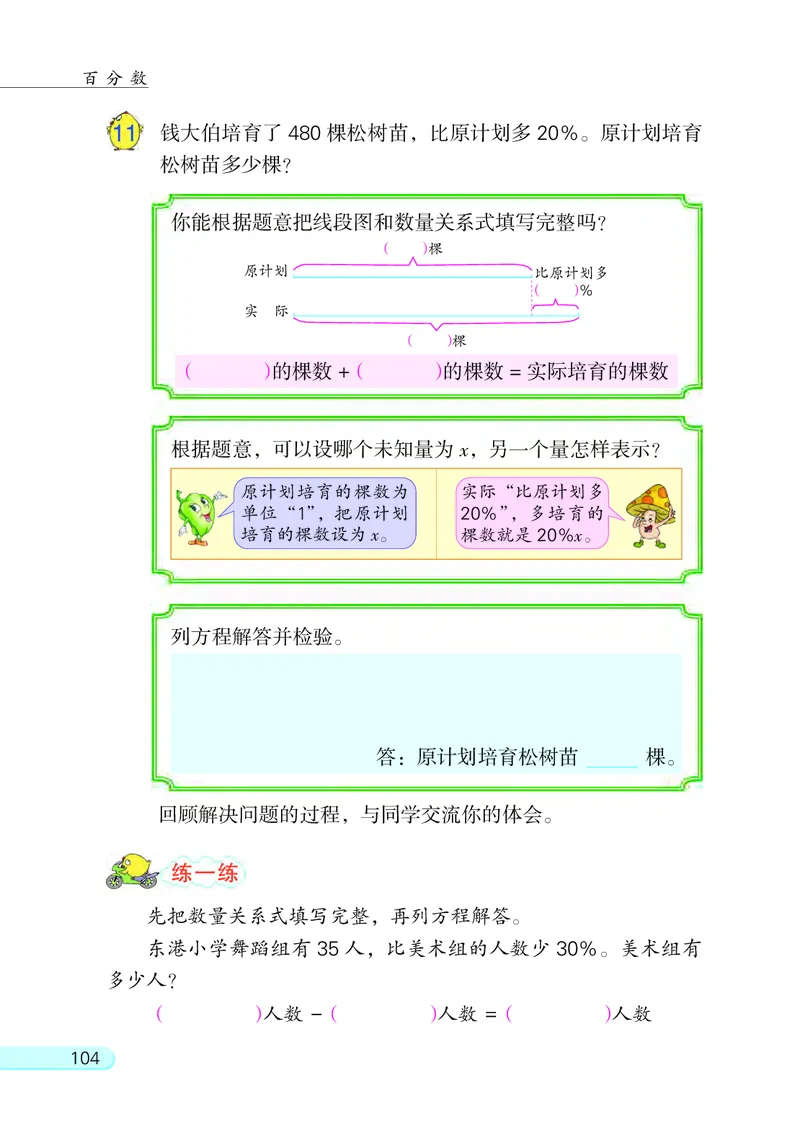
11 钱大伯培育了 480 棵松树苗, 比原计划多 20%。 原计划培育
松树苗多少棵?
你能根据题意把线段图和数量关系式填写完整吗?
( )棵
原计划 比原计划多
( )%
实 际
( )棵
( )的棵数 +( )的棵数 = 实际培育的棵数
根据题意, 可以设哪个未知量为 x, 另一个量怎样表示?
原计划培育的棵数为 实际“比原计划多
单位“1”, 把原计划 20%”, 多培育的
培育的棵数设为x。 棵数就是 20%x。
列方程解答并检验。
答: 原计划培育松树苗 棵。
回顾解决问题的过程, 与同学交流你的体会。
练一练
先把数量关系式填写完整, 再列方程解答。
东港小学舞蹈组有 35 人, 比美术组的人数少 30%。 美术组有
多少人?
( )人数 -( )人数 =( )人数
104百 分 数
练习十七
1. 解方程。
x + 60% x = 48 x - 25% x = 27 x - 35% x = 0.52
2. 谷丰旅游公司去年上半年的营业额是 230 万元, 下半年的营业额
占全年的 54%。 去年全年的营业额是多少万元?
3.(1)一桶油, 用去 25%, 正好用去 2.5 千克。 这桶油重多少千克?
(2)一桶油, 用去 25%, 还剩 7.5 千克。 这桶油重多少千克?
4. 解方程。
2 1 2 1 1 1
x + x = x - x =
15 6 5 2 3 10
5. 东方村今年水稻产量是 38.5 吨, 比去年增产 10%。 去年水稻产
量是多少吨?
6. 一件毛衣现在售价 51 元, 比原来降价 15%。 原来售价多少元?
7. 华光玩具商店上个月售出电动轮船 240 艘。
售出的电动轮船比电 售出的电动轮船比电
动汽车少 20%, 售 动飞机多 20%, 售
出电动汽车多少辆? 出电动飞机多少架?
8.
建造这座污水处
理池实际投资比
原计划节约10%。
(1)节约了 4.8 万元, 原计划投资多少万元?
(2)实际投资 43.2 万元, 原计划投资多少万元?
3 1 8 8 9 1 3
9.( - )÷ ÷[ -( + )]
4 2 15 49 8 8 7
105百 分 数
10.
桃树和梨树一共有 96 棵, 根据下面
的条件算出桃树和梨树各有多少棵。
(1)桃树的棵数是梨树的 3 倍。
1
(2)梨树的棵数是桃树的 。
3
11. 育新苗圃柏树苗的占地面积是松树苗的 80%, 两种树苗共占地
9 公顷。 两种树苗各占地多少公顷?
12. 同学们种蓖麻的棵数是种向日葵棵数的 75%。
(1)向日葵和蓖麻一共种了 147 棵, 向日葵和蓖麻各有多少棵?
(2)种的向日葵比蓖麻多 21 棵, 向日葵和蓖麻各有多少棵?
13.(1) 织女星的运行速度是 14 千米/秒, 相当于牛郎星运行速度的
7
。 牛郎星的运行速度是多少?
13
(2) 织女星的运行速度是 14 千米/秒, 比牛郎星的运行速度慢
6
。 牛郎星的运行速度是多少?
13
7
14. 新民食品厂九月份生产的牛奶饼干比果汁饼干少 吨, 牛奶饼
2
5
干的吨数是果汁饼干的 。 两种饼干各生产多少吨?
6
1
15. 小星看一本课外书, 第一天看了全书的 , 第二天看了全书的
6
1
, 两天一共看了 33 页。 这本书有多少页?
5
1
学校田径队女生人数原来占 , 后来有 6 名女生加入, 这样
3
4
女生人数就占田径队总人数的 。 现在田径队有女生多少人?
9
106百 分 数
整理与练习
回顾与整理
小组讨论:
1. 举例说说什么是百分数, 百分数与分数、 比有什么联系和区别。
2. 说说你对生活中一些常见百分率的理解。 怎样求一个数是另
一个数的百分之几?
3. 通过解决有关百分数的实际问题, 你有哪些体会和收获?
练习与应用
1. 下面是第六次全国人口普查公布的我国人口的一些数据。 先读一
读表中的百分数, 再回答问题。
性 别 年龄/岁 民 族
男 女 0~14 15~64 65及以上 汉族 少数民族
大约占总人
51.3% 48.7% 16.6% 74.5% 8.9% 91.5% 8.5%
口的百分数
(1) 我国人口中, 男性多还是女性多? 男性人口与总人口的比是
几比几? 女性人口与总人口的比呢?
(2)从年龄和民族看, 你还能知道些什么?
2.
3 4
分 数
8 9
小 数 0.7 1.45
百分数 17.5%
3. 几种体育运动每小时的耗氧量如下表:
运动项目 打篮球 游 泳 散 步
耗氧量(/ 升/时) 90 100 60
(1)散步时每小时的耗氧量比游泳少百分之几? 比打篮球呢?
(2)打篮球时每小时的耗氧量比游泳少百分之几? 比散步呢?
107百 分 数
4. 先填空, 再说说哪一种原料的出油率最高。
榨油原料 花生仁 大 豆 油菜籽
原料的千克数 160 200
出油的千克数 40 48
出油率 16% 40%
5. 番茄中的水分大约占 90%, 糖分大约占 3%。 5 千克番茄中大
约含水和糖各多少千克?
6. 据统计, 我国陆栖脊椎动物大约有 2070 种, 占世界陆栖脊椎动
物的 9.8%。 世界陆栖脊椎动物大约有多少种?(用计算器计算,
得数保留整数)
7. 清江饭店五月份的营业额是 64 万元。 按规定, 要缴纳 5%的营
业税, 还要按营业税额的 7%缴纳城市维护建设税。 五月份应
缴纳城市维护建设税多少万元?
8. 乘坐飞机的每位旅客, 携带行李超过 20 千克的部分, 每千克要
按飞机票原价的 1.5%购买行李票。 张芳从南京乘飞机到北京,
票价打七折后是 707 元。 南京到北京飞机票的原价是多少元?
张芳带了 30 千克行李, 应付行李费多少元?
9. 解方程。
x + 30% x = 26 x - 15% x = 170 x + 80% x = 7.2
10.(1) 某市修建一条 12 千米长的高架公路,已经修了全长的60%,
还有多少千米没有修?
(2) 某市修建一条高架公路, 已经修了全长的 60%, 还有 4.8
千米没有修。 这条高架公路长多少千米?
11.(1) 某市居民用水价格原来是每立方米1.5元, 现在提高了20%,
提价后每立方米水价多少元?
(2) 某市居民用水价格提高 20%后, 每立方米水价 1.8 元。 提
价前每立方米水价多少元?
108百 分 数
12. 黄铜是铜和锌的合金, 其中铜的含量是 68%。 一块黄铜里含锌
16 千克, 这块黄铜重多少千克?
13. 我国的淡水鱼类大约有 840 种, 比海洋鱼类少 74%。 我国的海
洋鱼类大约有多少种?(得数保留整数)
探索与实践
14. 在一个盘里铺几层滤纸或纱布, 喷洒
适量的水, 并均匀地铺上 50 粒黄豆或
蚕豆种子做发芽试验。 每天记录发芽的
种子数, 7天后算出发芽率。
时 间 第 1 天 第2天 第3天 第4天 第5天 第6天 第7天
发芽的种子数
15. 调查本班同学参加课外体育锻炼的情况, 并填写下表。
每周锻炼时间 不足 2小时 2 ~ 4小时 超过 4 小时
人 数
占被调查人数的百分之几
16. 从报刊、 电视、 网络等媒体中收集一些百分数, 说说它们的含
义, 与同学交流。
评价与反思
能联系生活实例理解百分数的意义, 并联系分数、
☆☆☆☆☆
比等知识进行思考
能主动探索分数、 小数和百分数互相改写的方法,
☆☆☆☆☆
正确进行改写
能根据百分数的意义, 正确理解实际问题的数量
☆☆☆☆☆
关系, 主动探索解决问题的方法, 反思解题结果的
合理性
109互联网的普及
阅 读 与 讨 论
你知道互联网吗? 利用互联网可以做哪些事?
可以在网上查 可以在网上阅 可以在网上与同
找资料, 学习 读新闻, 了解 学联系, 还可以
各种知识。 国家大事。 下载音乐……
互联网在日常生活中应用非常广泛, 它给我们的生活带来了很
大的方便。 2002 年, 我国互联网接入宽带用户仅 0.03 亿户, 上网
人数也只有 0.59 亿人。 随着时代的发展, 互联网的普及率* 不断上
升。 下面是 2002 ~ 2012 年关于互联网的一些统计数据:
年 份 2002 2004 2006 2008 2010 2012
接入宽带用户/亿户 0.03 0.25 0.51 0.83 1.26 1.75
上网人数/亿人 0.59 0.94 1.37 2.98 4.57 5.64
互联网普及率/% 4.6 7.3 10.5 22.6 34.3 42.1
读了这一段文字, 你有什么感想?
统 计 与 分 析
你们班同学中互联网的普及情况怎么样? 全班同学的家庭呢?
可以从哪些方面了解这些问题?
*互联网普及率是指某个地区(或国家)的互联网上网人数与该地区(或国家)的人口
总数的比。
110综合与实践
统计同学家庭 统计全班上网的 还可以统计全
中接入宽带的 人数, 并算出班 班同学家庭成
户数有多少。 级的普及率。 员的上网情况。
先分小组进行调查, 再整理数据, 完成下表。
家庭户数 接入互联网宽带的户数 占全班家庭户数的百分比
总人数 上网人数 上网人数占总人数的百分比
班级同学
全班家庭成员
通过上面的统计, 你认为你们班同学
家庭互联网的普及情况怎么样?
如果要了解你们班同学用互联网做些什么, 可以怎样设计调查
表? 怎样收集和整理数据?
调查并收集、 整理数据, 完成下表, 并说说有什么想法。
查阅资料 学习知识 阅读新闻 联系同学 下载音乐
人 数
占上网人数的百分比
回 顾 与 反 思
回顾上面的活动过程, 你有什么收获和体会?
通过统计, 能了解互 从互联网普及率的变 要充分利用网络
联网在全班同学家庭 化, 看出我国社会的 资源, 合理安排
中的普及情况。 发展越来越快。 上网时间。
111整 理 与 复 习
本学期我们学习了分数的哪些运算? 还学习了有关比和百分
数的哪些知识? 你能用这些知识解决哪些实际问题?
1. 读出下面的百分数, 并说出它的含义。
(1) 2011 年我国农村居民人均纯收入 6977 元, 比 2010 年增长
17.9%。
(2)2011 年, 中国人均水资源占有量是 1730 多立方米, 大约相
当于世界人均水平的 25%。
(3)李师傅某天生产的零件经过检验, 合格率是 100%。
( )
2.(1)125% = =( ):( )
( )
( )
(2)0.45 =( )% =( ):( )=
( )
3. 根据下面的条件, 你能写出哪些比?
(1)10 千克什锦糖中, 有花生糖 3 千克, 奶糖 2 千克, 水果糖 5
千克。
(2)小华 5 分钟走了 350 米,小芳 6 分钟走了 360 米。
4. 先化简, 再求比值。
28 3.6
300: 125 0.45: 0.9
21 9
5. 直接写出得数。
6 7 4 1 1 11
× = 15 × = ÷ = ÷ 22 =
7 9 5 4 2 12
5 5 3 5 3 1 1 1
÷ = × = + = - =
8 12 10 6 4 2 3 4
112整理与复习
6. 计算下面各题。
5 9 12 14 7 21 1 2
× × ÷ ÷
12 20 7 15 15 25 4 3
3 5 3 3 10 7 5
× × ÷ 6 × ÷ 7 ÷
4 9 10 5 7 12 6
7. 下面各题, 怎样算简便就怎样算。
2 5 2 7 5 11 8 2 1 4
+ × ( - )÷ � ÷[( + )× ]
3 8 5 6 9 8 9 5 10 3
5 2 5 5 5 1 5 1 4 5
- - 5 ÷ - × � × + ×
3 7 7 7 7 5 12 5 5 12
5 2
8. 李叔叔骑自行车 分钟行了 千米。
4 5
(1)他平均每分钟行多少千米? 行 1 千米需要多少分钟?
(2)他 20分钟能行多少千米? 行 20 千米需要多少分钟?
9.(1)李桥小学食堂五、 六月用煤量的比是 7: 8, 两个月一共用煤
3
吨。 五、 六月各用煤多少吨?
4
(2) 东湖塘小学食堂五、 六月用煤量的比是 7: 8, 五月用煤
3
吨。 六月用煤多少吨?
4
10. 用 250 克死海的海水能制出 75 克盐, 用 250 克东海的海水能
制出 15 克盐。 死海海水的含盐率是多少? 东海呢?
11. 计算后填空, 再说说这些商品分别是打几折出售的。
原 价/元 90 320 80
实际售价/元 81 220 60
降价百分之几 15% 12%
113整理与复习
12.《中华人民共和国个人所得税法实施条例》规定, 个人月工资收
入超过 3500 元的部分, 应缴纳个人所得税。 马莉每月工资
4200 元, 超过的部分按 3%缴纳个人所得税。
(1)马莉每月应缴纳个人所得税多少元?
(2) 2012 年1 月, 她把节余的 15000 元存入银行, 定期五年,
年利率是 5.50%。 到期后, 应得利息多少元?
13. 湖滨小区的花圃里种植了三种花, 面积如下表:
品 种 杜 鹃 月 季 绣 球
面积/平方米 45 25 20
(1)每种花各占花圃总面积的百分之几?
(2)杜鹃花的面积比月季花多百分之几?
(3)月季花的面积比杜鹃花少百分之几? 比绣球花多百分之几?
14.(1) 张大伯家承包的荒山总面积是 150 公顷, 其中 20%种果树,
剩下的种松树。 种松树的面积是多少公顷?
(2) 张大伯家承包了一片荒山, 其中 20%种果树, 其余的 120
公顷全部种松树。 他家承包的荒山总面积是多少公顷?
2 1 1
15. 食堂运来 吨煤, 用去 吨后, 又用去余下的 。 又用去多
3 4 3
少吨?
16. 少先队员收集植物标本和昆虫标本共
60 件, 植物标本的件数是昆虫标本
1
的 。 两种标本各收集了多少件?
2
17. 动物园有一头大象和一头小象, 小象每天需要的食物是大象的
1
, 比大象少 240 千克。 这两头象每天各需要食物多少千克?
3
114整理与复习
长方体和正方体各有什么特征? 怎样计算它们的表面积和体
积? 举例说说运用这些知识能解决哪些实际问题?
18. 在括号里填合适的单位。
(1)一本数学书的体积大约是 240( )。
(2)一间教室的容积大约是 150( )。
(3)一个书包的体积大约是 14( )。
(4)一个茶叶罐的容积大约是 900( )。
19. 3.05 立方米 =( )立方分米 60 毫升 =( )升
450 立方厘米 =( )立方分米 0.8 升 =( )立方厘米
20. 写出表中物体的形状是长方体还是正方体, 再求出它们的表面
积和体积。
长 宽 高 形 状 表面积 体 积
8厘米 6厘米 4厘米
6厘米 4厘米 4厘米
5厘米 5厘米 5厘米
21. 右边是一个正方体的展开图。 你能
1 2 3
说出这个正方体每组相对的面分别
4 5 6
是几号和几号吗?
22. 一个无盖的长方体玻璃鱼缸, 长 5 分米, 宽 4 分米, 高 3 分米。
(1)做这个鱼缸至少需要玻璃多少平方分米?
(2)在鱼缸里注入 40 升水, 水深多少分米?(玻璃的厚度忽略
不计)
(3) 再往水里放入一些鹅卵石, 水面
上升了 0.3 分米。 鹅卵石的体积
一共是多少立方分米?
115整理与复习
你在生活中发现了哪些数学问题? 你能运用所学的数学知识
和方法解决这些问题吗?
23.(1)我们校园的面积大约是( )平方米, 其中绿化面积大约是
( )平方米, 校园的绿化覆盖率是( )%。
(2) 我们班女生有( )人, 占全班总人数的( )%; 男生有
( )人, 占全班总人数的( )%。 男生人数是女生人数的
( )%, 女生人数是男生人数的( )%。
24. 把长26厘米、 宽18厘米的长方形纸, 从四个角各
剪去一个边长4厘米的正方形, 再折成一个无盖的
长方体纸盒。 这个纸盒的容积是多少立方厘米?
25. 芳芳把 154 个同样的小正方体堆成了三堆。 第一堆比第三堆少
24 个, 第二堆比第三堆少 14 个。 三堆各有多少个小正方体?
第一堆 第二堆 第三堆
回顾自己本学期学习的表现, 能得几个★, 就把几个☆涂上
颜色。
知道学会了什么和还有哪些疑问
☆ ☆ ☆ ☆ ☆
有条理地表达思考过程, 乐于与同学交流
☆ ☆ ☆ ☆ ☆
主动发现和提出问题, 能运用所学知识和方法解决问题
☆ ☆ ☆ ☆ ☆
对学习的内容有兴趣, 遇到困难不轻易放弃
☆ ☆ ☆ ☆ ☆
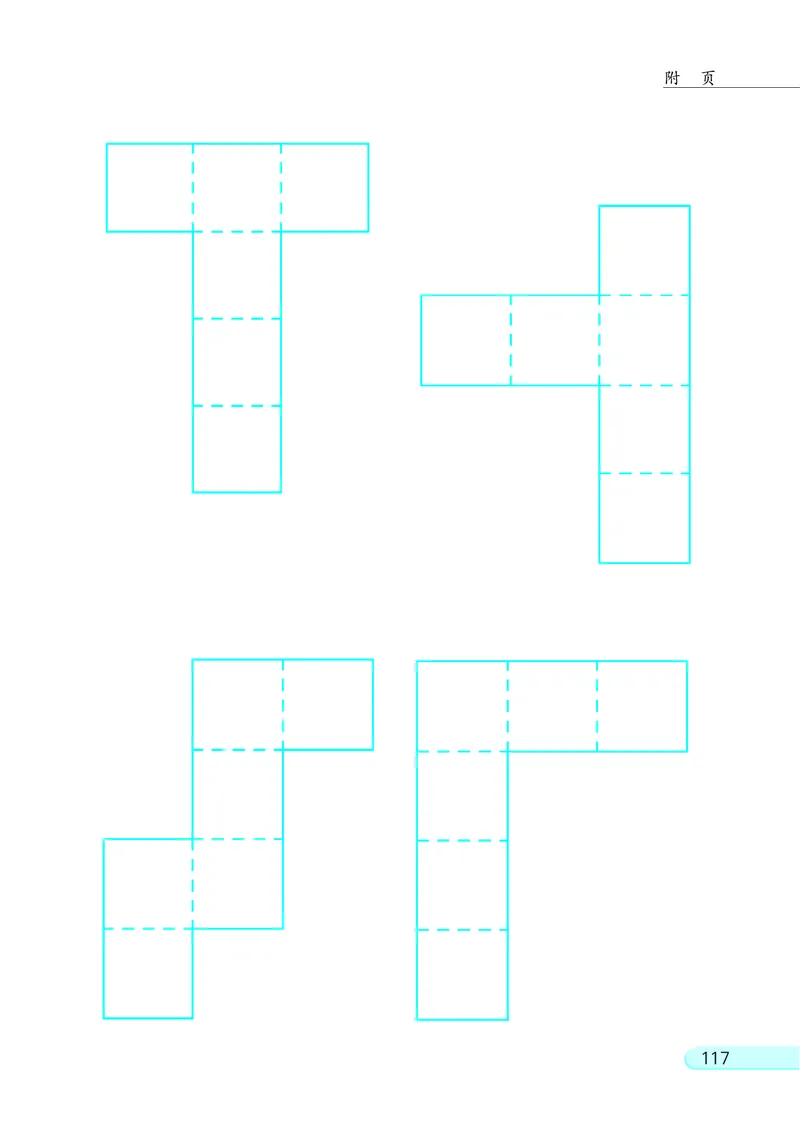
116附 页
117附 页
118附 页
119附 页
120后 记
依据 《义务教育数学课程标准 (2011 年版)》, 我们对原有的
义务教育课程标准小学数学实验教科书进行了修订。 修订时, 充
分考虑未来社会对公民数学素养的要求, 广泛吸收小学数学教学
改革中创造的先进教学方法与经验, 认真分析和研究各方面提出
的建议, 致力促进小学生的数学学习与全面发展。
教科书的主编是孙丽谷、 王林, 副主编是凌国伟、 陈春圣;
主审是盛大启, 副主审是沈重予、 李继海。 本册教科书由楚平、
李新等执笔修订。
本套教科书凝聚了参与课程改革实验的广大教师和教育工作
者的理性思考与实践智慧。 我们衷心地感谢所有对教科书及其修
订工作提出过建议、 提供过帮助和支持的专家、 学者、 教研员和
教师; 真诚地希望大家对教科书提出意见和建议, 并将意见和建
议及时反馈给我们。 联系方式如下: 南京市定淮门大街 11 号商会
大厦 B2104 室 南京东方数学教育科学研究所 (邮政编码:
210036), 025-86217370(电话), sjxsjcz@vip.sina.com(电子信箱)。
南京东方数学教育科学研究所
江苏省中小学教学研究室
2013 年 5 月