文档内容
http://t.cn/Ri466E4
苏教版六年级(上)段测数学试卷
一.选择(每题1分,共15分).得分
1.将棱长1米的正方体切成棱长1分米的正方体,切成的正方体排成一排长( )米.
A.1 B.10 C.100 D.1000
2.一个地窖能容纳6立方米的红薯,这个地窖的( )是6立方米.
A.体积B.容积 C.表面积 D.占地面积
3.两根同样长的铁丝,第一根用去它的 ,第二根用去了 米,( )剩得多?
A.第一根 B.第二根 C.同样多 D.无法确定
4.我们在画长方体时一般只画出三个面,这是因为长方体( )
A.只有三个面 B.只能看到三个面
C.最多只能看到三个面
5.至少要用( )个小正方体才能拼成一个较大的正方体.
A.4 B.8 C.9 D.16
6.将一个正方体钢坯锻造成长方体,它们的( )
A.体积相等,表面积不相等 B.体积不相等,表面积相等
C.体积和表面积都相等 D.表面积相等,体积不相等
7.一个正方体的棱长5厘米,如果棱长扩大3倍,则它的表面积扩大( )
A.3倍 B.9倍 C.15倍D.27倍
8.下面哪种不是正方体的展开图(每格都是正方形)( )
A. B. C. D.
9.下面几种说法中,错误的是( )
A.正方体和长方体的体积都可以用V=sh来进行计算
B.在杯里装满水时,杯里水的体积就是杯子的容积
C.一个棱长1分米的正方体可以切成1000个棱长1厘米的小正方体
D.表面积相等的两个长方体,它们的体积一定相等
10.A是一个非零的自然数,下列算式中得数最大的是( )
A.A×1B.A× C.A× D.A×0.999
11.妈妈买回一桶油,每天约用这桶油的 ,一周后,还剩下这桶油的( )
A. B. C.
12.六(3)班男生人数的 和女生人数的 相等,那么男女生人数相比,( )
A.男生多 B.女生多 C.一样多 D.无法确定
13.一个正方体纸盒的底面周长是 米,这个纸盒的体积是( )立方米.
A. B. C. D.
教育 1http://t.cn/Ri466E4
14.方华和王宁参加滑冰训练,方华每分钟滑 千米,王宁每小时滑15千米.谁滑的速
度快,( )
A.方华快 B.王宁快 C.一样快 D.无法比较
15.男生比女生少6人,女生比男生多 ,男生有( )人.
A.2 B.3 C.18 D.9
二.计算
16.直接写出得数.
﹣
2.4÷0.5= 2.7×4= 0.22=
=
1﹣ +
+ = 3×0.25= 0.33=
=
17.解方程.
0.6χ÷2=1.8
2.7χ﹣1.8χ=2.34
2χ﹣0.3=2.3.
18.下面各题,怎样简便就怎样算.
× ×
35× ×
﹣ + ﹣
12.5×3.2×0.25.
19.如图是一个有盖的长方体纸盒的展开图,求它的体积.
三.填空(每空1分,共23分)
20. 立方米= 立方分米
小时= 分
7.06升= 升 毫升;
250立方分米= 升.
教育 2http://t.cn/Ri466E4
22.一块橡皮的体积约是10 ;
手机屏幕的大小约12 ;
一台冰箱的高度约180 ,
容积约420 .
23.做一个长5cm,宽3cm,高1cm的长方体纸盒,至少需要纸板 cm2.
24.3米长的绳子平均分成5段,每段是全长的 ,每段长 .
25. 与 互为倒数; 的倒数是1;0.25的倒数是 .
26.棱长 分米的正方体的表面积是 平方分米,体积是 立方分
米.
27.一堆沙土重 吨,用去了 ,用去了 吨,还剩总数的 .
28.一根60厘米长的铁丝,如果做一个正方体模型,这个正方体的棱长是 厘
米;如果做一个长8厘米.宽5厘米的长方体模型,这个长方体的高是 厘米.
29.把一个正方体木块的表面全涂成红色,然后平均切成27个大小相等的正方体(如图),
那么,两个面是红色的小正方体有 个.
30.有一块长40厘米,宽20厘米的长方形铁皮,如果在它的四角分别切掉一个边长为5
厘米的正方形,余下部分做一个无盖长方体容器,这个容器的容积是 立方厘
米.
31.一根电线长10米,先用去它的 ,再用去 米,这根电线比原来短了 米.
四.操作
32.一台拖拉机每小时耕地 公顷, 小时耕地多少公顷?先在图上用阴影表示出来,再
列式计算.列式计算: .
四.只列式不计算:
33.一长方体长240厘米,横截面是边长5厘米的正方形,它的体积是多少立方厘米.列
式: .
34.一块长方形地,长56米,宽是长的 .这块地的面积是多少平方米?列式:
.
教育 3http://t.cn/Ri466E4
35.六年级一班的人数比六年级二班多 ,二班有48人,一班比二班多多少人?列式:
.
五.解决问题
36.一种长方体通风管,长3米,通风口长4分米,宽5分米.做10节这样的通风管共需
铁皮多少平方米?
37.五年级一班举行1分钟跳绳比赛,小红跳了120下,是小芳的 ,小芳跳了多少下?
38.学校读书节期间共收到240份自办小报,其中有 的小报获奖,一等奖占获奖总数的
.获一等奖的作品有多少件?
39.如图,有一个长6分米、宽4分米、高2分米的长方体硬纸箱,用绳子将箱子捆扎起
来,打结处共用2分米.一共要用绳子多少分米?
40.做一个长方体的玻璃缸(无盖),长8分米,宽4分米,高6分米,至少需要多少平
方分米的玻璃?
41.把一块棱长是0.6米的正方形钢坯,锻成横截面面积是0.08平方米的长方体钢材,锻
成的钢材长 米.
42.一个长方体水箱从里面量长5分米,宽4分米,水深1.8分米,当一个不规则的石块浸
没水中时,这时水上升2.5厘米,这个石块的体积是多少立方分米?
43.国庆期间为美化街道环境,新建了如图所示的花坛:高0.8米,底面是边长为1.2米的
正方形,四周用木条围成.
(1)这个花坛占地多少平方米?
(2)用泥土填满这个花坛,大约需要多少泥土?(木条的厚度忽略不计)
(3)做这样一个花坛,四周大约需要木条多少平方米?
教育 4http://t.cn/Ri466E4
苏教版六年级(上)段测数学试卷
参考答案与试题解析
一.选择(每题1分,共15分).得分
1.将棱长1米的正方体切成棱长1分米的正方体,切成的正方体排成一排长( )米.
A.1 B.10 C.100 D.1000
【考点】简单的立方体切拼问题.
【分析】根据正方体的体积计算公式,分别计算出棱长为1米的正方体的体积和棱长为1
分米的小正方体的体积;然后根据求一个数是另一个是的几倍,用除法进行解答即可.
【解答】解:1米=10分米,
(10×10×10)÷(1×1×1)
=1000÷1
=1000(个)
1×1000=1000(米)
切成的正方体排成一排长1000米.
故选:D.
2.一个地窖能容纳6立方米的红薯,这个地窖的( )是6立方米.
A.体积B.容积 C.表面积 D.占地面积
【考点】体积、容积及其单位.
【分析】根据容积的意义,物体所能容纳物体的体积叫做这个物体的容积,一个地窖能容
纳6立方米的红薯,这个地窖的容积是6立方米.
【解答】解:一个地窖能容纳6立方米的红薯,这个地窖的容积是6立方米.
故选:B.
3.两根同样长的铁丝,第一根用去它的 ,第二根用去了 米,( )剩得多?
A.第一根 B.第二根 C.同样多 D.无法确定
【考点】分数的意义、读写及分类.
【分析】由于不知道两根铁丝的具体长度,所以无法确定哪根剩下的长:
如果两根铁丝同长1米,则第一根用去的为1× = 米,即两根用去的同样长,则剩下的
同样长;
如果两根铁丝长多于1米,则第一根用去它的 多于 米,即第一根用去的长,则第二根
剩下的长;
如果两根铁丝长少于1米,则第一根用去它的 少于 米,即第二根用去的长,则第一根
剩下的长.
【解答】解:由于不知道两根铁丝的具体长度,所以无法确定哪根剩得多.
故选:D.
教育 5http://t.cn/Ri466E4
4.我们在画长方体时一般只画出三个面,这是因为长方体( )
A.只有三个面 B.只能看到三个面
C.最多只能看到三个面
【考点】长方体的特征.
【分析】长方体的特征是:6个面都是长方形(特殊情况有两个相对的面是正方形),相
对的面的面积相同.再根据观察物体的方法,从某个角度观察一个长方体最多能看到它的
3个面.由此解答.
【解答】解:根据长方体的特征和观察物体的角度及观察的范围,最多能看长方体的3个
面.
答:这是因为长方体最多只能看到它的3个面.
故选:C.
5.至少要用( )个小正方体才能拼成一个较大的正方体.
A.4 B.8 C.9 D.16
【考点】简单的立方体切拼问题;正方体的特征.
【分析】将若干个小正方体,摆成一个大正方体,那么这个正方体的每个棱长上至少有2
个小正方体,由此即可计算得出小正方体的总个数.
【解答】解:根据小正方体拼组大正方体的特点可知:将若干个小正方形,摆成一个大正
方体,那么这个正方体的每个棱长上至少有2个小正方体,
所以组成的这个大正方体中,小正方体的个数至少有2×2×2=8(个);
故选:B.
6.将一个正方体钢坯锻造成长方体,它们的( )
A.体积相等,表面积不相等 B.体积不相等,表面积相等
C.体积和表面积都相等 D.表面积相等,体积不相等
【考点】长方体和正方体的体积.
【分析】根据体积的意义,物体所占空间的大小叫做物体的体积,因此可知,将一个正方
体钢坯锻造成长方体,它们的形状变了,但体积不变.据此解答.
【解答】解:将一个正方体钢坯锻造成长方体,它们的形状变了,即表面积变了,但体积
不变.
故选:A.
7.一个正方体的棱长5厘米,如果棱长扩大3倍,则它的表面积扩大( )
A.3倍 B.9倍 C.15倍D.27倍
【考点】长方体和正方体的表面积.
【分析】根据正方体的表面积=棱长×棱长×6,再根据积的变化规律,积扩大的倍数等于
两个因数扩大倍数的乘积,由此解答.
【解答】解:根据正方体的表面积的计算方法和积的变化规律得:
如果正方体的棱长扩大3倍,它的表面积就扩大3×3=9倍;
故选:B.
8.下面哪种不是正方体的展开图(每格都是正方形)( )
教育 6http://t.cn/Ri466E4
A. B. C. D.
【考点】正方体的展开图.
【分析】根据正方体的展开图的种类1﹣4﹣1型;2﹣3﹣1型;3﹣3型;2﹣2﹣2型可知
A.B.D都能折成正方体,所以C不是正方体的展开图.
【解答】解:下面哪种不是正方体的展开图:C.
故答案为:C.
9.下面几种说法中,错误的是( )
A.正方体和长方体的体积都可以用V=sh来进行计算
B.在杯里装满水时,杯里水的体积就是杯子的容积
C.一个棱长1分米的正方体可以切成1000个棱长1厘米的小正方体
D.表面积相等的两个长方体,它们的体积一定相等
【考点】长方体和正方体的体积.
【分析】A,因为正方形的边长乘边长等于底面积,长方体的长乘宽等于底面积,所以正
方体和长方体的体积都可以用V=sh来进行计算.
B,根据容积的意义,某容器所能容纳别的物体的体积叫做这个容器的容积.因此,在杯
里装满水时,杯里水的体积就是杯子的容积.
C,1分米=10厘米,根据正方体的体积公式:v=a3,棱长1分米的正方体体积是1立方分
米,所以一个棱长1分米的正方体可以切成1000个棱长1厘米的小正方体.
D,可以举出表面积相等的两个长方体,但体积不相等的反例,继而得出结论.
【解答】解:根据分析得:
A,正方体和长方体的体积都可以用V=sh来进行计算.这种说法是正确的.
B,在杯里装满水时,杯里水的体积就是杯子的容积.这种说法是正确的.
C,一个棱长1分米的正方体可以切成1000个棱长1厘米的小正方体.这种说法是正确的.
D,如:长宽高分别为2,4,6的长方体表面积为:(2×4+2×6+4×6)×2=88,体积为:
2×4×6=48;
长宽高分别为2,2,10的长方体表面积为:(2×2+2×10+2×10)×2=88,体积为:
2×2×10=40.
故表面积相等的两个长方体,体积一定相等的说法是错误的.
故选:D.
10.A是一个非零的自然数,下列算式中得数最大的是( )
A.A×1B.A× C.A× D.A×0.999
【考点】分数大小的比较;分数乘法.
【分析】一个因数相同,都是A,且不为0,比较另一个因数,另一个因数越大,积就越
大,由此求解.
【解答】解:一个因数都是A,(A>0),比较另一个因数:
>1
所以A× 的积最大.
教育 7http://t.cn/Ri466E4
故选:C.
11.妈妈买回一桶油,每天约用这桶油的 ,一周后,还剩下这桶油的( )
A. B. C.
【考点】分数四则复合应用题.
【分析】妈妈买回一桶油,每天约用这桶油的 ,一周共7天,根据乘法的意义,一周共
用了全部的 ×7,根据分数减法的意义,用单位“1”减去这7天用的占全部的分率,即
得还剩下全部的几分之几.
【解答】解:1﹣ ×7
=1﹣
=
即还剩下全部的 .
故选:A.
12.六(3)班男生人数的 和女生人数的 相等,那么男女生人数相比,( )
A.男生多 B.女生多 C.一样多 D.无法确定
【考点】分数大小的比较.
【分析】根据“男生人数的 和女生人数的 正好相等,”知道男生人数× =女生人数×
,再逆用比例的基本性质得出男生人数和女生人数的比,再根据比的基本性质化简得出
男女生的人数相比的结果.
【解答】解:男生人数× =女生人数×
男生人数:女生人数=
男生人数:女生人数=8:7
所以男生的人数多.
故选:A.
喜子7的1商铺(淘宝店):http://t.cn/Ri466E4 微店5:http://shop83755268.vpubao.com/
13.一个正方体纸盒的底面周长是 米,这个纸盒的体积是( )立方米.
A. B. C. D.
【考点】长方体和正方体的体积.
教育 8http://t.cn/Ri466E4
【分析】已知正方体底面的周长是 米,根据正方形的边长=周长÷4,据此可以求出正方
体的棱长,再根据正方体的体积公式:v=a3,把数据代入公式解答.
【解答】解: (米),
(立方米),
答:这个纸盒的体积是 立方米.
故选:B.
14.方华和王宁参加滑冰训练,方华每分钟滑 千米,王宁每小时滑15千米.谁滑的速
度快,( )
A.方华快 B.王宁快 C.一样快 D.无法比较
【考点】简单的行程问题.
【分析】首先根据速度×时间=路程,用方华每分钟滑的路程乘以60,求出方华每小时滑
多少千米;然后把它和王宁的速度比较大小,判断出谁滑的速度快即可.
【解答】解:1小时=60分钟
=16(千米)
因为16>15,
所以方华滑的速度快.
答:方华滑的速度快.
故选:A.
15.男生比女生少6人,女生比男生多 ,男生有( )人.
A.2 B.3 C.18 D.9
【考点】分数除法应用题.
【分析】把男生的人数看成单位“1”,女生比男生多 ,它对应的数量是6人,由此用除
法求出男生的人数.
【解答】解:6÷ =18(人)
答:男生有18人.
二.计算
16.直接写出得数.
﹣
2.4÷0.5= 2.7×4= 0.22=
=
1﹣ +
+ = 3×0.25= 0.33=
=
教育 9http://t.cn/Ri466E4
【考点】分数的加法和减法;小数乘法.
【分析】根据分数、小数四则运算的计算法则进行计算即可.
【解答】解:
﹣ =
2.4÷0.5=4.8 2.7×4=10.8 0.22=0.04
1﹣ + =
+ = 3×0.25=0.75 0.33=0.027
17.解方程.
0.6χ÷2=1.8
2.7χ﹣1.8χ=2.34
2χ﹣0.3=2.3.
【考点】方程的解和解方程.
【分析】(1)根据等式的性质,方程两边同时乘2,然后再同时除以0.6即可解答.
(2)先计算2.7x﹣1.8x=0.9x,方程两边同时除以0.9即可解答.
(3)根据等式的性质,方程两边同时加上0.3,然后再同时除以2计算即可.
【解答】解:(1)0.6χ÷2=1.8
0.6χ÷2×2=1.8×2
0.6χ÷0.6=3.6÷0.6
x=6
(2)2.7χ﹣1.8χ=2.34
0.9x÷0.9=2.34÷0.9
x=2.6
(3)2χ﹣0.3=2.3
2χ﹣0.3+0.3=2.3+0.3
2x÷2=2.6÷2
x=1.3
18.下面各题,怎样简便就怎样算.
× ×
35× ×
﹣ + ﹣
12.5×3.2×0.25.
【考点】分数的四则混合运算.
【分析】(1)按照从左向右的顺序进行计算;
(2)根据乘法结合律进行简算;
教育 10http://t.cn/Ri466E4
(3)根据加法交换律和结合律进行简算;
(4)根据乘法交换律和结合律进行简算.
【解答】解:(1) × ×
= ×
= ;
(2)35× ×
=35×( × )
=35×
=20;
(3) ﹣ + ﹣
=( + )﹣( + )
=1﹣
= ;
(4)12.5×3.2×0.25
=12.5×(4×0.8)×0.25
=(12.5×0.8)×(4×0.25)
=10×1
=10.
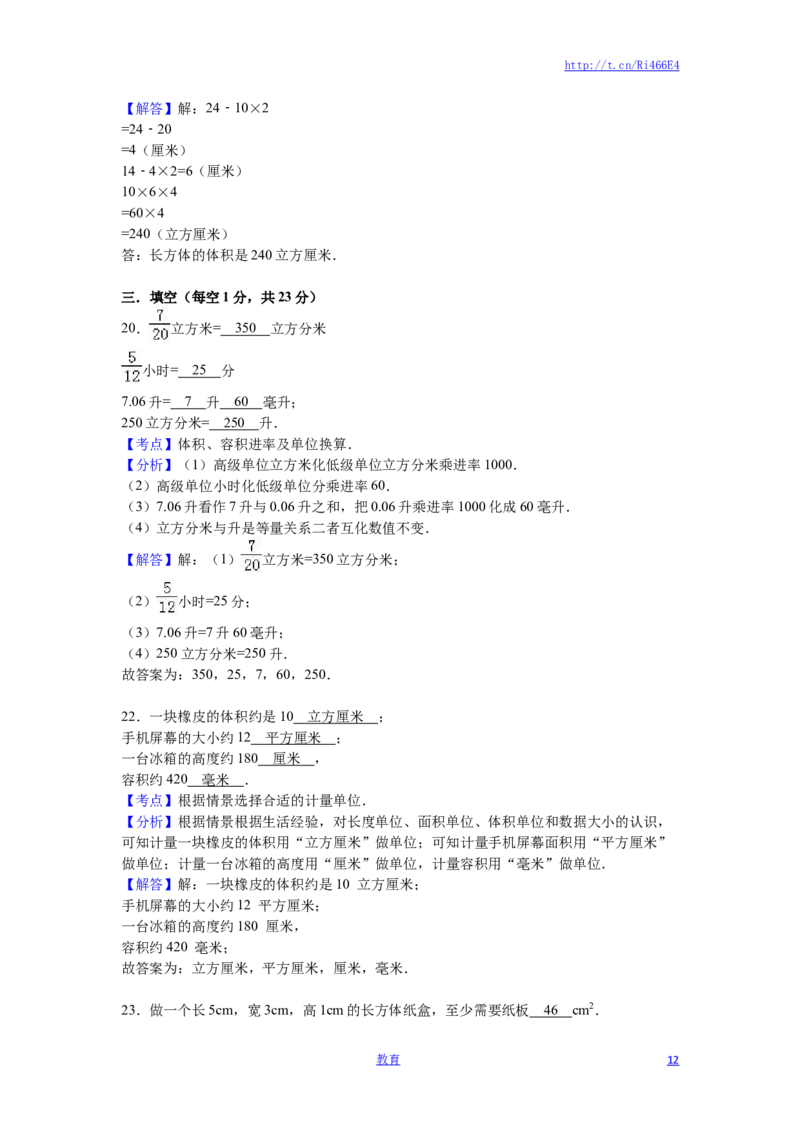
19.如图是一个有盖的长方体纸盒的展开图,求它的体积.
【考点】长方体的展开图;长方体和正方体的体积.
【分析】根据图形知道,长方体的长是10厘米,宽是14﹣4×2=6厘米,高是24﹣
10×2=4厘米,长方体的体积=长×宽×高,把数代入体积公式计算即可解答.
教育 11http://t.cn/Ri466E4
【解答】解:24﹣10×2
=24﹣20
=4(厘米)
14﹣4×2=6(厘米)
10×6×4
=60×4
=240(立方厘米)
答:长方体的体积是240立方厘米.
三.填空(每空1分,共23分)
20. 立方米= 35 0 立方分米
小时= 2 5 分
7.06升= 7 升 6 0 毫升;
250立方分米= 25 0 升.
【考点】体积、容积进率及单位换算.
【分析】(1)高级单位立方米化低级单位立方分米乘进率1000.
(2)高级单位小时化低级单位分乘进率60.
(3)7.06升看作7升与0.06升之和,把0.06升乘进率1000化成60毫升.
(4)立方分米与升是等量关系二者互化数值不变.
【解答】解:(1) 立方米=350立方分米;
(2) 小时=25分;
(3)7.06升=7升60毫升;
(4)250立方分米=250升.
故答案为:350,25,7,60,250.
22.一块橡皮的体积约是10 立方厘米 ;
手机屏幕的大小约12 平方厘米 ;
一台冰箱的高度约180 厘米 ,
容积约420 毫米 .
【考点】根据情景选择合适的计量单位.
【分析】根据情景根据生活经验,对长度单位、面积单位、体积单位和数据大小的认识,
可知计量一块橡皮的体积用“立方厘米”做单位;可知计量手机屏幕面积用“平方厘米”
做单位;计量一台冰箱的高度用“厘米”做单位,计量容积用“毫米”做单位.
【解答】解:一块橡皮的体积约是10 立方厘米;
手机屏幕的大小约12 平方厘米;
一台冰箱的高度约180 厘米,
容积约420 毫米;
故答案为:立方厘米,平方厘米,厘米,毫米.
23.做一个长5cm,宽3cm,高1cm的长方体纸盒,至少需要纸板 4 6 cm2.
教育 12http://t.cn/Ri466E4
【考点】长方体和正方体的表面积.
【分析】根据长方体的表面积公式:s=(ab+ah+bh)×2,把数据代入公式解答即可.
【解答】解:(5×3+5×1+3×1)×2
=(15+5+3)×2
=23×2
=46(平方厘米),
答:至少需要纸板46平方厘米.
故答案为:46.
24.3米长的绳子平均分成5段,每段是全长的 ,每段长 米 .
【考点】分数的意义、读写及分类.
【分析】把这条绳子的长度看作单位“1”,把它平均分成5段,每段是这条绳子全长的 ;
求每段长,根据平均分除法的意义,用这条绳子的长度除以平均分成的段数或根据分数乘
法的意义,用这条绳子的长度乘每段所占的分率.
【解答】解:1÷5= ,
3÷5= (米)或3× = (米).
即3米长的绳子平均分成5段,每段是全长的 ,每段长 米.
故答案为: , 米.
25. 与 互为倒数; 1 的倒数是1;0.25的倒数是 4 .
【考点】倒数的认识.
【分析】先把小数化为分数,再运用倒数的求法解答.
【解答】解: 与 互为倒数;1的倒数是1;0.25= , 的倒数是4.
故答案为: ;1;4.
26.棱长 分米的正方体的表面积是 平方分米,体积是 立方分米.
【考点】长方体和正方体的表面积;长方体和正方体的体积.
【分析】根据正方体的表面积公式:s=6a2,体积公式:v=a3,把数据分别代入公式解答.
【解答】解: = (平方分米),
= (平方分米),
答:它的表面积是 平方分米,体积是 立方分米.
教育 13http://t.cn/Ri466E4
故答案为: , .
27.一堆沙土重 吨,用去了 ,用去了 吨,还剩总数的 .
【考点】分数乘法应用题.
【分析】把这堆土总重看作单位“1”,用去了 ,运用乘法即可求出用去了多少吨,剩下
的分率为:1﹣ ;据此解答即可.
【解答】解: × = (吨)
1﹣ =
答:用去了 吨,还剩总数的 .
故答案为: , .
28.一根60厘米长的铁丝,如果做一个正方体模型,这个正方体的棱长是 5 厘米;如
果做一个长8厘米.宽5厘米的长方体模型,这个长方体的高是 2 厘米.
【考点】正方体的特征;长方体的特征.
【分析】(1)根据正方体的特征,12条的棱的长度都相等,已知一根铁丝长60厘米,如
果做一个正方体框架,也就是正方体的棱长总和是60厘米,用棱长总和÷12=棱长;
(2)长方体所有的棱长之和就等于铁丝的长,再依据长方体的棱长和=(长+宽+高)
×4,即可求出长方体的高.
【解答】解:60÷12=5(厘米),
答:正方体的棱长为5厘米;
(2)60÷4﹣8﹣5
=15﹣8﹣5
=2(厘米),
答:这个长方体的高是2厘米.
故答案为:5,2.
29.把一个正方体木块的表面全涂成红色,然后平均切成27个大小相等的正方体(如图),
那么,两个面是红色的小正方体有 1 2 个.
【考点】染色问题.
教育 14http://t.cn/Ri466E4
【分析】根据正方体表面涂色的特点,分别得出切割后的小正方体涂色面的排列特点:
(1)三面涂色的在每个顶点处;(2)两面涂色的在每条棱长上(除去顶点处的小正方
体);(3)一面涂色的都在每个面上(除去棱长上的小正方体);(4)没有涂色的都在
内部.
【解答】解:两面涂色的在每条棱长上(除去顶点处的小正方体),有:
(3﹣2)×12
=1×12
=12(个)
答:两个面是红色的小正方体有12个.
故答案为:12.
30.有一块长40厘米,宽20厘米的长方形铁皮,如果在它的四角分别切掉一个边长为5
厘米的正方形,余下部分做一个无盖长方体容器,这个容器的容积是 150 0 立方厘米.
【考点】长方体和正方体的体积.
【分析】根据题意,做成的盒子的长是(40﹣5×2)厘米,宽是(20﹣5×2)厘米,高是
5厘米,利用长方体的容积(体积)公式:v=abh,即可求出这个盒子的容积是多少立方厘
米.
【解答】解:(40﹣5×2)×(20﹣5×2)×5
=30×10×5
=1500(立方厘米),
答:这个容器的容积是1500立方厘米.
故答案为:1500.
31.一根电线长10米,先用去它的 ,再用去 米,这根电线比原来短了 2. 2 米.
【考点】分数四则复合应用题.
【分析】一根电线长10米,第一次用去全长的 ,求一个数的几分之几是多少,用乘法,
则第一次用了15× 米,第二次用去 米,所以两次共用了10× + 米,用去的米数即
得比原来短的米数,由此解答即可.
【解答】解:10× +
=2+0.2
=2.2(米)
答:这根电线比原来短了 2.2米;
故答案为:2.2.
四.操作
32.一台拖拉机每小时耕地 公顷, 小时耕地多少公顷?先在图上用阴影表示出来,再
列式计算.列式计算: × = (公顷) .
教育 15http://t.cn/Ri466E4
【考点】分数乘法应用题.
【分析】首先根据题意,把所给的图形看作1公顷,根据分数的意义,把它平均分成4份,
取其中的3份,表示出每小时耕地的面积;然后把这台拖拉机每小时耕地的面积看作单位
“1”,把它平均分成5份,取其中的2份,画出每小时耕地面积的 是多少;最后把这台
拖拉机每小时耕地的面积看作单位“1”,根据分数乘法的意义,用拖拉机每小时耕地的面
积乘以 ,求出 小时耕地多少公顷即可.
【解答】解:如图, ,
× = (公顷)
答: 小时耕地 公顷.
故答案为: × = (公顷).
四.只列式不计算:
33.一长方体长240厘米,横截面是边长5厘米的正方形,它的体积是多少立方厘米.列
式: 5 × 5 × 240=600 0 (立方厘米). .
【考点】长方体和正方体的体积.
【分析】根据长方体的体积公式:v=sh,把数据代入公式解答即可.
【解答】解:5×5×240
=25×240
=6000(立方厘米),
答:它的体积是6000立方厘米.
故答案为:5×5×240=6000(立方厘米).
34.一块长方形地,长56米,宽是长的 .这块地的面积是多少平方米?列式: 56×
×56 .
【考点】长方形、正方形的面积.
【分析】根据求一个数的几分之几是多少用乘法计算,用56乘 可求出长方形的宽,再根
据长方形的面积=长×宽可求出这块地的面积是多少平方米.据此解答.
【解答】解:56× ×56
=40×56
教育 16http://t.cn/Ri466E4
=2240(平方米)
答:这块地的面积是2240平方米.
故答案为:56× ×56.
35.六年级一班的人数比六年级二班多 ,二班有48人,一班比二班多多少人?列式:
48× .
【考点】分数乘法应用题.
【分析】首先根据题意,把六年级二班的人数看作单位“1”,要求一班比二班多多少人,
即求48人的 是多少,根据分数乘法的意义,用48乘以 即可.
【解答】解:48× =2(人)
答:一班比二班多2人.
故答案为:48× .
五.解决问题
36.一种长方体通风管,长3米,通风口长4分米,宽5分米.做10节这样的通风管共需
铁皮多少平方米?
【考点】长方体、正方体表面积与体积计算的应用.
【分析】要求做10节这样的通风管共需铁皮多少平方米,即求10个长方体通风管的侧面
积,根据长方体的侧面积=底面周长×高,求出1节这样的通风管共需铁皮,再乘以10,
解答即可.
【解答】解:4分米=0.4米,3分米=0.3米
3×(0.4+0.3)×2×10
=6×0.7×10
=42(平方米)
答:做10节这样的通风管共需铁皮42平方米.
37.五年级一班举行1分钟跳绳比赛,小红跳了120下,是小芳的 ,小芳跳了多少下?
【考点】分数除法应用题.
【分析】把小芳跳的看作单位“1”,小芳的 是120下,根据除法的意义,用120除以 ,
即可得小芳跳了多少下.
【解答】解:120÷ =160(下),
答:小芳跳了160下.
教育 17http://t.cn/Ri466E4
38.学校读书节期间共收到240份自办小报,其中有 的小报获奖,一等奖占获奖总数的
.获一等奖的作品有多少件?
【考点】分数四则复合应用题.
【分析】收到240份自办小报,其中有 的小报获奖,把小报总数看成单位“1”,根据分
数乘法的意义,用小报总数乘 就是小报获奖总数,其中一等奖占获奖总数的 ,根据分
数乘法的意义,可求得获一等奖的作品数量.
【解答】解:240× ×
=90×
=36(件)
答:获一等奖的作品有36件.
39.如图,有一个长6分米、宽4分米、高2分米的长方体硬纸箱,用绳子将箱子捆扎起
来,打结处共用2分米.一共要用绳子多少分米?
【考点】长方体的特征.
【分析】根据长方体的特征,相对的棱的长度相等,由图形可知:所需绳子的长度等于2
条长+4条宽+6条高+打结用的2分米,据此解答.
【解答】解:6×2+4×4+2×6+2
=12+16+12+2
=42(分米),
答:一共用绳子42分米.
40.做一个长方体的玻璃缸(无盖),长8分米,宽4分米,高6分米,至少需要多少平
方分米的玻璃?
【考点】长方体、正方体表面积与体积计算的应用.
【分析】根据题意可知,鱼缸是没有盖的,它是由5个面围成的,根据长方体的表面积的
计算方法即可求出需要玻璃多少平方分米.据此解答.
【解答】解:8×4+8×6×2+6×4×2
=32+96+48
=176(平方分米)
答:至少需要176平方分米的玻璃.
41.把一块棱长是0.6米的正方形钢坯,锻成横截面面积是0.08平方米的长方体钢材,锻
成的钢材长 2. 7 米.
【考点】长方体和正方体的体积.
教育 18http://t.cn/Ri466E4
【分析】根据体积的意义,物体所占空间的大小叫做物体的体积.由题意可知,把一块棱
长是0.6米的正方形钢坯,锻成横截面面积是0.08平方米的长方体钢材,只是形状改变了,
但是体积没有变;因此用正方体的体积除以底面积即可求出长度.正方体的体积公式
v=a3,长方体的体积公式v=sh,由此列式解答.
【解答】解:0.6×0.6×0.6÷0.08
=0.216÷0.08,
=2.7(米);
答:锻成的钢材长2.7米.
故答案为:2.7.
42.一个长方体水箱从里面量长5分米,宽4分米,水深1.8分米,当一个不规则的石块浸
没水中时,这时水上升2.5厘米,这个石块的体积是多少立方分米?
【考点】长方体、正方体表面积与体积计算的应用.
【分析】由题意可知:这个石块的体积就等于上升部分的水的体积,利用长方体的体积
V=abh,代入数据即可求出这个石块的体积.
【解答】解:2.5厘米=0.25分米
5×4×0.25
=20×0.25
=5(立方分米)
答:这个石块的体积是5立方分米.
43.国庆期间为美化街道环境,新建了如图所示的花坛:高0.8米,底面是边长为1.2米的
正方形,四周用木条围成.
(1)这个花坛占地多少平方米?
(2)用泥土填满这个花坛,大约需要多少泥土?(木条的厚度忽略不计)
(3)做这样一个花坛,四周大约需要木条多少平方米?
【考点】长方形的周长;长方形、正方形的面积.
【分析】(1)求这个花坛占地多少平方米,实际是求花坛的底面积,利用正方形的面积:
S=a2解答即可;
(2)求花坛里大约有多少立方米的泥土,就是求它的容积,再利用长方体的体积(容积)
公式:V=abh,解答即可;
(3)求四周大约需要木条多少平方米,就是求花坛的表面积,根据长方体的表面积公式求
出5个面的面积即可.
【解答】解:(1)1.2×1.2=1.44(平方米)
答:这个花坛占地1.44平方米.
(2)1.2×1.2×.8
=1.44×0.8
=1.152(立方米)
答:大约需要1.152立方米的泥土.
(3)1.2×4×0.8+0.8×0.8
教育 19http://t.cn/Ri466E4
=3.84+0.64
=4.48(平方米)
答:四周大约需要木条4.48平方米.
教育 20http://t.cn/Ri466E4
2016年8月20日
教育 21