文档内容
2020年湖南省张家界市中考数学试卷
一、选择题(本大题共8个小题,每小题3分,满分24分,在每小题给出的四个选项中,只有
一项是符合题目要求的)
1.(3分) 的倒数是( )
A.﹣ B. C.2020 D.﹣2020
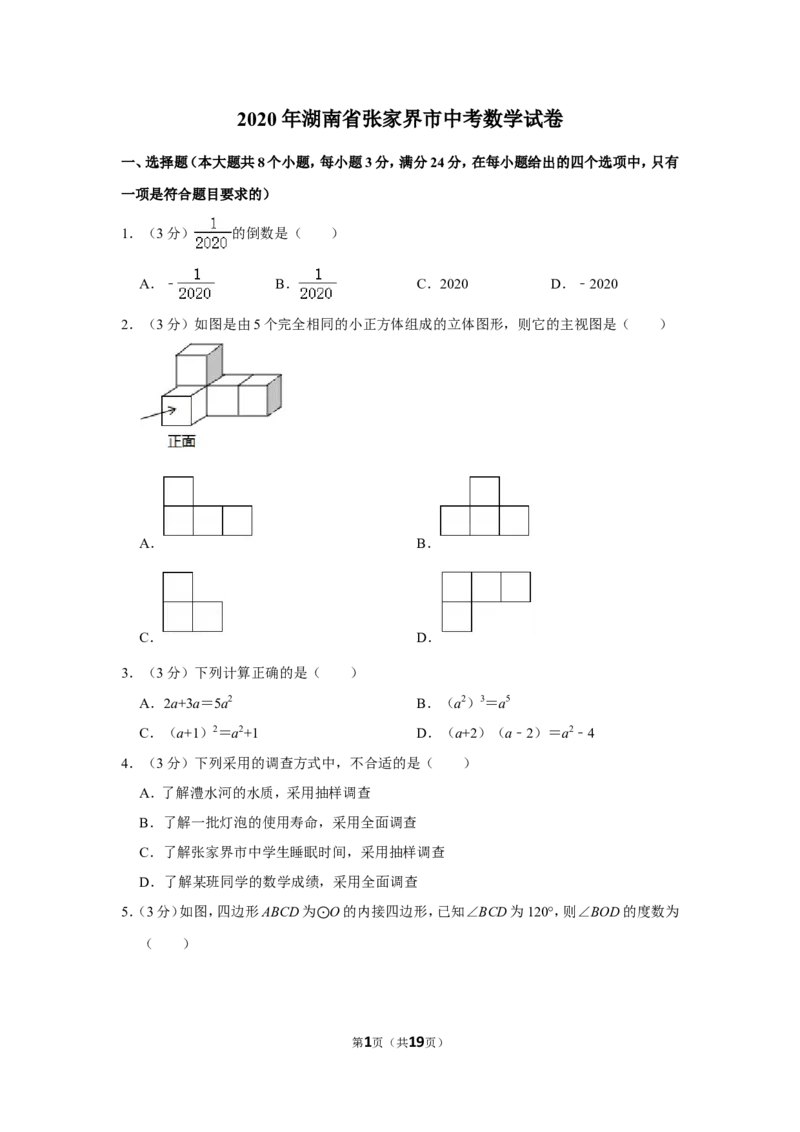
2.(3分)如图是由5个完全相同的小正方体组成的立体图形,则它的主视图是( )
A. B.
C. D.
3.(3分)下列计算正确的是( )
A.2a+3a=5a2 B.(a2)3=a5
C.(a+1)2=a2+1 D.(a+2)(a﹣2)=a2﹣4
4.(3分)下列采用的调查方式中,不合适的是( )
A.了解澧水河的水质,采用抽样调查
B.了解一批灯泡的使用寿命,采用全面调查
C.了解张家界市中学生睡眠时间,采用抽样调查
D.了解某班同学的数学成绩,采用全面调查
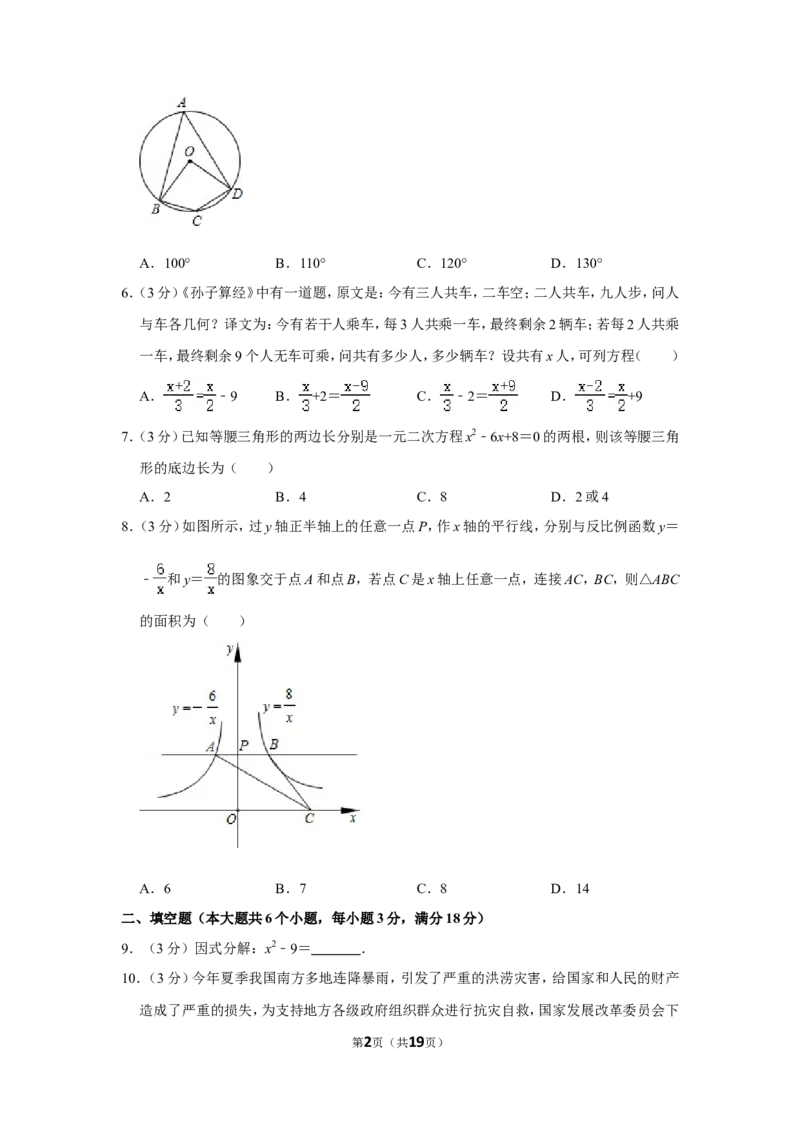
5.(3分)如图,四边形ABCD为 O的内接四边形,已知∠BCD为120°,则∠BOD的度数为
( ) ⊙
第1页(共19页)A.100° B.110° C.120° D.130°
6.(3分)《孙子算经》中有一道题,原文是:今有三人共车,二车空;二人共车,九人步,问人
与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车;若每2人共乘
一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )
A. ﹣9 B. +2= C. ﹣2= D. +9
7.(3分)已知等腰三角形的两边长分别是一元二次方程x2﹣6x+8=0的两根,则该等腰三角
形的底边长为( )
A.2 B.4 C.8 D.2或4
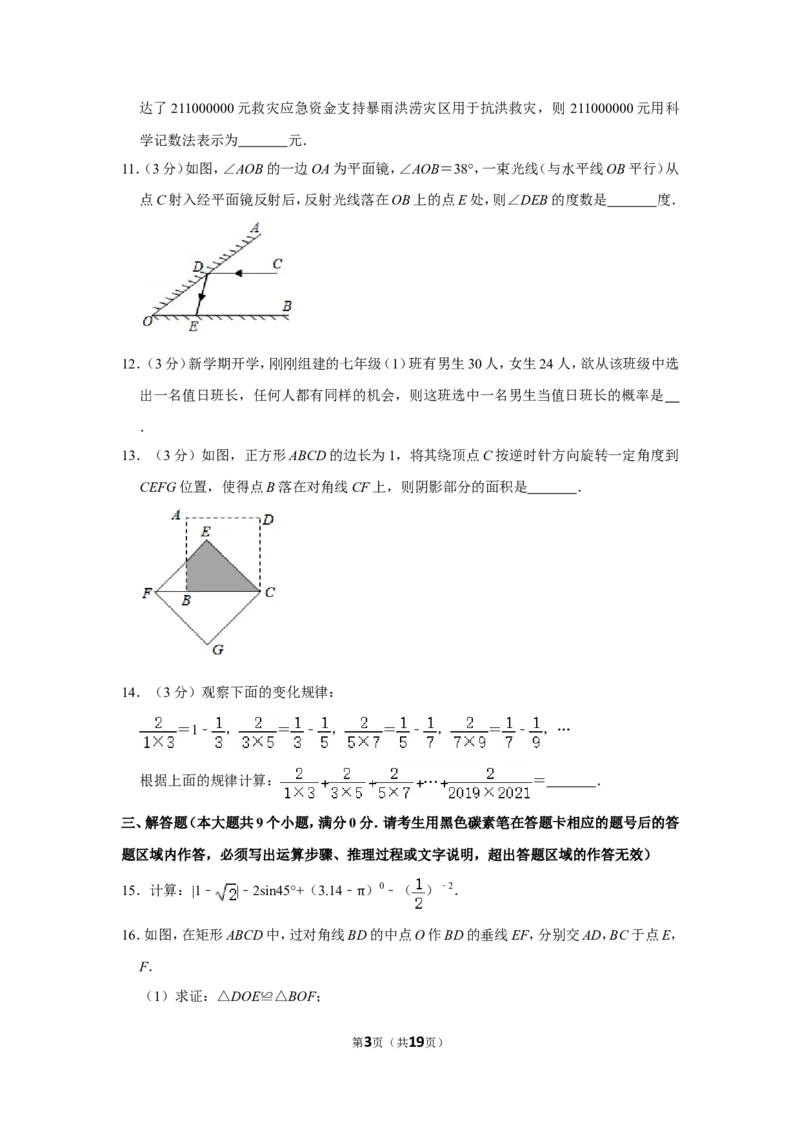
8.(3分)如图所示,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数y=
﹣ 和y= 的图象交于点A和点B,若点C是x轴上任意一点,连接AC,BC,则△ABC
的面积为( )
A.6 B.7 C.8 D.14
二、填空题(本大题共6个小题,每小题3分,满分18分)
9.(3分)因式分解:x2﹣9= .
10.(3分)今年夏季我国南方多地连降暴雨,引发了严重的洪涝灾害,给国家和人民的财产
造成了严重的损失,为支持地方各级政府组织群众进行抗灾自救,国家发展改革委员会下
第2页(共19页)达了211000000元救灾应急资金支持暴雨洪涝灾区用于抗洪救灾,则 211000000元用科
学记数法表示为 元.
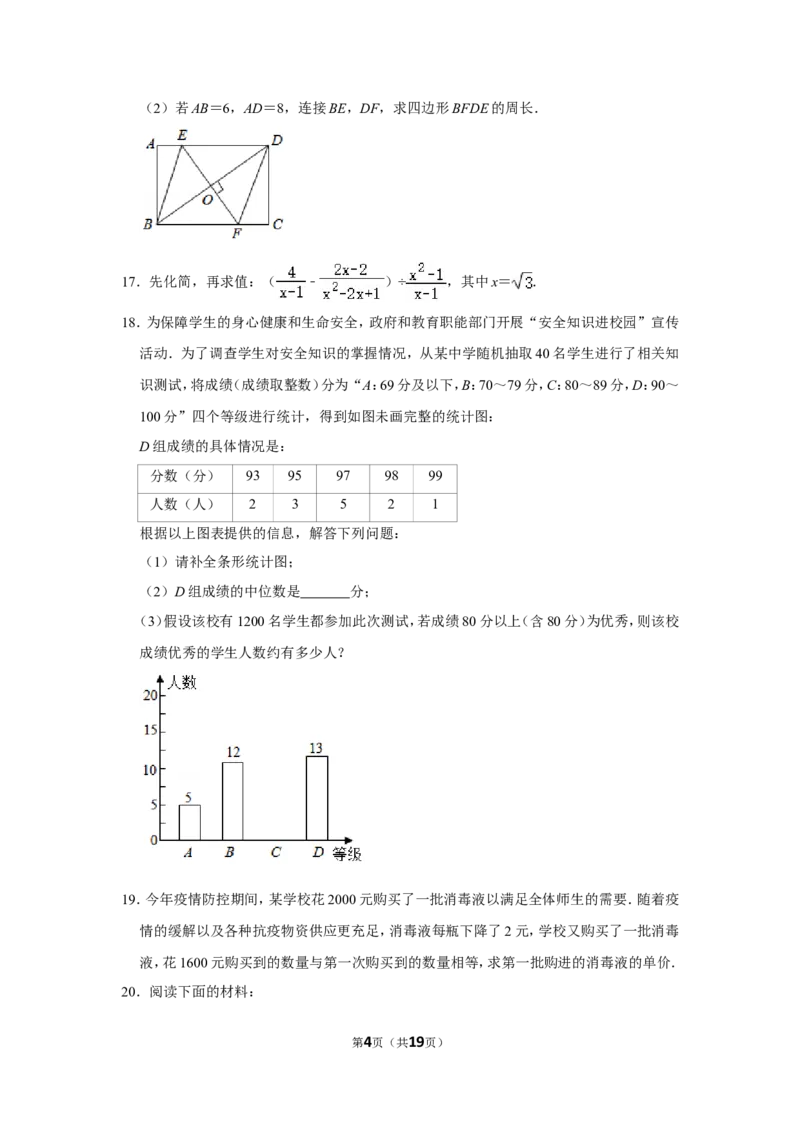
11.(3分)如图,∠AOB的一边OA为平面镜,∠AOB=38°,一束光线(与水平线OB平行)从
点C射入经平面镜反射后,反射光线落在OB上的点E处,则∠DEB的度数是 度.
12.(3分)新学期开学,刚刚组建的七年级(1)班有男生30人,女生24人,欲从该班级中选
出一名值日班长,任何人都有同样的机会,则这班选中一名男生当值日班长的概率是
.
13.(3分)如图,正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度到
CEFG位置,使得点B落在对角线CF上,则阴影部分的面积是 .
14.(3分)观察下面的变化规律:
=1﹣ , = ﹣ , = ﹣ , = ﹣ ,…
根据上面的规律计算: = .
三、解答题(本大题共9个小题,满分0分.请考生用黑色碳素笔在答题卡相应的题号后的答
题区域内作答,必须写出运算步骤、推理过程或文字说明,超出答题区域的作答无效)
15.计算:|1﹣ |﹣2sin45°+(3.14﹣ )0﹣( )﹣2.
π
16.如图,在矩形ABCD中,过对角线BD的中点O作BD的垂线EF,分别交AD,BC于点E,
F.
(1)求证:△DOE≌△BOF;
第3页(共19页)(2)若AB=6,AD=8,连接BE,DF,求四边形BFDE的周长.
17.先化简,再求值:( ﹣ )÷ ,其中x= .
18.为保障学生的身心健康和生命安全,政府和教育职能部门开展“安全知识进校园”宣传
活动.为了调查学生对安全知识的掌握情况,从某中学随机抽取40名学生进行了相关知
识测试,将成绩(成绩取整数)分为“A:69分及以下,B:70~79分,C:80~89分,D:90~
100分”四个等级进行统计,得到如图未画完整的统计图:
D组成绩的具体情况是:
分数(分) 93 95 97 98 99
人数(人) 2 3 5 2 1
根据以上图表提供的信息,解答下列问题:
(1)请补全条形统计图;
(2)D组成绩的中位数是 分;
(3)假设该校有1200名学生都参加此次测试,若成绩80分以上(含80分)为优秀,则该校
成绩优秀的学生人数约有多少人?
19.今年疫情防控期间,某学校花2000元购买了一批消毒液以满足全体师生的需要.随着疫
情的缓解以及各种抗疫物资供应更充足,消毒液每瓶下降了2元,学校又购买了一批消毒
液,花1600元购买到的数量与第一次购买到的数量相等,求第一批购进的消毒液的单价.
20.阅读下面的材料:
第4页(共19页)对于实数a,b,我们定义符号min{a,b}的意义为:当a<b时,min{a,b}=a;当a≥b时,
min{a,b}=b,如:min{4,﹣2}=﹣2,min{5,5}=5.
根据上面的材料回答下列问题:
(1)min{﹣1,3}= ;
(2)当min 时,求x的取值范围.
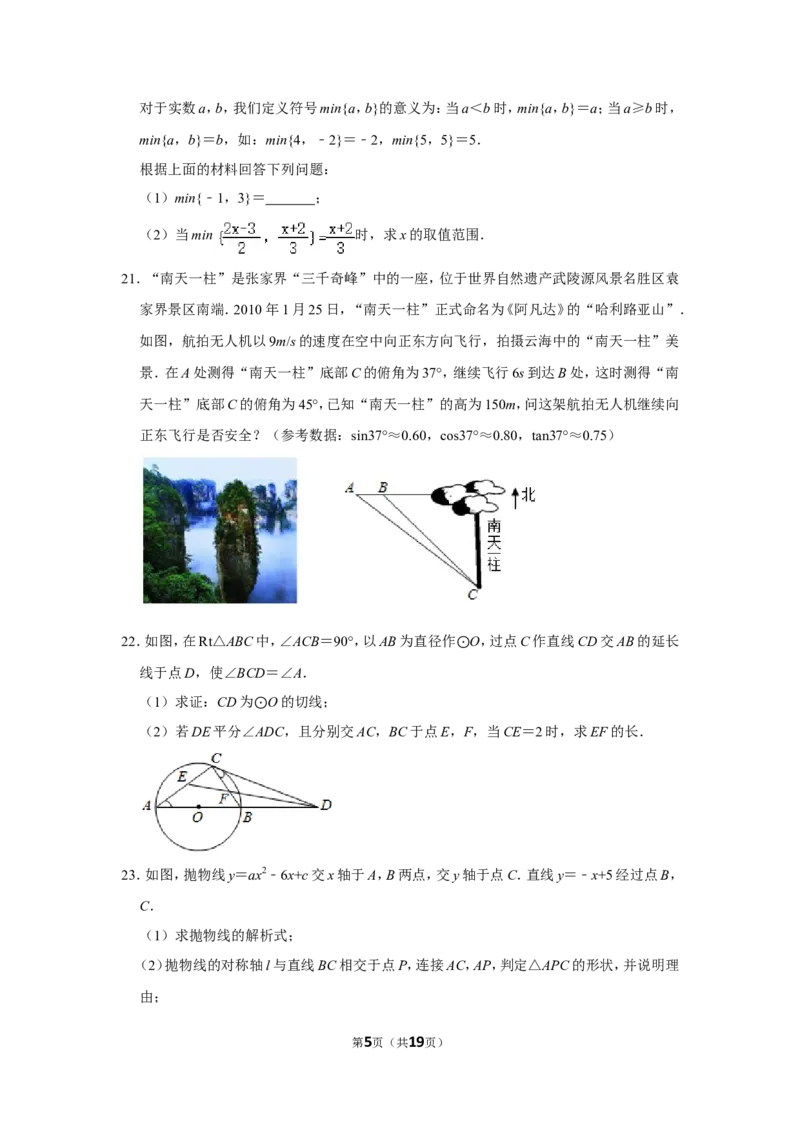
21.“南天一柱”是张家界“三千奇峰”中的一座,位于世界自然遗产武陵源风景名胜区袁
家界景区南端.2010年1月25日,“南天一柱”正式命名为《阿凡达》的“哈利路亚山”.
如图,航拍无人机以9m/s的速度在空中向正东方向飞行,拍摄云海中的“南天一柱”美
景.在A处测得“南天一柱”底部C的俯角为37°,继续飞行6s到达B处,这时测得“南
天一柱”底部C的俯角为45°,已知“南天一柱”的高为150m,问这架航拍无人机继续向
正东飞行是否安全?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
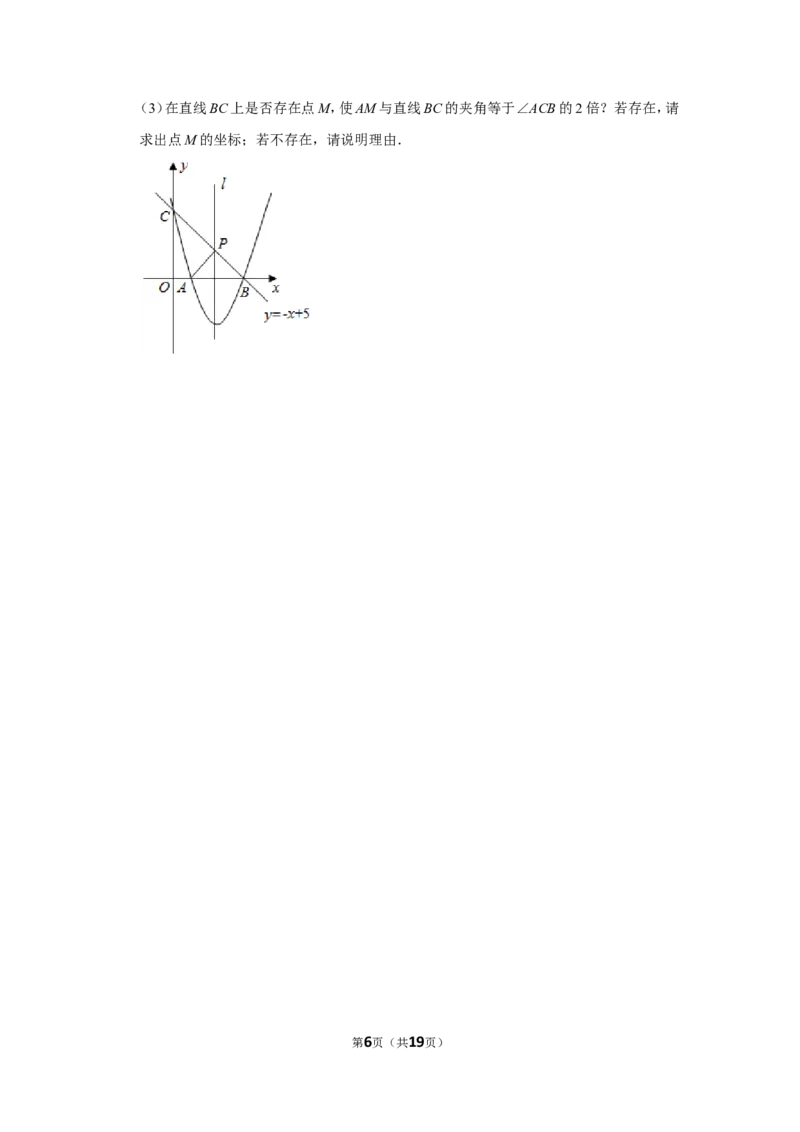
22.如图,在Rt△ABC中,∠ACB=90°,以AB为直径作 O,过点C作直线CD交AB的延长
线于点D,使∠BCD=∠A. ⊙
(1)求证:CD为 O的切线;
(2)若DE平分∠⊙ADC,且分别交AC,BC于点E,F,当CE=2时,求EF的长.
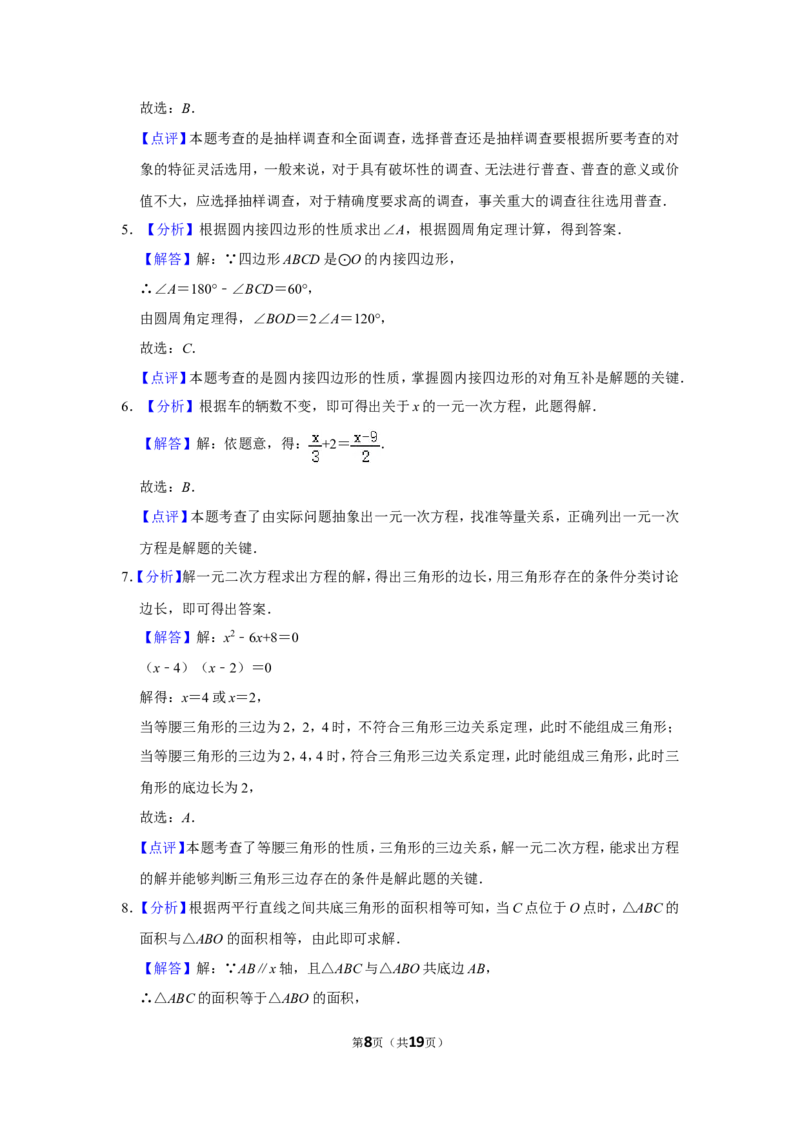
23.如图,抛物线y=ax2﹣6x+c交x轴于A,B两点,交y轴于点C.直线y=﹣x+5经过点B,
C.
(1)求抛物线的解析式;
(2)抛物线的对称轴l与直线BC相交于点P,连接AC,AP,判定△APC的形状,并说明理
由;
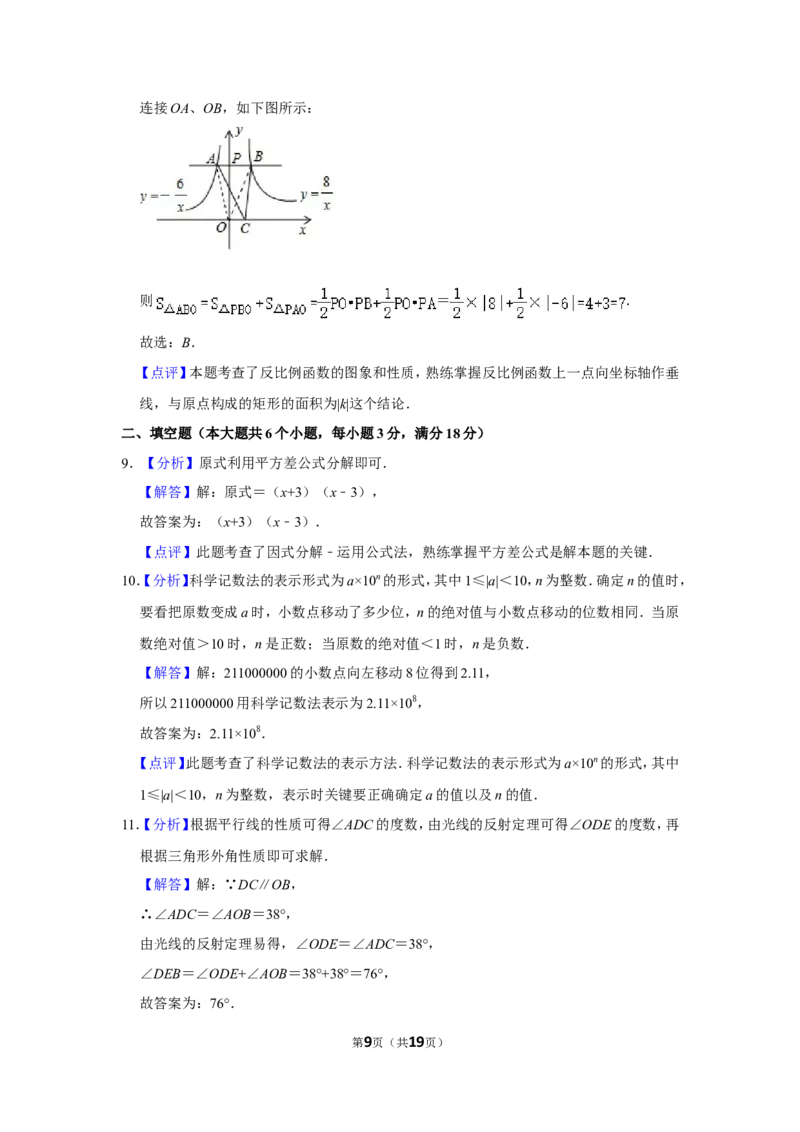
第5页(共19页)(3)在直线BC上是否存在点M,使AM与直线BC的夹角等于∠ACB的2倍?若存在,请
求出点M的坐标;若不存在,请说明理由.
第6页(共19页)2020年湖南省张家界市中考数学试卷
参考答案与试题解析
一、选择题(本大题共8个小题,每小题3分,满分24分,在每小题给出的四个选项中,只有
一项是符合题目要求的)
1.【分析】根据倒数之积等于1可得答案.
【解答】解: 的倒数是2020,
故选:C.
【点评】此题主要考查了倒数,解题的关键是掌握倒数定义.
2.【分析】根据从正面看得到的图形是主视图,可得答案.
【解答】解:从正面看有三列,从左到右依次有2、1、1个正方形,图形如下:
故选:A.
【点评】本题考查了简单组合体的三视图,解题时注意从正面看得到的图形是主视图.
3.【分析】根据合并同类项、幂的乘方、完全平方公式和平方差公式逐一进行判断即可
【解答】解:A、2a+3a=5a,故原式错误;
B、(a2)3=a6,故原式错误;
C、(a+1)2=a2+2a+1,故原式错误;
D、(a+2)(a﹣2)=a2﹣4,故原式正确,
故选:D.
【点评】此题考查了合并同类项、幂的乘方、完全平方公式和平方差公式,熟练掌握公式及
法则是解本题的关键.
4.【分析】根据调查对象的特点,结合普查得到的调查结果比较准确,但所费人力、物力和时
间较多,而抽样调查得到的调查结果接近准确数值,从而可得答案.
【解答】解:了解澧水河的水质,采用普查不太可能做到,所以采用抽样调查,故A合适,
了解一批灯泡的使用寿命,不宜采用全面调查,因为调查带有破坏性,故B不合适,
了解张家界市中学生睡眠时间,工作量大,宜采用抽样调查,故C合适,
了解某班同学的数学成绩,采用全面调查.合适,故D合适,
第7页(共19页)故选:B.
【点评】本题考查的是抽样调查和全面调查,选择普查还是抽样调查要根据所要考查的对
象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价
值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
5.【分析】根据圆内接四边形的性质求出∠A,根据圆周角定理计算,得到答案.
【解答】解:∵四边形ABCD是 O的内接四边形,
∴∠A=180°﹣∠BCD=60°, ⊙
由圆周角定理得,∠BOD=2∠A=120°,
故选:C.
【点评】本题考查的是圆内接四边形的性质,掌握圆内接四边形的对角互补是解题的关键.
6.【分析】根据车的辆数不变,即可得出关于x的一元一次方程,此题得解.
【解答】解:依题意,得: +2= .
故选:B.
【点评】本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次
方程是解题的关键.
7.【分析】解一元二次方程求出方程的解,得出三角形的边长,用三角形存在的条件分类讨论
边长,即可得出答案.
【解答】解:x2﹣6x+8=0
(x﹣4)(x﹣2)=0
解得:x=4或x=2,
当等腰三角形的三边为2,2,4时,不符合三角形三边关系定理,此时不能组成三角形;
当等腰三角形的三边为2,4,4时,符合三角形三边关系定理,此时能组成三角形,此时三
角形的底边长为2,
故选:A.
【点评】本题考查了等腰三角形的性质,三角形的三边关系,解一元二次方程,能求出方程
的解并能够判断三角形三边存在的条件是解此题的关键.
8.【分析】根据两平行直线之间共底三角形的面积相等可知,当C点位于O点时,△ABC的
面积与△ABO的面积相等,由此即可求解.
【解答】解:∵AB∥x轴,且△ABC与△ABO共底边AB,
∴△ABC的面积等于△ABO的面积,
第8页(共19页)连接OA、OB,如下图所示:
则 = .
故选:B.
【点评】本题考查了反比例函数的图象和性质,熟练掌握反比例函数上一点向坐标轴作垂
线,与原点构成的矩形的面积为|k|这个结论.
二、填空题(本大题共6个小题,每小题3分,满分18分)
9.【分析】原式利用平方差公式分解即可.
【解答】解:原式=(x+3)(x﹣3),
故答案为:(x+3)(x﹣3).
【点评】此题考查了因式分解﹣运用公式法,熟练掌握平方差公式是解本题的关键.
10.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,
要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原
数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:211000000的小数点向左移动8位得到2.11,
所以211000000用科学记数法表示为2.11×108,
故答案为:2.11×108.
【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中
1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
11.【分析】根据平行线的性质可得∠ADC的度数,由光线的反射定理可得∠ODE的度数,再
根据三角形外角性质即可求解.
【解答】解:∵DC∥OB,
∴∠ADC=∠AOB=38°,
由光线的反射定理易得,∠ODE=∠ADC=38°,
∠DEB=∠ODE+∠AOB=38°+38°=76°,
故答案为:76°.
第9页(共19页)【点评】本题考查平行线的性质、三角形外角性质和光线的反射定理,掌握入射角=反射
角是解题的关键.
12.【分析】先求出全班的学生数,再根据概率公式进行求解即可.
【解答】解:全班共有学生30+24=54(人),
其中男生30人,
则这班选中一名男生当值日班长的概率是 = .
故答案为: .
【点评】本题考查了简单的概率计算,如果一个事件有n种可能,而且这些事件的可能性相
同,其中事件A出现m种结果,那么事件A的概率P(A)= .
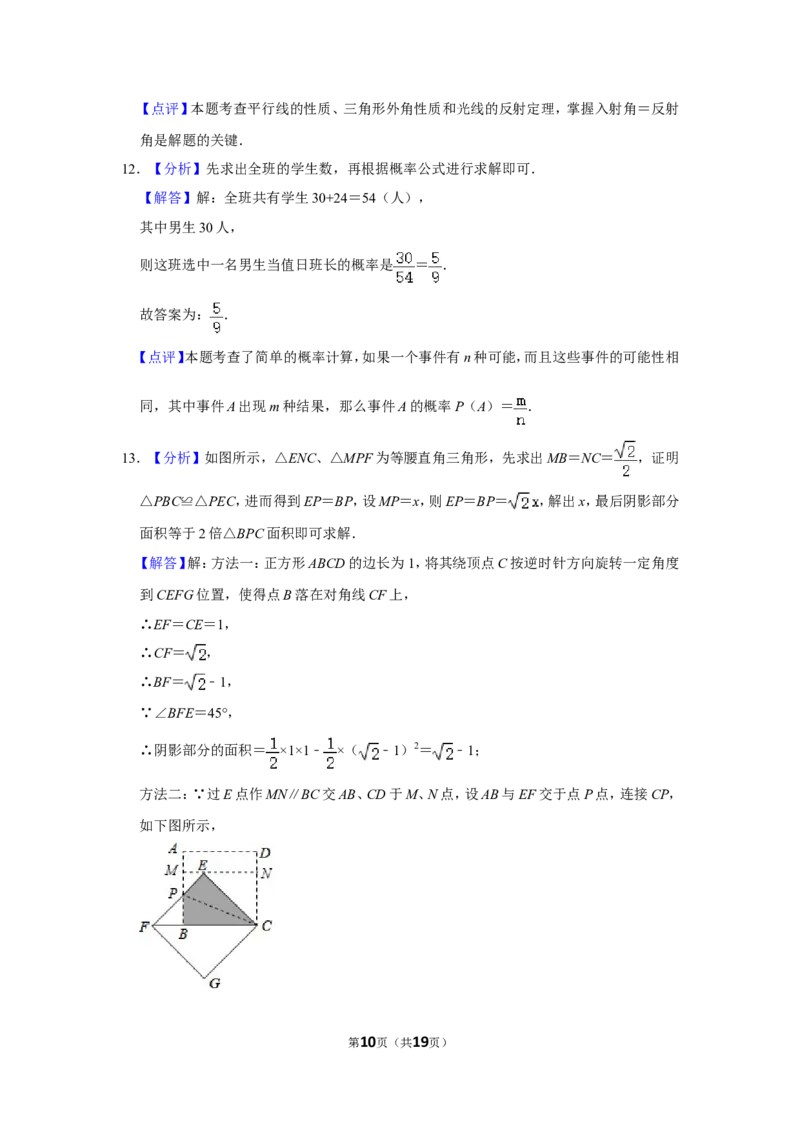
13.【分析】如图所示,△ENC、△MPF为等腰直角三角形,先求出MB=NC= ,证明
△PBC≌△PEC,进而得到EP=BP,设MP=x,则EP=BP= ,解出x,最后阴影部分
面积等于2倍△BPC面积即可求解.
【解答】解:方法一:正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度
到CEFG位置,使得点B落在对角线CF上,
∴EF=CE=1,
∴CF= ,
∴BF= ﹣1,
∵∠BFE=45°,
∴阴影部分的面积= ×1×1﹣ ×( ﹣1)2= ﹣1;
方法二:∵过E点作MN∥BC交AB、CD于M、N点,设AB与EF交于点P点,连接CP,
如下图所示,
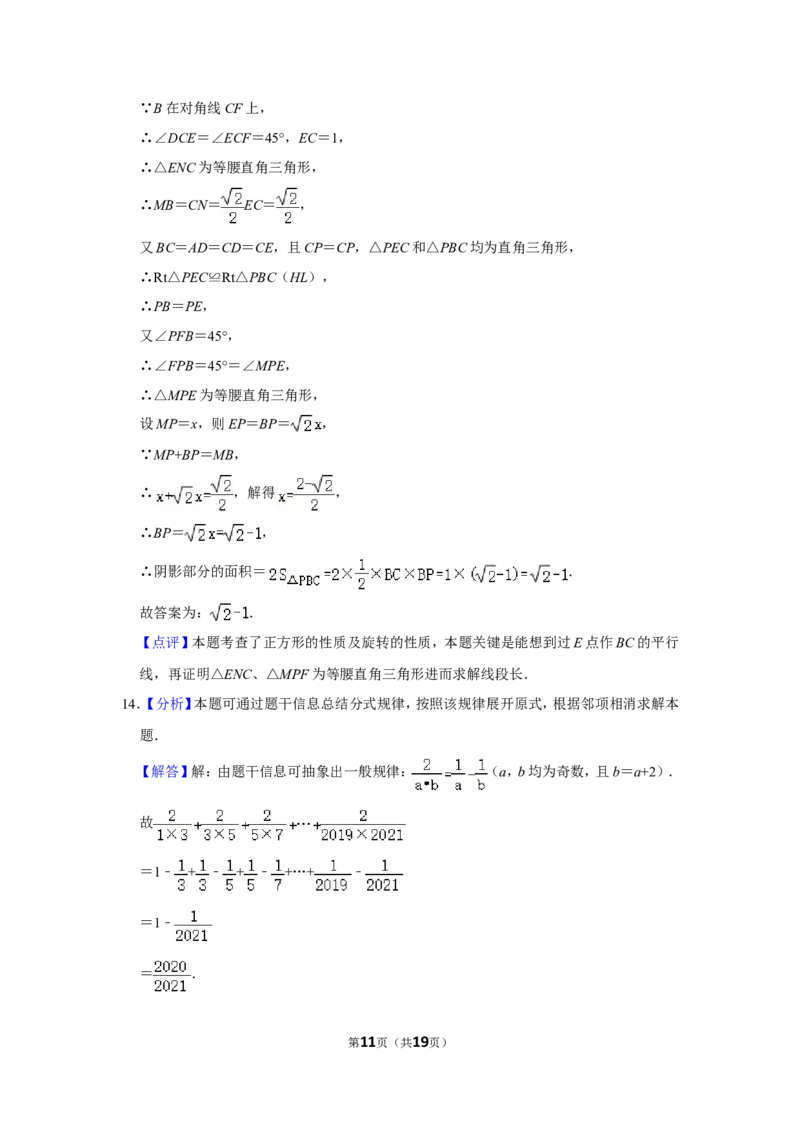
第10页(共19页)∵B在对角线CF上,
∴∠DCE=∠ECF=45°,EC=1,
∴△ENC为等腰直角三角形,
∴MB=CN= EC= ,
又BC=AD=CD=CE,且CP=CP,△PEC和△PBC均为直角三角形,
∴Rt△PEC≌Rt△PBC(HL),
∴PB=PE,
又∠PFB=45°,
∴∠FPB=45°=∠MPE,
∴△MPE为等腰直角三角形,
设MP=x,则EP=BP= ,
∵MP+BP=MB,
∴ ,解得 ,
∴BP= ,
∴阴影部分的面积= .
故答案为: .
【点评】本题考查了正方形的性质及旋转的性质,本题关键是能想到过E点作BC的平行
线,再证明△ENC、△MPF为等腰直角三角形进而求解线段长.
14.【分析】本题可通过题干信息总结分式规律,按照该规律展开原式,根据邻项相消求解本
题.
【解答】解:由题干信息可抽象出一般规律: (a,b均为奇数,且b=a+2).
故
=1﹣ + ﹣ + ﹣ +…+ ﹣
=1﹣
= .
第11页(共19页)故答案: .
【点评】本题考查规律型:数字的变化类,规律的抽象总结,解答该类型题目需要准确识别
题干所给的例子包含何种规律,严格按照该规律求解.
三、解答题(本大题共9个小题,满分0分.请考生用黑色碳素笔在答题卡相应的题号后的答
题区域内作答,必须写出运算步骤、推理过程或文字说明,超出答题区域的作答无效)
15.【分析】根据绝对值的性质,特殊角的三角函数值,零次幂,负整数指数幂进行运算即可.
【解答】解:原式= ﹣1﹣2× +1﹣4
= ﹣1﹣ +1﹣4
=﹣4.
【点评】本题考查了绝对值的性质、特殊角的三角函数值、零次幂、负整数指数幂,熟知以
上运算是解题的关键.
16.【分析】(1)根据矩形的性质可得BO=DO,∠EOD=∠FOB,∠EDO=∠FBO,即可证的
两个三角形全等;
(2)设AE=x,根据已知条件可得AE=8﹣x,由(1)可推得△EBO≌△EDO,可得ED=
EB,可证得四边形EBFD是菱形,根据勾股定理可得BE的长,即可求得周长;
【解答】(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,DO=BO,
∴∠EDO=∠FBO,
又∵EF⊥BD,
∴∠EOD=∠FOB=90°,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(ASA);
(2)解:∵由(1)可得,ED∥BF,ED=BF,
∴四边形BFDE是平行四边形,
∵BO=DO,EF⊥BD,
∴ED=EB,
第12页(共19页)∴四边形BFDE是菱形,
根据AB=6,AD=8,设AE=x,可得BE=ED=8﹣x,
在Rt△ABE中,根据勾股定理可得:BE2=AB2+AE2,
即(8﹣x)2=x2+62,
解得: ,
∴ ,
∴四边形BFDE的周长= .
【点评】本题主要考查了矩形的性质应用,结合菱形的判定与性质、全等三角形的判定进
行求解是解题的关键.
17.【分析】括号内后面的分式分子、分母先分解因式,约分后进行分式的减法运算,然后再进
行分式的除法运算进行化简,最后把x的值代入进行计算即可.
【解答】解:( ﹣ )÷
=
=
=
= ,
当 时,原式= =1.
【点评】本题考查了分式的混合运算﹣﹣化简求值,涉及了二次根式的运算、分式的约分、
分式的除法运算、减法运算等,熟练掌握各运算法则是解题的关键.
18.【分析】(1)用总人数减去A、B、D三组的人数和即可得出C组的人数,然后补全条形统
计图即可;
(2)D组共有13人,把数据按照从小到大(从大到小)的顺序排列,找到中间第七个数据
即可;
(3)用1200乘以80分以上的人数所占的比例即可得出人数.
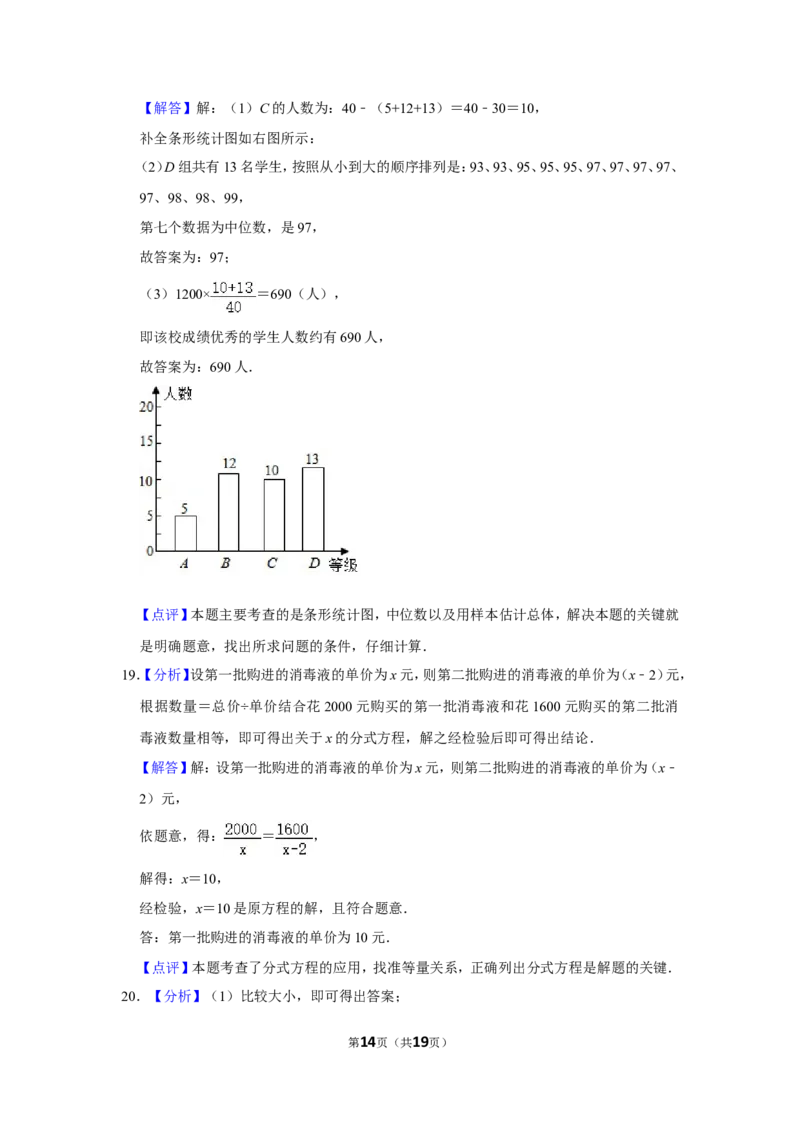
第13页(共19页)【解答】解:(1)C的人数为:40﹣(5+12+13)=40﹣30=10,
补全条形统计图如右图所示:
(2)D组共有13名学生,按照从小到大的顺序排列是:93、93、95、95、95、97、97、97、97、
97、98、98、99,
第七个数据为中位数,是97,
故答案为:97;
(3)1200× =690(人),
即该校成绩优秀的学生人数约有690人,
故答案为:690人.
【点评】本题主要考查的是条形统计图,中位数以及用样本估计总体,解决本题的关键就
是明确题意,找出所求问题的条件,仔细计算.
19.【分析】设第一批购进的消毒液的单价为x元,则第二批购进的消毒液的单价为(x﹣2)元,
根据数量=总价÷单价结合花2000元购买的第一批消毒液和花1600元购买的第二批消
毒液数量相等,即可得出关于x的分式方程,解之经检验后即可得出结论.
【解答】解:设第一批购进的消毒液的单价为x元,则第二批购进的消毒液的单价为(x﹣
2)元,
依题意,得: = ,
解得:x=10,
经检验,x=10是原方程的解,且符合题意.
答:第一批购进的消毒液的单价为10元.
【点评】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
20.【分析】(1)比较大小,即可得出答案;
第14页(共19页)(2)根据题意判断出 ,解不等式即可判断x的取值范围.
【解答】解:(1)由题意得min{﹣1,3}=﹣1;
故答案为:﹣1;
(2)由题意得:
3(2x﹣3)≥2(x+2)
6x﹣9≥2x+4
4x≥13
x≥ ,
∴x的取值范围为x≥ .
【点评】本题考查的是一元一次不等式的应用,根据题意理解新定义的计算公式是解题的
关键.
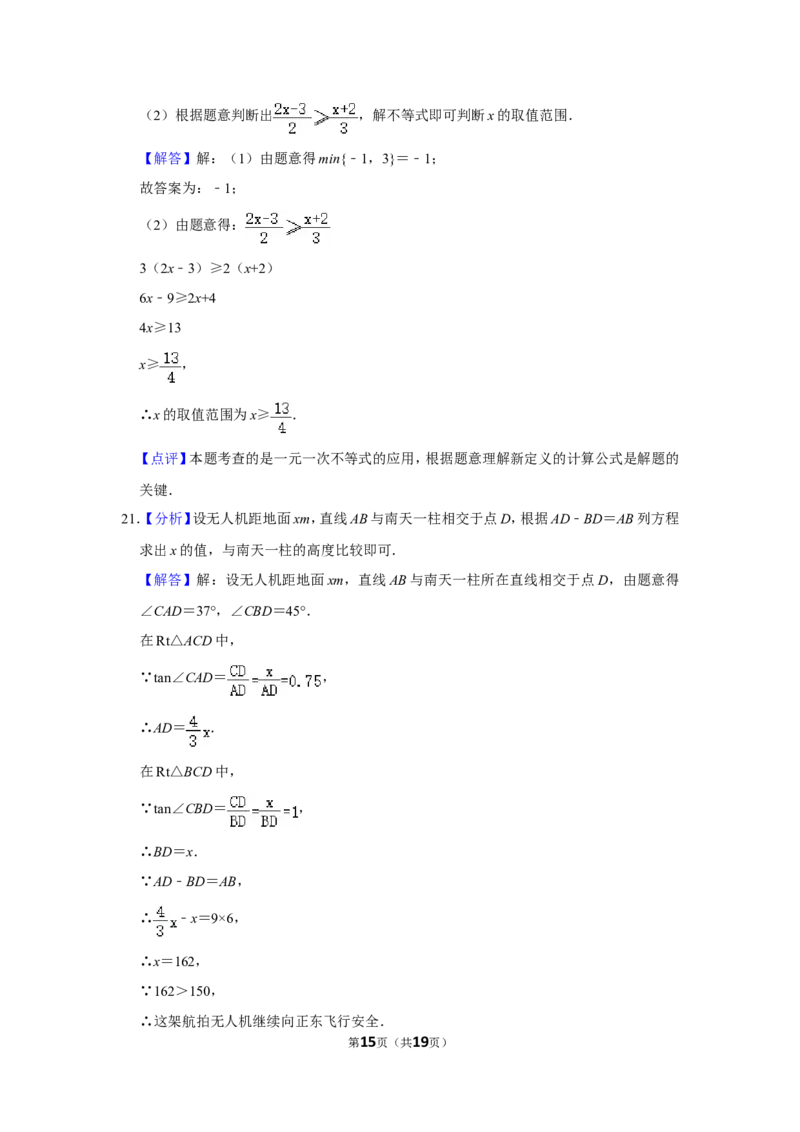
21.【分析】设无人机距地面xm,直线AB与南天一柱相交于点D,根据AD﹣BD=AB列方程
求出x的值,与南天一柱的高度比较即可.
【解答】解:设无人机距地面xm,直线AB与南天一柱所在直线相交于点D,由题意得
∠CAD=37°,∠CBD=45°.
在Rt△ACD中,
∵tan∠CAD= ,
∴AD= .
在Rt△BCD中,
∵tan∠CBD= ,
∴BD=x.
∵AD﹣BD=AB,
∴ ﹣x=9×6,
∴x=162,
∵162>150,
∴这架航拍无人机继续向正东飞行安全.
第15页(共19页)【点评】本题考查解直角三角形的应用﹣仰角俯角问题,解题的关键是学会添加常用辅助
线,构造直角三角形解决问题,学会用构建方程的思想思考问题.
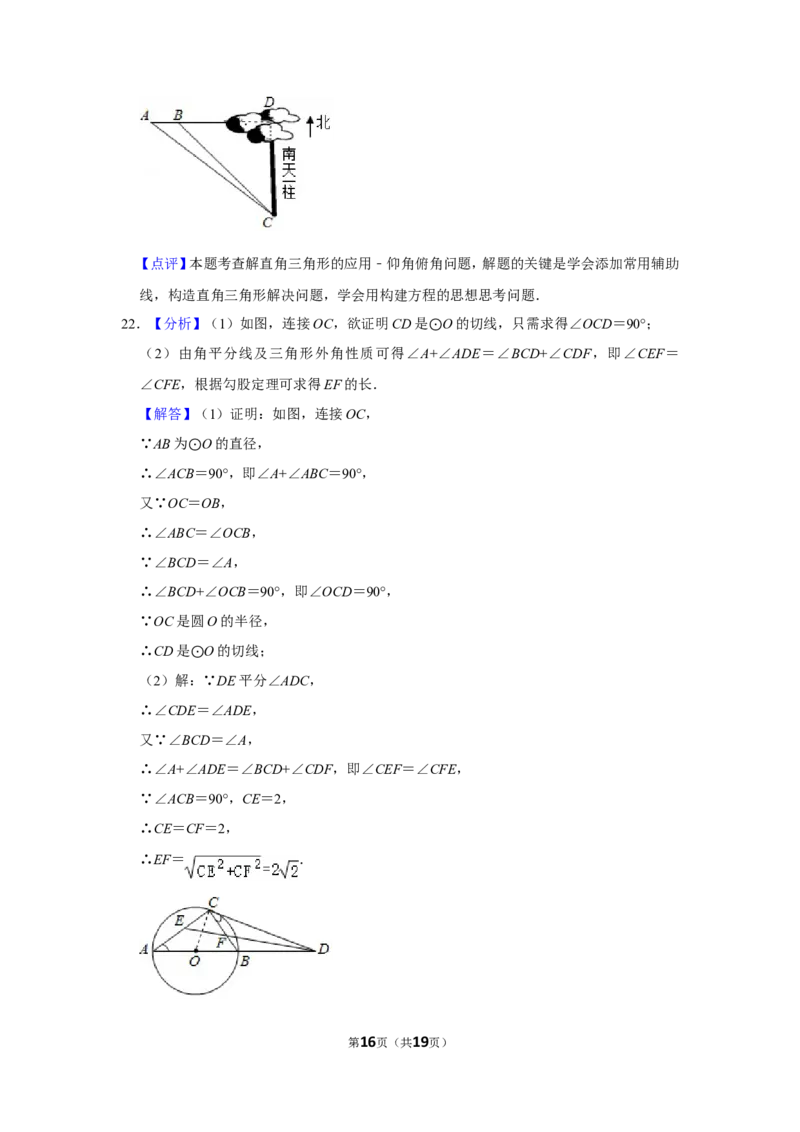
22.【分析】(1)如图,连接OC,欲证明CD是 O的切线,只需求得∠OCD=90°;
(2)由角平分线及三角形外角性质可得∠A⊙+∠ADE=∠BCD+∠CDF,即∠CEF=
∠CFE,根据勾股定理可求得EF的长.
【解答】(1)证明:如图,连接OC,
∵AB为 O的直径,
∴∠ACB⊙=90°,即∠A+∠ABC=90°,
又∵OC=OB,
∴∠ABC=∠OCB,
∵∠BCD=∠A,
∴∠BCD+∠OCB=90°,即∠OCD=90°,
∵OC是圆O的半径,
∴CD是 O的切线;
(2)解:⊙∵DE平分∠ADC,
∴∠CDE=∠ADE,
又∵∠BCD=∠A,
∴∠A+∠ADE=∠BCD+∠CDF,即∠CEF=∠CFE,
∵∠ACB=90°,CE=2,
∴CE=CF=2,
∴EF= .
第16页(共19页)【点评】此题主要考查切线的判定方法、角平分线及三角形外角性质和勾股定理,熟练进
行推理论证是解题关键.
23.【分析】(1)先根据直线y=﹣x+5经过点B,C,即可确定B、C的坐标,然后用待定系数
法解答即可;
(2)先求出A、B的坐标结合抛物线的对称性,说明三角形APB为等腰三角形;再结合OB
=OC得到∠ABP=45°,进一步说明∠APB=90°,则∠APC=90°即可判定△APC的形状;
(3)作AN⊥BC于N,NH⊥x轴于H,作AC的垂直平分线交BC于M1,AC于E;然后说明
△ANB为等腰直角三角形,进而确定N的坐标;再求出AC的解析式,进而确定M E的解
1
析式;然后联立直线BC和M E的解析式即可求得M 的坐标;在直线BC上作点M 关于
1 1 1
N点的对称点M ,利用中点坐标公式即可确定点M 的坐标.
2 2
【解答】解:(1)∵直线y=﹣x+5经过点B,C,
∴当x=0时,可得y=5,即C的坐标为(0,5).
当y=0时,可得x=5,即B的坐标为(5,0).
∴ .
解得 .
∴该抛物线的解析式为y=x2﹣6x+5;
(2)△APC为直角三角形,理由如下:
∵解方程x2﹣6x+5=0,则x =1,x =5.
1 2
∴A(1,0),B(5,0).
∵抛物线y=x2﹣6x+5的对称轴l为x=3,
∴△APB为等腰三角形.
∵C的坐标为(0,5),B的坐标为(5,0),
∴OB=CO=5,即∠ABP=45°.
∵PA=PB,∴∠PAB=∠ABP=45°,
∴∠ABP=45°.
∴∠APB=180°﹣45°﹣45°=90°.
∴∠APC=180°﹣90°=90°.
∴△APC为直角三角形;
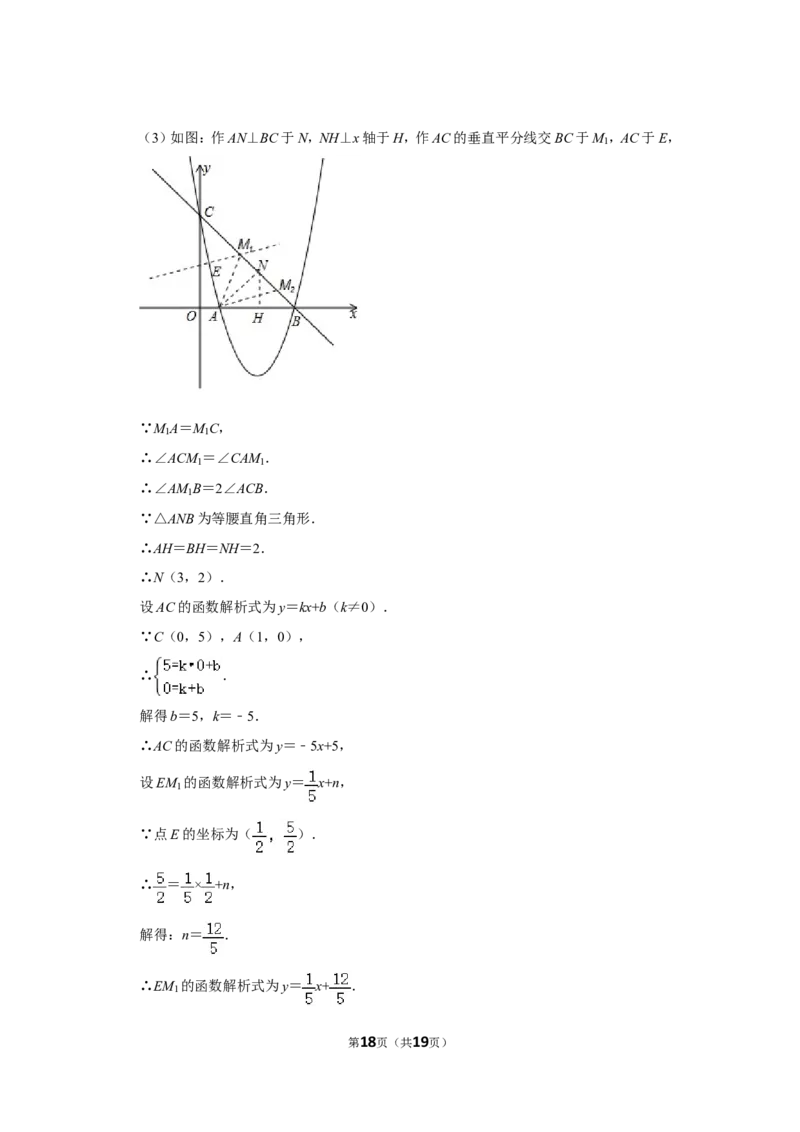
第17页(共19页)(3)如图:作AN⊥BC于N,NH⊥x轴于H,作AC的垂直平分线交BC于M ,AC于E,
1
∵M A=M C,
1 1
∴∠ACM =∠CAM .
1 1
∴∠AM B=2∠ACB.
1
∵△ANB为等腰直角三角形.
∴AH=BH=NH=2.
∴N(3,2).
设AC的函数解析式为y=kx+b(k≠0).
∵C(0,5),A(1,0),
∴ .
解得b=5,k=﹣5.
∴AC的函数解析式为y=﹣5x+5,
设EM 的函数解析式为y= x+n,
1
∵点E的坐标为( ).
∴ = × +n,
解得:n= .
∴EM 的函数解析式为y= x+ .
1
第18页(共19页)∵ .
解得 .
∴M 的坐标为( );
1
在直线BC上作点M 关于N点的对称点M ,
1 2
设M (a,﹣a+5),
2
则有:3= ,解得a= .
∴﹣a+5= .
∴M 的坐标为( , ).
2
综上,存在使AM与直线BC的夹角等于∠ACB的2倍的点,且坐标为M( ),M
1 2
( , ).
【点评】本题属于二次函数与几何的综合题,主要考查了待定系数法确定函数解析式、等
腰直角三角形的判定与性质、一次函数图象、三角形外角等知识,考查知识点较多,综合
应用所学知识成为解答本题的关键.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/9/17 11:11:32;用户:18366185883;邮箱:18366185883;学号:22597006
第19页(共19页)