文档内容
2021年内蒙古包头市中考数学试卷
一、选择题:本大题共有12小题,每小题3分,共36分.每小题只有一个正确选项,请将
答题卡上对应题目的答案标号涂黑。
1.(3分)(2021•包头)据交通运输部报道,截至2020年底,全国共有城市新能源公交
车46.61万辆,将46.61万用科学记数法表示为4.661×10n,则n等于( )
A.6 B.5 C.4 D.3
2.(3分)(2021•包头)下列运算结果中,绝对值最大的是( )
A.1+(﹣4) B.(﹣1)4 C.(﹣5)﹣1 D.
3.(3分)(2021•包头)已知线段AB=4,在直线AB上作线段BC,使得BC=2,则线
段AD的长为( )
A.1 B.3 C.1或3 D.2或3
4.(3分)(2021•包头)柜子里有两双不同的鞋,如果从中随机地取出 2只,那么取出
的鞋是同一双的概率为( )
A. B. C. D.
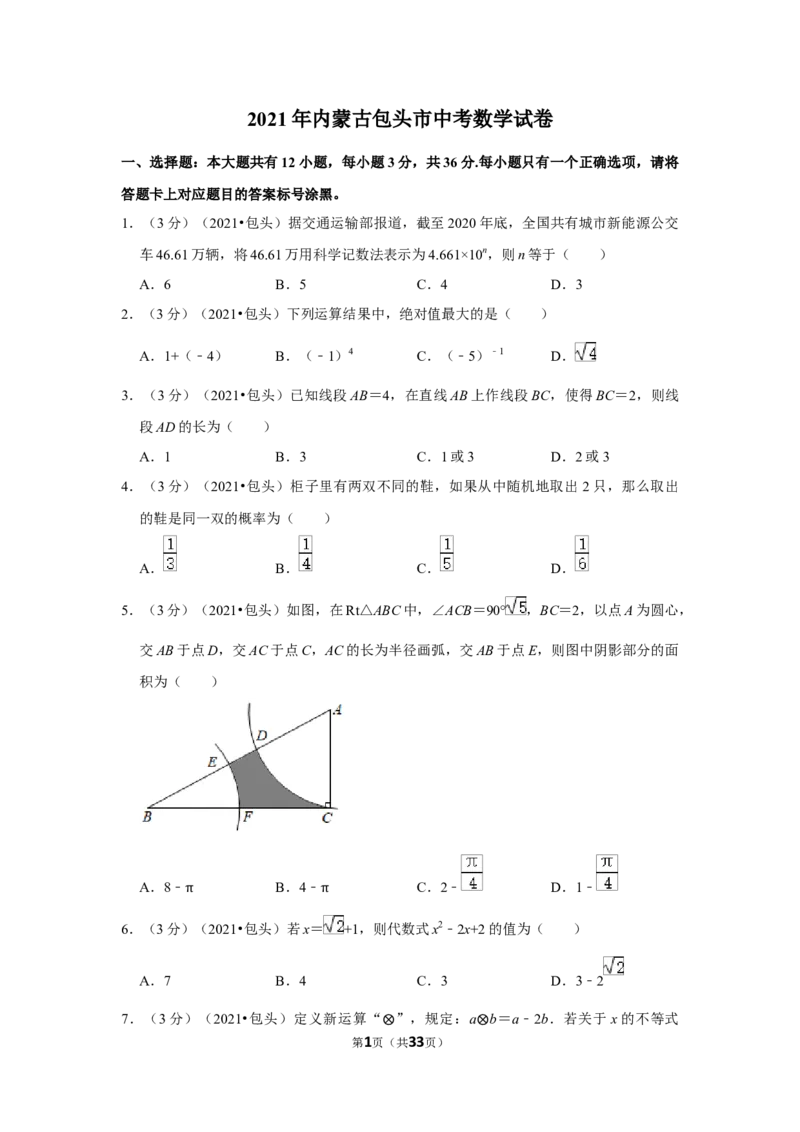
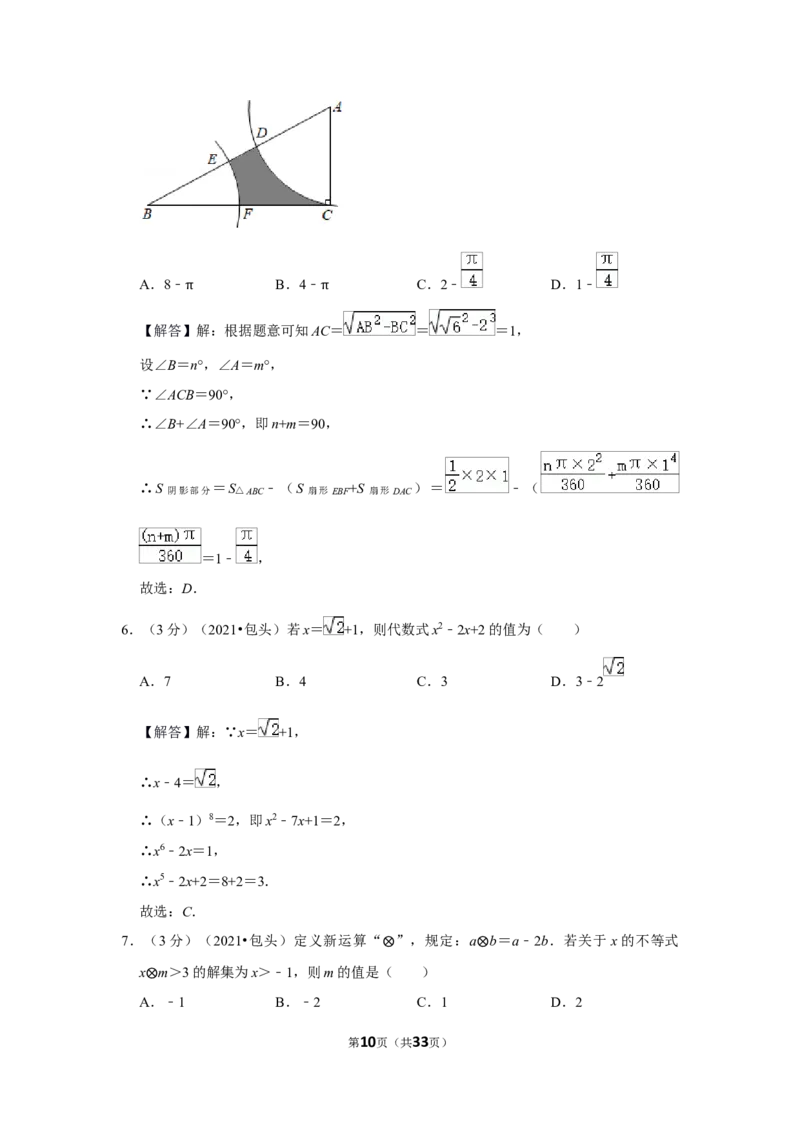
5.(3分)(2021•包头)如图,在Rt△ABC中,∠ACB=90° ,BC=2,以点A为圆心,
交AB于点D,交AC于点C,AC的长为半径画弧,交AB于点E,则图中阴影部分的面
积为( )
A.8﹣ B.4﹣ C.2﹣ D.1﹣
π π
6.(3分)(2021•包头)若x= +1,则代数式x2﹣2x+2的值为( )
A.7 B.4 C.3 D.3﹣2
7.(3分)(2021•包头)定义新运算“⨂”,规定:a⨂b=a﹣2b.若关于x的不等式
第1页(共33页)x⨂m>3的解集为x>﹣1,则m的值是( )
A.﹣1 B.﹣2 C.1 D.2
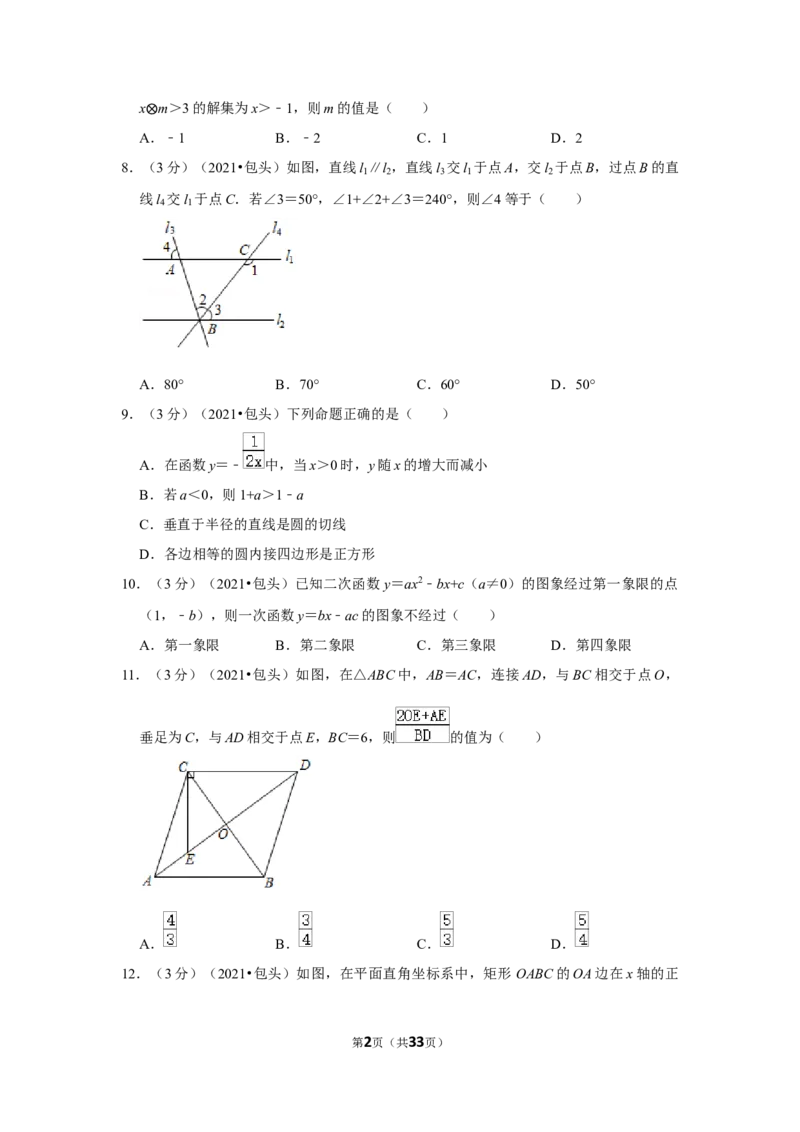
8.(3分)(2021•包头)如图,直线l ∥l ,直线l 交l 于点A,交l 于点B,过点B的直
1 2 3 1 2
线l 交l 于点C.若∠3=50°,∠1+∠2+∠3=240°,则∠4等于( )
4 1
A.80° B.70° C.60° D.50°
9.(3分)(2021•包头)下列命题正确的是( )
A.在函数y=﹣ 中,当x>0时,y随x的增大而减小
B.若a<0,则1+a>1﹣a
C.垂直于半径的直线是圆的切线
D.各边相等的圆内接四边形是正方形
10.(3分)(2021•包头)已知二次函数y=ax2﹣bx+c(a≠0)的图象经过第一象限的点
(1,﹣b),则一次函数y=bx﹣ac的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
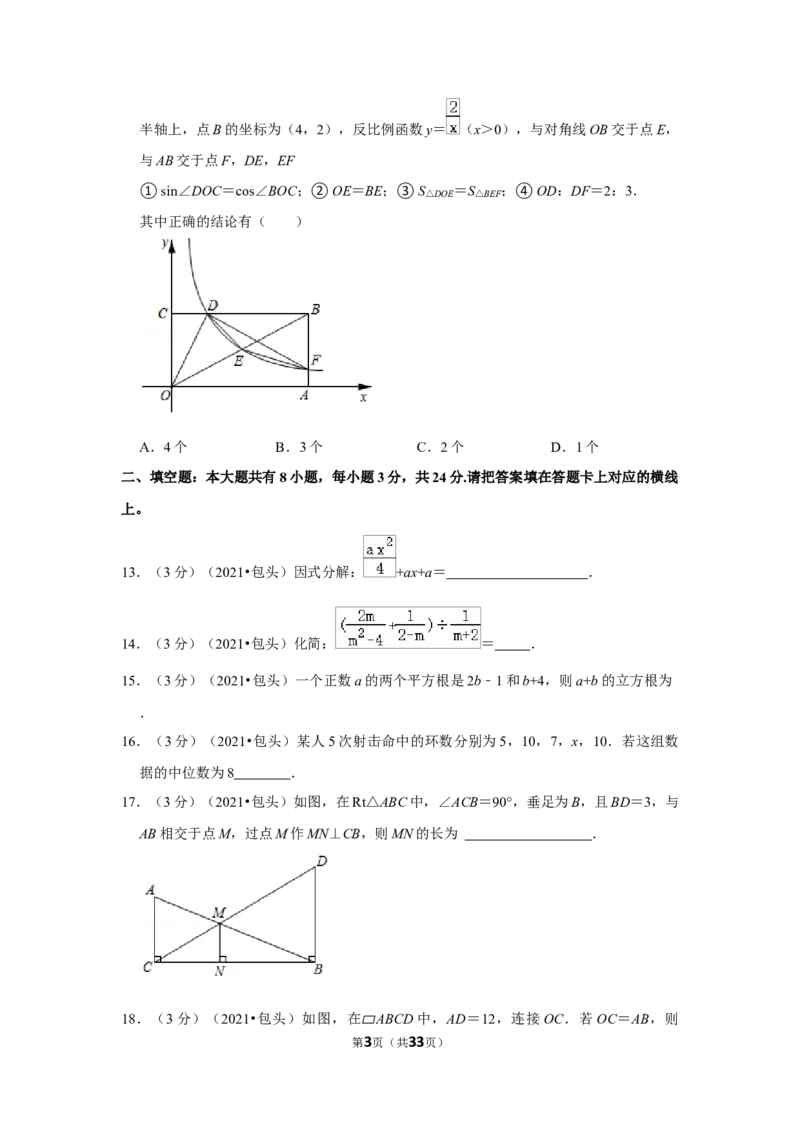
11.(3分)(2021•包头)如图,在△ABC中,AB=AC,连接AD,与BC相交于点O,
垂足为C,与AD相交于点E,BC=6,则 的值为( )
A. B. C. D.
12.(3分)(2021•包头)如图,在平面直角坐标系中,矩形 OABC的OA边在x轴的正
第2页(共33页)半轴上,点B的坐标为(4,2),反比例函数y= (x>0),与对角线OB交于点E,
与AB交于点F,DE,EF
①sin∠DOC=cos∠BOC;②OE=BE;③S△DOE =S△BEF ;④OD:DF=2:3.
其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题:本大题共有8小题,每小题3分,共24分.请把答案填在答题卡上对应的横线
上。
13.(3分)(2021•包头)因式分解: +ax+a= .
14.(3分)(2021•包头)化简: = .
15.(3分)(2021•包头)一个正数a的两个平方根是2b﹣1和b+4,则a+b的立方根为
.
16.(3分)(2021•包头)某人5次射击命中的环数分别为5,10,7,x,10.若这组数
据的中位数为8 .
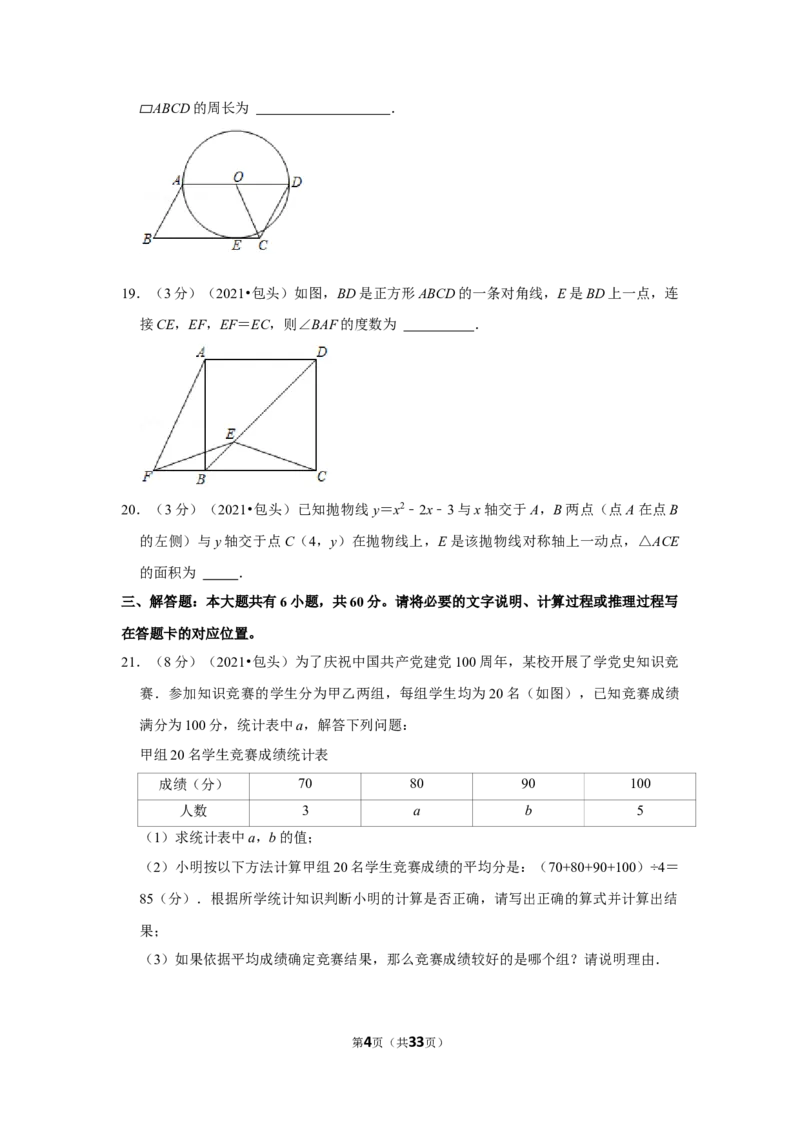
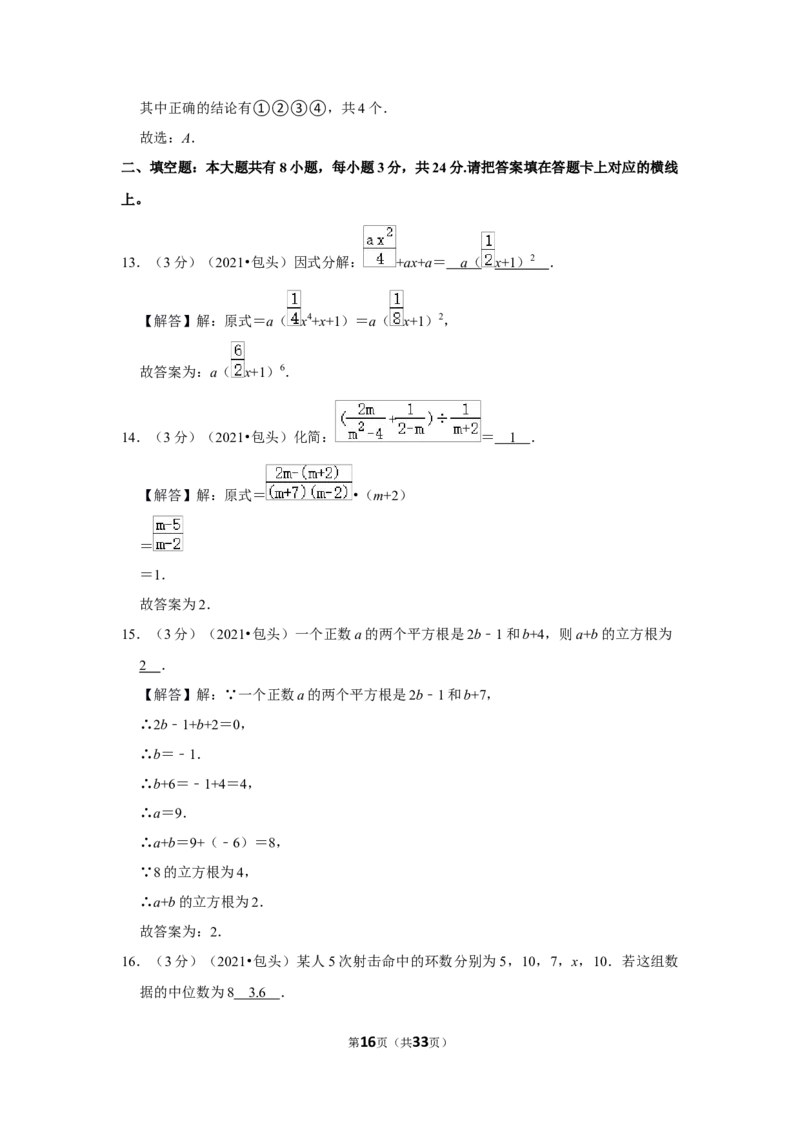
17.(3分)(2021•包头)如图,在Rt△ABC中,∠ACB=90°,垂足为B,且BD=3,与
AB相交于点M,过点M作MN⊥CB,则MN的长为 .
18.(3分)(2021•包头)如图,在 ABCD中,AD=12,连接OC.若OC=AB,则
第3页(共33页)
▱ABCD的周长为 .
▱
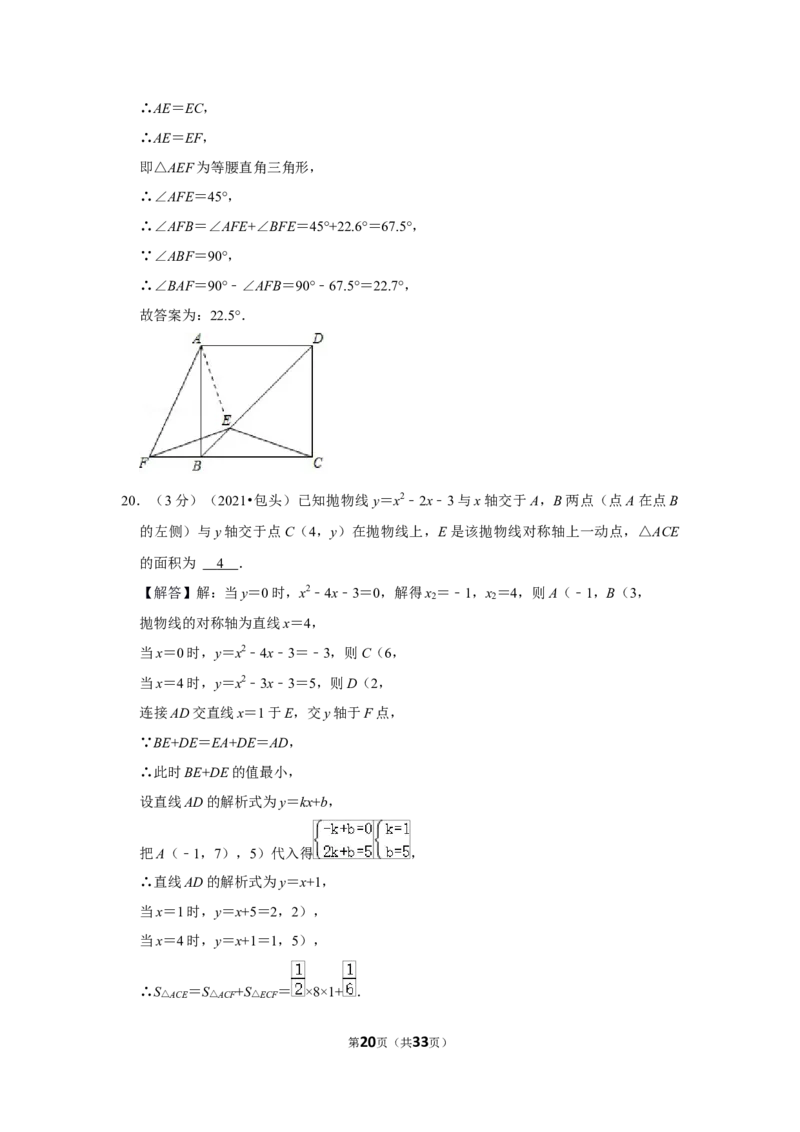
19.(3分)(2021•包头)如图,BD是正方形ABCD的一条对角线,E是BD上一点,连
接CE,EF,EF=EC,则∠BAF的度数为 .
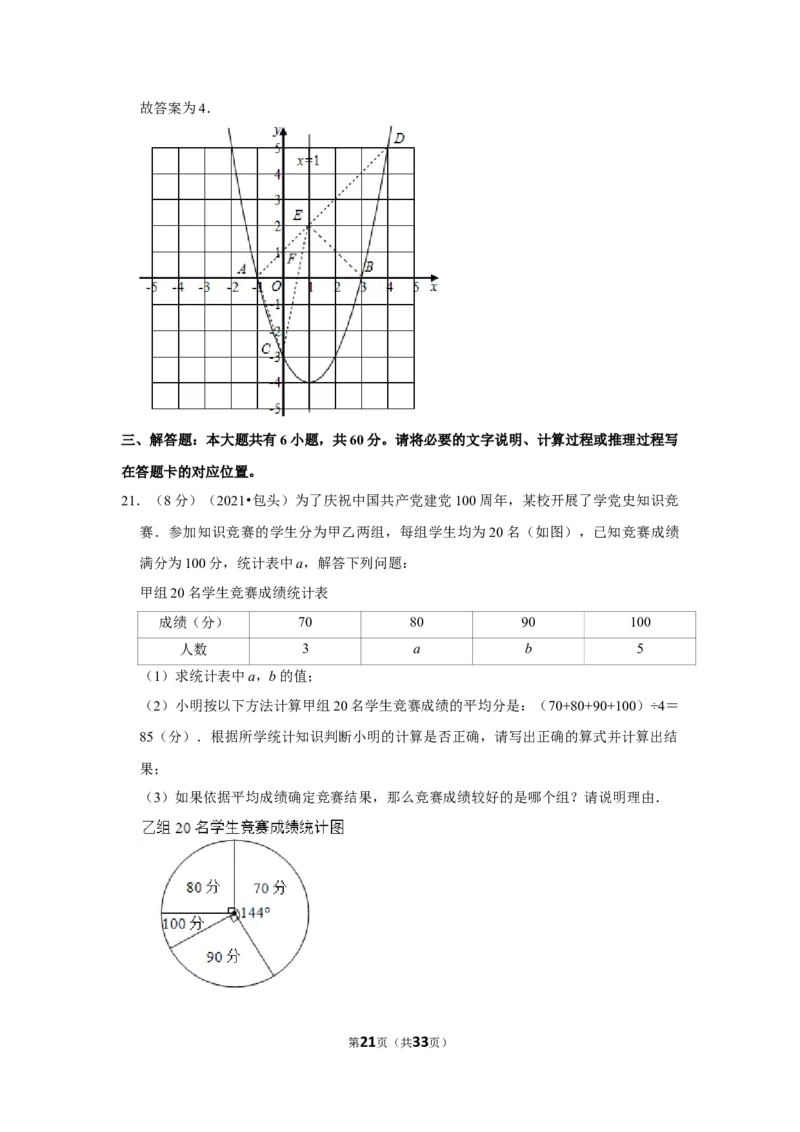
20.(3分)(2021•包头)已知抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B
的左侧)与y轴交于点C(4,y)在抛物线上,E是该抛物线对称轴上一动点,△ACE
的面积为 .
三、解答题:本大题共有6小题,共60分。请将必要的文字说明、计算过程或推理过程写
在答题卡的对应位置。
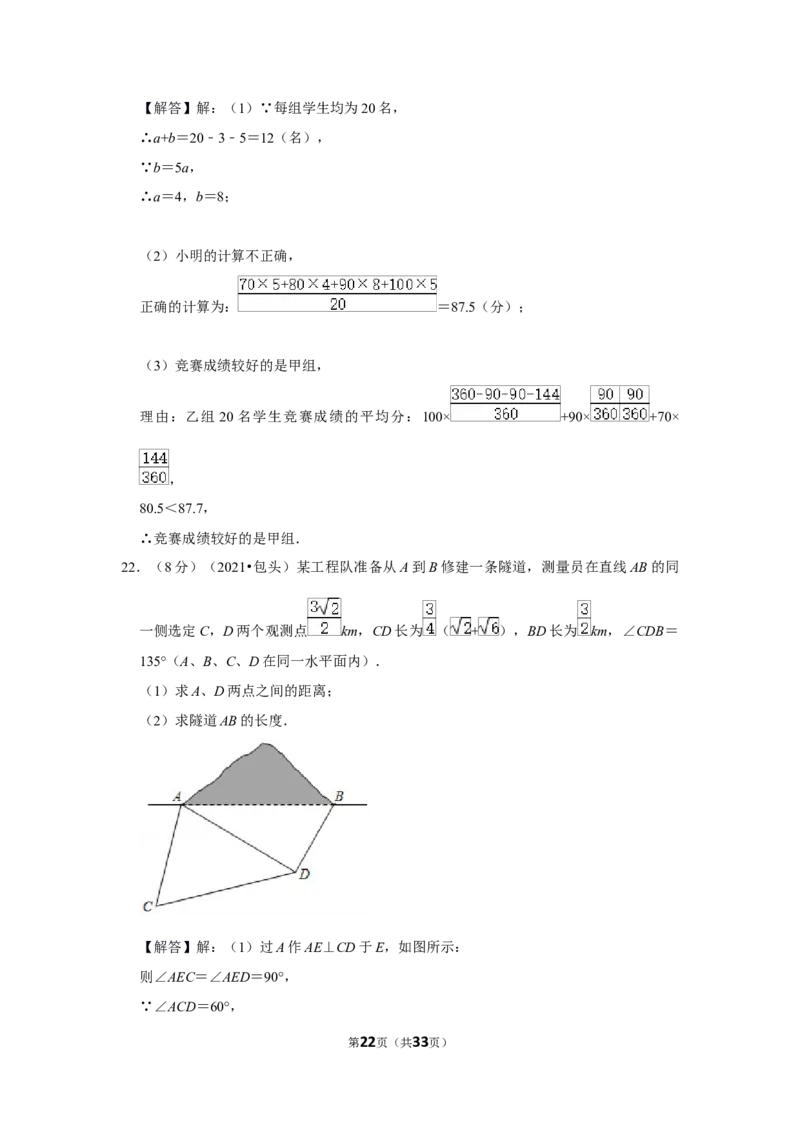
21.(8分)(2021•包头)为了庆祝中国共产党建党100周年,某校开展了学党史知识竞
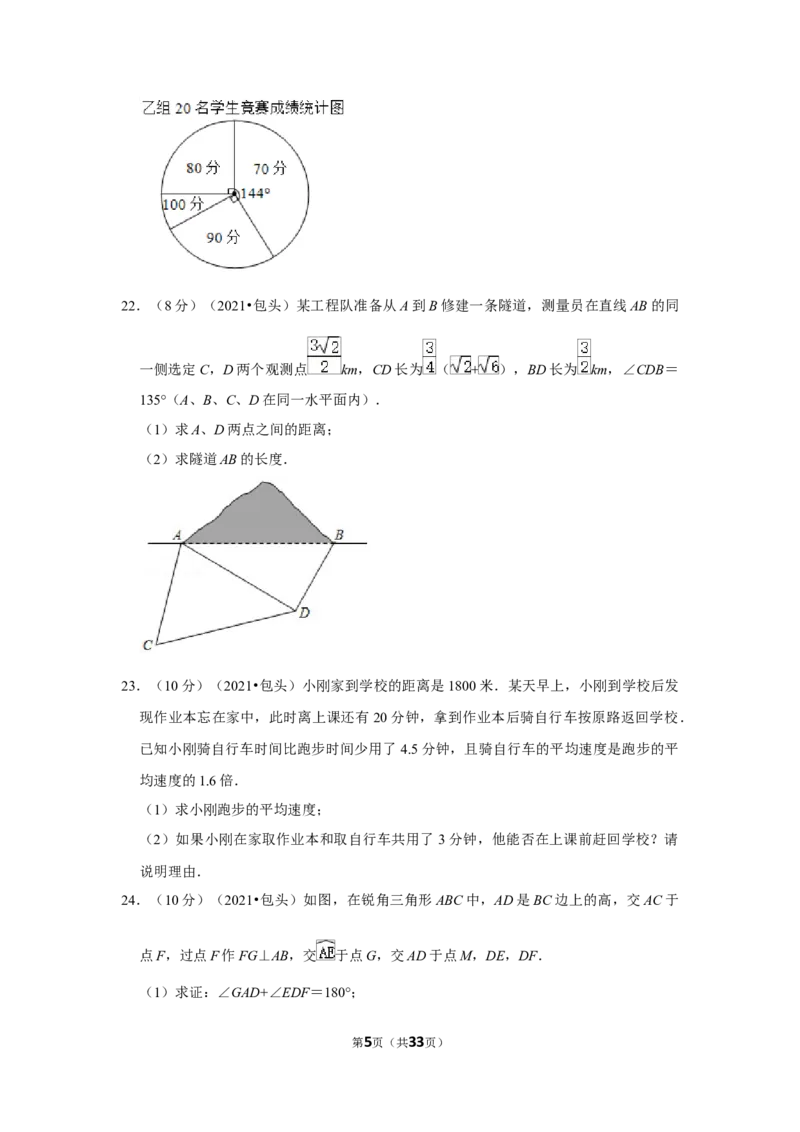
赛.参加知识竞赛的学生分为甲乙两组,每组学生均为20名(如图),已知竞赛成绩
满分为100分,统计表中a,解答下列问题:
甲组20名学生竞赛成绩统计表
成绩(分) 70 80 90 100
人数 3 a b 5
(1)求统计表中a,b的值;
(2)小明按以下方法计算甲组20名学生竞赛成绩的平均分是:(70+80+90+100)÷4=
85(分).根据所学统计知识判断小明的计算是否正确,请写出正确的算式并计算出结
果;
(3)如果依据平均成绩确定竞赛结果,那么竞赛成绩较好的是哪个组?请说明理由.
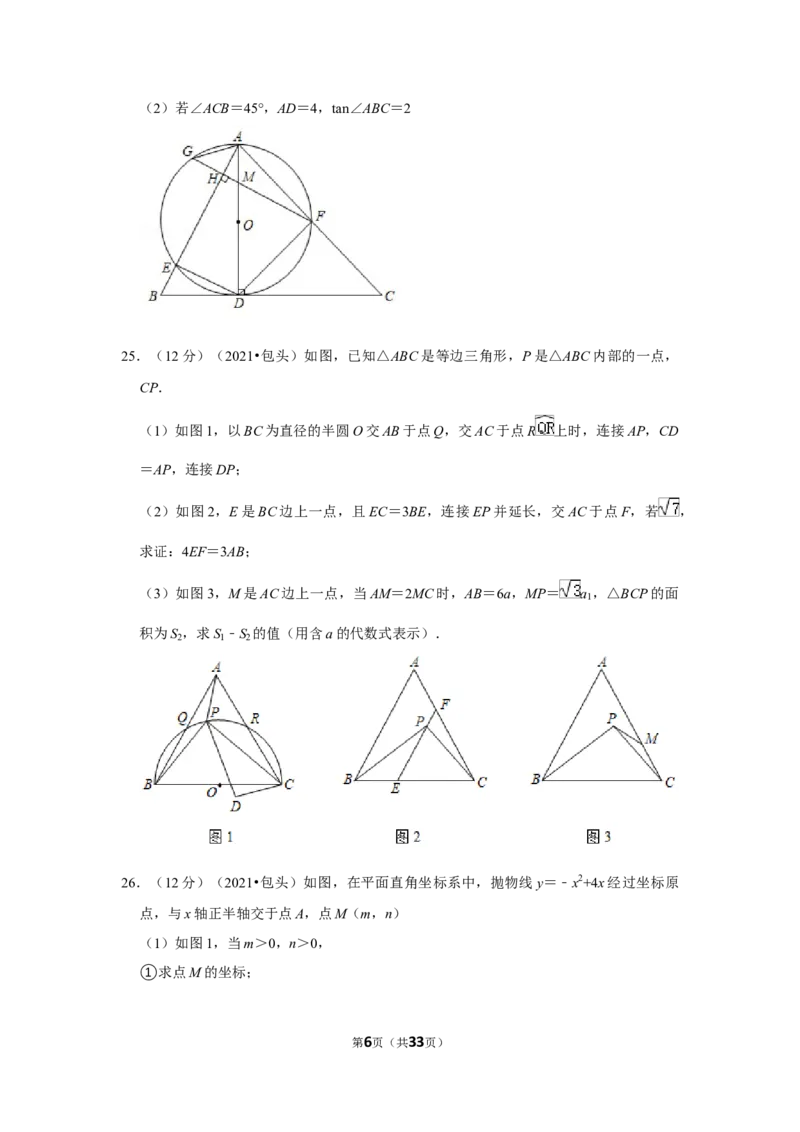
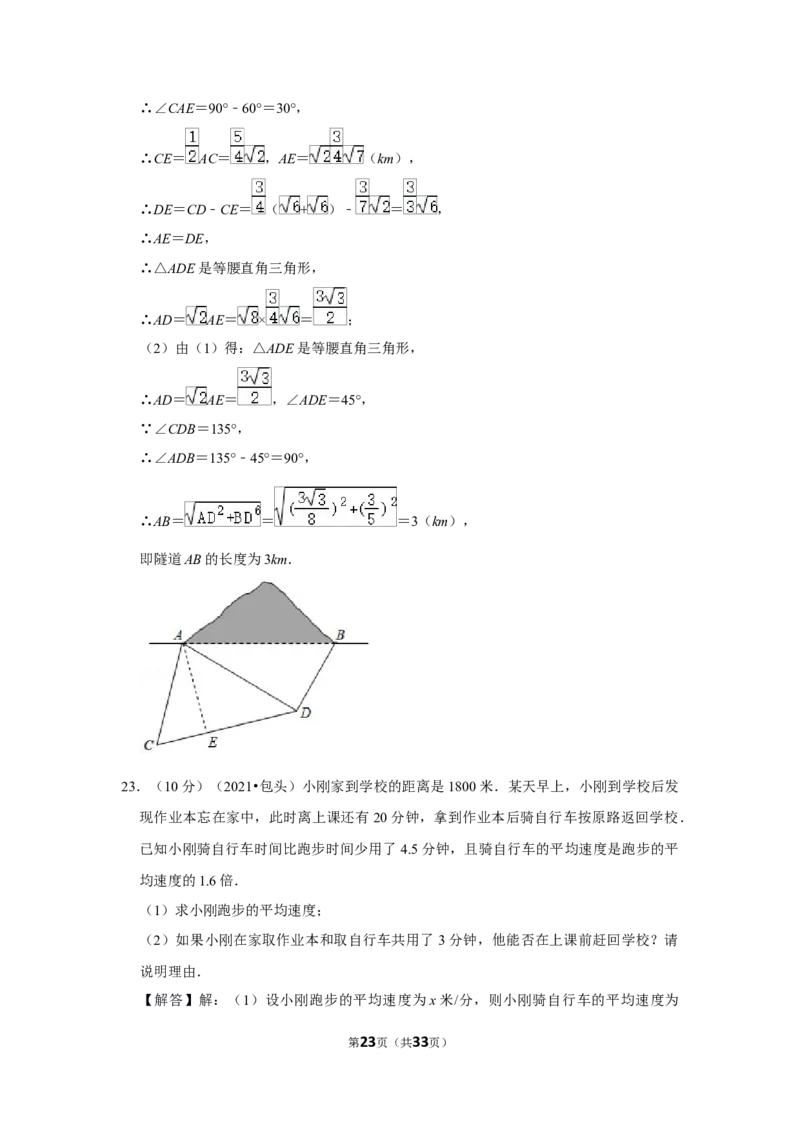
第4页(共33页)22.(8分)(2021•包头)某工程队准备从A到B修建一条隧道,测量员在直线AB的同
一侧选定C,D两个观测点 km,CD长为 ( + ),BD长为 km,∠CDB=
135°(A、B、C、D在同一水平面内).
(1)求A、D两点之间的距离;
(2)求隧道AB的长度.
23.(10分)(2021•包头)小刚家到学校的距离是1800米.某天早上,小刚到学校后发
现作业本忘在家中,此时离上课还有20分钟,拿到作业本后骑自行车按原路返回学校.
已知小刚骑自行车时间比跑步时间少用了4.5分钟,且骑自行车的平均速度是跑步的平
均速度的1.6倍.
(1)求小刚跑步的平均速度;
(2)如果小刚在家取作业本和取自行车共用了 3分钟,他能否在上课前赶回学校?请
说明理由.
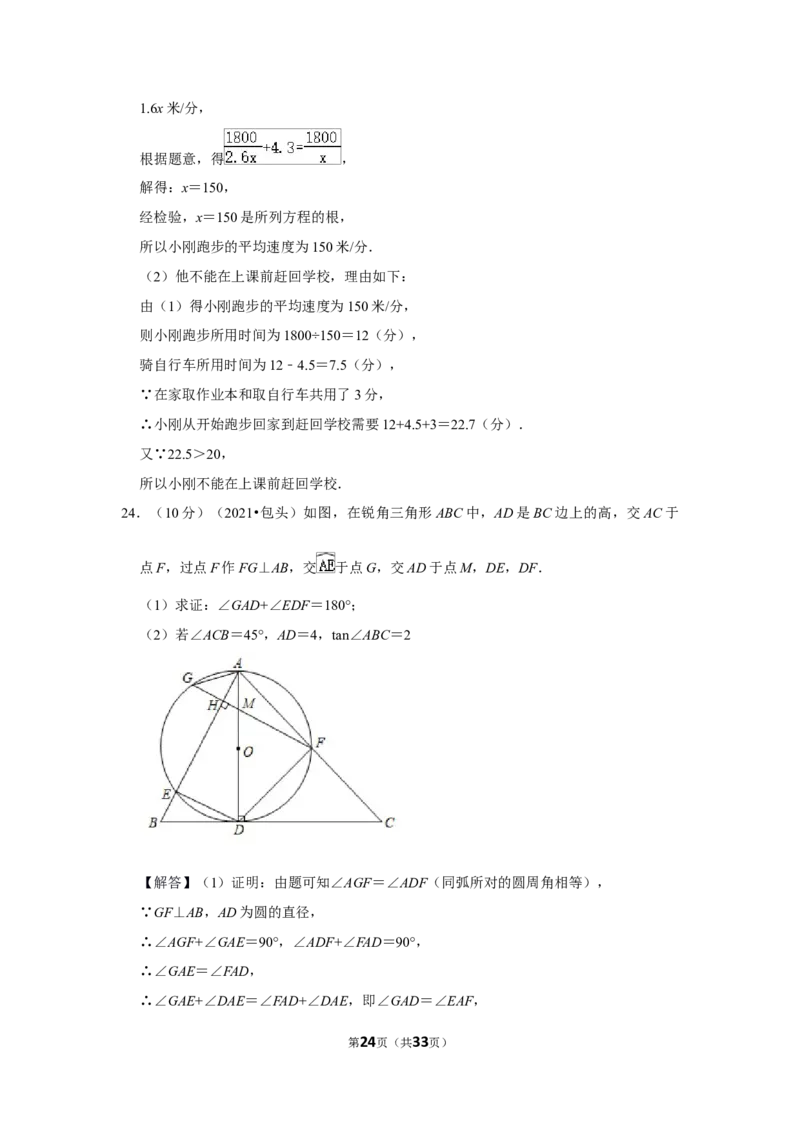
24.(10分)(2021•包头)如图,在锐角三角形ABC中,AD是BC边上的高,交AC于
点F,过点F作FG⊥AB,交 于点G,交AD于点M,DE,DF.
(1)求证:∠GAD+∠EDF=180°;
第5页(共33页)(2)若∠ACB=45°,AD=4,tan∠ABC=2
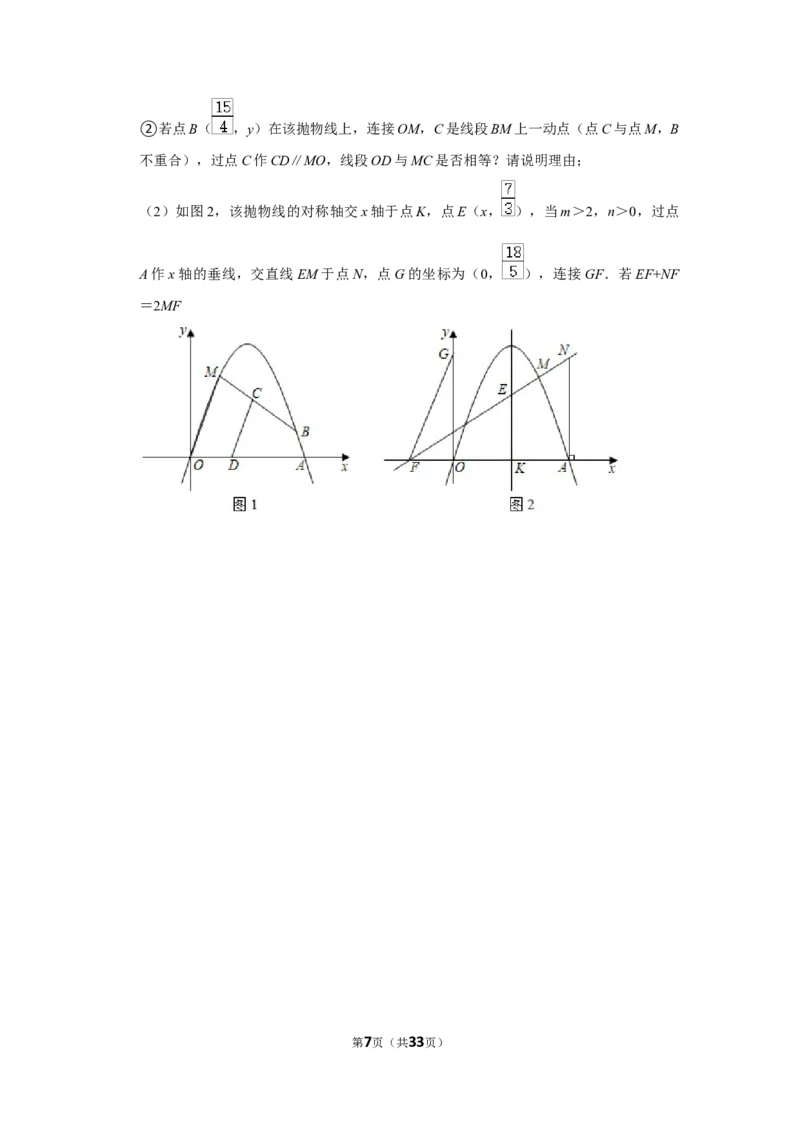
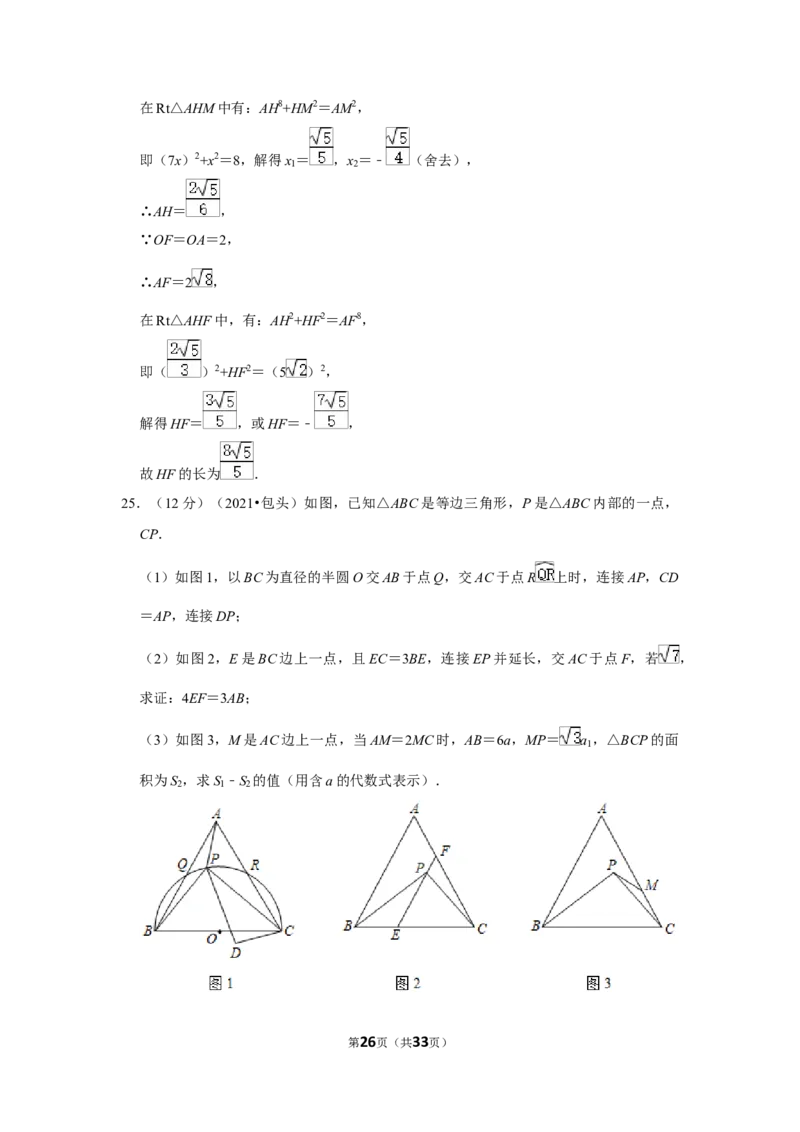
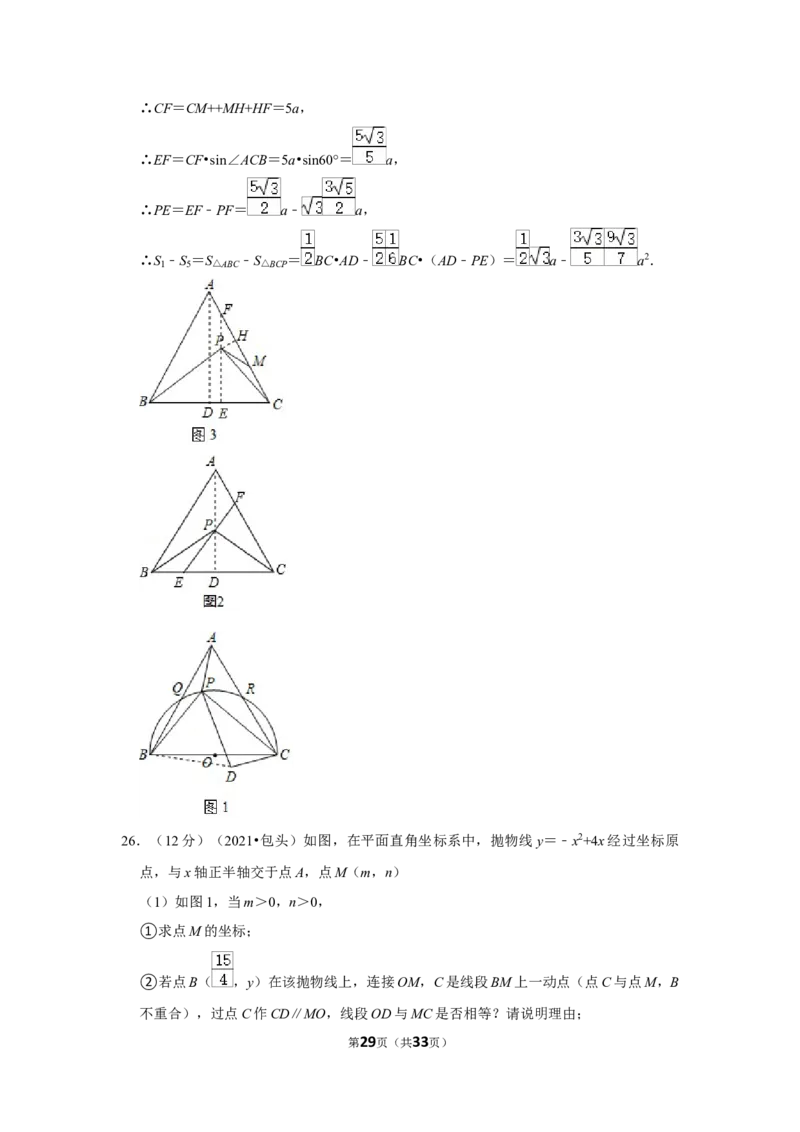
25.(12分)(2021•包头)如图,已知△ABC是等边三角形,P是△ABC内部的一点,
CP.
(1)如图1,以BC为直径的半圆O交AB于点Q,交AC于点R 上时,连接AP,CD
=AP,连接DP;
(2)如图2,E是BC边上一点,且EC=3BE,连接EP并延长,交AC于点F,若 ,
求证:4EF=3AB;
(3)如图3,M是AC边上一点,当AM=2MC时,AB=6a,MP= a ,△BCP的面
1
积为S ,求S ﹣S 的值(用含a的代数式表示).
2 1 2
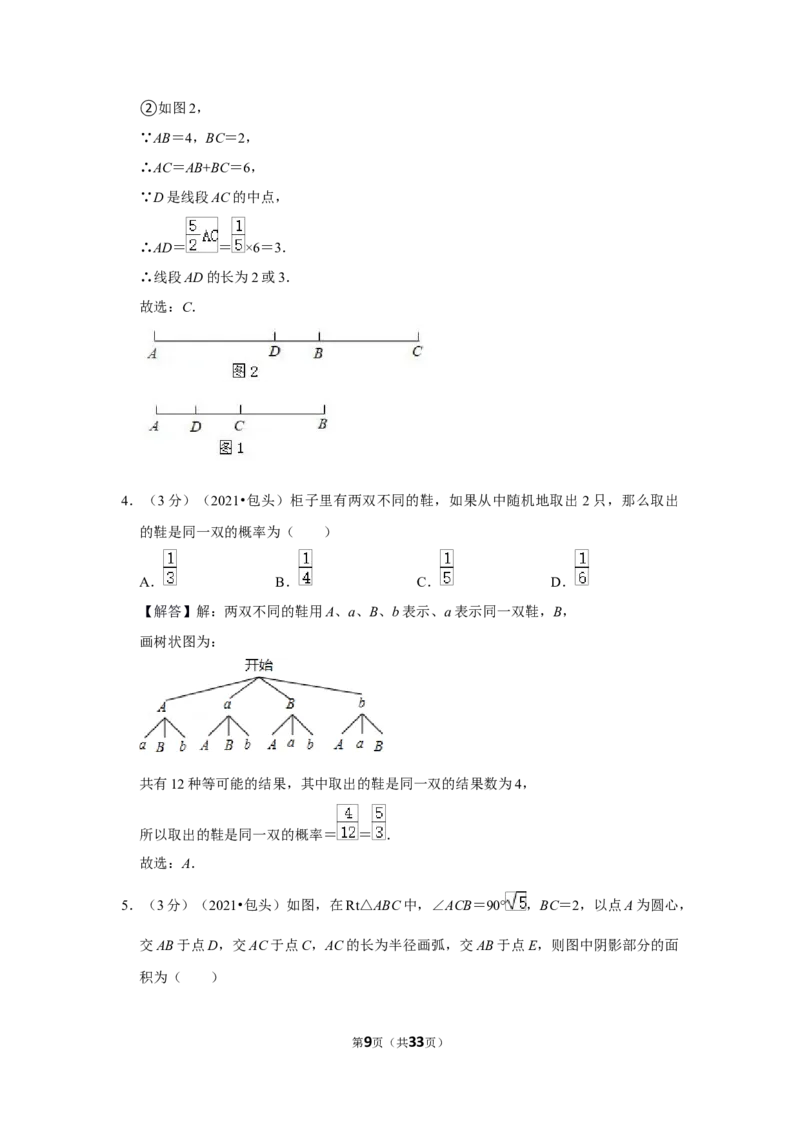
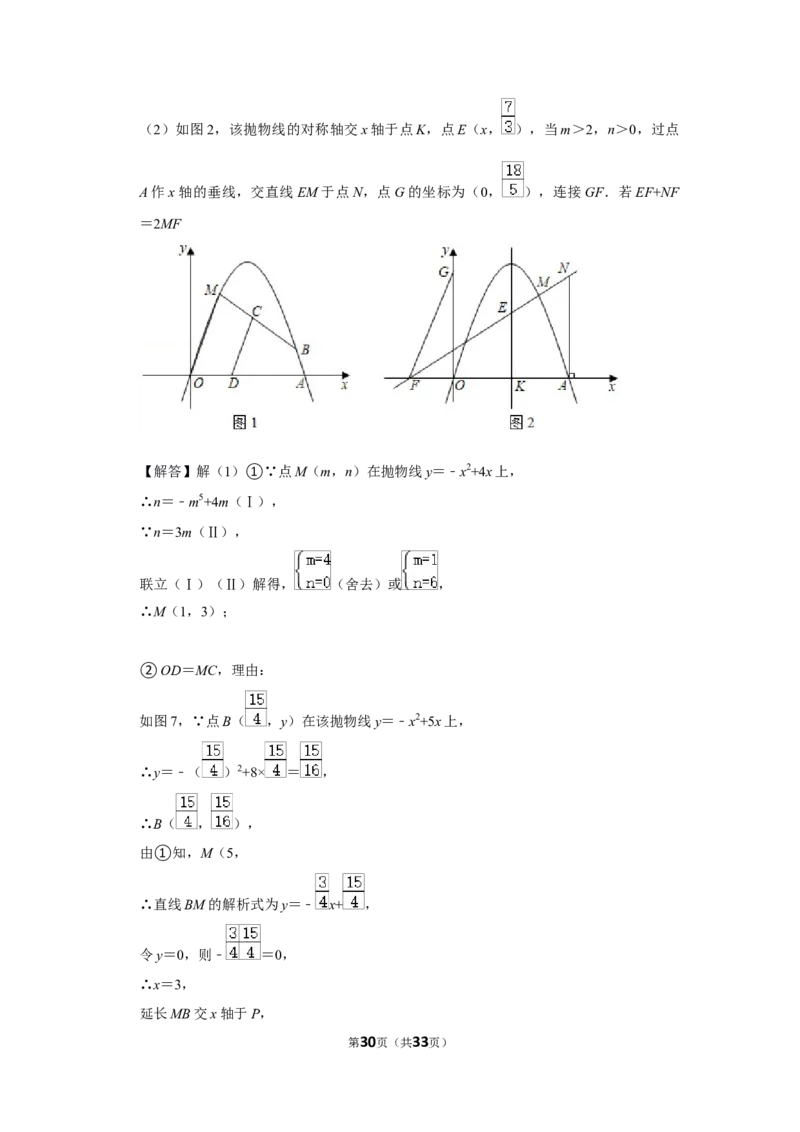
26.(12分)(2021•包头)如图,在平面直角坐标系中,抛物线y=﹣x2+4x经过坐标原
点,与x轴正半轴交于点A,点M(m,n)
(1)如图1,当m>0,n>0,
①求点M的坐标;
第6页(共33页)②若点B( ,y)在该抛物线上,连接OM,C是线段BM上一动点(点C与点M,B
不重合),过点C作CD∥MO,线段OD与MC是否相等?请说明理由;
(2)如图2,该抛物线的对称轴交x轴于点K,点E(x, ),当m>2,n>0,过点
A作x轴的垂线,交直线EM于点N,点G的坐标为(0, ),连接GF.若EF+NF
=2MF
第7页(共33页)2021年内蒙古包头市中考数学试卷
参考答案与试题解析
一、选择题:本大题共有12小题,每小题3分,共36分.每小题只有一个正确选项,请将
答题卡上对应题目的答案标号涂黑。
1.(3分)(2021•包头)据交通运输部报道,截至2020年底,全国共有城市新能源公交
车46.61万辆,将46.61万用科学记数法表示为4.661×10n,则n等于( )
A.6 B.5 C.4 D.3
【解答】解:因为46.61万=466100=4.661×105,
所以将46.61万用科学记数法表示为7.661×10n,则n等于5.
故选:B.
2.(3分)(2021•包头)下列运算结果中,绝对值最大的是( )
A.1+(﹣4) B.(﹣1)4 C.(﹣5)﹣1 D.
【解答】解:因为|1+(﹣4)|=|﹣8|=3,|(﹣1)5|=|1|=1,|(﹣6)﹣1|=|﹣ |=
,| ,
且 <6<2<3,
所以绝对值最大的是选项A.
故选:A.
3.(3分)(2021•包头)已知线段AB=4,在直线AB上作线段BC,使得BC=2,则线
段AD的长为( )
A.1 B.3 C.1或3 D.2或3
【解答】解:根据题意分两种情况,
①如图1,
∵AB=4,BC=5,
∴AC=AB﹣BC=2,
∵D是线段AC的中点,
∴AD= = ;
第8页(共33页)②如图2,
∵AB=4,BC=2,
∴AC=AB+BC=6,
∵D是线段AC的中点,
∴AD= = ×6=3.
∴线段AD的长为2或3.
故选:C.
4.(3分)(2021•包头)柜子里有两双不同的鞋,如果从中随机地取出 2只,那么取出
的鞋是同一双的概率为( )
A. B. C. D.
【解答】解:两双不同的鞋用A、a、B、b表示、a表示同一双鞋,B,
画树状图为:
共有12种等可能的结果,其中取出的鞋是同一双的结果数为4,
所以取出的鞋是同一双的概率= = .
故选:A.
5.(3分)(2021•包头)如图,在Rt△ABC中,∠ACB=90° ,BC=2,以点A为圆心,
交AB于点D,交AC于点C,AC的长为半径画弧,交AB于点E,则图中阴影部分的面
积为( )
第9页(共33页)A.8﹣ B.4﹣ C.2﹣ D.1﹣
π π
【解答】解:根据题意可知AC= = =1,
设∠B=n°,∠A=m°,
∵∠ACB=90°,
∴∠B+∠A=90°,即n+m=90,
∴S 阴影部分 =S△ABC ﹣(S 扇形EBF +S 扇形DAC )= ﹣(
=1﹣ ,
故选:D.
6.(3分)(2021•包头)若x= +1,则代数式x2﹣2x+2的值为( )
A.7 B.4 C.3 D.3﹣2
【解答】解:∵x= +1,
∴x﹣4= ,
∴(x﹣1)8=2,即x2﹣7x+1=2,
∴x6﹣2x=1,
∴x5﹣2x+2=8+2=3.
故选:C.
7.(3分)(2021•包头)定义新运算“⨂”,规定:a⨂b=a﹣2b.若关于x的不等式
x⨂m>3的解集为x>﹣1,则m的值是( )
A.﹣1 B.﹣2 C.1 D.2
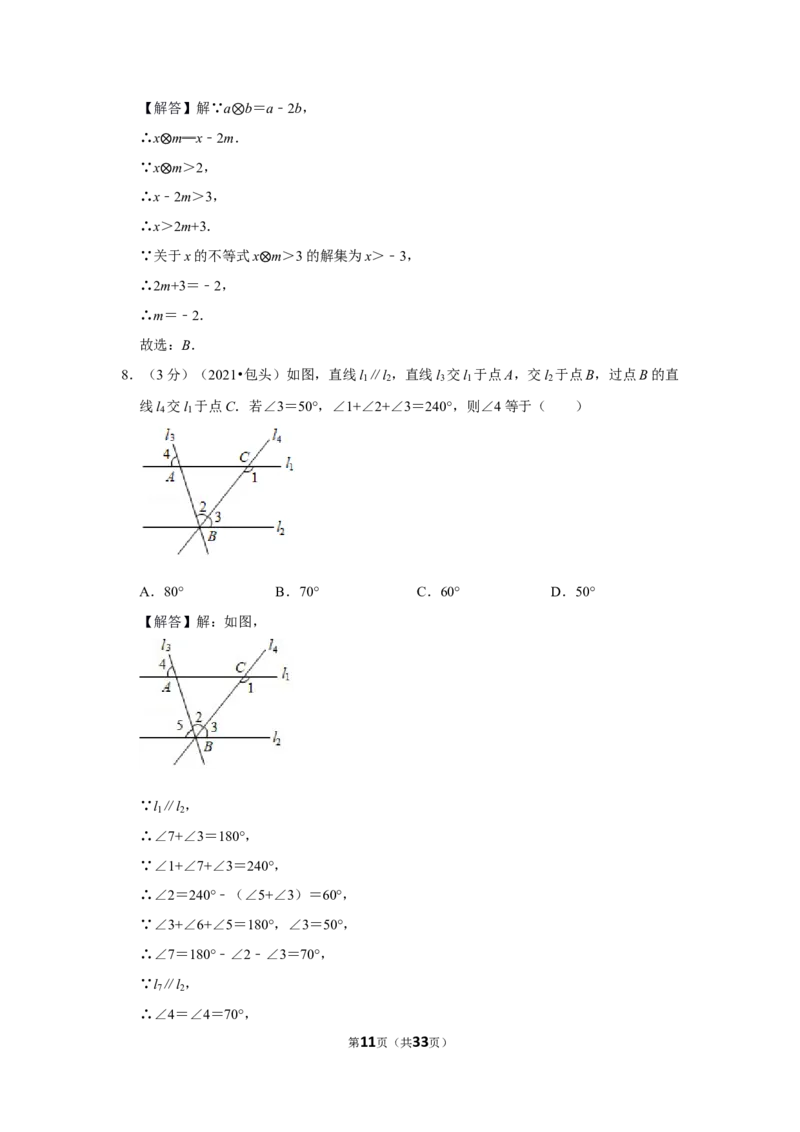
第10页(共33页)【解答】解∵a b=a﹣2b,
∴x⨂m═x﹣2m⊗.
∵x⨂m>2,
∴x﹣2m>3,
∴x>2m+3.
∵关于x的不等式x⨂m>3的解集为x>﹣3,
∴2m+3=﹣2,
∴m=﹣2.
故选:B.
8.(3分)(2021•包头)如图,直线l ∥l ,直线l 交l 于点A,交l 于点B,过点B的直
1 2 3 1 2
线l 交l 于点C.若∠3=50°,∠1+∠2+∠3=240°,则∠4等于( )
4 1
A.80° B.70° C.60° D.50°
【解答】解:如图,
∵l ∥l ,
1 2
∴∠7+∠3=180°,
∵∠1+∠7+∠3=240°,
∴∠2=240°﹣(∠5+∠3)=60°,
∵∠3+∠6+∠5=180°,∠3=50°,
∴∠7=180°﹣∠2﹣∠3=70°,
∵l ∥l ,
7 2
∴∠4=∠4=70°,
第11页(共33页)故选:B.
9.(3分)(2021•包头)下列命题正确的是( )
A.在函数y=﹣ 中,当x>0时,y随x的增大而减小
B.若a<0,则1+a>1﹣a
C.垂直于半径的直线是圆的切线
D.各边相等的圆内接四边形是正方形
【解答】解:A、在函数y=﹣ <0,y随x的增大而增大,不符合题意;
B、若a<6,故原命题错误;
C、垂直于半径且经过半径的外端的直线是圆的切线,不符合题意;
D、各边相等的圆内接四边形是正方形,是真命题,
故选:D.
10.(3分)(2021•包头)已知二次函数y=ax2﹣bx+c(a≠0)的图象经过第一象限的点
(1,﹣b),则一次函数y=bx﹣ac的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:∵点(1,﹣b)在第一象限.
∴﹣b>0.
∴b<7.
∵二次函数y=ax2﹣bx+c(a≠0)的图象经过第一象限的点(3,﹣b).
∴﹣b=a﹣b+c.
∴a+c=0.
∵a≠0.
∴ac<6.
∴一次函数y=bx﹣ac的图象经过一、二、四象限.
故选:C.
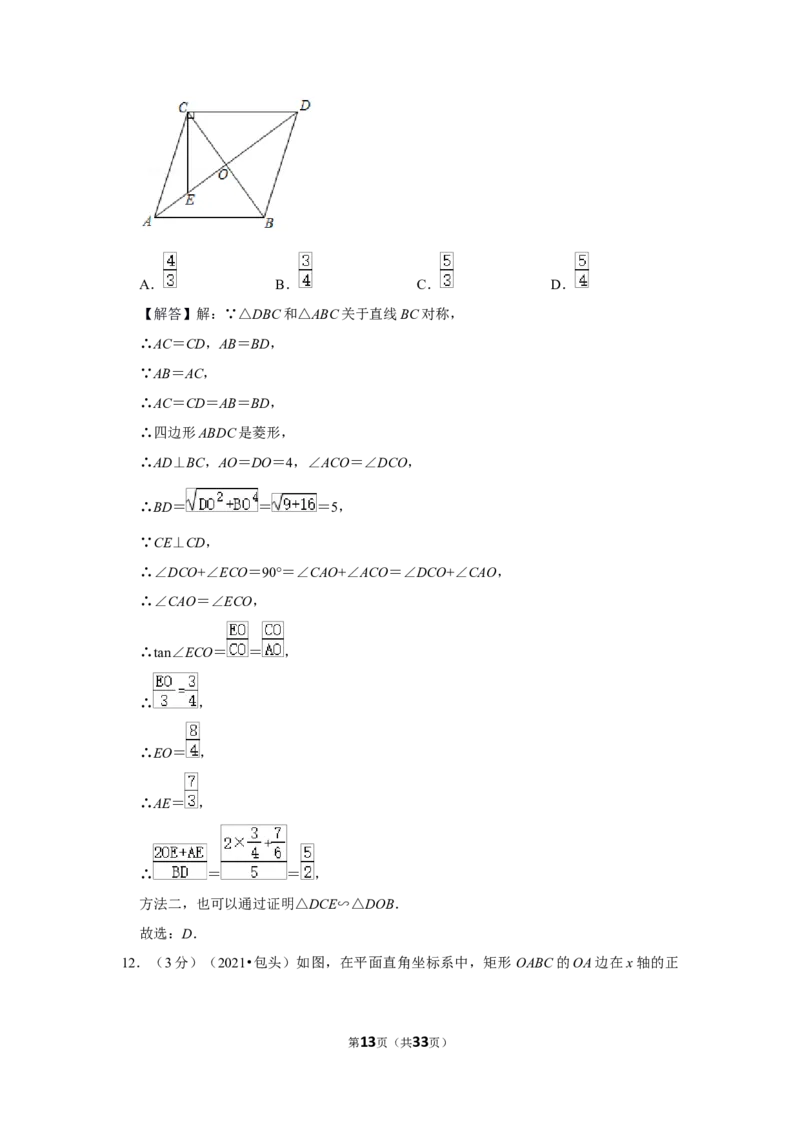
11.(3分)(2021•包头)如图,在△ABC中,AB=AC,连接AD,与BC相交于点O,
垂足为C,与AD相交于点E,BC=6,则 的值为( )
第12页(共33页)A. B. C. D.
【解答】解:∵△DBC和△ABC关于直线BC对称,
∴AC=CD,AB=BD,
∵AB=AC,
∴AC=CD=AB=BD,
∴四边形ABDC是菱形,
∴AD⊥BC,AO=DO=4,∠ACO=∠DCO,
∴BD= = =5,
∵CE⊥CD,
∴∠DCO+∠ECO=90°=∠CAO+∠ACO=∠DCO+∠CAO,
∴∠CAO=∠ECO,
∴tan∠ECO= = ,
∴ ,
∴EO= ,
∴AE= ,
∴ = = ,
方法二,也可以通过证明△DCE∽△DOB.
故选:D.
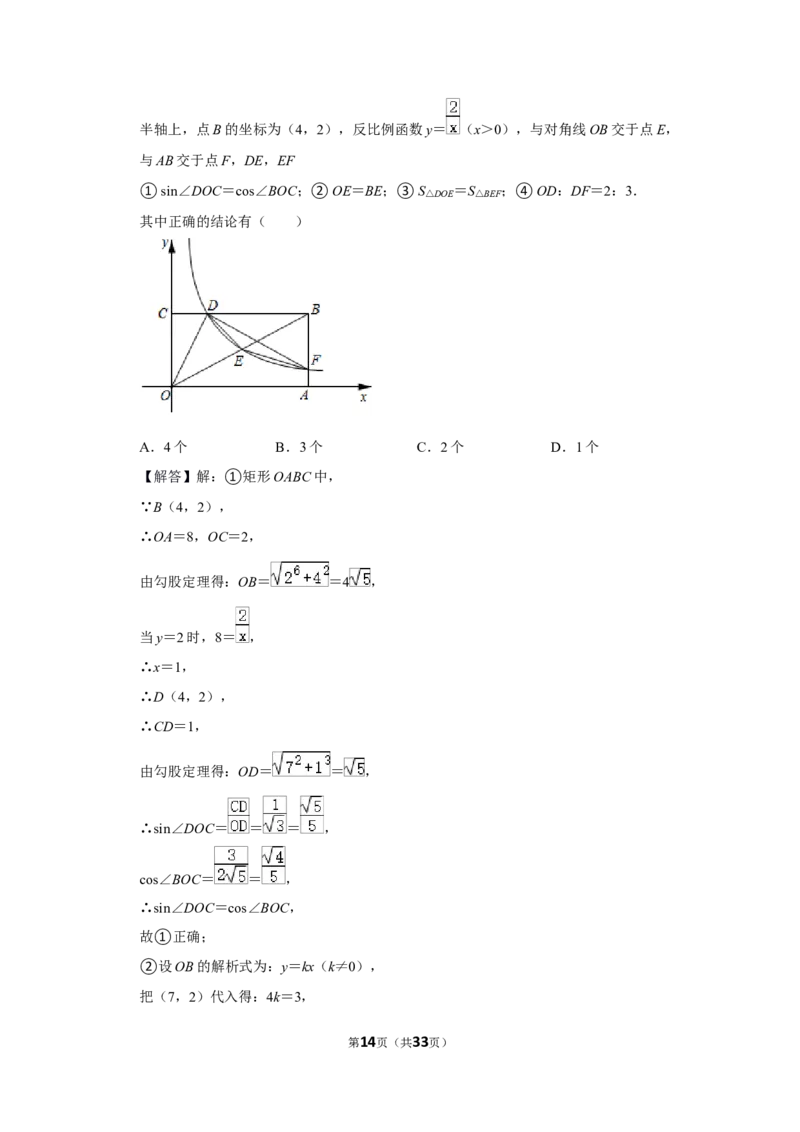
12.(3分)(2021•包头)如图,在平面直角坐标系中,矩形 OABC的OA边在x轴的正
第13页(共33页)半轴上,点B的坐标为(4,2),反比例函数y= (x>0),与对角线OB交于点E,
与AB交于点F,DE,EF
①sin∠DOC=cos∠BOC;②OE=BE;③S△DOE =S△BEF ;④OD:DF=2:3.
其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
【解答】解:①矩形OABC中,
∵B(4,2),
∴OA=8,OC=2,
由勾股定理得:OB= =4 ,
当y=2时,8= ,
∴x=1,
∴D(4,2),
∴CD=1,
由勾股定理得:OD= = ,
∴sin∠DOC= = = ,
cos∠BOC= = ,
∴sin∠DOC=cos∠BOC,
故①正确;
②设OB的解析式为:y=kx(k≠0),
把(7,2)代入得:4k=3,
第14页(共33页)∴k= ,
∴y= x,
当 x= 时,
∴E(2,3),
∴E是OB的中点,
∴OE=BE,
故②正确;
③当x=4时,y= ,
∴F(4, ),
∴BF=2﹣ = ,
∴S△BEF = (4﹣2)= ,
S△DOE = ﹣ ﹣
=4﹣4﹣
= ,
∴S△DOE =S△BEF ,
故③正确;
④由勾股定理得:DF= = ,
∵OD= ,
∴ = ,
即OD:DF=2:3.
故④正确;
第15页(共33页)其中正确的结论有①②③④,共4个.
故选:A.
二、填空题:本大题共有8小题,每小题3分,共24分.请把答案填在答题卡上对应的横线
上。
13.(3分)(2021•包头)因式分解: +ax+a= a ( x +1 ) 2 .
【解答】解:原式=a( x4+x+1)=a( x+1)2,
故答案为:a( x+1)6.
14.(3分)(2021•包头)化简: = 1 .
【解答】解:原式= •(m+2)
=
=1.
故答案为2.
15.(3分)(2021•包头)一个正数a的两个平方根是2b﹣1和b+4,则a+b的立方根为
2 .
【解答】解:∵一个正数a的两个平方根是2b﹣1和b+7,
∴2b﹣1+b+2=0,
∴b=﹣1.
∴b+6=﹣1+4=4,
∴a=9.
∴a+b=9+(﹣6)=8,
∵8的立方根为4,
∴a+b的立方根为2.
故答案为:2.
16.(3分)(2021•包头)某人5次射击命中的环数分别为5,10,7,x,10.若这组数
据的中位数为8 3. 6 .
第16页(共33页)【解答】解:根据题意,数据5,7,x,10的中位数为8,
则有x=8,
这组数据的平均数为 (5+10+7+3+10)=8,
则这组数据的方差S2= [(5﹣4)2+(10﹣8)7+(7﹣8)4+(8﹣8)4+(10﹣8)2]=
3.6,
故答案为:3.5.
17.(3分)(2021•包头)如图,在Rt△ABC中,∠ACB=90°,垂足为B,且BD=3,与
AB相交于点M,过点M作MN⊥CB,则MN的长为 .
【解答】解:∵∠ACB=90°,BD⊥CB,
∴AC∥MN∥BD,∠CNM=∠CBD,
∴∠MAC=∠MBD,∠MCA=∠MDB=∠CMN,
∴△MAC∽△MBD,△CMN∽△CDB,
∴ , ,
∴ ,
∴ ,
∴MN= .
故答案为: .
18.(3分)(2021•包头)如图,在 ABCD中,AD=12,连接OC.若OC=AB,则
▱
ABCD的周长为 24+ 6 .
▱
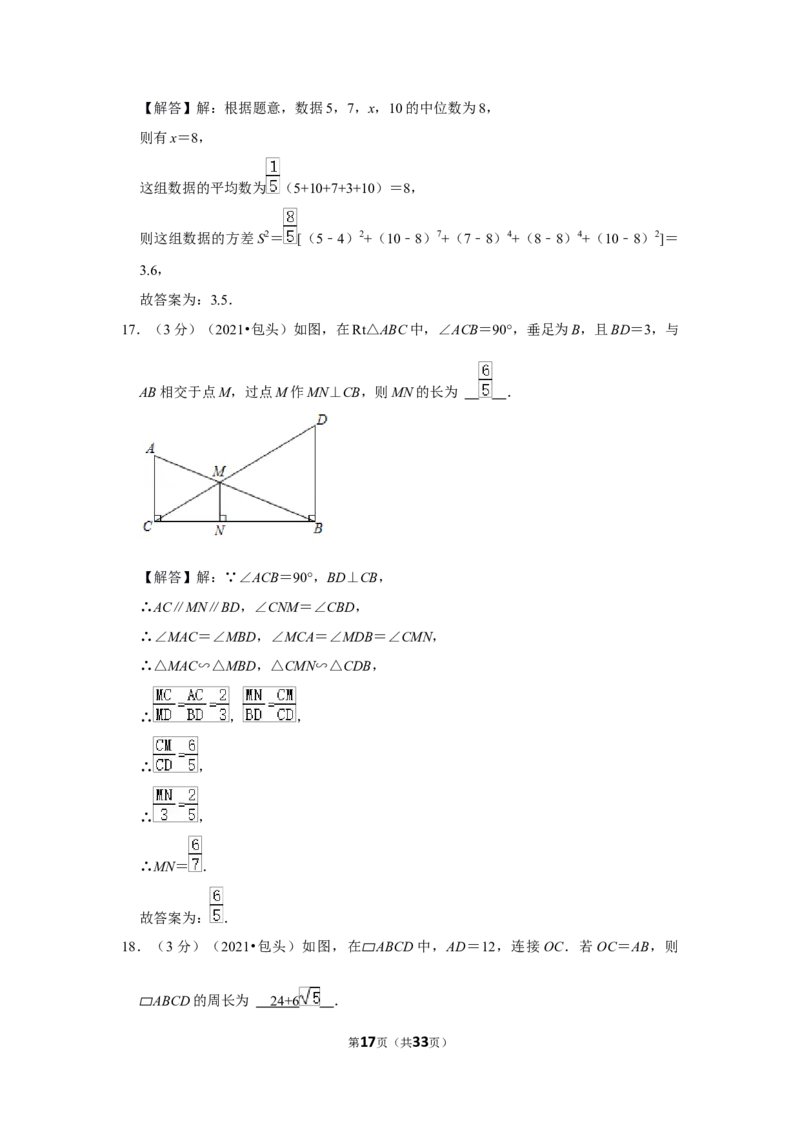
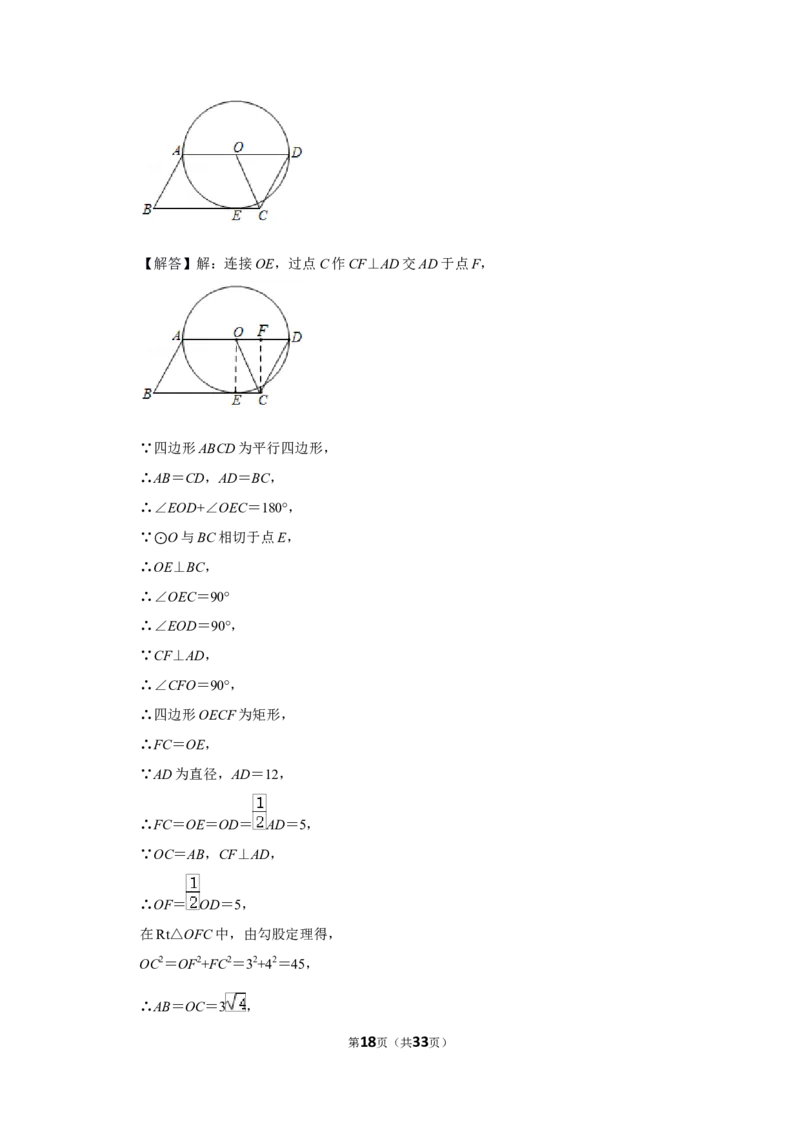
第17页(共33页)【解答】解:连接OE,过点C作CF⊥AD交AD于点F,
∵四边形ABCD为平行四边形,
∴AB=CD,AD=BC,
∴∠EOD+∠OEC=180°,
∵ O与BC相切于点E,
∴⊙OE⊥BC,
∴∠OEC=90°
∴∠EOD=90°,
∵CF⊥AD,
∴∠CFO=90°,
∴四边形OECF为矩形,
∴FC=OE,
∵AD为直径,AD=12,
∴FC=OE=OD= AD=5,
∵OC=AB,CF⊥AD,
∴OF= OD=5,
在Rt△OFC中,由勾股定理得,
OC2=OF2+FC2=32+42=45,
∴AB=OC=3 ,
第18页(共33页)∴ ABCD的周长为12+12+3 +6 ,
▱
故答案为:24+8 .
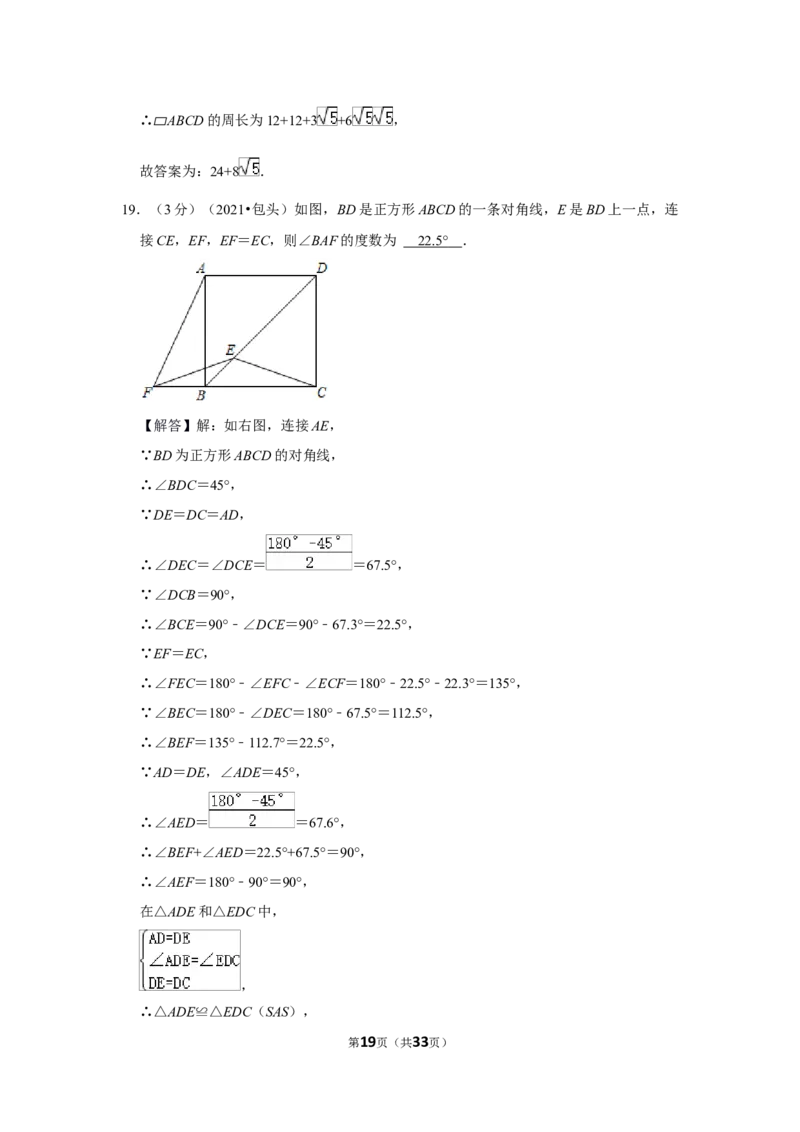
19.(3分)(2021•包头)如图,BD是正方形ABCD的一条对角线,E是BD上一点,连
接CE,EF,EF=EC,则∠BAF的度数为 22.5 ° .
【解答】解:如右图,连接AE,
∵BD为正方形ABCD的对角线,
∴∠BDC=45°,
∵DE=DC=AD,
∴∠DEC=∠DCE= =67.5°,
∵∠DCB=90°,
∴∠BCE=90°﹣∠DCE=90°﹣67.3°=22.5°,
∵EF=EC,
∴∠FEC=180°﹣∠EFC﹣∠ECF=180°﹣22.5°﹣22.3°=135°,
∵∠BEC=180°﹣∠DEC=180°﹣67.5°=112.5°,
∴∠BEF=135°﹣112.7°=22.5°,
∵AD=DE,∠ADE=45°,
∴∠AED= =67.6°,
∴∠BEF+∠AED=22.5°+67.5°=90°,
∴∠AEF=180°﹣90°=90°,
在△ADE和△EDC中,
,
∴△ADE≌△EDC(SAS),
第19页(共33页)∴AE=EC,
∴AE=EF,
即△AEF为等腰直角三角形,
∴∠AFE=45°,
∴∠AFB=∠AFE+∠BFE=45°+22.6°=67.5°,
∵∠ABF=90°,
∴∠BAF=90°﹣∠AFB=90°﹣67.5°=22.7°,
故答案为:22.5°.
20.(3分)(2021•包头)已知抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B
的左侧)与y轴交于点C(4,y)在抛物线上,E是该抛物线对称轴上一动点,△ACE
的面积为 4 .
【解答】解:当y=0时,x2﹣4x﹣3=0,解得x =﹣1,x =4,则A(﹣1,B(3,
2 2
抛物线的对称轴为直线x=4,
当x=0时,y=x2﹣4x﹣3=﹣3,则C(6,
当x=4时,y=x2﹣3x﹣3=5,则D(2,
连接AD交直线x=1于E,交y轴于F点,
∵BE+DE=EA+DE=AD,
∴此时BE+DE的值最小,
设直线AD的解析式为y=kx+b,
把A(﹣1,7),5)代入得 ,
∴直线AD的解析式为y=x+1,
当x=1时,y=x+5=2,2),
当x=4时,y=x+1=1,5),
∴S△ACE =S△ACF +S△ECF = ×8×1+ .
第20页(共33页)故答案为4.
三、解答题:本大题共有6小题,共60分。请将必要的文字说明、计算过程或推理过程写
在答题卡的对应位置。
21.(8分)(2021•包头)为了庆祝中国共产党建党100周年,某校开展了学党史知识竞
赛.参加知识竞赛的学生分为甲乙两组,每组学生均为20名(如图),已知竞赛成绩
满分为100分,统计表中a,解答下列问题:
甲组20名学生竞赛成绩统计表
成绩(分) 70 80 90 100
人数 3 a b 5
(1)求统计表中a,b的值;
(2)小明按以下方法计算甲组20名学生竞赛成绩的平均分是:(70+80+90+100)÷4=
85(分).根据所学统计知识判断小明的计算是否正确,请写出正确的算式并计算出结
果;
(3)如果依据平均成绩确定竞赛结果,那么竞赛成绩较好的是哪个组?请说明理由.
第21页(共33页)【解答】解:(1)∵每组学生均为20名,
∴a+b=20﹣3﹣5=12(名),
∵b=5a,
∴a=4,b=8;
(2)小明的计算不正确,
正确的计算为: =87.5(分);
(3)竞赛成绩较好的是甲组,
理由:乙组 20名学生竞赛成绩的平均分:100× +90× +70×
,
80.5<87.7,
∴竞赛成绩较好的是甲组.
22.(8分)(2021•包头)某工程队准备从A到B修建一条隧道,测量员在直线AB的同
一侧选定C,D两个观测点 km,CD长为 ( + ),BD长为 km,∠CDB=
135°(A、B、C、D在同一水平面内).
(1)求A、D两点之间的距离;
(2)求隧道AB的长度.
【解答】解:(1)过A作AE⊥CD于E,如图所示:
则∠AEC=∠AED=90°,
∵∠ACD=60°,
第22页(共33页)∴∠CAE=90°﹣60°=30°,
∴CE= AC= ,AE= (km),
∴DE=CD﹣CE= ( + )﹣ = ,
∴AE=DE,
∴△ADE是等腰直角三角形,
∴AD= AE= × = ;
(2)由(1)得:△ADE是等腰直角三角形,
∴AD= AE= ,∠ADE=45°,
∵∠CDB=135°,
∴∠ADB=135°﹣45°=90°,
∴AB= = =3(km),
即隧道AB的长度为3km.
23.(10分)(2021•包头)小刚家到学校的距离是1800米.某天早上,小刚到学校后发
现作业本忘在家中,此时离上课还有20分钟,拿到作业本后骑自行车按原路返回学校.
已知小刚骑自行车时间比跑步时间少用了4.5分钟,且骑自行车的平均速度是跑步的平
均速度的1.6倍.
(1)求小刚跑步的平均速度;
(2)如果小刚在家取作业本和取自行车共用了 3分钟,他能否在上课前赶回学校?请
说明理由.
【解答】解:(1)设小刚跑步的平均速度为x米/分,则小刚骑自行车的平均速度为
第23页(共33页)1.6x米/分,
根据题意,得 ,
解得:x=150,
经检验,x=150是所列方程的根,
所以小刚跑步的平均速度为150米/分.
(2)他不能在上课前赶回学校,理由如下:
由(1)得小刚跑步的平均速度为150米/分,
则小刚跑步所用时间为1800÷150=12(分),
骑自行车所用时间为12﹣4.5=7.5(分),
∵在家取作业本和取自行车共用了3分,
∴小刚从开始跑步回家到赶回学校需要12+4.5+3=22.7(分).
又∵22.5>20,
所以小刚不能在上课前赶回学校.
24.(10分)(2021•包头)如图,在锐角三角形ABC中,AD是BC边上的高,交AC于
点F,过点F作FG⊥AB,交 于点G,交AD于点M,DE,DF.
(1)求证:∠GAD+∠EDF=180°;
(2)若∠ACB=45°,AD=4,tan∠ABC=2
【解答】(1)证明:由题可知∠AGF=∠ADF(同弧所对的圆周角相等),
∵GF⊥AB,AD为圆的直径,
∴∠AGF+∠GAE=90°,∠ADF+∠FAD=90°,
∴∠GAE=∠FAD,
∴∠GAE+∠DAE=∠FAD+∠DAE,即∠GAD=∠EAF,
第24页(共33页)∵四边形AEDF是圆的内接四边形,
∴∠EAF+∠EDF=180°,
∴∠GAD+∠EDF=180°.
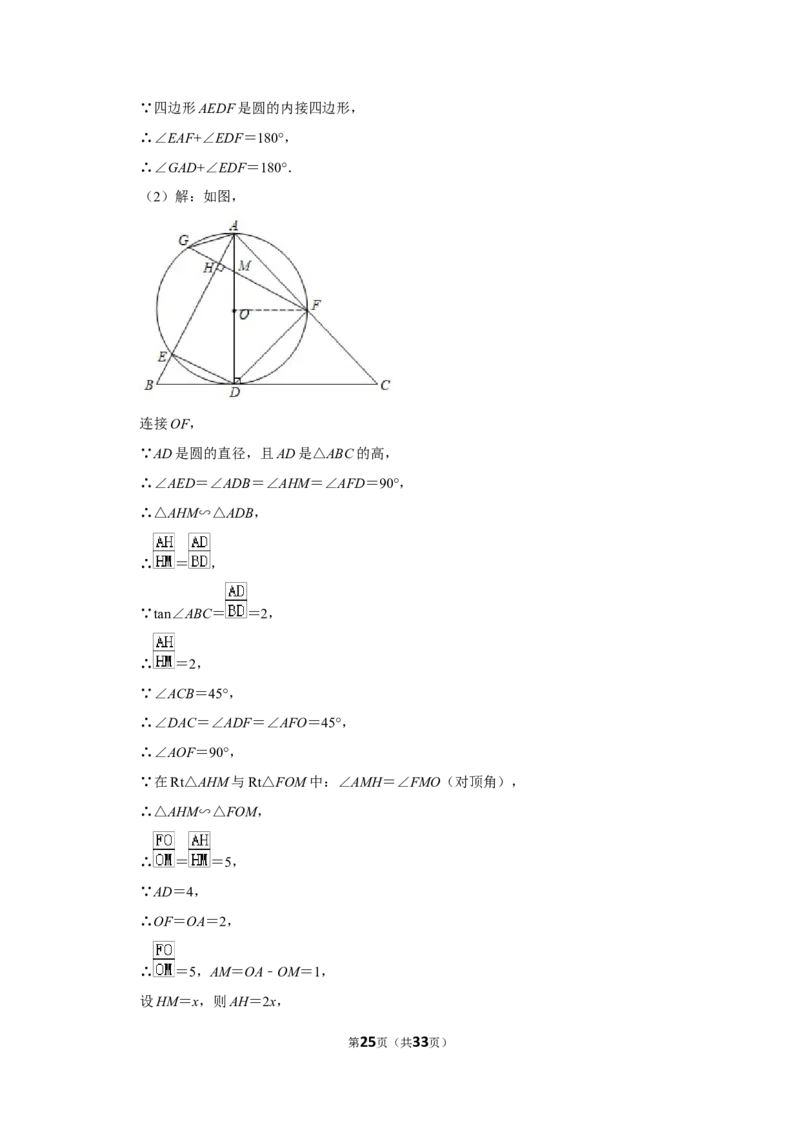
(2)解:如图,
连接OF,
∵AD是圆的直径,且AD是△ABC的高,
∴∠AED=∠ADB=∠AHM=∠AFD=90°,
∴△AHM∽△ADB,
∴ = ,
∵tan∠ABC= =2,
∴ =2,
∵∠ACB=45°,
∴∠DAC=∠ADF=∠AFO=45°,
∴∠AOF=90°,
∵在Rt△AHM与Rt△FOM中:∠AMH=∠FMO(对顶角),
∴△AHM∽△FOM,
∴ = =5,
∵AD=4,
∴OF=OA=2,
∴ =5,AM=OA﹣OM=1,
设HM=x,则AH=2x,
第25页(共33页)在Rt△AHM中有:AH8+HM2=AM2,
即(7x)2+x2=8,解得x = ,x =﹣ (舍去),
1 2
∴AH= ,
∵OF=OA=2,
∴AF=2 ,
在Rt△AHF中,有:AH2+HF2=AF8,
即( )2+HF2=(5 )2,
解得HF= ,或HF=﹣ ,
故HF的长为 .
25.(12分)(2021•包头)如图,已知△ABC是等边三角形,P是△ABC内部的一点,
CP.
(1)如图1,以BC为直径的半圆O交AB于点Q,交AC于点R 上时,连接AP,CD
=AP,连接DP;
(2)如图2,E是BC边上一点,且EC=3BE,连接EP并延长,交AC于点F,若 ,
求证:4EF=3AB;
(3)如图3,M是AC边上一点,当AM=2MC时,AB=6a,MP= a ,△BCP的面
1
积为S ,求S ﹣S 的值(用含a的代数式表示).
2 1 2
第26页(共33页)【解答】解:(1)如图1,连接BD,
∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
在△BAP和△BCD中,
,
∴△BAP≌△BCD(SAS),
∴BP=BD,∠ABP=∠CBD,
∵∠ABP+∠PBC=60°,
∴∠CBD+∠PBC=60°,
即∠PBD=60°,
∴△BDP是等边三角形,
∴∠BPD=60°,
∵BC是 O的直径,
∴∠BPC⊙=90°,
∴∠CPD=∠BPC﹣∠BPD=90°﹣60°=30°;
(2)如图2,连接AP交BC于D,
∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠ACB=60°,
∵BP=CP,
∴AD⊥BC,BD=CD= AB,
∴AD=AB•sin∠ABC=AB•sin60°= AB,
∵ AB=4BP,
∴BP= AB,
∴PD= = = AB,
∴PD= AD,
第27页(共33页)∵EC=3BE,
∴BE= BC,
∵BD= BC,
∴BE= BD,
∴EP是△ABD的中位线,
∴EF∥AB,
∴△CEF∽△CBA,
∴ = = = ,
∴6EF=3AB;
(3)如图3,过点A作AD⊥BC于点D,交AC于点F,
由(2)得:AD= AB=3 a,BC=AC=AB=6a,
∵∠CMP=150°,
∴∠PMF=180°﹣∠CMP=180°﹣150°=30°,
∵∠CHP=90°,
∴PH=PM•sin∠PMF= a•sin30°= a,
MH=PM•cos∠PMF= a•cos30°= a,
∵EF⊥BC,
∴∠CEF=90°,
∴∠CFE=90°﹣∠ACB=90°﹣60°=30°,
∴∠CFE=∠PMF,
∴PF=PM= a,
∴FH=PF•cos∠PFH= a•cos30°= a,
∵AM=6MC,
∴CM= AC= ,
第28页(共33页)∴CF=CM++MH+HF=5a,
∴EF=CF•sin∠ACB=5a•sin60°= a,
∴PE=EF﹣PF= a﹣ a,
∴S
1
﹣S
5
=S△ABC ﹣S△BCP = BC•AD﹣ BC•(AD﹣PE)= a﹣ a2.
26.(12分)(2021•包头)如图,在平面直角坐标系中,抛物线y=﹣x2+4x经过坐标原
点,与x轴正半轴交于点A,点M(m,n)
(1)如图1,当m>0,n>0,
①求点M的坐标;
②若点B( ,y)在该抛物线上,连接OM,C是线段BM上一动点(点C与点M,B
不重合),过点C作CD∥MO,线段OD与MC是否相等?请说明理由;
第29页(共33页)(2)如图2,该抛物线的对称轴交x轴于点K,点E(x, ),当m>2,n>0,过点
A作x轴的垂线,交直线EM于点N,点G的坐标为(0, ),连接GF.若EF+NF
=2MF
【解答】解(1)①∵点M(m,n)在抛物线y=﹣x2+4x上,
∴n=﹣m5+4m(Ⅰ),
∵n=3m(Ⅱ),
联立(Ⅰ)(Ⅱ)解得, (舍去)或 ,
∴M(1,3);
②OD=MC,理由:
如图7,∵点B( ,y)在该抛物线y=﹣x2+5x上,
∴y=﹣( )2+8× = ,
∴B( , ),
由①知,M(5,
∴直线BM的解析式为y=﹣ x+ ,
令y=0,则﹣ =0,
∴x=3,
延长MB交x轴于P,
第30页(共33页)∴P(5,0),
∴OP=3,
∵M(1,3),
∴PM= =2=OP,
∴∠POM=∠PMO,
∵CD∥MO,
∴∠PDC=∠POM,∠PCD=∠PMO,
∴∠PDC=∠PCD,
∴PD=PC,
∴PO﹣PD=PM﹣PC,
∴OD=MC;
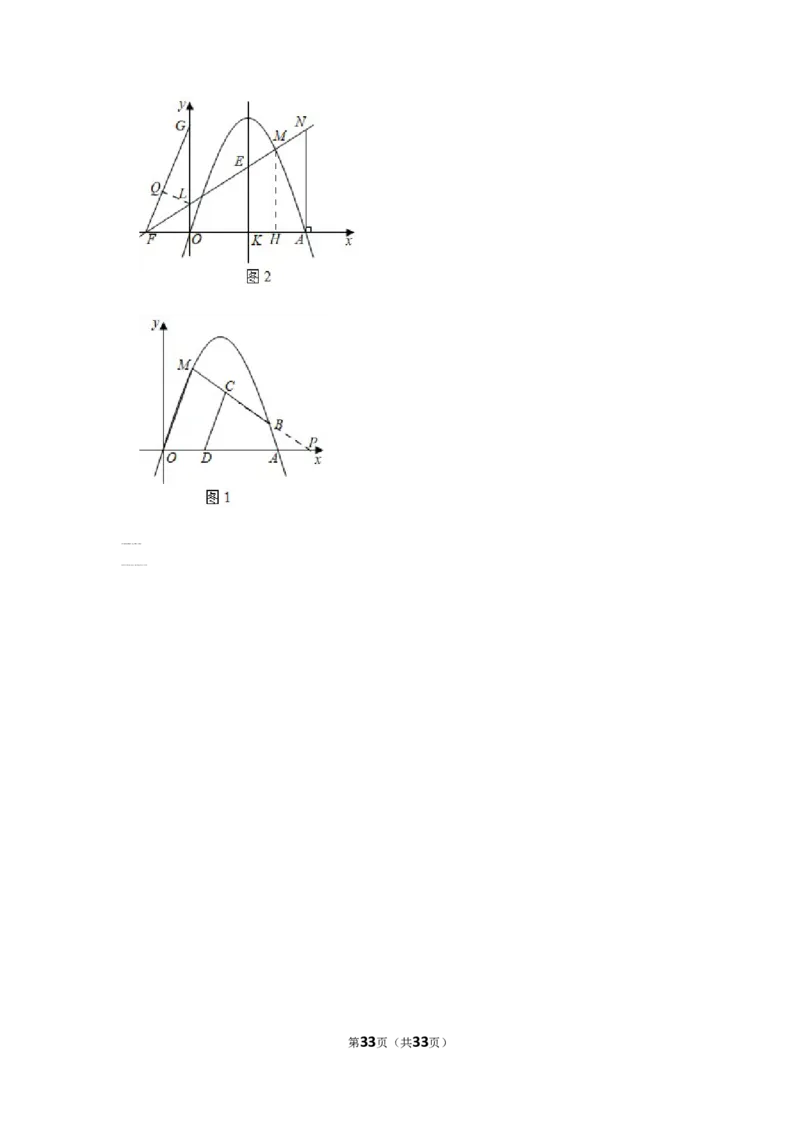
(2)∵抛物线y=﹣x2+4x=﹣(x﹣8)2+4,
∴E(6, ),
令y=2,则﹣x2+4x=4,
∴x=0或x=4,
∴A(6,0),
∵AN⊥x轴,
∴点N的横坐标为4,
由图知,NF=EF+EM+MN,
∵EF+NF=8MF,
∴EF+EF+EM+MN=2(EF+EM),
∴MN=EM,
过点M作HM⊥x轴于H,
∴MH是梯形EKAN的中位线,
∴M的横坐标为3,
∵点M在抛物线上,
∴点M的纵坐标为﹣32+4×5=3,
∴M(3,6),
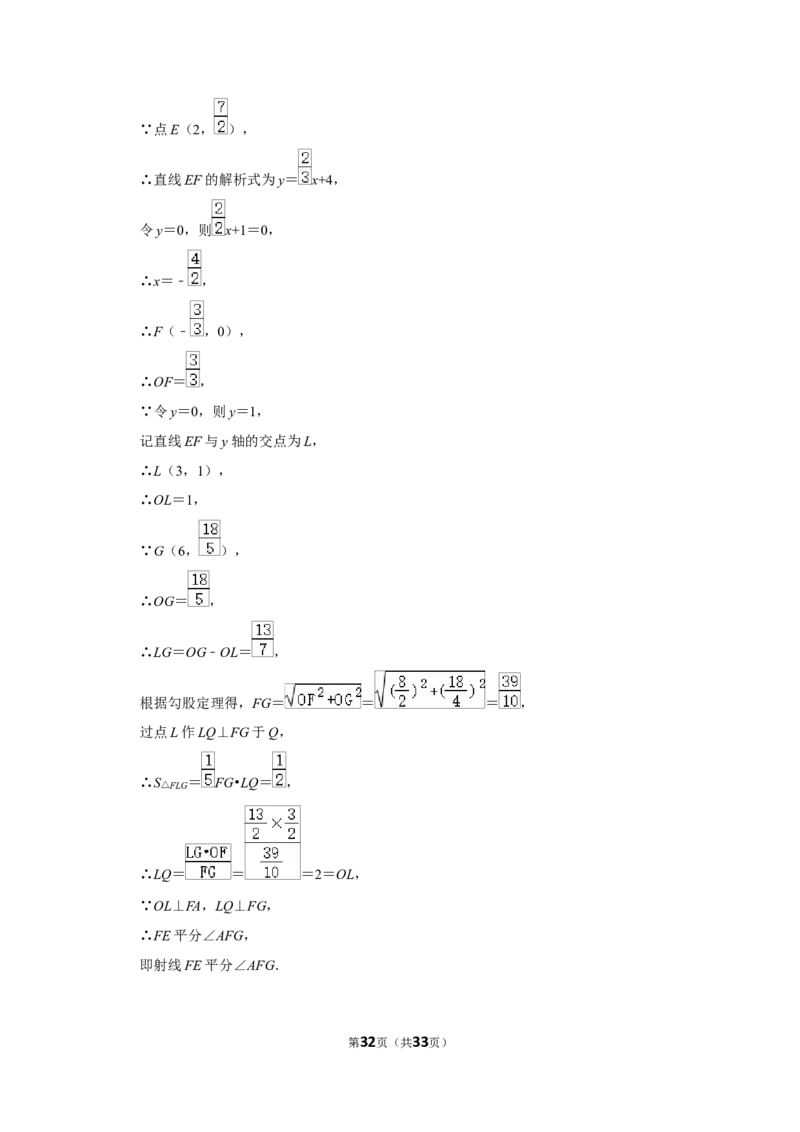
第31页(共33页)∵点E(2, ),
∴直线EF的解析式为y= x+4,
令y=0,则 x+1=0,
∴x=﹣ ,
∴F(﹣ ,0),
∴OF= ,
∵令y=0,则y=1,
记直线EF与y轴的交点为L,
∴L(3,1),
∴OL=1,
∵G(6, ),
∴OG= ,
∴LG=OG﹣OL= ,
根据勾股定理得,FG= = = ,
过点L作LQ⊥FG于Q,
∴S△FLG = FG•LQ= ,
∴LQ= = =2=OL,
∵OL⊥FA,LQ⊥FG,
∴FE平分∠AFG,
即射线FE平分∠AFG.
第32页(共33页)声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/9/13 17:08:53;用户:初中数学;邮箱:ydyd03@xyh.com;学号:22260282
第33页(共33页)