文档内容
2021 年广东省初中学业水平考试数学
本试卷共4页,25小题,满分120分,考试用时90分钟.
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的准考证号、姓名、考场号和座位号填写
在答题卡上.用2B铅笔在“考场号”和“座位号”栏相应位置填涂自己的考场号和座位号.将
条形码粘贴在答题卡“条形码粘贴处”·
2.作管选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;
如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位
置上:如需改动,先划掉原来的答案,然后再写上新的答案:不准使用铅笔和涂改液.不按以上要
求作答的答案无效.
4.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.下列实数中,最大的数是( )
A. B. C. D.
【答案】A
【解析】考查实数的大小比较,涉及有理数、无理数、绝对值
2.据国家卫生健康委员会发布,截至2021年5月23日,31个省(区、市)及新疆生产建
设兵团累计报告接种新冠病毒疫苗 万剂次,将“ 万”用科学记数法表示
为( )
A. B.
C. D.
【答案】D
【解析】考查科学记数法的表示方法,一般把大于10的数表示成
3.同时掷两枚质地均匀的骰子,则两枚骰子向上的点数之和为 的概率是( )
A. B. C. D.
【答案】B
【解析】如图,总事件有36种,和为7的事件有6种,所以4.已知 , ,则 ( )
A. B. C. D.
【答案】D
【解析】 ,考查幂的运算公式的灵活变形
5.若 ,则 ( )
A. B. C. D.
【答案】B
【解析】因为 ,且 ,
所以 ,
所以 , ,所以 ,考查绝对值、二次根式的非负性。
6.下列图形是正方体展开图的个数为( )
A. 个 B. 个 C. 个 D. 个
【答案】C
【解析】考查正方体展开图的11种样式的记忆,第一个属于2-3-1样式,第三个属于2-2-2样式,
第三个属于3-3样式
7.如题 图, 是 的直径,点 为圆上一点, , 的平分线交 于点D,
,则 的直径为( )
A. B. C. D.
【答案】B
【 解 析 】 作 于 H 点 , 根 据 角 平 分 线 的 性 质 可 得 , 而
,
易得 ,所以直径 ,考查圆中的计算(结合角平分线、三角函
数)
8.设 的整数部分为 ,小数部分为 ,则 的值是( )
A. B. C. D.【答案】A
【解析】易得 ,所以 即( ),因此可得 ,
,所以 ,考查实数的整数部分、小数
部分的转化,以及平方差公式的运算
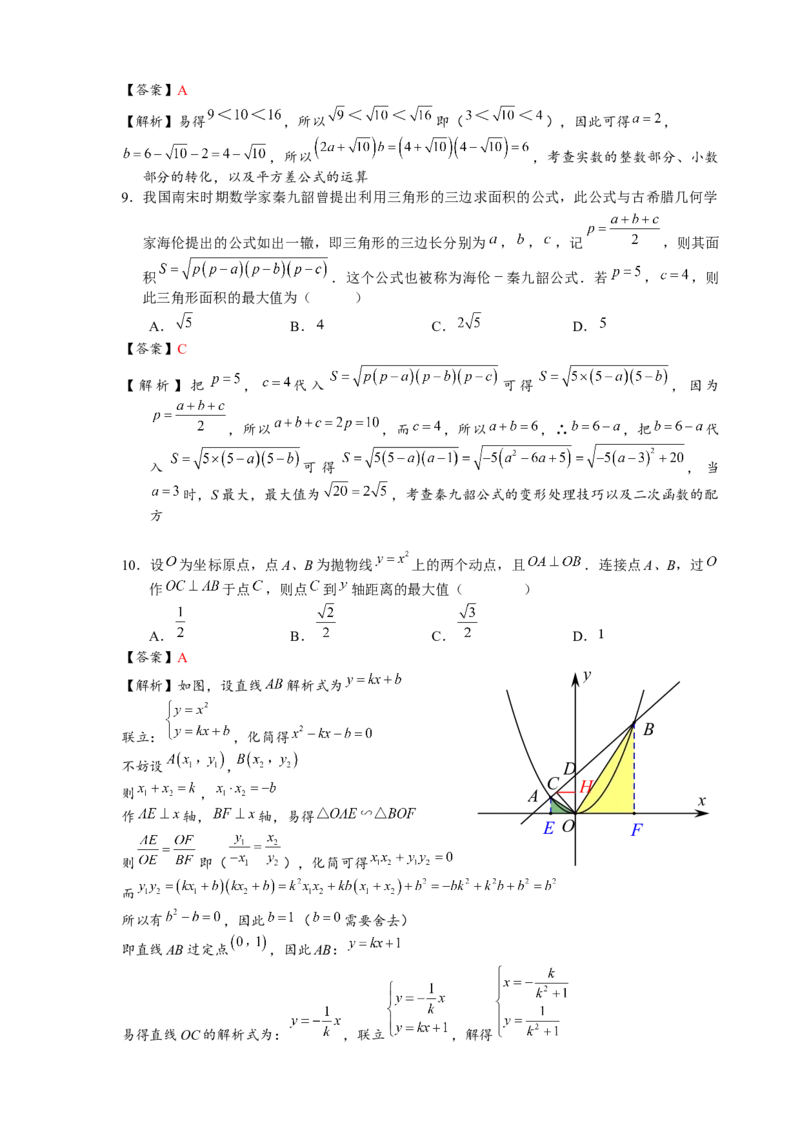
9.我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学
家海伦提出的公式如出一辙,即三角形的三边长分别为 , , ,记 ,则其面
积 .这个公式也被称为海伦 秦九韶公式.若 , ,则
此三角形面积的最大值为( )
A. B. C. D.
【答案】C
【解析】把 , 代入 可得 ,因为
,所以 ,而 ,所以 ,∴ ,把 代
入 可 得 , 当
时,S最大,最大值为 ,考查秦九韶公式的变形处理技巧以及二次函数的配
方
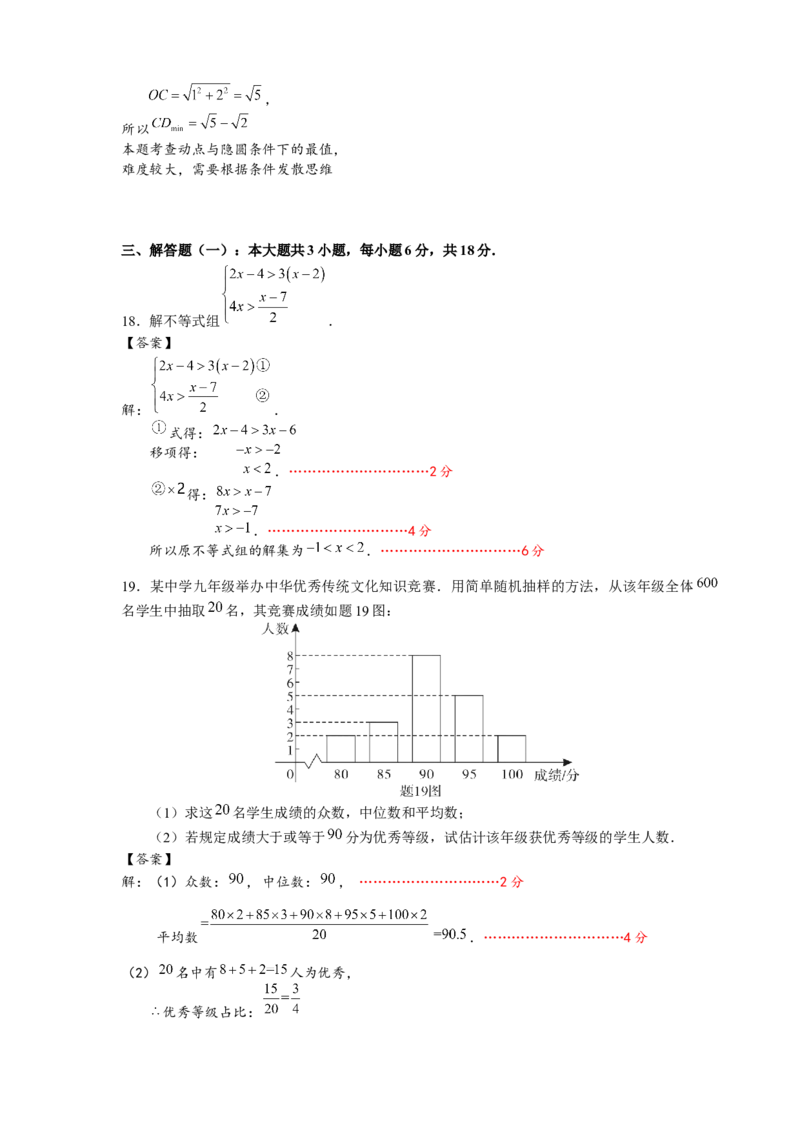
10.设 为坐标原点,点A、B为抛物线 上的两个动点,且 .连接点A、B,过
作 于点 ,则点 到 轴距离的最大值( )
A. B. C. D.
【答案】A
y
【解析】如图,设直线 解析式为
B
联立: ,化简得
不妨设 , D
C H
则 , A x
作 轴, 轴,易得
E O F
则 即( ),化简可得
而
所以有 ,因此 ( 需要舍去)
即直线AB过定点 ,因此AB:
易得直线OC的解析式为: ,联立 ,解得即
点C到y轴距离 ,则 ,化简可得 ,由于关于k的一元
二次方程有实数根,因此满足 ,即 ,因此 ,因此
本题考查二次函数与一定函数结合时过定点背景下的最值求法,涉及相似三角形、一元二次方程
等多个考点
二、填空题:本大题7小题,每小题4分,共28分.
11.二元一次方程组 的解为_________.
【答案】
【解析】 ,①+②可得 ③,①-③得, ,把 代入③得
因此 ,考查二元一次方程组的解法
12.把抛物线 向左平移 个单位长度,再向下平移 个单位长度,得到的抛物线的解析
式为_________.
【答案】
【解析】考查二次函数的图象变换,根据“上加下减,左加右减”可得平移后的解析式为
,化简即得
13.如题 图,等腰直角三角形 中, , .分别以点B、点C为圆心,线段
长的一半为半径作圆弧,交 、 、 于点D、E、F,则图中阴影部分的面积为
_________.
【答案】
【解析】 ,考查阴影面积的求法(主要还是用整
体减去局部)
14.若一元二次方程 ( , 为常数)的两根 , 满足 , ,
则符合条件的一个方程为_________.【答案】 (答案不唯一)
【解析】不妨设 , ,则满足题意的其中一个方程是 ,本题考查一元二次方
程根与系数的关系(已知两根范围,表达原方程,需要有逆推的思维)
15.若 且 ,则 _________.
【答案】
【解析】因为 ,且
因此
而 ,可得
因此 ,所以
本题考查完全平方公式的变形运算以及因式分解的技巧
16.如题 图,在 中, , , .过点 作 ,垂足为 ,
则 _________.
12
D
【答案】
C
【解析】作 ,在 中, H
4 10
5 4 5
由等积法可得
A B
3
E
易得 , , , 12
∴
∴
17.在 中, , , .点 为平面上一个动点, ,则
线段 长度的最小值为_____.
【答案】
【解析】如图1,根据 , (定弦定角),作 的外接圆O,连接OC,交
于 (图2),此时CD的值最小,根据 ,得 ,因此
,作 ,可得 ,所以 ,所以
A A
D
D
45°
45°
2 O 2 OA A
D
D
45°
45°
2 O 2 O
,
所以
本题考查动点与隐圆条件下的最值,
难度较大,需要根据条件发散思维
三、解答题(一):本大题共3小题,每小题6分,共18分.
18.解不等式组 .
【答案】
解: .
式得:
移项得:
.…………………………2分
得:
.…………………………4分
所以原不等式组的解集为 .…………………………6分
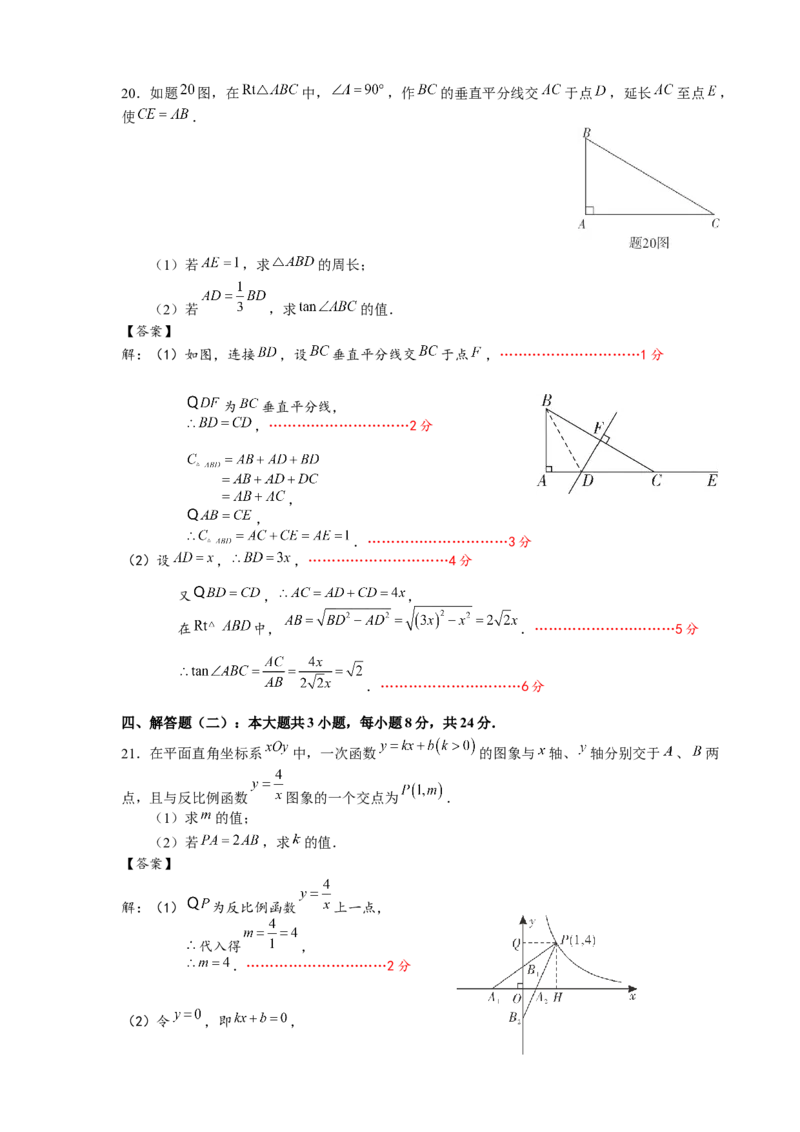
19.某中学九年级举办中华优秀传统文化知识竞赛.用简单随机抽样的方法,从该年级全体
名学生中抽取 名,其竞赛成绩如题19图:
(1)求这 名学生成绩的众数,中位数和平均数;
(2)若规定成绩大于或等于 分为优秀等级,试估计该年级获优秀等级的学生人数.
【答案】
解:(1)众数: ,中位数: , …………………………2分
平均数 .…………………………4分
(2) 名中有 人为优秀,
优秀等级占比:该年级优秀等级学生人数为: (人)
答:该年级优秀等级学生人数为 人.…………………………6分20.如题 图,在 中, ,作 的垂直平分线交 于点 ,延长 至点 ,
使 .
(1)若 ,求 的周长;
(2)若 ,求 的值.
【答案】
解:(1)如图,连接 ,设 垂直平分线交 于点 ,…………………………1分
为 垂直平分线,
,…………………………2分
,
,
.…………………………3分
(2)设 , ,…………………………4分
又 , ,
在 中, .…………………………5分
.…………………………6分
四、解答题(二):本大题共3小题,每小题8分,共24分.
21.在平面直角坐标系 中,一次函数 的图象与 轴、 轴分别交于 、 两
点,且与反比例函数 图象的一个交点为 .
(1)求 的值;
(2)若 ,求 的值.
【答案】
解:(1) 为反比例函数 上一点,
代入得 ,
.…………………………2分
(2)令 ,即 ,, ,
令 , , ,
.
由图象得,可分为以下两种情况,
① 在 轴正半轴时, ,
,
过 作 轴交 轴于点 ,又 , ,
, ,
,
,
,
, .…………………………5分
② 的 轴负半轴时, ,过 作 轴,
, , ,
,
,
, ,
,
,…………………………7分
综上, 或 .…………………………8分
22.端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习
俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜 元,某商家用 元购进的猪肉 粽 和
用 元购进的豆沙粽盒数相同.在销售中,该商家发现猪肉粽每盒售价 元时, 每天可售
出 盒;每盒售价提高 元时,每天少售出 盒.
(1)求猪肉粽和豆沙粽每盒的进价;
(2)设猪肉粽每盒售价 元( ), 表示该商家每天销售猪肉粽的利润(单
位:元),求 关于 的函数解析式并求最大利润.
【答案】
解:(1)设猪肉粽每盒进价 元,则豆沙粽没和进价 元.…………………………1分
则 …………………………2分
解得: ,经检验 是方程的解.…………………………3分
猪肉粽每盒进价 元,豆沙粽每盒进价 元.…………………………4分(2)由题意得,当 时,每天可售 盒.
当猪肉粽每盒售 元时,每天可售 盒. ……………………5分
…………………………6分
∵ ,且 时,y随x的增大而增大
∴当 时, 取最大值,最大值为 元.…………7分
答: 关于 的函数解析式为 ,且最大利润为 元.
……………2分
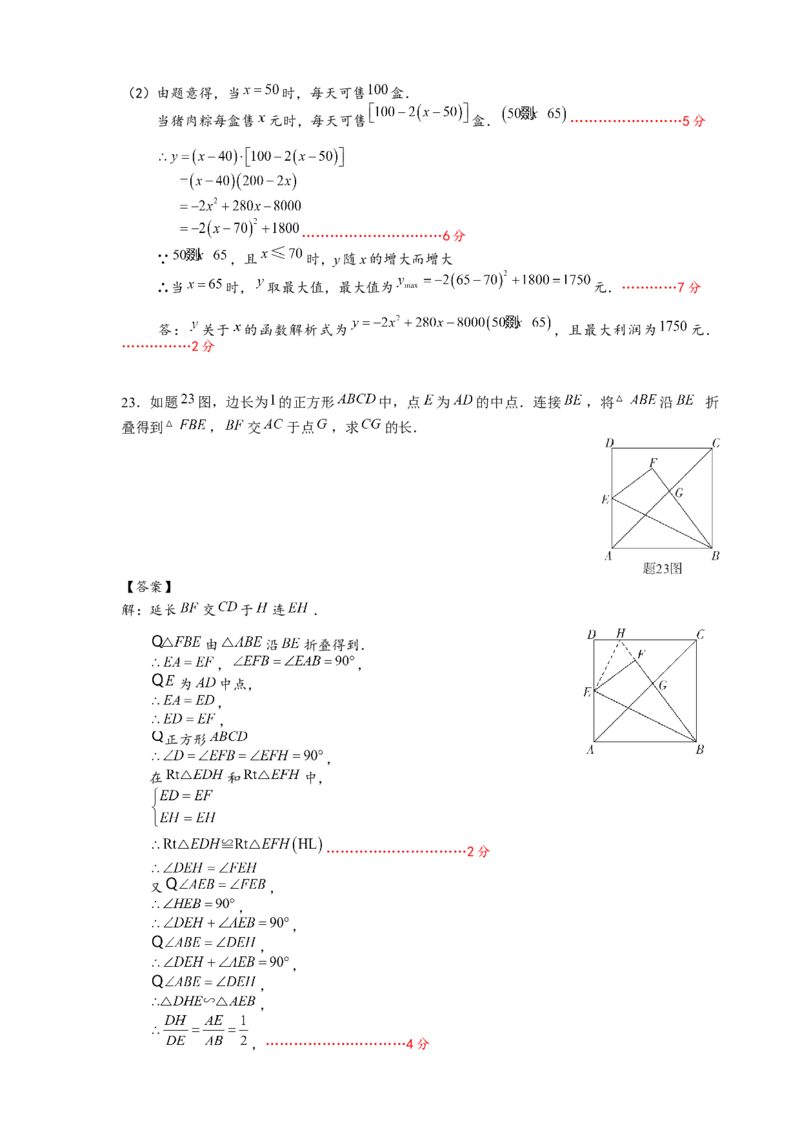
23.如题 图,边长为 的正方形 中,点 为 的中点.连接 ,将 沿 折
叠得到 , 交 于点 ,求 的长.
【答案】
解:延长 交 于 连 .
由 沿 折叠得到.
, ,
为 中点,
,
,
正方形
,
在 和 中,
…………………………2分
又 ,
,
,
,
,
,
,
,…………………………4分,
,
,…………………………6分
由勾股定理得: .…………………………7分
.…………………………8分
备注:本题用其他解法,且过程严谨,亦可以给满分
五、解答题(三):本大题共2小题,每小题10分,共20分.
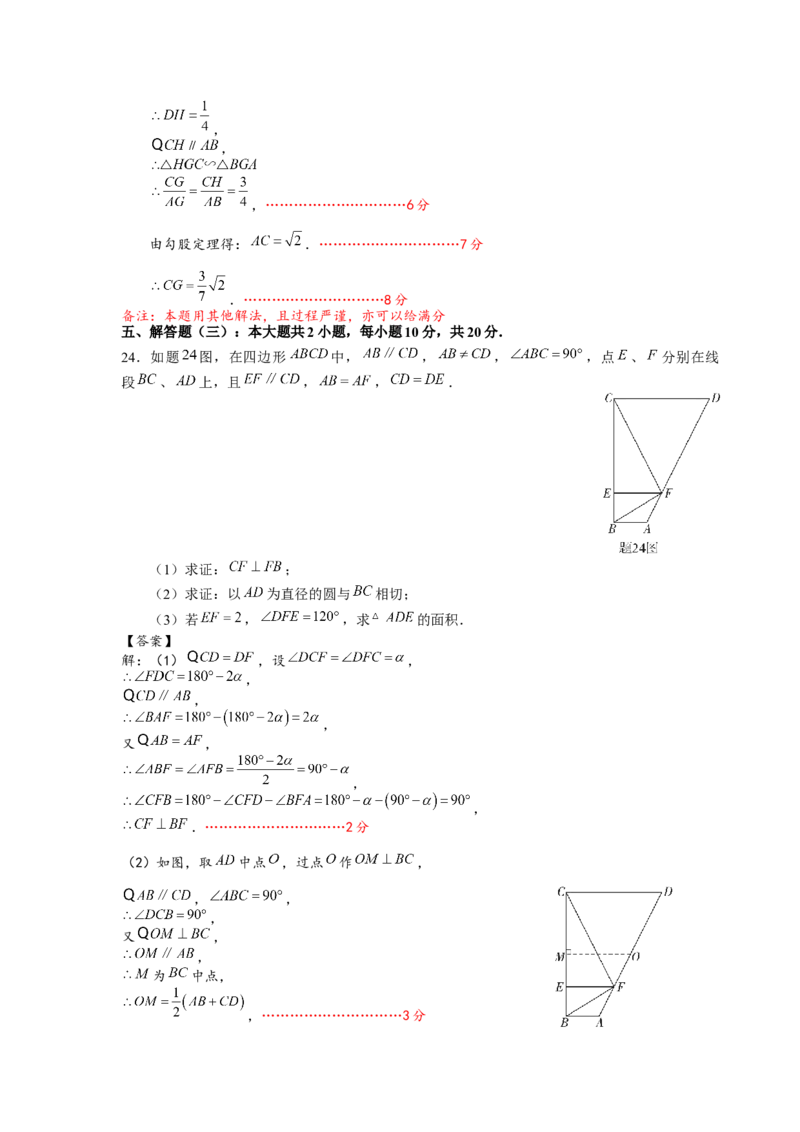
24.如题 图,在四边形 中, , , ,点 、 分别在线
段 、 上,且 , , .
(1)求证: ;
(2)求证:以 为直径的圆与 相切;
(3)若 , ,求 的面积.
【答案】
解:(1) ,设 ,
,
,
,
又 ,
,
,
.…………………………2分
(2)如图,取 中点 ,过点 作 ,
, ,
,
又 ,
,
为 中点,
,…………………………3分,
又 , ,
,
∴ …………………………5分
又 ,
以 为直径的圆与 相切.…………………………6分
(3) , , ,
, , ,
又 ,
为等边三角形, ,…………………………7分
由(2)得: ,
,
,
,在 中, .
在 中, ,…………………………8分
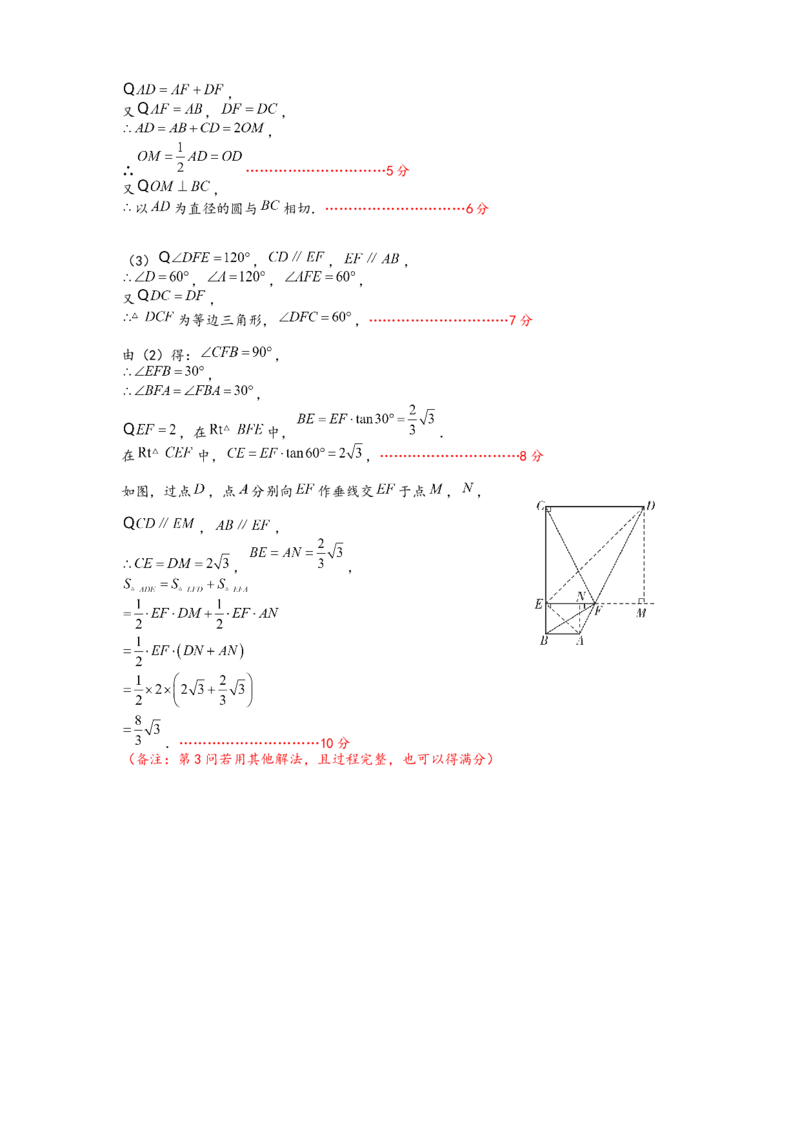
如图,过点 ,点 分别向 作垂线交 于点 , ,
, ,
, ,
.…………………………10分
(备注:第3问若用其他解法,且过程完整,也可以得满分)25.已知二次函数 的图象过点 ,且对任意实数 ,都有
.
(1)求该二次函数的解析式;
(2)若(1)中二次函数图象与 轴的正半轴交点为 ,与 轴交点为 ;点 是(1)
中二次函数图象上的动点.问在 轴上是否存在点 ,使得以 、 、 、
为顶点的四边形是平行四边形.若存在,求出所有满足条件的点 的坐标;若不
存在,请说明理由.
【答案】
解:(1)令 ,解得 ,
当 时, ,
必过 ,…………………………1分
又 过 ,
,
,
又 ,
,
,
且 ,
,
,
,
, ,…………………………2分
.…………………………3分
(2)由(1)可知: , ,设 , ,
①当 为对角线时,
,解得 (舍), ,
,即 .…………………………5分
②当 为对角线时,
,解得 (舍) ,
,即 .…………………………7分
③当 为对角线时,,解得 , ,
或 ,
, .…………………………9分
综上所述: 点坐标为 或 或 或 .…………………10
分