文档内容
2021年广西玉林市中考数学试卷
一、选择题:本大题共12小题,每小题3分,共36分,在每小题给出的四个选项中,只
有一项是符合题目要求的,把正确答案的标号填(涂)在答题卡内相应的位置上.
1.计算:﹣1+2的结果是( )
A.1 B.﹣1 C.3 D.﹣3
2.我市今年中考报名人数接近101000人,将数据101000用科学记数法表示是( )
A.10.1×104 B.1.01×105 C.1.01×106 D.0.101×106
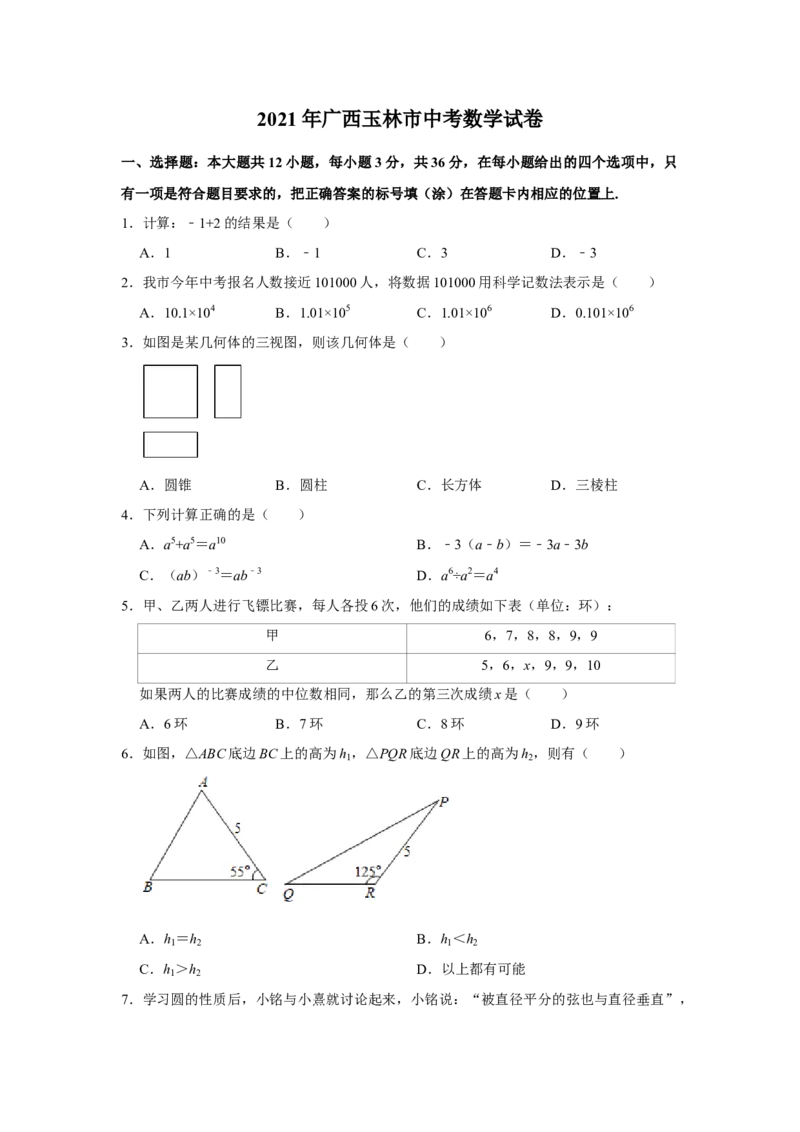
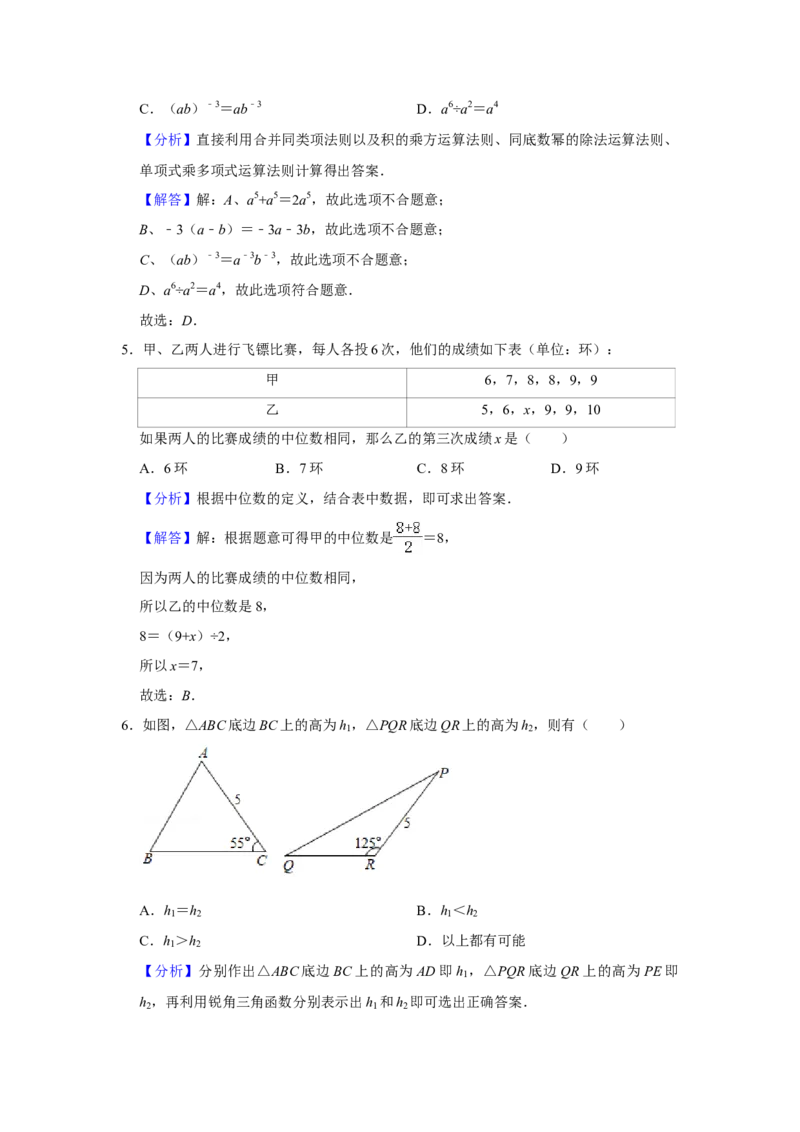
3.如图是某几何体的三视图,则该几何体是( )
A.圆锥 B.圆柱 C.长方体 D.三棱柱
4.下列计算正确的是( )
A.a5+a5=a10 B.﹣3(a﹣b)=﹣3a﹣3b
C.(ab)﹣3=ab﹣3 D.a6÷a2=a4
5.甲、乙两人进行飞镖比赛,每人各投6次,他们的成绩如下表(单位:环):
甲 6,7,8,8,9,9
乙 5,6,x,9,9,10
如果两人的比赛成绩的中位数相同,那么乙的第三次成绩x是( )
A.6环 B.7环 C.8环 D.9环
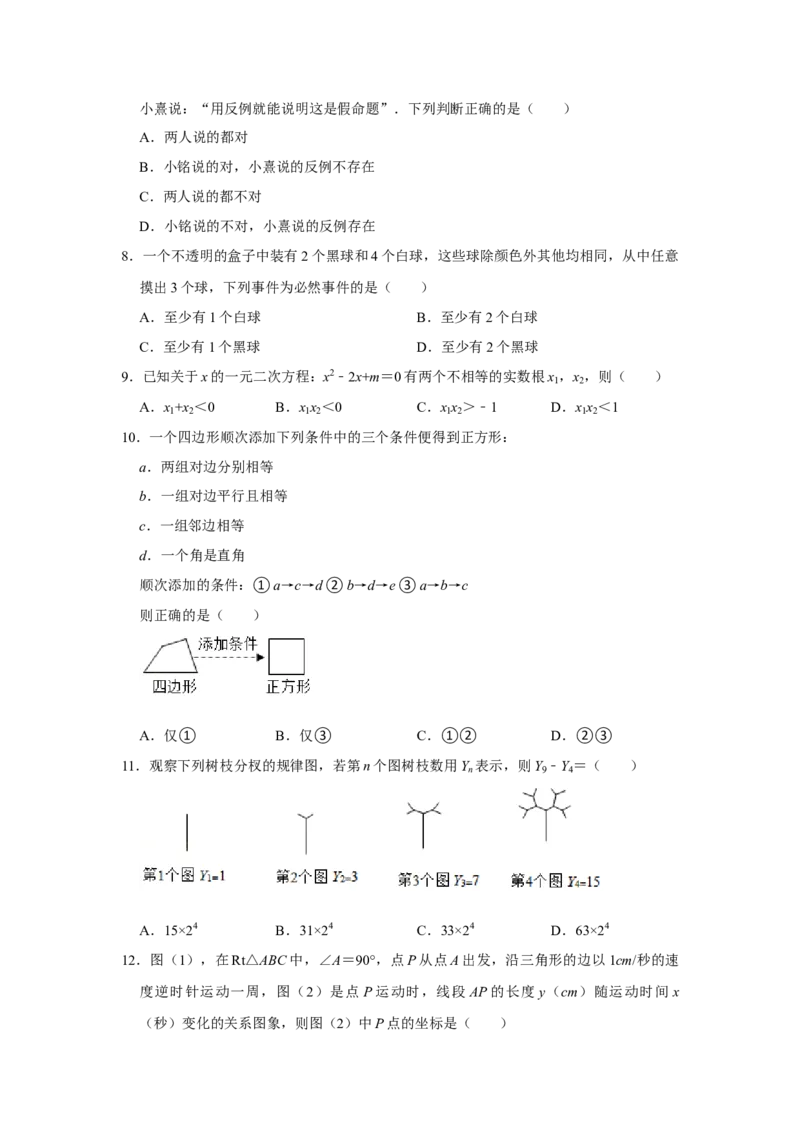
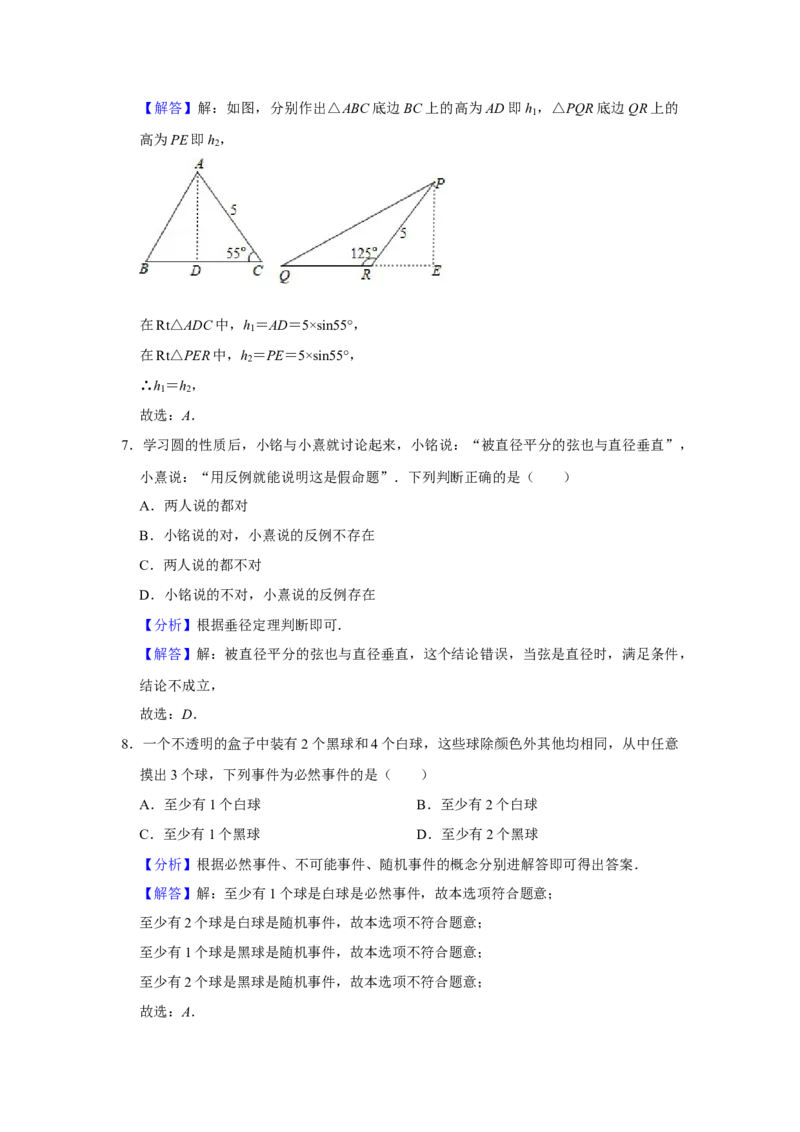
6.如图,△ABC底边BC上的高为h ,△PQR底边QR上的高为h ,则有( )
1 2
A.h =h B.h <h
1 2 1 2
C.h >h D.以上都有可能
1 2
7.学习圆的性质后,小铭与小熹就讨论起来,小铭说:“被直径平分的弦也与直径垂直”,小熹说:“用反例就能说明这是假命题”.下列判断正确的是( )
A.两人说的都对
B.小铭说的对,小熹说的反例不存在
C.两人说的都不对
D.小铭说的不对,小熹说的反例存在
8.一个不透明的盒子中装有2个黑球和4个白球,这些球除颜色外其他均相同,从中任意
摸出3个球,下列事件为必然事件的是( )
A.至少有1个白球 B.至少有2个白球
C.至少有1个黑球 D.至少有2个黑球
9.已知关于x的一元二次方程:x2﹣2x+m=0有两个不相等的实数根x ,x ,则( )
1 2
A.x +x <0 B.x x <0 C.x x >﹣1 D.x x <1
1 2 1 2 1 2 1 2
10.一个四边形顺次添加下列条件中的三个条件便得到正方形:
a.两组对边分别相等
b.一组对边平行且相等
c.一组邻边相等
d.一个角是直角
顺次添加的条件:①a→c→d②b→d→e③a→b→c
则正确的是( )
A.仅① B.仅③ C.①② D.②③
11.观察下列树枝分杈的规律图,若第n个图树枝数用Y 表示,则Y ﹣Y =( )
n 9 4
A.15×24 B.31×24 C.33×24 D.63×24
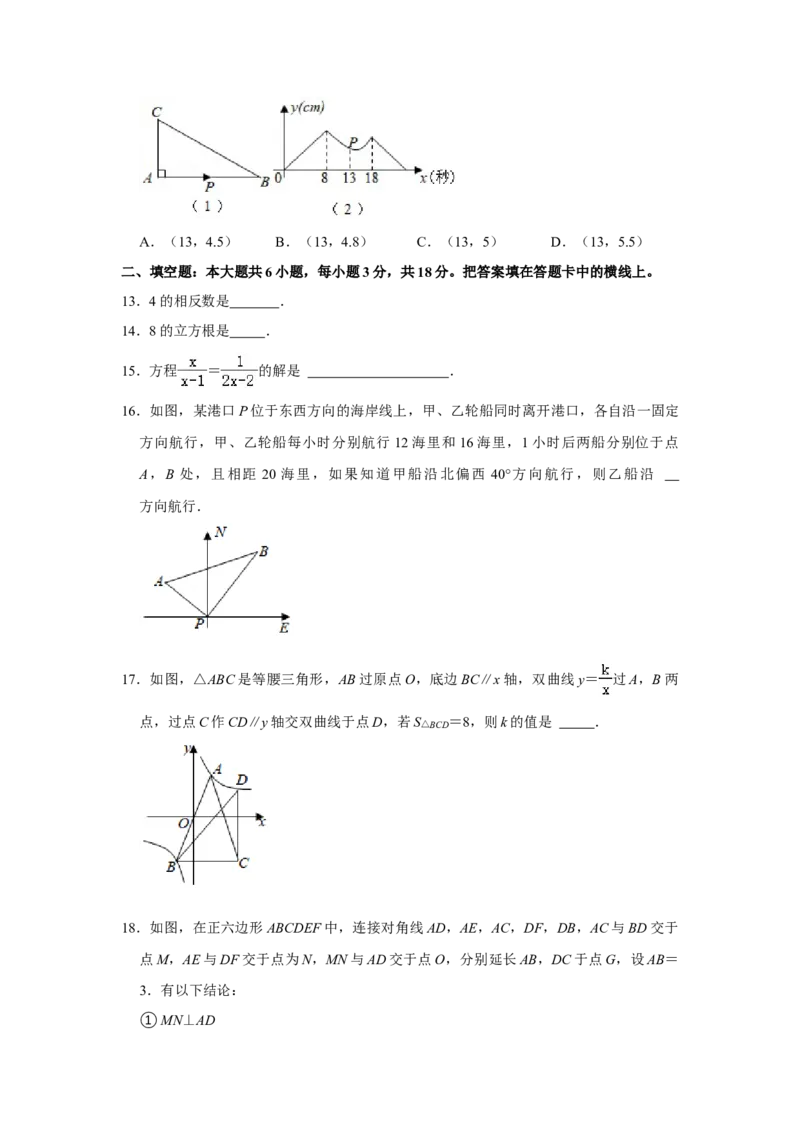
12.图(1),在Rt△ABC中,∠A=90°,点P从点A出发,沿三角形的边以1cm/秒的速
度逆时针运动一周,图(2)是点P运动时,线段AP的长度y(cm)随运动时间x
(秒)变化的关系图象,则图(2)中P点的坐标是( )A.(13,4.5) B.(13,4.8) C.(13,5) D.(13,5.5)
二、填空题:本大题共6小题,每小题3分,共18分。把答案填在答题卡中的横线上。
13.4的相反数是 .
14.8的立方根是 .
15.方程 = 的解是 .
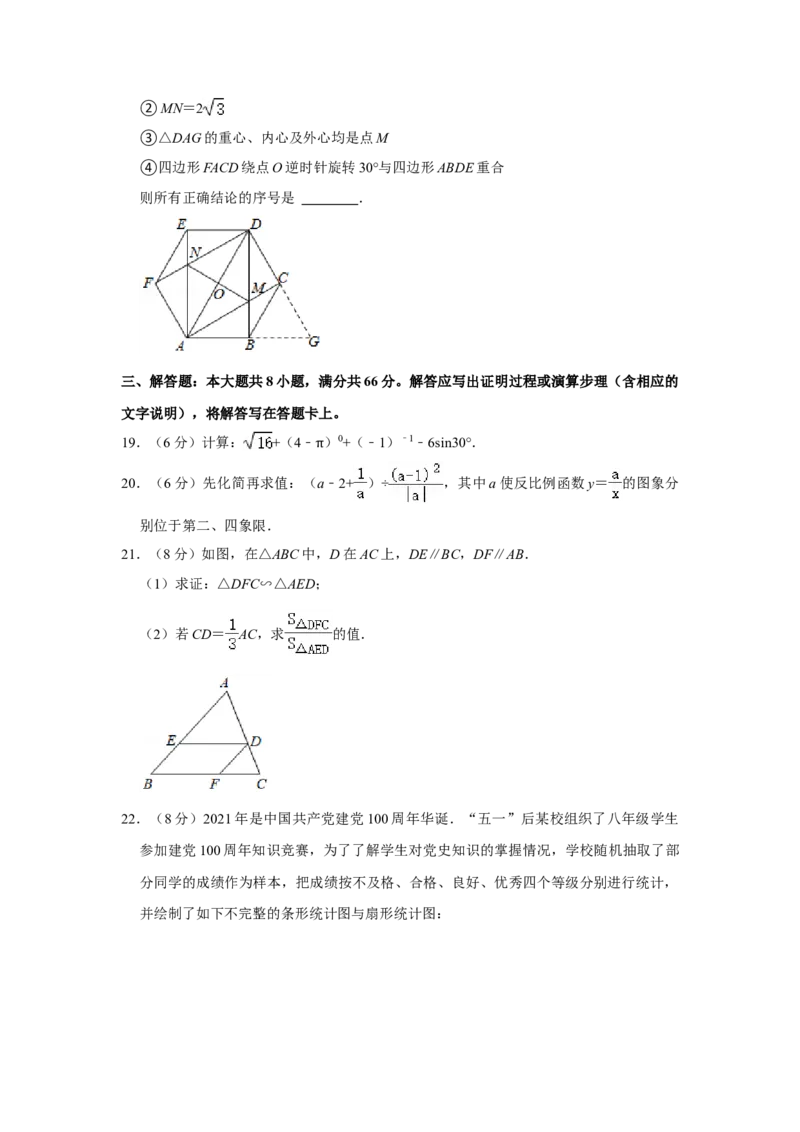
16.如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定
方向航行,甲、乙轮船每小时分别航行 12海里和16海里,1小时后两船分别位于点
A,B 处,且相距 20 海里,如果知道甲船沿北偏西 40°方向航行,则乙船沿
方向航行.
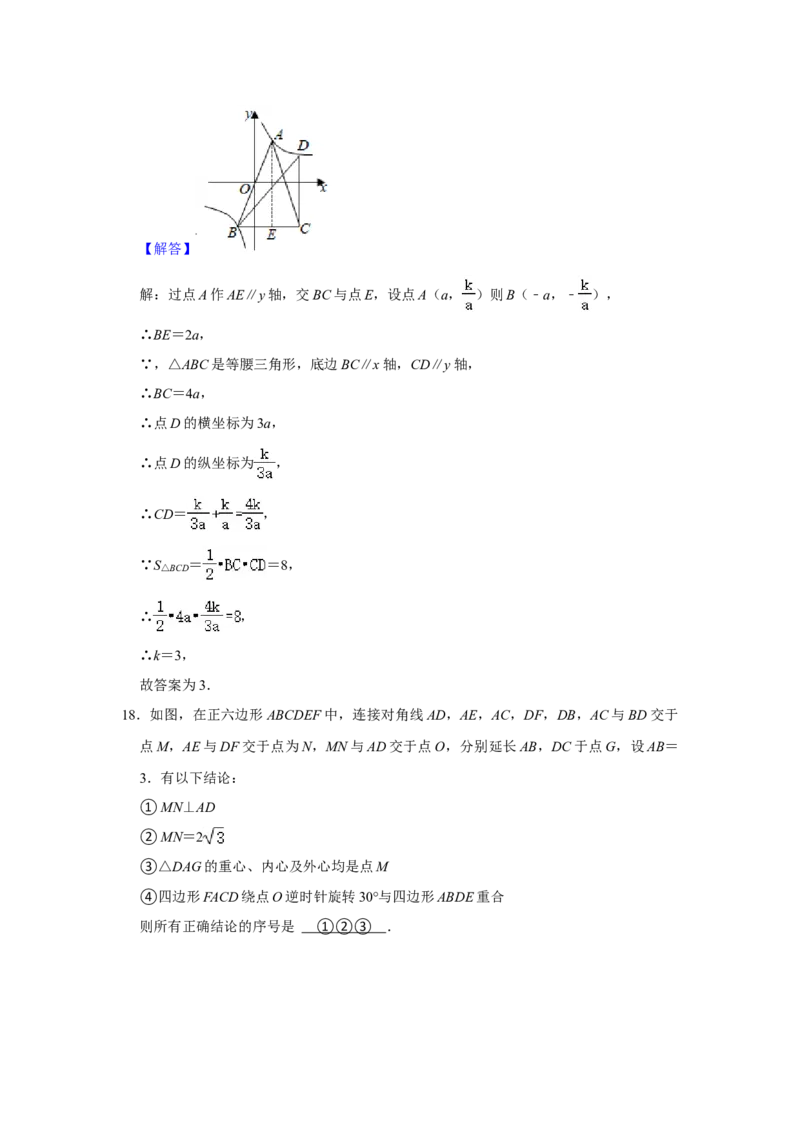
17.如图,△ABC是等腰三角形,AB过原点O,底边BC∥x轴,双曲线y= 过A,B两
点,过点C作CD∥y轴交双曲线于点D,若S△BCD =8,则k的值是 .
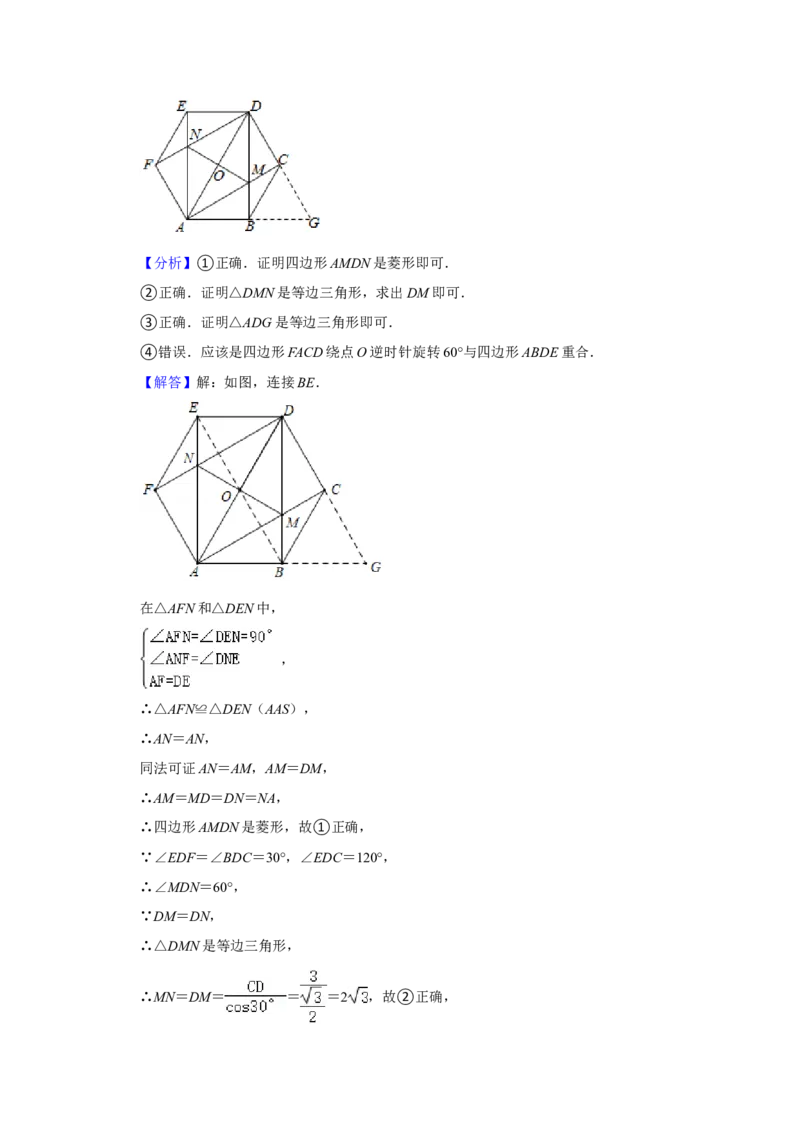
18.如图,在正六边形ABCDEF中,连接对角线AD,AE,AC,DF,DB,AC与BD交于
点M,AE与DF交于点为N,MN与AD交于点O,分别延长AB,DC于点G,设AB=
3.有以下结论:
①MN⊥AD②MN=2
③△DAG的重心、内心及外心均是点M
④四边形FACD绕点O逆时针旋转30°与四边形ABDE重合
则所有正确结论的序号是 .
三、解答题:本大题共8小题,满分共66分。解答应写出证明过程或演算步理(含相应的
文字说明),将解答写在答题卡上。
19.(6分)计算: +(4﹣ )0+(﹣1)﹣1﹣6sin30°.
π
20.(6分)先化简再求值:(a﹣2+ )÷ ,其中a使反比例函数y= 的图象分
别位于第二、四象限.
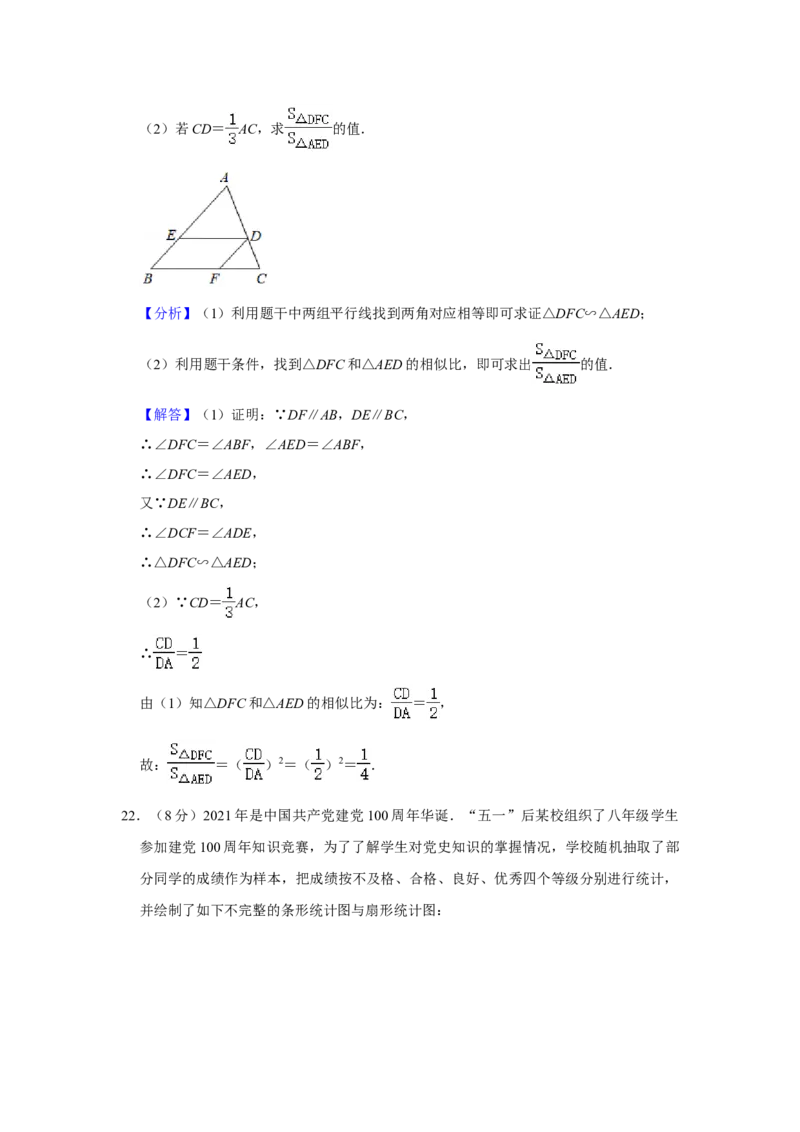
21.(8分)如图,在△ABC中,D在AC上,DE∥BC,DF∥AB.
(1)求证:△DFC∽△AED;
(2)若CD= AC,求 的值.
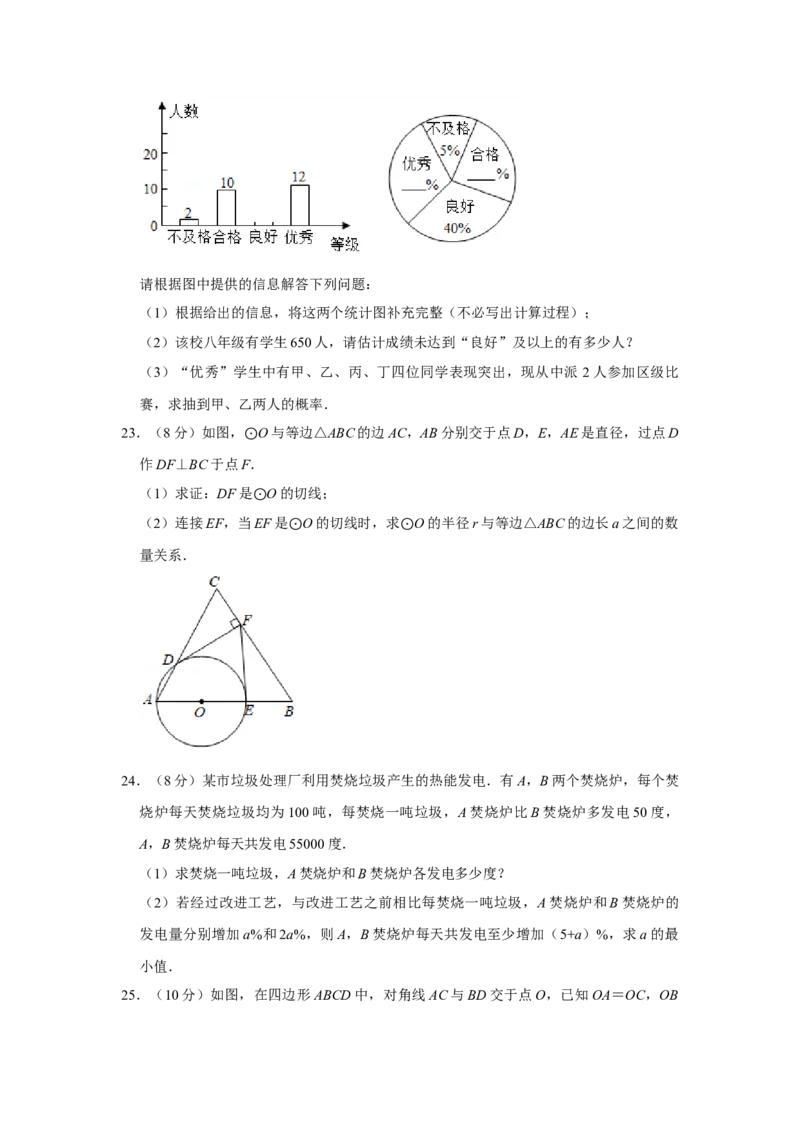
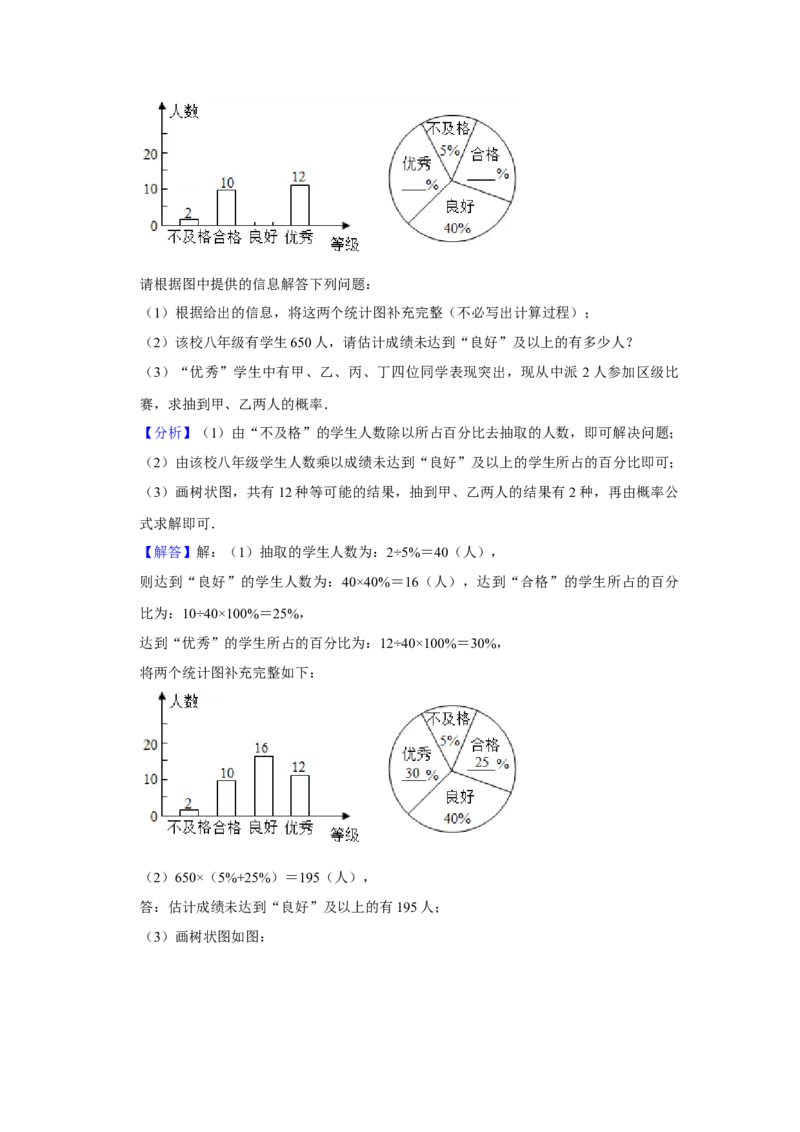
22.(8分)2021年是中国共产党建党100周年华诞.“五一”后某校组织了八年级学生
参加建党100周年知识竞赛,为了了解学生对党史知识的掌握情况,学校随机抽取了部
分同学的成绩作为样本,把成绩按不及格、合格、良好、优秀四个等级分别进行统计,
并绘制了如下不完整的条形统计图与扇形统计图:请根据图中提供的信息解答下列问题:
(1)根据给出的信息,将这两个统计图补充完整(不必写出计算过程);
(2)该校八年级有学生650人,请估计成绩未达到“良好”及以上的有多少人?
(3)“优秀”学生中有甲、乙、丙、丁四位同学表现突出,现从中派 2人参加区级比
赛,求抽到甲、乙两人的概率.
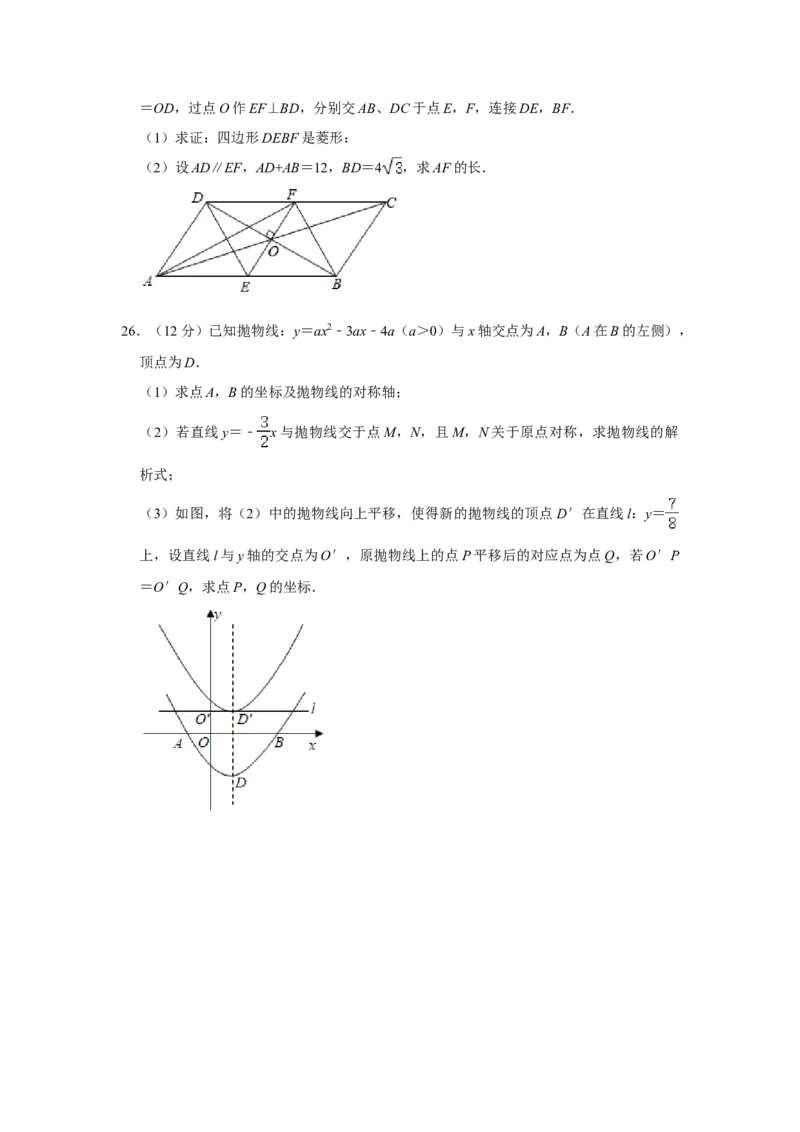
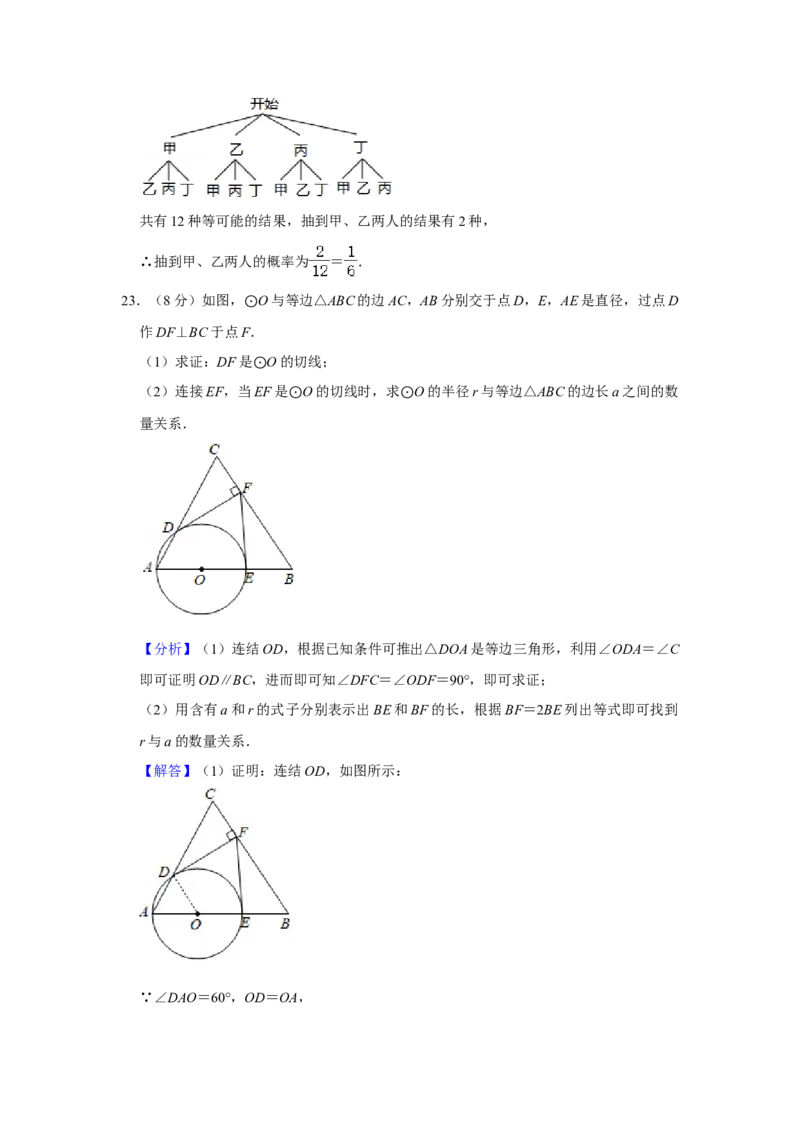
23.(8分)如图, O与等边△ABC的边AC,AB分别交于点D,E,AE是直径,过点D
作DF⊥BC于点F⊙.
(1)求证:DF是 O的切线;
(2)连接EF,当⊙EF是 O的切线时,求 O的半径r与等边△ABC的边长a之间的数
量关系. ⊙ ⊙
24.(8分)某市垃圾处理厂利用焚烧垃圾产生的热能发电.有A,B两个焚烧炉,每个焚
烧炉每天焚烧垃圾均为100吨,每焚烧一吨垃圾,A焚烧炉比B焚烧炉多发电50度,
A,B焚烧炉每天共发电55000度.
(1)求焚烧一吨垃圾,A焚烧炉和B焚烧炉各发电多少度?
(2)若经过改进工艺,与改进工艺之前相比每焚烧一吨垃圾,A焚烧炉和B焚烧炉的
发电量分别增加a%和2a%,则A,B焚烧炉每天共发电至少增加(5+a)%,求a的最
小值.
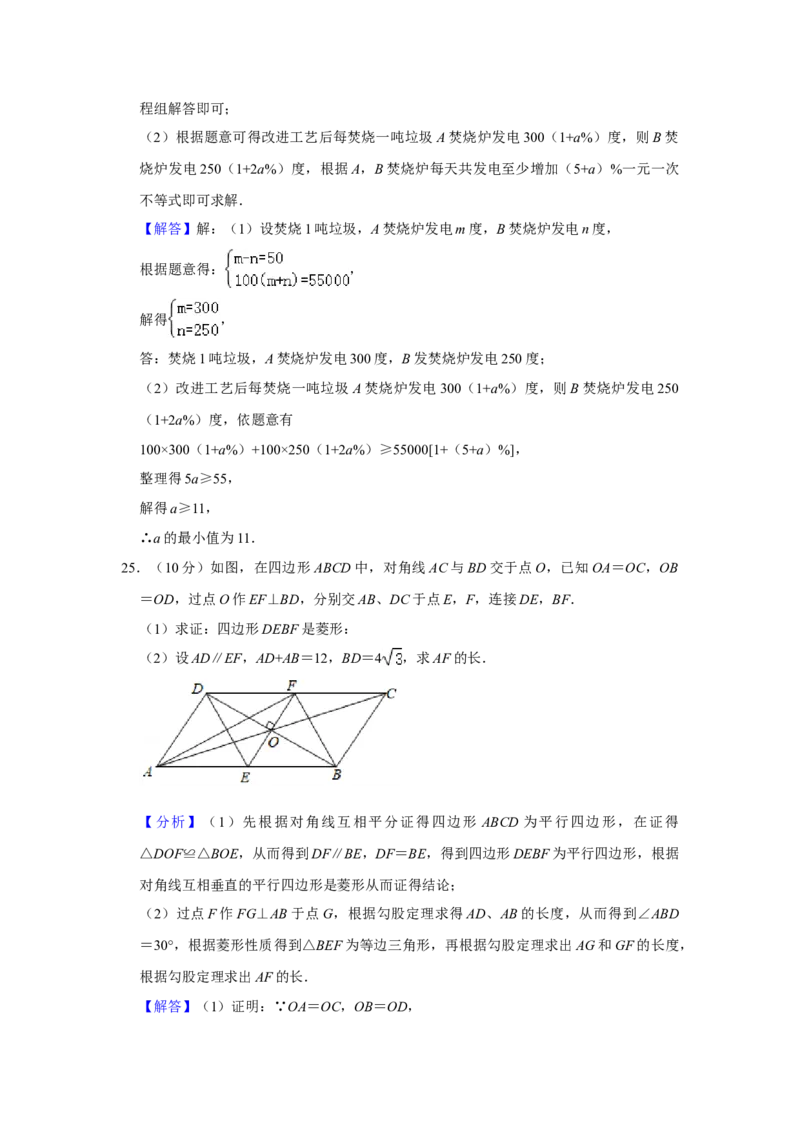
25.(10分)如图,在四边形ABCD中,对角线AC与BD交于点O,已知OA=OC,OB=OD,过点O作EF⊥BD,分别交AB、DC于点E,F,连接DE,BF.
(1)求证:四边形DEBF是菱形:
(2)设AD∥EF,AD+AB=12,BD=4 ,求AF的长.
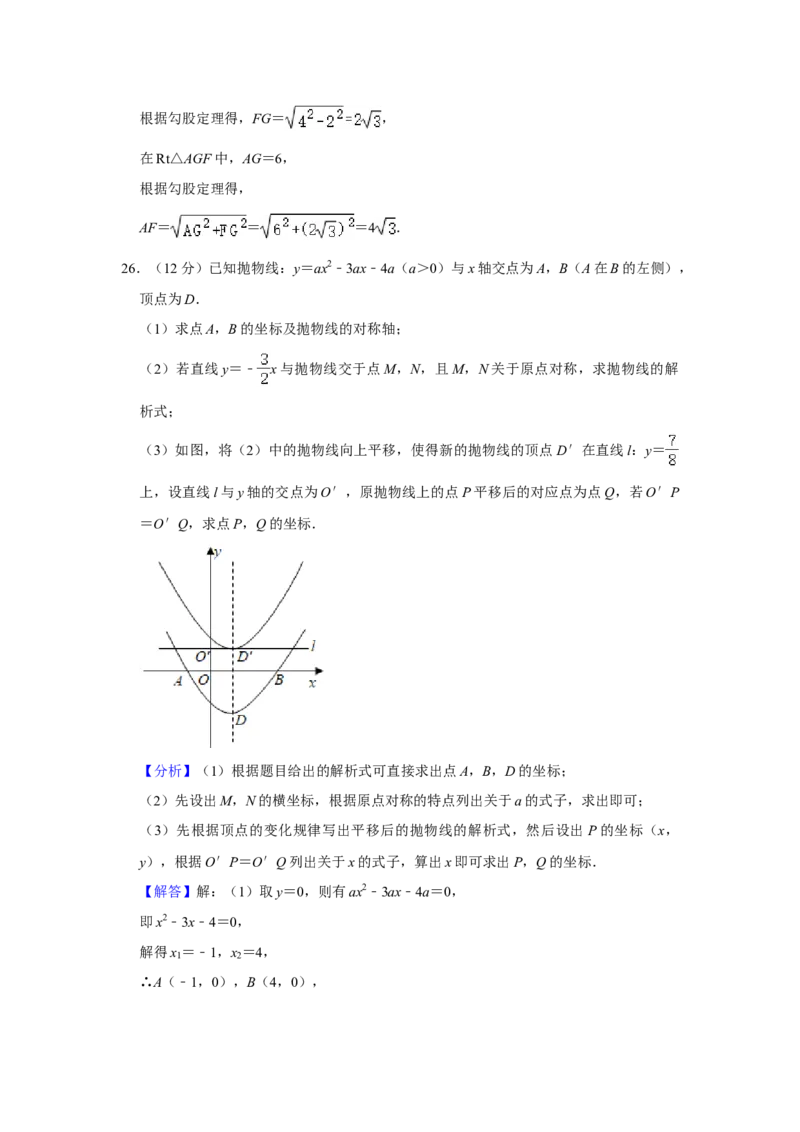
26.(12分)已知抛物线:y=ax2﹣3ax﹣4a(a>0)与x轴交点为A,B(A在B的左侧),
顶点为D.
(1)求点A,B的坐标及抛物线的对称轴;
(2)若直线y=﹣ x与抛物线交于点M,N,且M,N关于原点对称,求抛物线的解
析式;
(3)如图,将(2)中的抛物线向上平移,使得新的抛物线的顶点D′在直线l:y=
上,设直线l与y轴的交点为O′,原抛物线上的点P平移后的对应点为点Q,若O′P
=O′Q,求点P,Q的坐标.2021年广西玉林市中考数学试卷
参考答案与试题解析
一、选择题:本大题共12小题,每小题3分,共36分,在每小题给出的四个选项中,只
有一项是符合题目要求的,把正确答案的标号填(涂)在答题卡内相应的位置上.
1.计算:﹣1+2的结果是( )
A.1 B.﹣1 C.3 D.﹣3
【分析】直接利用有理数加减运算法则:绝对值不等的异号加减,取绝对值较大的加数
符号,并用较大的绝对值减去较小的绝对值进行计算得出答案.
【解答】解:﹣1+2=1.
故选:A.
2.我市今年中考报名人数接近101000人,将数据101000用科学记数法表示是( )
A.10.1×104 B.1.01×105 C.1.01×106 D.0.101×106
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的
值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相
同.
【解答】解:101000=1.01×105,
故选:B.
3.如图是某几何体的三视图,则该几何体是( )
A.圆锥 B.圆柱 C.长方体 D.三棱柱
【分析】该几何体的主视图与左视图、俯视图均为矩形,易得出该几何体的形状.
【解答】解:该几何体的主视图为矩形,左视图为矩形,俯视图是一个矩形,且三个矩
形大小不一,
故该几何体是长方体.
故选:C.
4.下列计算正确的是( )
A.a5+a5=a10 B.﹣3(a﹣b)=﹣3a﹣3bC.(ab)﹣3=ab﹣3 D.a6÷a2=a4
【分析】直接利用合并同类项法则以及积的乘方运算法则、同底数幂的除法运算法则、
单项式乘多项式运算法则计算得出答案.
【解答】解:A、a5+a5=2a5,故此选项不合题意;
B、﹣3(a﹣b)=﹣3a﹣3b,故此选项不合题意;
C、(ab)﹣3=a﹣3b﹣3,故此选项不合题意;
D、a6÷a2=a4,故此选项符合题意.
故选:D.
5.甲、乙两人进行飞镖比赛,每人各投6次,他们的成绩如下表(单位:环):
甲 6,7,8,8,9,9
乙 5,6,x,9,9,10
如果两人的比赛成绩的中位数相同,那么乙的第三次成绩x是( )
A.6环 B.7环 C.8环 D.9环
【分析】根据中位数的定义,结合表中数据,即可求出答案.
【解答】解:根据题意可得甲的中位数是 =8,
因为两人的比赛成绩的中位数相同,
所以乙的中位数是8,
8=(9+x)÷2,
所以x=7,
故选:B.
6.如图,△ABC底边BC上的高为h ,△PQR底边QR上的高为h ,则有( )
1 2
A.h =h B.h <h
1 2 1 2
C.h >h D.以上都有可能
1 2
【分析】分别作出△ABC底边BC上的高为AD即h ,△PQR底边QR上的高为PE即
1
h ,再利用锐角三角函数分别表示出h 和h 即可选出正确答案.
2 1 2【解答】解:如图,分别作出△ABC底边BC上的高为AD即h ,△PQR底边QR上的
1
高为PE即h ,
2
在Rt△ADC中,h =AD=5×sin55°,
1
在Rt△PER中,h =PE=5×sin55°,
2
∴h =h ,
1 2
故选:A.
7.学习圆的性质后,小铭与小熹就讨论起来,小铭说:“被直径平分的弦也与直径垂直”,
小熹说:“用反例就能说明这是假命题”.下列判断正确的是( )
A.两人说的都对
B.小铭说的对,小熹说的反例不存在
C.两人说的都不对
D.小铭说的不对,小熹说的反例存在
【分析】根据垂径定理判断即可.
【解答】解:被直径平分的弦也与直径垂直,这个结论错误,当弦是直径时,满足条件,
结论不成立,
故选:D.
8.一个不透明的盒子中装有2个黑球和4个白球,这些球除颜色外其他均相同,从中任意
摸出3个球,下列事件为必然事件的是( )
A.至少有1个白球 B.至少有2个白球
C.至少有1个黑球 D.至少有2个黑球
【分析】根据必然事件、不可能事件、随机事件的概念分别进解答即可得出答案.
【解答】解:至少有1个球是白球是必然事件,故本选项符合题意;
至少有2个球是白球是随机事件,故本选项不符合题意;
至少有1个球是黑球是随机事件,故本选项不符合题意;
至少有2个球是黑球是随机事件,故本选项不符合题意;
故选:A.9.已知关于x的一元二次方程:x2﹣2x+m=0有两个不相等的实数根x ,x ,则( )
1 2
A.x +x <0 B.x x <0 C.x x >﹣1 D.x x <1
1 2 1 2 1 2 1 2
【分析】根据判别式的意义得到△=(﹣2)2﹣4m>0,解得m<1,再利用根与系数的
关系得到x +x =2,x x =m,然后对各选项进行判断.
1 2 1 2
【解答】解:根据题意得△=(﹣2)2﹣4m>0,解得m<1,
所以x +x =2,x x =m<1.
1 2 1 2
故选:D.
10.一个四边形顺次添加下列条件中的三个条件便得到正方形:
a.两组对边分别相等
b.一组对边平行且相等
c.一组邻边相等
d.一个角是直角
顺次添加的条件:①a→c→d②b→d→e③a→b→c
则正确的是( )
A.仅① B.仅③ C.①② D.②③
【分析】①由条件a可得到四边形是平行四边形,添加c得到平行四边形是菱形,再添
加d得到菱形是正方形,①正确;
②由条件b得到四边形是平行四边形,添加d平行四边形是矩形,再添加c矩形是正方
形,②正确;
③由a和b都可得到四边形是平行四边形,再添加c得到平行四边形是菱形,不能得到
四边形是正方形,③不正确.
【解答】解:①由a得到两组对边分别相等的四边形是平行四边形,添加c即一组邻边
相等的平行四边形是菱形,再添加d即一个角是直角的菱形是正方形,故①正确;
②由b得到一组对边平行且相等的四边形是平行四边形,添加d即有一个角是直角的平
行四边形是矩形,再添加c即一组邻边相等的矩形是正方形,故②正确;
③由a得到两组对边分别相等的四边形是平行四边形,添加b得到一组对边平行且相等
的平行四边形仍是平行四边形,再添加c即一组邻边相等的平行四边形是菱形,不能得
到四边形是正方形,故③不正确;故选:C.
11.观察下列树枝分杈的规律图,若第n个图树枝数用Y 表示,则Y ﹣Y =( )
n 9 4
A.15×24 B.31×24 C.33×24 D.63×24
【分析】根据已知图中规律可得:Y =1+2+22+23+24+25+26+27+•••+2n﹣1,相减可得结论.
n
【解答】解:由题意得:
第1个图:Y =1,
1
第2个图:Y =3=1+2,
2
第3个图:Y =7=1+2+22,
3
第4个图:Y =15=1+2+22+23,
4
•••
第9个图:Y =1+2+22+23+24+25+26+27+28,
9
∴Y ﹣Y =24+25+26+27+28=24(1+2+22+23+24)=24×(3+4+8+16)=24×31.
9 4
故选:B.
12.图(1),在Rt△ABC中,∠A=90°,点P从点A出发,沿三角形的边以1cm/秒的速
度逆时针运动一周,图(2)是点P运动时,线段AP的长度y(cm)随运动时间x
(秒)变化的关系图象,则图(2)中P点的坐标是( )
A.(13,4.5) B.(13,4.8) C.(13,5) D.(13,5.5)
【分析】图(2)中的图象有三段,正好对应图(1)中的线段AB,BC,AC,所以AB
=8,BC=10,当x=13时,则P点为BC的中点,根据直角三角形斜边上的中线等于
斜边的一半,求得此时AP的长度,即图(2)中点P的纵坐标y.
【解答】解:由图象可知:AB=8,BC=18﹣8=10,
当x=13时,即点运动了13>8,∴此时点P在线段BC上,BP=13﹣8=5,
则P点为BC的中点,
又因为∠A=90°,
所以AP= BC=5.
所以图(2)中P的坐标为(13,5).
故选:C.
二、填空题:本大题共6小题,每小题3分,共18分。把答案填在答题卡中的横线上。
13.4的相反数是 ﹣ 4 .
【分析】根据只有符号不同的两个数互为相反数,可得一个数的相反数.
【解答】解:4的相反数是﹣4,
故答案为:﹣4.
14.8的立方根是 2 .
【分析】利用立方根的定义计算即可得到结果.
【解答】解:8的立方根为2,
故答案为:2.
15.方程 = 的解是 x = .
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可
得到分式方程的解.
【解答】解:去分母得:2x=1,
解得:x= ,
检验:当x= 时,2(x﹣1)≠0,
∴分式方程的解为x= .
故答案为:x= .
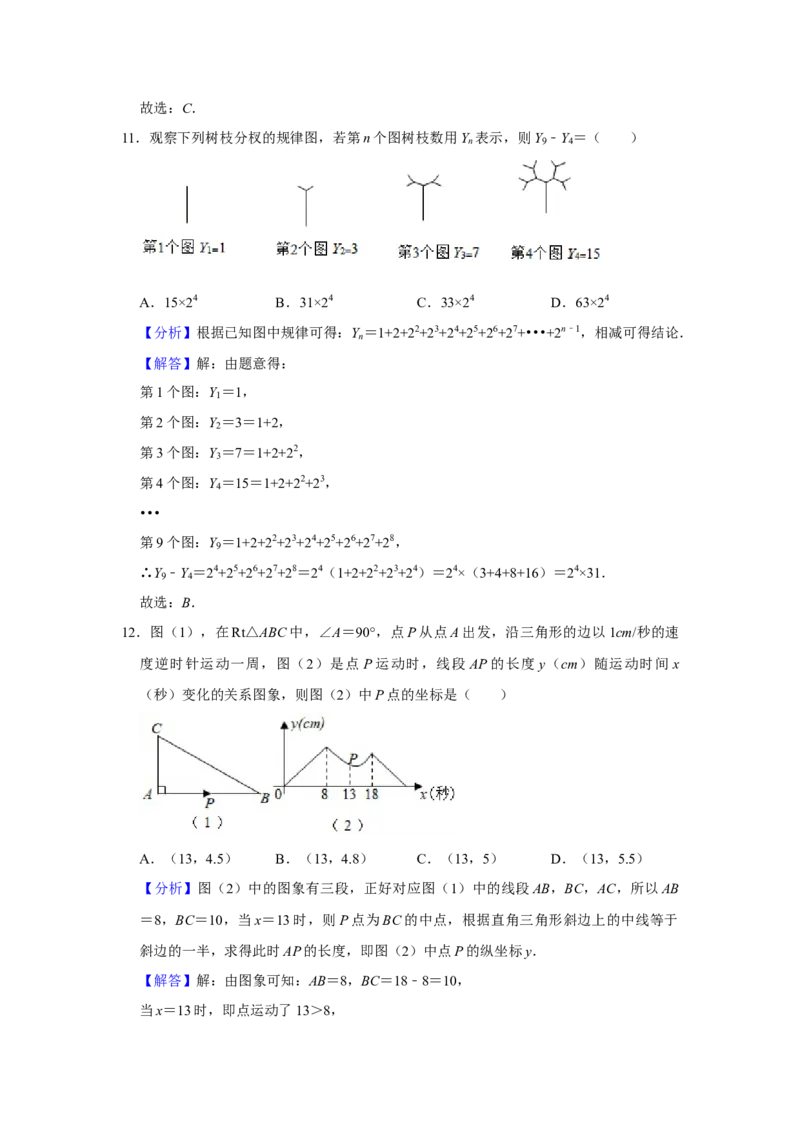
16.如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定
方向航行,甲、乙轮船每小时分别航行 12海里和16海里,1小时后两船分别位于点
A,B处,且相距20海里,如果知道甲船沿北偏西40°方向航行,则乙船沿 北偏东
50° 方向航行.【分析】根据题意即可知AP=12,BP=16,AB=20,利用勾股定理的逆定理可推出
△APB是直角三角形,由甲船沿北偏西40°方向航行,即可推出乙船的航行方位角.
【解答】解:由题意可知:AP=12,BP=16,AB=20,
∵122+162=202,
∴△APB是直角三角形,
∴∠APB=90°,
由题意知∠APN=40°,
∴∠BPN=90°﹣∠APN=90°﹣40°=50°,
即乙船沿北偏东50°方向航行,
故答案为:北偏东50°.
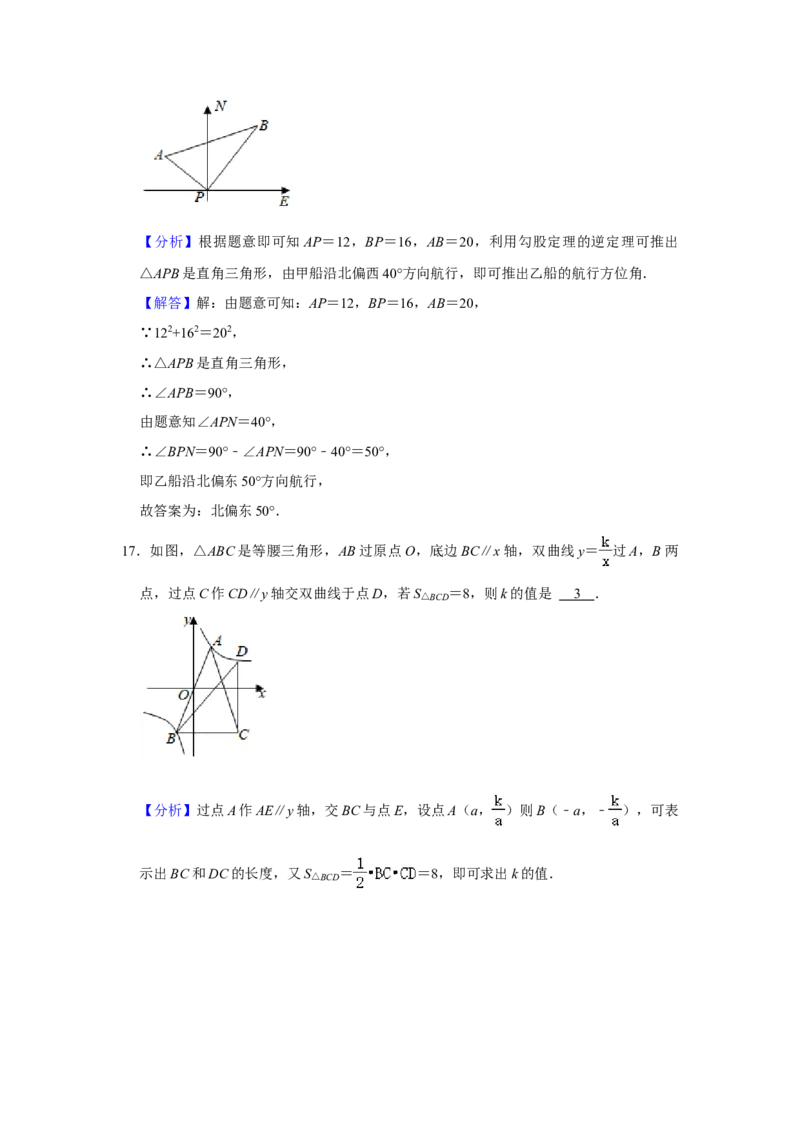
17.如图,△ABC是等腰三角形,AB过原点O,底边BC∥x轴,双曲线y= 过A,B两
点,过点C作CD∥y轴交双曲线于点D,若S△BCD =8,则k的值是 3 .
【分析】过点A作AE∥y轴,交BC与点E,设点A(a, )则B(﹣a,﹣ ),可表
示出BC和DC的长度,又S△BCD = =8,即可求出k的值.【解答】
解:过点A作AE∥y轴,交BC与点E,设点A(a, )则B(﹣a,﹣ ),
∴BE=2a,
∵,△ABC是等腰三角形,底边BC∥x轴,CD∥y轴,
∴BC=4a,
∴点D的横坐标为3a,
∴点D的纵坐标为 ,
∴CD= ,
∵S△BCD = =8,
∴ ,
∴k=3,
故答案为3.
18.如图,在正六边形ABCDEF中,连接对角线AD,AE,AC,DF,DB,AC与BD交于
点M,AE与DF交于点为N,MN与AD交于点O,分别延长AB,DC于点G,设AB=
3.有以下结论:
①MN⊥AD
②MN=2
③△DAG的重心、内心及外心均是点M
④四边形FACD绕点O逆时针旋转30°与四边形ABDE重合
则所有正确结论的序号是 ①②③ .【分析】①正确.证明四边形AMDN是菱形即可.
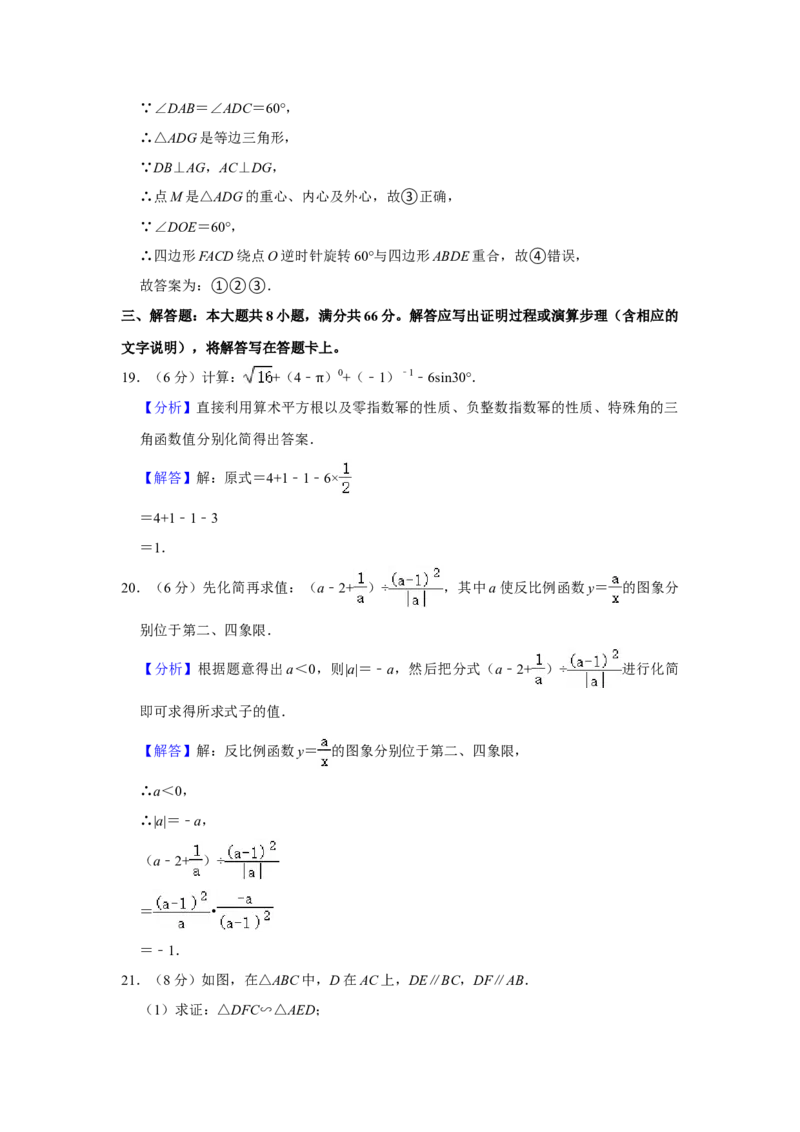
②正确.证明△DMN是等边三角形,求出DM即可.
③正确.证明△ADG是等边三角形即可.
④错误.应该是四边形FACD绕点O逆时针旋转60°与四边形ABDE重合.
【解答】解:如图,连接BE.
在△AFN和△DEN中,
,
∴△AFN≌△DEN(AAS),
∴AN=AN,
同法可证AN=AM,AM=DM,
∴AM=MD=DN=NA,
∴四边形AMDN是菱形,故①正确,
∵∠EDF=∠BDC=30°,∠EDC=120°,
∴∠MDN=60°,
∵DM=DN,
∴△DMN是等边三角形,
∴MN=DM= = =2 ,故②正确,∵∠DAB=∠ADC=60°,
∴△ADG是等边三角形,
∵DB⊥AG,AC⊥DG,
∴点M是△ADG的重心、内心及外心,故③正确,
∵∠DOE=60°,
∴四边形FACD绕点O逆时针旋转60°与四边形ABDE重合,故④错误,
故答案为:①②③.
三、解答题:本大题共8小题,满分共66分。解答应写出证明过程或演算步理(含相应的
文字说明),将解答写在答题卡上。
19.(6分)计算: +(4﹣ )0+(﹣1)﹣1﹣6sin30°.
【分析】直接利用算术平方根π以及零指数幂的性质、负整数指数幂的性质、特殊角的三
角函数值分别化简得出答案.
【解答】解:原式=4+1﹣1﹣6×
=4+1﹣1﹣3
=1.
20.(6分)先化简再求值:(a﹣2+ )÷ ,其中a使反比例函数y= 的图象分
别位于第二、四象限.
【分析】根据题意得出a<0,则|a|=﹣a,然后把分式(a﹣2+ )÷ 进行化简
即可求得所求式子的值.
【解答】解:反比例函数y= 的图象分别位于第二、四象限,
∴a<0,
∴|a|=﹣a,
(a﹣2+ )÷
= •
=﹣1.
21.(8分)如图,在△ABC中,D在AC上,DE∥BC,DF∥AB.
(1)求证:△DFC∽△AED;(2)若CD= AC,求 的值.
【分析】(1)利用题干中两组平行线找到两角对应相等即可求证△DFC∽△AED;
(2)利用题干条件,找到△DFC和△AED的相似比,即可求出 的值.
【解答】(1)证明:∵DF∥AB,DE∥BC,
∴∠DFC=∠ABF,∠AED=∠ABF,
∴∠DFC=∠AED,
又∵DE∥BC,
∴∠DCF=∠ADE,
∴△DFC∽△AED;
(2)∵CD= AC,
∴ =
由(1)知△DFC和△AED的相似比为: = ,
故: =( )2=( )2= .
22.(8分)2021年是中国共产党建党100周年华诞.“五一”后某校组织了八年级学生
参加建党100周年知识竞赛,为了了解学生对党史知识的掌握情况,学校随机抽取了部
分同学的成绩作为样本,把成绩按不及格、合格、良好、优秀四个等级分别进行统计,
并绘制了如下不完整的条形统计图与扇形统计图:请根据图中提供的信息解答下列问题:
(1)根据给出的信息,将这两个统计图补充完整(不必写出计算过程);
(2)该校八年级有学生650人,请估计成绩未达到“良好”及以上的有多少人?
(3)“优秀”学生中有甲、乙、丙、丁四位同学表现突出,现从中派 2人参加区级比
赛,求抽到甲、乙两人的概率.
【分析】(1)由“不及格”的学生人数除以所占百分比去抽取的人数,即可解决问题;
(2)由该校八年级学生人数乘以成绩未达到“良好”及以上的学生所占的百分比即可;
(3)画树状图,共有12种等可能的结果,抽到甲、乙两人的结果有2种,再由概率公
式求解即可.
【解答】解:(1)抽取的学生人数为:2÷5%=40(人),
则达到“良好”的学生人数为:40×40%=16(人),达到“合格”的学生所占的百分
比为:10÷40×100%=25%,
达到“优秀”的学生所占的百分比为:12÷40×100%=30%,
将两个统计图补充完整如下:
(2)650×(5%+25%)=195(人),
答:估计成绩未达到“良好”及以上的有195人;
(3)画树状图如图:共有12种等可能的结果,抽到甲、乙两人的结果有2种,
∴抽到甲、乙两人的概率为 = .
23.(8分)如图, O与等边△ABC的边AC,AB分别交于点D,E,AE是直径,过点D
作DF⊥BC于点F⊙.
(1)求证:DF是 O的切线;
(2)连接EF,当⊙EF是 O的切线时,求 O的半径r与等边△ABC的边长a之间的数
量关系. ⊙ ⊙
【分析】(1)连结OD,根据已知条件可推出△DOA是等边三角形,利用∠ODA=∠C
即可证明OD∥BC,进而即可知∠DFC=∠ODF=90°,即可求证;
(2)用含有a和r的式子分别表示出BE和BF的长,根据BF=2BE列出等式即可找到
r与a的数量关系.
【解答】(1)证明:连结OD,如图所示:
∵∠DAO=60°,OD=OA,∴△DOA是等边三角形,
∴∠ODA=∠C=60°,
∴OD∥BC,
又∵∠DFC=90°,
∴∠ODF=90°,
∴OD⊥DF,
即DF是 O的切线;
(2)设半⊙径为r,等边△ABC的边长为a,
由(1)可知:AD=r,则CD=a﹣r,BE=a﹣2r
在Rt△CFD中,∠C=60°,CD=a﹣r,
∴CF= ,
∴BF=a﹣ ,
又∵EF是 O的切线,
∴△FEB是⊙直角三角形,且∠B=60°,∠EFB=30°,
∴BF=2BE,
∴a﹣ (a﹣r)=2(a﹣2r),
解得:a=3r,
即r= ,
∴ O的半径r与等边△ABC的边长a之间的数量关系为:r= .
⊙
24.(8分)某市垃圾处理厂利用焚烧垃圾产生的热能发电.有A,B两个焚烧炉,每个焚
烧炉每天焚烧垃圾均为100吨,每焚烧一吨垃圾,A焚烧炉比B焚烧炉多发电50度,
A,B焚烧炉每天共发电55000度.
(1)求焚烧一吨垃圾,A焚烧炉和B焚烧炉各发电多少度?
(2)若经过改进工艺,与改进工艺之前相比每焚烧一吨垃圾,A焚烧炉和B焚烧炉的
发电量分别增加a%和2a%,则A,B焚烧炉每天共发电至少增加(5+a)%,求a的最
小值.
【分析】(1)设焚烧1吨垃圾,A焚烧炉发电m度,B焚烧炉发电n度,根据“每焚烧
一吨垃圾,A焚烧炉比B焚烧炉多发电50度,A,B焚烧炉每天共发电55000度”列方程组解答即可;
(2)根据题意可得改进工艺后每焚烧一吨垃圾 A焚烧炉发电300(1+a%)度,则B焚
烧炉发电250(1+2a%)度,根据A,B焚烧炉每天共发电至少增加(5+a)%一元一次
不等式即可求解.
【解答】解:(1)设焚烧1吨垃圾,A焚烧炉发电m度,B焚烧炉发电n度,
根据题意得: ,
解得 ,
答:焚烧1吨垃圾,A焚烧炉发电300度,B发焚烧炉发电250度;
(2)改进工艺后每焚烧一吨垃圾A焚烧炉发电300(1+a%)度,则B焚烧炉发电250
(1+2a%)度,依题意有
100×300(1+a%)+100×250(1+2a%)≥55000[1+(5+a)%],
整理得5a≥55,
解得a≥11,
∴a的最小值为11.
25.(10分)如图,在四边形ABCD中,对角线AC与BD交于点O,已知OA=OC,OB
=OD,过点O作EF⊥BD,分别交AB、DC于点E,F,连接DE,BF.
(1)求证:四边形DEBF是菱形:
(2)设AD∥EF,AD+AB=12,BD=4 ,求AF的长.
【分析】(1)先根据对角线互相平分证得四边形 ABCD 为平行四边形,在证得
△DOF≌△BOE,从而得到DF∥BE,DF=BE,得到四边形DEBF为平行四边形,根据
对角线互相垂直的平行四边形是菱形从而证得结论;
(2)过点F作FG⊥AB于点G,根据勾股定理求得AD、AB的长度,从而得到∠ABD
=30°,根据菱形性质得到△BEF为等边三角形,再根据勾股定理求出AG和GF的长度,
根据勾股定理求出AF的长.
【解答】(1)证明:∵OA=OC,OB=OD,∴四边形ABCD为平行四边形,
∴AB∥CD,
∴∠ABD=∠CDB,
在△BOE和△DOF中,
,
∴BE=DF,
∵BE∥DF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形;
(2)过点F作FG⊥AB于点G,如图,
∵AD∥EF,EF⊥BD,
∴∠ADB=90°,
∴在Rt△ABD中,AD2+BD2=AB2,
∵AD+AB=12,BD=4 ,
∴AD2+(4 )2=(12﹣AD)2,
解得AD=4,AB=8,
∴∠ABD=30°,
∵四边形DEBF是菱形,
∴∠EBF=2∠ABD=60°,
∴△BEF是等边三角形,
∵OB=OD,EF∥AD,
∴AE=BE=4,
∵FG⊥BE,
∴EG=BG=2,
在Rt△BGF中,BF=4,BG=2,根据勾股定理得,FG= ,
在Rt△AGF中,AG=6,
根据勾股定理得,
AF= = =4 .
26.(12分)已知抛物线:y=ax2﹣3ax﹣4a(a>0)与x轴交点为A,B(A在B的左侧),
顶点为D.
(1)求点A,B的坐标及抛物线的对称轴;
(2)若直线y=﹣ x与抛物线交于点M,N,且M,N关于原点对称,求抛物线的解
析式;
(3)如图,将(2)中的抛物线向上平移,使得新的抛物线的顶点D′在直线l:y=
上,设直线l与y轴的交点为O′,原抛物线上的点P平移后的对应点为点Q,若O′P
=O′Q,求点P,Q的坐标.
【分析】(1)根据题目给出的解析式可直接求出点A,B,D的坐标;
(2)先设出M,N的横坐标,根据原点对称的特点列出关于a的式子,求出即可;
(3)先根据顶点的变化规律写出平移后的抛物线的解析式,然后设出P的坐标(x,
y),根据O′P=O′Q列出关于x的式子,算出x即可求出P,Q的坐标.
【解答】解:(1)取y=0,则有ax2﹣3ax﹣4a=0,
即x2﹣3x﹣4=0,
解得x =﹣1,x =4,
1 2
∴A(﹣1,0),B(4,0),对称轴为直线x= ,
(2)设M的横坐标为x ,N的横坐标为x ,
1 2
根据题意得: ,
即 ,
,
又∵M,N关于原点对称,
∴ ,
∴a= ,
∴ ,
(3)∵ ,
由题意得向上平移后的抛物线解析式为 ,
∴抛物线向上平移了四个单位,
设P(x, ),则Q(x, ),
由题意得O'(0, ),
∵O′P=O′Q,
∴ ,
解得 , ,
若 ,则y= ,
∴P( ,﹣ ),Q( , ),
若 ,
则y= ,
∴P( , ),Q( , ),
综上,P( ,﹣ ),Q( , )或P( , ),Q( , ).