文档内容
方法精讲-资料 3
(笔记)
主讲教师:戚七
授课时间:2024.03.15
粉笔公考·官方微信方法精讲-资料 3(笔记)
学习任务:
1.课程内容:比重、平均数
2.授课时长:3小时
3.对应讲义:第 214~225页
4.重点内容:
(1)现期比重、基期比重的计算公式及拓展
(2)两期比重的升降判断及数值计算
(3)不同条件下的现期平均数计算、基期平均数及两期平均数问题
第五节 比重
【注意】比重、平均数统称为比例,都可以表达为“A/B”的形式,比重=部
分/整体,平均数=总数/份数,因为初始列式形式一样,所以有很多相似的公式
和技巧。为了便于总结和记忆,统一把所有比例形式的分子称为A、分母称为 B;
分子的增长率用a 表示,分母的增长率用b 表示。
比重
基本术语
1.现期比重
2.基期比重
3.两期比重的比较与计算
“比重=部分(A)/整体(B)”基础三量关系
①比重=部分/整体
【引例1】某班总共 500人,其中女生100 人,求女生占全班总人数的比重。
②整体=部分/比重
【引例2】某班女生 100人,占全班总人数的 20%,求全班有多少人。
③部分=整体*比重
1【引例 3】某班总共 500 人,已知女生占全班总人数的 20%,求女生有多少
人。
【注意】比重:生活化的概念,指的是部分在整体中所占的比例关系。
1.比重=部分(A)/整体(B)。
例:某班总共 500人,其中女生100人,求女生占全班总人数的比重。
答:女生占比=女生人数/全班人数=100/500=1/5=20%。
2.整体=部分/比重。
例:某班女生 100人,占全班总人数的 20%,求全班有多少人。
答:全班人数=部分/比重=100/20%=500 人。
3.部分=整体*比重。
例:某班总共 500人,已知女生占全班总人数的 20%,求女生有多少人。
答:女生人数=全班人数*比重=500*20%=100 人。
比重=部分(A)/总体(B)
题型识别:A占 B的比重,(B中A所占的比重)
第三产业占GDP 的比重
在总收入中工资收入占的比重
【注意】比重:
1.题型识别:“占”字有两个作用。
(1)“占”字可以表示比重的含义,出现“占”字,为比重问题。“占”字
是比重题型识别的关键字。
(2)“占”字可以帮助我们快速识别谁是分子 A、谁是分母B。
①表述往往为“部分占整体”。比如“A 占B的比重”,“占”前为 A,故A为
分子;“占”后为B,故B为分母。
②有时候会出现倒装语序,表述往往为“整体中部分所占的比重”。比如“B
中A所占的比重”,可以翻译为“A占B的比重”。
2.例:
(1)第三产业占 GDP的比重。
答:出现“占”字,“占”前为A,“占”后为 B,比重=第三产业/GDP。
2(2)在总收入中工资收入占的比重。
答:倒装语序,可以翻译为“工资收入占总收入的比重”,工资收入为 A,总
收入为B,比重=工资收入/总收入。
概念引申(比重的特殊表述形式)
①A对B的增长贡献率=部分A的增长量/整体B的增长量
问:2020年工作收入对总收入的增长贡献率是多少?
②在资料分析中,利润率=利润/收入;在数量关系中,利润率=利润/成本
【注意】概念引申(比重的特殊表述形式):
1.A对B的增长贡献率:
(1)贡献率本身就是一个比重,A对 B的贡献率=A/B。
(2)A对B的增长贡献率=部分A的增长量/整体B的增长量。
(3)例:2020 年工作收入对总收入的增长贡献率是多少?
答:工作收入为 A,总收入为 B,工资收入的增长量为 5000-4500=500 元,
总收入的增长量为 11000-10000=1000 元,工作收入对总收入的增长贡献率为
500/1000=50%。
2.利润率:
(1)在数量关系中,利润率=利润/成本。数量关系研究的是成本很清晰的
小本买卖。
(2)在资料分析中,利润率=利润/收入。资料分析研究的是一个行业、区
域、全国,很难清晰界定成本,而且在真实数据中,收入-成本≠利润,收入包
括很多部分,比如成本、利润、税收……,故资料分析研究的是收入利润率。利
润是收入的一个部分,“利润/收入”相当于“部分/整体”的形式,故利润率也
是一种比重。
比重
1.现期比重
32.基期比重
3.两期比重的比较与计算
【注意】比重:
1.现期比重。
2.基期比重。
3.两期比重的比较与计算。
现期比重
题型识别:问题时间与材料时间一致+A 占B的比重
公式:比重=部分(A)/整体(B)
速算技巧:截位直除
【注意】现期比重:识别题型至关重要。
1.题型识别:问题时间与材料时间一致+A占B的比重。
2.公式:比重=部分(A)/整体(B)。
3.速算技巧:截位直除。
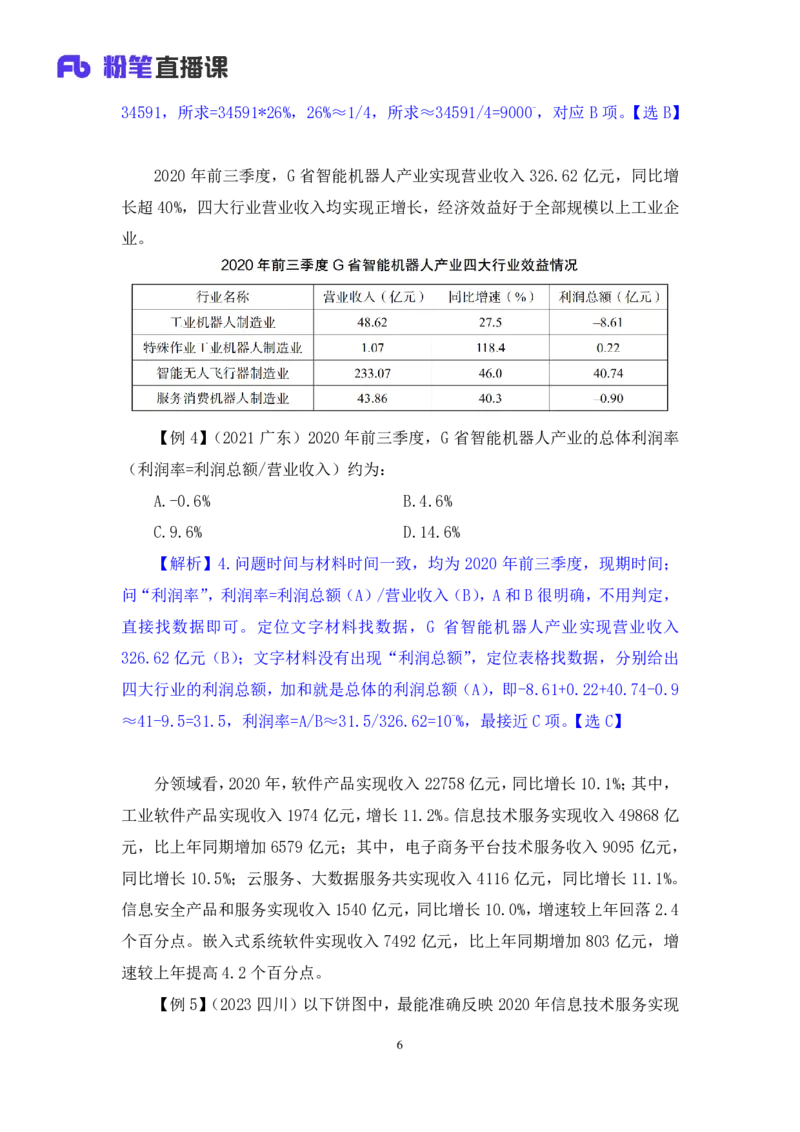
【例1】(2023 上海)2020 年,江浙沪地区年人均教育文化娱乐支出在年人
均消费支出中的占比约为:
A.5% B.7%
C.9% D.15%
4【解析】1.问题时间为 2020 年,材料时间包括 2020 年,现期时间;出现
“占比”,为现期比重问题。问“……在……中的占比”,应该是“部分在总体中
的占比”,故“人均教育文化娱乐支出”为部分(A),“人均消费支出”为整体(B),
对应材料找数据,现期比重=A/B=3380/37303,选项首位各不相同,选项差距大,
截两位计算,原式转化为 3380/37≈9%,对应 C项。【选 C】
2021年,中国跨境电商交易规模达 14.2 万亿元,占我国货物进出口总额的
比例为36.3%。其中出口跨境电商交易规模 11万亿元,同比增速 13.4%;进口跨
境电商交易规模3.2 万亿元,同比增速 14.3%。2017—2022年第一季度,中国跨
境电商领域共发生 262次投资,投资总金额 654.91亿元。
【例2】(2023 山东)2021年,我国全年的货物进出口总额约为多少万亿元?
A.36 B.39
C.42 D.45
【解析】2.问题时间和材料时间一致,根据“2021年,中国跨境电商交易规
模达14.2万亿元,占我国货物进出口总额的比例为 36.3%”,占前为部分(A),
占后为总体(B),则 B=A/36.3%=14.2/36.3%,首位接近商4,对应 B 项。【选 B】
【例3】(2023 联考)2021年,我国消费最多的母婴商品金额约为:
A.9638亿元 B.8994 亿元
C.7852亿元 D.4186 亿元
【解析】3.问题时间和材料时间一致,为现期时间;问“消费最多的母婴商
品金额”,可以看占比,占比最大的是服装鞋帽(26%),给出 2021 年的总体为
534591,所求=34591*26%,26%≈1/4,所求≈34591/4=9000-,对应 B 项。【选 B】
2020 年前三季度,G 省智能机器人产业实现营业收入 326.62 亿元,同比增
长超40%,四大行业营业收入均实现正增长,经济效益好于全部规模以上工业企
业。
【例 4】(2021 广东)2020 年前三季度,G 省智能机器人产业的总体利润率
(利润率=利润总额/营业收入)约为:
A.-0.6% B.4.6%
C.9.6% D.14.6%
【解析】4.问题时间与材料时间一致,均为 2020 年前三季度,现期时间;
问“利润率”,利润率=利润总额(A)/营业收入(B),A和B很明确,不用判定,
直接找数据即可。定位文字材料找数据,G 省智能机器人产业实现营业收入
326.62亿元(B);文字材料没有出现“利润总额”,定位表格找数据,分别给出
四大行业的利润总额,加和就是总体的利润总额(A),即-8.61+0.22+40.74-0.9
≈41-9.5=31.5,利润率=A/B≈31.5/326.62=10-%,最接近C项。【选 C】
分领域看,2020 年,软件产品实现收入 22758亿元,同比增长10.1%;其中,
工业软件产品实现收入1974亿元,增长11.2%。信息技术服务实现收入 49868亿
元,比上年同期增加 6579 亿元;其中,电子商务平台技术服务收入 9095 亿元,
同比增长 10.5%;云服务、大数据服务共实现收入 4116 亿元,同比增长 11.1%。
信息安全产品和服务实现收入1540亿元,同比增长10.0%,增速较上年回落 2.4
个百分点。嵌入式系统软件实现收入 7492 亿元,比上年同期增加 803 亿元,增
速较上年提高4.2 个百分点。
【例5】(2023 四川)以下饼图中,最能准确反映 2020年信息技术服务实现
6收入中,电子商务平台技术服务收入(黑色),云服务、大数据服务收入(竖线)
和其他收入(白色)占比关系的是:
A. B.
C. D.
【解析】5.选项为饼形图,给2020年、问2020年,现期比重。总体是信息
技术服务实现收入,电子商务平台是黑色部分(9095亿元),云服务、大数据服
务收入是竖线部分(4116 亿元),其他收入是白色部分。根据数据,已知可知黑
色大于竖线,排除 A、B 项。看 C、D 项的差异,C 项:黑色+竖线<总体的 1/4,
D 项:黑色+竖线>总体的 1/4,总体的 1/4=49868*(1/4)=12000+,黑色+竖线
=9095+4116=13000+,13000+>12000+→黑色+竖线>总体的 1/4,对应 D 项。【选
D】
比重中的饼图问题
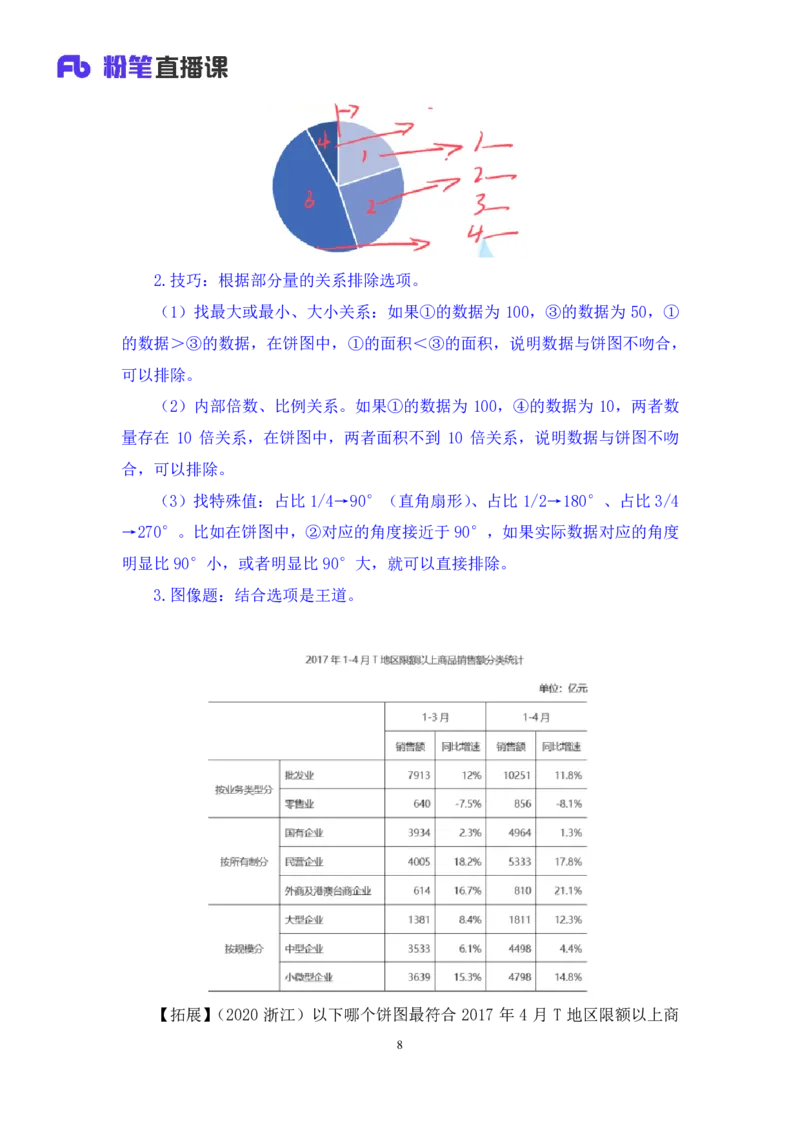
构图原则:12 点钟方向,顺时针旋转依次排布
技巧——分析部分量的关系进行排除:
(1)找最大或最小、大小关系
(2)内部倍数、比例关系
(3)找特殊值(1/4、1/2、3/4)
图像题——结合选项是王道
【注意】比重中的饼图问题:
1.构图原则:以 12 点钟方向为起点,顺时针旋转与图例依次对应。比如题
干是①→②→③→④的顺序,则依次对应如图区域。
72.技巧:根据部分量的关系排除选项。
(1)找最大或最小、大小关系:如果①的数据为 100,③的数据为 50,①
的数据>③的数据,在饼图中,①的面积<③的面积,说明数据与饼图不吻合,
可以排除。
(2)内部倍数、比例关系。如果①的数据为 100,④的数据为 10,两者数
量存在 10 倍关系,在饼图中,两者面积不到 10 倍关系,说明数据与饼图不吻
合,可以排除。
(3)找特殊值:占比1/4→90°(直角扇形)、占比1/2→180°、占比3/4
→270°。比如在饼图中,②对应的角度接近于 90°,如果实际数据对应的角度
明显比90°小,或者明显比 90°大,就可以直接排除。
3.图像题:结合选项是王道。
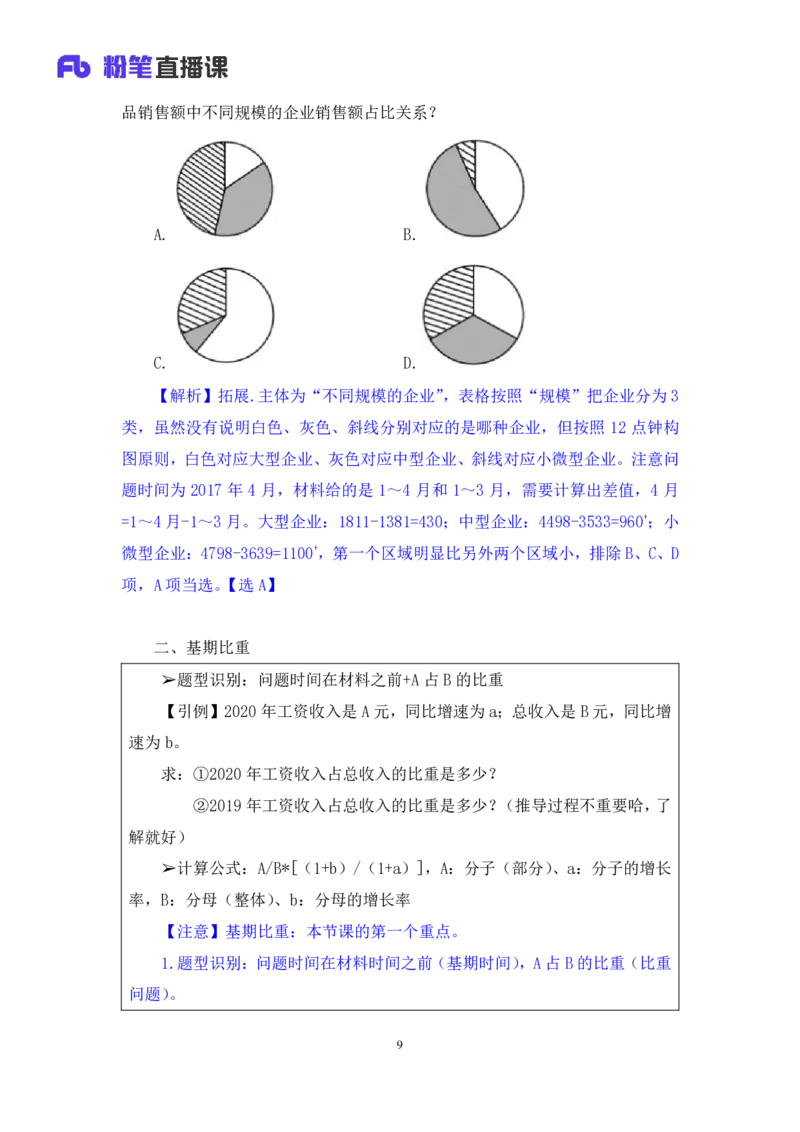
【拓展】(2020 浙江)以下哪个饼图最符合 2017 年 4 月 T 地区限额以上商
8品销售额中不同规模的企业销售额占比关系?
A. B.
C. D.
【解析】拓展.主体为“不同规模的企业”,表格按照“规模”把企业分为 3
类,虽然没有说明白色、灰色、斜线分别对应的是哪种企业,但按照 12 点钟构
图原则,白色对应大型企业、灰色对应中型企业、斜线对应小微型企业。注意问
题时间为 2017 年 4 月,材料给的是 1~4 月和 1~3 月,需要计算出差值,4 月
=1~4月-1~3月。大型企业:1811-1381=430;中型企业:4498-3533=960+;小
微型企业:4798-3639=1100+,第一个区域明显比另外两个区域小,排除B、C、D
项,A项当选。【选 A】
二、基期比重
➢题型识别:问题时间在材料之前+A 占B的比重
【引例】2020 年工资收入是 A元,同比增速为 a;总收入是B 元,同比增
速为b。
求:①2020年工资收入占总收入的比重是多少?
②2019年工资收入占总收入的比重是多少?(推导过程不重要哈,了
解就好)
➢计算公式:A/B*[(1+b)/(1+a)],A:分子(部分)、a:分子的增长
率,B:分母(整体)、b:分母的增长率
【注意】基期比重:本节课的第一个重点。
1.题型识别:问题时间在材料时间之前(基期时间),A占B的比重(比重
问题)。
92.引例:2020 年工资收入是 A元,同比增速为 a;总收入是B 元,同比增
速为b。
(1)2020年工资收入占总收入的比重是多少?
答:问题时间与材料时间一致,均为 2020年,现期时间;出现“占”字,
求现期比重。“占”前为 A,“占”后为B,比重=工资收入/总收入=A/B。
(2)2019年工资收入占总收入的比重是多少?
答:问题时间为 2019年,材料时间为 2020年,基期时间;出现“占”字,
求基期比重。基期比重=2019年A/2019年 B,给出现期量、r,根据“基期量=
现期量/(1+r)”,基期比重=[A/(1+a)]÷[B/(1+b)]=[A/(1+a)]*[(1+b)
/B]=A/B*[(1+b)/(1+a)],除以一个分数等于乘以这个分数的倒数,可以得
到基期比重公式,需要记住公式,推导过程不重要。
3.计算公式:A/B*[(1+b)/(1+a)],A 为分子(部分)、a 为分子的增
长率,B为分母(整体)、b为分母的增长率。记忆方法:“A/B”就是现期比重,
后半部分为“1+增长率”上下颠倒。
基期比重——A/B*[(1+b)/(1+a)]列式练习(只列式,先不考虑计算)
【练习 1】(2016 联考)2013 年 11 月我国货物周转总量中,水运周转量占
比在以下哪个范围?
2018 年 1~10 月份,全国房地产开发投资 99325 亿元,同比增长 9.7%,增
速比 1~9 月份回落 0.2 个百分点。其中,住宅投资 70370 亿元,增长 13.7%,
增速回落0.3个百分点。住宅投资占房地产开发投资的比重为 70.8%。
【练习2】(2019 青海)2017年1~10 月,住宅投资占房地产开发投资的比
重约为:
10【注意】基期比重“A/B*[(1+b)/(1+a)]”的列式练习:
1.练习1:问题时间为 2013年,材料时间为 2014年,基期时间;出现“占”
字,求基期比重。比重=“占”前/“占”后=水运周转量(A、a)/货物周转总量
(B、b),对应表格找数据,所求=8204.1/16409.2*[(1+8.6%)/(1+12.5%)]。
2.练习2:问题时间为 2017年,材料时间为2018年,基期时间;出现“占”
字,求基期比重。比重=“占”前/“占”后=住宅投资(A、a)/房地产开发投资
(B、b),对应材料找数据,所求=70370/99325*[(1+9.7%)/(1+13.7%)],这
个列式虽然是正确的,但不是最好的,注意“(2018年1~10月)住宅投资占房
地产开发投资的比重为 70.8%”,直接给出现期比重 A/B=70.8%,可以直接列式为
“70.8%*[(1+9.7%)/(1+13.7%)]”,两种列式对比,后者又好列、又好算。
速算技巧:
选项差距大:所有数字截两位直除
选项差距小:①计算 A/B(截位直除)
②分析(1+b)/(1+a)与1的大小关系,结合选项确定答案
【注意】速算技巧:
1.选项差距大:所有数字截两位直除,可以结合微调,先约分、再计算。
2.选项差距小:理论上需要截三位计算,截三位不能微调,也不好约分,截
位直除不能方便计算,有新的技巧。
(1)计算A/B(截位直除),注意材料有没有直接给出A/B。
(2)分析(1+b)/(1+a)与 1的大小关系,结合选项确定答案。a、b都是
增长率,常见的增长率都是 10%、20%等,算出来 1+a、1+b 基本都是 1.x,所以
(1+b)/(1+a)的结果要么比 1 大一点、要么比 1 小一点,此时结合选项就能
分析出结果。
(3)例:50%*[(1+5%)/(1+3%)]。
A.51% B.49%
答:(1+5%)/(1+3%)=大数/小数>1,原式=50%*1+>50%,对应 A项。
A/B*[(1+b)/(1+a)]计算练一练
11【练习1】(2019 青海)70.8%*[(1+9.7%)/(1+13.7%)]
A.68.4% B.70.8%
C.72.8% D.73.4%
【练习2】(2017 广东)20%*[(1+7.5%)/(1+9.7%)]
A.16.6% B.19.6%
C.22.6% D.25.6%
【练习3】(2016 联考)8204.1/16409.2*[(1+8.6%)/(1+12.5%)]
A.低于40% B.40%~50%
C.50%~60% D.高于60%
【练习4】(2015 河北)3991/47993*[(1+10.7%)/(1+47.4%)]
A.6.25% B.8.11%
C.8.32% D.10.70%
【注意】速算技巧练习:
1.(2019青海)70.8%*[(1+9.7%)/(1+13.7%)]。
A.68.4% B.70.8%
C.72.8% D.73.4%
答:(1+9.7%)/(1+13.7%)=小数/大数<1,原式=70.8%*1-<70.8%,只有
A项满足,A项当选。
2.(2017广东)20%*[(1+7.5%)/(1+9.7%)]。
A.16.6% B.19.6%
C.22.6% D.25.6%
答:(1+7.5%)/(1+9.7%)=小数/大数<1,原式=20%*1-<20%,排除 C、D
项;(1+7.5%)/(1+9.7%)=1.075/1.097,虽然比 1小,但只比 1小一点,20%*0.8+=A
项,(1+7.5%)/(1+9.7%)=90+%,A项太小,B 项当选。
3.(2016联考)8204.1/16409.2*[(1+8.6%)/(1+12.5%)]。
A.低于40% B.40%~50%
C.50%~60% D.高于60%
答:现期比重=8204.1/16409.2=50%,(1+8.6%)/(1+12.5%)=小数/大数<
1,原式=50%*1-<50%,排除 C、D 项;(1+8.6%)/(1+12.5%)=1.086/1.125,只
12比 1 小一点,50%*0.8-=A 项,1.086/1.125 远远大于 0.8,A 项太小,B 项当选。
4.(2015河北)3991/47993*[(1+10.7%)/(1+47.4%)]。
A.6.25% B.8.11%
C.8.32% D.10.70%
答:现期比重=3991/47993≈4000/48000=1/12≈8.3%,(1+10.7%)/(1+47.4%)
=小数/大数<1,原式=8.3%*1-<8.3%,排除 C、D 项;(1+10.7%)/(1+47.4%)
=1.107/1.474≈1/1.5=2/3,结果比 8.3%小很多,B 项很接近 8.3%,排除 B 项,
A项当选。
2020 年江苏省实现以新产业、新业态、新模式为主要内容的“三新”经济
增加值 25177 亿元,比上年增长 5.6%,比全省地区生产总值的增速快 1.5 个百
分点,占全省地区生产总值的比重为 24.5%。全省战略性新兴产业产值增长 11.0%,
快于规模以上工业 5.5个百分点。其中新能源汽车、数字创意、新能源和高端装
备制造业的产值增速分别为 21.0%、19.8%、15.6%和 15.5%。……全省网上零售
额 10602 亿元,增长 10.0%。其中,实物商品网上零售额增长 13.9%,增速比上
年快5.2个百分点,占社会消费品零售总额 37086亿元的比重为24.9%,提高 2.7
个百分点。
【例 1】(2022 江苏) 2019 年江苏省“三新”经济增加值占全省地区生产
总值的比重是:
A.20.5% B.24.2%
C.27.1% D.30.0%
【解析】1.问题时间在材料时间之前,基期时间;求比重,基期比重问题,
公式:A/B*[(1+b)/(1+a)],定位材料找数据,所求=24.5%*(1+4.1%)/(1+5.6%),
(1+4.1%)/(1+5.6%)和1非常接近,结果接近 24.5%,对应B项。【选B】
2022年,规模以上工业企业中,分行业看:采矿业实现利润总额 15573.6亿
元,同比增长 48.6%;制造业实现利润总额 64150.2 亿元,同比下降 13.4%;电
力、热力、燃气及水生产和供应业实现利润总额 4314.7亿元,同比增长 41.8%。
2022年,在 41个工业大类行业中,利润总额由高到低的前十个行业的利润情况
13如下:……医药制造业实现利润总额 4288.7 亿元,同比下降 31.8%;石油和天
然气开采业实现利润总额 3545亿元,同比增长 109.8%;通用设备制造业实现利
润总额3250.3亿元,同比增长 0.4%;电力、热力生产和供应业实现利润总额 3154
亿元,同比增长86.3%。
【例2】(2023 联考)2021 年,石油和天然气开采业利润总额占采矿业利润
总额的:
A.不足10% B.10%~20%之间
C.20%~30%之间 D.30%以上
【解析】2.问题时间在材料时间之前,基期时间;求比重,基期比重问题,
公式:A/B*[(1+b)/(1+a)],定位材料找数据,所求=(3545/15573.6)*[(1+48.6%)
/(1+109.8%)],选项差距大,直接截位,原式转化为 35/16*15/21≈5/3=1.6,
估算量级,3500+/15000+=25+%,25+%*1.4/2+,结果对应B项。【选B】
基期比重
题型识别:问题时间在材料之前+A占 B的比重
计算公式:A/B*[(1+b)/(1+a)]
A:分子(部分)、a:分子的增长率,B:分母(整体)、b:分母的增长率
速算技巧:
选项差距大:所有数字截两位直除(先约再算)
选项差距小:①计算 A/B(截位直除)
②分析(1+b)/(1+a)与 1的大小关系,结合选项确定答案
*77小提醒:
1.找找材料是否给出现期比重 A/B的值
2.计算A/B:相当于做一步除法,只截分母即可
【注意】基期比重总结:
1.题型识别:问题时间在材料时间之前(基期时间)+A占B的比重(比重问
题)。
2.计算公式:A/B*[(1+b)/(1+a)],记忆“现期比重*(1+r)上下颠倒”。
A为分子(部分)、a为分子的增长率;B为分母(整体)、b为分母的增长率。
143.速算技巧:
(1)选项差距大:直接截位计算。
(2)选项差距小:先计算 A/B(截位直除,如果直接给出A/B,直接用即可),
再分析(1+b)/(1+a)与1的大小关系,结合选项确定答案。
4.注意:
(1)找找材料是否给出现期比重 A/B 的值。
(2)计算A/B:相当于做一步除法,只截分母即可。
三、两期比重
【注意】两期比重:两期指的就是现期和基期。
两期比重比较——升降判断
题型识别:两个时间相比+比重+上升/下降
【识别 1】(2017 联考)2013 年 1~9 月,苏中工业用电量占江苏省工业用
电总量的比重与去年相比:
A.提高 B.降低
C.不变 D.无法判断
【识别 2】(2018 四川下)2018 年 1~3 月出货量占全国手机出货量比重高
于上年水平的有几类?
A.0 B.1
C.2 D.3
比较:现期比重=A/B,基期比重=A/B*[(1+b)/(1+a)]
升降判断:a>b,比重上升;a<b,比重下降;a=b,比重不变。
a:分子(部分量)的增长率
b:分母(整体量)的增长率
比较增长率,需要带符号进行比较
【引例】2020 年总收入 10 万元,同比增长 10%;工资收入 8 万,同比增长
5%。
判断:2020年工资收入占总收入的比重比上年上升(回 1)还是下降(回 2)?
15比重变化判断练习:上升(回 1),下降(回 2),不变(回3)
【注意】两期比重比较:升降判断,不涉及计算。
1.题型识别:两个时间相比+比重+上升/下降。
2.例:
(1)识别 1:(2017联考)2013年1~9月,苏中工业用电量占江苏省工业
用电总量的比重与去年相比:
A.提高 B.降低
C.不变 D.无法判断
答:出现“……占……的比重”,两个时间(2013 年1~9月、去年)+比重
+提高/降低,为两期比重的比较问题。
(2)识别 2:(2018四川下)2018年1~3月出货量占全国手机出货量比重
高于上年水平的有几类?
A.0 B.1
C.2 D.3
答:出现“……占……的比重”,两个时间(2018 年1~3月、上年)+比重
+高于,为两期比重的比较问题。
3.两期比重比较:升降判断。
(1)分析:现期比重>基期比重→A/B>A/B*[(1+b)/(1+a)]→(A/B)
*1>A/B*[(1+b)/(1+a)]→1>(1+b)/(1+a)→1+a>1+b→a>b,比重上
升,二者可以相互推出。
(2)小于、等于也是同样的道理,记住结论即可。
4.升降判断:a 是分子(部分)的增长率,b 是分母(整体)的增长率,带
着符号进行比较。
16(1)a>b,比重上升。
(2)a<b,比重下降。
(3)a=b,比重不变。
5.引例:2020 年总收入 10 万元,同比增长 10%;工资收入 8 万,同比增长
5%。判断:2020年工资收入占总收入的比重比上年上升还是下降?
答:出现“……占……的比重”,两个时间(2020年、上年)+比重+上升/下
降,为两期比重的比较问题,没问计算,找到a、b,比较大小即可。比重=“占”
前/“占”后=工资收入(A、a)/总收入(B、b),工资收入的增长率为 a=5%,总
收入的增长率为b=10%,a<b,比重下降。
6.比重变化判断练习:
(1)a=10%、b=5%:a>b,比重上升。
(2)a=10%、b=-5%:a>b,比重上升。
(3)a=-10%、b=10%:a<b,比重下降。
(4)a=-10%、b=-5%:a<b,比重下降。
(5)a=-15%、b=-35%:a>b,比重上升。
据对全国 6.4 万家规模以上文化及相关产业企业调查,2021 年前三季度,
上述企业实现营业收入84205亿元,按可比口径计算,同比增长21.8%;两年平
均增长10.0%
分行业类别营业收入情况:新闻信息服务 9847 亿元,同比增长 22.1%;内
容创作生产17693 亿元,同比增长18.6%;创意设计服务13787亿元,同比增长
24.0%;文化传播渠道 9309 亿元,同比增长 30.1%;文化投资运营 359 亿元,同
比增长 13.8%;文化娱乐休闲服务 916 亿元,同比增长 35.3%;文化辅助生产和
中介服务11441亿元,同比增长18.3%;文化装备生产4880亿元,同比增长17.8%;
文化消费终端生产 15974亿元,同比增长22.0%。
【例1】(2023 联考)与上一年相比,2021 年前三季度分行业类别中,占全
国6.4万家规模以上文化及相关产业企业营业总收入比重增加的行业个数是:
A.3个 B.4 个
C.5个 D.6 个
17【解析】1.两个时间(上一年、2021年)+“占”字+增加,两期比重比较问
题。“占”前为A,增长率为 a;“占”后为 B,增长率为b,问增加,找 a>b的,
定位材料找数据,b=21.8%,找增长率大于21.8%的有几个,满足的有5个(22.1%、
24.0%、30.1%、35.3%、22.0%),对应C项。【选C】
2018年前三季度,S省社会物流总额35357.26 亿元,同比增长 6.4%,增速
比上半年放缓 0.7 个百分点。其中,工业品物流总额 16636.15 亿元,同比增长
0.2%,增速比上半年放缓 2.1 个百分点;外部流入(含进口)货物物流总额
17357.31亿元,同比增长 12.1%,增速比上半年加快 0.8个百分点;农产品物流
总额 875.06 亿元,同比增长 11.6%,增速比上半年加快 0.5 个百分点;单位与
居民物品物流总额 457.86 亿元,同比增长 40.7%,增速比上半年放缓 3 个百分
点;再生资源物流总额 30.88 亿元,同比下降 7.0%,降幅比上半年扩大 4.3 个
百分点。
【例 2】(2020 国考)在工业品物流、外部流入(含进口)货物物流、农产
品物流、单位与居民物品物流和再生资源物流中,2018 年前三季度物流总额占
社会物流总额的比重高于上年水平的有几类?
A.4 B.3
C.2 D.1
【解析】2.两个时间+比重+高于,两期比重比较问题。找 a>b 的,占前为
部分(A、a),占后为总体(B、b),社会物流总额的增长率 b=6.4%,满足的有3
个(12.1%、11.6%、40.7%),对应B项。【选 B】
比重问法连连看
2020年老师总收入 B元,同比增长率为 b;其中买猫粮花费 A元,同比增长
率为a。
2020年买猫粮花费占总收入的比重?
2019年买猫粮花费占总收入的比重?
2020年买猫粮花费占总收入的比重比上年上升还是下降?
2020 年买猫粮花费占总收入的比重比上年同期上升/下降了多少个百分点?
18【注意】比重问法连连看:2020年老师总收入 B元,同比增长率为 b;其中
买猫粮花费A元,同比增长率为 a。
1.2020年买猫粮花费占总收入的比重?
答:问题时间与材料时间一致,均为 2020 年,现期时间;问“……占……
的比重”,求现期比重,计算“A/B”。
2.2019年买猫粮花费占总收入的比重?
答:问题时间为 2020年,材料时间为 2019年,基期时间;问“……占……
的比重”,求基期比重,计算“A/B*[(1+b)/(1+a)]”。
3.2020年买猫粮花费占总收入的比重比上年上升还是下降?
答:出现“……占……的比重”,两个时间(2020 年、上一年)+比重+上升
/下降,找到a、b,比较大小即可,a>b→比重上升,a<b→比重下降。
4.2020 年买猫粮花费占总收入的比重比上年同期上升/下降了多少个百分
点?
答:出现“……占……的比重”,两个时间(2020 年、上一年)+比重+上升
/下降+百分点,百分点是两个百分数的差值,比重本身就是百分数,两期比重差
=2020 年比重-2019 年比重=A/B-A/B*[(1+b)/(1+a)]=A/B*[1-(1+b)/
(1+a)]=A/B*[(1+a)/(1+a)-(1+b)/(1+a)]=A/B*[(a-b)/(1+a)],
可以得到两期比重差公式。
两期比重计算——上升/下降几个百分点
题型识别:两个时间相比+比重+上升/下降几个百分点
计算公式:两期比重差=A/B-A/B*[(1+b)/(1+a)]=A/B*[(a-b)/(1+a)]
解题技巧:第一步,判升降(a>b,上升;a<b,下降)
第二步,定大小:绝对值一般小于|a-b|
a:分子(部分量)的增长率 b:分母(整体量)的增长率
【识别】2015 年一季度,该省园区企业上缴税金占主营业务收入的比重比
上年同期:
A.上升了0.1 个百分点 B.上升了3.1个百分点
C.下降了0.1 个百分点 D.下降了3.1个百分点
19推导过程其实不重要,重点还是记结论:判升降,定大小(一般小于|a-b|)
比重升降几个百分点=现期比重- 基期比重
A/B*[(a-b)/(1+a)]=A/B*[1/(1+a)]*(a-b)
因为 A/B(比重)<1,而且 1/(1+a)(a>0)<1,所以|A/B*[(a-b)/
(1+a)]|<|a-b|
【注意】两期比重计算——上升/下降几个百分点:
1.题型识别:两个时间相比+比重+上升/下降几个百分点。
2.计算公式:两期比重差=A/B*[(a-b)/(1+a)]。
3.解题技巧:a是分子(部分)的增长率,b是分母(整体)的增长率。
(1)第一步:判升降,a>b,上升;a<b,下降。
(2)第二步:定大小,绝对值一般小于|a-b|。
4.例:2015 年一季度,该省园区企业上缴税金占主营业务收入的比重比上
年同期:
A.上升了0.1 个百分点 B.下降了0.1个百分点
C.上升了3.1 个百分点 D.下降了3.1个百分点
答:出现“……占……的比重”,两个时间(2015 年一季度、上年同期)+比
重+上升/下降+百分点,求两期比重差。如果 a=14.1%、b=11.0%,判升降,a>b,
比重上升,排除 B、D 项;定大小,比重差<|a-b|=|14.1%-11.0%|=3.1%,只有
C项满足,C项当选。
5.原理:推导过程其实不重要,重点还是记住结论:判升降、定大小(一般
小于|a-b|)。两期比重差=现期比重- 基期比重=A/B*[(a-b)/(1+a)]=A/B*[1/
(1+a)]*(a-b)。A/B=现期比重=部分/整体,一定小于1,故A/B=1-。
(1)若a>0,则 1+a>1,故1/(1+a)=1-,原式=1-*1-*(a-b),数值一定
会变小,比如1-*5%=5-%,1-*(-5%)=-5-%,比重差<|a-b|。
(2)若a<0,这种情况不是很多,而且资料分析用的都是真实数据,即使
a 是负的,也是下降得比较少,则 1+a 只会比 1 小一点,故 1/(1+a)也只是比
1大一点;现期比重(A/B)通常比1小很多,故 A/B*[1/(1+a)]基本上都比 1
小,比重差<|a-b|。
20五年来,我国积极推进网络强国和数字中国建设,着力深化数字经济与实体
经济融合,为打造数字经济新优势、增强经济发展新动能提供有力支撑。2022年,
我国电信业务收入累计完成 1.58万亿元,比上年增长 8%,较 2018年增长超 2800
亿元。
2022年移动数据流量业务收入 6397亿元,比上年增长 0.3%,在电信业务收
入中占比约为40.5%。数据中心、云计算、大数据、物联网等新兴业务快速发展,
对我国电信业务拉动作用持续增强。2022年新兴业务收入达 3072亿元,在电信
业务收入中占比由上年的 16.1%提升至 19.4%。其中,数据中心、云计算、大数
据、物联网业务比上年分别增长 11.5%、118.2%、58%和24.7%。
【例 3】(2023 广东)与 2021 年相比,2022 年我国移动数据流量业务收入
在电信业务收入中的占比( )。
A.增加了约3 个百分点 B.减少了约3个百分点
C.增加了约13 个百分点 D.减少了约13个百分点
【解析】3.两个时间(2021 年、2022 年)+比重(占比)+增加/减少+百分
点,是两期比重计算问题。比重=移动数据流量业务收入(A、a)/电信业务收入
(B、b),已知移动数据流量业务收入增长率 a=0.3%、电信业务收入增长率 b=8%,
a<b,占比减少,排除 A、C项;结果<|a-b|=|0.3%-8%|=7.7%,选择 B 项。【选
B】
2015 年 3 月末,国有企业资产总额 1054875.4 亿元,所有者权益合计
369109.1 亿元,同比增长 12.2%,其中,中央企业资产总额 554658.3 亿元,所
有者权益为191354.4 亿元,同比增长10.7%。
【拓展】(2016 浙江)2015年 3月末,中央企业所有者权益占国有企业总体
比重比上年同期约:
A.下降了0.7 个百分点 B.下降了1.5个百分点
C.上升了0.7 个百分点 D.上升了1.5个百分点
【解析】拓展.出现“……占……的比重”,两个时间(2015年 3月末、上年
同期)+比重+上升/下降+百分点,为两期比重的计算问题。(1)判升降:比重=
“占”前/“占”后=中央企业所有者权益(A、a)/国有企业总体所有者权益(B、
21b),对应材料找数据,中央企业所有者权益的增长率为a=10.7%,国有企业总体
所有者权益的增长率为 b=12.2%,a<b,比重下降,排除 C、D项。(2)定大小:
比重差<|a-b|=|10.7%-12.2%|=1.5%,下降了不到 1.5 个百分点,排除 B 项,A
项当选。【选A】
两期比重计算——上升/下降几个百分点
题型识别:两个时间相比+比重+上升/下降几个百分点
计算公式:两期比重差=A/B*[(a-b)/(1+a)]
解题步骤:①判升降(a>b,上升;a<b,下降)
②定大小:绝对值一般小于|a-b|
a:分子的增长率 b:分母的增长率
注:1.若a>0,且选项中只有一个小于|a-b|,直接选即可。
2.若选项中有多个小于|a-b|或a<0,代入公式分析、计算
2020 年 1~2 月,我国境内投资者共对全球 147 个国家和地区的 1733 家境
外企业进行了非金融类直接投资,累计实现投资 1078.6 亿元人民币,同比增长
1.8%。对外投资主要流向租赁和商务服务业、批发和零售业、制造业和采矿业等
传统投资领域,占对境外企业非金融类直接投资的比重分别为 40.8%、15.1%、
11.3%和 8.9%。其中流向租赁和商务服务业的投资额同比增长 43.2%,成为增速
最高的领域。
【例 4】(2021 国考)2020 年 1~2 月,租赁和商务服务业对外投资额占对
境外企业非金融类直接投资额的比重比上年同期约:
A.上升了3个百分点 B.上升了12个百分点
C.下降了3个百分点 D.下降了12个百分点
【解析】4.出现“……占……的比重”,两个时间+比重+上升/下降+百分点,
为两期比重的计算问题。(1)判升降:比重=“占”前/“占”后=租赁和上午服
务业对外投资额(A、a)/对境外企业非金融类直接投资额(B、b),对应材料找
数据,a=43.2%,b=1.8%,a>b,比重下降,排除 C、D项。(2)定大小:比重差
<|a-b|=|43.2%-1.8%|=41.4%,A、B项都满足,无法排除;代入公式估算,现期
22比重 A/B=40.8%,所求=40.8%*41.4%/(1+43.2%)≈0.16/1.4=0.1+,对应 B 项。
【选B】
两期比重计算——上升/下降几个百分点
题型识别:两个时间相比+比重+上升/下降几个百分点
计算公式:两期比重差=A/B*[(a-b)/(1+a)]
解题步骤:①判升降(a>b,上升;a<b,下降)
②定大小:绝对值一般小于|a-b|
a:分子的增长率 b:分母的增长率
注:1.若a>0,且选项中只有一个小于|a-b|,直接选即可。
2.若选项中有多个小于|a-b|或a<0,代入公式分析、计算
【注意】两期比重计算总结:
1.题型识别:两个时间相比+比重+上升/下降几个百分点
2.解题步骤:
(1)判升降:a>b,比重上升;a<b,比重下降。
(2)定大小:绝对值一般小于|a-b|。
(3)能选直接选,选不出来再套公式,即“A/B*[(a-b)/(1+a)]”,一般
不用计算,大致分析即可。
比重总结
A占B→A/B→看时间:
现在时间→现期比重→直接除
过去时间→基期比重→A/B*[(1+b)/(1+a)]→①根据选项差距,截位直
除计算“A/B”
②分析“(1+b)/(1+a)”与1的大小关系,结合选项选择
与上年比较→单纯比较→A(增速a)/B(增速 b)→a>b,上升;a<b,下
降→还要计算→①判升降,②定大小代入公式(一般小于|a-b|)
【注意】比重总结:
1.题型识别:出现“占”字,结合时间,判断具体题型。
232.现期比重:计算“A/B”,饼图按照12点钟构图原则进行排除。
3.基期比重:计算“A/B*[(1+b)/(1+a)]”,记清楚公式,直接代入公式,
不能在考试时推导,注意材料是否直接给出“A/B”,直接给则直接用,没给则代
入公式。
4.两期比重:
(1)比重:找到 a、b,比较大小即可。
(2)计算:判升降、定大小(一般<|a-b|),能选直接选,选不出来再套
公式,即“A/B*[(a-b)/(1+a)]”,一般不用计算,大致分析即可。
第六节 平均数
【注意】比重和平均数有很多相似之处(包括公式和技巧),但也会有些差
异。在学习过程中要注意不同之处,重点记忆不同之处,其次要区分相同之处,
相同的公式和技巧可以合并记忆。基本上到后半节课的后半段,会有同学比较懵,
知识点混乱,但无论是什么状态,都要坚持到最后,结课之前老师会对两个知识
点进行梳理区分。
基本术语
现期平均数
基期平均数
两期平均数的比较与计算
【注意】平均数——基本术语:了解基本术语和基础概念。
平均数指多个数的平均值,即多个数的总和(A)/数的个数(B)
题型识别:均、每、单位。
AB区分:
人均收入=收入/人数。
单位面积产量=产量/面积。
平均每人次客运旅客运输距离=运输距离/人次。
其他区分技巧:
24单位:
例——售价:元/平方米。
常识:
谁是1谁就是分母。
【注意】平均数:平均数指多个数的平均值,多个数的总和(A)/个数(B)。
1.题型识别:均、每、单位。出现关键字要会识别。
2.A、B区分:平均数=后/前。后对应分子 A,前对应分母B。
(1)人均收入=收入/人数。有两个词,“人”和“收入”,用后面的词除
以前面的词。靠后的收入为 A,靠前的人数为 B。
(2)单位面积产量=产量/面积。靠后的产量为A,靠前的面积为B。
(3)平均每人次客运旅客运输距离=运输距离/人次。运输距离靠后为 A,人
次靠前为B。
3.其他区分技巧:有些题目没有明确的给出“后/前”。
(1)从单位入手:比如售价的单位是“元/平方米”。“元”即钱数(A),
“平方米”即面积(B)。
(2)常识:最本质的方法,谁是“1”谁就是分母。用这种方法永远不会识
别错误。平均数就是把总数分到多少份,所求为每一份是多少,谁是 1份,谁就
是分母。比如人均收入即每一个人的收入,则人数为分母 B;单位面积产量即 1
份面积对应的产量,面积为分母 B;平均每人次客运旅客运输距离即每个人次的
距离,人次为分母 B。
平均数
1.现期平均数
2.基期平均数
3.两期平均数的比较与计算
现期平均数
识别:问题时间与材料时间一致+平均(均/每/单位)。
题型:1.已知多个数的总和:平均数=总数(A)/个数(B)。
25速算:截位直除。
【注意】现期平均数:将时间与平均数问题分开识别。
1.识别:问题时间与材料时间一致+平均(均/每/单位)。
2.题型:已知总和,平均数=总数(A)/个数(B)。
3.速算:截位直除。
2021 年 H 省共有电子商务平台 87 个,在本省电商平台上实现交易金额为
5354.93亿元,同比增长 41.0%,收取的平台交易服务费为 3.17亿元,同比增长
49.5%。从地区分布来看,2021年本地电子商务平台拥有量最多的为 Z市,有 44
个平台,实现交易金额 4239.04亿元。
【例 1】(2023 国考)2021 年,H 省除 Z 市外其他地区的电子商务平台平均
每个平台实现的交易金额约为多少亿元?
A.5 B.12
C.26 D.62
【解析】1.出现“平均”,平均数问题。平均数=后(金额)/前(个数),对
应材料找数据,所求=A/B=(5354.93-4239.04)/(87-44)=1106/43=2+,对应A
项。【选A】
2021年上半年,湖北省 676家规上信息软件业企业中营业收入前 20的企业
共实现营业收入355.46 亿元,同比增长 8.3%,拉动规上服务业营业收入增长 1.1
个百分点。
【例2】(2022 湖北选调)2021年上半年湖北省规上信息软件业中营业收入
前20的企业,平均每家每月营业收入约为多少亿元?
A.1.18 B.2.25
C.2.32 D.2.96
【解析】2.问题时间 2021年上半年,与材料时间一致,现期时间,出现“平
均每”,为平均数问题。“每家”→每 1家,家数是分母 B,“每月”→每 1个月,
月数也是分母 B,故家数和月数均为分母 B,营业收入为分子 A,所求为营业收
入/(家数*月数)。对应材料找数据,A=355.46 亿元,“前20的企业”,家数=20
26家。若认为是12个月就掉坑了,因为问题时间为 2021年上半年,共 6个月。所
求=355.46/(20*6)=360-/120=3-,对应D 项。【选D】
现期平均数
识别:问题时间与材料时间一致+平均(均/每/单位)。
题型:2.分别给多个数,求平均数。
【引例】小狗今天吃了 5 次猫粮,求每次吃猫粮的平均值:7g、10g、12g、
8g、18g。
速算:削峰填谷
第一步:划定基准,找峰找谷
基准:找一个接近平均值、相对好算的数
第二步:计算,用峰填谷
平均数=基准+剩余的和/n
【注意】现期平均数:
1.识别:问题时间与材料时间一致+平均(均/每/单位)。
2.题型:分别给多个数,求平均数。
3.速算:削峰填谷。
(1)第一步:划定基准,找峰找谷。基准值没有严格意义上的标准,找一
个接近平均值、相对好算的数,一般会找偏整数的数字作为基准值。
(2)第二步:计算,用峰填谷。平均数=基准+剩余的和/n。
4.引例:小狗今天吃了 5 次猫粮,求每次吃猫粮的平均值:7g、10g、12g、
8g、18g。
答:找平均值,数值均在 10 左右,假设基准值为 10,峰谷分别为-3、0、
+2、-2、+8,峰谷互填,-3+0+2-2+8=+5,即实际值比假设的值一共多5,平摊到
每一次,平均数=基准+剩余的和/n=10+5/5=11。
27【拓展1】(2017 联考)表二中的各营销事件美誉度平均得分约为:
A.89.85 B.88.6
C.86.7 D.83.3
【解析】拓展 1.求平均分,总共 10个数,求平均值,考虑削峰填谷。假设
基准值为 90(可以找基准值为 88,但一般取比较好算的数字为基准值),则峰
谷为-1、-3、-2、+1、-2、0、0、-1、-2、-4,峰谷互填,抵消之后还剩-7-7=-
14,10 个数字一共为-14,则平均数=90+(-14)/10=90-1.4=88.6,对应 B 项。
【选B】
【拓展2】(2017 广东)2015~2016年,平均每季度大约有多少企业认为自
身综合经营状况良好或稳定?
A.77.2% B.78.3%
C.79.6% D.82.8%
【解析】拓展 2.求2015~2016 年所有数据的平均值,材料数据从 2014年4
28季度开始,2014 年 4 季度的数据不需要看,所求为后面八个季度的平均值,观
察到图像中有横线作为标准,找比较居中的 78%作为基准值,峰谷为+1.5%、-0.8%、
+0.2%、-1.8%、-0.1%、-1.5%、+3.1%、+1.5%,峰谷互填,还剩下 4.7%-2.6%=2.1%,
8 个数共正 2.1%,平均数=78%+2.1%/8=78%+0.25+%=78.25+%,最接近 B 项。【选
B】
想不想算得更快?
*77敲黑板:速算的灵魂——选项为王!
【注意】
1.资料分析要想做得快,要记住“选项为王”。削峰填谷如果结合选项,计
算速度会更快。
2.结合选项分析拓展 1:表格中最大的数字是 91,最小的数字是 86,观察
选项,可以排除D项(最小的数是 86,因此平均数不可能是 83),题目中只有一
个86,其他的数据都在 86以上,故平均数不可能是 86.7,排除C项。除了 A项
以外的选项,其余数据均是小数点后 1 位,只有 A 项是小数点后 2 位。已知 10
个数字之和为整数,整数/10 只能计算到小数点后 1 位,排除 A 项,选择 B 项。
3.结合选项分析拓展 2:最大的数字是 81.1%,最小的数字是 76.2%,排除 D
项。只有 1 个数据大于 79.6%,排除 C 项。只有两个数据比 77.2%小,且存在一
个比77.1%大很多的数(81.1%),说明峰远大于谷,排除 A项,选择 B项。
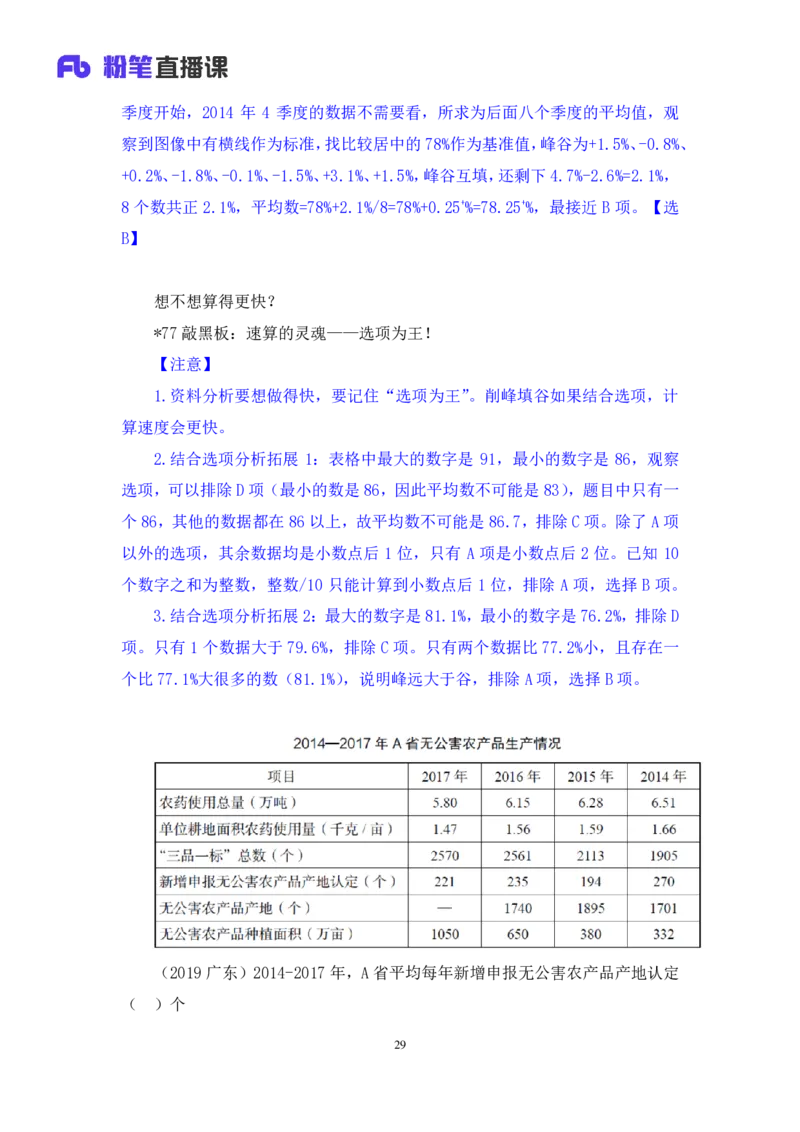
(2019广东)2014-2017年,A省平均每年新增申报无公害农产品产地认定
( )个
29A.184 B.202
C.221 D.230
【解析】拓展 3.出现“平均每年”,平均数问题。最小的是 194,平均数不
可能是 184、202,排除 A、B 项;以 221 为基准值,235 多了 14,194 少了 27,
270多了49,峰>谷,填不平,排除 C项,对应 D项。【选D】
【拓展 4】(2024 国考)2017—2022 年,全国移动数据流量 业务收入总额
在以下哪个范围内?
A.不到3.4万亿元 B.超过3.6万亿元
C.3.4万亿—3.5 万亿元之间 D.3.5 万亿—3.6万亿元之间
【解析】拓展 4.2017 年~2022 年一共 6 年,B 项总额超过 3.6 万亿元,说
明平均每年超过6000 亿元,结合表格数据,峰>谷,明显超过 6000,对应 B项。
【选B】
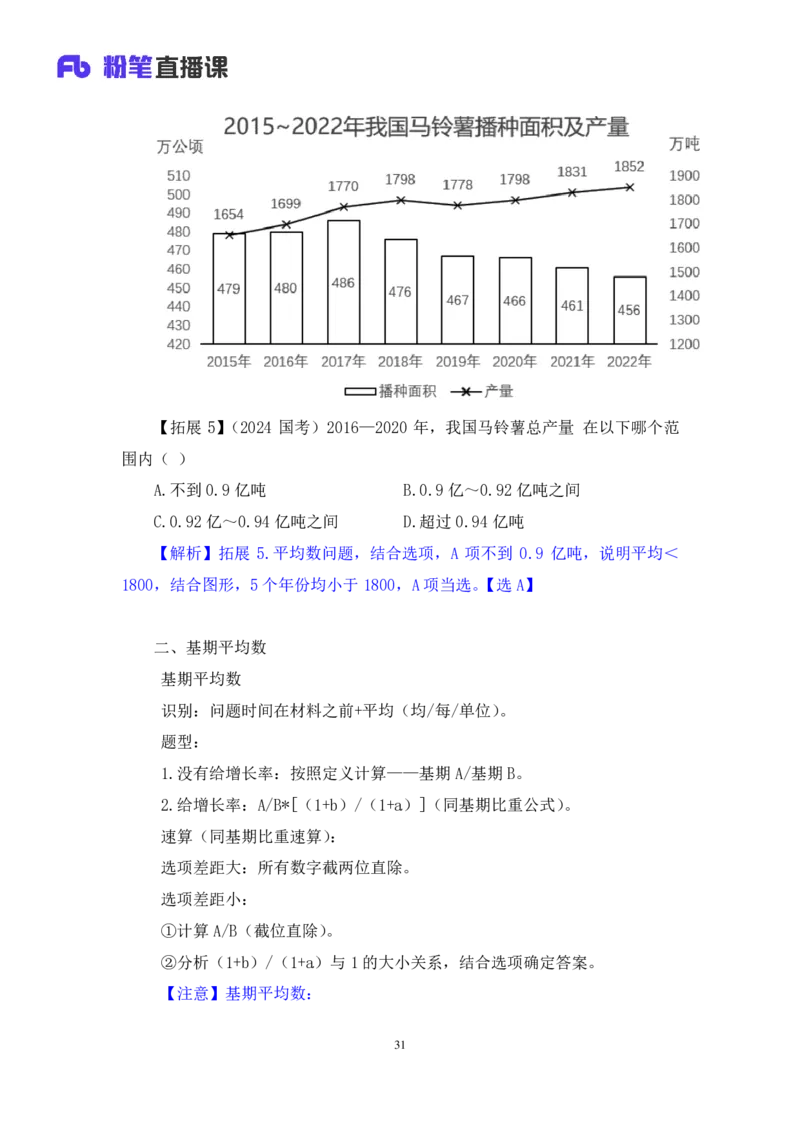
30【拓展 5】(2024 国考)2016—2020 年,我国马铃薯总产量 在以下哪个范
围内( )
A.不到0.9亿吨 B.0.9 亿~0.92亿吨之间
C.0.92亿~0.94 亿吨之间 D.超过0.94亿吨
【解析】拓展 5.平均数问题,结合选项,A 项不到 0.9 亿吨,说明平均<
1800,结合图形,5个年份均小于1800,A 项当选。【选 A】
二、基期平均数
基期平均数
识别:问题时间在材料之前+平均(均/每/单位)。
题型:
1.没有给增长率:按照定义计算——基期A/基期B。
2.给增长率:A/B*[(1+b)/(1+a)](同基期比重公式)。
速算(同基期比重速算):
选项差距大:所有数字截两位直除。
选项差距小:
①计算A/B(截位直除)。
②分析(1+b)/(1+a)与1的大小关系,结合选项确定答案。
【注意】基期平均数:
311.识别:问题时间在材料之前+平均(均/每/单位)。基期时间+平均数问
法→基期平均数。
2.题型:
(1)没有给增长率:按照定义计算,基期 A/基期 B→[A/(1+a)]÷[B/
(1+b)]→A/B*[(1+b)/(1+a)]。
(2)给增长率:A/B*[(1+b)/(1+a)](同基期比重公式)。
3.速算(同基期比重速算):
(1)选项差距大:所有数字截两位直除。
(2)选项差距小:
①计算A/B(截位直除)。
②分析(1+b)/(1+a)与1的大小关系,结合选项确定答案。
2020年1—6月,全国电池制造业主要产品中,锂离子电池产量 71.5亿只,
同比增长1.3%;铅酸蓄电池产量 9635.6万千伏安时,同比增长 6.1%;原电池及
原电池组(非扣式)产量 178.2亿只,同比下降 0.7%。
【例3】(2022 国考)2019 年上半年,全国铅酸蓄电池月均产量约为多少亿
千伏安时?
A.0.13 B.0.14
C.0.15 D.0.16
【解析】3.问题时间在材料时间之前,求月均产量,产量为 A,月份数为 B,
上半年有6个月,基期 A/B=9635.6/(1+6.1%)÷6=1606/1.06,选项差距小,精
确计算,结果为15 开头,对应C项。【选C】
2017年全国共有各级各类民办学校17.76万所,占全国学校总数的34.57%;
各类民办教育在校生达 5120.47 万人,比上年增长 6.12%。其中:民办幼儿园
16.04 万所,比上年增长 4.00%;在园儿童 2572.34 万人,比上年增长 5.53%。
民办普通小学 6107 所,比上年增长 2.21%;在校生 814.17 万人,比上年增长
7.65%。民办初中 5277 所,比上年增长 3.78%;在校生 577.68 万人,比上年增
长 8.42%。民办普通高中 3002 所,比上年增长 7.71%;在校生 306.26 万人,比
32上年增长9.74%。民办中等职业学校 2069 所,比上年下降 2.17%;在校生 197.33
万人,比上年增长 7.16%。
【例 4】(2020 北京)2016 年平均每所民办中等职业学校在校生人数约为:
A.871人 B.991 人
C.1091人 D.1181 人
【解析】4.平均数问题,民办中等职业学校对应 B、b,在校生人数对应 A、
a,定位材料找数据,套公式:197.33/2069*(1-2.17%)/(1+7.16%),先算前面
部分,转化为197.33/207=95 开头,(1-2.17%)/(1+7.16%)<1,所求=95*1-,
结合选项,只有A 项符合。【选A】
三、两期平均数
两期平均数比较——升降判断
题型识别:两个时间相比+平均数+升降
升降判断:
(1)a>b,平均数上升;
(2)a<b,平均数下降;
(3)a=b,平均数不变。
a:分子(总数 A)的增长率
b:分母(份数 B)的增长率
【注意】两期平均数比较——升降判断:
1.题型识别:两个时间相比+平均数+升降。
2.升降判断:比较 A/B和A/B*[(1+b)/(1+a)]的大小关系,与两期比重
比较一样,比较过程中需要带符号。
(1)a>b,平均数上升。
(2)a<b,平均数下降。
(3)a=b,平均数不变。
(4)a:分子(总数 A)的增长率;b:分母(份数 B)的增长率。
2021年上半年,我国进口集成电路 3123 亿块,同比增长 28.4%;进口额 1979
33亿美元,增长 28.3%。出口集成电路 1514 亿块,增长 34.5%;出口额 664 亿美
元,增长32.0%。
【例1】(2022 江苏)能够从上述资料中推出的是:
A.略
B.略
C.2021年上半年,我国集成电路出口平均价格同比有所提高
D.略
【解析】1.问题时间与材料时间一致,同比→与上年相比,两个时间+平均
价格+有所提高,两期平均数比较问题。提高→a>b,“出口平均价格”→钱数(出
口增长率)对应A、a,平均出口每 1个东西,因此出口数量对应B、b,a=32.0%
<b=34.5%,说法错误。【不选】
2017 年,S 市服务业小微样本企业总体实现营业收入 105.39 亿元,同比增
长 3.1%,比 2016 年回落了 15.7 个百分点,户均实现营业收入 510.63 万元。
2017 年,S 市服务业小微样本企业总体营业税金及附加为 1.09 亿元,同比下降
29.5%;缴纳增值税 2.30亿元,同比增长 11.6%,户均缴纳增值税 11.16万元。
【例2】(2020 四川)能够从上述资料中推出的是:
A.略
B.略
C.略
D.2017年,S市服务业小微样本企业平均每万元营业收入缴纳营业税金及附
加高于上年水平
【解析】2.出现“平均每”,平均数问题;高于上年即 a>b,营业收入为 B、
b,缴纳营业税金及附加为 A、a。定位材料找数据,a=-29.5%<b=3.1%,为低于,
说法错误。【不选】
平均数问法连连看
2021年戚七家拥有 B只小猫咪,同比增长率为 b。吃掉了 A个罐头,同比增
长率为a。
342021年和2020 年平均每只猫吃掉了多少个罐头?
2021年平均每只猫吃掉的罐头数同比增长了( )个?
2021年平均每只猫吃掉的罐头数同比增长了( )%?
【注意】平均数问法连连看:2021 年戚七家拥有 B 只小猫咪,同比增长率
为b。吃掉了A个罐头,同比增长率为 a。
1.2021年和2020 年平均每只猫吃掉了多少个罐头?
答:若问2021 年为现期平均数,“平均每只猫吃掉了多少个罐头”→“每 1
只猫吃掉的罐头”,平均数=罐头(A)/猫(B),2021年是现期时间→A/B,2020
年是基期时间→A/B*[(1+b)/(1+a)]。
2.2021年平均每只猫吃掉的罐头数同比增长了( )个?
答:增长了( )个,增长+单位→增长量,平均每→平均数问题,本题为
平均数增长量问题,增长量=现期- 基期。所求=现期平均数- 基期平均数=A/B-
A/B*[(1+b)/(1+a)],同两期比重差公式推导,整理后的公式为 A/B*[(a-b)
/(1+a)],平均数的增长量,与两期比重差的公式是一样的。
3.2021年平均每只猫吃掉的罐头数同比增长了( )%?
答:增长+%→增长率,r=增长量/基期量,平均数的 r=平均数的增长量/平均
数的基期量,平均数的增长量=A/B*[(a-b)/(1+a)],平均数的基期量=A/B*[(1+b)
/(1+a)],平均数的 r={A/B*[(a-b)/(1+a)]}÷{A/B*[(1+b)/(1+a)]}=
(a-b)/(1+b)→平均数的增长率。
平均数的增长率
识别:平均/每/单位+增长+%
公式:平均数增长率 r=(a-b)/(1+b)(a是分子的增长率,b 是分母的增
长率)
做题逻辑:
①确定分子、分母(谁÷谁)
②代入公式:r=(a-b)/(1+b)
【注意】平均数的增长率:
1.识别:平均/每/单位+增长+%。
352.公式:平均数增长率 r=(a-b)/(1+b)(a是分子的增长率,b是分母的
增长率)。
(1)现期平均数、基期平均数、平均数的增长量,三个都是量,公式都和
A、B 有关,但是平均数增长率的公式与现期的 A、B 无关,只与增长率 a、b 有
关。
(2)基期平均数=A/B*[(1+b)/(1+a)]、平均数增长量=A/B*[(a-b)/
(1+a)],公式中的分母都是(1+a),只有平均数增长率公式的分母为(1+b),
是唯一一个分母为(1+b)的公式。
3.做题逻辑:平均数问题,谁是 1谁是分母 B。
(1)确定分子、分母(谁/谁),找到 A、B,A对应的增长率为 a,B对应的
增长率为b。
(2)代入公式:r=(a-b)/(1+b)。
2018年前三季度,S省社会物流总额35357.26 亿元,同比增长 6.4%,增速
比上半年放缓 0.7 个百分点。其中,工业品物流总额 16636.15 亿元,同比增长
0.2%,增速比上半年放缓 2.1 个百分点;外部流入(含进口)货物物流总额
17357.31亿元,同比增长 12.1%,增速比上半年加快 0.8个百分点;农产品物流
总额 875.06 亿元,同比增长 11.6%,增速比上半年加快 0.5 个百分点;单位与
居民物品物流总额 457.86 亿元,同比增长 40.7%,增速比上半年放缓 3 个百分
点;再生资源物流总额 30.88 亿元,同比下降 7.0%,降幅比上半年扩大 4.3 个
百分点。
2018年前三季度,S省社会物流总费用 2682.1亿元,同比增长 6.3%,比上
半年放缓0.9个百分点。其中:物流运输环节总费用1854.6亿元,同比增长6.3%;
保管环节总费用 612.4 亿元,同比增长 6.4%;管理环节总费用 214.9 亿元,同
比增长6.4%。
【例3】(2020 国考)2018 年前三季度,平均每万元社会物流总额产生的物
流费用比上年同期:
A.上升了不到 1% B.上升了1%以上
C.下降了不到 1% D.下降了1%以上
36【解析】3.问题时间为 2018 年前三季度,平均每+比上年同期+上升/下降+%,
平均数增长率问题,公式:r=(a-b)/(1+b)。“平均每 1 万元社会物流总额产
生的物流费用”,谁是 1谁是分母B,物流费用为 A,物流总额B,物流费用增长
率对应 a,物流总额增长率对应 b。结合材料找数据,a=6.3%,b=6.4%,代入公
式:r=(a-b)/(1+b)=(6.3%-6.4%)/(1+6.4%)=-0.1%/1.06<0,负号代表
下降,排除A、B项;0.1%/1.06<0.1%,下降不到 1%,对应C项。【选 C】
平均数总结
均、每、单位 XX→A/B→看时间:
现在时间→现期平均数→直接除,注意“月均”、“日均”
过去时间→基期平均数→A/B*[(1+b)/(1+a)]。
①根据选项差距,截位直除计算“A/B”
②根据“(1+b)/(1+a)”与1的大小关系,结合选项选择
与上年比较→单纯比较→A/B,A→增速 a、B→增速 b,a>b,上升;a<b,
下降
→还要计算→代入公式:
增长率:r=(a-b)/(1+b)(考查较多)
增长量:A/B*[(a-b)/(1+a)]
【注意】平均数总结:均、每、单位 XX→A/B(谁是1谁是分母)→看时间。
1.现在时间→现期平均数→直接除(或削峰填谷),注意“月均”、“日均”。
2.过去时间→基期平均数→A/B*[(1+b)/(1+a)]。
(1)根据选项差距,截位直除计算“A/B”。
(2)分析“(1+b)/(1+a)”与1的大小关系,结合选项选择。
3.与上年比较:
(1)单纯比较:A/B,A→增速a、B→增速 b。a>b,上升;a<b,下降。
(2)还要计算:代入公式。
①增长率(平均数+升/降+%):r=(a-b)/(1+b)。
②增长量(平均数+升/降+单位):A/B*[(a-b)/(1+a)]。
37【注意】比例小结:
1.识别:
(1)比重:“占”字。“占”前/“占”后=A/B。
(2)平均数:均、每、单。谁是 1份谁是分母 B。
2.现期比重和平均数的公式:A/B。可以记忆为现期比例问题。
3.基期:A/B*[(1+b)/(1+a)],基期比例问题公式也是一样的。
4.两期:
(1)比较:比较的是 a、b。比例为 a/b,分子上升的越快,分数值越大,
分母上升的越快,分数值越小。
①比重:a>b,比重上升;a<b,比重下降;a=b,比重不变。
②平均数:a>b,平均数上升;a<b,平均数下降;a=b,平均数不变。
(2)计算:
①两期比重差:第一步,判升降;第二步,定大小,结果<|a-b|,或者代
入公式计算。公式:A/B*[(a-b)/(1+a)]。
②平均数:平均数增长量=A/B*[(a-b)/(1+a)];平均数增长率=(a-b)
/(1+b)。
5.比重差=现期比重- 基期比重,可以理解为比重的增长量;平均数增长量
=现期平均数- 基期平均数。二者的公式是一样的。
38注:A现期分子,B现期分母;a分子增长率,b分母增长率
【注意】两期比重差和平均数增长量的和公式通用,但技巧不通用。在比重
差中,A/B的结果一定小于 1,因此差值<|a-b|。但平均数的增长量中,平均数
A/B 不一定小于 1,因此不能用这个结论。判升降定大小,只适用于两期比重差
的计算。
【注意】重点区分两期比例部分:
1.题型区分:先通过关键字,判定题目是比重问题(占、率)还是平均数问
题(均、每、单位)。
2.如果是比重问题,只有一种考法,即两期比重差,即使选项中有百分号(属
于出题不严谨),也属于两期比重差问题。可以用技巧,判升降、定大小,技巧
无法解出答案就代公式。
3.如果是平均数问题,有两种情况:升/降+单位→平均数的增长量、升/降
+%→平均数的增长率。
39专项巩固——题型识别
1.(2020山东)2017年J省海洋生产总值占全国的比重比上年( )百分
点。
A.上升了约0.2 个 B.上升了约2个
C.下降了约0.2 个 D.下降了约2个
2.(2019 北京)2016 年全社会餐饮业平均每个经营单位的从业人数比上年
约:
A.减少了2% B.减少了15%
C.增加了2% D.增加了15%
3.(2017四川下)2014年铁路旅客平均每人次周转距离比 2013 年多约( )
公里?
A.15 B.25
C.34 D.44
4.(2017 四川下)2015 年,纺织行业规模以上企业主营业务利润率(利润
总额/主营业务收入)比上年约:
A.上升0.02个百分点 B.上升0.4个百分点
C.下降0.02个百分点 D.下降0.4个百分点
5.(2018 辽宁)2018 年全国谷物总产量占全国粮食总产量的比重,较上一
年约:
A.增长了0.19% B.减少了0.19%
C.增长了 0.26% D.减少了0.26%
【注意】专项巩固——题型识别:只区分题型(比重差、平均数增长量、平
均数增长率)。
1.出现“占”字,比重问题,只能是比重差。
2.平均每+增加/减少+%,为平均数的增长率。
3.平均每+多+公里(单位),为平均数的增长量。
4.利润率是比重,为比重差问题。
5.出现“占”,只能是比重差问题,出现%是因为出题人命题不严谨,实际应
该为“个百分点”。
402017 年,全省全年完成快递业务量 100.51 亿件,同比增长 31.0%。其中,
同城快递业务量增长 29.3%,异地快递业务量增长 33.0%,国际和港澳台地区快
递业务量增长33.1%。
【练习1】(2019 国考)2017年A省快递业务中,业务量占总业务量比重高
于上年水平的分类是:
A.仅国际和港澳台地区快递
B.异地快递、国际和港澳台地区快递
C.仅同城快递
D.同城快递、异地快递
【解析】练习 1.问比重高于上年水平的,两期比重比较问题,找 a>b 的。
“占”前快递业务量为 A,增长率为 a;“占”后总业务量为 B,增长率为 b,结
合材料,“全省全年完成快递业务量 100.51 亿件,同比增长 31.0%”,则 b=31.0%,
a (29.3%)<31.0%,a (33.0%)>31.0%,a (33.1%)>31.0%,只有
同城 异地 港澳台
异地快递、国际和港澳台地区快递满足,对应 B项。【选B】
2014年某区限额以上第三产业单位共 674家,实际收入 1059.1 亿元,同比
增长4.5%;实现利润总额 13.5亿元,同比增长 11.9%;从业人员达到 58631人,
同比下降4.3%。
【练习2】(2019 北京)2014年该区限额以上第三产业单位平均每名从业人
员创造的利润比上年约:
A.下降了7% B.下降了17%
C.上升了7% D.上升了17%
【解析】练习 2.问题时间是2014年,与材料时间一致,出现“平均每”,选
项为上升/下降+%,为平均数的增长率问题,公式:r=(a-b)/(1+b)。“平均每
名”→“平均每 1 名从业人员”,谁是 1 谁是分母 B,利润为 A、a,从业人员为
B、b,已知“实现利润总额 13.5亿元,同比增长 11.9%;从业人员达到 58631人,
同比下降 4.3%”,则 a=11.9%、b=-4.3%,列式:[11.9%-(-4.3%)]/[1+(-
4.3%)]=16.2%/1->0,说明上升,排除 A、B 项;16.2%/1-=16.2+%,对应 D 项。
41【选D】
下节课18:50 开始答疑
作业:
1.巩固:今天讲的题下次课之前再做一遍
整理笔记(思考公式间关联)
2.预习:倍数、特殊增长率
明天的你一定会感激今天努力的自己。
【答案汇总】
现期比重1-5:CBBCD
基期比重1-2:BB
两期比重1-4:CBBB
现期平均数1-4:ADCA
基期平均数:CA
两期平均数1-3:不选不选C
42遇见不一样的自己
Be your better self
43