文档内容
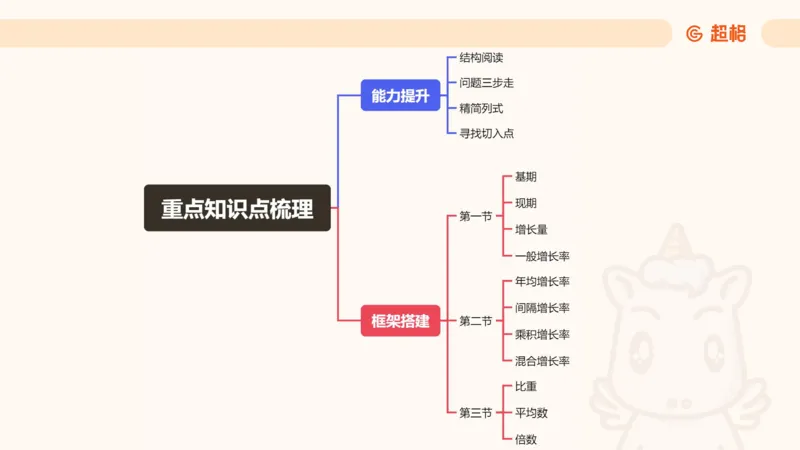
联考超大杯(重点知识点梳理)
牟立志框架搭建基期基期
① 识别:计算 → 一个时间(过去)+ 主体
比较 → 一个时间(过去)+ 最多 / 最少
② 公式:
基期 = 现期 - 增长量
增长量
基期 =
增长率
现期
基期 =
增长率
1 +基期
③ 题型:
计算类
Ⅰ已知现期、增长量,计算基期
Ⅱ 已知增长量、增长率,计算基期
Ⅲ 已知现期、增长率,计算基期基期
③ 题型:
计算类
Ⅰ已知现期、增长量,计算基期 → 高减低加
例1:2024 年,照照体重 180 斤,同比增加 10 斤,则 2023 年照照体重为:
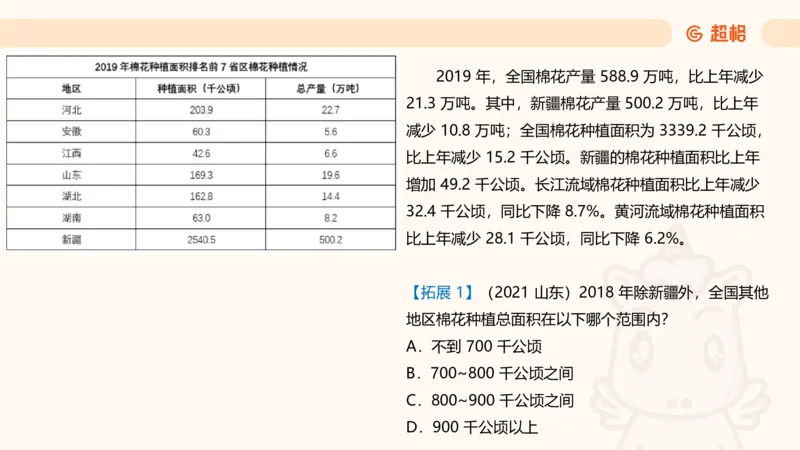
例2:2024 年,帅志体重 160 斤,同比减少 10 斤,则 2023 年帅志体重为:2019 年,全国棉花产量 588.9 万吨,比上年减少
21.3 万吨。其中,新疆棉花产量 500.2 万吨,比上年
减少 10.8 万吨;全国棉花种植面积为 3339.2 千公顷,
比上年减少 15.2 千公顷。新疆的棉花种植面积比上年
增加 49.2 千公顷。长江流域棉花种植面积比上年减少
32.4 千公顷,同比下降 8.7%。黄河流域棉花种植面积
比上年减少 28.1 千公顷,同比下降 6.2%。
【拓展 1】(2021 山东)2018 年除新疆外,全国其他
地区棉花种植总面积在以下哪个范围内?
A.不到 700 千公顷
B.700~800 千公顷之间
C.800~900 千公顷之间
D.900 千公顷以上基期
③ 题型:
计算类
Ⅱ 已知增长量、增长率,计算基期 → 基期 = 增长量 ÷ 增长率
考的很少,一般棉花种植材料会涉及(2016 年)从棉区看,黄河、长江流域棉区延续 2015 年减产较多的趋势。其中,黄河流域棉花
播种面积减少 147. 8 千公顷,下降约 14. 3%;单产每公顷增加 63. 3 公斤,提高约 6. 0%;产量减
少 10. 0 万吨,下降约 9. 2%。长江流域棉花播种面积减少 160. 7 千公顷,下降约 19. 8%;单产每
公顷减少 68. 3 公斤,下降约 5. 9%;产量减少 23. 0 万吨,下降约 24. 6%。
【例 1】(2021 四川下)2015 年,黄河流域的棉花单产为:
A. 1118 公斤/公顷
B. 1092 公斤/公顷
C. 1055 公斤/公顷
D. 1003 公斤/公顷基期
③ 题型:
计算类
Ⅲ 已知现期、增长率,计算基期 → 看差距,用厂除
差距大,厂除两位
差距小,厂除三位
差距极小( 选项前两位相同 ),精算,选调生考试偶尔出现2023 年一季度,新疆外贸进出口总值 680. 7 亿元,同比增长 80. 3%。其中,出口 584. 7 亿元,
同比增长 86. 9%。3 月当月,新疆外贸进出口总值 236. 9 亿元,同比增长 70%。其中,出口 203. 4
亿元,同比增长 78. 9%;进口33. 5 亿元,同比增长 30. 8%。
【例 2】(2024 联考)2022 年 3 月,新疆外贸出口值约为:
A. 126 亿元
B. 114 亿元
C. 139 亿元
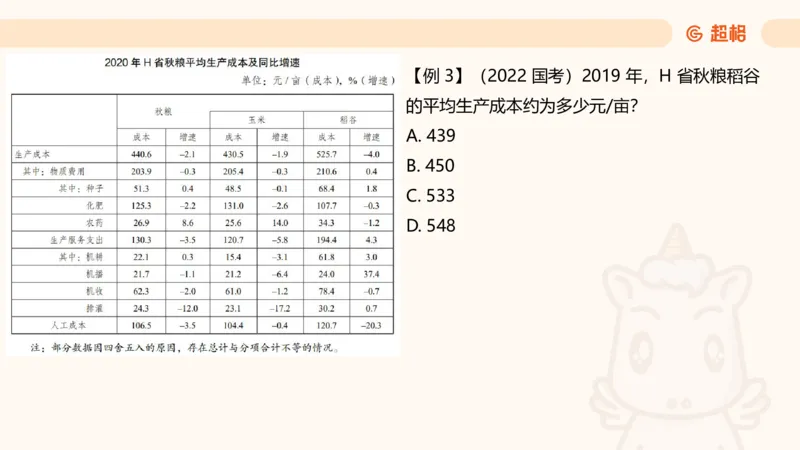
D. 160 亿元【例 3】(2022 国考)2019 年,H 省秋粮稻谷
的平均生产成本约为多少元/亩?
A. 439
B. 450
C. 533
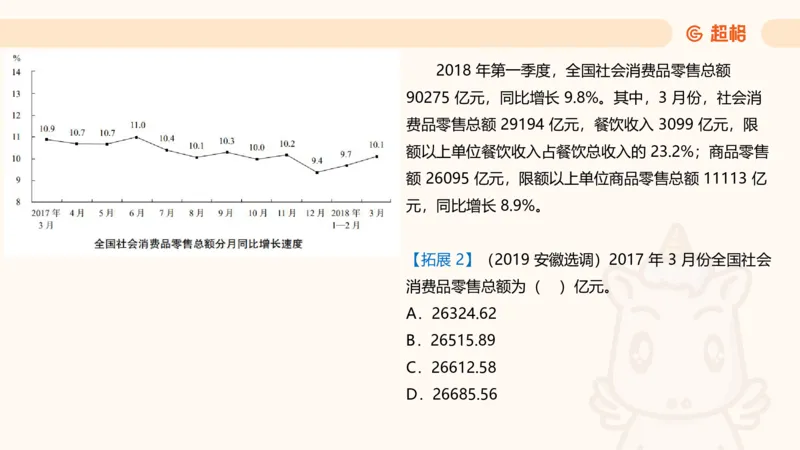
D. 5482018 年第一季度,全国社会消费品零售总额
90275 亿元,同比增长 9.8%。其中,3 月份,社会消
费品零售总额 29194 亿元,餐饮收入 3099 亿元,限
额以上单位餐饮收入占餐饮总收入的 23.2%;商品零售
额 26095 亿元,限额以上单位商品零售总额 11113 亿
元,同比增长 8.9%。
【拓展 2】(2019 安徽选调)2017 年 3 月份全国社会
消费品零售总额为( )亿元。
A.26324.62
B.26515.89
C.26612.58
D.26685.56框架积累
基期计算(复杂类)
现期
给增长率,一般考查“ 基期 = ”
增长率
1 +
不给增长率,给比重,想转化:基期部分 = 基期总体 × 基期比重
基期部分
基期总体 =
基期比重
例 1:2024 年帅志的总收入为 100 元,其中工资同比增长 10%,占总收入的 60%,2023 年帅志的工资为多少元?
例 2:2024 年帅志的总收入为 100 元,同比增长 10%,其中工资占总收入的 60%,较上年提高 5 个百分点
2023 年帅志的工资为多少元?2021 年,我国估值在 100 亿美元及以上的独角兽企业 15 家合计估值为 7280 亿美元,占据全
部独角兽企业估值的 54. 03%。
【例 4】(2023 上海)若 2021 年我国独角兽企业市场总估值较 2018 年增长了 32. 21%,则 2018
年我国独角兽企业市场总估值约为( )亿美元。
A. 22750
B. 13474
C. 12630
D. 101912023 年第 14 周,H 市流感哨点监测医院(哨点医院)共报告流感样病例 5187 例,本周监测门诊就诊病人总数 86749 例,比上周增加 5.
76%,流感样病例的就诊比例(ILI%)为 5. 98%。
(一)哨点医院 ILI%监测情况
本周哨点医院共报告流感样病例总数为 5187 例,比上周增加 4. 49%,比去年同期减少 56. 16%,其中国家级哨点医院 455 例,比上周减
少 6. 57%,比去年同期减少 55. 04%。城区哨点医院 1899 例,比上周减少 19. 40%,比去年同期减少 55. 46%;郊区、县(市)哨点医院
3288 例,比上周增加 26. 07%,比去年同期减少 56. 55%。本周全市哨点医院 ILI%为 5. 98%,比上周低 0. 07 个百分点,其中国家级哨点医院
ILI%为 2. 12%,比上周高 0. 23个百分点。城区哨点医院 ILI%为 4. 45%,比上周低 0. 56 个百分点;郊区、县(市)哨点医院 ILI%为 7. 46%,
比上周高 0. 01 个百分点。
(二)哨点医院 ILI%纵向比较
2023 年第 14 周全市哨点医院 ILI%为 5. 98%,比 2022 年同期低 7. 56 个百分点,比 2021 年同期低 0. 66 个百分点,其中国家级哨点医
院 ILI%为 2. 12%,比 2022 年同期低 3. 36 个百分点,比 2021 年同期低 4. 67 个百分点。城区哨点医院 ILI%为 4. 45%,比 2022 年同期低 6.
81 个百分点,比 2021 年同期低 2. 08 个百分点;郊区、县(市)哨点医院 ILI%为 7. 46%,比 2022 年同期低 7. 82 个百分点,比 2021 年同
期高 0. 54 个百分点。
【例 5】(2024 浙江)2022 年第 14 周,H 市哨点医院监测门诊就诊病人总数约多少例?
A. 87000
B. 89000
C. 91000
D. 93000基期
③ 题型:
计算类
Ⅲ 已知现期、增长率,计算基期和差 → 先估算,再厂除
平时多练速算练习,进可口算,退可厂除2021 年,中国向“一带一路”沿线国家出口纺织品服装 1137. 9 亿美元,同比增长 24. 5%,较
2019 年增长 17. 3%;同时,中国自“一带一路”沿线国家进口纺织品服装 131. 6 亿美元,同比增
长 24. 5%。
【例 6】(2023 国考)2020 年,中国对“一带一路”沿线国家纺织品服装贸易顺差额约为多少亿美
元?
A. 1129
B. 1253
C. 808
D. 10062021 年 1-9 月,我国机床工具进出口总额 242. 6 亿美元,同比增长 32. 8%。其中,机床工具
商品进口 105. 2亿美元,同比增长 23. 7%;出口 137. 4 亿美元,同比增长 40. 8%。
【例 7】(2022 联考)2020 年 1-9 月,我国机床工具贸易状况为:
A. 顺差 10 亿美元以上
B. 顺差不到 10 亿美元
C. 逆差 10 亿美元以上
D. 逆差不到 10 亿美元基期
③ 题型:
计算类
Ⅲ 已知现期、增长率,计算间隔基期 → 先算间隔增长率,再厂除
选项差距大,间隔增长率估算至十位
选项差距小,间隔增长率估算至个位2015 年国民经济和社会发展统计公报。公报显示,全年全国居民人均可支配收入 21966 元,比
上年增长 8. 9%,增长率下降 1. 2 个百分点。按常住地分,2015 年城镇居民人均可支配收入 31195
元,比上年增长 8. 2%,增长率比 2014 年下降 0. 8 个百分点;农村居民人均可支配收入 11422 元,
比上年增长 8. 9%,增长率比 2014年下降 2. 3 个百分点。
【例 8】(2020 四川下)2013 年,城镇居民人均可支配收入约为多少万元?
A. 1. 9
B. 2. 2
C. 2. 6
D. 3基期
③ 题型:
比较类
Ⅰ已知现期、增长量,计算基期 → 高减低加
Ⅱ 已知现期、增长率,先分析(现期大,增长率小,基期大),再比较截至 2019 年 12 月底,G 省移动电话期末用户 1. 65 亿户,下降 1. 7%;4G 期末用户 1. 43 亿
户,增长 2. 3%。互联网宽带接入期末用户 3802 万户,增长 2. 7%;移动互联网期末用户 1. 42 亿
户,下降 8. 2%。
【例 9】(2021 广东)2018 年末,下列 G 省的电信业务用户数量最多的是:
A. 移动电话期末用户
B. 4G 期末用户
C. 互联网宽带接入期末用户
D. 移动互联网期末用户框架梳理(拿出纸和笔,一起写)现期现期
① 识别:若保持增长量 / 增长率不变,求以后
② 公式:现期 = 基期 + 增长量
现期 = 基期 ×(1 + 增长率)例 1:2024 年,帅志的体重为 160 斤,同比增加 20 斤
现期
若保持 2024 年的同比增长量不变,哪一年,帅志体重达到 210 斤 ?
③ 题型:
例 2:2024 年,帅志的体重为 160 斤,同比增加 25 斤
追赶类(保持增长量不变)
照照的体重为 200 斤,同比增加 10 斤
若保持 2024 年的同比增长量不变,哪一年,帅志体重超过照照 ?
找差距 → 目标 - 现在
补差距 → 追定量:所需年份数 = 差距 ÷ 增长量
追变量:所需年份数 = 差距 ÷ 增长量差
年份数不为整,往大取整
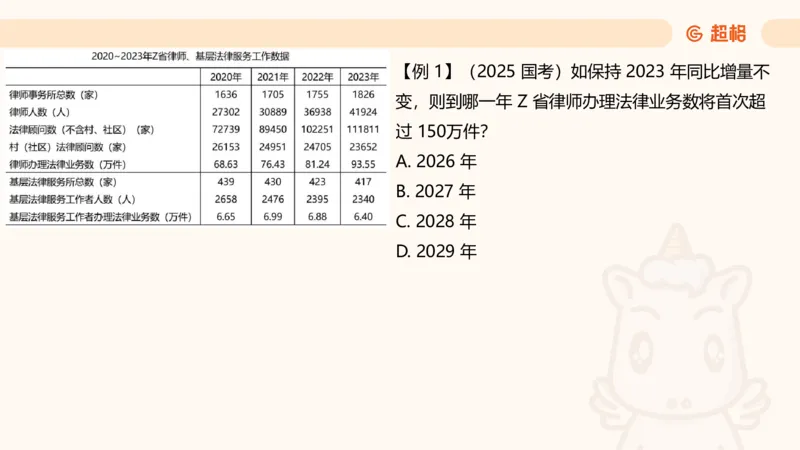
算年份 → 所求年份 = 基期年份 + 所需年份数【例 1】(2025 国考)如保持 2023 年同比增量不
变,则到哪一年 Z 省律师办理法律业务数将首次超
过 150万件?
A. 2026 年
B. 2027 年
C. 2028 年
D. 2029 年【例 2】(2024 国考)如 2022 年内每个月移动电
话用户数增量和蜂窝物联网终端用户数增量均为固
定值,则 2022 年蜂窝物联网终端用户数第一次超
过移动电话用户数是在哪个季度?
A. 第一季度
B. 第二季度
C. 第三季度
D. 第四季度现期
③ 题型:
计算类(保持增长率不变)
Ⅰ 给增长率
Ⅱ 不给增长率现期
③ 题型:
计算类(保持增长率不变)
Ⅰ 给增长率 → 现期 = 基期 ×(1 + 增长率),选项差距小,拆分截至 2018 年底,中国人工智能市场规模约为 238. 2 亿元,同比增长率达到 56. 6%。从中国人
工智能企业地域分布情况来看,北京企业数量最多,企业数量为 368 家;其次为广东,人工智能企业
数量为 185 家;排名第三的是上海,数量为 131 家。
【例 3】(2020 联考)若按照 2018 年同比增长率,到 2019 年底中国人工智能市场规模约为:
A. 363 亿元
B. 371 亿元
C. 373 亿元
D. 383 亿元现期
③ 题型:
计算类(保持增长率不变)
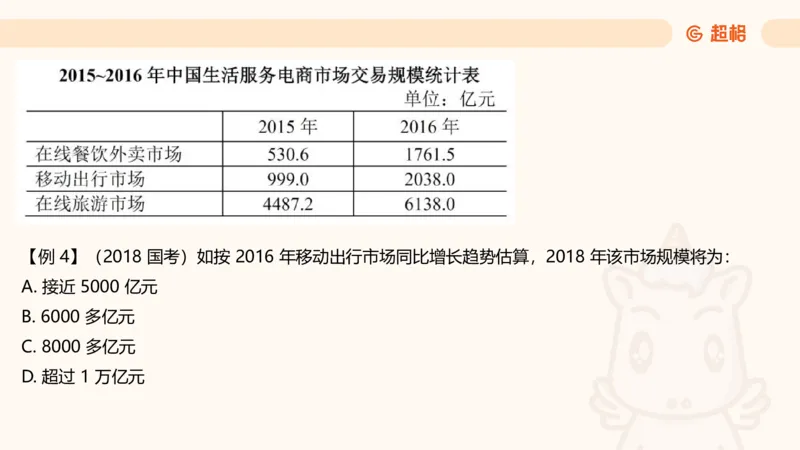
Ⅱ 不给增长率 → 现期、基期倍数明显,算倍数,乘倍数【例 4】(2018 国考)如按 2016 年移动出行市场同比增长趋势估算,2018 年该市场规模将为:
A. 接近 5000 亿元
B. 6000 多亿元
C. 8000 多亿元
D. 超过 1 万亿元现期
③ 题型:
计算类(保持增长率不变)
Ⅱ 不给增长率 → 现期、基期倍数不明显,算增长量,按增长量不变计算,结果怕偏小选大
例:2023 年、2024 年帅志的工资分别为 100 元、110 元
若保持 2024 年的同比增长量不变,2025 年,帅志的工资为 _____ 元
若保持 2024 年的同比增长率不变,2025 年,帅志的工资为 _____ 元
A.115 B.118 C.120 D.121
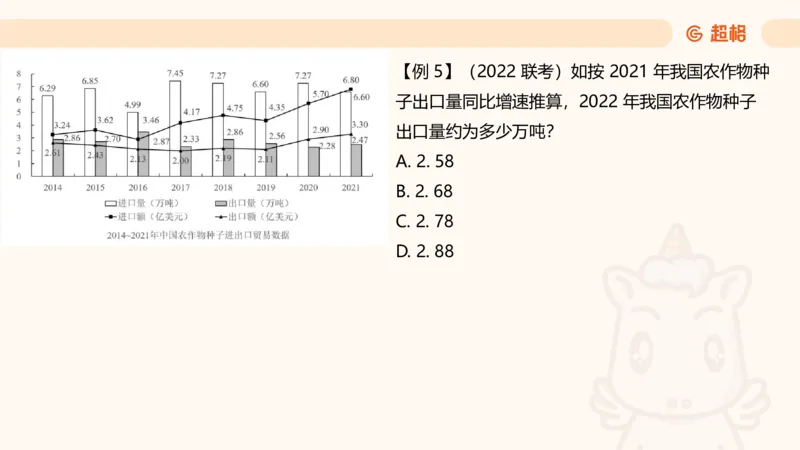
A.115 B.120 C.121 D.125【例 5】(2022 联考)如按 2021 年我国农作物种
子出口量同比增速推算,2022 年我国农作物种子
出口量约为多少万吨?
A. 2. 58
B. 2. 68
C. 2. 78
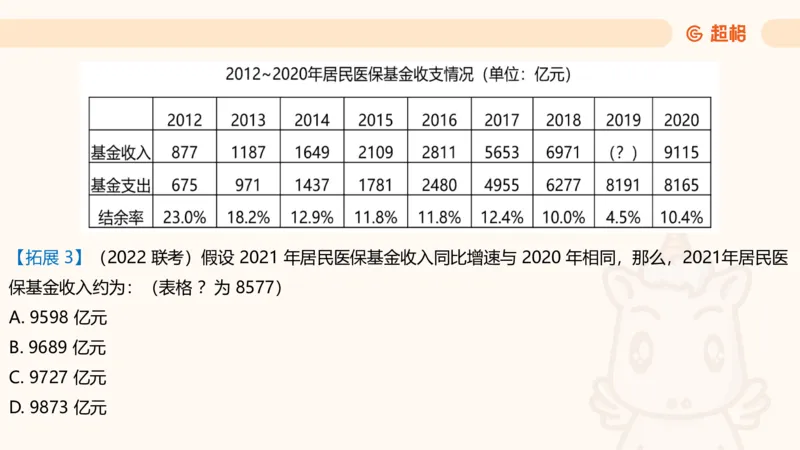
D. 2. 88【拓展 3】(2022 联考)假设 2021 年居民医保基金收入同比增速与 2020 年相同,那么,2021年居民医
保基金收入约为:(表格 ?为 8577)
A. 9598 亿元
B. 9689 亿元
C. 9727 亿元
D. 9873 亿元框架梳理(拿出纸和笔,一起写)增长量增长量
① 识别:计算 → 两个时间 + 主体 + 增长 + 单位
比较 → 增长最多 / 少
② 公式:增长量 = 现期 - 基期
增长量 = 基期 × 增长率
现期
增长量 = × 增长率
增长率
1 +增长量
③ 题型:
计算类
Ⅰ 已知现期、基期,计算增长量( 主体为多个数加和、特定增长量、年均增长量 )
Ⅱ 已知现期、增长率,计算增长量( 百化分求增长量、增长量的倍数、每增长 N 一个百分点对应增长量 )增长量
③ 题型:
计算类
Ⅰ 已知现期、基期,计算增长量,主体为多个数加和
方法一:先加再减(凑整或高位叠加)
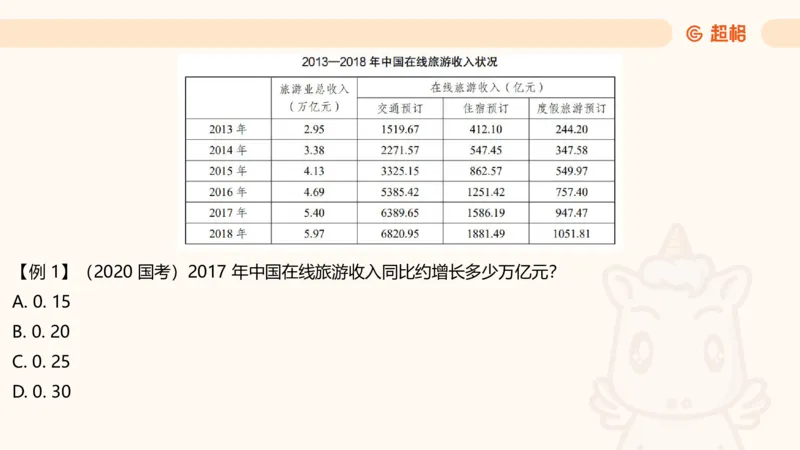
方法二:先减再加(抵消)【例 1】(2020 国考)2017 年中国在线旅游收入同比约增长多少万亿元?
A. 0. 15
B. 0. 20
C. 0. 25
D. 0. 30增长量
③ 题型:
计算类
Ⅰ 已知现期、基期,计算特定增长量(增长量大于某一数值的有几个)
方法一:现期 - 基期 > 特定增长量
方法二:基期 + 特定增长量 < 现期
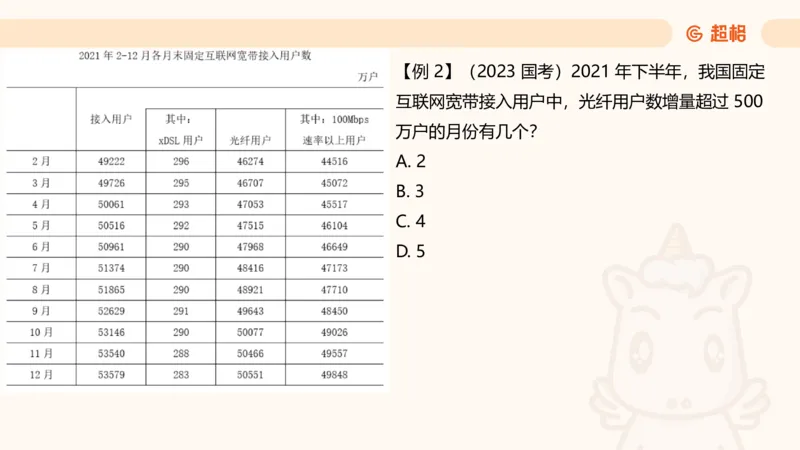
注:时间段中第一年的增长量千万别忽略【例 2】(2023 国考)2021 年下半年,我国固定
互联网宽带接入用户中,光纤用户数增量超过 500
万户的月份有几个?
A. 2
B. 3
C. 4
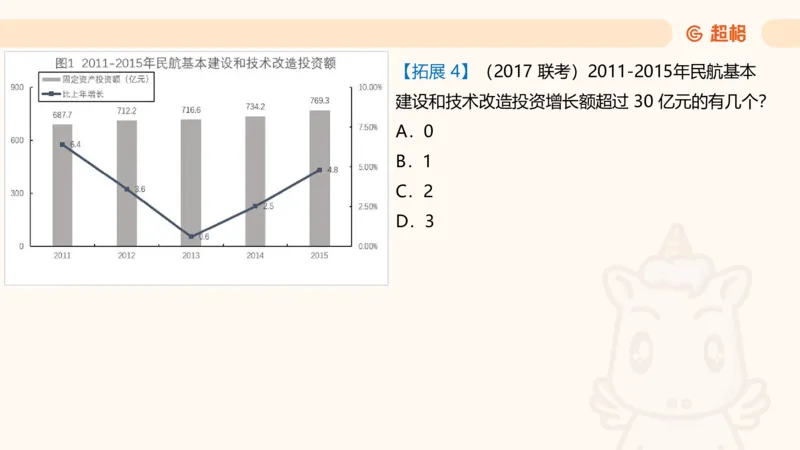
D. 5【拓展 4】(2017 联考)2011-2015年民航基本
建设和技术改造投资增长额超过 30 亿元的有几个?
A.0
B.1
C.2
D.3增长量
③ 题型:
计算类
Ⅰ 已知现期、基期,计算年均增长量
年 年
非限定:除江苏省考以为外,2016-2020 年,志哥工资的年均增长量 →
2020 −2016
年4 年
限定:所有考试,十三五( 2016-2020 年 ),志哥工资的年均增长量 →
2020 −2015
年 年5
限定:在江苏省考中,2016-2020 年,志哥工资的年均增长量 →
2020 −2015
52022 年,京津冀地区生产总值合计 10. 0 万亿元,是 2013 年的 1. 8 倍。其中,北京、河北跨
越 4 万亿元量级,均为 4. 2 万亿元,分别是 2013 年的 2. 0 倍和 1. 7 倍;天津 1. 6 万亿元,是
2013 年的 1. 6 倍。京津冀第一产业、第二产业、第三产业增加值占生产总值比重构成由 2013 年的
6. 2∶35. 7∶58. 1 变化为 2022 年的 4. 8∶29. 6∶65. 6。京津冀三地第三产业增加值占生产总值比
重分别为 83. 8%、61. 3%和 49. 4%,较 2013 年分别提高 4. 3、7. 2 和 8. 4 个百分点。
【例 3】(2024 国考)以 2013 年为基期,则 2013-2022 年京津冀地区生产总值年均约增加多少万
亿元?
A. 1. 1
B. 0. 9
C. 0. 7
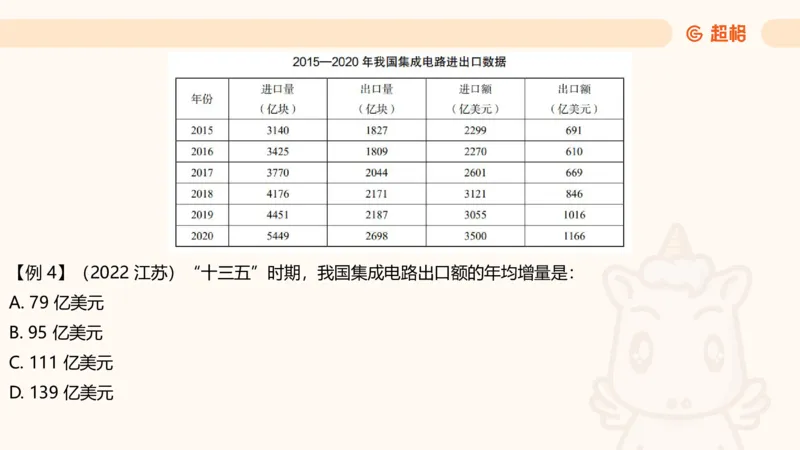
D. 0. 5【例 4】(2022 江苏)“十三五”时期,我国集成电路出口额的年均增量是:
A. 79 亿美元
B. 95 亿美元
C. 111 亿美元
D. 139 亿美元增长量
③ 题型:
计算类
Ⅱ 已知现期、增长率,计算增长量,百化分求增长量
现期 现期
方法:|r|= → 增长量 = 、减少量 =
1
+ 1 − 1
技巧一:误差 ≈ 现期 × 增长率差距
技巧二:|r|≤ 5%,且选项差距大,增长量 ≈ 现期 × 增长率2023 年上半年,全国办理机动车转让登记业务 1134 万辆。其中,办理汽车转让登记业务1057
万辆,同比增长 5.3%;异地直接办理交易登记二手小客车 157 万辆。
【例 5】(2025 四川)2023 年上半年,我国办理汽车转让登记业务同比增加:
A. 不到 40 万辆
B. 40 多万辆
C. 50 多万辆
D. 60 万辆以上2023 年前 5 个月,汽车出口带动天津口岸整体出口同比增加。汽车出口占同期天津口岸出口商
品总值的2. 2%,较上年同期提升 0. 3 个百分点。1-5 月民营企业出口活力明显,民营企业出口约 10.
6 万辆,同比增长 64. 3%,占同期天津口岸汽车出口总量的 61. 6%,占比较上年同期提升 13 个百
分点。新能源汽车出口成为新的增长点,出口约 11 万辆,同比增长 50. 2%。
【例 6】(2024 联考)2023 年 1-5 月,民营企业出口汽车同比约增加了多少万辆?
A. 3
B. 4
C. 5
D. 62019 年 1-10 月,江苏民航机场旅客吞吐量 4901 万人次,同比增长 13. 4%,增速比华东地区
(六省一市)高 6. 2 个百分点,比上海高 9. 7 个百分点,比浙江高 5. 7 个百分点,比山东高 4. 4 个
百分点,比福建高 8. 7 个百分点,比江西高 6. 9 个百分点,与安徽持平。
【例 7】(2020 江苏)2019 年 1-10 月,江苏民航机场旅客吞吐量同比增加:
A. 398 万人次
B. 435 万人次
C. 579 万人次
D. 657 万人次2022 年,我国废钢铁、废有色金属等十个品种(详见表格)再生资源回收总重量约为 37067. 7
万吨,同比下降 2. 62%,回收总金额约为 13140. 6 亿元,同比下降 4. 05%。2022 年废有色金属中
废铅回收重量同比增长 5. 56%。2022 年我国报废机动车回收数量 399. 1 万辆,同比增长 32. 9%,
回收数量占我国机动车保有量的 9. 57%。
【例 8】(2024 联考)相比 2021 年,2022 年我国十个品种再生资源回收总金额同比下降了约:
A. 511 亿元
B. 532 亿元
C. 555 亿元
D. 578 亿元截至 2024 年 2 月,我国公共充电桩数量为 282. 6 万台,环比增加 4. 4 万台,同比增长 51. 3%。
其中直流充电桩 123. 9 万台,环比增长 2. 1%;交流充电桩 158. 6 万台,环比增长 1. 2%。
【例 9】(2025 天津)截至 2024 年 2 月,我国交流充电桩数量环比增量比直流充电桩数量环比增
量:
A. 低不到 1 万台
B. 低 1 万台以上
C. 高不到 1 万台
D. 高 1 万台以上2023 年,互联网企业互联网业务累计收入居前 5 名的省级行政区为北京(5721. 4 亿元,增长 4.
2%)、上海(4167. 8 亿元,增长 17. 5%)、浙江(1955. 9 亿元,增长 4. 8%)、广东(1754. 5
亿元,下降 4. 6%)和天津(981. 7 亿元,增长 20. 3%)。全国互联网企业互联网业务增速实现正增
长的省级行政区有 16 个,数量较 2022年全年增长 3 个。
【例 10】(2025 天津)2023 年,互联网企业互联网业务累计收入居前 5 名的省级行政区完成互联
网业务收入比上年:
A. 减少了不到 500 亿元
B. 减少了 500 亿元以上
C. 增长了不到 500 亿元
D. 增长了 500 亿元以上增长量
③ 题型:
计算类
Ⅱ 已知现期、增长率,计算增长量之间的倍数
情况一:增长率相差 10 个百分点以内,且选项差距大,A 增长量 ÷ B 增长量 ≈ ( A ÷ B )×( a ÷ b )
情况二:增长率相差 10 个百分点以上,分别百化分求增长量,再求倍数2021 年上半年,全市社会消费品零售总额 9048. 44 亿元,比去年同期增加了 2104. 14 亿元。
分行业看,批发和零售业零售额 8287. 13 亿元,同比增长 28. 4%;住宿和餐饮业零售额 761. 31 亿
元,同比增长 54. 0%。2021年上半年,全市网上商店零售额 1485. 72 亿元,比去年同期增加 259.
92 亿元。
【例 11】(2023 浙江)2021 年上半年,S 市批发和零售业零售额同比增量约是住宿和餐饮业的多
少倍?
A. 3
B. 5
C. 7
D. 92019 年,A 市居民人均可支配收入 28920 元,比上年增长 9. 6%。按常住地分,城镇居民人均
可支配收入37939 元;农村居民人均可支配收入 15133 元。全市居民人均消费支出 20774 元,比上
年增长 7. 9%。按常住地分,城镇居民人均消费支出 25785 元;农村居民人均消费支出 13112 元。
全市居民恩格尔系数为 32. 1%,比上年下降 0. 2 个百分点。其中城镇为 31. 2%,农村为 34. 9%。
【例 12】(2022 四川下)2019 年,A 市居民人均可支配收入同比增量约是同期人均消费支出同比
增量的多少倍?
A. 1. 1
B. 1. 4
C. 1. 7
D. 2. 2增长量
③ 题型:
计算类
Ⅱ 已知现期、增长率,计算每增长 N 个百分点,对应的增长量
第一步:计算基期
第二步:基期 × N%2017 年,J 省海洋生产总值为 7217 亿元,比上年增长 9. 2%,海洋生产总值占地区生产总值的
8. 4%,2017年,全省沿海沿江港口完成货物吞吐量 20. 4 亿吨,同比增长 8. 3%;集装箱吞吐量
1698. 8 万标箱,同比增长 5. 5%。
【例 13】(2020 山东)2017 年 J 省海洋生产总值同比每增长 1 个百分点,当年其海洋生产总值约
增加:
A. 66 亿元
B. 72 亿元
C. 726 亿元
D. 776 亿元增长量
③ 题型:
比较类
Ⅰ 已知现期、基期,比较增长量
Ⅱ 已知现期、增长率,比较增长量增长量
③ 题型:
比较类
Ⅰ 已知现期、基期,比较增长量
柱状图 → 看高度差,高度差越大,增长量越大
折线图 → 看斜率,斜率越大,增长量越大
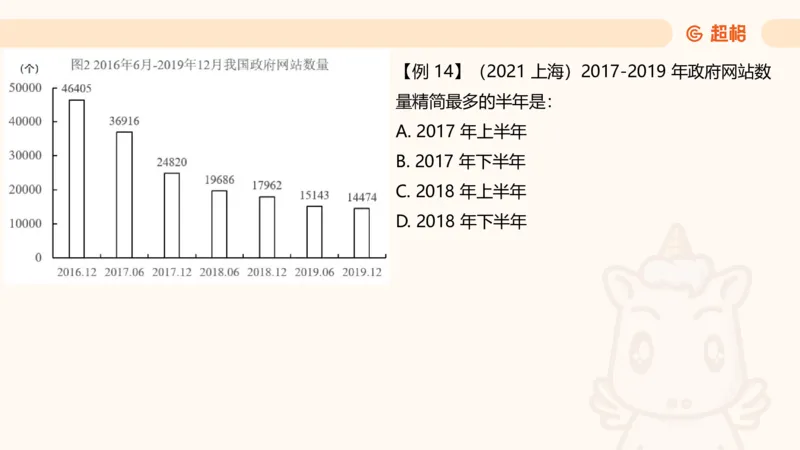
看不出,别硬看,直接算【例 14】(2021 上海)2017-2019 年政府网站数
量精简最多的半年是:
A. 2017 年上半年
B. 2017 年下半年
C. 2018 年上半年
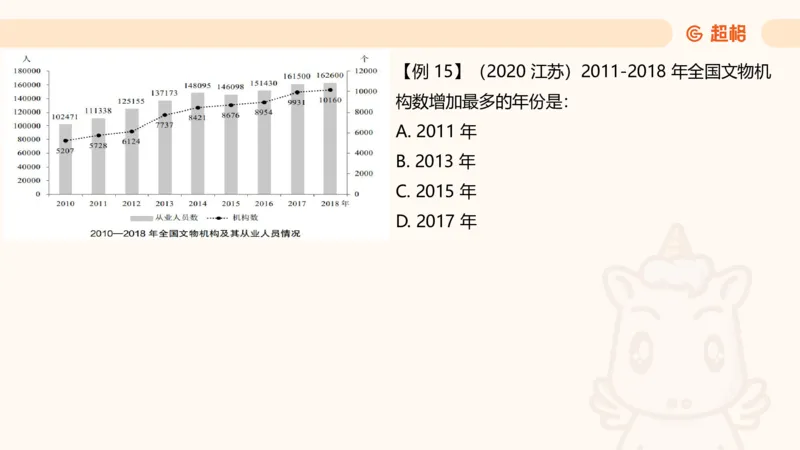
D. 2018 年下半年【例 15】(2020 江苏)2011-2018 年全国文物机
构数增加最多的年份是:
A. 2011 年
B. 2013 年
C. 2015 年
D. 2017 年增长量
③ 题型:
比较类
Ⅱ 已知现期、增长率,比较增长量
大大则大,一大一小,百化分,倍数关系差距大,也可分析倍数
例1:帅志工资上升 10 元,照照工资下降 12 元,_____ 工资的增长量大?
例2:帅志工资下降 10 元,照照工资下降 12 元,_____ 工资的增长量大?2021 年,中国对美国、东盟、欧盟和日本的纺织品服装出口合计 1724. 9 亿美元。其中,对美
国出口额为563. 5 亿美元,同比增长 4. 0%;向东盟十国出口纺织品服装 491. 2 亿美元,同比增长
24. 9%;对欧盟 27 国出口纺织品服装 469. 9 亿美元,同比下降 11. 1%;对日本出口纺织品服装
200. 3 亿美元,同比下降 7. 2%。
【例 16】(2023 国考)将①美国、②东盟十国、③欧盟 27 国和④日本按 2021 年自中国进口纺织
品服装金额同比增量从高到低排列,以下正确的是:
A. ①②③④
B. ①②④③
C. ②①③④
D. ②①④③知识点总结
进口、出口的易错点
遇到进口、出口的主体,看是否有分割词,有分割词,注意分割词前后主客体顺序,顺序改变,名词改变
没有,无需多虑
例1:(2018 国考)平均每个东欧国家的进口额高于平均每个 例2:(2021 四川)2017 年,表中国家和地区自上海
西亚、北非国家的进口额 市货物进口额同比增速超过 10% 的有多少个?框架梳理(拿出纸和笔,一起写)一般增长率一般增长率
① 识别:计算 → 两个时间 + 主体 + 增长 + 百分数或倍数,又名增速、增幅
比较 → 增长最快 / 慢
增长量
② 公式:增长率 =
基期一般增长率
③ 题型:
计算类
Ⅰ 给百分点型
Ⅱ 给具体量型
Ⅲ 特定增长率一般增长率
③ 题型:
计算类
Ⅰ 给百分点型(给现期增长率以及与基期增长率间百分点的关系,求基期增长率)
第一步:高减低加
第二步:增速 / 增幅上升 / 下降,有负号,带负号
降幅扩大 / 收窄,带绝对值算降幅,再转化增长率例1:2024 年增长 10 %,增速比上年同期降低 6 个百分点,则 2023 年增长率为 _____
例2:2024 年下降 10%,增速比上年同期提高 6 个百分点,则 2023 年增长率为 _____
例3:2024 年增长 10%,增幅比上年同期降低 6 个百分点,则 2023 年增长率为 _____
例4:2024 年下降 10%,增幅比上年同期降低 6 个百分点,则 2023 年增长率为 _____
例5:2024 年下降 10%,降幅比上年同期扩大 6 个百分点,则 2023 年增长率为 _____
例6:2024 年下降 10%,降幅比上年同期收窄 6 个百分点,则 2023 年增长率为 _____一般增长率
③ 题型:
计算类
Ⅱ 给具体量
现期、基期、增长量,任知其二,代公式
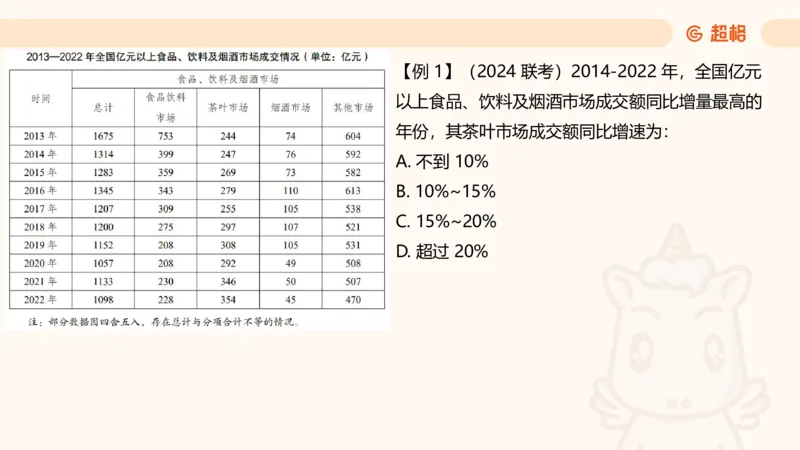
注意优化列式习惯【例 1】(2024 联考)2014-2022 年,全国亿元
以上食品、饮料及烟酒市场成交额同比增量最高的
年份,其茶叶市场成交额同比增速为:
A. 不到 10%
B. 10%~15%
C. 15%~20%
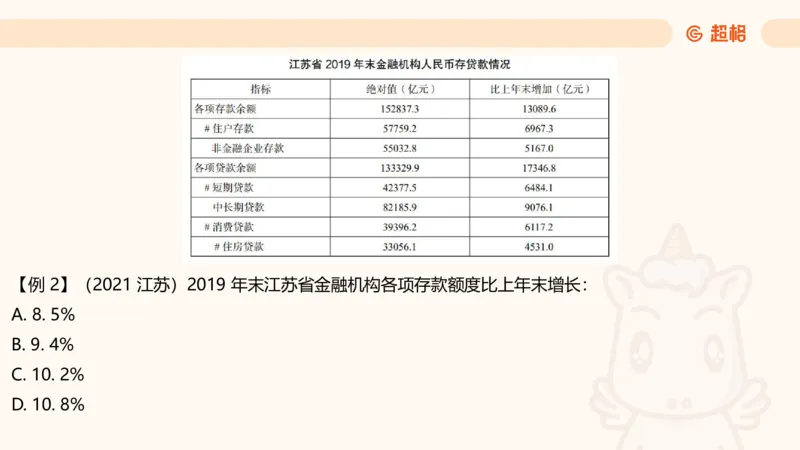
D. 超过 20%【例 2】(2021 江苏)2019 年末江苏省金融机构各项存款额度比上年末增长:
A. 8. 5%
B. 9. 4%
C. 10. 2%
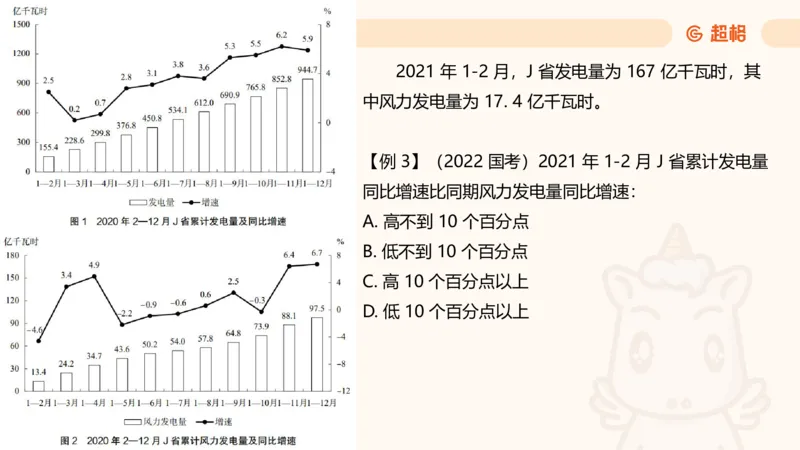
D. 10. 8%2021 年 1-2 月,J 省发电量为 167 亿千瓦时,其
中风力发电量为 17. 4 亿千瓦时。
【例 3】(2022 国考)2021 年 1-2 月 J 省累计发电量
同比增速比同期风力发电量同比增速:
A. 高不到 10 个百分点
B. 低不到 10 个百分点
C. 高 10 个百分点以上
D. 低 10 个百分点以上一般增长率
③ 题型:
计算类
Ⅲ 特定增长率
给现期、基期,简单题 → 看前三位(无须四舍五入),口算增长量,计算增长率
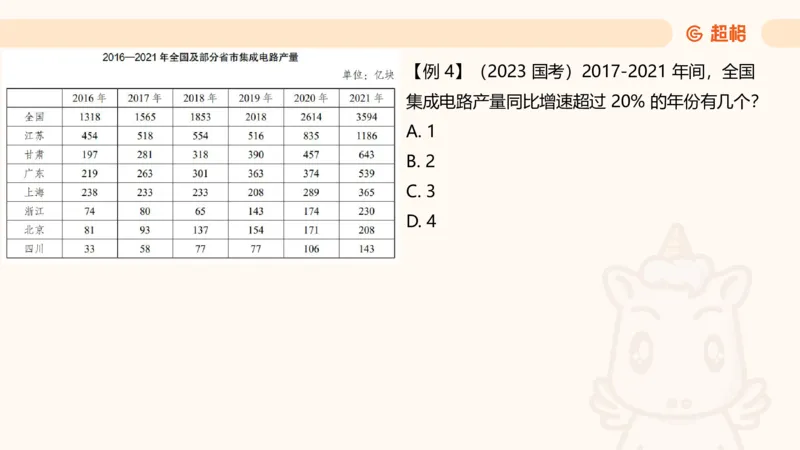
复杂题 →“ 基期 × 特定增长率 ”与“ 增长量 ”比较【例 4】(2023 国考)2017-2021 年间,全国
集成电路产量同比增速超过 20% 的年份有几个?
A. 1
B. 2
C. 3
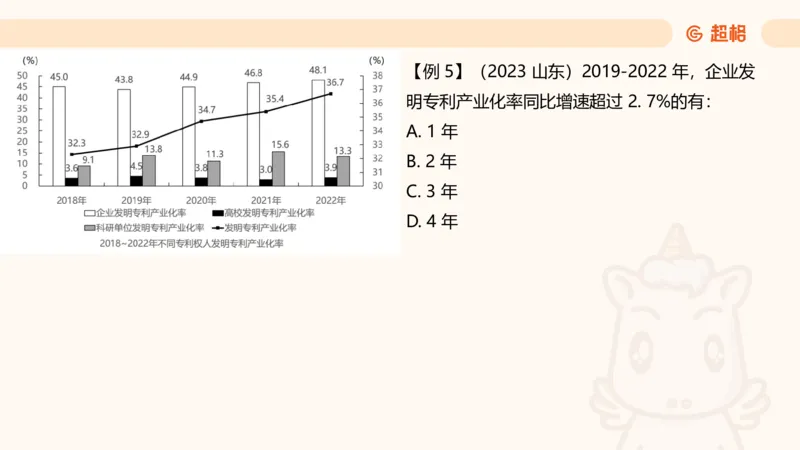
D. 4【例 5】(2023 山东)2019-2022 年,企业发
明专利产业化率同比增速超过 2. 7%的有:
A. 1 年
B. 2 年
C. 3 年
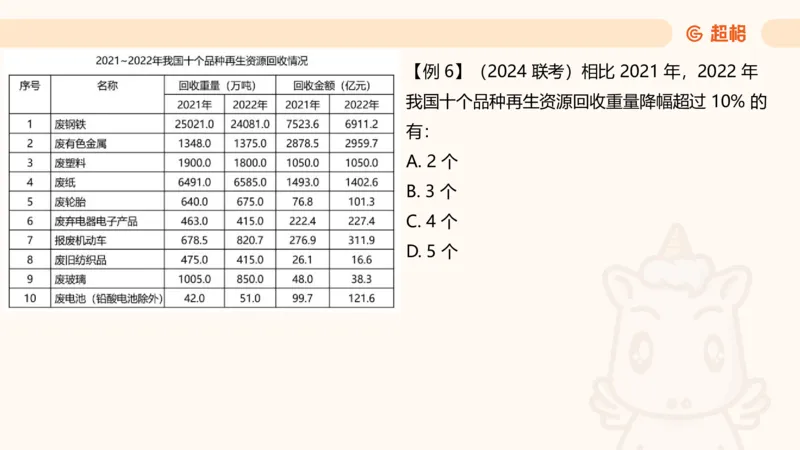
D. 4 年【例 6】(2024 联考)相比 2021 年,2022 年
我国十个品种再生资源回收重量降幅超过 10% 的
有:
A. 2 个
B. 3 个
C. 4 个
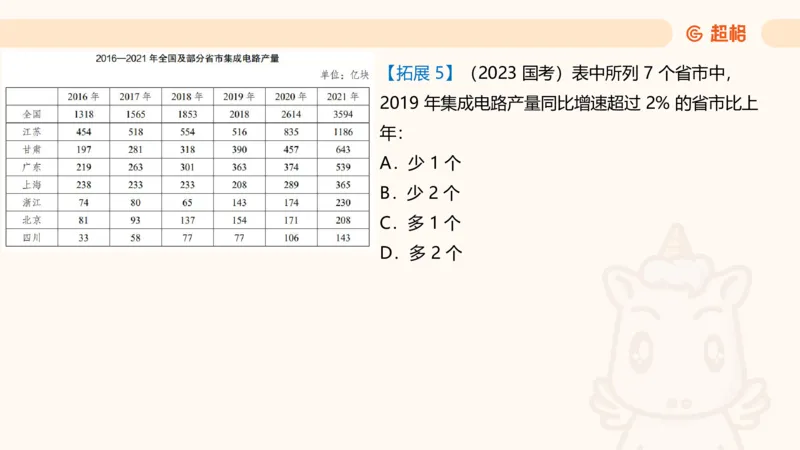
D. 5 个【拓展 5】(2023 国考)表中所列 7 个省市中,
2019 年集成电路产量同比增速超过 2% 的省市比上
年:
A.少 1 个
B.少 2 个
C.多 1 个
D.多 2 个一般增长率
③ 题型:
计算类
Ⅲ 特定增长率
给现期、增长量,增长率 >100% → 2 × 增长量 > 现期
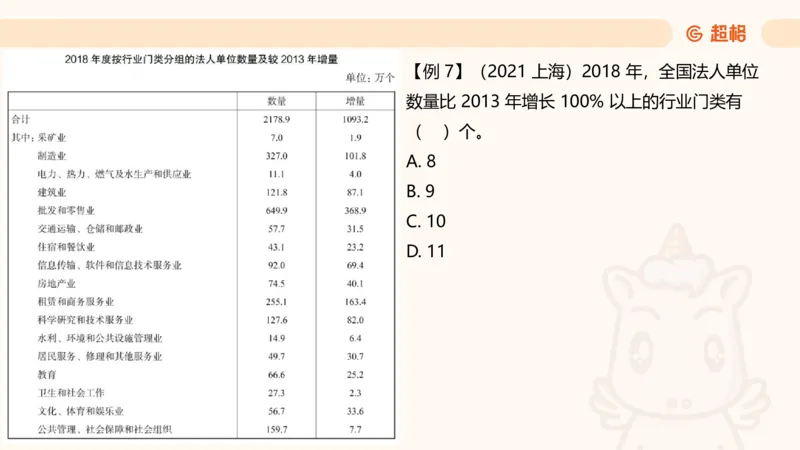
增长率 > 1% → 101 × 增长量 > 现期【例 7】(2021 上海)2018 年,全国法人单位
数量比 2013 年增长 100% 以上的行业门类有
( )个。
A. 8
B. 9
C. 10
D. 11一般增长率
③ 题型:
比较类
Ⅰ 给现期、基期
Ⅱ 给现期、增长量一般增长率
③ 题型:
比较类
Ⅰ 给现期、基期,倍数关系明显,比较倍数,倍数大,增长率大
倍数关系不明显,比增长率,看前三位,口算增长量,先分析,再比较
技巧:材料为柱状图,高度差占柱子比例越大,当年增长率越大【例 8】(2025 四川)以下各年份中,年末全国
平均每万人群众文化设施建筑面积同比增速最快
的是:
A. 2012 年
B. 2013 年
C. 2014 年
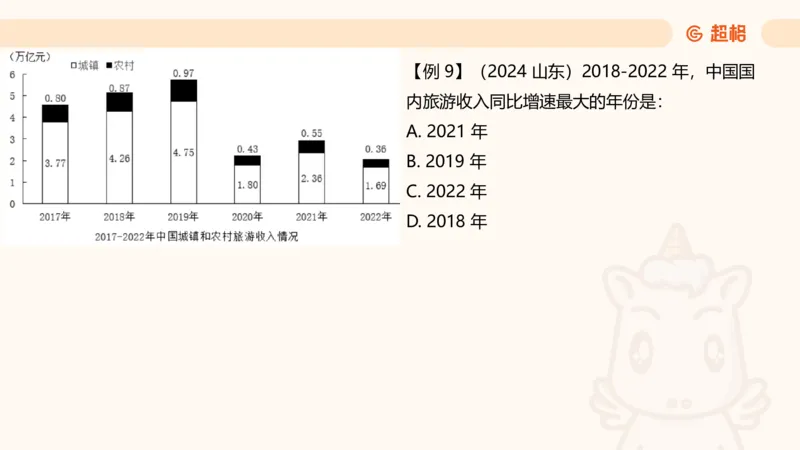
D. 2019 年【例 9】(2024 山东)2018-2022 年,中国国
内旅游收入同比增速最大的年份是:
A. 2021 年
B. 2019 年
C. 2022 年
D. 2018 年一般增长率
③ 题型:
比较类
增长量
Ⅱ 给现期、增长量,比较 “ ”,仅限比较时可用
现期2022 年,S 省各级 12315 工作机构共接收诉求 220. 4 万件,同比增长 21. 41%。其中,投诉
55. 6 万件、举报 26. 3 万件、咨询 138. 5 万件,比上一年分别增加 14. 0 万件、8. 9 万件、16. 0 万
件。
【例 10】(2024 国考)将 S 省各级 12315 工作机构接收的投诉、举报和咨询三类诉求量按 2022
年同比增速从高到低排序,以下正确的是:
A. 投诉量、举报量、咨询量
B. 咨询量、投诉量、举报量
C. 举报量、咨询量、投诉量
D. 举报量、投诉量、咨询量框架梳理(拿出纸和笔,一起写)坚持不是固执,而是选择
放弃不是洒脱,而是结果