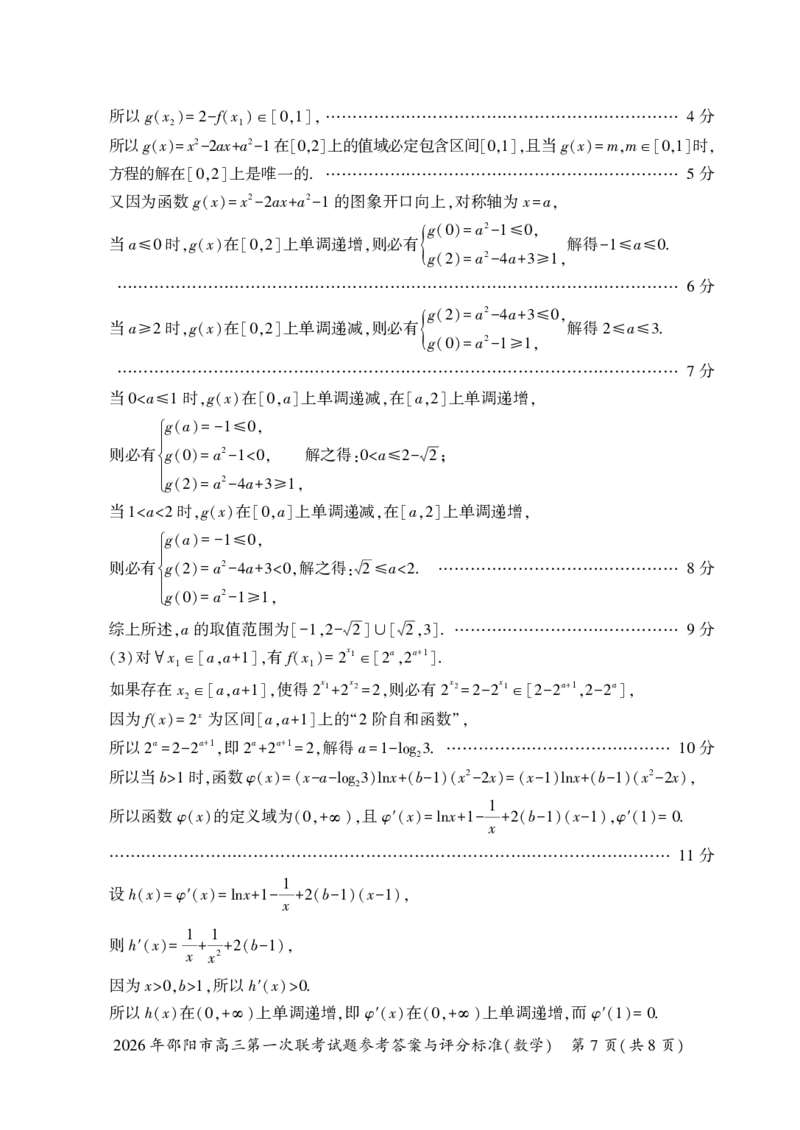数学答案(1)(1)_2026年1月_260130湖南省2026年邵阳市高三第一次联考试题卷（全科）_2026年湖南省邵阳市高三第一次联考数学试卷

2026 年邵阳市高三第一次联考试题参考答案与评分标准 数 学 一、选择题(本大题共 小题,每小题 分,共 分 在每小题给出的四个选项中,只有一项 8 5 40 . 是符合题目要求的) 题号 1 2 3 4 5 6 7 8 答案 D C A A B B D C . 【解析】由 f(x) x 2 ,得 ax 2. 设 y ax 的图象与 y 2 的图象的交点为 8 C = -ax =0 = x 1 = = x A(x ,2 ).由g(x) x 2 ,得 x 2.设 y x 的图象与 y 2 的图象的交点为 1 x = - x=0 loga = x 2=loga = x 1 loga B(x ,2 ).因为y ax 的图象与y x的图象关于直线y x对称,y 2的图象也关于直 2 x 1= 2=loga = = x 2 线y x对称,所以点A与点B关于直线y x对称,故x 2,x x x 64.当a 时,x ; = = 2=x 1+32 2= 1+x =2 1=1 1 1 当a [ , )时,x ( , ].函数y x 64在( , ]上单调递减,所以 x x [ , ). ∈ 2 +∞ 1∈ 0 1 = + x 0 1 1+32 2∈ 65 +∞ 故选项 正确. C 二、选择题(本大题共 小题,每小题 分,共 分.在每小题给出的选项中,有多项符合题 3 6 18 目要求.全部选对的得 分,部分选对的得部分分,有选错的得 分) 6 0 题号 9 10 11 答案 BC ABD AD . 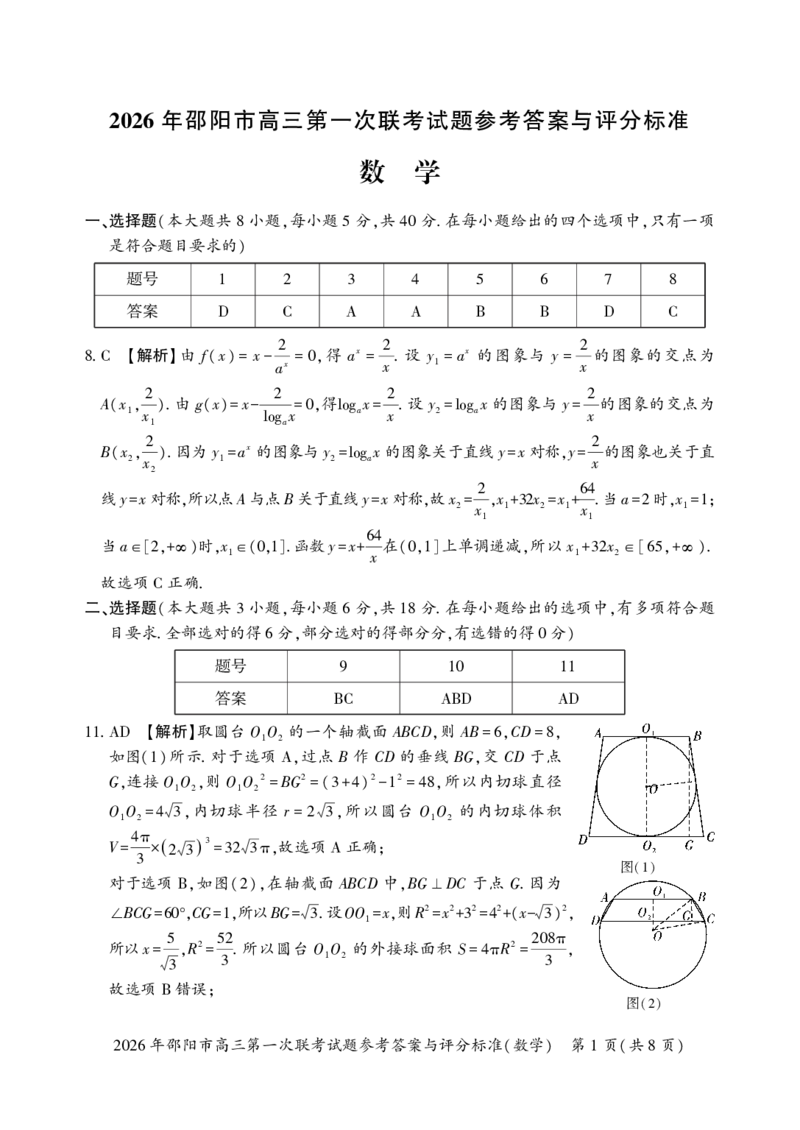【解析】取圆台 O O 的一个轴截面 ABCD,则 AB ,CD , 11 AD 1 2 =6 =8 如图( )所示. 对于选项 ,过点 B 作 CD 的垂线 BG,交 CD 于点 1 A G,连接O O ,则 O O 2 BG2 ( )2 2 ,所以内切球直径 1 2 1 2 = = 3+4 -1 =48 O O ,内切球半径 r ,所以圆台 O O 的内切球体积 1 2=4 3 =2 3 1 2 V 4π ( ) 3 ,故选项 正确; = × 2 3 =32 3π A 3 图 对于选项 ,如图( ),在轴截面 ABCD 中,BG DC 于点 G. 因为 (1) B 2 ⊥ BCG °,CG ,所以BG .设OO x,则R2 x2 2 2 (x )2, ∠ =60 =1 = 3 1= = +3 =4 + - 3 所以x 5,R2 52. 所以圆台 O O 的外接球面积 S R2 208π, = = 1 2 =4π = 3 3 3 故选项 错误; B 图 (2) 年邵阳市高三第一次联考试题参考答案与评分标准(数学) 第 页(共 页) 2026 1 8R3 对于选项 ,因为500π 4π ,所以 R . 如图( )所示,当外接 C = =5 3 3 3 球球心点 O 在 O O 之间时,圆台 O O 的母线 BC 2 2 1 2 1 2 = 7 +1 = ,圆台的表面积 S 2 2 ( ) 50=5 2 =π×3 +π×4 +π 3+4 ×5 2 = . 25π+35 2π 当外接球球心点 O 在 O O 的延长线上时,如图( )所示,圆台 1 2 4 图 (3) O O 的母线BC 2 2 ,圆台的表面积 S 2 2 1 2 = 1 +1 = 2 =π×3 +π×4 + ( ) ,故选项 错误; π 3+4 × 2=25π+7 2π C 对于选项 ,外接球半径 R ,由选项 分析可知,圆台的高 D = 5 C O O 或 . 所以圆台的体积 V π(r2 r2 r r )h,当 h 时, 1 2=7 1 = 1+ 2+ 1 2 =7 3 V 259π;当h 时,V 37π,故选项 正确. = =1 = D 3 3 图 三、填空题(本大题共 小题,每小题 分,共 分) (4) 3 5 15 . . . 12 30 13 3 14 8 . 【解析】如图( )所示,将正四面体ABCD补全为正方体. 14 8 5 以点A为坐标原点,建立空间直角坐标系,则 A( , , ), 0 0 0 B( , , ),C ( , , ), D( , , ). 设 M(x,y,z), 则 4 4 0 0 4 4 4 0 4 MA2 MB2 x2 y2 z2 (x )2 (y )2 z2,MC2 MD2 x2 + = + + + -4 + -4 + + = + (y )2 (z )2 (x )2 y2 (z )2. 因为 MA2 MB2 -4 + -4 + -4 + + -4 + = MC2 MD2,所以z ,即点M构成的平面截正四面体所得 + =2 的截面为正方形 PQRS,边长为 ,故截面面积为 2 2 . 2 2×2 2=8 图 (5) 四、解答题(本大题共 小题,共 分.解答应写出文字说明、证明过程或演算步骤) 5 77 . 分 15 (13 ) 解: 在 ABC中 因为 2B A B C 2C 所以由正弦定理和余弦定理 (1) △ , sin +3sin cos sin -2sin =0, a2 c2 b2 得 b2 ac + - c2 .所以b2 a2 c2. 分 : +3 · ac -2 =0 =3 - ……………………………………… 2 2 因为a c 所以b2 .故a2 b2 c2 ABC为直角三角形. 分 = 2, =2, =2 + = ,△ ………………… 4 所以 ABC的外接圆的半径为 . 分 △ 1 …………………………………………………… 6 因为 A 2 又A 所以 A 2A 5. 分 (2) cos = , ∈(0,π), sin = 1-cos = ……………………… 7 3 3 b2 c2 a2 因为 A + - 2 所以 b2 c2 a2 bc.又b2 a2 c2 且b 所以c2 c . cos = bc = , 3 +3 -3 =4 =3 - , =2, -4 +4=0 2 3 分 …………………………………………………………………………………………… 10 年邵阳市高三第一次联考试题参考答案与评分标准(数学) 第 页(共 页) 2026 2 8所以c S 1bc A 1 5 2 5. 分 =2, △ ABC= sin = ×2×2× = …………………………………… 13 2 2 3 3 . 分 16 (15 ) 解: 取棱PA的中点Q 连接EQ BQ 如图 所示 (1) , , , (6) , 则QE AD QE 1AD. ∥ , = 2 又因为BC AD BC 1AD ∥ , = , 2 所以QE BC 四边形QBCE为平行四边形 图 􀱀 , , (6) 所以EC QB. 分 ∥ …………………………………………………………………………… 3 又因为QB 平面PAB EC 平面PAB 所以EC 平面PAB. 分 ⊂ , ⊄ , ∥ ……………………… 5 如图 所示 以点A为坐标原点 分别以AB AD AP (2) (7) , , , , 所在直线为x轴 y轴 z轴建立空间直角坐标系 , , , 则A B C P D . (0,0,0), (1,0,0), (1,1,0), (0,0,2), (0,2,0) 则A→C A→P P→D . 分 =(1,1,0), =(0,0,2), =(0,2,-2) … 6 取线段AC的中点为F 连接BF 由题意可知 , , : ( ) BF 平面PAC 可得B→F 1 1 则取平面 PAC 的 ⊥ , = - , ,0 , 2 2 一个法向量为m B→F . 分 图 =2 =(-1,1,0) ……………… 8 (7) 假设在棱PD上存在点E 使得平面PAC与平面EAC的夹角的余弦值为 3 , , 3 设P→E λP→D λ 则A→E A→P P→E λ λ . 分 = (0≤ ≤1), = + =(0,2 ,2-2 ) …………………………… 9 设n x y z 为平面EAC的一个法向量 =( , , ) , {n A→E λy λ z · =2 +(2-2 ) =0, 则 取y λ =1- , n A→C x y . · = + =0 {x λ 得 = -1,所以n λ λ λ . 分 z λ. =( -1,1- ,- ) ………………………………………………… 11 =- 设平面PAC与平面EAC的夹角为θ , m n λ λ 则 θ · 1- +1- 3. cos = m n = λ 2 λ 2 λ2 = | |·| | 2· ( -1) +(1- ) + 3 解得λ 舍 或λ 2. 分 =2( ) = ……………………………………………………………… 14 3 此时点E为棱PD上靠近点D的三等分点. 分 ………………………………………… 15 年邵阳市高三第一次联考试题参考答案与评分标准(数学) 第 页(共 页) 2026 3 8. 分 17 (15 ) 解: 设事件A 为 第 i 轮比赛甲班团队获胜 由题意得 P A 2 i .设事 (1) i “ ”, ( i )= ( =1,2,3) 3 件C表示 当比赛结束时恰好进行了 轮比赛 且甲班团队获得冠军 因为每轮比赛的 “ 3 , ”, 结果相互独立 则 , ( ) 3 P C P A A A P A P A P A 2 8. ( )= ( 1 2 3)= ( 1) ( 2) ( 3)= = 3 27 故甲班团队获得冠军的概率为8 . 分 …………………………………………………… 3 27 由题意得 事件A 为 第i 轮比赛乙班团队获胜 P A 1 i X 的 (2)(ⅰ) , i “ ”, ( i)= ( =1,2,3), 3 所有可能值为 . 3,5 ( ) ( ) 3 3 所以P X P A A A A A A P A A A P A A A 2 1 1. ( =3)= ( 1 2 3∪ 1 2 3)= ( 1 2 3)+ ( 1 2 3)= + = 3 3 3 分 …………………………………………………………………………………………… 5 P X P X 2. ( =5)= 1- ( =3)= 3 所以X的分布列为 X 3 5 P 1 2 3 3 分 ……………… 7 所以E X 1 2 13. 分 ( )= 3× +5× = ………………………………………………………… 8 3 3 3 设事件E表示 比赛轮数不限制 甲班团队获得冠军 .设比赛过程中 甲班团队与 (ⅱ) “ , ” , 乙班团队累积得分的分差为Y P Y k 表示 Y k 时最终甲班团队获得冠军的概率 其 , ( = ) = , 中k { }.由题意知P Y P Y P Y P E . ∈ -3,-2,-1,0,1,2,3 ( =3)= 1, ( =-3)= 0, ( =0)= ( ) 分 …………………………………………………………………………………………… 10 根据全概率公式有 P Y k 2P Y k 1P Y k k . 分 ( = )= ( = +1)+ ( = -1), ∈{-2,-1,0,1,2} ……………………… 11 3 3 所以P Y k P Y k 1 P Y k P Y k 迭代得 ( = +1)- ( = )= [ ( = )- ( = -1)], 2 所以P Y P Y 1 P Y P Y 1 P Y P Y ( =3)- ( =2)= [ ( =2)- ( =1)]= [ ( =1)- ( =0)] 2 4 1 P Y P Y 1 P Y P Y = [ ( =0)- ( =-1)]= [ ( =-1)- ( =-2)] 8 16 1 P Y P Y 1P Y . = [ ( =-2)- ( =-3)]= ( =-2) 32 32 年邵阳市高三第一次联考试题参考答案与评分标准(数学) 第 页(共 页) 2026 4 8所以P Y P Y 1P Y ( =3)- ( =2)= ( =-2), 32 P Y P Y 1P Y P Y P Y 1P Y ( =2)- ( =1)= ( =-2), ( =1)- ( =0)= ( =-2), 16 8 P Y P Y 1P Y P Y P Y 1P Y . ( =0)- ( =-1)= ( =-2), ( =-1)- ( =-2)= ( =-2) 4 2 累加得P Y P Y 1 1 1 1 1 P Y 31P Y . 分 ( =3)- ( =-2)=( + + + + )· ( =-2)= ( =-2) … 13 32 16 8 4 2 32 所以P Y 32P Y 32. ( =-2)= ( =3)= 63 63 故P Y 1P Y 1P Y P Y 7P Y 7 32 8. ( =0)= ( =-2)+ ( =-2)+ ( =-2)= ( =-2)= × = 4 2 4 4 63 9 即P E 8. ( )= 9 故若比赛轮数不限制 甲班团队获得冠军的概率为8 . 分 , ……………………………… 15 9 . 分 18 (17 ) 解: 因为 ABF 的周长为 AB AF BF AF AF BF BF a a a (1) △ 1 | |+| 1|+| 1|=| 2|+| 1|+| 2|+| 1|=2 +2 =4 =8, 所以a . 分 =2 ……………………………………………………………………………… 2 c c 又e 1 所以c . = a = = , =1 2 2 所以b2 a2 c2 = - =3, x2 y2 所以椭圆E的方程为 . 分 + =1 ……………………………………………………… 4 4 3 由 知 F 由题意知 直线l与坐标轴不垂直. (2)(ⅰ) (1) , 2(1,0), , 设直线l x my m A x y B x y C x y D x y . : = +1( ≠0), ( 1, 1), ( 2, 2), ( 3, 3), ( 4, 4) x2 y2 将x my 代入 整理得 m2 y2 my . 分 = +1 + =1, (3 +4) +6 -9=0 ………………………… 5 4 3 m 则Δ y y 6 y y 9 . >0, 1+ 2=- m2 , 1 2=- m2 3 +4 3 +4 y y m 所以y 1+ 2 3 x my 4 . M= =- m2 , M= M+1= m2 2 3 +4 3 +4 ( m ) ( m2 m ) 所以M 4 3 同理可得N 4 3 . 分 m2 ,- m2 , m2 , m2 …………………………… 6 3 +4 3 +4 4 +3 4 +3 m2 4 4 所以 x M- x N 3 m2 +4 - 4 m2 +3 4 m2 -4. 分 y y = m m = m ………………………………………………… 7 M- N 3 3 7 - m2 - m2 3 +4 4 +3 年邵阳市高三第一次联考试题参考答案与评分标准(数学) 第 页(共 页) 2026 5 8m2 ( m ) m2 所以直线MN的方程为x 4 4 -4 y 3 即x 4( -1)y 4 - m2 = m + m2 , = m + , 3 +4 7 3 +4 7 7 ( ) 所以直线MN过定点 4 . 分 ,0 ………………………………………………………… 9 7 连接 AD 设 H 为线段 AD 的中点 直 (ⅱ) , , 线NR MR 分别与 AD 相交于点 S T 连接 , , , NH MH RH NA MD 如图 所示. , , , , , (8) 因为M N H分别为AB CD AD的中点 , , , , , 所以MH BD NH AC. ∥ , ∥ 则S S S S . △ NAR= △ HAR, △ MDR= △ HDR 所以S S S S . △ NAS= △ RSH, △ MDT= △ RTH 故S S . 分 图 △ MNR= 四边形MNAD ……………… 12 (8) m2 由 知 AB m2 y y m2 y y 2 y y 12(1+ ) (ⅰ) ,| |= 1+ | 1- 2|= (1+ )[( 1+ 2) -4 1 2] = m2 , 3 +4 m2 同理可得 CD 12(1+ ) 分 | |= m2 , ………………………………………………………… 14 3+4 m2 2 所以S S 1 ND AM 1 AB CD 18(1+ ) △ MNR = 四边形MNAD= | |×| |= | |×| |= m2 m2 2 8 (3 +4)(3+4 ) m2 2 18(1+ ) 72 分 ≥( m2 m2 ) 2 = ,………………………………………………… 16 3 +4+3+4 49 2 当且仅当 m2 m2 时 即m 时 等号成立. 3 +4=4 +3 , =±1 , 所以 MNR的面积的最小值为72. 分 △ …………………………………………………… 17 49 . 分 19 (17 ) 解: 对于 x 有f x x . 分 (1) ∀ 1∈[2,26], ( 1)=log3( 1+1)∈[1,3] ………………………… 1 如果存在x 使得 x x . 2∈[2,26], log3( 1+1)+log3( 2+1)= 3 则必有 x x log3( 2+1)= 3-log3( 1+1)∈[0,2], 令x 则x 1=26, 2=0∉[2,26], 所以f x 不是 阶自和函数 . 分 ( ) “3 ” ……………………………………………………… 3 函数f x 4 在区间 上的值域为 . (2) ( )=x [0,2] [1,2] +2 因为f x 4 是g x x2 ax a2 在区间 上的 阶和函数 . ( )=x ( )= -2 + -1 [0,2] “2 ” +2 所以对任意x 总存在唯一的x 使得f x g x 成立 1∈[0,2], 2∈[0,2], ( 1)+ ( 2)= 2 , 年邵阳市高三第一次联考试题参考答案与评分标准(数学) 第 页(共 页) 2026 6 8所以g x f x 分 ( 2)= 2- ( 1)∈[0,1],………………………………………………………… 4 所以g x x2 ax a2 在 上的值域必定包含区间 且当g x m m 时 ( )= -2 + -1 [0,2] [0,1], ( )= , ∈[0,1] , 方程的解在 上是唯一的. 分 [0,2] ………………………………………………………… 5 又因为函数g x x2 ax a2 的图象开口向上 对称轴为x a ( )= -2 + -1 , = , {g a2 当a 时 g x 在 上单调递增 则必有 (0)= -1≤0, 解得 a . ≤0 , ( ) [0,2] , g a2 a -1≤ ≤0 (2)= -4 +3≥1, 分 …………………………………………………………………………………………… 6 {g a2 a 当a 时 g x 在 上单调递减 则必有 (2)= -4 +3≤0,解得 a . ≥2 , ( ) [0,2] , g a2 2≤ ≤3 (0)= -1≥1, 分 …………………………………………………………………………………………… 7 当 a 时 g x 在 a 上单调递减 在 a 上单调递增 0< ≤1 , ( ) [0, ] , [ ,2] , ìg a ï ( )= -1≤0, ï 则必有íg a2 解之得 a ï (0)= -1<0, :0< ≤2- 2; ï îg a2 a (2)= -4 +3≥1, 当 a 时 g x 在 a 上单调递减 在 a 上单调递增 1< <2 , ( ) [0, ] , [ ,2] , ìg a ï ( )= -1≤0, ï 则必有íg a2 a 解之得 a . 分 ï (2)= -4 +3<0, : 2≤ <2 ……………………………………… 8 ï îg a2 (0)= -1≥1, 综上所述 a的取值范围为 . 分 , [-1,2- 2]∪[ 2,3] …………………………………… 9 对 x a a 有f x x 1 a a +1 . (3) ∀ 1∈[ , +1], ( 1)= 2 ∈[2 ,2 ] 如果存在x a a 使得 x 1 x 2 则必有 x 2 x 1 a +1 a 2∈[ , +1], 2 +2 =2, 2 =2-2 ∈[2-2 ,2-2 ], 因为f x x 为区间 a a 上的 阶自和函数 ( )= 2 [ , +1] “2 ”, 所以 a a +1 即 a a +1 解得a . 分 2 =2-2 , 2 +2 =2, =1-log23 …………………………………… 10 所以当b 时 函数φ x x a x b x2 x x x b x2 x >1 , ( )=( - -log23)ln +( -1)( -2 )=( -1)ln +( -1)( -2 ), 所以函数φ x 的定义域为 且φ′ x x 1 b x φ′ . ( ) (0,+∞), ( )=ln +1-x +2( -1)( -1), (1)= 0 分 …………………………………………………………………………………………… 11 设h x φ′ x x 1 b x ( )= ( )=ln +1-x +2( -1)( -1), 则h′ x 1 1 b ( )= x +x2 +2( -1), 因为x b 所以h′ x . >0, >1, ( )>0 所以h x 在 上单调递增 即φ′ x 在 上单调递增 而φ′ . ( ) (0,+∞) , ( ) (0,+∞) , (1)= 0 年邵阳市高三第一次联考试题参考答案与评分标准(数学) 第 页(共 页) 2026 7 8所以当 x 时 φ′ x φ x 单调递减 当x 时 φ′ x φ x 单调递增. 0< <1 , ( )<0, ( ) , >1 , ( )>0, ( ) 而φ b 当x 且x 时 φ x φ . (1)= 1- <0, >0 →0 , ( )>0, (2)=ln2>0 所以 x x . 分 0< 1<1< 2<2 …………………………………………………………………… 12 设F x φ x φ x x 则F x x x x2 ( )= ( )- (2- ),0< <1, ( )=( -1)ln(2 - )>0, 所以φ x φ x 又φ x φ x ( 1)> (2- 1), ( 1)= ( 2)= 0, 所以φ x 所以φ x φ x . (2- 1)<0, ( 2)> (2- 1) 因为x x 且φ x 在 上单调递增 2>1,2- 1>1 ( ) (1,+∞) , 所以x x 即x x . 分 2>2- 1, 1+ 2>2 …………………………………………………………… 13 x 设t x x 1 则t′ x -1 ( )=ln +x -1, ( )= x2 , 所以当 x 时 t′ x t x 单调递减 0< <1 , ( )<0, ( ) , 当x 时 t′ x t x 单调递增. >1 , ( )>0, ( ) 所以t x t 则 x 1. ( )≥ (1)= 0, ln ≥1-x ( ) x 3 因为x2 x x 1 ( -1) -2 - +x -3 = x , 所以当 x 时 x2 x x 1 当x 时 x2 x x 1 . 分 0< <1 , -2 < +x -3, >1 , -2 > +x -3 ……………………… 14 ì ( ) ( ) ï φ x x 1 b x 1 ïï0= ( 1)<( 1-1) 1-x +( -1) 1+x -3 , 所以í 1 1 ï ( ) ( ) ïï φ x x 1 b x 1 î0= ( 2)>( 2-1) 1-x +( -1) 2+x -3 , 2 2 {bx 2 b x b 整理得 1 +(1-3 ) 1+ >0, ① bx 2 b x b 2 +(1-3 ) 2+ <0, ② 由 得 x x b x x b 分 ①-② ,( 1- 2)[ ( 1+ 2)+1-3 ]>0, ………………………………………… 16 因为x x 所以b x x b 所以x x 1. 1< 2, ( 1+ 2)+1-3 <0, 1+ 2<3-b 综上得证. 分 ……………………………………………………………………………… 17 注:解答题有其他解法酌情给分. 年邵阳市高三第一次联考试题参考答案与评分标准(数学) 第 页(共 页) 2026 8 8