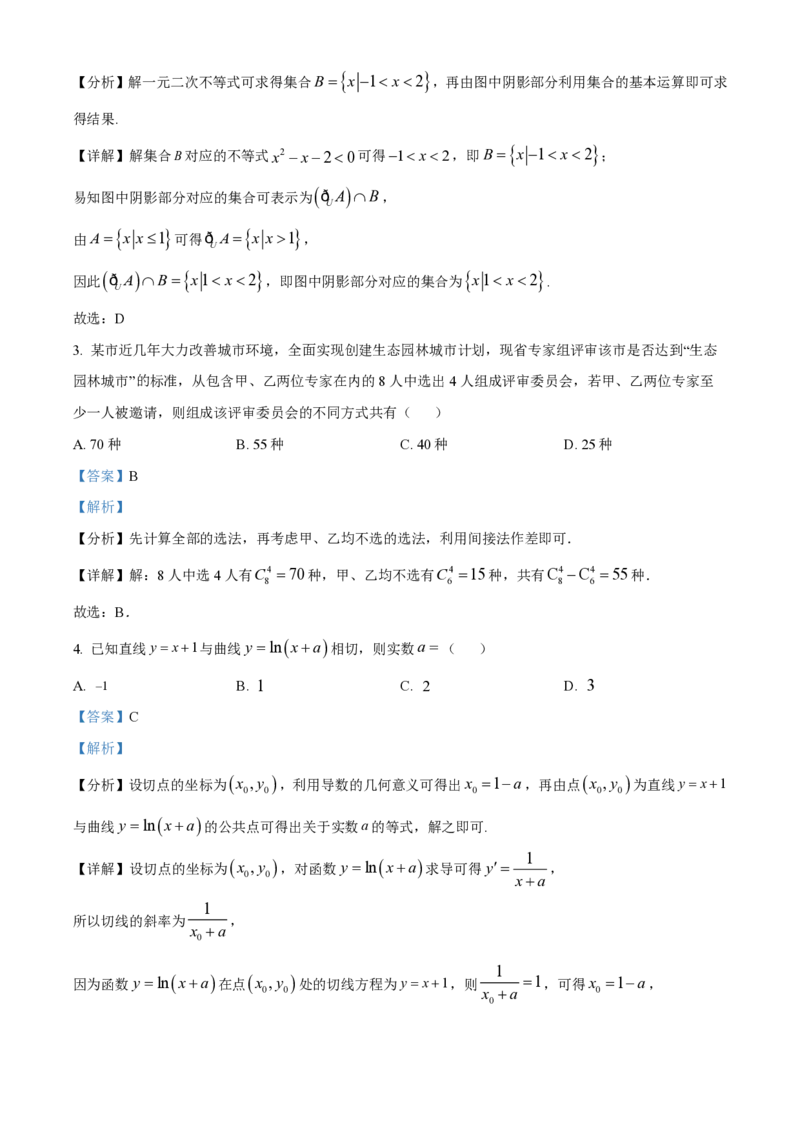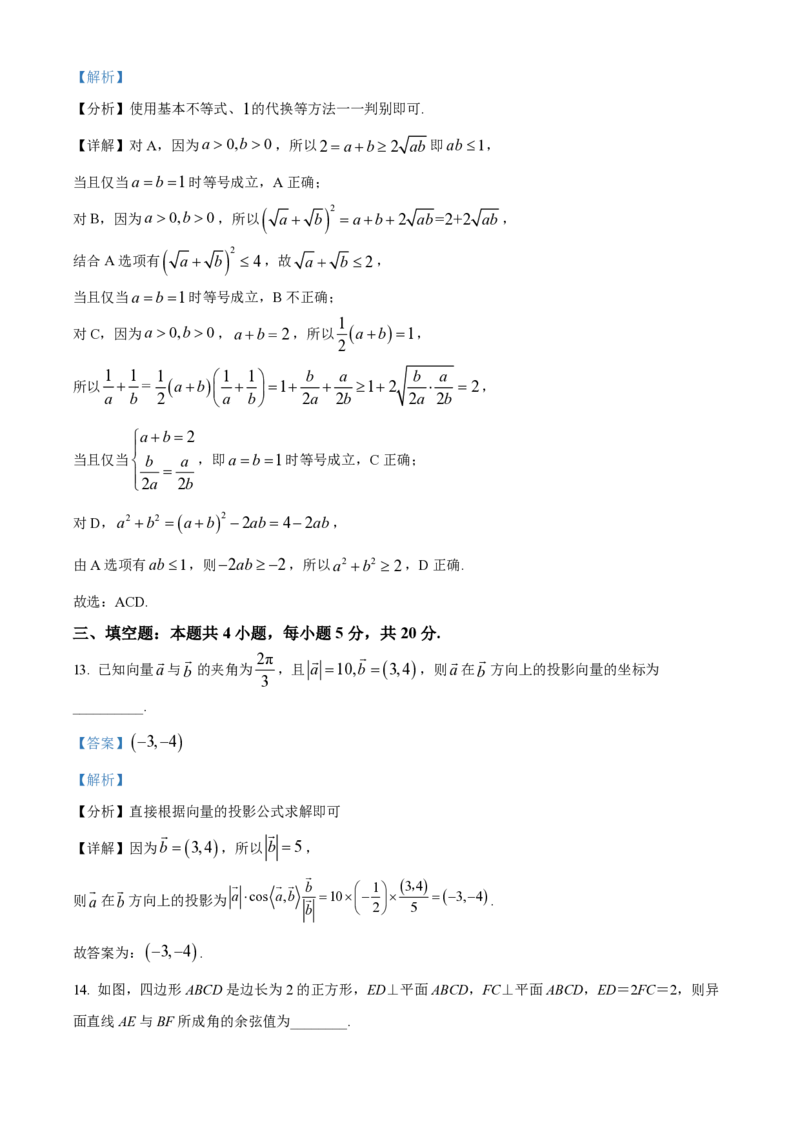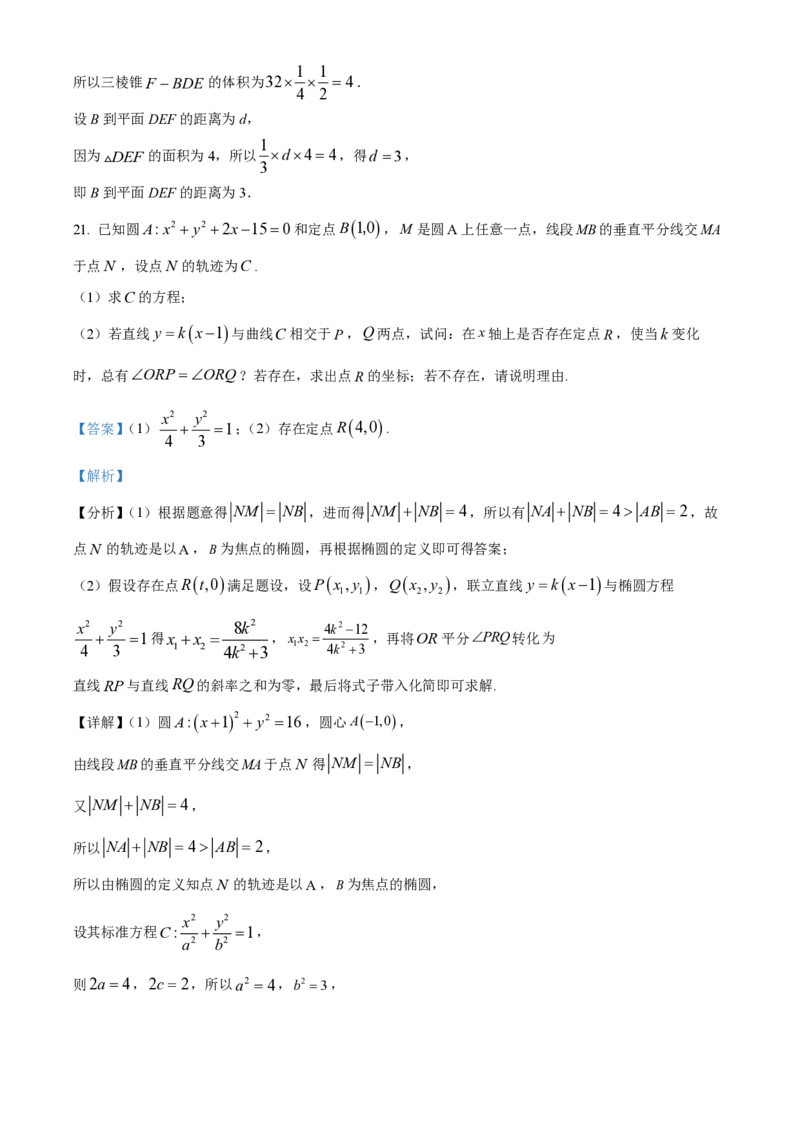云南省红河州开远市第一中学2024届高三上学期开学考试数学解析(1)_2023年9月_029月合集_2024届云南省红河州开远市第一中学高三上学期开学考试

开远市第一中学校 2023 年秋季学期高三年级开学考试
数学
考生注意：
1.本试满分 150分，考试时间 120分钟.
2.回答选择题时，选出每小题答案后，用 2B铅笔把答题卡上对应题目的答案标号涂黑.如需
改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上，写在
本试卷上无效.超出答题区域书写的答案无效，在试卷、草稿纸上作答无效.
一、选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项
是符合题目要求的.
2i
1. 已知i为虚数单位，若复数ai （ aR ）为纯虚数，则复数 z 2ai 在复平面上对应的点（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
【答案】D
【解析】
2i
【分析】化简复数 ，由纯虚数概念可解得a的值，从而得出结论.
ai
2i (2i)(ai) 2a1 2a
【详解】由    i为纯虚数,
ai a2 1 a2 1 a2 1
2a1 2a 1
则实部 0, 虚部  0, 解得 a  ,
a2 1 a2 1 2
则复数z 1i，在复平面上对应的点在第四象限.
故选: D.
2. 设全集U R，B  x x2 x20  ，A  x x1  ，则图中阴影部分对应的集合为（ ）
       
A. x x1 B. x1 x2 C. x x1 D. x1 x2
【答案】D
【解析】 
【分析】解一元二次不等式可求得集合B x 1 x2 ，再由图中阴影部分利用集合的基本运算即可求
得结果.
 
【详解】解集合B对应的不等式x2 x20可得1 x2，即B x 1 x2 ；
易知图中阴影部分对应的集合可表示为 ð A B，
U
   
由A x x1 可得ð A x x1 ，
U
因此 ð AB  x1 x2  ，即图中阴影部分对应的集合为  x1 x2  .
U
故选：D
3. 某市近几年大力改善城市环境，全面实现创建生态园林城市计划，现省专家组评审该市是否达到“生态
园林城市”的标准，从包含甲、乙两位专家在内的8人中选出4人组成评审委员会，若甲、乙两位专家至
少一人被邀请，则组成该评审委员会的不同方式共有（ ）
A. 70种 B. 55种 C. 40种 D. 25种
【答案】B
【解析】
【分析】先计算全部的选法，再考虑甲、乙均不选的选法，利用间接法作差即可．
【详解】解：8人中选4人有C4 70种，甲、乙均不选有C4 15种，共有C4 C4 55种．
8 6 8 6
故选：B．
4. 已知直线yx1与曲线y lnxa 相切，则实数a （ ）
A. 1 B. 1 C. 2 D. 3
【答案】C
【解析】
【分析】设切点的坐标为 x ,y  ，利用导数的几何意义可得出x 1a，再由点 x ,y  为直线yx1
0 0 0 0 0
与曲线y lnxa 的公共点可得出关于实数a的等式，解之即可.
1
【详解】设切点的坐标为 x ,y  ，对函数y lnxa 求导可得y ，
0 0 xa
1
所以切线的斜率为 ，
x a
0
1
因为函数y lnxa 在点 x ,y  处的切线方程为yx1，则 1，可得x 1a，
0 0 x a 0
0又因为点 x ,y  为直线yx1与曲线y lnxa 的公共点，
0 0
则y  x 1lnx a ，即2aln1，解得a2.
0 0 0
故选：C.
5. 已知抛物线C：y2 12x的焦点为F ，抛物线C上有一动点P，Q4,2 ，则 PF  PQ 的最小
值为（ ）
A. 5 B. 6 C. 7 D. 8
【答案】C
【解析】
【分析】抛物线的准线l的方程为x3，过P作PM l于M ，根据抛物线的定义可知 PF  PM ，则
当Q,P,M 三点共线时，可求 PM  PQ 得最小值，答案可得.
【详解】解：抛物线C：y2 12x的焦点为F3,0 ，准线l的方程为x3，
如图，过P作PM l于M ，
由抛物线的定义可知 PF  PM ，所以 PF  PQ  PM  PQ
则当Q,P,M 三点共线时， PM  PQ 最小为347.
所以 PF  PQ 的最小值为7.
故选：C.
1 2
6. 若函数 f(x) x3x2  在区间(a1,a5)内存在最小值，则实数a的取值范围是（ ）
3 3
A. [－5,1) B. (－5,1)
C. [－2,1) D. (－2,1)
【答案】C【解析】
【分析】先求出函数的极值点，要使函数在区(a1,a5)内存在最小值，只需极小值点在该区间内，且
在端点处的函数值不能超过极小值．
【详解】由 f(x) x2 2x，令 f(x)0，可得x2或x0，
由 f(x)0得：x<2或x0，由 f(x)0得：2 x0，
所以函数 f(x)在(,2)上单调递增，在(2,0)上单调递减，在(0,)上单调递增，
2
所以函数在x0处取得极小值 f(0) ，
3
1 2 2
令 f x x3x2   ，解得x0或x3，
3 3 3
若函数 f(x)在(a1,a5)内存在最小值，则3a10a5，得2a1．
故选：C
S S
7. 在等差数列{a }中，a 2023，其前n项和为S ，若 12  10 2，则S （ ）
n 1 n 12 10 2023
A. 2023 B. 2022 C. 2021 D. 2020
【答案】A
【解析】
【分析】由等差数列的求和公式可求得
a 
的公差为d，再由等差数列的求和公式即可求解.
n
【详解】设等差数列
a 
的公差为d，
n
1211 109
S S 12a  d 10a  d
因为 12  10 2，所以 1 2 1 2 ，
12 10  2
12 10
可得：d 2，
20222023
所以S 20232023 22023.
2023 2
故选：A.
1
8. 在平面直角坐标系中，已知点P3,4 为角终边上一点，若cos ，0,π ，则
3
sin（ ）
38 2 38 2
A. B.
15 1546 2 6 24
C. D.
15 15
【答案】D
【解析】
【分析】利用三角函数的定义求出角的正弦值和余弦值，求出的取值范围，利用同角三角函数的
基本关系求出sin 的值，再利用两角差的正弦公式可求得sin的值.
3 3
【详解】因为点P3,4 为角终边上一点，由三角函数定义可得cos  ，
32 42 5
4 4  3 
sin   ,1，
 
32 42 5

2

π π
易知为第一象限角，不妨设  ，
3 2
π 3π 1 π π
因为0,π ，则  ，因为cos 0，则  ，
3 2 3 3 2
2
1 2 2
所以，sin 1cos2  1  ，
 
3 3
所以，sinsinsincoscossin
2 2 3 1 4 6 24
     .
3 5 3 5 15
故选：D.
二、多选题：本题共 4小题，每小题 5分，共 20 分.在每小题给出的选项中，有多项符合题
目要求.全部选对的得 5分，部分选对的得 2分，有选错的得 0分.
9. 下列说法正确的有（ ）
A. 若一组样本数据
x,y i 1,2,3,,n
线性相关，则用最小二乘法得到的经验回归直线必经过样本中
i i
 
心点 x,y
B. 根据分类变量X 与Y 的成对样本数据，计算得到2 5.028，依据0.05的独立性检验
x 3.841，则推断X 与Y 无关不成立，即认为X 与Y 有关联，此推断犯错误的概率不大于0.05
0.05
C.
若随机变量和满足21，则E2E1，D4D1D. 若随机变量X ~ N  100,2 ，且PX 1200.84，则P100 X 1200.34
【答案】ABD
【解析】
【分析】根据回归方程的性质判断A，根据独立性检验的思想判断B，根据期望与方差的性质判断C，根据
正态分布的性质判断D.
【详解】对于A：若一组样本数据
x,y i 1,2,3,,n
线性相关，
i i
 
则用最小二乘法得到的经验回归直线必经过样本中心点 x,y ，故A正确；
对于B：因为2 5.0283.841 x ，所以有95%的把握可判断分类变量X 与Y 有关联，
0.05
此推断犯错误的概率不大于0.05，故B正确；
对于C：若随机变量和满足21，则E2E1，D4D，故C错误；
对于D：若随机变量X ~ N  100,2 ，且PX 1200.84，
则P100 X 120 PX 120PX 1000.840.50.34，故D正确；
故选：ABD
10. 已知三棱锥 ABCD的各顶点都在球 O 上，点 M，N 分别是 AC，CD 的中点， AB平面 BCD，
CD2AB2BC 2，AD 6，则下列说法正确的是（ ）
A. 三棱锥ABCD的四个面均为直角三角形
B. 球O的表面积为6
1
C. 直线BD与平面ABC所成角的正切值是
2
3
D. 点O到平面BMN的距离是
3
【答案】ABD
【解析】
【分析】根据线面垂直的性质和勾股定理的逆定理可得△ABC、△ABD、△DBC、△ACD为直角三角形，
进而判断A；根据三棱锥外接球的结构求出球的半径，利用球的表面积公式计算即可判断B；结合线面角
的定义即可判断C；根据三棱锥等体积法求出点O到平面BMN的距离，进而得出平面BMN被球O所截
的截面圆的半径，利用圆的面积公式计算即可判断D.【详解】
AB⊥平面BCD，∴△ABC、△ABD为直角三角形，
∵AB=1，BC=1，AD 6，由勾股定理得AC  2 ，BD 5，
又∵BC=1，CD=2，则BC2 CD2  BD2，AC2 CD2  AD2，
∴△DBC、△ACD为直角三角形，故A正确；
三棱锥A-BCD可看作由长、宽、高分别为2、1、1的长方体截得，O为AD的中点，球O的直径为
22 12 12  6，
2
 6 
故球O的表面积S 4  6，故B正确；
 
2
 
CD
直线BD与平面ABC所成角的平面角为∠DBC，∴tanDBC  2，所以C不正确；
BC
1 2 1 6
在Rt△ABC中，BM  AC  ，在△ACD中，MN  AD ，又BN  2 ，∴△BMN为直角
2 2 2 2
1 6 2 3
三角形，S     ，
△BMN 2 2 2 4
设点O到平面BMN的距离为h，由于O到平面BMN的距离与C到平面BMN的距离相等，∴
1 1 1
V V V ，则 S  AB S h，
OBMN CBNM MBCN 3 △BCN 2 3 △BMN
1 1 1 1 3
3
则  11   h，解得h ，故D正确，
3 2 2 3 4 3
故选：ABD．
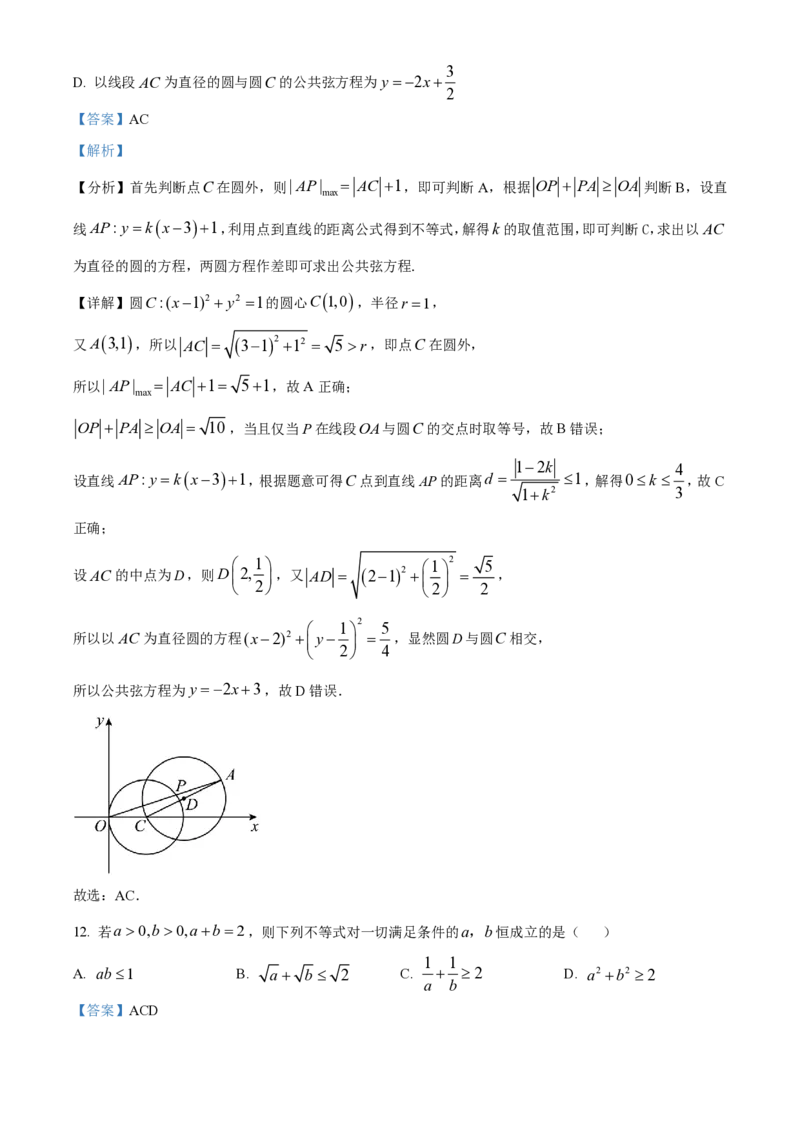
11. 已知圆C:(x1)2  y2 1,A3,1 ，点P为圆C上一动点，O为坐标原点，则下列说法中正确的是（ ）
A. AP 的最大值为 51
B. OP  PA 的最小值为2 2
 4
C. 直线AP的斜率范围为  0, 
 33
D. 以线段AC为直径的圆与圆C的公共弦方程为y 2x
2
【答案】AC
【解析】
【分析】首先判断点C在圆外，则| AP|  AC 1，即可判断A，根据 OP  PA  OA 判断B，设直
max
线AP: y kx31，利用点到直线的距离公式得到不等式，解得k的取值范围，即可判断C，求出以AC
为直径的圆的方程，两圆方程作差即可求出公共弦方程.
【详解】圆C:(x1)2  y2 1的圆心C1,0 ，半径r 1，
又A3,1 ，所以 AC  312 12  5 r，即点C在圆外，
所以| AP|  AC 1 51，故A正确；
max
OP  PA  OA  10 ，当且仅当P在线段OA与圆C的交点时取等号，故B错误；
12k 4
设直线AP: y kx31，根据题意可得C点到直线AP的距离d  1，解得0k  ，故C
1k2 3
正确；
 1 1 2 5
设AC的中点为D，则D  2, ，又 AD  212     ，
 2 2 2
2
 1 5
所以以AC为直径圆的方程(x2)2 

y

 ，显然圆D与圆C相交，
 2 4
所以公共弦方程为y 2x3，故D错误．
故选：AC．
12. 若a 0,b0,ab2，则下列不等式对一切满足条件的a，b恒成立的是（ ）
1 1
A. ab1 B. a  b  2 C.  2 D. a2 b2 2
a b
【答案】ACD【解析】
【分析】使用基本不等式、1的代换等方法一一判别即可.
【详解】对A，因为a 0,b0，所以2ab2 ab 即ab1，
当且仅当a b1时等号成立，A正确；
 2
对B，因为a 0,b0，所以 a  b ab2 ab=2+2 ab，
 2
结合A选项有 a  b 4，故 a  b 2，
当且仅当a b1时等号成立，B不正确；
1
对C，因为a 0,b0，ab2，所以 ab1，
2
1 1 1 1 1 b a b a
所以  = ab  1  12  2，
 
a b 2 a b 2a 2b 2a 2b
ab2

当且仅当 b a ，即a b1时等号成立，C正确；


2a 2b
对D，a2 b2 ab2 2ab42ab，
由A选项有ab1，则2ab2，所以a2 b2 2，D正确.
故选：ACD.
三、填空题：本题共 4小题，每小题 5分，共 20 分.
13. 已知向量a  与b  的夹角为 2π ，且 a  10,b  3,4，则a  在b  方向上的投影向量的坐标为
3
__________.
【答案】
3,4
【解析】
【分析】直接根据向量的投影公式求解即可
 
【详解】因为b 3,4，所以 b 5，

   b  1 3，4
则a  在b  方向上的投影为 a cos a,b  10  3,4 .
b  2 5
故答案为：
3,4
.
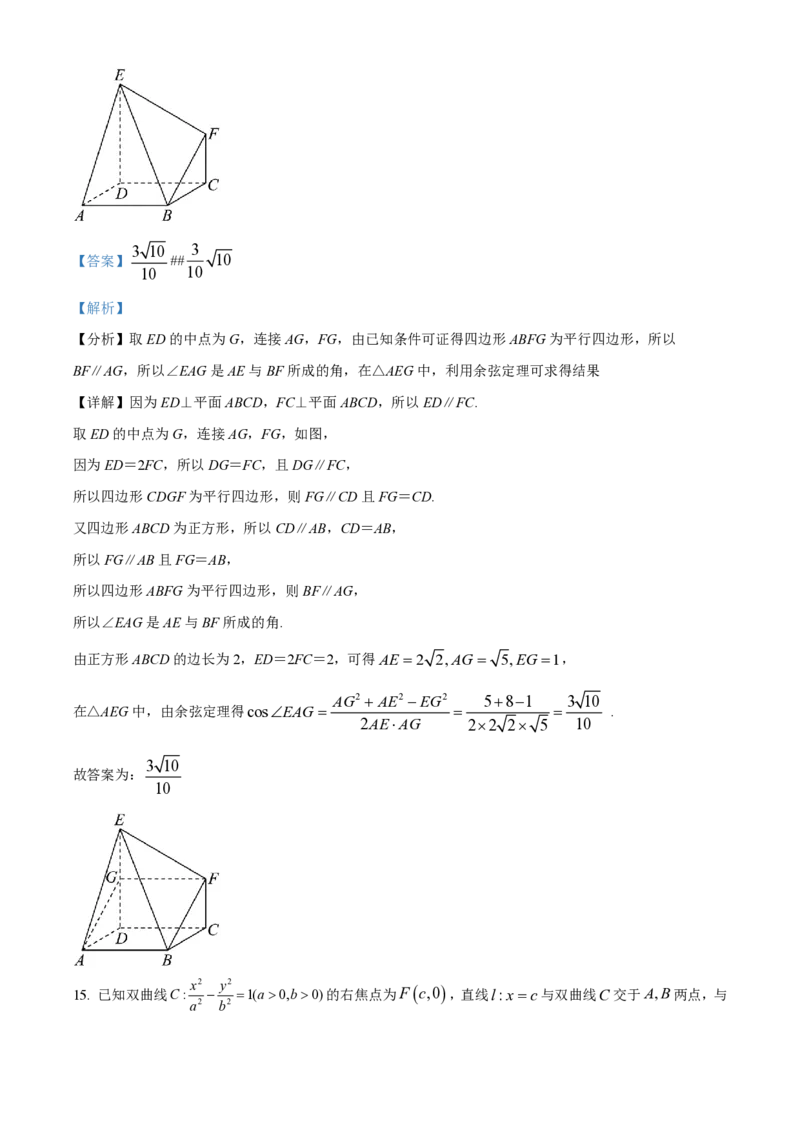
14. 如图，四边形ABCD是边长为2的正方形，ED⊥平面ABCD，FC⊥平面ABCD，ED＝2FC＝2，则异
面直线AE与BF所成角的余弦值为________.3 10 3
【答案】 ## 10
10 10
【解析】
【分析】取ED的中点为G，连接AG，FG，由已知条件可证得四边形ABFG为平行四边形，所以
BF∥AG，所以∠EAG是AE与BF所成的角，在△AEG中，利用余弦定理可求得结果
【详解】因为ED⊥平面ABCD，FC⊥平面ABCD，所以ED∥FC.
取ED的中点为G，连接AG，FG，如图，
因为ED＝2FC，所以DG＝FC，且DG∥FC，
所以四边形CDGF为平行四边形，则FG∥CD且FG＝CD.
又四边形ABCD为正方形，所以CD∥AB，CD＝AB，
所以FG∥AB且FG＝AB，
所以四边形ABFG为平行四边形，则BF∥AG，
所以∠EAG是AE与BF所成的角.
由正方形ABCD的边长为2，ED＝2FC＝2，可得AE 2 2,AG  5,EG 1，
AG2  AE2 EG2 581 3 10
在△AEG中，由余弦定理得cosEAG    .
2AEAG 22 2 5 10
3 10
故答案为：
10
15. 已知双曲线C:
x2

y2
1(a0,b0)的右焦点为Fc,0 ，直线l:xc与双曲线C交于A,B两点，与
a2 b2双曲线C的渐近线交于D,E两点，若 DE 2 AB ，则双曲线C的离心率是_________．
2 3 2
【答案】 ## 3
3 3
【解析】
【分析】利用双曲线通径长和与渐近线交点情况可得 AB , DE ,由 DE 2 AB 和a,b,c关系可求得
c2b，a= 3b，由此可求得离心率．
b
【详解】由双曲线方程可得其渐近线方程为：y x，
a
直线l:xc

 AB 为双曲线的通径，则
xc xc
  2b2
由x2 y2 得 b2 ，则 AB  ，
  1  y  a
a2 b2  a
xc xc
  2bc
由 b 得 bc ，则 DE 
y  x y  a
 
 a  a
2bc 4b2
由 DE 2 AB 得： 
a a
即c2b
所以a c2 b2  3b，
c 2 3
所以离心率e 
a 3
2 3
故答案为：
3
π
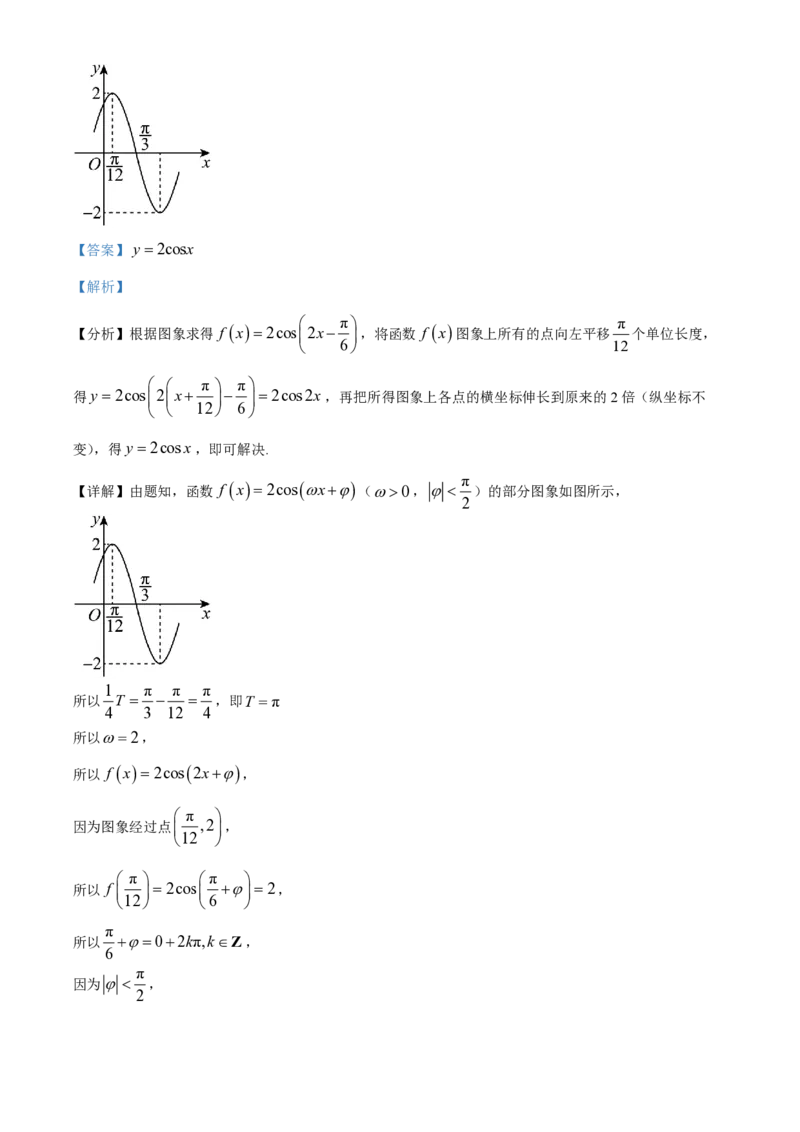
16. 已知函数 f x2cosx （0， ）的部分图象如图所示，将函数 f x 图象上所有
2
π
的点向左平移 个单位长度，再把所得图象上各点的横坐标伸长到原来的2倍（纵坐标不变），所得函数
12
图象的解析式为______．【答案】y 2cosx
【解析】
 π π
【分析】根据图象求得 f x2cos  2x ，将函数 f x 图象上所有的点向左平移 个单位长度，
 6 12
  π  π
得y 2cos

2

x



2cos2x，再把所得图象上各点的横坐标伸长到原来的2倍（纵坐标不
  12 6
变），得y 2cosx，即可解决.
π
【详解】由题知，函数 f x2cosx （0， ）的部分图象如图所示，
2
1 π π π
所以 T    ，即T π
4 3 12 4
所以2，
所以 f x2cos2x ，
 π 
因为图象经过点 ,2 ，
12 
 π  π 
所以 f   2cos    2，
12 6 
π
所以 02kπ,kZ，
6
π
因为 ，
2π
所以 ，
6
 π
所以 f x2cos  2x ，
 6
π
将函数 f x 图象上所有的点向左平移 个单位长度，
12
  π  π
得y 2cos

2

x



2cos2x，
  12 6
再把所得图象上各点的横坐标伸长到原来的2倍（纵坐标不变），
得y 2cosx，
所以所得函数图象的解析式为y 2cosx，
故答案为：y 2cosx
四、解答题：本题共 6小题，共 70分.解答应写出文字说明、证明过程或演算步骤.
3  a2 c2 b2
17. 已知△ABC的内角A，B，C所对边分别为a，b，c，且sinA .
2bc
（1）求B的大小；
（2）若△ABC为钝角三角形，且b 3，求△ABC的周长的取值范围.
π
【答案】（1）
3
 
（2） 2 3,3 3
【解析】
【分析】（1）根据正余弦定理，将条件变形，求角B的大小；
（2）根据正弦定理，将周长表示为三角函数，根据函数的定义域，求周长的取值范围.
【小问1详解】
a2 c2 b2
根据余弦定理可知， cosB，
2ac
32accosB 3acosB 3sinAcosB
所以sinA ，即sinA sinA ，
2bc b sinB
π
则tanB
3,B0,π
，所以B ；
3
【小问2详解】π 2π
设A  , ，
2 3 
a c b 3
   2
根据正弦定理可知sin A sinC sinB π ，
sin
3
2π 
所以a2sinA,c2sinC 2sin  A ，
 3 
2π 
所以周长abc2sinA2sin

A

 3
 3 
 3 1 
2sinA2 cosA sinA 3
 
2 2
 
3sinA 3cosA 3
 π
2 3sin

A

 3,
 6
π 2π π 2π 5π
因为A  , ,A   , ，
2 3  6  3 6 
 π 1 3  π
所以sin  A    ,   ，所以2 32 3sin  A   33 3，
 6  2 2   6
 
所以 ABC的周长为 2 3,3 3 .

18. 已知S 为数列 a  的前n项和，S 2a 4n2．
n n n n
（1）证明：数列
a 4
为等比数列；
n
 2n  1
（2）设数列 的前n项和为T ，证明：T  ．
 a a  n n 6
n n1
【答案】（1）证明见解析
（2）证明见解析
【解析】
a 4
【分析】（1）取n1计算a 2，a S S 2a 2a 4得到 n 2，得到证明.
1 n n n1 n n1 a 4
n1
2n 1 1 1 
（2）确定a 432n 4，变换    ，利用裂项求和计算得到证明.
n a a 332n 4 32n14
n n1【小问1详解】
a S 2a 412，a 2，a 46．
1 1 1 1 1
由S 2a 4n2，得S 2a 4n12,n2，
n n n1 n1
a
n
S
n
S
n1
2a
n
4n2

2a
n1
412

2a
n
2a
n1
4,n2，
a 4 2a 44
所以a 2a 4,n2，故 n  n1 2,n2，
n n1 a 4 a 4
n1 n1
所以数列
a 4
是以6为首项，2为公比的等比数列．
n
【小问2详解】
a 462n1 32n 4，
n
2n 2n 1 1 1 
故 a a   32n 4    32n14   3  32n 4  32n14 ，
n n1
2 22 2n
所以T
n

a a

a a



a a
1 2 2 3 n n1
1 1 1 1 1 1 1  1 1 1 1
               ．
3 2 8 8 20 32n 4 32n14 6 3 32n14 6
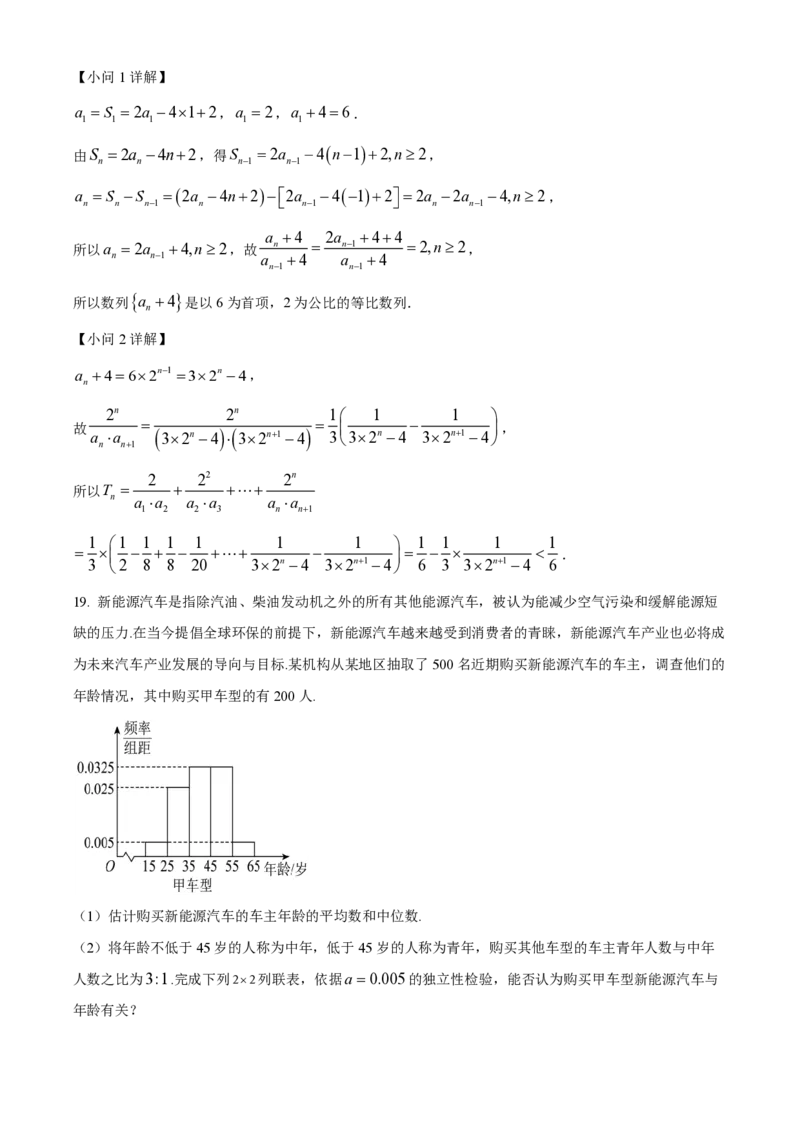
19. 新能源汽车是指除汽油、柴油发动机之外的所有其他能源汽车，被认为能减少空气污染和缓解能源短
缺的压力.在当今提倡全球环保的前提下，新能源汽车越来越受到消费者的青睐，新能源汽车产业也必将成
为未来汽车产业发展的导向与目标.某机构从某地区抽取了500名近期购买新能源汽车的车主，调查他们的
年龄情况，其中购买甲车型的有200人.
（1）估计购买新能源汽车的车主年龄的平均数和中位数.
（2）将年龄不低于45岁的人称为中年，低于45岁的人称为青年，购买其他车型的车主青年人数与中年
人数之比为3:1.完成下列22列联表，依据a 0.005的独立性检验，能否认为购买甲车型新能源汽车与
年龄有关？青年 中年 合计
甲车型
其他车型
合计
（3）用分层抽样的方法从购买甲车型的样本中抽取8人，再从中随机抽取4人，记青年有X 人，求X 的
分布列和数学期望.
nad bc2
附：2  nabcd .
abcdacbd
a 0.100 0.050 0.010 0.005
x 2.706 3.841 6.635 7.879
a
【答案】（1）40.75,41.15
（2）有95%的把握认为购买甲车型新能源汽车与年龄有关.
5
（3）分布列见解析, E(X) .
2
【解析】
【分析】（1）根据频率分布直方图计算购买新能源汽车的车主年龄的平均数和中位数;
（2）根据分布列和已知条件求出购买甲车型和其他车型的青年、中年人数，可得列联表，然后计算卡方，
查表可作出判断；
（3）先计算各层所抽取人数，然后由超几何分布概率公式求概率可得分布列，再根据期望公式可解.
【小问1详解】
购 买 新 能 源 汽 车 的 车 主 年 龄 的 平 均 数 为
200.00510+300.02510+400.032510+500.032510+600.00510=40.75,
设购买新能源汽车的车主年龄的中位数为t,
0.05+0.250.5,0.05+0.250.3250.5,

0.05+0.25t350.03250.5,t 41.15
【小问2详解】由直方图可知，购买甲车型的青年人数为200(0.0050.0250.0325)10125人，中年人数为
20012575人，
3
购买其他车型的青年人数为(500200) 225人，中年人数为30022575人，
31
于是的22列联表：
青年 中年 合计
甲车型 125 75 200
其他车型 225 75 300
合计 350 150 500
500(1257522575)2 125
因为2   8.9297.879，
350150200300 14
所以，有95%的把握认为购买甲车型新能源汽车与年龄有关.
【小问3详解】
用分层抽样的方法从购买甲车型的样本中抽取8人，
125 75
则青年有8 5人，中年有8 3人，所以X 的可能取值为1,2,3,4.
200 200
C1C3 5 1 C2C2 30 3
PX 1 5 3   ，PX 2 5 3   ，
C4 70 14 C4 70 7
8 8
C3C1 30 3 C4C0 5 1
PX 3 5 3   ，PX 4 5 3   ，
C4 70 7 C4 70 14
8 8
所以X 的分布列为：
X 1 2 3 4
1 3 3 1
P
14 7 7 14
1 3 3 1 5
所以E(X)1 2 3 4  .
14 7 7 14 2
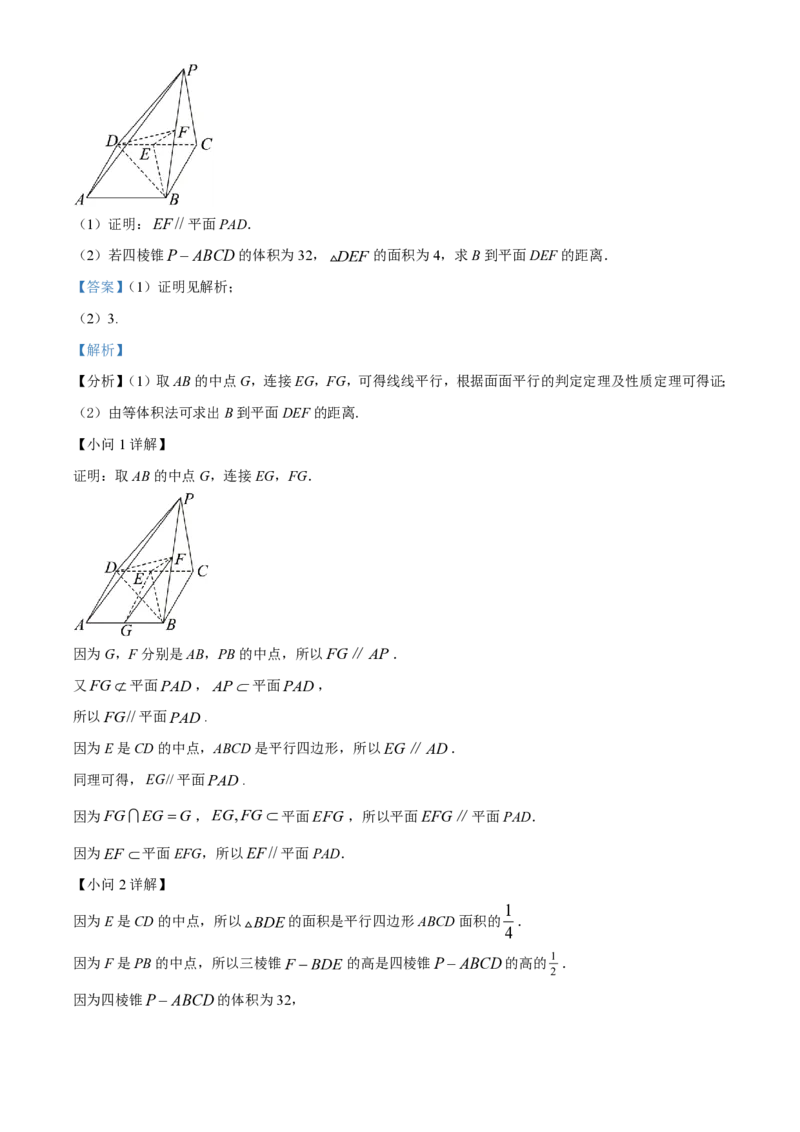
20. 如图，在四棱锥PABCD中，底面ABCD是平行四边形，E，F分别是CD，PB的中点．（1）证明：EF//平面PAD．
（2）若四棱锥PABCD的体积为32， DEF 的面积为4，求B到平面DEF的距离．

【答案】（1）证明见解析；
（2）3.
【解析】
【分析】（1）取AB的中点G，连接EG，FG，可得线线平行，根据面面平行的判定定理及性质定理可得证；
（2）由等体积法可求出B到平面DEF的距离.
【小问1详解】
证明：取AB的中点G，连接EG，FG．
因为G，F分别是AB，PB的中点，所以FG∥AP．
又FG平面PAD，AP平面PAD，
所以FG//平面PAD.
因为E是CD的中点，ABCD是平行四边形，所以EG∥AD．
同理可得，EG//平面PAD.
因为FG

EG G，EG,FG 平面EFG ，所以平面EFG∥平面PAD．
因为EF 平面EFG，所以EF//平面PAD．
【小问2详解】
1
因为E是CD的中点，所以 BDE的面积是平行四边形ABCD面积的 ．

4
1
因为F是PB的中点，所以三棱锥F BDE 的高是四棱锥PABCD的高的 ．
2
因为四棱锥PABCD的体积为32，1 1
所以三棱锥F BDE 的体积为32  4．
4 2
设B到平面DEF的距离为d，
1
因为 DEF 的面积为4，所以 d44，得d 3，

3
即B到平面DEF的距离为3．
21. 已知圆A:x2  y2 2x150和定点B1,0 ，M 是圆A上任意一点，线段MB的垂直平分线交MA
于点N ，设点N 的轨迹为C.
（1）求C的方程；
（2）若直线y kx1 与曲线C相交于P，Q两点，试问：在x轴上是否存在定点R，使当k变化
时，总有ORPORQ？若存在，求出点R的坐标；若不存在，请说明理由.
x2 y2
【答案】（1） 
1；（2）存在定点R4,0
.
4 3
【解析】
【分析】（1）根据题意得 NM  NB ，进而得 NM  NB 4，所以有 NA  NB 4 AB 2，故
点N 的轨迹是以A，B为焦点的椭圆，再根据椭圆的定义即可得答案；
（2）假设存在点Rt,0 满足题设，设Px ,y  ，Qx ,y  ，联立直线y kx1 与椭圆方程
1 1 2 2
x2 y2 8k2 4k2 12
 1得x x  ，xx  ，再将OR平分PRQ转化为
4 3 1 2 4k23 1 2 4k2 3
直线RP与直线RQ的斜率之和为零，最后将式子带入化简即可求解.
【详解】（1）圆A:x12  y2 16，圆心A1,0，
由线段MB的垂直平分线交MA于点N 得 NM  NB ，
又 NM  NB 4，
所以 NA  NB 4 AB 2，
所以由椭圆的定义知点N 的轨迹是以A，B为焦点的椭圆，
x2 y2
设其标准方程C:  1，
a2 b2
则2a4，2c2，所以a2 4，b2 3，x2 y2
所以曲线C:  1.
4 3
（2）设存在点Rt,0
满足题设，
x2 y2
联立直线y kx1 与椭圆方程  1消y得
4 3
 4k2 3  x2 8k2x  4k2 12  0，
设Px ,y  ，Qx ,y  ，
1 1 2 2
8k2 4k2 12
则由韦达定理得x x  ①，xx  ②，
1 2 4k23 1 2 4k2 3
由题设知OR平分PRQ直线RP与直RQ的倾斜角互补，
即直线RP与直线RQ的斜率之和为零，
y y
即 1  2 0，即x y x y ty  y 0，
x t x t 1 2 2 1 1 2
1 2
即2kx x 1tkx x 2tk 0③，
1 2 1 2
t4k
把①、②代入③并化简得 0，即 t4k 0④，
4k2 3
所以当k变化时④成立，只要t 4即可， 所以存在定点R4,0 满足题设.
【点睛】本题考查利用定义法求椭圆的方程，椭圆中的定点问题，考查运算能力与化归转化思想，是中档
题.
22. 已知函数 f xax2 4x2lnxaR ．
（1）讨论函数 f x 的单调性；
（2）若a2，证明： f x2x2lnx2  ex 2x  ．
【答案】（1）答案不唯一，具体见解析
（2）证明见解析
【解析】
【分析】（1）分类讨论参数a的取值范围，利用导数求解函数 f(x)的单调性；
lnx ex
（2）代入a2，化简不等式，通过构造函数gx1 ，hx ，利用导数求解函数
x x2g(x),h(x)的最值，将不等式转化为hx  gx 即可求证.
min max
【小问1详解】
2 2ax2 4x2
解：由题可知，x(0,)， fx2ax4  ．
x x
4x2  1 1 
若a0， fx ，所以 f x 在 0, 上单调递增，在 , 上单调递减；
x  2 2 
若a<0，令 fx0，解得x  1 1a 0或x  1 1a 0（舍），
1 a 2 a
 1 1a  1 1a 
所以 f x 在0, 上单调递增，在 ,上单调递减；
   
a a
   
若a0，当1616a0，即a1时， fx0在 0, 上恒成立，所以 f x 在 0, 上单
调递增；
 1 1a 
当0a1时，令 fx0，解得x  1 1a 或x  1 1a ，所以 f x 在0, 上单调递
1 a 2 a   a  
1 1a 1 1a  1 1a 
增，在 , 上单调递减，在 ,上单调递增；
   
a a a
   
【小问2详解】
证明：若a2，要证 f x2x2lnx2  ex 2x  ，即证x2 xlnxex，即证1 lnx  ex ．
x x2
lnx 1lnx
令函数gx1 ，则gx ．
x x2
令gx0，得x0,e ；令gx0，得xe,
．
1
所以gx 在 0,e 上单调递增，在 e, 上单调递减，所以gx  ge1 ，
max e
ex exx2
令函数hx ，则hx ．
x2 x3
当x0,2 时，hx0；当x2, 时，hx0．
e2
所以hx 在 0,2 上单调递减，在2,上单调递增，所以hx h2 ．
min 4e2  1
因为   1  0，所以hx  gx ，
4  e min max