云南省红河州开远市第一中学2024届高三上学期开学考试数学(1)_2023年9月_029月合集_2024届云南省红河州开远市第一中学高三上学期开学考试

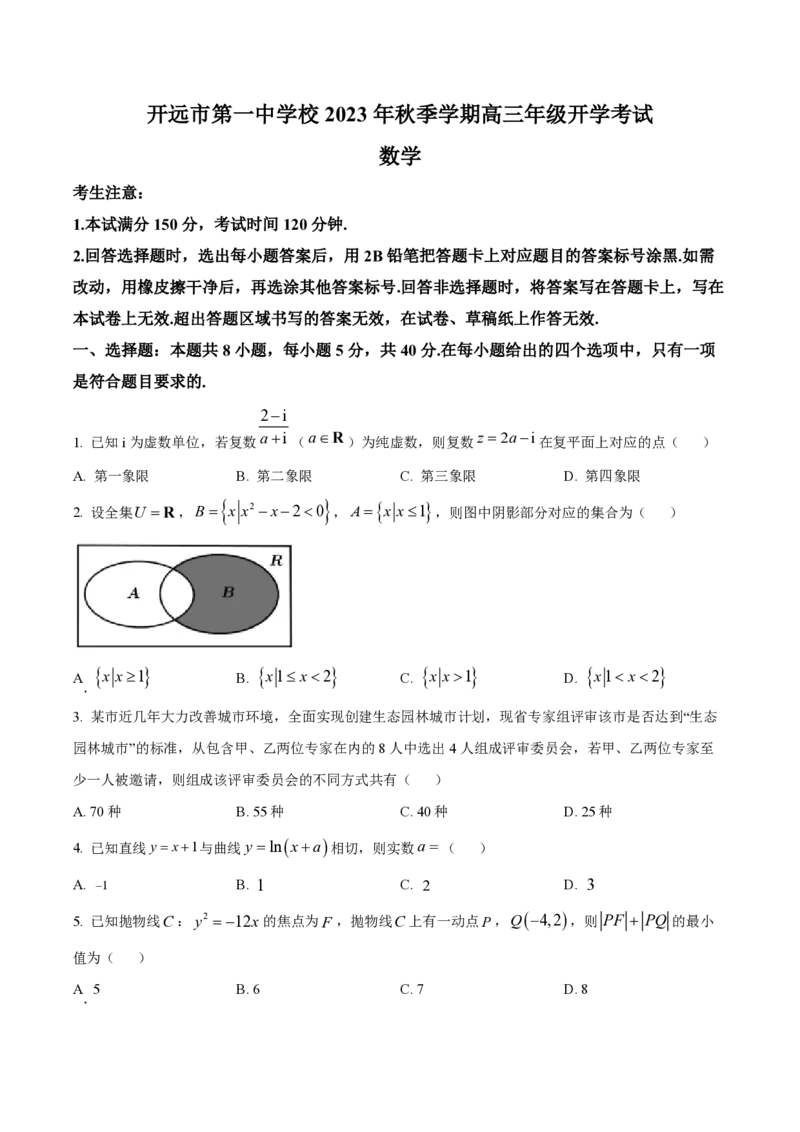
开远市第一中学校 2023 年秋季学期高三年级开学考试 数学 考生注意： 1.本试满分 150分，考试时间 120分钟. 2.回答选择题时，选出每小题答案后，用 2B铅笔把答题卡上对应题目的答案标号涂黑.如需 改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上，写在 本试卷上无效.超出答题区域书写的答案无效，在试卷、草稿纸上作答无效. 一、选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项 是符合题目要求的. 2i 1. 已知i为虚数单位，若复数ai （ aR ）为纯虚数，则复数 z 2ai 在复平面上对应的点（ ） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 2. 设全集U R，B  x x2 x20  ，A  x x1  ，则图中阴影部分对应的集合为（ ）         A x x1 B. x1 x2 C. x x1 D. x1 x2 . 3. 某市近几年大力改善城市环境，全面实现创建生态园林城市计划，现省专家组评审该市是否达到“生态 园林城市”的标准，从包含甲、乙两位专家在内的8人中选出4人组成评审委员会，若甲、乙两位专家至 少一人被邀请，则组成该评审委员会的不同方式共有（ ） A. 70种 B. 55种 C. 40种 D. 25种 4. 已知直线yx1与曲线y lnxa 相切，则实数a （ ） A. 1 B. 1 C. 2 D. 3 5. 已知抛物线C：y2 12x的焦点为F ，抛物线C上有一动点P，Q4,2 ，则 PF  PQ 的最小 值为（ ） A 5 B. 6 C. 7 D. 8 .1 2 6. 若函数 f(x) x3x2  在区间(a1,a5)内存在最小值，则实数a的取值范围是（ ） 3 3 A. [－5,1) B. (－5,1) C. [－2,1) D. (－2,1) S S 7. 在等差数列{a }中，a 2023，其前n项和为 S ，若 12  10 2，则S （ ） n 1 n 12 10 2023 A. 2023 B. 2022 C. 2021 D. 2020 1 8. 在平面直角坐标系中，已知点P3,4 为角终边上一点，若cos ，0,π ，则 3 sin（ ） 38 2 38 2 A. B. 15 15 46 2 6 24 C. D. 15 15 二、多选题：本题共 4小题，每小题 5分，共 20 分.在每小题给出的选项中，有多项符合题 目要求.全部选对的得 5分，部分选对的得 2分，有选错的得 0分. 9. 下列说法正确的有（ ） A. 若一组样本数据 x,y i 1,2,3,,n 线性相关，则用最小二乘法得到的经验回归直线必经过样本中 i i   心点 x,y B. 根据分类变量X 与Y 的成对样本数据，计算得到2 5.028，依据0.05的独立性检验 x 3.841，则推断X 与Y 无关不成立，即认为X 与Y 有关联，此推断犯错误的概率不大于0.05 0.05 C. 若随机变量和满足21，则E2E1，D4D1 D. 若随机变量X ~ N  100,2 ，且PX 1200.84，则P100 X 1200.34 10. 已知三棱锥 ABCD的各顶点都在球 O 上，点 M，N 分别是 AC，CD 的中点， AB平面 BCD， CD2AB2BC 2，AD 6，则下列说法正确的是（ ） A. 三棱锥ABCD的四个面均为直角三角形 B. 球O的表面积为6 1 C. 直线BD与平面ABC所成角的正切值是 2 3 D. 点O到平面BMN的距离是 311. 已知圆C:(x1)2  y2 1,A3,1 ，点P为圆C上一动点，O为坐标原点，则下列说法中正确的是（ ） A. AP 的最大值为 51 B. OP  PA 的最小值为2 2  4 C. 直线AP的斜率范围为  0,   3 3 D. 以线段AC为直径的圆与圆C的公共弦方程为y 2x 2 12. 若a 0,b0,ab2，则下列不等式对一切满足条件的a，b恒成立的是（ ） 1 1 A. ab1 B. a  b  2 C.  2 D. a2 b2 2 a b 三、填空题：本题共 4小题，每小题 5分，共 20 分. 13. 已知向量a  与b  的夹角为 2π ，且 a  10,b  3,4，则a  在b  方向上的投影向量的坐标为 3 __________. 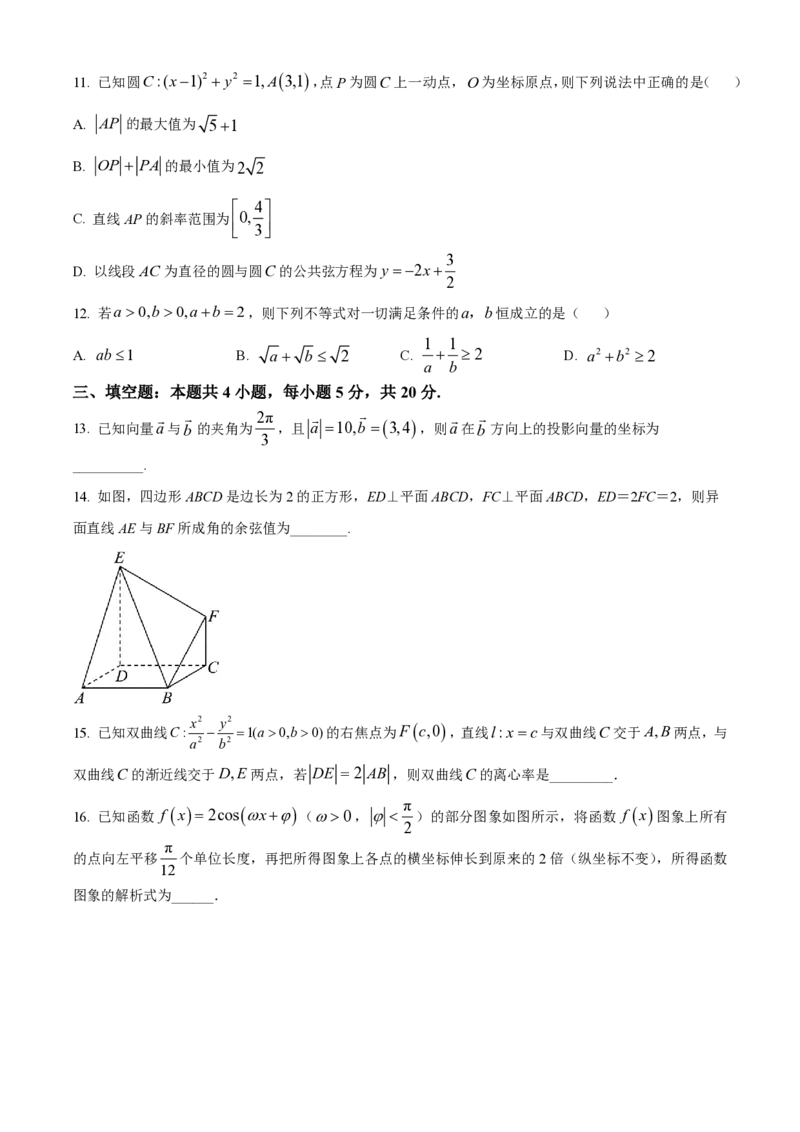14. 如图，四边形ABCD是边长为2的正方形，ED⊥平面ABCD，FC⊥平面ABCD，ED＝2FC＝2，则异 面直线AE与BF所成角的余弦值为________. 15. 已知双曲线C: x2  y2 1(a0,b0)的右焦点为Fc,0 ，直线l:xc与双曲线C交于A,B两点，与 a2 b2 双曲线C的渐近线交于D,E两点，若 DE 2 AB ，则双曲线C的离心率是_________． π 16. 已知函数 f x2cosx （0， ）的部分图象如图所示，将函数 f x 图象上所有 2 π 的点向左平移 个单位长度，再把所得图象上各点的横坐标伸长到原来的2倍（纵坐标不变），所得函数 12 图象的解析式为______．四、解答题：本题共 6小题，共 70分.解答应写出文字说明、证明过程或演算步骤. 3  a2 c2 b2 17. 已知△ABC的内角A，B，C所对边分别为a，b，c，且sinA . 2bc （1）求B的大小； （2）若△ABC为钝角三角形，且b 3，求△ABC的周长的取值范围. 18. 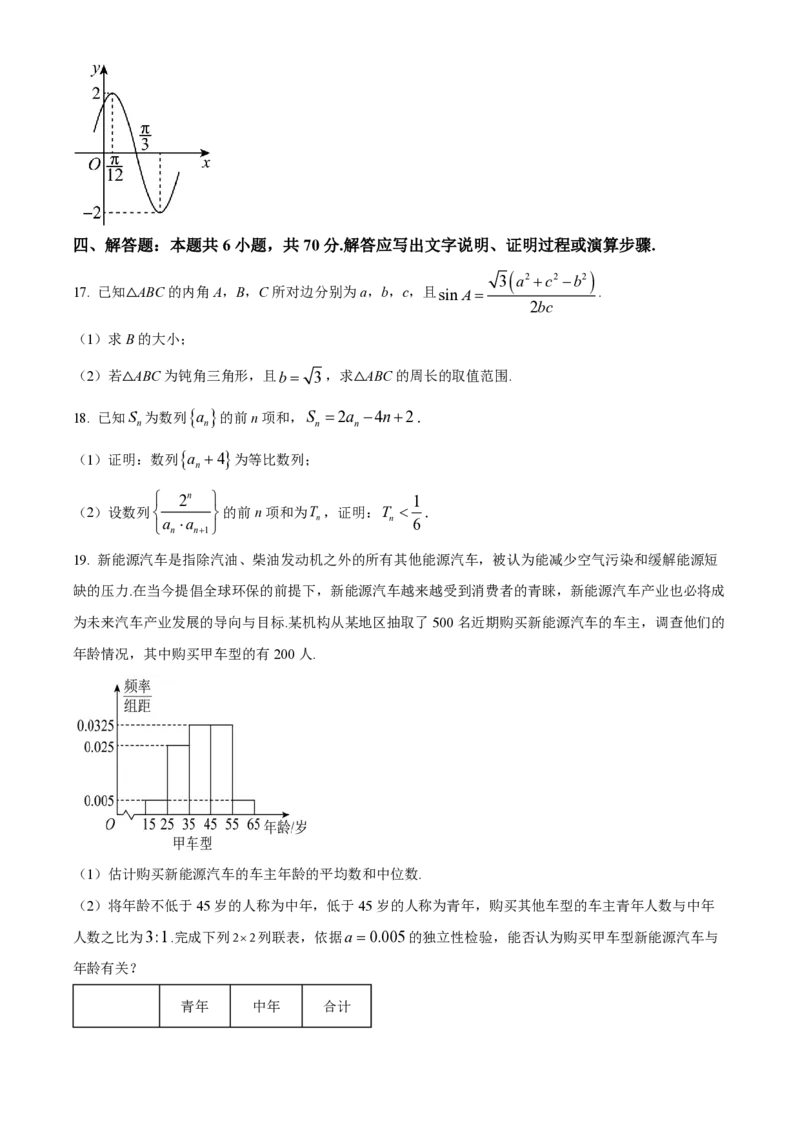已知S 为数列 a  的前n项和，S 2a 4n2． n n n n （1）证明：数列 a 4 为等比数列； n  2n  1 （2）设数列 的前n项和为T ，证明：T  ．  a a  n n 6 n n1 19. 新能源汽车是指除汽油、柴油发动机之外的所有其他能源汽车，被认为能减少空气污染和缓解能源短 缺的压力.在当今提倡全球环保的前提下，新能源汽车越来越受到消费者的青睐，新能源汽车产业也必将成 为未来汽车产业发展的导向与目标.某机构从某地区抽取了500名近期购买新能源汽车的车主，调查他们的 年龄情况，其中购买甲车型的有200人. （1）估计购买新能源汽车的车主年龄的平均数和中位数. （2）将年龄不低于45岁的人称为中年，低于45岁的人称为青年，购买其他车型的车主青年人数与中年 人数之比为3:1.完成下列22列联表，依据a 0.005的独立性检验，能否认为购买甲车型新能源汽车与 年龄有关？ 青年 中年 合计甲车型 其他车型 合计 （3）用分层抽样的方法从购买甲车型的样本中抽取8人，再从中随机抽取4人，记青年有X 人，求X 的 分布列和数学期望. nad bc2 附：2  nabcd . 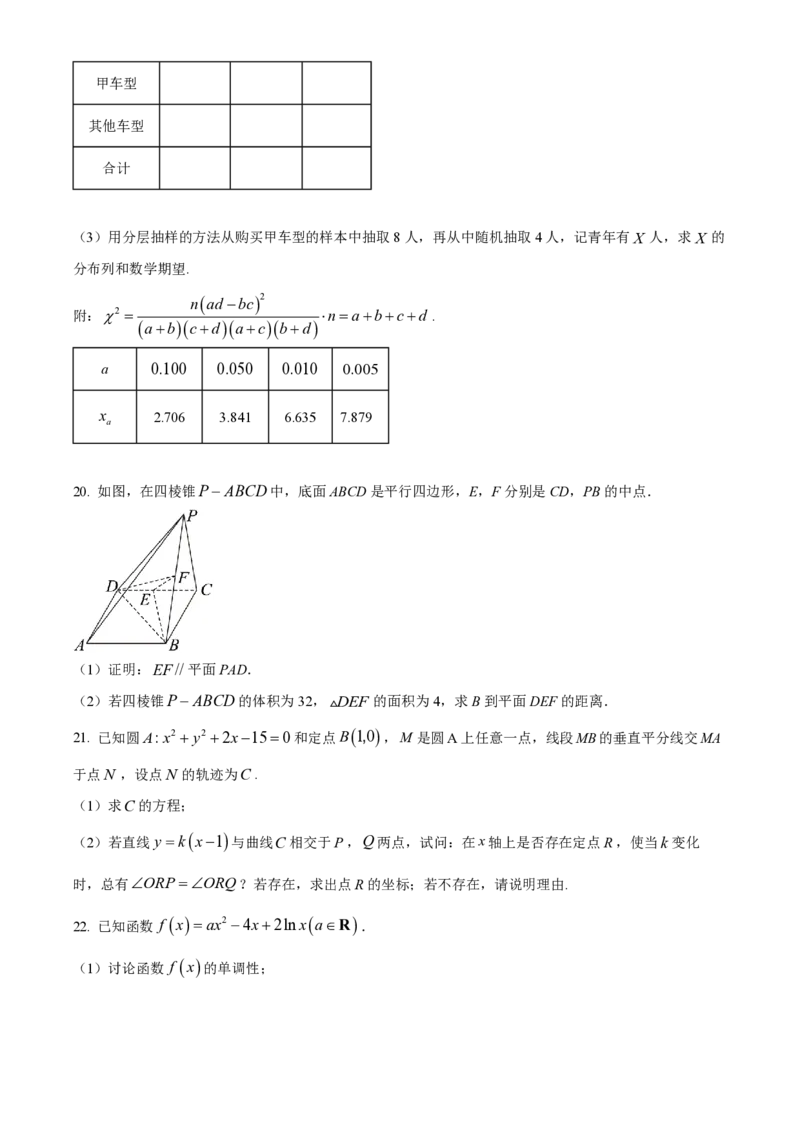abcdacbd a 0.100 0.050 0.010 0.005 x 2.706 3.841 6.635 7.879 a 20. 如图，在四棱锥PABCD中，底面ABCD是平行四边形，E，F分别是CD，PB的中点． （1）证明：EF//平面PAD． （2）若四棱锥PABCD的体积为32， DEF 的面积为4，求B到平面DEF的距离．  21. 已知圆A:x2  y2 2x150和定点B1,0 ，M 是圆A上任意一点，线段MB的垂直平分线交MA 于点N ，设点N 的轨迹为C. （1）求C的方程； （2）若直线y kx1 与曲线C相交于P，Q两点，试问：在x轴上是否存在定点R，使当k变化 时，总有ORPORQ？若存在，求出点R的坐标；若不存在，请说明理由. 22. 已知函数 f xax2 4x2lnxaR ． （1）讨论函数 f x 的单调性；