2024届南宁市高中毕业班适应性测试数学答案(1)_2024年5月_025月合集_2024届广西届南宁市高三二模（金太阳459C）

2024 届南宁市初中毕业班适应性测试 数学参考答案 一、选择题（本大题共12小题，每小题3分，共36分） 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A B A C A B D A C B D C 二、填空题（本大题共6小题，每小题2分，共12分 ） 1 13．x(x-5)； 14．x≥3； 15． ； 16．（0，6）； 17．25； 18．nm2． 3 三、解答题（本大题共72分） 19．（本题满分6分） 解：原式＝9（1）+2，·····························3分 ＝-9+2，·····································4分 ＝-7．········································6分 20．（本题满分6分） 解：原式＝a2 2abb2 2abb2，·············2分 ＝a2 4ab．································4分 1 当a＝2，b＝- 时， 4 1 原式＝22 42（ ），·····················5分 4 ＝4-2 ＝2．··········································6分 21．（本题满分10分） （1）如图所示，CE即为所求；·····················5分 （2）证明：∵在Rt△ABC中，∠ACB=90°，∠A=40°， ∴∠B=90°-40°=50°．··················6分 又点D为AB中点， ∴CD=BD．·······························7分 （第21题图） ∴∠B=∠DCB=50° ．·················8分 ∵CE平分∠BCD， 1 ∴∠BCE= ∠BCD=25°．··········· 9分 2 ∴∠AEC=∠B+∠BCE=75°．········10分 数学参考答案 第1页（共4页） {#{QQABAYCUggAoAIJAARhCQQ2QCAMQkBEACAoGhFAEIAAByAFABAA=}#}22．（本题满分10分） （1）m＝40，a＝12，n%＝40%；·················3分 （2）他的说法是错误的．···························· 4分 理由如下： ∵在参加测试的40名学生测试成绩中，排在最中间的两个分数都是85， 8585 ∴中位数为 85．·····················6分 2 ∵84＜85， ∴有一半以上的同学成绩超过了84分．···7分 ∴小邕的说法是错误的． （3）解：500×(40%+30%)＝350（人）············9分 答：估计本年级中食品安全意识良好的学生人数为350人．····················10分 23．（本题满分10分） （1）证明：∵AB∥DE， ∴∠B＝∠E．······································ 1分 又BF＝CE， ∴BF+FC＝CE+FC，即BC=EF．·············2分 在△ABC和△DEF中 ABDE  BE，·····································3分  BC EF ∴△ABC≌△DEF（SAS）．···················4分 （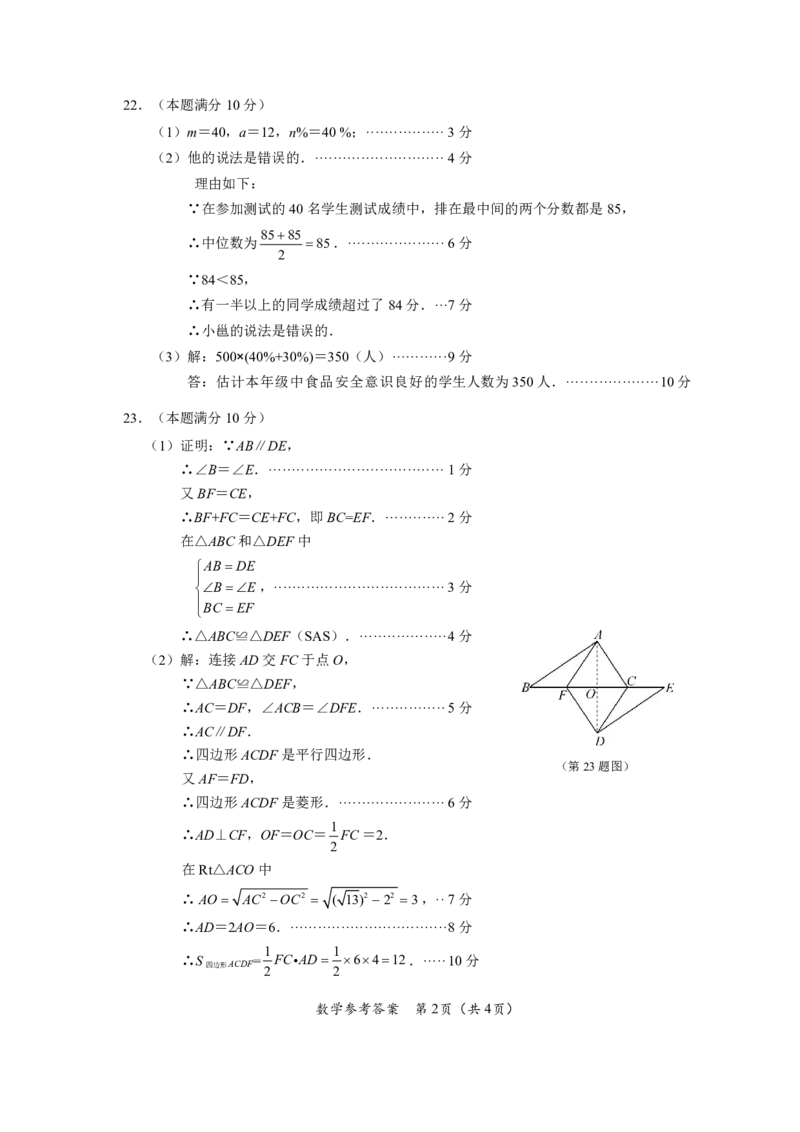2）解：连接AD交FC于点O， ∵△ABC≌△DEF， ∴AC＝DF，∠ACB＝∠DFE．················5分 ∴AC∥DF． ∴四边形ACDF是平行四边形． （第23题图） 又AF＝FD， ∴四边形ACDF是菱形．·······················6分 1 ∴AD⊥CF，OF＝OC＝ FC＝2． 2 在Rt△ACO中 ∴AO AC2 OC2  ( 13)2 22 3，··7分 ∴AD＝2AO＝6．··································8分 1 1 ∴S = FCAD 6412．·····10分 四边形ACDF 2 2 数学参考答案 第2页（共4页） {#{QQABAYCUggAoAIJAARhCQQ2QCAMQkBEACAoGhFAEIAAByAFABAA=}#}24．（本题满分10分） （1）解：设团购群1《儒林外史》和《简爱》的单价分别是x元、y元；············1分 3x2y12220 由题意得： ，·····3分 4x3y288 x48 解得  ．···························5分 y32 答：团购群1《儒林外史》和《简爱》的单价分别是48元、32元．············6分 （2）解：团购群1：（4832）150.784（0 元）， ·······································7分 团购群2：7015105（0 元） 1050-40393（0 元），····8分 ∵840＜930，·································9分 ∴选择团购群1购买更合算．············10分 25．（本题满分10分） （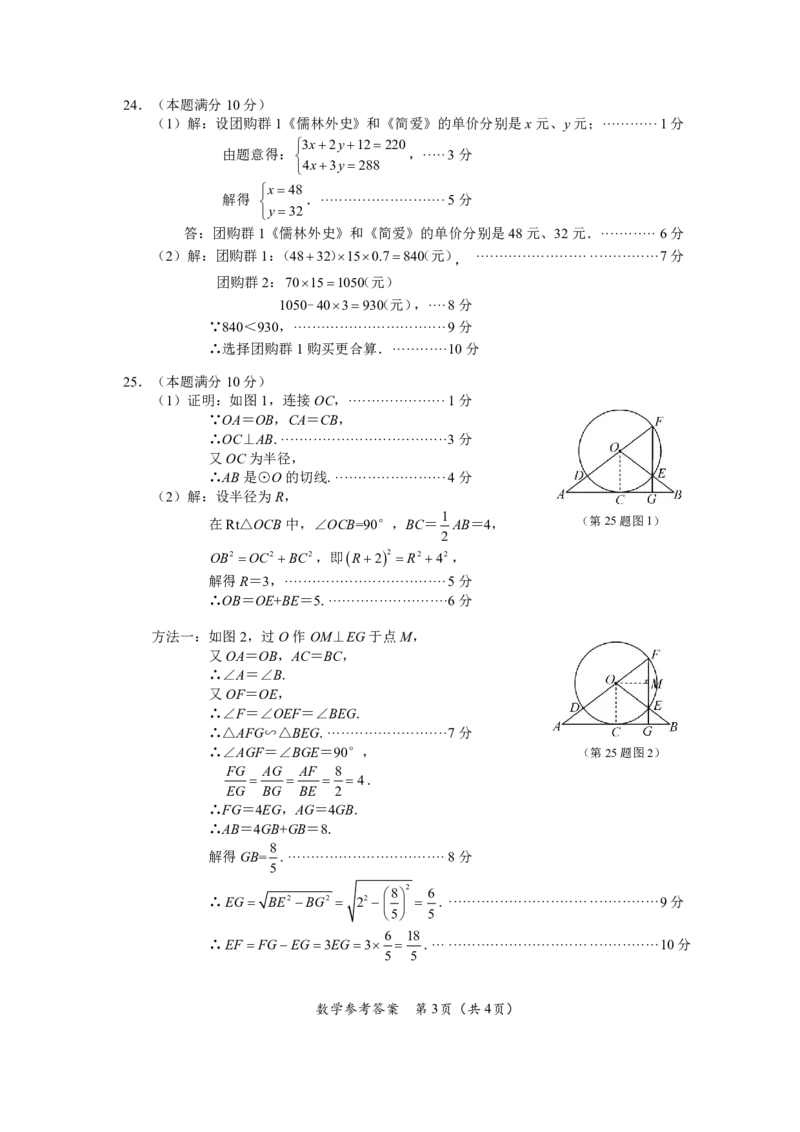1）证明：如图1，连接OC，·····················1分 ∵OA＝OB，CA＝CB， ∴OC⊥AB.····································3分 又OC为半径， ∴AB是⊙O的切线.························4分 （2）解：设半径为R， 在Rt△OCB中，∠OCB=90°，BC＝ 1 AB＝4， （第25题图1） 2 OB2 OC2 BC2，即R22 R242， 解得R＝3，···································5分 ∴OB＝OE+BE＝5.··························6分 方法一：如图2，过O作OM⊥EG于点M， 又OA＝OB，AC＝BC， ∴∠A＝∠B. 又OF＝OE， ∴∠F＝∠OEF＝∠BEG. ∴△AFG∽△BEG.··························7分 ∴∠AGF＝∠BGE＝90°， （第25题图2） FG AG AF 8     4. EG BG BE 2 ∴FG＝4EG，AG＝4GB. ∴AB＝4GB+GB＝8. 8 解得GB= .··································8分 5 2 8 6 ∴EG BE2 BG2  22    .·············································9分 5 5 6 18 ∴EF FGEG3EG3  .················································10分 5 5 数学参考答案 第3页（共4页） {#{QQABAYCUggAoAIJAARhCQQ2QCAMQkBEACAoGhFAEIAAByAFABAA=}#}方法二：如图3，连接DE， OD OE 3 ∵∠DOE＝∠AOB，   ， OA OB 5 ∴△DOE∽△AOB.·························7分 DE OE 3 ∴   . AB OB 5 24 ∴DE= .····································8分 （第25题图3） 5 ∵DF是⊙O直径， ∴∠DEF＝90°.·····························9分 2 24 18 ∴EF  DF2 DE2  62    .··········································10分  5  5 26．（本题满分10分） （1）解：由题意可知，抛物线顶点为（2，2），经过B（0，1.2） 设抛物线的解析式为yax222···············································1分 将点B（0，1.2）代入，得1.2a0222， 1 解得 a .·············································································2分 5 1 ∴抛物线的解析式为y x222.············································3分 5 （2）队伍排列时，最高的队员在正中间其位置的横坐标为2， 其余同学按照从高到低的顺序在其两侧对称排列. 身高为1.68与1.73的队员所在位置的横坐标分别为1.5与2.5，···············4分 身高为1.60的队员所在位置的横坐标分别为1与3； ∵1.8＜2， ∴身高最高的队员可以通过.·····························································5分 1 1 由题意，把x1.5代入y x222中，得y 1.52221.95. 5 5 ∵1.95＞1.73＞1.68， ∴可以通过.····································· ·············································6分 1 1 由题意，把x1代入y x222中，得y 12221.8. 5 5 ∵1.8＞1.60， ∴可以通过.····································· ·············································7分 综上所述，所有队员都可以通过. 1 （3）由题意，把y1.60代入 y x222中， 5 1 则1.6 x222.·····································································8分 5 解得x 2 2,x 2＋ 2 （舍去）.···················································9分 1 1 ∵2 2＞0.5， ∴最左边的跳绳队员与离他最近的甩绳队员之间距离的取值范围： 2 2＜x≤1.································· ·············································10分 数学参考答案 第4页（共4页） {#{QQABAYCUggAoAIJAARhCQQ2QCAMQkBEACAoGhFAEIAAByAFABAA=}#}