文档内容
哈三中 2023—2024 学年度上学期
高三学年第二次验收考试数学试卷
考试说明:
(1)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分.考试时间为120
分钟;
(2)第Ⅰ卷,第Ⅱ卷试题答案均答在答题卡上,交卷时只交答题卡.
第Ⅰ卷(选择题,共60分)
一、选择题(共60分)
(一)单项选择题(共8小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题
目要求的)
1.已知集合 , ,则( )
A. B. C. D.
2.已知 的终边上有一点 ,则 的值为( )
A. B. C. D.
3.已知 , ,则 ( )
A.25 B.5 C. D.
4.已知命题 , ,命题 , ,若命题 , 都是真命题,
实数 的取值范围是( )
A. B. C. D. 或
5.已知函数 和 的图象与直线 交点的横坐标分别 , ,则 ( )
A.1 B.2 C.3 D.4
6.小明在调查某班小学生每月的人均零花钱时,得到了下列一组数据:
月份 2 3 4 5 6 …
元 1.40 2.56 5.31 11 21.30 …
请从模型 ,模型 中选择一个合适的函数模型,并预测小学生零花钱首次超过300元的月份为
学科网(北京)股份有限公司( )(参考数据: , )
A.8 B.9 C.10 D.11
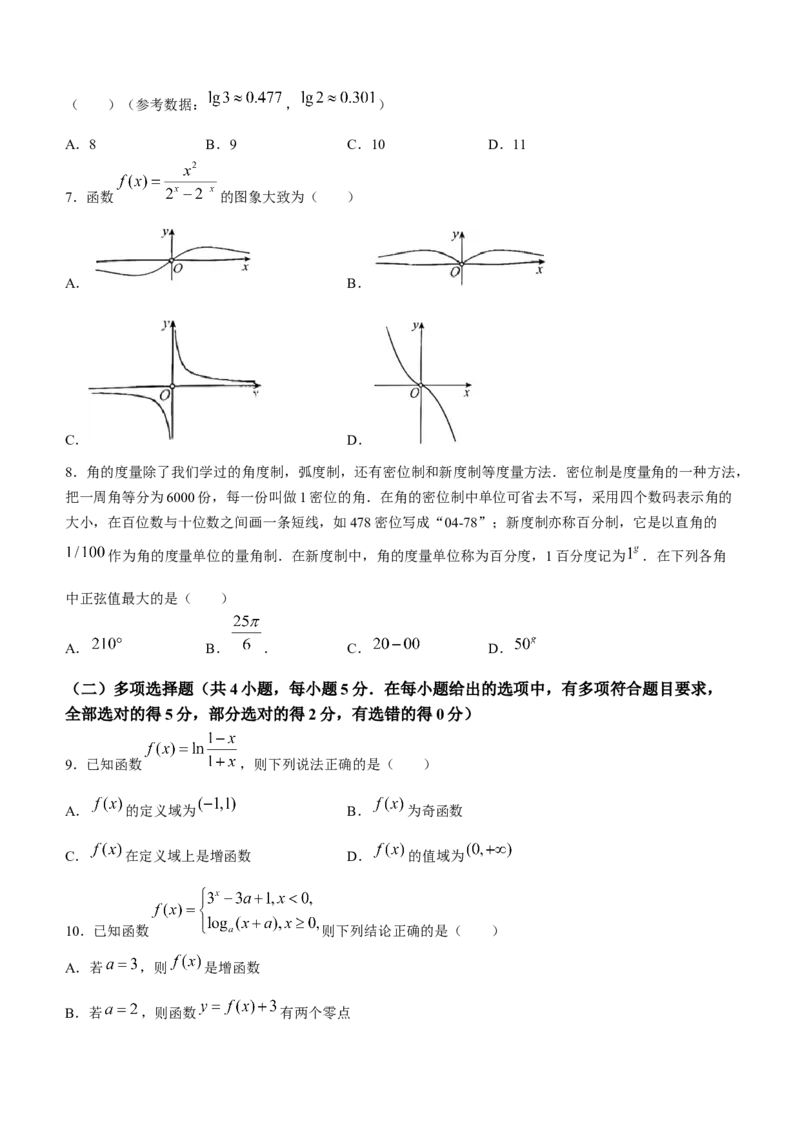
7.函数 的图象大致为( )
A. B.
C. D.
8.角的度量除了我们学过的角度制,弧度制,还有密位制和新度制等度量方法.密位制是度量角的一种方法,
把一周角等分为6000份,每一份叫做1密位的角.在角的密位制中单位可省去不写,采用四个数码表示角的
大小,在百位数与十位数之间画一条短线,如478密位写成“04-78”;新度制亦称百分制,它是以直角的
作为角的度量单位的量角制.在新度制中,角的度量单位称为百分度,1百分度记为 .在下列各角
中正弦值最大的是( )
A. B. . C. D.
(二)多项选择题(共4小题,每小题5分.在每小题给出的选项中,有多项符合题目要求,
全部选对的得5分,部分选对的得2分,有选错的得0分)
9.已知函数 ,则下列说法正确的是( )
A. 的定义域为 B. 为奇函数
C. 在定义域上是增函数 D. 的值域为
10.已知函数 则下列结论正确的是( )
A.若 ,则 是增函数
B.若 ,则函数 有两个零点
学科网(北京)股份有限公司C.若 ,则 的值域为
D.若 有最大值,则实数 的取值范围是
11.已知函数 为偶函数,在 时, 单调递减,且 .若 ,
, ,则下列正确的有( )
A. B. C. D.
12.函数 的定义域为 , ,且 为奇函数,当 时, ,
则下列说法正确的是( )
A. 在 上单调递增
B.
C.若关于 的方程 在区间 上的所有实数根之和为 ,则
D.函数 有2个零点
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题5分,共20分.将答案填在答题卡相应的位置上)
13.已知幂函数 在 上单调递增,则 __________.
14.函数 与 的图象交点为 .若 , ,则 __________.
15.明清时期,浙江、苏州、四川等地盛产折扇,题字作画亦兴于此.这一精湛的技艺从明代开始传入欧洲,
风行世界.如图是折扇的示意图,其中 , . 为 的中点,则扇面(图中扇
环)部分的面积是__________ .
学科网(北京)股份有限公司16.若存在常数 ,使得对函数 的定义域 内的任意 , ,都有
成立,则称函数 是在其定义域 上是“ -利普希兹函数”.若函数
是“ -利普希兹函数”,则 的最小值为__________.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.已知 , 是关于 的一元二次方程 的两根.
(1)求 的值;
(2)若 ,求 的值.
18.已知 , .
(1)当 , 时,求函数 的值域;
(2)若对任意的 , 恒成立,求实数 的取值范围.
19.已知 , ,其中 , .
(1)求 的值;
(2)求 的值.
20.苍苍黑土,漭漭龙江.北国骊珠,普育名庠.2023年10月6日,哈三中将迎来建校百年庆典.某公司为
哈三中百年校庆设计了文创产品,并批量生产进行售卖.经市场调研发现,若本季度在原材料上多投入 万
元,产品销售周可增加 千个,其中 每千个的销售价格为 万元,另外每生
产1千个吉祥物还需要投入其他成本0.5万元.
(1)写出该公司本季度增加的利润 与 (单位:万元)之间的函数关系;
(2)当 为多少万元时,该公司在本季度增加的利润最大?最大为多少万元?
21.已知函数 为偶函数.
(1)求实数 的值;
学科网(北京)股份有限公司(2)判断 的单调性,并解不等式 ;
(3)设 ,若方程 有解.求实数 的取值范围.
22.已知函数 , .
(1)当 时,求函数 在点 处的切线方程;
(2)若函数 有两个零点 , ,求实数 的取值范围;
(3)在(2)的条件下,证明: .
哈三中 2023—2024 学年度上学期
高三学年第二次验收考试数学答案
1—4BCBD 5—8BCAC
9.AB 10.ACD 11.ACD 12.BD
13.2 14.3 15. 16.
17.(1) (2)
18.(1) (2)
19.(1) (2)
20.(1) (2) ,
学科网(北京)股份有限公司21.(1) , 单调递减, 单调递增
(2) (3)
22.(1) (2) (3)略
学科网(北京)股份有限公司