文档内容
五年(2019-2023)年高考真题分项汇编
专题 17 数系扩充及复数引入
复数是高考中必出题型,一般是小题出现,主要形式是选题题前三题形式出现。
考点01 复数的概念以及基本意义
考点02 复数的四则运算
考点 01 复数的概念以及基本意义
1.(2023年北京卷·)在复平面内,复数 对应的点的坐标是 ,则 的共轭复数 ( )
.
A B. C. D.
【答案】D
【解析】: 在复平面对应的点是 ,根据复数的几何意义, ,
由共轭复数的定义可知, .
故选:D
2.(2023年新课标全国Ⅰ卷·)已知 ,则 ( )
A. B. C.0 D.1
【答案】A
【解析】:因为 ,所以 ,即 .
故选:A.
3.(2023年全国乙卷理科·)设 ,则 ( )
A. B. C. D.
【答案】B
【解析】:由题意可得 ,
则 .
故选:B.4.(2021年高考浙江卷·)已知 , ,(i为虚数单位),则 ( )
A. B.1 C. D.3
【答案】C
【解析】: ,利用复数相等的充分必要条件可得: ,故选C.
5.(2020年浙江省高考数学试卷·第2题)已知a∈R,若a–1+(a–2)i(i为虚数单位)是实数,则a= ( )
A.1 B.–1 C.2 D.–2
【答案】C
【解析】:因为 为实数,所以 ,故选:C
6.(2021年新高考全国Ⅱ卷)复数 在复平面内对应的点所在的象限为 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】A
【解析】: ,所以该复数对应的点为 ,该点在第一象限,故选
A.
7.(2022高考北京卷·)若复数z满足 ,则 ( )
A.1 B.5 C.7 D.25
【答案】B
【解析】:由题意有 ,故 .故选,B.
8.(2019·全国Ⅱ·理·)设 ,则在复平面内 对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】C
【解析】∵ ,∴ ,对应坐标 ,是第三象限.
9.(2023年新课标全国Ⅱ卷·)在复平面内, 对应的点位于 ( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】A
【解析】:因为 ,
则所求复数对应的点为 ,位于第一象限.故选:A.
10.(2020北京高考·)在复平面内,复数 对应的点的坐标是 ,则 ( ).
A. B. C. D.
【答案】B 【解析】由题意得 , .故选:B.二 填空
1.(2020年高考课标Ⅱ卷)设复数 , 满足 , ,则 =__________.
【答案】
【解析】:方法一:设 , ,
,
,又 ,所以 , ,
.故答案为: .
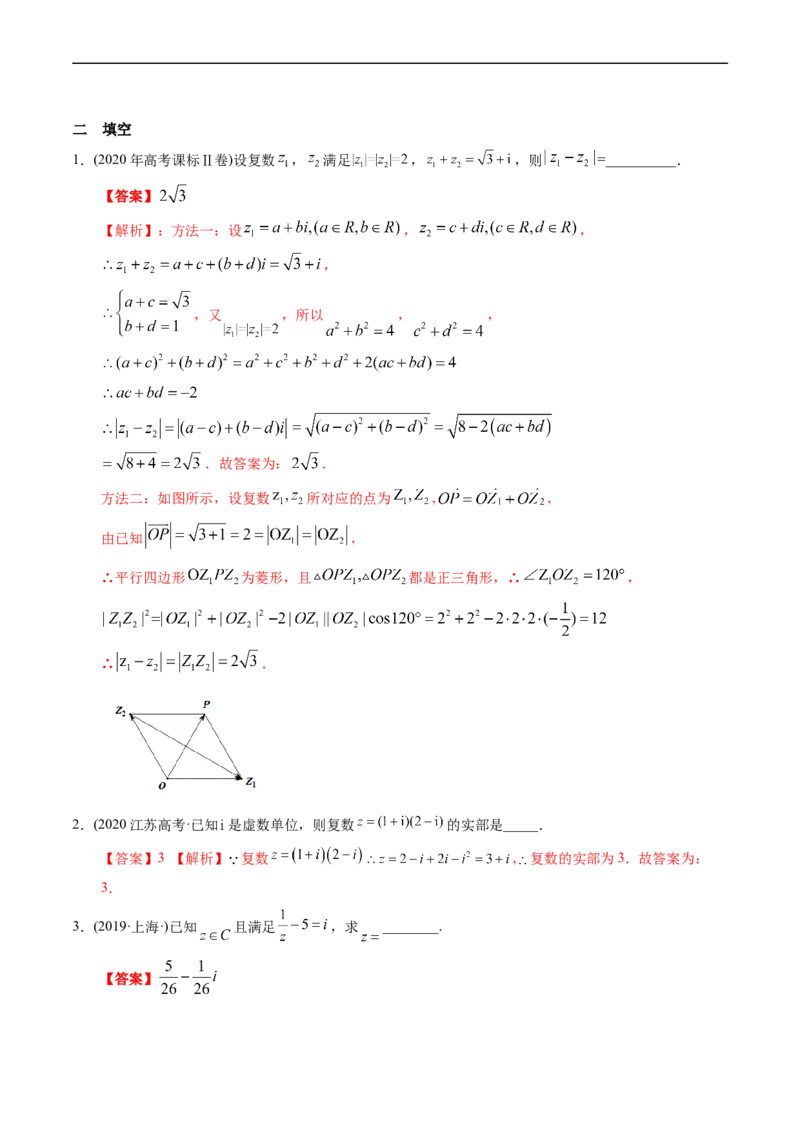
方法二:如图所示,设复数 所对应的点为 , ,
由已知 ,
∴平行四边形 为菱形,且 都是正三角形,∴ ,
∴ .
2.(2020江苏高考·已知 是虚数单位,则复数 的实部是_____.
【答案】3 【解析】 复数 , 复数的实部为3.故答案为:
3.
3.(2019·上海·)已知 且满足 ,求 ________.
【答案】【解析】 , .
4.(2019·浙江·)复数 ( 为虚数单位),则 .
【 答 案 】 【 解 析 】 解 法 一 : 由 于 , 则
.解法二: .
5.(2019·江苏·)已知复数 的实部为 ,其中 为虚数单位,则实数 的值是______.
【答案】2【解析】因为 的实部为 , .
考点 02 复数的四则运算
1.(2022新高考全国I卷·)若 ,则 ( )
A. B. C.1 D.2
【答案】D
【解析】:由题设有 ,故 ,故 , 故选:D
2.(2022年高考全国甲卷数学)若 ,则 ( )
A. B. C. D.
【答案】C【解析】
故选 :C
3.(2022年浙江省高考数学试题·)已知 ( 为虚数单位),则 ( )
A. B. C. D.
【答案】B
【解析】: ,而 为实数,故 ,故选,B.
4.(2022新高考全国II卷·) ( )
A. B. C. D.
【答案】.D
【解析】: . 故选 D.5.(2021高考北京·)在复平面内,复数 满足 ,则 ( )
A. B. C. D.
【答案】D
【解析】:由题意可得: .故选:D.
6.(2021年新高考Ⅰ卷·)已知 ,则 ( )
A. B. C. D.
【答案】C
【解析】:因为 ,故 ,故 ,故选C.
7.(2021年高考全国乙卷理科·)设 ,则 ( )
A. B. C. D.
【答案】C
【解析】:设 ,则 ,则 ,
所以, ,解得 ,因此, .故选:C.
8.(2021年高考全国甲卷理科·)已知 ,则 ( )
A. B. C. D.
【答案】B
【解析】: ,
.故选:B.
9.(2020年高考课标Ⅰ卷理科·)若z=1+i,则|z2–2z|= ( )
A.0 B.1 C. D.2
【答案】D
【解析】由题意可得: ,则 .
故 .故选:D.
10.(2020年高考课标Ⅲ卷)复数 虚部是 ( )A. B. C. D.
【答案】D
解析:因为 ,
所以复数 的虚部为 .
故选:D.
【点晴】本题主要考查复数的除法运算,涉及到复数的虚部的定义,是一道基础题.
11.(2020年新高考全国Ⅰ卷(山东)·第2题) ( )
A.1 B.−1 C.i D.−i
【答案】D 【解析】: 故选:D
12.(2020年新高考全国卷Ⅱ数学) = ( )
A. B. C. D.
【答案】B【解析】:
13.(2020天津高考·) 是虚数单位,复数 _________.
【答案】 【解析】 .故答案为: .
14.(2019·全国Ⅲ·)若 ,则 ( )
A. B. C. D.
【答案】D【解析】根据复数运算法则, ,故选D.
另解:由常用结论 ,得 ,则 ,故选D.
二、填空题
1.(2023年天津卷·)已知 是虚数单位,化简 的结果为_________.
【答案】
【解析】:由题意可得 .故答案为: .
2.(2021高考天津·) 是虚数单位,复数 _____________.【答案】 【解析】: . 故答案为: .