21级高三雅安市三诊数学（文）答案_2024年5月_01按日期_10号_2024届四川省雅安市高三下学期第三次诊断性考试_四川省雅安市2023-2024学年高三三诊数学（文）试题

雅安市高 2021 级第三次诊断性考试 数学（文科）参考答案 一、选择题（本大题共 12小题，每小题 5分，共 60分） BDDDA CCBCA BD 二、填空题(本大题共 4 小题，每小题 5 分，共 20分) 4 13. 4 14. 15 15. 3 16. 29 三、解答题(本大题共 6 小题，共 70 分) 1 17.(1)∵b  acosC  c， 2 1 由正弦定理得sinB sin AcosC  sinC sin(AC) sin AcosC cosAsinC， 2 1 ∴ sinC  cosAsinC. ∵sinC  0， 2 1  ∴cosA ，∴A .··················································6分 2 3 (2) 由已知得ABAC  cbcosA3，故bc  6. 由余弦定理得a2 b2 c2 2bccosAb2 c2 bc  2bcbc bc  6， 当且仅当b  c  6时，a有最小值 6 .····································12分 18.（1）每月使用跑腿服务不低于5次的消费者年龄的平均数为 200.02810300.03010400.02210500.0201033.4， 设每月使用同城配送服务不低于5的消费者年龄的中位数为a， 则0.02810 a25 0.0300.5 ，解得a 32.3.··························6分 （2）补全的22列联表如下： 年龄段I 年龄段II 合计 使用同城配送服务频率高 145 105 250 使用同城配送服务频率低 255 295 550 合计 400 400 800 800  145295105255 2 所以K2  9.3096.635． 400400550250 所以，有99%的把握认为同城配送服务的使用频率高低与年龄段有关．·············12分 19.（1）证明：因为 ， 为线段 的中点， 所以 ，···························································1分 在等腰梯形 中，作 于 ，则由 得 ， 数学（文科）答案 1/4 {#{QQABaYSAggiAQJJAARgCQQkACAMQkAGAAKoOQBAMMAAAiRFABCA=}#}所以 ，所以 ， 因为 ，所以 所以 ∽ ，所以 ， 所以 ，所以 ，·····································3分 因为 ， ， 所以 平面 ，·················································4分 因为 在平面 内，所以 ，································5分 因为 ， 在平面 内，所以 平面 .·······6分 （2）因为 ， ，所以 ， ， 取 的中点 ，连接 ，则 ，因为 平面 ，所以 ， 又 所以 平面 ，·································7分 PDM 为直线 PD 与平面 ABCD 所成的角， 3 1 1 在正PAC中，PM  ，又因为DM  BC  ， 2 2 2 5 10 在RtPDM 中，PD2 PM2 DM2  ，PD  ， 2 2 3 PM 3 10 2 sinPDM    . 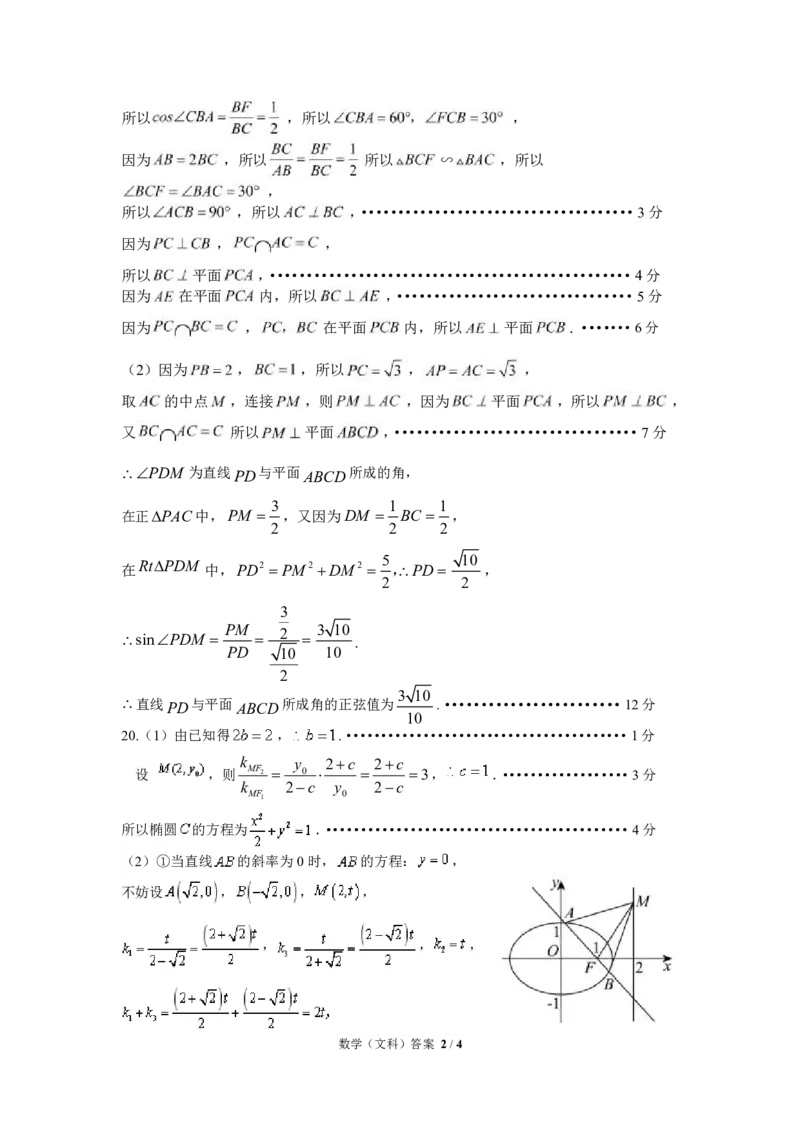PD 10 10 2 3 10 直线 PD 与平面 ABCD 所成角的正弦值为 .························12分 10 20.（1）由已知得 ， .········································1分 k y 2c 2c 设 ，则 MF 2  0   3， ．··················3分 k 2c y 2c MF 0 1 所以椭圆 的方程为 ．···········································4分 （2）①当直线 的斜率为0时， 的方程： ， 不妨设 ， ， ， ， ， ， 数学（文科）答案 2/4 {#{QQABaYSAggiAQJJAARgCQQkACAMQkAGAAKoOQBAMMAAAiRFABCA=}#}所以 ；·························································5分 ②当直线 的斜率不为0时，如图，设 的方程： ， ， ． 由 ，得 ． 则 ， .········································7分 ,·····························10分 又 ，所以 ．···············································11分 综上， ．所以 ， ， 成等差数列.···························12分 21.(1)依题意， ， 令 ，得 ， 因为 ， 所以当 时， ， 在 上单调递减； 当 时， ， 故 在 上单调递增； 当 时， 有解， 综上， ．·························································4分 （2）依题意，由 ， 得 ， 即 ，················································6分 设 ， ， 则 设 ，则 ， 当 时， ， 单调递增； 所以在 上， ，且 ，   当 a0，即a 时，h'(x)0，h(x)在  0, 上单调递减，h(x)h(0)，不符合 2 2 题意，舍去，······························································8分 ②当 ，即 时， （I）若 ，即 ， 数学（文科）答案 3/4 {#{QQABaYSAggiAQJJAARgCQQkACAMQkAGAAKoOQBAMMAAAiRFABCA=}#}，使得 ，当 时， ，h(x) 在 内单调递减， ，不符合题意，舍去，········································10分 （II）若 ，即 ， 恒成立， 在 上单调递增，则 ，符合题意． 综上，实数 的取值范围为 ．···········································12分 22.（1）曲线 是以 为圆心的半圆， 所以半圆的极坐标方程为 ， 曲线 以 为圆心的圆，转换为极坐标方程为 . 故半圆 ，圆 的极坐标方程分别为： ， 5分 （2）由（1）得： . 点 到直线 的距离 . 所以 其中 ，当 时， 的面积的最大值为4.···········10分 23.（1）当 时，不等式为 ， 当 时， 可以化为 ，解得 ； 当 时， 可以化为 ，得 ； 当 时， 可以化为 ，解得 ，不等式不成立； 综上,可得不等式 的解集为 ·································5分 （2）当 时， 当 时等号成立，由 可得 （舍）或 ，故 , 由柯西不等式可得 ，即得 当且仅当 时，即 时取等号．·······························10分 数学（文科）答案 4/4 {#{QQABaYSAggiAQJJAARgCQQkACAMQkAGAAKoOQBAMMAAAiRFABCA=}#}