2025届高二年级下学期见面考试原卷(1)_2024年4月_01按日期_6号_2024届新结构高考数学合集_新高考19题（九省联考模式）数学合集140套

2025 届高二年级下学期见面考试 学校:___________姓名：___________班级：___________考号：___________ 一、单选题 1．已知抛物线C：x2 =4y的焦点为F，准线为l，则焦点F 到准线l的距离为（ ） A．1 B．2 C．4 D．8 3−i 2．设z= ，则 z =（ ） 1+2i A．2 B． 3 C． 2 D．1  π 3．为了得到函数y=2sin3x的图象，只要把函数y=2sin3x+ 图象上所有的点（ ）  5 π π A．向左平移 个单位长度 B．向右平移 个单位长度 5 5 π π C．向左平移 个单位长度 D．向右平移 个单位长度 15 15 4．已知各项均为正数的等比数列{a }的前4项和为15，且a =3a +4a ，则a =（ ） n 5 3 1 3 A．16 B．8 C．4 D．2 5．设A(2,−1)，B(4,1)，则以线段AB为直径的圆的方程为（ ） A．(x−3)2+y2 =4 B．(x−3)2+y2 =2 C．(x+3)2+y2 =2 D．(x+3)2+y2 =8 6．已知A,B,C为球O的球面上的三个点，⊙O 为ABC的外接圆，若⊙O 的面积为4π，AB=BC = AC =OO ， 1 1 1 则球O的表面积为（ ） A．64π B．48π C．36π D．32π 2x−1 7．若 f (x)=(x+a)ln 为偶函数，则a=（ ）． 2x+1 1 A．−1 B．0 C． D．1 2 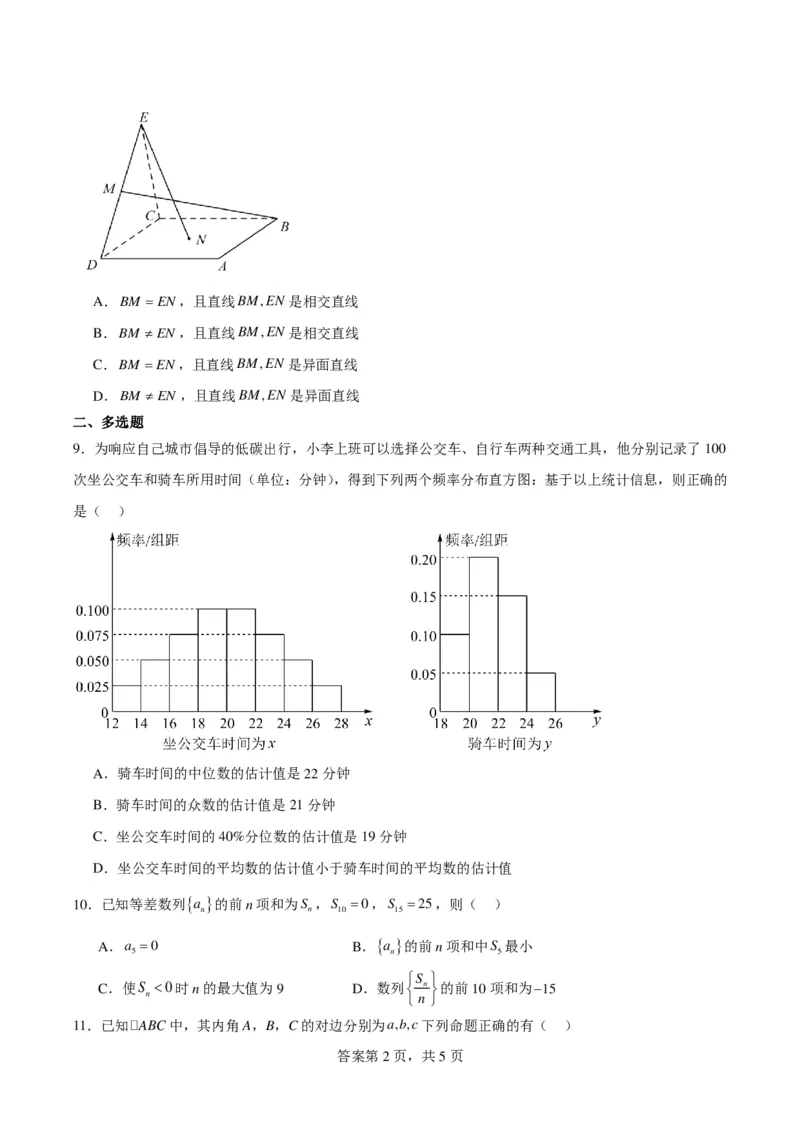8．如图，点N 为正方形ABCD的中心，∆ECD为正三角形，平面ECD⊥平面ABCD,M 是线段ED的中点， 则（ ） 答案第1页，共5页 学科网（北京）股份有限公司A．BM =EN，且直线BM,EN 是相交直线 B．BM ≠EN ，且直线BM,EN是相交直线 C．BM =EN，且直线BM,EN 是异面直线 D．BM ≠EN ，且直线BM,EN是异面直线 二、多选题 9．为响应自己城市倡导的低碳出行，小李上班可以选择公交车、自行车两种交通工具，他分别记录了100 次坐公交车和骑车所用时间（单位：分钟），得到下列两个频率分布直方图：基于以上统计信息，则正确的 是（ ） A．骑车时间的中位数的估计值是22分钟 B．骑车时间的众数的估计值是21分钟 C．坐公交车时间的40%分位数的估计值是19分钟 D．坐公交车时间的平均数的估计值小于骑车时间的平均数的估计值 10．已知等差数列{a }的前n项和为S ，S =0，S =25，则（ ） n n 10 15 A．a =0 B．{a }的前n项和中S 最小 5 n 5 S  C．使S <0时n的最大值为9 D．数列 n的前10项和为−15 n  n  11．已知ABC中，其内角A，B，C的对边分别为a,b,c下列命题正确的有（ ） 答案第2页，共5页A．若A> B，则cosA>cosB π B．若A= ，a=4，则ABC外接圆半径为4 6 C．若a=2bcosC，则ABC为直角三角形 2π 3 3 D．若b=1，c=3，A= ，则S = 3 △ABC 4 x2 y2 12．已知椭圆C: + =1,F,F 分别为它的左右焦点，A,B分别为它的左右顶点，点P是椭圆上的一个动 25 9 1 2 点，下列结论中正确的有（ ） π A．存在P使得∠FPF = 1 2 2 1 B．cos∠FPF 的最小值为− 1 2 8 9 C．直线PA与直线PB斜率乘积为定值 25 D．PF ⊥PF ，则△FPF 的面积为9 1 2 1 2 三、填空题      13．已知向量a=(1,3),b=(3,4)，若(a−λb)⊥b，则λ= ． 14．记ABC的内角A，B，C的对边分别为a，b，c，面积为 3 ，B=60°，a2+c2 =3ac，则b= ． x2 15．已知双曲线C: − y2 =1(m>0)的一条渐近线为 3x+my=0，则C的焦距为 ． m 16．已知点S,A,B,C均在半径为2的球面上，ABC是边长为3的等边三角形，SA⊥平面ABC，则 SA= ． 四、解答题 17．记S 为等差数列{a }的前n项和，已知S =－a ． n n 9 5 （1）若a =4，求{a }的通项公式； 3 n （2）若a >0，求使得S ≥a 的n的取值范围． 1 n n 18．直三棱柱ABCABC 中，AA = AB= AC =2,AA ⊥ AB,AC ⊥ AB，D为AB 的中点，E为AA 的中点， 1 1 1 1 1 1 1 1 F为CD的中点． (1)求证：EF//平面ABC； (2)求直线BE与平面CCD所成角的正弦值； 1 答案第3页，共5页 学科网（北京）股份有限公司(3)求平面ACD与平面CCD夹角的余弦值． 1 1 19．为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成A,B两组，每 组100只，其中A组小鼠给服甲离子溶液，B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔 浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如 下直方图： 记C为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到P(C)的估计值为0.70. （1）求乙离子残留百分比直方图中a,b的值； （2）分别估计甲、乙离子残留百分比的平均值（同一组中的数据用该组区间的中点值为代表）. cosA sin2B 20．记ABC的内角A，B，C的对边分别为a，b，c，已知 = ． 1+sinA 1+cos2B 2π (1)若C= ，求B； 3 a2 + b2 (2)求 的最小值． c2 答案第4页，共5页21．已知{a }的前n项和为S ，a =2，且满足______，现有以下条件： n n 1 4n+1−4 ①2a +22a +23a +⋅⋅⋅+2na = ；②S =2a −2；③S −2S =2 1 2 3 n 3 n n n+1 n 请在三个条件中任选一个，补充到上述题目中的横线处，并求解下面的问题： (1)求数列{a }的通项公式； n 2n+1 3 (2)若b =nlog a ，求 的前n项和T ，并证明： ≤T <1． n 2 n+1  b2  n 4 n n x2 y2 2 22．已知椭圆 + =1的左右焦点分别为F，F ，离心率为 ，P是椭圆上一点，且△PFF 面积的最 a2 b2 1 2 2 1 2 大值为1. (1)求椭圆的方程；   (2)过F 的直线交椭圆于M，N两点，求FM⋅FN 的取值范围 2 1 1 答案第5页，共5页 学科网（北京）股份有限公司