2024届湖北十一校第二次联考数学答案_2024年3月_013月合集_2024届湖北省十一校高三下学期第二次联考_湖北省十一校2024届高三下学期第二次联考数学

2024 届高三湖北十一校第二次联考 数学参考答案及评分细则 命题学校：鄂南高中 命题人：李环宇 易红艳 汪勇谋 审题人：鄂南高中 雷松柏 黄石二中 万莲艳 题号 1 2 3 4 5 6 7 8 9 10 11 答案 A B B C A D D C ACD AC ABC 1.M =(−5,2 ) ,N =[ 0,+∞) ∴M N =[ 0,2 ) 选：A 2.设z =a+bi,(a,b∈R)，由 z+2i = z ，得|a+(b+2)i|=|a+bi|, a2 +(b+2)2 =a2 +b2，解得b=−1，∴ z的虚部为−b=1 选：B  π tanα−1 2tanα 3 3. 由tan α−  = =2，得tanα=−3，∴sin2α= =−  4 1+tanα 1+tan2α 5 选：B     2   3  4.由 a = b = a−b 得向量a,b的夹角为60，a⋅(a+b)=a +ab= |a|2 2 1   1  2    2 3  （a+b)2 = (a +2ab+b )= |a|2 2 2 2 选：C 5.由题意得，动点M 的轨迹是线段AB的中垂面与平面α的交线， B 2 可得线段AM 的最小值为4 2× =4 2 A M α 选：A 6．x2C0 +ax⋅C1(−x )+(−1 )⋅C2(−x )2 ，所以x2的系数为1−6a−15=−2，所以a=−2 6 6 6 选：D   7．设P ( x,y )，PA⋅PB=3a2，得P得轨迹方程为圆C: x2 + y2 =4a2，所以圆C和已 a2 +2a+5≥0 知圆相交即可，圆心距r −r ≤ 0C ≤r +r ，其中r =a,r =2a，得 2 1 1 2 1 2 7a2 −2a−5≥0 得a≥1 选：D 1 {#{QQABBQCEogAgAIBAABhCQQlgCAMQkACACAoGAEAAsAIASBFABAA=}#}x x x y x 8．参变分离得ay≥ x ( ln y−lnx )−x，∴a≥ ( ln y−lnx )− ，∴a≥ ln − y y y x y y lnt−1 lnx−1 设t = ，得a≥ ,t∈( 0,+∞)，设g(x)= ,x∈( 0,+∞)，求导讨论单调性，可 x t x 1 得a≥ e2 选：C ( ) 9．X  N 100,1.52 可知期望为100，方差为1.52， C选项P ( X <µ+σ)= P ( X >µ−σ)正确 D选项P (µ−2σ< X <µ+σ)= P (µ−σ< X <µ+2σ)正确 选：ACD 10．第i行是以a 为首项，以( i+1 )为公差的等差数列， i1 ∴a =a +( j−1 )⋅i =( i+1 )+( j−1 )⋅i =i⋅ j+1，C正确 ij i1 可知A正确，对于B选项 a =i⋅ j+1=65,∴i⋅ j =64=20×26 =21×25 =22×24 =23×23 =24×22 =25×21 =26×20 ij 故共出现7次，B错误 对于D选项，令n=1,2，检验可知错误. 选：AC 11．A选项易知正确 B选项，如图可知 GF =G A,GF =GD,∴G A+GD=GF +GF =( a−c )+( a+c )=2a 1 1 1 1 2 1 1 1 1 1 1 2 ∴OO = AD=2a得证 1 2 C选项，∆OOF ,OF =c,OO =a,∠OOF =θ得证 1 1 1 1 1 1 θ θ AG D选项，可知∠AOF =θ,∠AOG = , ∆O AG 中，tan = 1 ，所以错误. 1 1 1 1 2 1 1 2 R 选：ABC 2 {#{QQABBQCEogAgAIBAABhCQQlgCAMQkACACAoGAEAAsAIASBFABAA=}#}12. 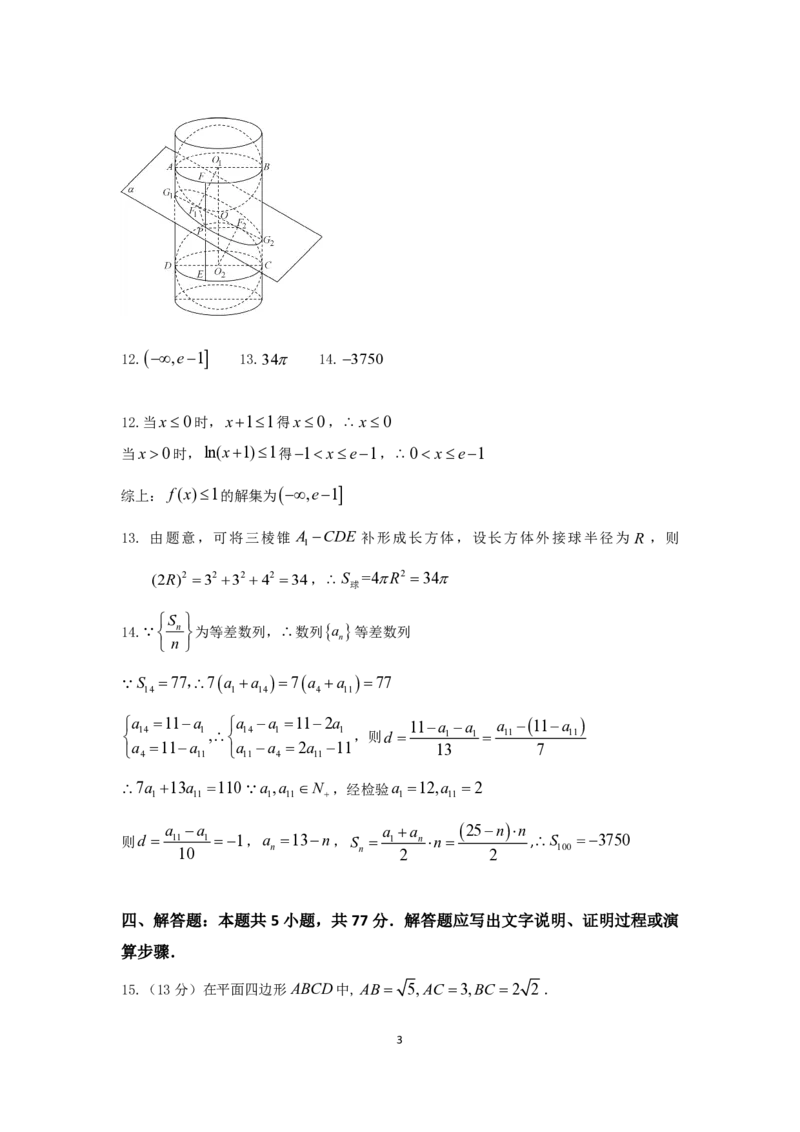(−∞,e−1 ] 13.34π 14.−3750 12.当x≤0时，x+1≤1得x≤0，∴ x≤0 当x>0时，ln(x+1)≤1得−1< x≤e−1，∴0< x≤e−1 综上： f(x)≤1的解集为 (−∞,e−1 ] 13. 由题意，可将三棱锥 A −CDE 补形成长方体，设长方体外接球半径为 R ，则 1 (2R)2 =32 +32 +42 =34，∴S =4πR2 =34π 球 S  14. n为等差数列，∴数列{a }等差数列  n  n S =77，∴7 ( a +a )=7 ( a +a )=77 14 1 14 4 11 a =11−a a −a =11−2a 11−a −a a −( 11−a )  14 1,∴ 14 1 1 ，则d = 1 1 = 11 11 a =11−a a −a =2a −11 13 7 4 11 11 4 11 ∴7a +13a =110a ,a ∈N ，经检验a =12,a =2 1 11 1 11 + 1 11 a −a a +a ( 25−n )⋅n 则d = 11 1 =−1，a =13−n，S = 1 n ⋅n= ,∴S =−3750 10 n n 2 2 100 四、解答题：本题共 5 小题，共 77 分．解答题应写出文字说明、证明过程或演 算步骤． 15.（13分）在平面四边形ABCD中,AB= 5,AC =3,BC =2 2． 3 {#{QQABBQCEogAgAIBAABhCQQlgCAMQkACACAoGAEAAsAIASBFABAA=}#}(1)求cos∠BCA的值; 12 21 (2)若cos∠BCD=− ,cos∠ADC =− 求AD的长． 13 5 AC2 +BC2 −AB2 解：（1）在 ∆ABC中，由余弦定理可得：cos∠BCA= 2AC⋅BC 9+8−5 2 ∴cos∠BCA= = ; ................5分 2×3×2 2 2 (2)sin∠ACD=sin (∠BCD−∠BCA )=sin∠BCDcos∠BCA−cos∠BCDsin∠BCA 5 2 12 2 17 2 = ⋅ + ⋅ = 13 2 13 2 26 2 sin∠ADC = 1−cos2∠ADC = .................9分 5 AC AD 在∆ACD中，由正弦定理可得： = sin∠ADC sin∠ACD 3 AD 255 ∴ = ⇒ AD= 2 ................13分 2 17 2 52 5 26 16.（15 分）如图所示,平面 ACFE ⊥平面 ABCD，且四边形 ACFE是矩形，在四边形 ABCD中，∠ADC =120,2AB=2AD=2CD= BC =6. → 2 → (1) 若EM = EF ,求证：AM //平面BDF ； 3 π (2) 若BF 与平面ABCD所成角为 ，求平面BED与平面BCF 所成锐二面角的余弦值. 6 E M F A D C B （第16题图） （1）证明：连接BD AC O 与 交于点  AD=CD=3,∠ADC =120 4 {#{QQABBQCEogAgAIBAABhCQQlgCAMQkACACAoGAEAAsAIASBFABAA=}#}∴∠DCA=30,AC =3 3 又AB=3，BC =6 ∴∠CAB=90,∠ACB=30 ∴四边形ABCD是等腰梯形 ............... 3分 ， 1 AD//BC且AD= BC 2 1 1 ∴ ∴AO= AC = EF =MF 四边形AOFM 是平行四边形 ............... 6分 3 3 ∴ AM //OF 又AM ⊄面BDF,OF ⊂面BDF， ∴ AM //平面BDF ............7分 （2）平面ACFE ⊥平面ABCD，且四边形ACFE是矩形 ∴ AE ⊥ 平面ABCD π 建立如图所示空间直角坐标系，由BF 与平面ABCD所成角为 6 ，得CF =2 3.... 8分 3 3 3 ∴ B(0,3,0) C(3 3,0,0) F(3 3,0,2 3) E(0,0,2 3) D( ,− ,0) 2 2 → → 3 3 9 BE =(0,−3,2 3) BD=( ,− ,0) 2 2 → → BC =(3 3,−3,0) BF =(3 3,−3,2 3) ......... 9 分 (0,−3,2 3)⋅(x,y,z)=−3y+2 3z =0 →  设平面BED的法向量为n =(x,y,z)，则 1 3 3 9 3 3 9 ( ,− ,0)⋅(x,y,z)= x− y =0  2 2 2 2 ∴ → n =(2 3,2, 3) ......... 11分 1 → 设平面BCF的法向量为n =(x,y,z)， 2  (3 3,−3,0)⋅(x,y,z)=3 3x−3y =0 则 (3 3,−3,2 3)⋅(x,y,z)=3 3x−3y+2 3z =0 ∴ → n =(1，3,0) ......... 13分 2 → → ∴ |n n | 2 57 cosθ= 1 2 = ......... 15分 → → 19 |n ||n | 1 2 17.（15 分）2023 年12 月 30 号，长征二号丙/远征一号S 运载火箭在酒泉卫星发射中心点 火起飞，随后成功将卫星互联网技术实验卫星送入预定轨道，发射任务获得圆满完成，此次 任务是长征系列运载火箭的第505次飞行，也代表着中国航天2023年完美收官。某市一调 研机构为了了解当地学生对我国航天事业发展的关注度，随机的从本市大学生和高中生中抽 5 {#{QQABBQCEogAgAIBAABhCQQlgCAMQkACACAoGAEAAsAIASBFABAA=}#}取一个容量为n的样本进行调查，调查结果如下表： 附： α 0.1 0.05 0.025 0.01 0.001 x a 2.706 3.841 5.024 6.635 10.828 n(ad−bc)2 χ2 = ，其中n=a+b+c+d． (a+b)(c+d)(a+c)(b+d) （1）完成上述列联表，依据小概率值α=0.05的独立性检验，认为关注航天事业发展与学生 群体有关，求样本容量n的最小值？ （2）该市为了提高本市学生对航天事业的关注，举办了一次航天知识闯关比赛，包含三个 问题，有两种答题方案选择： 方案一：回答三个问题，至少答出两个可以晋级； 方案二：在三个问题中，随机选择两个问题，都答对可以晋级. 3 2 1 已知小华同学答出三个问题的概率分别是 ，， ，小华回答三个问题正确与否相互独立， 4 3 2 则小华应该选择哪种方案晋级的可能性更大？（说明理由） 解：（1） 6 {#{QQABBQCEogAgAIBAABhCQQlgCAMQkACACAoGAEAAsAIASBFABAA=}#}零假设为H ：关注航天事业发展与学生群体无关 0 n n n n n( ⋅ − )2 根据列联表中的数据，经计算得到χ2 = 2 5 510 = 8n .............4分 7n 3n 3n 2n 63 ⋅ ⋅ ⋅ 10 10 5 5 因为依据小概率值α=0.05的独立性检验，认为关注航天事业发展与学生群体有关 8n 所以χ2 = >3.841⇒n>30.25 .....................6分 63 由题可知，n是10的倍数，∴n =40 .....................7分 min 3 2 1 （2）记小华同学答出三个问题的事件分别A,B,C,则P ( A )= ,P ( B )= ,P ( C )= 4 3 2 记选择方案一通过的概率为P 1 P=P ( ABC ) +P ( ABC ) +P ( ABC ) +P ( ABC ) 1 3 2 1 3 1 1 1 2 1 3 2 1 17 = ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ = ....................11分 4 3 2 4 3 2 4 3 2 4 3 2 24 记选择方案二通过的概率为P 2 1 1 1 P = P ( AB )+ P ( BC )+ P ( AC ) 2 3 3 3 13 2 2 1 3 1 29 = ⋅ + ⋅ + ⋅ =   34 3 3 2 4 2 72 P > P ,∴小华应该选择方案一 ....................15分 1 2 x2 y2 1 18.（17分）已知椭圆M ： + =1(a >b>0)的离心率为 , A,B分别为椭圆的左顶 a2 b2 2 3 点和上顶点，F 为左焦点，且ABF的面积为 . 1 1 2 （1）求椭圆M 的标准方程； （2）设椭圆M 的右顶点为C，P是椭圆M 上不与顶点重合的动点： 3 （i）若点P(1, ),点D在椭圆M 上且位于x轴下方，直线PD交x轴于点F ，设APF和 2 7 {#{QQABBQCEogAgAIBAABhCQQlgCAMQkACACAoGAEAAsAIASBFABAA=}#}3 CDF 的面积分别为S ,S ,若S −S = ，求点D的坐标； 1 2 1 2 2 （ii）若直线AB与直线CP交于点Q，直线BP交x轴于点N ，求证：2k −k 为定值， QN QC 并求出此定值. y Q B P N A O C x （第18（ii）题图） c 1 =  a 2 解：（1）由题意得 ， ...........1分 1 3 (a−c)b= 2 2 解得a =2,c=1 ...........2分 ∴ x2 y2 椭圆M 的标准方程为 + =1 ...........4分 4 3 (2)（i）连接PC, 1 3 3 S −S =S −S = ×4× −S = ...........6分 1 2 APC DPC 2 2 DPC 2 ∴ 3 1 S = = S =S DPC 2 2 APC OPC ∴ 3 OD//PC k =− ...........8分 OD 2  3 y =− x  3  2 ∴ 3 直线OD的方程为y =− x，联立 得x =1 D(1,− ) .......10分 2 x2 y2 D 2 + =1  4 3 （其它方法酌情给分） （ii）设直线QC的斜率为k，则直线QC的方程为：y =k(x−2) y =k(x−2) 3  直线AB的方程为y = (x+2)，由 3 得 2 y = (x+2)  2 2(2k+ 3) 4 3k Q( , ) ...........11分 2k− 3 2k− 3 8 {#{QQABBQCEogAgAIBAABhCQQlgCAMQkACACAoGAEAAsAIASBFABAA=}#}y =k(x−2)  由x2 y2 得（3+4k2)x2 −16k2x+16k2 −12=0  + =1  4 3 16k2 −12 ∴ 8k2 −6 −12k 2x = P( , ) ...........13分 P 3+4k2 3+4k2 3+4k2 ∴ −4 3k2 −12k−3 3 直线BP的方程为:y = x+ 3 8k2 −6 ∴ 2(2k− 3) N( ,0) ...........15分 2k+ 3 4 3k ∴ 2k− 3 8 3k+12 1 3 k = = = k+ QN 2(2k+ 3) 2(2k− 3) 16 3 2 4 − 2k− 3 2k+ 3 ∴ 3 2k −k = ...........17分 QN QC 2 为定值 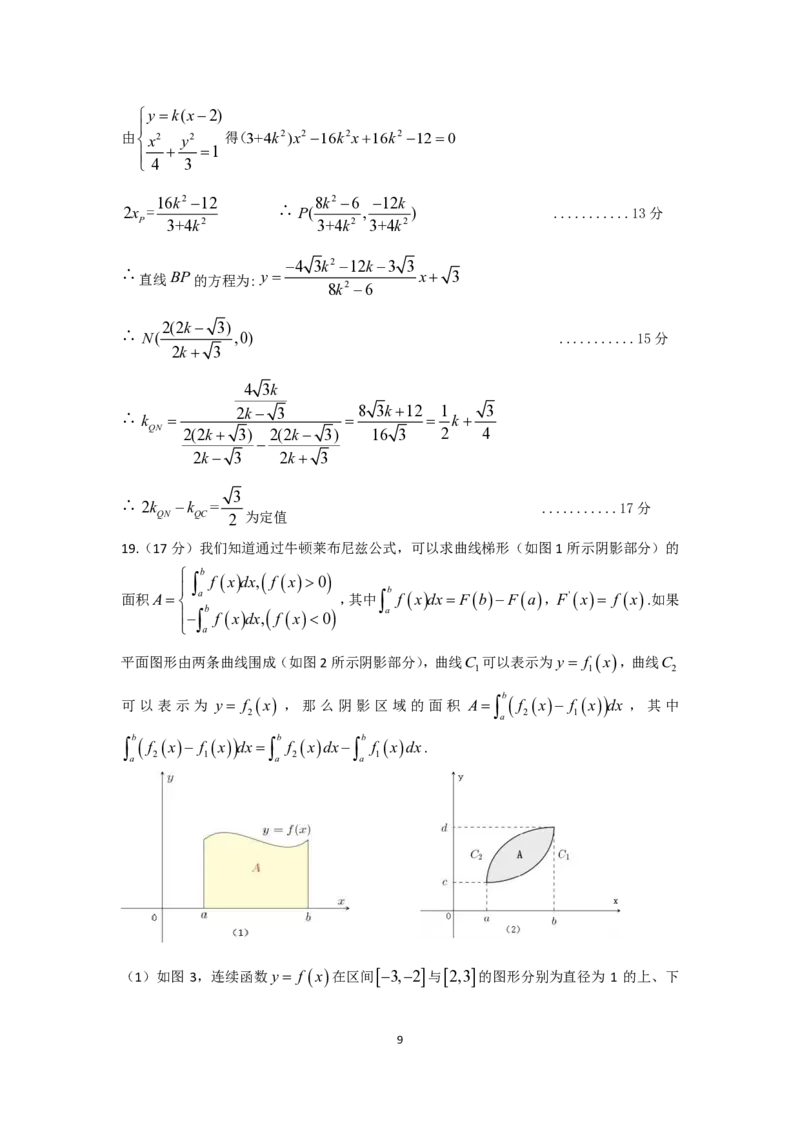19.（17分）我们知道通过牛顿莱布尼兹公式，可以求曲线梯形（如图1所示阴影部分）的  ∫ b f ( x ) dx, ( f ( x )>0 ) 面积A=   a ，其中∫ b f ( x ) dx= F ( b )−F ( a )，F'( x )= f ( x ) .如果 −∫ b f ( x ) dx, ( f ( x )<0 ) a  a 平面图形由两条曲线围成（如图2所示阴影部分），曲线C 可以表示为y = f ( x )，曲线C 1 1 2 可以表示为 y = f ( x ) ，那么阴影区域的面积 A=∫ b( f ( x )− f ( x )) dx ，其中 2 2 1 a ∫ b( f ( x )− f ( x )) dx=∫ b f ( x ) dx−∫ b f ( x ) dx. 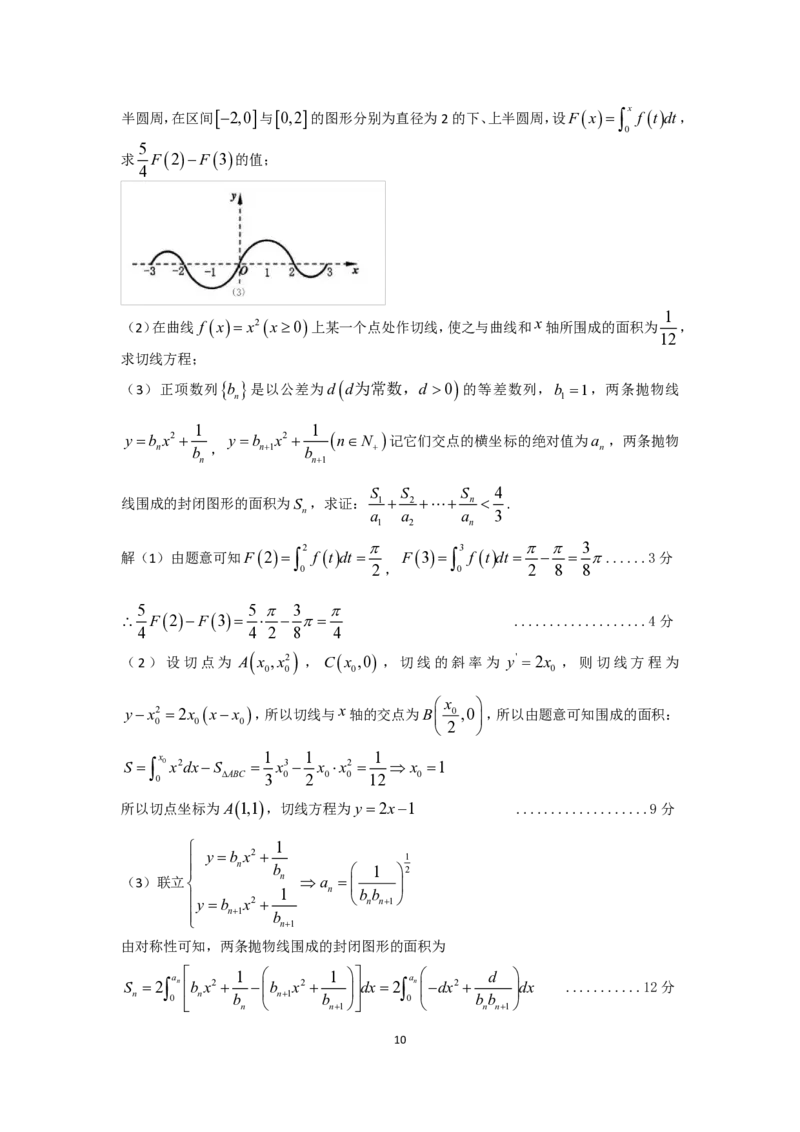2 1 2 1 a a a （1）如图 3，连续函数y = f ( x )在区间[−3,−2 ]与[ 2,3 ]的图形分别为直径为 1 的上、下 9 {#{QQABBQCEogAgAIBAABhCQQlgCAMQkACACAoGAEAAsAIASBFABAA=}#}半圆周，在区间[−2,0 ]与[ 0,2 ]的图形分别为直径为2的下、上半圆周，设F ( x )=∫ x f ( t ) dt， 0 5 求 F ( 2 )−F ( 3 )的值； 4 1 （2）在曲线 f ( x )= x2( x≥0 )上某一个点处作切线，使之与曲线和x轴所围成的面积为 ， 12 求切线方程； （3）正项数列{ b }是以公差为d ( d为常数，d >0 ) 的等差数列，b =1，两条抛物线 n 1 1 1 y =b x2 + y =b x2 + ( n∈N )记它们交点的横坐标的绝对值为a ，两条抛物 n b ， n+1 b + n n n+1 S S S 4 线围成的封闭图形的面积为S ，求证： 1 + 2 +⋅⋅⋅+ n < . n a a a 3 1 2 n 解（1）由题意可知F ( 2 )=∫ 2 f ( t ) dt = π F ( 3 )=∫ 3 f ( t ) dt = π − π = 3 π......3分 0 2 ， 0 2 8 8 5 5 π 3 π ∴ F ( 2 )−F ( 3 )= ⋅ − π= ...................4分 4 4 2 8 4 （2）设切点为 A ( x ,x2 ) ， C ( x ,0 ) ，切线的斜率为 y' =2x ，则切线方程为 0 0 0 0  x  y−x2 =2x ( x−x )，所以切线与x轴的交点为B 0 ,0，所以由题意可知围成的面积： 0 0 0  2  x 1 1 1 S =∫ 0 x2dx−S = x3− x ⋅x2 = ⇒ x =1 0 ∆ABC 3 0 2 0 0 12 0 所以切点坐标为A ( 1,1 )，切线方程为y =2x−1 ...................9分  1   y =b n x2 + b  1  1 2 （3）联立 n ⇒a =   y =b x2 + 1 n b n b n+1    n+1 b n+1 由对称性可知，两条抛物线围成的封闭图形的面积为 a  1  1  a  d  S =2∫ n b x2 + −b x2 + dx=2∫ n −dx2 + dx ...........12分 n 0  n b n  n+1 b n+1  0  b n b n+1  10 {#{QQABBQCEogAgAIBAABhCQQlgCAMQkACACAoGAEAAsAIASBFABAA=}#}d d dx 令 f ( x )=−dx2 + ,F' ( x )= f ( x ) ,⇒ F ( x )=− x3 + +C（C为常数） b b 3 b b n n+1 n n+1 3 3 ∴∫ a n f ( x )= F ( a )−F ( 0 )=− d a3 + da n = 2d   1   2 ∴S = 4d   1   2 0 n 3 n b b 3 b b  n 3 b b  n n+1 n n+1 n n+1 S 4d 1 4 1 1  ∴ n = ⋅ =  −  ....................15分 a 3 b b 3b b  n n n+1 n n+1 S S S 4 1 1 1 1 1 1  4 1 1  4 则 1 + 2 +⋅⋅⋅+ n =  − + − +⋅⋅⋅+ − =  − < ...17分 a a a 3b b b b b b  3b b  3 1 2 n 1 2 2 3 n n+1 1 n+1 11 {#{QQABBQCEogAgAIBAABhCQQlgCAMQkACACAoGAEAAsAIASBFABAA=}#}