文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(全国卷专用)
黄金卷02(文科)
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.设集合 , ,则 ( )
A. B. C. D.
【答案】D
【分析】由分式不等式的解法,解出集合 ,根据集合的交集运算,可得答案.
【详解】由不等式 ,则等价于 ,解得 ,
所以 ,由 ,则 .
故选:D.
2.设复数 ,其共扼复数为 ,则 ( )
A. B. C.2 D.
【答案】A
【分析】由复数的除法,计算得 和 ,再由复数模的计算公式,计算 .
【详解】复数 ,其共扼复数 ,
, .
故选:A
3.已知 , 是两条不同直线, 是平面,且 , ,“ ”是“ ”的( )A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】B
【分析】根据直线与平面的关系即可结合必要不充分条件的判定求解.
【详解】一条直线平行平面,但这条直线不一定和平面内的直线平行,所以由 ,不能得到 ,
而 , , ,则 ,
所以“ ”是“ ”的必要不充分条件,
故选:B
4.( 2023·四川泸州·统考一模)若 , ,则 ( )
A. B. C. D.
【答案】C
【分析】利用两角和(差)的余弦公式求出 ,再由二倍角公式计算可得.
【详解】因为 , ,
所以 ,
所以 ,所以 ,
所以
.
故选:C
5.已知正方形 的边长为 , 在边 上,则 的最大值为( )
A.1 B. C.2 D.
【答案】C
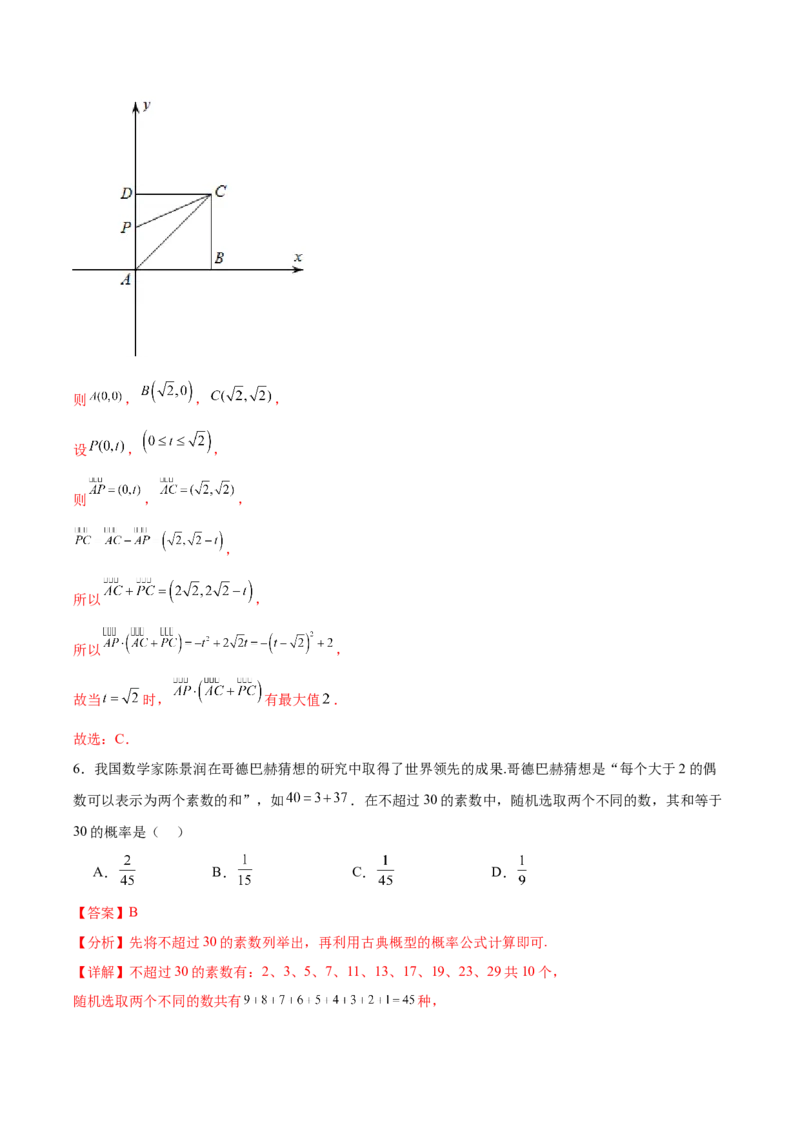
【分析】建立平面直角坐标系,得出 , , 的坐标,设出点 坐标,利用坐标运算求解即可.
【详解】由题意,建立如图所示坐标系,则 , , ,
设 , ,
则 , ,
,
所以 ,
所以 ,
故当 时, 有最大值 .
故选:C.
6.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶
数可以表示为两个素数的和”,如 .在不超过30的素数中,随机选取两个不同的数,其和等于
30的概率是( )
A. B. C. D.
【答案】B
【分析】先将不超过30的素数列举出,再利用古典概型的概率公式计算即可.
【详解】不超过30的素数有:2、3、5、7、11、13、17、19、23、29共10个,
随机选取两个不同的数共有 种,其中和等于30的有 这3种情况,
所以在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是 .
故选:B.
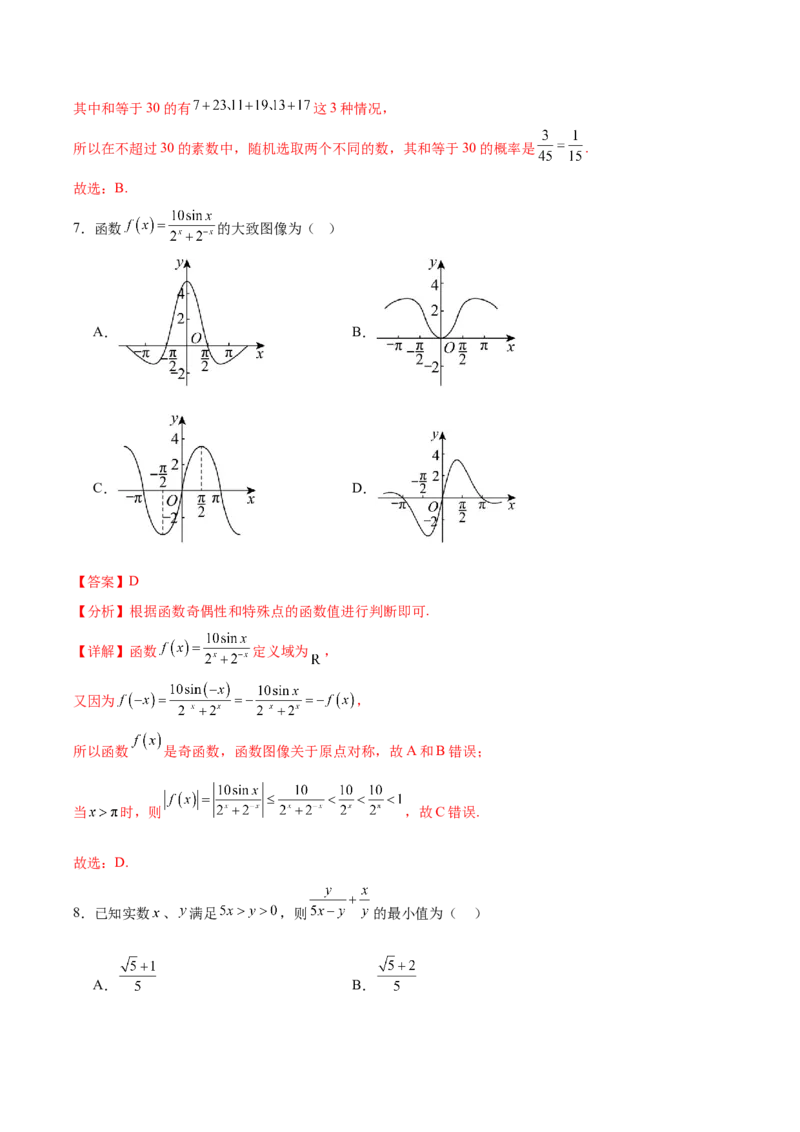
7.函数 的大致图像为( )
A. B.
C. D.
【答案】D
【分析】根据函数奇偶性和特殊点的函数值进行判断即可.
【详解】函数 定义域为 ,
又因为 ,
所以函数 是奇函数,函数图像关于原点对称,故A和B错误;
当 时,则 ,故C错误.
故选:D.
8.已知实数 、 满足 ,则 的最小值为( )
A. B.C. D.
【答案】C
【分析】由已知可得出 ,可得出 ,再利用基本不等式可求出所求代
数式的最小值.
【详解】因为 ,所以 ,即 ,
所以 ,
当且仅当 ,即 时等号成立,
所以 的最小值为 .
故选:C.
9.A,B,C,D是球O的球面上四点, ,球心O是 的中点,四面体 的体积
为 ,则球O的表面积为( )
A. B. C. D.
【答案】B
【分析】利用棱锥的体积公式结合球的表面积公式计算即可.
【详解】由题意可知 为球O的直径,设D到面 的距离为 ,
易知等边 的面积为 ,所以 ,则球心O到面 的距离为1,
设 面 ,易知H为等边 的外心,
所以 ,
故 .
故选:B
10.已知 分别为双曲线 的左、右焦点,过 与双曲线的一条渐近线平行的直线
交双曲线于点 ,若 ,则双曲线的离心率为( )
A.3 B. C. D.2
【答案】C
【分析】设过 与双曲线的一条渐近线 平行的直线交双曲线于点 ,运用双曲线的定义和条件可得
, , ,再由渐近线的斜率和余弦定理,结合离心率公式,计算即可得到所求值.
【详解】设过 与双曲线的一条渐近线 平行的直线交双曲线于点 ,
由双曲线的定义可得 ,
由 ,可得 , , ,由 可得 ,
在三角形 中,由余弦定理可得:
,
即有 ,化简可得 ,
所以双曲线的离心率 .
故选:C.
11.设首项为 的数列 的前n项和为 , ,且 ,则数列 的前23项
和为( )
A. B. C. D.
【答案】D
【分析】根据题意,推得 ,得到数列 为等差数列,求得 ,化简得到
,结合裂项法求和,即可求解.
【详解】由 , ,可得 ,
当 时, ,所以 ,可得 ,
又 ,所以数列 是以2为首项、 为公差的等差数列,
所以 ,得 ,于是 ,
所以数列 的前 项和为 .
故选:D.
12.若曲线 存在与直线 垂直的切线,则k的取值范围是( )
A. B. C. D.
【答案】D
【分析】对 求导后根据题意可得 在 上有解. 令 ,
求导判断单调性求得值域,从而可得不等式 ,求解即可.
【详解】对 求导得 ,
当 时,曲线 不存在与直线 垂直的切线,
当 时,若曲线 存在与直线 垂直的切线,
只需 在 上有解.
令 ,求导得 ,
所以当 时, ,当 时, ,
所以 在 上单调递减,在 上单调递增,
则 ,且当 时, ,所以 ,解得 ,
所以k的取值范围是 .
故选:D.
第 II 卷(非选择题)
二、填空题:本大题共4小题,每小题5分,共20分
13.已知 中, ,且 ,则 的面积是 .
【答案】3
【分析】根据给定条件,利用夹角公式求出 ,再利用三角形面积公式求解作答.
【详解】在 中, , ,
解得 ,而 ,因此 ,
所以 的面积 .
故答案为:3
14.若实数 满足约束条件 ,则 的最大值为 .
【答案】14
【分析】首先画出可行域,将目标函数变形根据其几何意义即可求得当 过点 时,取得最
大值为 .
【详解】根据题意画出满足约束条件的可行域如下图中着色部分所示:将目标函数 变形可得 ,
若 取得最大值,即直线 在 轴上的截距取得最小值,
将 平移到过点 时,直线 在 轴上的截距最小,
此时目标函数 有最大值为 .
故答案为:
15.若直线l: 与圆C: 相交于A,B两点, ,则直线l的斜率的
取值范围为 .
【答案】
【分析】先求得圆心和半径,根据 的范围列不等式,求得 的取值范围,进而求得直线 的斜率的取
值范围.
【详解】将圆C的方程 整理得 ,
圆心坐标为 ,半径为 ,
要求 , ,则圆心到直线的距离应小于等于 ,
∴ ,即 ( ),
∴ , ,设直线l的斜率为k,则 ,
∴ ,
直线l的斜率的取值范围是 .
故答案为:
16.已知 为偶函数,且当 时, ,其中 为 的导数,则不等式
的解集为 .
【答案】
【分析】根据给定条件,构造函数,利用导数探讨函数的单调性,再结合奇偶性求解不等式作答.
【详解】令函数 ,当 时, ,即函数 在 上单调递
减,
由 为偶函数,得 ,即函数 是奇函数,于是 在R上单调递减,
不等式 ,
因此 ,解得 ,所以原不等式的解集是 .
故答案为:
【点睛】关键点睛:根据条件构造函数,利用导数研究函数的单调性是解决本题的关键.
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)某校为了宣传垃圾分类知识,面向该校学生开展了“垃圾分类知识”网络问卷调查,每位学
生仅有一次参与机会,通过抽样,得到 100 人的得分情况,将样本数据分成
五组,并整理得到如下频率分布直方图;已知成绩的中位数为 75(1)求 的值,并求出成绩的平均数(同一组中的每个数据可用该组区间中点值代替);
(2)现用分层抽样从第四组和第五组按照比例抽选出 6 人进行垃圾分类知识竞答活动,再从中选出两人进
行一对一 ,求抽出的两人恰好来自同一组的概率.
【答案】(1) , ,
(2) .
【详解】(1) 中位数为 75 , ,
,.........................................................................................................................................2分
又 ,
,...........................................................................................................................................3分
则平均数为: ..............................................5分
(2)第四组与第五组人数的比为 ,
从第四组抽选4人,记为1,2,3,4,
从第五组抽选2人,记为 ,..........................................................................................................7分
所有基本事件为: ,
共15种,............................................................9分
来自同一组的有: ,共7种情况,................................10分
故恰好来自同一组的概率 .........................................................................................................12分
18.(12分)记 的内角A, , 所对的边分别是 , , ,已知 .
(1)求角 的大小;(2)若点 在边 上, 平分 , , ,求线段 长.
【答案】(1)
(2)
【详解】(1)由已知 ,根据正弦定理可得 ,................1分
因为 ,所以 ,故有 ,
则有 ,..................................................................................................................3分
因为 ,即 ,可知 ,可得 ,................................................5分
所以 ,则 .....................................................................................................................6分
(2)在 中,根据余弦定理可得 ,
即 ,解得 或 (舍去),.............................................................................8分
由题意可知: ,
由面积关系可得 ,
则 ,.........................................................................10分
即 ,可得 ...........................................................................................................12分
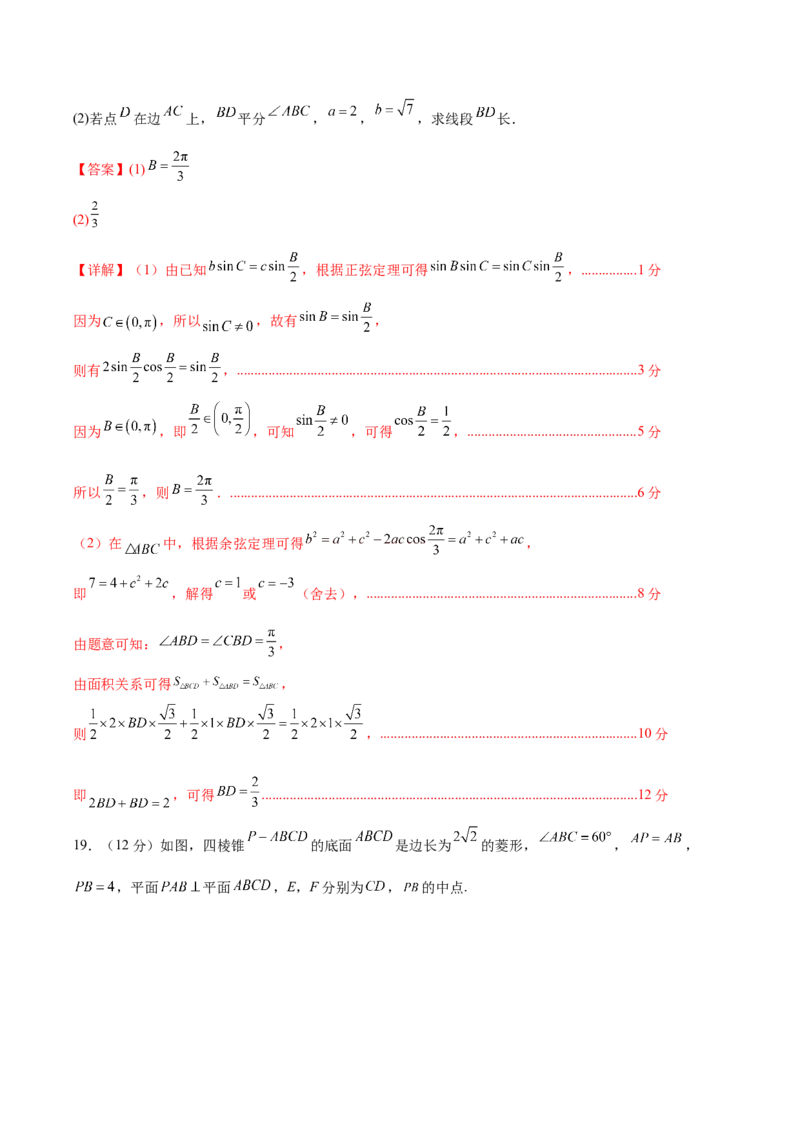
19.(12分)如图,四棱锥 的底面 是边长为 的菱形, , ,
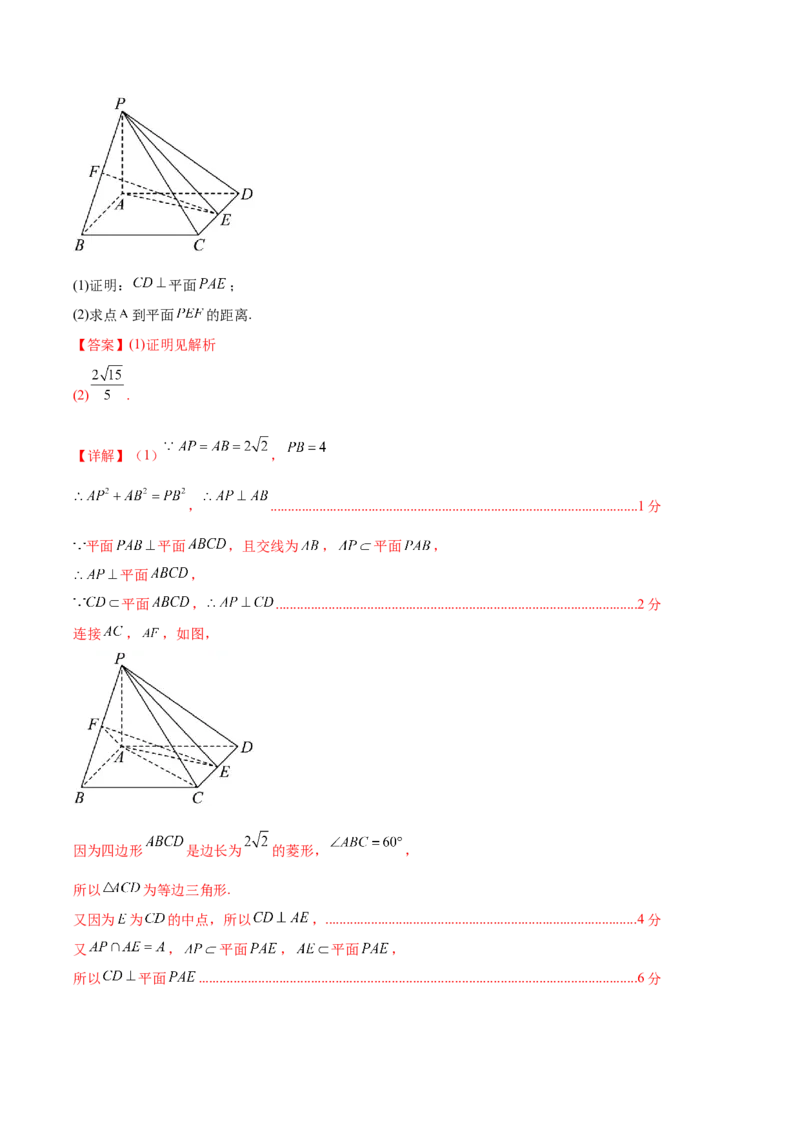
,平面 平面 ,E,F分别为 , 的中点.(1)证明: 平面 ;
(2)求点 到平面 的距离.
【答案】(1)证明见解析
(2) .
【详解】(1) ,
, .........................................................................................................1分
平面 平面 ,且交线为 , 平面 ,
平面 ,
平面 , .......................................................................................................2分
连接 , ,如图,
因为四边形 是边长为 的菱形, ,
所以 为等边三角形.
又因为 为 的中点,所以 ,.........................................................................................4分
又 , 平面 , 平面 ,
所以 平面 .............................................................................................................................6分(2)设点 到平面 的距离为 ,则 ,
因为 ,所以 ,又由(1)知 ,
又 , 平面 , 平面 ,所以 平面 ,...........................8分
又 平面 , 平面 ,所以 , ,
又 , ,
又由 , , , 平面 , 平面 ,
所以 平面 ,.........................................................................................................................10分
且 , ,
所以 ,即 ,
所以点 到平面 的距离为 .................................................................................................12分
20.(12分)设 , 为实数,且 ,函数 .
(1)讨论 的单调性;
(2)设 ,函数 ,试问 是否存在极小值点?若存在,求出 的极小值点;若不存
在,请说明理由.
【答案】(1)答案见解析
(2) 存在极小值点,且极小值点为
【详解】(1) , , ,...................................................................1分
当 时, , 在区间 上单调递增;...........................................................2分
当 ,且 时, , 单调递减;当 时, , 单调递增.................................................................................4分
综上,当 时, 在区间 上单调递增;
当 时, 在区间 上单调递减,在区间 上单调递增..................................5分
(2)当 时, , ,故 .
令 , ,所以 ,........................................................................6分
当 时, , 单调递减;
当 时, , 单调递增...................................................................................8分
又 , , ,
故 ,使得 .
当 时, , , 单调递增;
当 时, , , 单调递减;................................................................10分
当 时, , , 单调递增,
故 存在极小值点,且极小值点为 ......................................................................................12分
21.(12分)已知椭圆 的离心率为 ,且过点 .
(1)求椭圆 的标准方程.
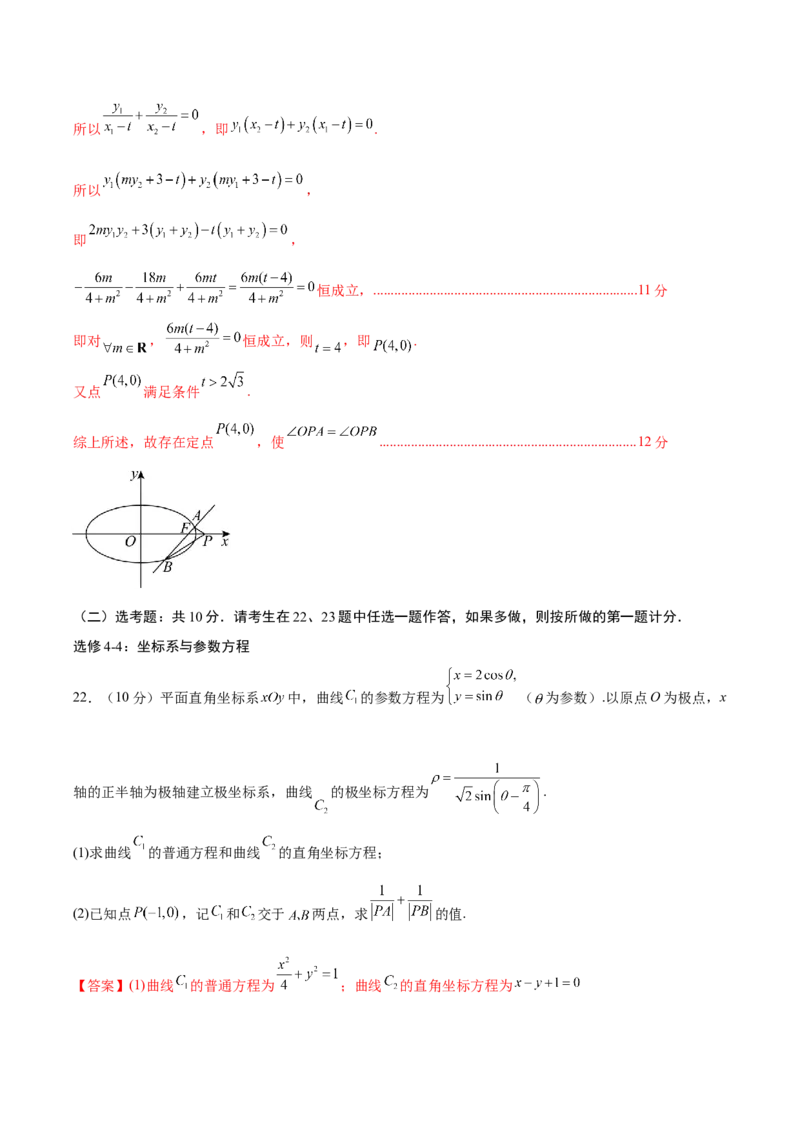
(2)已知过右焦点 的直线 与 交于 两点,在 轴上是否存在一个定点 ,使 ?若存在,
求出定点 的坐标;若不存在,请说明理由.【答案】(1)
(2)存在,
【详解】(1)因为 ,所以 .
所以椭圆 的方程为 .......................................................................................................2分
因为点 在椭圆 上,所以 ,解得 ,
所以 ............................................................................................................................................4分
所以椭圆 的标准方程为 .................................................................................................5分
(2)存在定点 ,使 .理由如下:
由(1)知, ,则点 .
设在 轴上存在定点 ,使 成立......................................................................6分
当直线 斜率为 时,直线右焦点 的直线 即 轴与 交于长轴两端点,
若 ,则 ,或 .....................................................................................7分
当直线 斜率不为 时,设直线 的方程为 ,.
由 消去 并整理,得 ,
则 ....................................................................................................9分
因为 ,所以 ,所以 ,即 .
所以 ,
即 ,
恒成立,...........................................................................11分
即对 , 恒成立,则 ,即 .
又点 满足条件 .
综上所述,故存在定点 ,使 .........................................................................12分
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.(10分)平面直角坐标系 中,曲线 的参数方程为 ( 为参数).以原点O为极点,x
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为 .
(1)求曲线 的普通方程和曲线 的直角坐标方程;
(2)已知点 ,记 和 交于 两点,求 的值.
【答案】(1)曲线 的普通方程为 ;曲线 的直角坐标方程为(2)
【详解】(1)已知曲线 ( 为参数),
则 ,由 消参得 ,
则曲线 的普通方程为 ..................................................................................................2分
由曲线 的极坐标方程为 ,
变形得 ,............................................................................................3分
即 ,且满足 ,
由互化公式 ,得 ,即 .
故曲线 的直角坐标方程为 ........................................................................................5分
(2)由于 在直线l上,
可设直线l的参数方程的标准形式为 (t为参数),
代入曲线 ,
化简得 , ,............................................................................................7分
设A,B对应的参数分别为 , ,则 , ,................................................................................................................8分
由于 ,故 ,
所以 .
故 的值为 .....................................................................................................................10分
选修4-5:不等式选讲
23.(10分)已知函数 .
(1)求不等式 的解集 ;
(2)若 是 的最小值,且正数 满足 ,证明: .
【答案】(1)
(2)证明见解析
【详解】(1) ................................................................1分
∴ 或 或 ,..................................................................3分
解得 或 或 ,
∴不等式的解集为 ;...........................................................................................5分
(2)证明:由 ,可得 的最小值为 ,...........................................6分则 , ,
∴
,当且仅当 时,等号成立,.............................................9分
∴ ..................................................................................................................10分