文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(新高考 卷专用)
Ⅰ
黄金卷03
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。
1.若集合 , ,则 ( )
A. B. C. D.
【答案】B
【详解】 , ,
,又 ,
.
故选:B.
2.已知 ( , 为虚数单位),若 是实数,则( )
A. B.
C. D.
【答案】A
【详解】因为 是实数,
所以 ,
故选:A
3.已知一个古典概型,其样本空间中共有12个样本点,其中事件 有6个样本点,事件 有4个样本点,
事件 有8个样本点,则 ( )
A. B. C. D.
【答案】D【分析】依题意计算可得 , , ,再由概率的加法公式计算即可得
.
【详解】根据概率公式计算可得 , , ;
由概率的加法公式可知 ,代入计算可得
故选:D
4.若一系列函数的解析式和值域相同,但定义域不相同,则称这些函数为“同值函数”.例如函数 ,
与函数 , 即为“同值函数”,给出下面四个函数,其中能够被用来构造“同值函
数”的是( )
A. B. C. D.
【答案】D
【详解】要想能够被用来构造“同值函数”,则要函数不单调,
ABC选项, 在R上单调递减, 在R上单调递增,
在 上单调递增,ABC错误;
D选项, 在 上单调递减,在 上单调递增,
不妨设 , 与函数 , ,两者的值域相同,为同值函数,D正确.
故选:D
5.已知抛物线 的焦点为 ,准线与 轴的交点为 ,点 在抛物线上,且 ,
,则 ( )
A. B. C. D.【答案】A
【详解】根据抛物线 ,得: ,
因为: ,得 三点共线,所以直线 过点 且斜率不为 ,故设直线 的方程为:
,
与抛物线方程 联立得: ,化简得: ,
设 ,此时 ,根据根与系数的关系得: .
由 ,知 ,即 ,化简得: ,
又因为点 在抛物线上,所以: ,
所以: ,所以 (舍去负值).
由 ,得: ,即: ,
所以: ,所以: ,所以: .
故选:A
6.设 , ,且 ,则( )
A. B. C. D.
【答案】A
【详解】因为 ,
所以 ,
所以 ,
即 .又 , ,
所以 ,即
或 ,即 (舍去).
故选:
7.已知数列 满足 ,且 ,则下列说法中错误的是( )
A.若 ,则 是等差数列
B.若 ,则 是等差数列
C.若 ,则 是等比数列
D.若 ,则 是等比数列
【答案】B
【详解】对于A项: ,得: ,
因为: ,所以得: ,
所以: 为等差数列,故A项正确;
对于B项: , ,所以: , ,
不满足等差数列,故B项错误;
对于C项: , ,所以: ,故: ,
数列 为等比数列,故C项正确
对于D项: ,得: ,
因为: ,所以: ,即: ,所以: 为等比数列,故D项正确.
故选:B.
8.设 , , ,则( )
A. B. C. D.
【答案】D
【详解】由题意可得 , , ,
设 , ,则 ,
故当 时, , 单调递增;
当 时, , 单调递减;
因为 , , ,且 ,
可得 , ,所以 .
故选:D.
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的
要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9.若圆 与直线 相切,且与圆 相切于点 ,则圆 的半径为( )
A.5 B.3 C. D.
【答案】BD
【分析】由已知得圆心在 轴,设圆心为 ,然后由圆与直线相切及过点 列方程组求得圆心后再求
得半径.
【详解】圆 的圆心为 ,半径为1,圆 与圆 相切于点 ,则圆心在 轴,设圆心为 ,
则由题意 ,解得 或 ,
时,半径为 , 时,半径为 ,
故选:BD.
10.《黄帝内经》中十二时辰养生法认为:子时的睡眠对一天至关重要(子时是指23点到次日凌晨1点).
相关数据表明,入睡时间越晚,沉睡时间越少,睡眠指数也就越低.根据某次的抽样数据,对早睡群体和
晚睡群体的睡眠指数统计如图,则下列说法错误的是( )
A.在睡眠指数 的人群中,早睡人数多于晚睡人数
B.早睡人群睡眠指数主要集中在
C.早睡人群睡眠指数的极差比晚睡人群睡眠指数的极差小
D.晚睡人群睡眠指数主要集中在
【答案】ACD
【详解】由图知,每一组中的早睡人群占比与晚睡人群占比都是以早睡与晚睡各自的总人数为基数的,
所以每一组中的早睡人数与晚睡人数不能从所占的百分比来判断,故选项A错误;
早睡人群睡眠指数主要集中在 ,晚睡人群睡眠指数主要集中在 ,选项B正确,选项D错误;
早睡人群睡眠指数的极差和晚睡人群睡眠指数的极差的大小无法确定,故选项C错误.
故选:ACD.
11.如图,四棱锥 中,底面 是正方形, 平面 , , , 分别是 ,
的中点, 是棱 上的动点,则( )A.
B.存在点 ,使 平面
C.存在点 ,使直线 与 所成的角为
D.点 到平面 与平面 的距离和为定值
【答案】ABD
【详解】依题意可知 两两相互垂直,以 为原点,建立如图所示空间直角坐标系,
设 ,
,设 , ,
所以 ,所以 ,A选项正确.
点 到平面 与平面 的距离和为 为定值,D选项正确.
, ,
设平面 的法向量为 ,
则 ,故可设 ,
要使 平面 , 平面 ,则 ,
解得 ,所以存在点 ,使 平面 ,B选项正确.
若直线 与直线 所成角为 ,
则 ,
,无解,所以C选项错误.
故选:ABD
12.定义在R上的函数 满足 为奇函数,函数 满足
,若 与 恰有2023个交点 ,则下列说法正
确的是( )
A. B. 为 的对称轴
C. D.
【答案】BCD
【分析】由 ,得函数 图象关于直线 对称,由 是奇函数,得 的图象关
于点 对称,从而得 是周期函数,4是它的一个周期,由 ,得 图象关于点
对称,从而知 与 的图象的交点关于点 对称,点 是它们的一个公共点,由此可判断各选项.
【详解】 ,则函数 图象关于直线 对称,B正确;
是奇函数,即 , ,则 的图象关于点 对称,
, ,C正确;
所以 ,从而 ,所以 是周期函数,4是它的一个周期, ,A错;
又 , 图象关于点 对称,因此 与 的图象的交点关于点 对称,点
是它们的一个公共点,
,D正确.
故选:BCD.
第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.已知向量 , ,则 在 上的投影向量的坐标为 .
【答案】
【详解】 , ,
则 在 上的投影向量为 .
故答案为:
14.已知双曲线 和椭圆 有相同的焦点,则 的最小值为 .
【答案】9
【详解】 的焦点坐标为 ,故 ,
故 ,
当且仅当 ,即 时,等号成立,
故 的最小值为9.
故答案为:915.已知函数 的部分图像如图所示,且关于 的不等式
的解集为 , ,则正偶数a的最小值为 .
【答案】4
【详解】由题意得 ,所以 ,
而 , ,所以 ,
而 ,故 ,所以 ,
又 过点 ,所以 ,即 ,
所以 ,则 ,
又 ,即 ,又 ,则 ,所以 ,
则 ,又 ,所以 ,则 ,
所以 ,
由 ,得 ,
所以 ,解得 ,当 时,在区间 内不存在正偶数,
当 时,在区间 内存在1个正偶数4,所以正偶数a的最小值为 .
故答案为: .
【点睛】关键点睛:本题解决的关键在于利用五点法求得 的解析式,从而解关于 的不等式,从而得
解.
16.已知函数 若函数 有4个零点.则实数 的取值
范围是 .
【答案】
【详解】当 且 时, , ,
当 且 时, ;当 时, .
故 在 , 上单调递减,在 上单调递增,
当 时, 取得极小值 ,
时, ; 时,
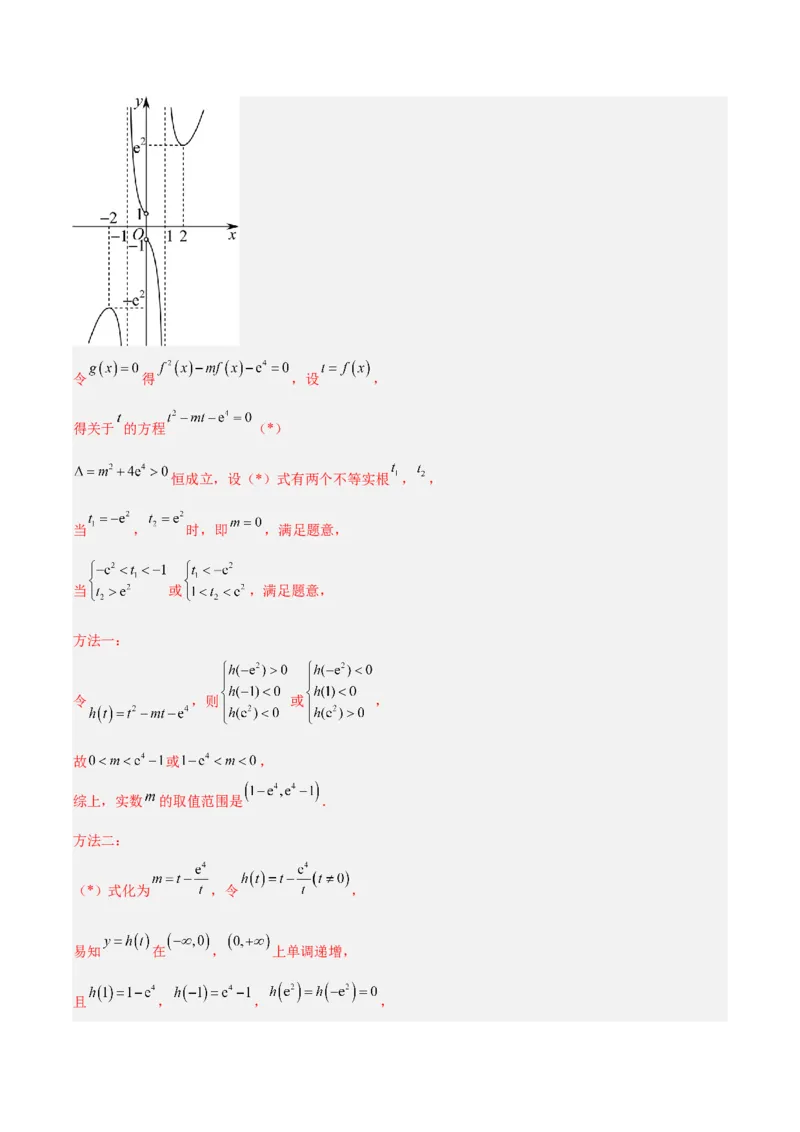
由 解析式可知, 为奇函数.画出 图象大致如下:令 得 ,设 ,
得关于 的方程 (*)
恒成立,设(*)式有两个不等实根 , ,
当 , 时,即 ,满足题意,
当 或 ,满足题意,
方法一:
令 ,则 或 ,
故 或 ,
综上,实数 的取值范围是 .
方法二:
(*)式化为 ,令 ,
易知 在 , 上单调递增,
且 , , ,其图象大致如图:
当 或 时,满足 或 ,
综上,实数 的取值范围是 .
【点睛】方法点睛:
导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.
注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问
题处理.通过构造一个适当的函数,利用它的单调性进行解题,是一种常用技巧.许多问题,如果运用这种
思想去解决,往往能获得简洁明快的思路,有着非凡的功效.
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.在 中,角 、 、 的对边分别为 、 、 ,且 ,
(1)求角 的大小;
(2)若 , ,求 的值.
【答案】(1) (2)
【详解】(1)解:因为 ,由正弦定理可得 ,
所以,
,
因为 、 ,所以, ,则 ,故 .
(2)解:因为 , , ,由余弦定理可得 ,则 ,
由正弦定理可得 ,所以, .
18.某娱乐节目闯关游戏共有三关,游戏规则如下,选手依次参加第一,二,三关,闯关成功可获得的奖
金分别为1000元、2000元、3000元.奖金可累加,若某关闯关成功,选手可以选择结束闯关游戏并获得相
应奖金,也可以选择继续闯关,若有任何一关闯关失败,则连同前面所得奖金全部归零,闯关游戏结束.选
手小刘参加闯关游戏,已知他第一,二,三关闯关成功的概率分别为 , , .第一关闯关成功选择继续
闯关的概率为 ,第二关闯关成功选择继续闯关的概率为 ,且每关闯关成功与否互不影响.
(1)求小刘第一关闯关成功,但所得总奖金为零的概率;
(2)设小刘所得奖金为X,求随机变量X的分布列及数学期望.
【答案】(1) ; (2)分布列见解析,数学期望为 元.
【详解】(1)由题意,要使小刘第一关闯关成功,但所得总奖金为零,
选择闯第二关且失败,或选择闯第二关且成功,又选择闯第三关且失败,
所以小刘第一关闯关成功,但所得总奖金为零的概率 .
(2)由题意, ,且 ,
, ,
,
X的分布列如下:
0 1000 3000 6000
元.19.在数列 中, , 是 的前n项和,且数列 是公差为 的等差数列.
(1)求 的通项公式;
(2)设 ,求数列 的前n项和 .
【答案】(1) (2)
【详解】(1)由已知得 , ,
所以 ,①
当 时, ,②
,得 ,
也符合该式,
所以 .
(2)由(1)得 ,
所以 ,③
,④
,得
.
故 .
20.已知矩形ABCD中,点E在边CD上,且 .现将 沿AE向上翻折,使点D到点P的位置,构成如图所示的四棱锥 .
(1)若点F在线段AP上,且 平面PBC,求 的值;
(2)若 ,求锐二面角 的余弦值.
【答案】(1)2 (2)
【详解】(1)点 为线段 上靠近点 的三等分点,满足 平面PBC,证明如下:
如图,过点 作 交 于点 ,连接 ,则 ,
又 , ,所以 .因为 ,所以 ,
所以四边形 为平行四边形,有 ,
又 平面 , 平面 ,所以 平面 .
此时有 .
(2) , 为等腰直角三角形,
, , , .
取 的中点 ,以 为坐标原点, 为 轴建立如图所示的空间直角坐标系,设 , , , ,
则 , ,
因为 , ,所以 ,解得 ,
则 , , ,
设平面 的法向量为 , 则 ,
不妨取 ,则 , ,
设平面 的一个法向量为 ,则 ,
则锐二面角 的的余弦值为 .
21.在 中,已知点 边上的中线长与 边上的中线长之和为 ,记
的重心G的轨迹为曲线C.
(1)求C的方程;
(2)若圆 ,过坐标原点O且与y轴不重合的任意直线 与圆 相交于点 ,直线
与曲线 的另一个交点分别是点 ,求 面积的最大值.【答案】(1) (2)
【详解】(1)设 的中点为S, 的中点为T,所以 , ,
所以 ,所以 ,
所以G点的轨迹是以 为焦点,长轴长 的椭圆.所以 ,
所以 , ,所以曲线C的方程为 .
.
(2)设直线 为 (不妨设 ),设 , ,
所以 , , ,
解得 ( 舍去),则 ,
由于AB是单位圆的直径,所以 ,
所以直线EN的斜率为 ,直线EN的方程为 ,
同理可求得 ,则 ,由上述分析可知 , ,而 ,
所以
,
所以 ,令 ,
当且仅当 , 时等号成立,
则 ,函数 在 上单调递增,
所以当 时, 取得最小值为 .
【点睛】关键点睛:在圆锥曲线中,求解三角形面积最值、范围等的有关问题,关键点有两点,第一点是
求得三角形面积的表达式,可考虑根与系数关系、点到直线的距离公式等等来进行求解;第二点根据面积
的表达式,使用基本不等式、二次函数等知识求得面积的最值或取值范围.
22.已知函数 .
(1)当 时,求曲线 在 处的切线方程;
(2)若 ,都有 ,求 的取值范围.
【答案】(1) (2)
【详解】(1)解:当 时, ,因为 ,
所以,曲线 在 处的切线方程是 ,即 .
(2)因为 ,都有 ,所以 .
设 ,则 .
记 ,设 ,则 ,
当 时, ,当 时, ,
所以 在 上单调递增,在 上单调递减,
所以 ,
所以 ,所以 在 上单调递减.
因为 ,当 时, ,当 时, ,
所以 在 上单调递增,在 上单调递减,
所以 ,所以, .
【点睛】方法点睛:对于 , 恒成立,则 ;对于 , 恒成立,则
;对于 , 有解,则 ;对于 , 有解,则 ;