文档内容
【赢在高考·黄金8卷】备战2024年高考数学模拟卷(新高考Ⅰ卷专用)
黄金卷07
(考试时间:120分钟 试卷满分:150分)
第 I 卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的。
1.已知全集 ,集合 ,则 ( )
A. B. C. D.
2.欧拉公式 (e为自然对数的底数, 为虚数单位)由瑞士数学家Euler(欧拉)首先发
现.它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,被称为“数学中的天桥”,则
( )
A. -1 B.1 C.- D.
3.若 为奇函数,则 的值为( )
A.-1 B.0 C.1 D.-1或1
4.已知向量 满足 ,且 ,则 在 上的投影向量为( )
A. B. C. D.
5.已知动点 在直线 上,过点 作圆 的一条切线,切点为 ,则 的最小值为
( )
A.1 B. C. D.2
6.“绿水青山,就是金山银山”,随着我国的生态环境越来越好,外出旅游的人越来越多.现有两位游客
慕名来江苏旅游,他们分别从“太湖鼋头渚、苏州拙政园、镇江金山寺、常州恐龙园、南京夫子庙、扬州
瘦西湖”这6个景点中随机选择1个景点游玩.记事件A为“两位游客中至少有一人选择太湖鼋头渚”,事件B为“两位游客选择的景点不同”,则 ( )
A. B. C. D.
7.玉琮是中国古代玉器中重要的礼器,神人纹玉琮王是新石器时代良渚文化的典型玉器, 年出土于
浙江省余杭市反山文化遗址.玉琮王通高 ,孔径 、外径 .琮体四面各琢刻一完整的兽面神
人图像.兽面的两侧各浅浮雕鸟纹.器形呈扁矮的方柱体,内圆外方,上下端为圆面的射,中心有一上下垂
直相透的圆孔.试估计该神人纹玉琮王的体积约为(单位: )( )
A. B. C. D.
8.如图,已知抛物线 ( )的焦点为 ,点 ( )是抛物线 上一点.以
为圆心的圆与线段 相交于点 ,与过焦点 且垂直于对称轴的直线交于点 , , ,直线
与抛物线 的另一交点为 ,若 ,则 ( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目的
要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
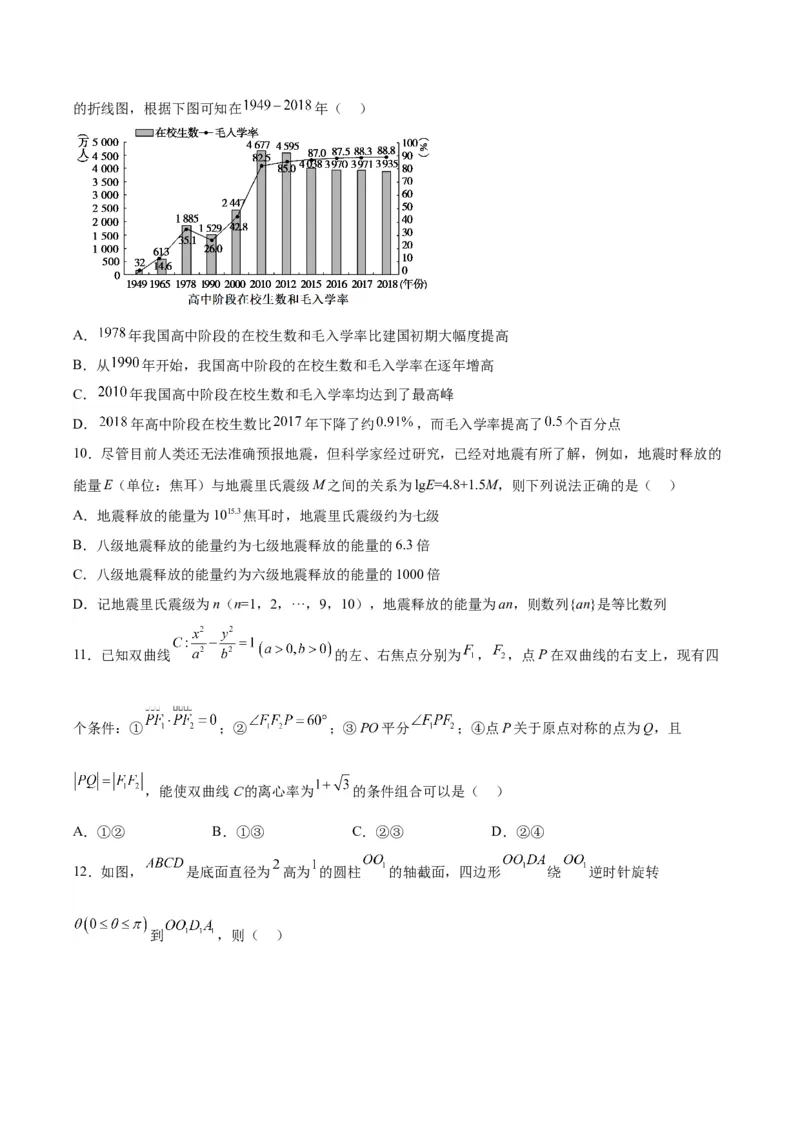
9.图是《2018年全国教育事业发展统计公报》中 年我国高中阶段在校生数条形图和毛入学率的折线图,根据下图可知在 年( )
A. 年我国高中阶段的在校生数和毛入学率比建国初期大幅度提高
B.从 年开始,我国高中阶段的在校生数和毛入学率在逐年增高
C. 年我国高中阶段在校生数和毛入学率均达到了最高峰
D. 年高中阶段在校生数比 年下降了约 ,而毛入学率提高了 个百分点
10.尽管目前人类还无法准确预报地震,但科学家经过研究,已经对地震有所了解,例如,地震时释放的
能量E(单位:焦耳)与地震里氏震级M之间的关系为lgE=4.8+1.5M,则下列说法正确的是( )
A.地震释放的能量为1015.3焦耳时,地震里氏震级约为七级
B.八级地震释放的能量约为七级地震释放的能量的6.3倍
C.八级地震释放的能量约为六级地震释放的能量的1000倍
D.记地震里氏震级为n(n=1,2,···,9,10),地震释放的能量为an,则数列{an}是等比数列
11.已知双曲线 的左、右焦点分别为 , ,点P在双曲线的右支上,现有四
个条件:① ;② ;③PO平分 ;④点P关于原点对称的点为Q,且
,能使双曲线C的离心率为 的条件组合可以是( )
A.①② B.①③ C.②③ D.②④
12.如图, 是底面直径为 高为 的圆柱 的轴截面,四边形 绕 逆时针旋转
到 ,则( )A.圆柱 的侧面积为
B.当 时,
C.当 时,异面直线 与 所成的角为
D. 面积的最大值为
第 II 卷(非选择题)
三、填空题:本题共4小题,每小题5分,共20分。
13.编号为1,2,3,4的四位同学,分别就座于编号为1,2,3,4的四个座位上,每位座位恰好坐一位
同学,则恰有两位同学编号和座位编号一致的坐法种数为 .
14.已知 ,则 .
15.已知 a>0,若 ,且 ,则a= .
16.已知函数 是偶函数,将 的图象沿 轴向左平移 个
单位,再将图象上所有点的横坐标伸长到原来的 倍(纵坐标不变),所得图象对应的函数为 .已
知 的图象相邻对称中心之间的距离为 ,则 ,若 的图象在其某对称轴处对
应的函数值为 ,则 在 上的最大值为 .
四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及验算步骤。
17.(本题满分10分)在① ;② ;③ 是 与 的等比中项,三个条件中任选一个,
补充在下面问题中,并给出解答.问题:已知 为公差不为零的等差数列,其前 项和为 为等比数列,其前 项和 为
常数, ,
(1)求数列 的通项公式;
(2)令 其中 表示不超过 的最大整数,求 的值.
注:如果选择多个条件分别解答,按第一个解答计分.
18.(本题满分12分)如图,平面四边形 ,点 , , 均在半径为 的圆上,且 .
(1)求 的长度;
(2)若 ,求 的面积.
19.(本题满分12分)2021年春晚首次采用“云”传播,“云”互动形式,实现隔空连线心意相通,全
球华人心连心“云团圆”,共享新春氛围,“云课堂”亦是一种真正完全突破时空限制的全方位互动性学
习模式.某市随机抽取200人对“云课堂”倡议的了解情况进行了问卷调查,记 表示了解, 表示不了
解,统计结果如下表所示:
(表一)
了解情况
人数 140 60
(表二)男 女 合计
80
4
0
合计
(1)请根据所提供的数据,完成上面的 列联表(表二),并判断是否有99%的把握认为对“云课
堂”倡议的了解情况与性别有关系;
(2)用样本估计总体,将频率视为概率,在男性市民和女性市民中各随机抽取4人,记“4名男性中恰有
3人了解云课堂倡议”的概率为 ,“4名女性中恰有3人了解云课堂倡议”的概率为 .试求出 与 ,
并比较 与 的大小.
附:临界值参考表的参考公式
,其中 )
20.(本题满分12分)如图,四棱锥 中, 平面 , , ,
,点 在线段 上,且 , 平面 .
(1)求证:平面 平面 ;
(2)若 ,求平面 和平面 所成锐二面角的余弦值.21.(本题满分12分)已知 分别是椭圆 的左、右焦点, 为椭圆的上顶点,
是面积为 的直角三角形.
(1)求椭圆 的方程;
(2)设圆 上任意一点 处的切线 交椭圆 于点 ,问: 是否为定值?若是,
求出此定值;若不是,说明理由.
22.(本题满分12分)已知函数 , .
(1)若 ,讨论 的单调性;
(2)若当 时, 恒成立,求 的取值范围.