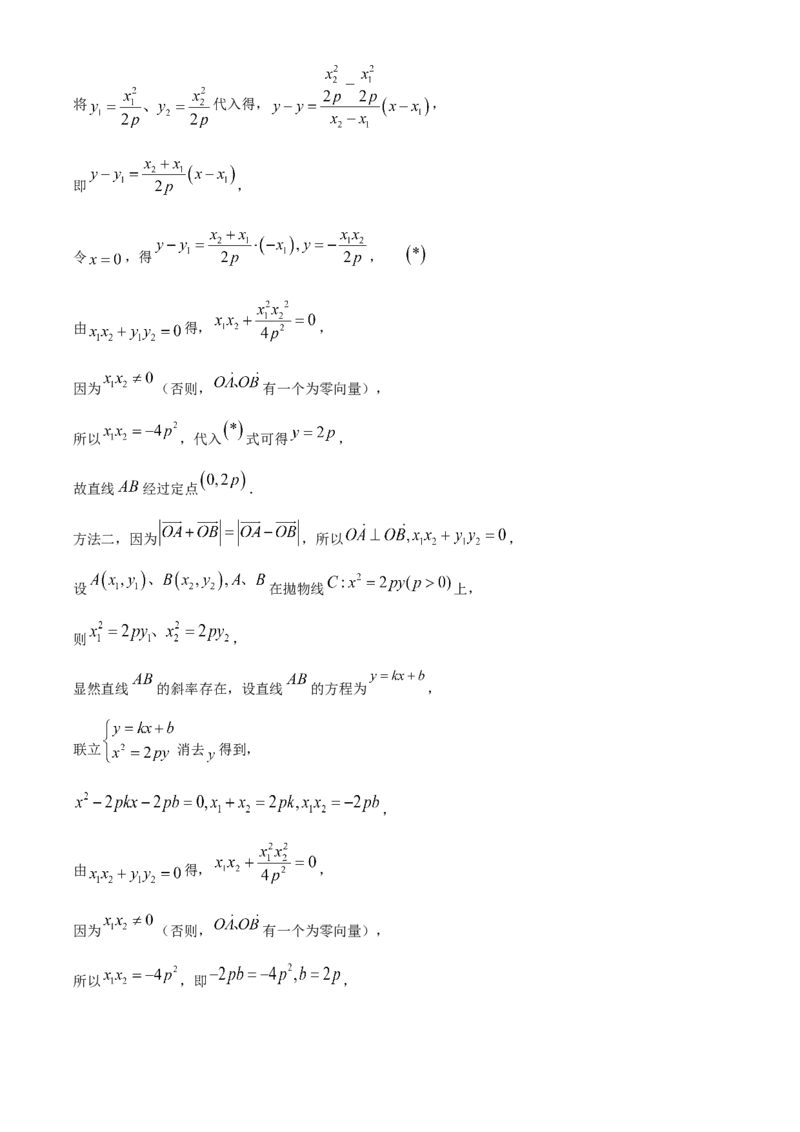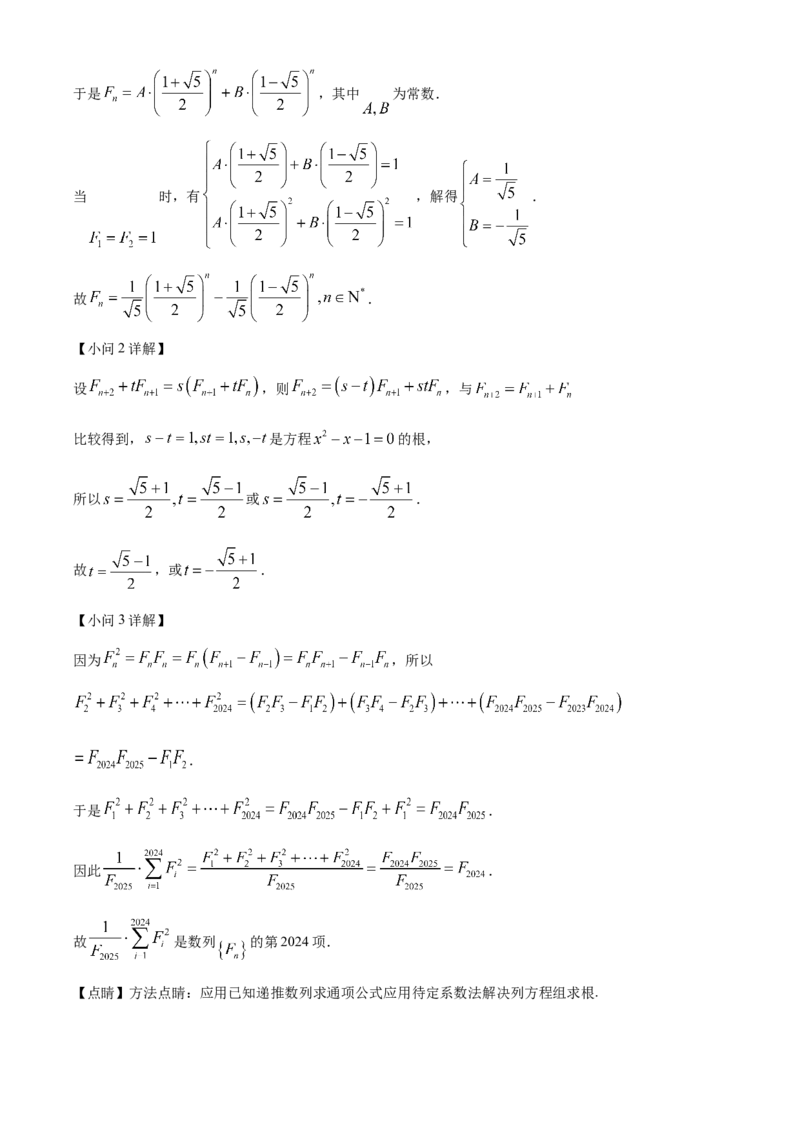文档内容
高二数学(人教版)
本试卷共4页,19题.全卷满分150分,考试时间120分钟.
考生注意事项:
1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在
答题卡上的指定位置.
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.写
在试卷、草稿纸和答题卡上的非答题区域均无效.
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸
和答题卡上的非答题区域均无效.
4.考试结束后,请将本试卷和答题卡一并上交.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 若 是离散型随机变量,则 ( )
A. B. C. 0 D.
2. 函数 的定义域为开区间 ,导函数 在 内的图象如图所示,则函数 在开区
间 内有极小值点( )
A. 1个 B. 2个 C. 3个 D. 4个
3. 某市旅游局对全市各旅游景区的环境进行综合治理,投入不同数额的经费( 千万元),得到各旅游景
区收益的增加值( 万元),对应数据如下表所示:
投人的治理经费 (单位:千万元) 1 2 3 4 5 6 7
收益的增加值 (单位:万元) 2 3 2 5 7 7 9
若 与 的回归直线方程为 ,则相应于点 的残差是( )A. B. 0.358 C. D. 8.642
4. 函数 在 上( )
A. 单调递增 B. 单调递减 C. 有增有减 D. 无法判定
的
5. 某班新年联欢会原定 5个节目已排成节目单,开演前又增加了两个新节目.如果将这两个节目插入原
节目单中,那么不同插法的种数为
A. 42 B. 30 C. 20 D. 12
6. 已知函数 是自然对数的底数.若曲线 在点 处的切
线方程是 ,则 的值是( )
A. B. C. D.
7. 甲乙两人分别掷两枚骰子,规则如下:若掷出的点数之和是3的倍数,则由原掷骰子的人继续掷;若掷
出的点数之和不是3的倍数,则由对方接着掷.第一次掷由甲开始,设第 次由甲掷的概率为 ,则 与
之间的关系是( )
.
A B.
C. D.
8. 设 分别是离心率为 的椭圆 的左、右焦点,过点 的直线交椭圆
于 两点,且 ,则 ( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符
合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 把一个正态曲线 沿着横轴方向向右移动2个单位,得到新的一条曲线 ,下列说法中正确的是(
)
A. 曲线 仍然是正态曲线
B. 曲线 和曲线 的最高点的纵坐标相等
C. 以曲线 为概率密度曲线的总体的期望比以曲线 为概率密度曲线的总体的期望小2
D. 以曲线 为概率密度曲线的总体的方差比以曲线 为概率密度曲线的总体的方差大2
10. 已知数列 的前 项和为 ,且 ,则下列结论中正确的是(
)
A. B. 是等比数列
C. D. 是递增数列
11. “曼哈顿距离”是由赫尔曼-闵可夫斯基使用在几何度量空间的几何学用语.在平面直角坐标系中,点
的 曼 哈 顿 距 离 为 : . 若 点 , 点 为 圆
上一动点,则( )
A. 点 和点 的曼哈顿距离为3
B. 设 ,则
C. 的最大值为
D. 的最大值为
三、填空题:本题共3小题,每小题5分,共15分.12. 已知随机变量 ,则 的值是___________
13. 在二项式 的展开式中,所有项的系数和为 ,则此二项式展开式中二项式系数之和
是___________.
14. 若不等式 对任意 恒成立,则整数 的最大值是___________.
四、解答题:共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知函数 ,其中 为自然对数 的底数.
(1)求 的极值;
(2)若 有两个零点,求 的取值范围.
16. 如图,在四棱锥 中,底面矩形 垂直于侧面 ,且 分别是棱
的中点, .
(1)证明: 平面 ;
的
(2)若 ,求二面角 正弦值.
17. 已知 为坐标原点, 是抛物线 上与点 不重合 的任意一点.
(1)设抛物线 的焦点为 ,若以 为圆心, 为半径的圆 交 的准线 于 两点,且
的面积为 ,求圆 的方程;
(2)若 是拋物线 上的另外一点,非零向量 满足 ,证明:直线 必经过一个定点.
18. 某市一些企业,由于没有技术更新业务受到形响,资金出现缺额,银行将给予低息贷款的扶持.银行
制定了评分标准,根据标准对这些企业进行评估,然后依据企业评估得分将这些企业分别定为优秀、良好、
合格、不合格四个等级,并根据等级分配相应的低息贷款数额.为了更好地掌握贷款总额,银行随机抽查
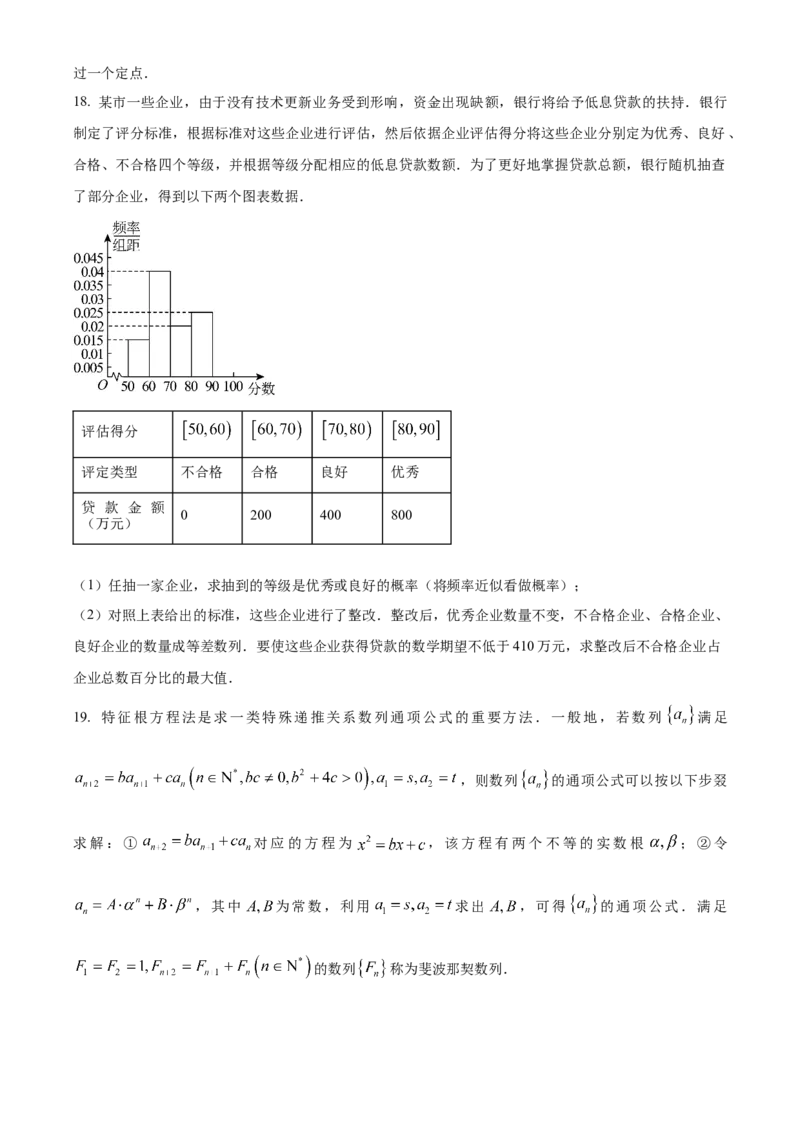
了部分企业,得到以下两个图表数据.
评估得分
评定类型 不合格 合格 良好 优秀
贷 款 金 额
0 200 400 800
(万元)
(1)任抽一家企业,求抽到的等级是优秀或良好的概率(将频率近似看做概率);
(2)对照上表给出的标准,这些企业进行了整改.整改后,优秀企业数量不变,不合格企业、合格企业、
良好企业的数量成等差数列.要使这些企业获得贷款的数学期望不低于410万元,求整改后不合格企业占
企业总数百分比的最大值.
19. 特征根方程法是求一类特殊递推关系数列通项公式的重要方法.一般地,若数列 满足
,则数列 的通项公式可以按以下步叕
求解:① 对应的方程为 ,该方程有两个不等的实数根 ;②令
,其中 为常数,利用 求出 ,可得 的通项公式.满足
的数列 称为斐波那契数列.(1)求数列 的通项公式;
(2)若存在非零实数 ,使得 为等比数列,求 的值;
(3)判定 是数列 的第几项,写出推理过程.高二数学(人教版)
本试卷共4页,19题.全卷满分150分,考试时间120分钟.
考生注意事项:
1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在
答题卡上的指定位置.
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.写
在试卷、草稿纸和答题卡上的非答题区域均无效.
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸
和答题卡上的非答题区域均无效.
4.考试结束后,请将本试卷和答题卡一并上交.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 若 是离散型随机变量,则 ( )
A. B. C. 0 D.
【答案】C
【解析】
【分析】根据随机变量的数学期望的性质计算即可.
【详解】 .
故选:C.
2. 函数 的定义域为开区间 ,导函数 在 内的图象如图所示,则函数 在开区
间 内有极小值点( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】A【解析】
【分析】由导函数的图象可知 在开区间 内有 个零点 , ,
分析导函数再零点左右的导数值(正、负),即可判断函数的极值点,从而得解.
【详解】从图形中可以看出, 在开区间 内有 个零点 , ,
在 处的两边 左正、右负,取得极大值;
在 处的两边 左负、右正,取值极小值;
在 处的两边 都为正,没有极值;
在 处的两边 左正、右负,取值极大值.
因此函数 在开区间 内的极小值点只有一个.
故选:A.
3. 某市旅游局对全市各旅游景区的环境进行综合治理,投入不同数额的经费( 千万元),得到各旅游景
区收益的增加值( 万元),对应数据如下表所示:
投人的治理经费 (单位:千万元) 1 2 3 4 5 6 7
收益的增加值 (单位:万元) 2 3 2 5 7 7 9
若 与 的回归直线方程为 ,则相应于点 的残差是( )
A. B. 0.358 C. D. 8.642
【答案】B
【解析】
【分析】先算出 ,代入回归直线方程为 ,可得 ,进而得到回归直线方程,当
时,求出 ,算出残差即可.
【详解】 ,
所以 ,当 时, ,因此残差为 .
故选:B.
4. 函数 在 上( )
A. 单调递增 B. 单调递减 C. 有增有减 D. 无法判定
【答案】B
【解析】
【分析】根据函数的导数即可分析函数单调性.
【详解】因为
,函数 在 上单调递减.
故选:B.
5. 某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目.如果将这两个节目插入原
节目单中,那么不同插法的种数为
A. 42 B. 30 C. 20 D. 12
【答案】A
【解析】
【详解】原定的5个节目之间有6个位.
当插入的这两个新节目在一起时,有 插法;
当插入的这两个新节目不在一起时,有 插法,
所以总的不同插法的种数为 种.
故选:A.
【点睛】关于排列和组合的题目,常用到捆绑法和插位法.捆绑法是将一些对象看作一个对象进行排列;
插位法是将一些对象进行排列后,再对剩下的对象进行排列.
6. 已知函数 是自然对数的底数.若曲线 在点 处的切
线方程是 ,则 的值是( )
A. B. C. D.【答案】C
【解析】
【分析】求导,根据函数在某点的切线方程得到 在点 处的切线方程可表示为:
,再由切线方程是 ,建立方程组求解.
【详解】因为 ,所以 .
在点 处的切线方程可表示为:
,
又因为曲线 在点 处的切线方程是 ,
所以 解得 .
故选:C.
7. 甲乙两人分别掷两枚骰子,规则如下:若掷出的点数之和是3的倍数,则由原掷骰子的人继续掷;若掷
出的点数之和不是3的倍数,则由对方接着掷.第一次掷由甲开始,设第 次由甲掷的概率为 ,则 与
之间的关系是( )
A. B.
C. D.
【答案】C
【解析】
【分析】据题意列出第 次由甲掷的两种情况,根据互斥事件判断可得到答案.
【详解】第 次由甲掷应该有两种情况:①第 次由甲掷,第 次继续由甲掷,此时概率为 ;
②第 次由乙掷,第 次由甲掷,此时概率为 .
由于这两种情况是互斥的,
因此 与 之间的关系式是 ,其中 .
故选:C.
8. 设 分别是离心率为 的椭圆 的左、右焦点,过点 的直线交椭圆
于 两点,且 ,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】根据题意,由椭圆的定义结合余弦定理代入计算,即可得到 ,从而得到结果.
【详解】因为 ,所以 .设 ,则 .
在 中, .
在 中, ,
所以 ,整理得, .
于是 .
故选:D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符
合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 把一个正态曲线 沿着横轴方向向右移动2个单位,得到新的一条曲线 ,下列说法中正确的是(
)
A. 曲线 仍然是正态曲线
B. 曲线 和曲线 的最高点的纵坐标相等
C. 以曲线 为概率密度曲线的总体的期望比以曲线 为概率密度曲线的总体的期望小2
D. 以曲线 为概率密度曲线的总体的方差比以曲线 为概率密度曲线的总体的方差大2
【答案】AB
【解析】
【分析】利用正态分布的图象与性质判定即可.
【详解】密度函数 ,向右移动2个单位后,密度函数 ,
曲线b仍然是正态曲线,最高点的纵坐标不变,故AB正确;
以曲线b为概率密度曲线的总体的期望值为 ,故C错误;
以曲线 为概率密度曲线的总体的方差不变.故D错误;
故选: AB.
10. 已知数列 的前 项和为 ,且 ,则下列结论中正确的是(
)
A. B. 是等比数列
C. D. 是递增数列
【答案】ACD
【解析】
【分析】由题中条件可得 ,判断 A;通过两式相减的 ,变形可得出,判断B;
根据求和公式结合作差法比较大小判断C,D;
【详解】对于A,由 得,
,所以 .A正确;
对于B,将 与 整体相减得, ,
所以 ,
又 ,即 ,
所以 .
因此 不是等比数列,B错误;
对于C,因为 ,
所以当 时, .
当 时, .
当 时, ,因此 ,C正确;
对于D,因 为,
所以 ,
所以 ,
因此 是递增数列,D正确;
故选:ACD.
11. “曼哈顿距离”是由赫尔曼-闵可夫斯基使用在几何度量空间的几何学用语.在平面直角坐标系中,点的 曼 哈 顿 距 离 为 : . 若 点 , 点 为 圆
上一动点,则( )
A. 点 和点 的曼哈顿距离为3
B. 设 ,则
C. 的最大值为
D. 的最大值为
【答案】ABD
【解析】
【分析】根据“曼哈顿距离”即可去判断选项A,根据 ,分类讨论去绝对值结合辅助角
公式可求判断选项B,C,D.
【详解】对A, ,A对;
因为 ,
所以 ,B对;
当 , 即 时 , 的 最 大 值 为 . 满 足
,
当 ,即 时, 的最大值为 .满足,则C错,D对,
故选ABD.
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知随机变量 ,则 的值是___________
【答案】
【解析】
【分析】根据二项分布的方差公式求得 ,再结合方差的性质公式得出
结果.
【详解】因为 ,
所以 .
故答案为: .
13. 在二项式 展开式中,所有项的系数和为 ,则此二项式展开式中二项式系数之和
的
是___________.
【答案】
【解析】
【分析】令 ,利用各项系数和求出 ,再利用二项式系数的性质即可求解.
【详解】在二项式 的展开式中,令 ,
得, ,
即, ,
解得, ,所以二项式系数和为 .
故答案为:16.
14. 若不等式 对任意 恒成立,则整数 的最大值是___________.
【答案】3
【解析】
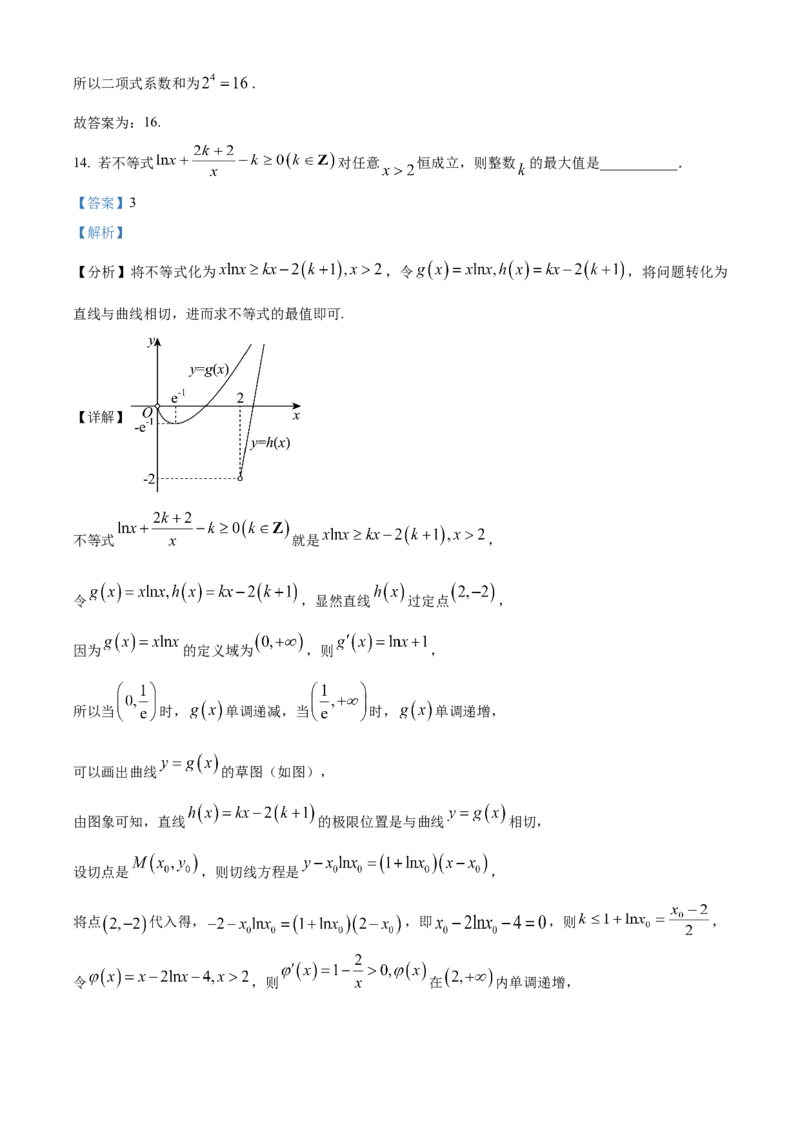
【分析】将不等式化为 ,令 ,将问题转化为
直线与曲线相切,进而求不等式的最值即可.
【详解】
不等式 就是 ,
令 ,显然直线 过定点 ,
因为 的定义域为 ,则 ,
所以当 时, 单调递减,当 时, 单调递增,
可以画出曲线 的草图(如图),
由图象可知,直线 的极限位置是与曲线 相切,
设切点是 ,则切线方程是 ,
将点 代入得, ,即 ,则 ,
令 ,则 在 内单调递增,又因为 ,在 中 ,于是
,故整数 的最大值是3.
故答案为: .
【点睛】本题考查了函数恒成立问题,直线与曲线相切应用,导数应用以及函数最值问题,体现了转化和
数形结合思想,是一道难题.
四、解答题:共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知函数 ,其中 为自然对数的底数.
(1)求 的极值;
(2)若 有两个零点,求 的取值范围.
【答案】(1)答案见解析
(2) .
【解析】
【分析】(1)先对函数进行求导,对参数分类讨论,求解函数极值;
(2)根据 有两个零点转化为 ,令 ,利用函数求导判断函
数 单调性和在不同范围内函数的值域求得 的取值范围.
【小问1详解】
.
当 时, 上单增,既没有极大值,也没有极小值.
在
当 时,令 ,则当 时, 在 上单减,
当 时, 在 上单增,
所以 的极小值为 ,没有极大值.
【小问2详解】
由 得, .令 .
则 ,当 时, 单增;
当 时, 单减.因此 .
显然当 时, ;当 时, .
当 时,直线 与函数 的图象有且仅有两个公共点,
即函数 有两个零点.
故 的取值范围是 .
16. 如图,在四棱锥 中,底面矩形 垂直于侧面 ,且 分别是棱
的中点, .
(1)证明: 平面 ;
(2)若 ,求二面角 的正弦值.
【答案】(1)证明见解析(2)
【解析】
【分析】(1)由面面垂直可得 平面 ,则 ,由几何知识可得 , ,
结合线面垂直的判定定理分析证明;
(2)建系标点,可得平面 、平面 的法向量,利用空间向量求二面角.
【小问1详解】
因为 为矩形,则 ,
且平面 平面 ,平面 平面 平面 ,
则 平面 ,且 平面 ,所以 .
连接 .
在 和 中, ,
可知 全等于 .则 ,
且 是 的中点,则 .
在 中, ,
而 是 的中点,则 .
且 , 平面 ,所以 平面 .
【小问2详解】以A为坐标原点, 所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系
,
则 ,可得 ,
由(1)知, 是平面 的法向量,
且平面 的法向量是 .
可得 .
所以二面角 的正弦值为 .
17. 已知 为坐标原点, 是抛物线 上与点 不重合的任意一点.
(1)设抛物线 的焦点为 ,若以 为圆心, 为半径的圆 交 的准线 于 两点,且
的面积为 ,求圆 的方程;
(2)若 是拋物线 上的另外一点,非零向量 满足 ,证明:直线 必经
过一个定点.
【答案】(1)
(2)证明见解析
【解析】
【分析】(1)求出 ,点 到准线 的距离 ,利用 求出 可得答案;(2)方法一,对 两边平方得 ,设 ,设直线
的方程为 ,结合抛物线方程得 ,再由
可得答案;方法二,对 两边平方得 ,设 ,设直
线 的方程为 与抛物线方程联立,利用韦达定理结合 可得答案.
【小问1详解】
准线 为 到 的距离是 .由对称性知,
是等腰直角三角形,斜边 ,
点 到准线 的距离 ,
,解得 ,
故圆 的方程为 ;
【小问2详解】
方法一,因为 ,
所以 ,
所以 ,
设 在抛物线 上,
则 .
显然直线 的斜率存在,
则直线 的方程为 ,将 代入得, ,
即 ,
令 ,得 ,
由 得, ,
因为 (否则, 有一个为零向量),
所以 ,代入 式可得 ,
故直线 经过定点 .
方法二,因为 ,所以 ,
设 在拋物线 上,
则 ,
显然直线 的斜率存在,设直线 的方程为 ,
联立 消去 得到,
,
由 得, ,
因为 (否则, 有一个为零向量),
所以 ,即 ,因此 就是 .故直线 经过定点 .
【点睛】方法点睛:求解直线过定点问题常用方法如下:(1)“特殊探路,一般证明”:即先通过特殊
情况确定定点,再转化为有方向、有目的的一般性证明;(2)“一般推理,特殊求解”:即设出定点坐
标,根据题设条件选择参数,建立一个直线系或曲线的方程,再根据参数的任意性得到一个关于定点坐标
的方程组,以这个方程组的解为坐标的点即为所求点;(3)求证直线过定点,常利用直线的点斜式方程
或截距式来证明.
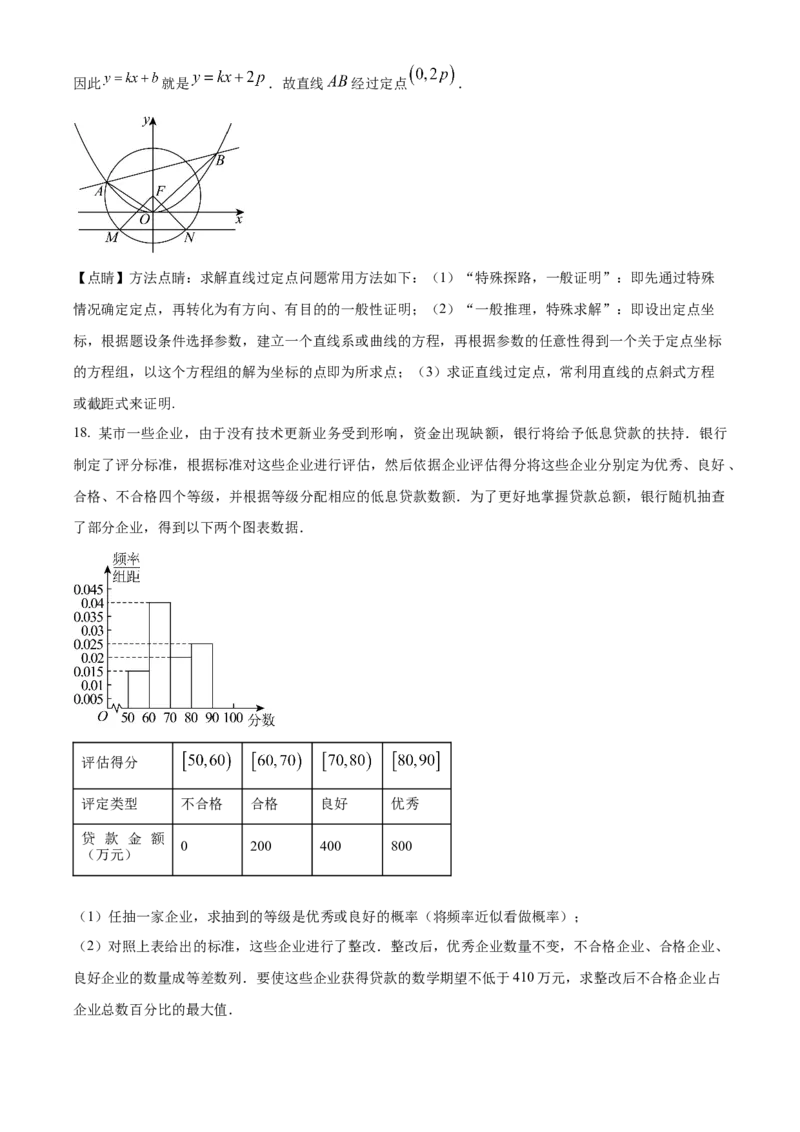
18. 某市一些企业,由于没有技术更新业务受到形响,资金出现缺额,银行将给予低息贷款的扶持.银行
制定了评分标准,根据标准对这些企业进行评估,然后依据企业评估得分将这些企业分别定为优秀、良好、
合格、不合格四个等级,并根据等级分配相应的低息贷款数额.为了更好地掌握贷款总额,银行随机抽查
了部分企业,得到以下两个图表数据.
评估得分
评定类型 不合格 合格 良好 优秀
贷 款 金 额
0 200 400 800
(万元)
(1)任抽一家企业,求抽到的等级是优秀或良好的概率(将频率近似看做概率);
(2)对照上表给出的标准,这些企业进行了整改.整改后,优秀企业数量不变,不合格企业、合格企业、
良好企业的数量成等差数列.要使这些企业获得贷款的数学期望不低于410万元,求整改后不合格企业占
企业总数百分比的最大值.【答案】(1)0.45
(2)
【解析】
【分析】(1)由频率分布直方图可得, 抽到不合格、合格、良好、优秀的概率,则可得抽到的等级是优秀
或良好的概率;
(2)设整改后,抽到不合格、合格、良好的概率分别为 ,则 也成等差数列,即 ,
又 ,可得 ,列出分布列,可求得 ,又数学期
望不低于410,列出不等式,即可解得不合格企业占企业总数百分比的最大值.
【小问1详解】
设任意抽取一家企业,抽到不合格、合格、良好、优秀的概率分别是 ,
则根据频率分布直方图可知,
.
故任抽一家企业,等级是优秀或良好的概率约为 .
【小问2详解】
设整改后,任意抽取一家企业,抽到不合格、合格、良好的概率分别为 ,
因为不合格企业、合格企业、良好企业的数量成等差数列,所以 也成等差数列,
即 ,又因为 ,所以 ,
设整改后一家企业获得的低息贷款为随机变量 ,则其分布列是
0 200 400 800
0.25 0.25
于是
,
因为 ,所以 ,解得 ,故整改后不合格企业占企业总数百分比的最大值是 .
19. 特征根方程法是求一类特殊递推关系数列通项公式的重要方法.一般地,若数列 满足
,则数列 的通项公式可以按以下步叕
求解:① 对应的方程为 ,该方程有两个不等的实数根 ;②令
,其中 为常数,利用 求出 ,可得 的通项公式.满足
的数列 称为斐波那契数列.
(1)求数列 的通项公式;
(2)若存在非零实数 ,使得 为等比数列,求 的值;
(3)判定 是数列 的第几项,写出推理过程.
【答案】(1)
(2) ,或 .
(3)第2024项,答案见解析
【解析】
【分析】(1)应用待定系数法求参即可;
(2)设数列为等比数列再应用待定系数法得出等式再求参;
(3)化简再应用裂项相消求和即可得出数列中的项.
【小问1详解】
由题意知, 对应的特征方程是 ,解得 .于是 ,其中 为常数.
当 时,有 ,解得 .
故 .
【小问2详解】
设 ,则 ,与
比较得到, 是方程 的根,
所以 或 .
故 ,或 .
【小问3详解】
因为 ,所以
.
于是 .
因此 .
故 是数列 的第2024项.
【点睛】方法点睛:应用已知递推数列求通项公式应用待定系数法解决列方程组求根.