文档内容
2024年新高考改革适应性练习 2(九省联考题型)
数学试题卷
考生须知
1. 本卷共5页,四大题19小题,满分150分,答题时间120分钟;
2. 答题时须在答题卡上填涂所选答案(选择题),或用黑色字迹的签字笔规范书写答案与步骤(非选择题),
答在本试题卷上或草稿纸上的答案均属无效;
3. 考试结束时,考生须一并上交本试题卷,答题卡与草稿纸.
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.)
1. 某旅行社为迎节日搞活动旅游,经市场调查,某旅游线路销量 (人)与旅游价格 (元/人)负相
关,则其回归直线方程可能是 𝑌𝑌 𝑋𝑋
A. B.
C.𝑌𝑌 = −80𝑋𝑋+1600 D.𝑌𝑌 = 80𝑋𝑋+1600
2. 已知𝑌𝑌复=数−列80𝑋𝑋−满16足00 ( 为虚数单位),则𝑌𝑌 = 80的𝑋𝑋前−11600项0 和是
𝑛𝑛
A. {𝑧𝑧 𝑛𝑛} 𝑧𝑧B𝑛𝑛.= i i C. {𝑧𝑧𝑛𝑛} D.
3. “棱1柱+的i相邻两个侧面是矩1−形i”是“该棱柱为直−棱1柱+”i 的 −1−i
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
4. 斐波那契数列指的是这样一个数列 : , ,记 除以4的
余数为 ,则 {𝐹𝐹𝑛𝑛} 𝐹𝐹1 = 𝐹𝐹2 = 1 𝐹𝐹𝑛𝑛 = 𝐹𝐹𝑛𝑛−1+𝐹𝐹𝑛𝑛−2 (𝑛𝑛 ≥ 3) 𝐹𝐹𝑛𝑛
A.0 𝐺𝐺 𝑛𝑛 𝐺𝐺2 0 24 =B.1 C.2 D.3
5. 曼哈顿距离(Manhattan Distance)是由十九世纪的赫尔曼·闵可夫斯基所创词汇,是种使用在几何
度量空间的几何学用语,用以标明两个点在标准坐标系上的绝对轴距总和.同一平面上的两点
, ,其“曼哈顿距离”
𝐴𝐴(𝑥𝑥1,𝑦𝑦1) 𝐵𝐵(𝑥𝑥2,𝑦𝑦2)
则所有与点 的“曼哈顿距离𝑑𝑑”𝐴𝐴𝐴𝐴等=于|𝑥𝑥21的−点𝑥𝑥2构|+成|𝑦𝑦的1图−形𝑦𝑦2的| 周长为
A.8 (1 ,2) B. C.4 D.
8√2 4√2
数学试题卷 第1页(共5页)
学科网(北京)股份有限公司6. 已知以 为中心的椭圆 ,其一个长轴顶点为 , 是 的一个靠近 的焦点,点 在 上,
设 是 𝑂𝑂以 为直径的 𝛺𝛺圆 , 是以 为半径 𝑀𝑀的 圆𝑁𝑁, 则 𝛺𝛺 与 的位 𝑀𝑀置 关系为 𝑃𝑃 𝛺𝛺
A. 𝜔𝜔相1 切 𝑃𝑃𝑁𝑁 B.相交𝜔𝜔 2 𝑂𝑂𝑀𝑀 C.相离 𝜔𝜔1 𝜔𝜔2D .无法确定
7. 将函数 向下平移 个单位长度得到 .若 有两个零
𝑥𝑥
𝑥𝑥𝑒𝑒 ,𝑥𝑥 ≤ 0
点 𝑓𝑓(𝑥𝑥)= � ,则 的值 不可能是 𝑚𝑚 (𝑚𝑚 ∈ 𝑅𝑅) 𝑔𝑔(𝑥𝑥) 𝑔𝑔(𝑥𝑥)
ln𝑥𝑥−𝑥𝑥+1,𝑥𝑥 > 0
A.𝑥𝑥1 1 , 𝑥𝑥2 ( 𝑥𝑥1 < 𝑥𝑥2) B 𝑥𝑥. 1+𝑥𝑥2 C. D.
1 1
2 1 −𝑒𝑒 −𝑒𝑒
8. 过正四面体 的顶点𝑒𝑒 作−截𝑒𝑒 面,若满足:①𝑒𝑒截面+是1等腰三角形:②𝑒𝑒 截−面1与底面 成 的
二面角.这样 𝐴𝐴𝐵𝐵的𝐴𝐴截𝐴𝐴 面个数为 𝐴𝐴 𝐵𝐵𝐴𝐴𝐴𝐴 75°
A.6 B.12 C.18 D.24
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得6分,部分选对的得3分,有选错的得0分.)
9. 在正六边形 中,
A. 𝐴𝐴𝐵𝐵𝐴𝐴𝐴𝐴𝐴𝐴 𝐹𝐹 B.
𝐴𝐴����𝐴𝐴�⃗−�𝐴𝐴���𝐴𝐴�⃗ =�𝐵𝐵���𝐹𝐹�⃗ 𝐴𝐴����𝐴𝐴�⃗+�𝐴𝐴���𝐴𝐴�⃗ = 3𝐴𝐴����𝐴𝐴�⃗
C. D. 在 上的投影向量为
2
10. 已知𝐴𝐴��直��𝐴𝐴�⃗线·𝐴𝐴����𝐵𝐵�⃗ =与��𝐴𝐴���𝐵𝐵�⃗�经过坐标原点 ,且 𝐴𝐴����𝐴𝐴�,⃗ 𝐴𝐴����𝐴𝐴�⃗ 均在圆 𝐴𝐴����𝐴𝐴�⃗
2 2
上,则以 下𝐴𝐴𝐴𝐴说 法 𝐵𝐵正𝐴𝐴确 的有 𝑂𝑂 𝐴𝐴𝐴𝐴 ⊥ 𝐵𝐵𝐴𝐴 𝐴𝐴,𝐵𝐵,𝐴𝐴,𝐴𝐴 𝑃𝑃:𝑥𝑥 −6𝑥𝑥+𝑦𝑦 −8𝑦𝑦−9 = 0
A.圆心 到直线 的距离的最小值为5
B.弦 𝑃𝑃 𝐴𝐴𝐴𝐴 的中点满足四点共圆
C.四 边𝐴𝐴𝐵𝐵形,𝐵𝐵𝐴𝐴,𝐴𝐴𝐴𝐴,的𝐴𝐴𝐴𝐴面 积的取值范围是
D. 𝐴𝐴𝐵𝐵𝐴𝐴𝐴𝐴 �6√34,43�
11. 对正6整|𝑂𝑂数𝐴𝐴|+,3|若𝑂𝑂𝐴𝐴其|不≥能2√ 被2|任𝑂𝑂𝐴𝐴意|一·|𝑂𝑂个𝐴𝐴完| 全平方数整除,则称其为“无平方因子数”,并记其的素因子
个数为 𝑁𝑁. 由所有“无平方因子数”构成的集合记作 .则数论函数“缪比乌斯函数”定义如下
𝑑𝑑𝑛𝑛 𝑆𝑆
1 ,𝑛𝑛 = 1
𝑑𝑑𝑛𝑛
𝜇𝜇(𝑛𝑛)= �(−1) ,𝑛𝑛 ∈𝑆𝑆
则下列运算正确的有
0 ,𝑛𝑛 ∉ 𝑆𝑆
A.
B.𝜇𝜇(1)+𝜇𝜇(2)= 0
𝜇𝜇(1)+𝜇𝜇(2)+𝜇𝜇(4) = 1
数学试题卷 第2页(共5页)
学科网(北京)股份有限公司C.
D.𝜇𝜇(1)+𝜇𝜇(2)+𝜇𝜇(4)+𝜇𝜇(8) = 0
𝑛𝑛
𝜇𝜇(1)+𝜇𝜇(2)+⋯+𝜇𝜇(2 )= 1 (𝑛𝑛 ≥ 4)
三、填空题(本题共3小题,每小题5分,共15分.)
12. 已知钝角 的面积为3, , ,则 的值是_________.
13. 若函数 △𝐴𝐴𝐵𝐵𝐴𝐴 𝐴𝐴𝐵𝐵 = 4 𝐴𝐴𝐴𝐴 = 1 的四个 𝐴𝐴���� 零𝐵𝐵�⃗·点𝐴𝐴���� 是𝐴𝐴�⃗ 以0为首项的等差数列,则
2 𝑥𝑥−3 3−𝑥𝑥
______ 𝑓𝑓__(𝑥𝑥_.)= (𝑥𝑥 −6𝑥𝑥+𝑚𝑚)(𝑒𝑒 +𝑒𝑒 −𝑛𝑛) 𝑚𝑚+ 𝑛𝑛 =
14. 若 一个三位数中的任意两个相邻数码的差不超过 1,则称其为“平稳数”,则所有“平稳数”的个
数为_________.
四、解答题(本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.)
15.(15分)
已知在 中,角 所对的边分别为 ,且 .
(1)求 △𝐴𝐴;𝐵𝐵𝐴𝐴 𝐴𝐴,𝐵𝐵,𝐴𝐴 𝑎𝑎,𝑏𝑏,𝑐𝑐 tan𝐴𝐴+tan𝐵𝐵−√3tan𝐴𝐴tan𝐵𝐵+√3 =0
(2)若 𝐴𝐴 ,求 面积 的最大值.
𝑎𝑎+𝑏𝑏 = 4 △𝐴𝐴𝐵𝐵𝐴𝐴 𝑆𝑆
16.(17分)
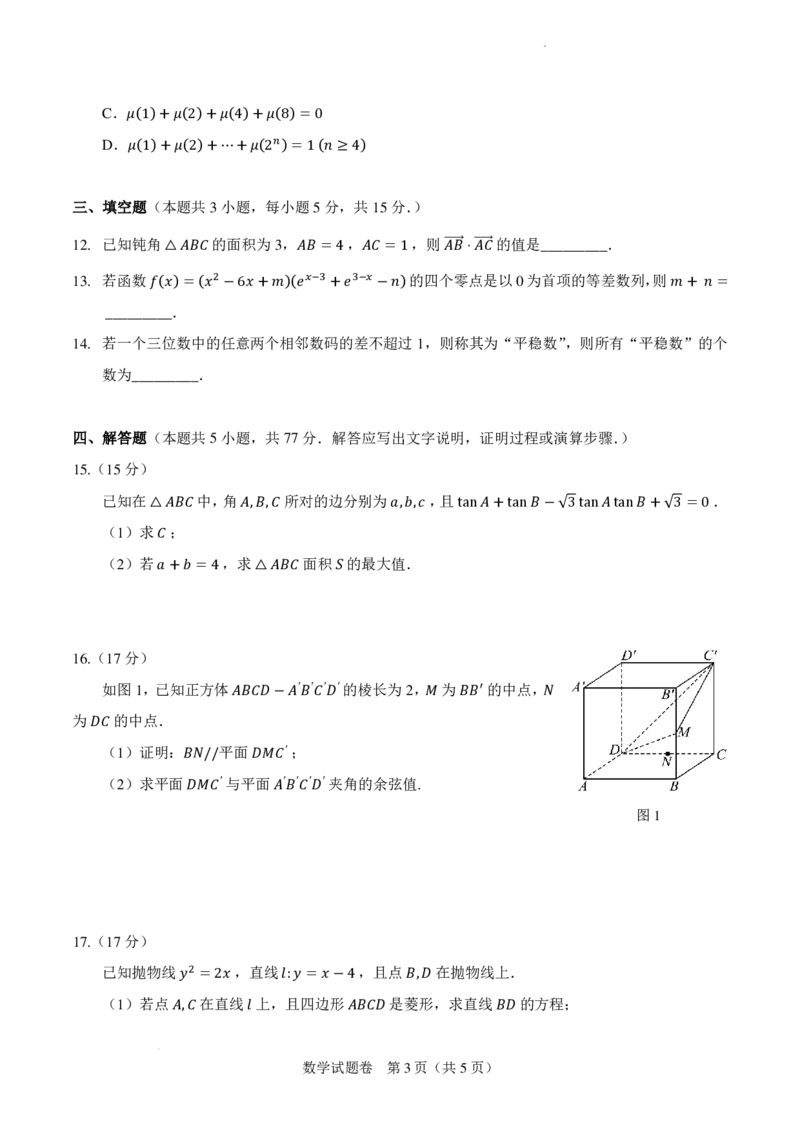
如图1,已知正方体 ′ ′ ′ ′的棱长为2, 为 的中点,
′
为 的中点. 𝐴𝐴𝐵𝐵𝐴𝐴𝐴𝐴−𝐴𝐴𝐵𝐵𝐴𝐴𝐴𝐴 𝑀𝑀 𝐵𝐵𝐵𝐵 𝑁𝑁
𝐴𝐴𝐴𝐴( 1)证明: 平面 ′;
(2)求平面𝐵𝐵𝑁𝑁//′ 与平 𝐴𝐴面𝑀𝑀𝐴𝐴′ ′ ′ ′夹角的余弦值.
𝐴𝐴𝑀𝑀𝐴𝐴 𝐴𝐴𝐵𝐵𝐴𝐴𝐴𝐴 图1
17.(17分)
已知抛物线 ,直线 ,且点 在抛物线上.
2
(1)若点 𝑦𝑦 =在2直𝑥𝑥线 上, 𝑙𝑙且:𝑦𝑦四=边𝑥𝑥形−4 是 菱𝐵𝐵,形𝐴𝐴 ,求直线 的方程;
𝐴𝐴,𝐴𝐴 𝑙𝑙 𝐴𝐴𝐵𝐵𝐴𝐴𝐴𝐴 𝐵𝐵𝐴𝐴
数学试题卷 第3页(共5页)
学科网(北京)股份有限公司(2)若点 为抛物线和直线 的交点(位于 轴下方),点 在直线 上,且四边形 是菱形,
求直线 的斜 𝐴𝐴率 . 𝑙𝑙 𝑥𝑥 𝐴𝐴 𝑙𝑙 𝐴𝐴𝐵𝐵𝐴𝐴𝐴𝐴
𝐵𝐵𝐴𝐴
18.(17分)
已知函数 .
𝑥𝑥
(1)若 𝑓𝑓(𝑥𝑥),=求𝑎𝑎 −log𝑎𝑎𝑥𝑥 过,𝑎𝑎点∈(0,1)的∪(切1,线+方∞)程 ;
(2)若 𝑎𝑎 = 𝑒𝑒在 其定 𝑦𝑦义=域𝑓𝑓上(𝑥𝑥没) 有零 (点0,,1)求 的取值范围.
𝑓𝑓(𝑥𝑥) 𝑎𝑎
19.(17分)
概率论中有很多经典的不等式,其中最著名的两个当属由两位俄国数学家马尔科夫和切比雪夫分
别提出的马尔科夫(Markov)不等式和切比雪夫(Chebyshev)不等式.马尔科夫不等式的形式如下:
设 为一个非负随机变量,其数学期望为 ,则对任意 ,均有
𝑋𝑋 𝐴𝐴(𝑋𝑋) 𝜀𝜀 > 0
𝐴𝐴(𝑋𝑋)
马尔科夫不等式给出了随机变量取值不𝑃𝑃(小𝑋𝑋于≥某𝜀𝜀)正≤数的概率上界,阐释了随机变量尾部取值概率与
𝜀𝜀
其数学期望间的关系.当 为非负离散型随机变量时,马尔科夫不等式的证明如下:
设 的分布列为 𝑋𝑋 其中 , ,
𝑋𝑋, 则对任意 𝑃𝑃(𝑋𝑋,= 𝑥𝑥𝑖𝑖)= 𝑝𝑝𝑖𝑖 (𝑖𝑖 = 1,2,…,𝑛𝑛) 𝑝𝑝𝑖𝑖 ∈ (0,+∞) 𝑝𝑝1+𝑝𝑝2+⋯+𝑝𝑝𝑛𝑛 = 1 𝑥𝑥𝑖𝑖 ∈
[0,+∞) 𝜀𝜀 > 0
𝑛𝑛
𝑥𝑥𝑖𝑖 1 1 𝐴𝐴(𝑋𝑋)
𝑃𝑃(𝑋𝑋 ≥ 𝜀𝜀)= �𝑝𝑝𝑖𝑖 ≤ � 𝑝𝑝𝑖𝑖 = � 𝑥𝑥𝑖𝑖𝑝𝑝𝑖𝑖 ≤ �𝑥𝑥𝑖𝑖𝑝𝑝𝑖𝑖 =
其中符号 𝑥𝑥𝑖𝑖≥𝜀𝜀 𝑥𝑥𝑖𝑖≥𝜀𝜀 𝜀𝜀 𝜀𝜀𝑥𝑥𝑖𝑖≥𝜀𝜀 𝜀𝜀 𝑖𝑖=1 𝜀𝜀
�𝐴𝐴𝑖𝑖
表示对所有满足 的指标 所对应的
𝑥𝑥
求
𝑖𝑖≥𝜀𝜀
和.
切比雪夫不等式的 𝑥𝑥𝑖𝑖形≥式𝜀𝜀 如下: 𝑖𝑖 𝐴𝐴𝑖𝑖
设随机变量的 数学期望为 ,方差为 ,则对任意 ,均有
𝑋𝑋 𝐴𝐴(𝑋𝑋) 𝐴𝐴(𝑋𝑋) 𝜀𝜀 > 0
𝐴𝐴(𝑋𝑋)
【类比探究】 𝑃𝑃(|𝑋𝑋−𝐴𝐴(𝑋𝑋)|≥ 𝜀𝜀)≤ 2
𝜀𝜀
(1)根据以上参考资料,证明切比雪夫不等式对离散型随机变量 成立;
𝑋𝑋
数学试题卷 第4页(共5页)
学科网(北京)股份有限公司【实际应用】
(2)已知正整数 .在一次抽奖游戏中,有 个不透明的箱子依次编号为 ,编号为
的箱子中 𝑛𝑛装≥有5编 号为 的 个大 𝑛𝑛 小、质地均相同的小球.主持人 1,邀2,…请,𝑛𝑛 位嘉宾从
每 𝑖𝑖 (个1箱≤子𝑖𝑖 ≤中𝑛𝑛随) 机抽取一个球,记从 编0,1号,…为,𝑖𝑖 的 箱𝑖𝑖+子1中 抽取的小球号码为 ,并记 𝑛𝑛
𝑖𝑖 𝑋𝑋𝑖𝑖
𝑛𝑛
𝑋𝑋𝑖𝑖
𝑋𝑋 = �
对任意的 ,是否总能保证 (假𝑖𝑖=设1 𝑖𝑖嘉宾和箱子数能任意多)?并证明你的结论.
【理论 𝑛𝑛 拓展】 𝑃𝑃(𝑋𝑋 ≤ 0.1𝑛𝑛)≥ 0.01
(3)已知 重伯努利试验中每次试验中事件 出现的概率 ,请用切比雪夫不等式估计
,使得事件 𝑛𝑛出 现的频率在0.74和0.76之间的概 𝐴𝐴率 不低于0.9 0𝑃𝑃.= 0.75
𝑛𝑛 𝐴𝐴
数学试题卷 第5页(共5页)
学科网(北京)股份有限公司