文档内容
2024年新高考新结构题型数学选填压轴好题汇编 02
一、单选题
1 (2024·广东·一模)已知函数hx
1
的定义域为R,且满足hx+1 +hx-1 =2,h2-x 是偶函数,
h2
103
=0,若n∈Z,则 h(n)= ( )
n=-103
A.202 B.204 C.206 D.208
2 (2024·高三·湖南·阶段练习)设方程2x⋅log 2 x =1的两根为x 1 ,x 2x 1 2 B.x> C.03
1 2 1 x 1 2 1 2
2
x2 y2 x2 y2
3 (2024·福建·二模)已知椭圆 + =1(a>b>0)与双曲线 - =1(m>0,n>0)有共同的
a2 b2 m2 n2
π
焦点F,F,且在第一象限内相交于点P,椭圆与双曲线的离心率分别为e ,e .若∠FPF= ,则e⋅e 的
1 2 1 2 1 2 3 1 2
最小值是
1 2 3 3
A. B. C. D.
2 2 2 2
2cos40°+cos80°
4 (2024·高三·湖南长沙·阶段练习)求值: = ( )
sin80°
3 3
A. 3 B. C.- 3 D.-
3 3
5 (2024·陕西安康·二模)宋代理学家周敦颐的《太极图》和《太极图说》是象数和义理结合的表达.《朱
子语类》卷七五:“太极只是一个混沦底道理,里面包含阴阳、刚柔、奇偶,无所不有”.太极图(如下图)将平
衡美、对称美体现的淋漓尽致.定义:对于函数fx ,若存在圆C,使得fx 的图象能将圆C的周长和面积
同时平分,则称fx 是圆C的太极函数.下列说法正确的是 ( )
①对于任意一个圆,其太极函数有无数个
②fx =log 2x+1
1
2
1
+ x是x2+y+1
2
2=1的太极函数
③太极函数的图象必是中心对称图形
④存在一个圆C,fx =sinx+cosx是它的太极函数
A.①④ B.③④ C.①③ D.②③
6 已知定义在[0,1]上的函数f(x)满足:
①f(0)=f(1)=0;
②对所有x,y∈[0,1],且x≠y,有f(x)-f(y)
1
< x-y
2
.
若对所有x,y∈[0,1],f(x)-f(y)
a2 b2
b>0)于P,M两点,Q为OP中点,过Q作x轴垂线,垂足为B,直线MB交椭圆于另一点N,直线PM,PN
1
的斜率分别为k,k ,若kk =- ,则椭圆离心率为 ( )
1 2 1 2 2
1 3 3 6
A. B. C. D.
2 3 2 3
1 x2 y2
11 (2024·高三·江苏南京·开学考试)斜率为 的直线l经过双曲线 - =1(a>0,b>0)的左焦
2 a2 b2
点F,与双曲线左,右两支分别交于A,B两点,以双曲线右焦点F 为圆心的圆经过A,B,则该双曲线的离
1 2
心率为 ( )
15
A. 2 B. 3 C. 5 D.
3
x2 y2
12 (2024·高三·湖南长沙·阶段练习)双曲线C: - =1的右支上一点P在第一象限,F,F 分别为
9 16 1 2
双曲线C的左、右焦点,I为△PFF 的内心,若内切圆I的半径为1,则△PFF 的面积等于 ( )
1 2 1 2
32 16
A.24 B.12 C. D.
3 3
13 (2024·高三·江苏无锡·开学考试)已知函数fx
x-1
=
, x<2
2x-3
,若方程f fx
2-1, x≥2
1
= 的实
2
根个数为 ( )
A.4 B.8 C.10 D.12
14 (2024·陕西咸阳·模拟预测)已知圆C 1 :x- 3 2+y2=r2(0b>c B.c>a>b C.a>c>b D.b>c>a
20 (2024·高三·重庆·阶段练习)将分别标有数字1,2,3,4,5的五个小球放入A,B,C三个盒子,每个
小球只能放入一个盒子,每个盒子至少放一个小球.若标有数字1和2的小球放入同一个盒子,且A盒子中
只放一个小球,则不同的放法数为 ( )
A.28 B.24 C.18 D.12
二、多选题
21 (2024·高三·广东·阶段练习)已知O为坐标原点,点F为抛物线C:y2=4x的焦点,点P4,4 ,直线l:
x=my+1交抛物线C于A,B两点(不与P点重合),则以下说法正确的是 ( )
A. FA
π
≥1 B.存在实数m,使得∠AOB<
2
2
C.若AF=2BF,则m=± D.若直线PA与PB的倾斜角互补,则m=-2
4
22 (2024·广东·一模)将圆柱OO 的下底面圆O 置于球O的一个水平截面内,恰好使得O 与水平截
1 2 1 1
面圆的圆心重合,圆柱OO 的上底面圆O 的圆周始终与球O的内壁相接(球心O在圆柱OO 内部).已
1 2 2 1 2
3
知球O的半径为3,OO= .若R为上底面圆O 的圆周上任意一点,设RO与圆柱OO 的下底面所成
1 2 2 1 2
的角为α,圆柱OO 的体积为V,则 ( )
1 2
π
A.α可以取到0,
2
27π
中的任意一个值 B.V= cos2α1+2sinα
2
81π
C.V的值可以是任意小的正数 D.V =
max 4
23 (2024·高三·湖南·阶段练习)已知体积为2的四棱锥P-ABCD,底面ABCD是菱形,AB=2,PA
=3,则下列说法正确的是 ( )π
A.若PA⊥平面ABCD,则∠BAD为
6
B.过点P作PO⊥平面ABCD,若AO⊥BD,则BD⊥PC
π
C.PA与底面ABCD所成角的最小值为
6
D.若点P仅在平面ABCD的一侧,且AB⊥AD,则P点轨迹长度为3 3π
24 (2024·高三·湖南长沙·阶段练习)已知函数fx
4
=x+1 ex-x-1 ,则下列说法正确的有
A. fx 有唯一零点 B. fx 无最大值
C. fx 在区间1,+∞ 上单调递增 D.x=0为fx 的一个极小值点
25 (2024·高三·山东济南·期末)已知函数fx 的定义域为R,且fx+y =fx +fy +1,f1 =0,
则 ( )
A. f0 =-1 B. fx 有最小值 C. f2024 =2023 D. fx +1是奇函数
26 (2024·高三·山东德州·期末)双曲线具有以下光学性质:从双曲线的一个焦点发出的光线,经双曲线
反射后,反射光线的反向延长线经过双曲线的另一个焦点.由此可得,过双曲线上任意一点的切线平分该
x2
点与两焦点连线的夹角.已知F,F 分别为双曲线C: -y2=1的左,右焦点,过C右支上一点
1 2 3
Ax 0 ,y 0 x 0 > 3 作双曲线的切线交x轴于点M,交y轴于点N,则 ( )
A.平面上点B4,1 ,AF 2 +AB 的最小值为 37-2 3
B.直线MN的方程为xx -3yy =3
0 0
C.过点F 1 作F 1 H⊥AM,垂足为H,则OH =2(O为坐标原点)
D.四边形AFNF 面积的最小值为4
1 2
27 (2024·高三·浙江杭州·专题练习)数列a n
1
满足a n+1 = 4 a n -6 3+6(n=1,2,3⋯),则 ( )
A.当a=3时,a
1 n
为递减数列,且存在M∈R,使a >M恒成立
n
B.当a=5时,a
1 n
为递增数列,且存在M≤6,使a M恒成立
n
D.当a=9时,a
1 n
递增数列,且存在M∈R,使a 0恒成立
B.函数gx 的极小值为0
C.若函数y=gx -m在其定义域内有两个不同的零点,则实数m的取值范围是0,1
D.对任意的x 1 ,x 2 ∈2,+∞ x+x ,都有f 1 2 2 ≤ fx 1 +fx 2 2
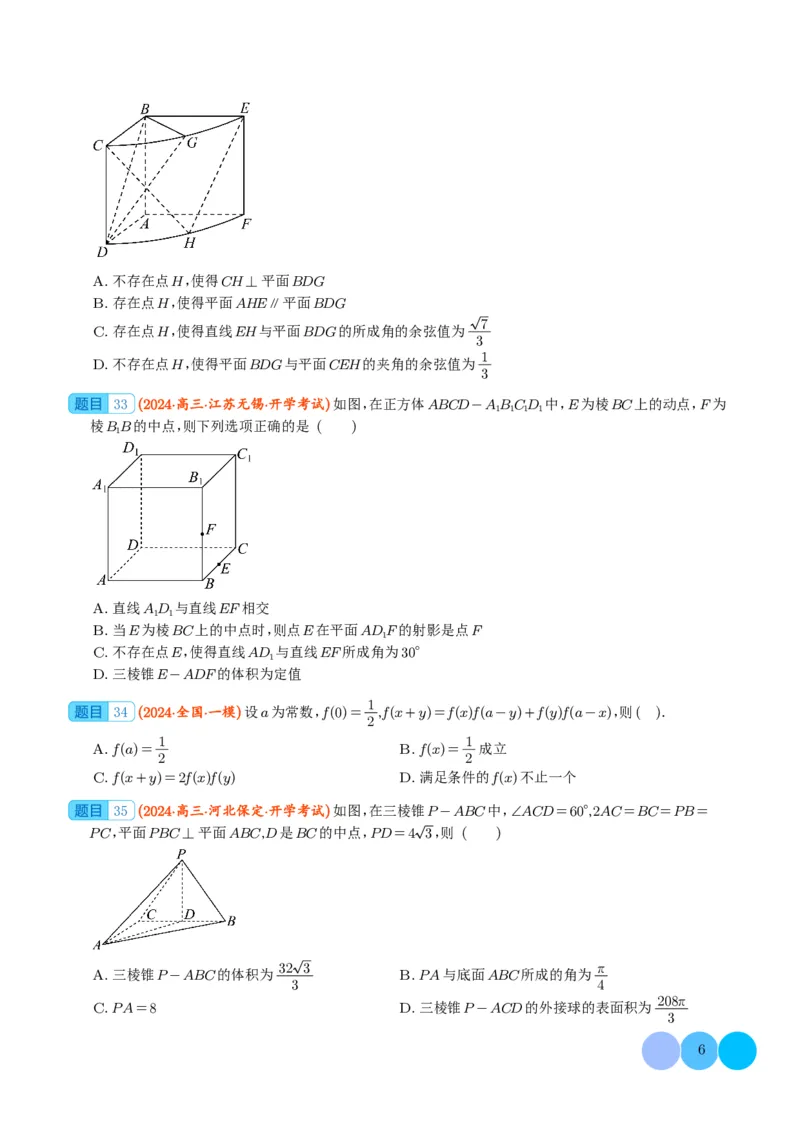
39 (2024·高三·山西·阶段练习)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠DAB
=60°,侧面PAD为正三角形,且平面PAD⊥平面ABCD,则 ( )
A.AD⊥PB
B.在棱PB上存在点M,使得AM⊥平面PBC
C.平面PAD与平面PBC的交线平行于平面ABCD
15
D.C到平面PBD的距离为
5
40 (2024·高三·山西·阶段练习)已知定义域为R的函数fx 的导函数为f x ,若函数f4x+1 和f
x+2 均为偶函数,且f 2 =-1,f1 =1,则 ( )
2023
A. f i
i=1
2024
=-1 B. f i
i=1
2023
=0 C. fi
i=1
2024
=2023 D. fi
i=1
=0
x2 y2
41 (2024·高三·重庆·阶段练习)如图,已知双曲线C: - =1(a>0,b>0)的左、右焦点分别为F
a2 b2 1
-3,0 ,F 23,0 ,点A在C上,点B在y轴上,A,F,B三点共线,若直线BF的斜率为 3,直线AF的斜率 2 1 15 3
为- ,则 ( )
11
3
A.C的渐近线方程为y=±2x B.C的离心率为
2
C. AB
8
=16 D.△ABF的面积为16 3 1
三、填空题
42 (2024·浙江·模拟预测)已知平面向量a、b、c、e,满足a⊥b,a
=2b
,c=a+b,e =1,若a
2
-6a
⋅
e
+8=0,则c
⋅e
-
1
c
2的最大值是
.
3
43 (2024·高三·山东菏泽·开学考试)已知cosα+β
1 α-β α+β
=- ,cosα+cosβ=1,则cos cos =
3 2 2
sinα+β
,
= .
sinα+sinβ
44 某同学在学习和探索三角形相关知识时,发现了一个有趣的性质:将锐角三角形三条边所对的外接
圆的三条圆弧(劣弧)沿着三角形的边进行翻折,则三条圆弧交于该三角形内部一点,且此交点为该三角形
的垂心(即三角形三条高线的交点).如图,已知锐角△ABC外接圆的半径为2,且三条圆弧沿△ABC三边
翻折后交于点P.若AB=3,则sin∠PAC= ;若AC:AB:BC=6:5:4,则PA+PB+PC的值为
.
45 (2024·高三·上海宝山·期中)如图,画一个正三角形,不画第三边;接着画正方形,对这个正方形,不
画第四边,接着画正五边形;对这个正五边形不画第五边,接着画正六边形;⋯⋯,这样无限画下去,形成一
条无穷伸展的等边折线.设第n条线段与第n+1条线段所夹的角为θ n n∈N*,θ n ∈0,π ,则θ = 2022
.46 (2024·全国·模拟预测)已知圆锥SO的母线SA=5,侧面积为15π,则圆锥SO的内切球半径为
;若正四面体A-BCD 能在圆锥SO内任意转动,则正四面体A-BCD 的最大棱长为 .
1 1 1 1 1 1 1 1
47 (2024·四川资阳·模拟预测)若函数fx
9
=ex+cosx+a-1 x存在最小值,则a的取值范围是
.
48 (2024·高三·山东青岛·期中)已知四边形ABCD,Fn∈N*
n
为边BC边上一点,连接AF 交BD于
n
E n∈N* n ,点E n 满足21+a n
E n F n -E n C=a n+1 -2
E B,其中a n n
是首项为1的正项数列,BC=λ ⋅ n
BF,则λ
n n
的前n项T= .
n
49 (2024·高三·江苏苏州·阶段练习)过抛物线y2=6x的焦点F的直线交抛物线于A,B两点,C在抛物
线的准线上,则∠ACB的最大值为 ;若△ACB为等边三角形,则其边长为 .
50 (2024·高三·江苏镇江·开学考试)如果函数fx 在区间a,b 上为增函数,则记为f(x)a,b ,函数
fx 在区间a,b 上为减函数,则记为f(x)
a,b
4 .已知x+
x
m,3 ,则实数m的最小值为 ;函数
fx =2x3-3ax2+12x+1,且f(x)
1,2
,f(x)2,3 ,则实数a= .
51 (2024·高三·江苏镇江·开学考试)已知AB是圆锥PO的底面直径,C是底面圆周上的一点,PC=
AB=2,AC= 3,则二面角A-PB-C的余弦值为 .
n+lnn=3
52 (2024·高三·江苏南京·开学考试)已知实数m,n满足
1+lnm=e2-lnm
,则mn= .
53 (2024·高三·江苏无锡·开学考试)“曼哈顿距离”是人脸识别中的一种重要测距方式,其定义如下:设
Ax 1 ,y 1 ,Bx 2 ,y 2 ,则A,B两点间的曼哈顿距离dA,B = x 1 -x 2+ y 1 -y 2 .已知M4,6 ,点N在圆C:x2
+y2+6x+4y=0上运动,若点P满足dM,P =2,则PN 的最大值为 .
54 (2024·高三·河北保定·开学考试)对于函数fx
1
,若在定义域内存在实数x,满足f
x
=-fx ,则
称fx 为“局部反比例对称函数”.若fx
1 1
= x3- mx2+m2-3
3 2
x+5的导函数f x 是定义在区间
2,+∞ 上的“局部反比例对称函数”,则实数m的最大值与最小值之差为 .
55 (2024·高三·河北保定·开学考试)已知平面向量a,b是非零向量,2a-b
⊥2a+b
,向量b在向
a⋅b
量a方向上的投影向量为-a,则 = ;向量a,b的夹角为 .
|a|2
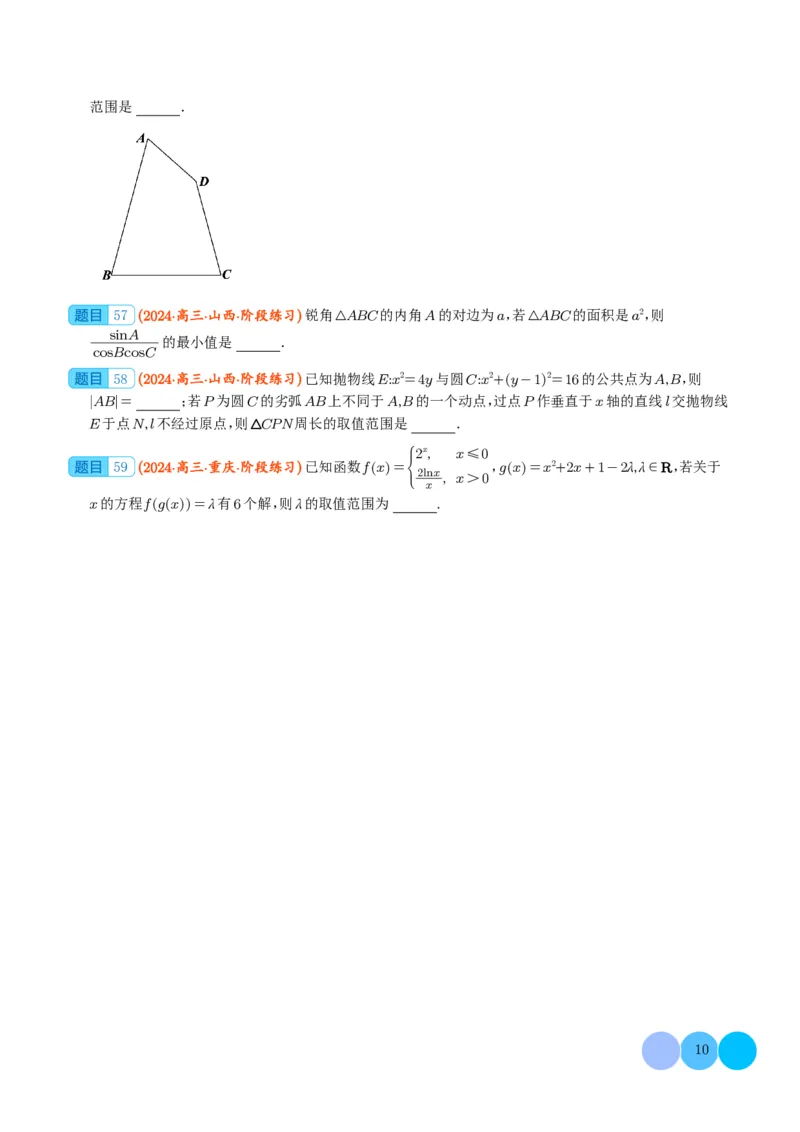
56 (2024·全国·高考真题)如图在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是 .
57 (2024·高三·山西·阶段练习)锐角△ABC的内角A的对边为a,若△ABC的面积是a2,则
sinA
的最小值是 .
cosBcosC
58 (2024·高三·山西·阶段练习)已知抛物线E:x2=4y与圆C:x2+y-1
10
2=16的公共点为A,B,则
AB = ;若P为圆C的劣弧AB上不同于A,B的一个动点,过点P作垂直于x轴的直线l交抛物线
E于点N,l不经过原点,则△CPN周长的取值范围是 .
59 (2024·高三·重庆·阶段练习)已知函数fx
2x, x≤0
=2lnx,
x>0
,gx
x
=x2+2x+1-2λ,λ∈R,若关于
x的方程f gx =λ有6个解,则λ的取值范围为 .