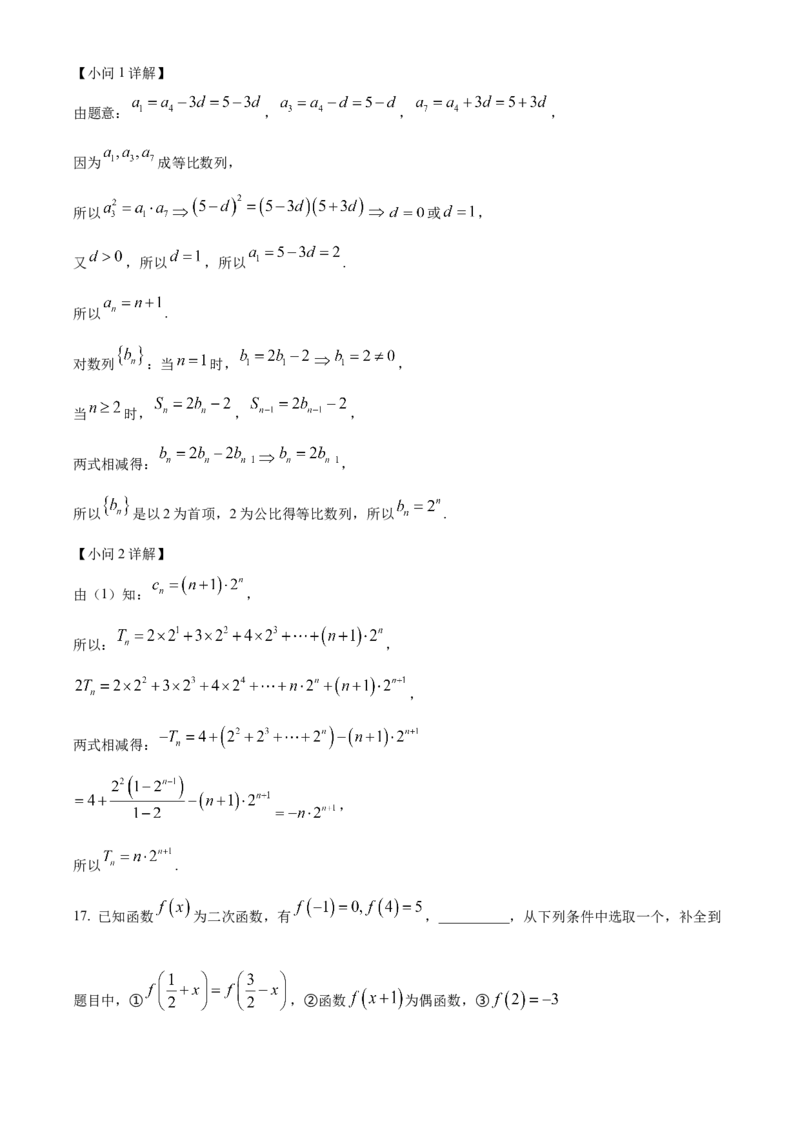江西省赣州市2023-2024学年高二下学期7月期末考试数学Word版含解析(1)_8月_240807江西省赣州市2023-2024学年高二下学期7月期末考试

赣州市 2023~2024 学年度第二学期期末考试 高二数学试卷 一､单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1. 已知集合 ，则 （ ） A. B. C. 或 D. 2. 已知命题 ，则 为（ ） A. B. C. D. 3. 正项等比数列 中， ，则 （ ） A. 1 B. 2 C. 3 D. 4 4. 已知函数 的定义域为 且导函数为 ，函数 的图象如图，则下列说法正确的是 （ ） A. 函数 的增区间是 B. 函数 的减区间是 C. 是函数的极大值点 D. 是函数的极大值点 5. “ ”是“函数 在 单调递增”的（ ） A. 充分不必要条件 B. 必要不充分条件C. 充要条件 D. 既不充分也不必要条件 6. 在人工智能神经网络理论中，根据不同的需要，设置不同激活神经单元的函数，其中函数 是比较 常用的一种，其解析式为 .关于函数 ，下列结论错误的是（ ） A. 有解 B. 是奇函数 C. 不是周期函数 D. 是单调递增函数 7. 已如 是函数 图像上的动点， 是直线 上的动点，则 两点间距离 的最小值为（ ） . A B. 4 C. D. 8. 设等差数列 的前 项和为 ，公差为 ，则下列结论正确的是（ ） A. B. 使得 成立的最小自然数 是20 C. D. 二､多选题：本题共3小题，每小题6分，共18分.在每小题给出选项中，有多项符合题目要 求.全部选对的得6分，部分选对的得部分分，有选错项得0分. 9. 已知 ，且 ， 都不为0，则下列不等式一定成立的是（ ） A. B. C. D. 10. 已知正数 满足 ，则下列结论正确的是（ ） A. 的最大值为1 B. 的最小值为4C. 的最小值为9 D. 的最小值为 11. 记方程 的实数解为 （ 是无理数）， 被称为在指数函数中的“黄金比例”.下列有关 的结 论正确的是（ ） A. B. C. D. 函数 的最小值为 三､填空题：本题共3小题，每小题5分，共15分. 12. 已知函数 是 上的奇函数， ，则 __________. 13. 数列 的前 项和为 ，若 ，则 __________. 14. 已知定义在 上的函数 满足 ，当 时， ，则 在 上的零点个数为__________个. 四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤. 15. 已知函数 的图象过点 ，且在点 处的切线恰好与直线 平行. （1）求函数 的解析式； （2）求 在 上的最大值和最小值.16. 已知等差数列 的公差 成等比数列，数列 的前 项和公式为 . （1）求数列 和 的通项公式： （2）设 ，求数列 的前 项和 . 17. 已知函数 为二次函数，有 ，__________，从下列条件中选取一个，补全到 题目中，① ，②函数 为偶函数，③ （1）求函数 的解析式； （2）若 ，若对任意的 ，总存在 ，使得 成立，求实数 的取值范围. 18. 已知函数 为 的导函数，记 ，其中 为常数. （1）讨论 的单调性； （2）若函数 有两个极值点 ， ①求 的取值范围； ②求证： . 19. 若在数列的每相邻两项之间插入此两项的和，形成新的数列，再把所得数列按照同样的方法不断构造 出新的数列.现对数列1，3进行构造，第一次得到数列1，4，3：第二次得到数列 ：依次构造， 第 次得到的数列的所有项之和记为 ，如 . （1）求 ；（2）求 的通项公式； （3）证明： .赣州市 2023~2024 学年度第二学期期末考试 高二数学试卷 一､单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1. 已知集合 ，则 （ ） A. B. C. 或 D. 【答案】A 【解析】 【分析】先解一元二次不等式，求解集合 ，再求交集即可. 【详解】因为 ，又 所以 . 故选：A. 2. 已知命题 ，则 为（ ） A. B. C. D. 【答案】D 【解析】 【分析】全称量词命题的否定，首先把全称量词改成存在量词，然后把后面结论改否定即可. 【详解】因为命题 是全称量词命题，则命题 为存在量词命题， 由全称量词命题的否定得，命题 ： . 故选：D. 3. 正项等比数列 中， ，则 （ ） A. 1 B. 2 C. 3 D. 4 【答案】B【解析】 【分析】根据等比数列的性质求出 即可得解. 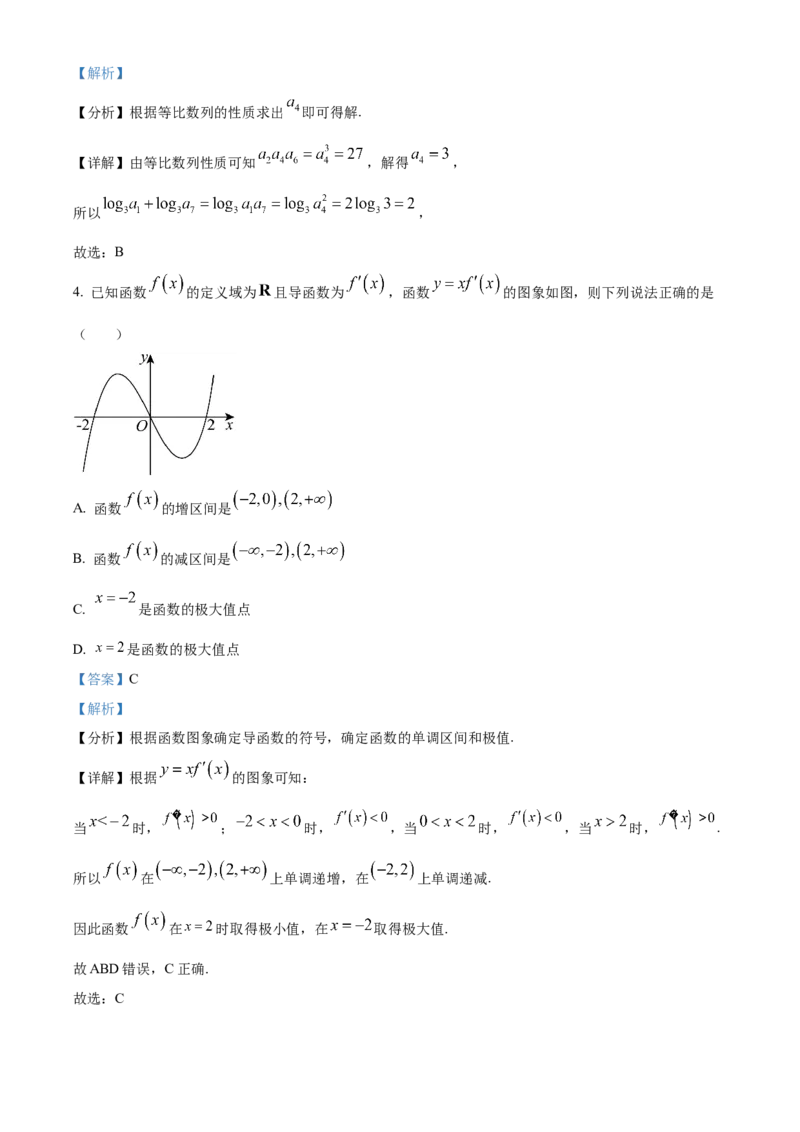【详解】由等比数列性质可知 ，解得 ， 所以 ， 故选：B 4. 已知函数 的定义域为 且导函数为 ，函数 的图象如图，则下列说法正确的是 （ ） A. 函数 的增区间是 B. 函数 的减区间是 C. 是函数的极大值点 D. 是函数的极大值点 【答案】C 【解析】 【分析】根据函数图象确定导函数的符号，确定函数的单调区间和极值. 【详解】根据 的图象可知： 当 时， ； 时， ，当 时， ，当 时， . 所以 在 上单调递增，在 上单调递减. 因此函数 在 时取得极小值，在 取得极大值. 故ABD错误，C正确. 故选：C5. “ ”是“函数 在 单调递增”的（ ） . A 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 【答案】B 【解析】 【分析】利用对数函数与复合函数的单调性计算即可. 【详解】由二次函数、对数函数的单调性及复合函数的单调性可知： 要满足函数 在 单调递增， 需要 ， 因为 ，所以“ ”是“函数 在 单调递增”的必要不充分条件． 故选：B． 6. 在人工智能神经网络理论中，根据不同的需要，设置不同激活神经单元的函数，其中函数 是比较 常用的一种，其解析式为 .关于函数 ，下列结论错误的是（ ） A. 有解 B. 是奇函数 C. 不是周期函数 D. 是单调递增函数 【答案】A 【解析】 【分析】考虑函数的值域可判断A，根据函数的奇偶性定义判断B，由复合函数的单调性分析可判断D， 由D结合周期定义判断C. 【详解】由 ， 因 ，则 ，可得 ，即 ，故A错误；因为 的定义域为 ，且 ，所以 是奇函数， 故B正确； ，因 是增函数， 是增函数且恒为正数，则 是减函数，故 是增函数，故D正确； 由D可知函数在 上单调递增，所以当 时， ，所以函数不是周期函数，故C 正确. 故选：A 7. 已如 是函数 图像上的动点， 是直线 上的动点，则 两点间距离 的最小值为（ ） A. B. 4 C. D. 【答案】C 【解析】 【分析】先求函数 斜率为 的切线，然后切线与直线 的距离即为所求. 【详解】因为 ，（ ），所以 ， 由 ，得 ，又 ， 所以 过 点的切线为： 即 . 直线 与 的距离为： 即为所求. 故选：C 8. 设等差数列 的前 项和为 ，公差为 ，则下列结论正确的是（ ）A. B. 使得 成立的最小自然数 是20 C. D. 【答案】C 【解析】 【分析】根据题意可知数列单调递减且 ，由通项公式化简可判断A，由等差数 列的性质及求和公式结合条件可判断B，根据 为递减数列即可判断C，由 的关系及 的 符号可判断D. 【详解】由公差为 可知，等差数列 为递减数列且 ， 对A， ，故A错误； 对B，因为 ，所以 ，所以 ，故B错误； 对C，因为 ，且 ，所以由一次函数单调性知 为单调递减数列， 所以 ，故C正确； 对D，由B知 ，且 ，所以 ， 因为 ， ，若 ，则 ，且 ， 即 ，即 ，而 ， ，显然矛盾，故 不成立，故D错误. 故选：C 二､多选题：本题共3小题，每小题6分，共18分.在每小题给出选项中，有多项符合题目要 求.全部选对的得6分，部分选对的得部分分，有选错项得0分. 9. 已知 ，且 ， 都不为0，则下列不等式一定成立的是（ ） A. B. C. D. 【答案】BC 【解析】 【分析】由不等式的性质和函数单调性，判断选项中的不等式是否成立. 【详解】当 时，有 ，A选项错误； ，则 ，得 ，B选项正确； ， ，得 ，C选项正确； 函数 在R上单调递减， ，则 ，D选项错误. 故选：BC 10. 已知正数 满足 ，则下列结论正确的是（ ） A. 的最大值为1 B. 的最小值为4 C. 的最小值为9 D. 的最小值为 【答案】ABD 【解析】【分析】根据均值不等式分别建立不等式解不等式可判断AB，先变形 为关于 的二次函数求最 值判断C，利用条件变形可得 ，转化 为关于 的式子由均值不等式判断D. 【详解】由正数 满足 ，可得 ，解得 ，即 ， 当且仅当 ，即 时等号成立，故A正确； 由正数 满足 ，可得 ， 解得 或 （舍去），当且仅当 ，即 时等号成立，故B正确； ，由A知 ， 由二次函数的单调性知 ，即 时， 的最小值为8，故C错误； 由 可得 ，即 ，所以 ， 所以 ，当且仅当 ，即 ， 时等号成立，故D正 确. 故选：ABD 11. 记方程 的实数解为 （ 是无理数）， 被称为在指数函数中的“黄金比例”.下列有关 的结 论正确的是（ ） A. B. C.D. 函数 的最小值为 【答案】ACD 【解析】 【分析】构建 ，利用导数判断其单调性，结合零点存在性定理分析判断 B选项，对于A： 对 ， ，取对数整理即可；对于C：根据二次函数单调性判断；对于D：结合不等式 分析可知 ，当且仅当 时，等号成立. 【详解】构建 ，则 为 的零点， 因为 ， 若 ，则 ，可知 在 内单调递减，且 ， 所以 在 内无零点； 若 ，则 ，可知 在内单调递增， 且 ，所以 在 内存在唯一零点 ； 对于选项A：因为 ， ，即 ， 两边取对数可得： ， ，故A正确； 对于选项B：由上可知 ，故B不正确； 对于选项C： 对称轴为 ，而 ，故 单调递增， 当 ， 最小值为 ，所以 ，故C正确；对于选项D：构建 ，则 ， 令 ，解得 ；令 ，解得 ； 可知 在 内单调递减，在 内单调递增， 则 ，可得 ，当且仅当 时，等号成立， 可得 ，令 ， 则 ， 当且仅当 ，即 时，等号成立， 所以 的最小值为 ，故D正确； 故选：ACD. 【点睛】方法点睛：对于函数零点的个数的相关问题，利用导数和数形结合的数学思想来求解．这类问题 求解的通法是： （1）构造函数，这是解决此类题的关键点和难点，并求其定义域； （2）求导数，得单调区间和极值点； （3）数形结合，挖掘隐含条件，确定函数图象与x轴的交点情况进而求解． 三､填空题：本题共3小题，每小题5分，共15分. 12. 已知函数 是 上的奇函数， ，则 __________. 【答案】2 【解析】 【分析】根据奇函数的定义得出 ，再由 解析式得解. 【详解】因为函数 是 上的奇函数，所以 ，所以 ， 故答案为：2 13. 数列 的前 项和为 ，若 ，则 __________. 【答案】 【解析】 【分析】先按通项进行分组求和，再由分式数列用裂项法求和，而数列 是周期为4的数列，所以 按每4个数一组求和即可. 【详解】由 得： ， 故答案为： . 14. 已知定义在 上的函数 满足 ，当 时， ，则 在 上的零点个数为__________个. 【答案】 【解析】 【分析】由题意可得函数为周期函数，再由一个周期内 内有两个零点，且一个零点小于1，一个大于 的 2，即可得出在 上 零点个数.【详解】由 可得 ， 所以周期 ， 当 时， ，令 ， 解得 ，即一个周期内有2个零点， 因为 ， 所以 在 上的零点个数为 . 故答案为： 四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤. 15. 已知函数 的图象过点 ，且在点 处的切线恰好与直线 平行. （1）求函数 的解析式； （2）求 在 上的最大值和最小值. 【答案】（1） （2）最大值为4；最小值为： 【解析】 【分析】（1）根据函数的图象过点 ，得到关于 的一个关系式，再根据函数在 处的导数为 ， 又得到关于 的一个关系式，可求 的值. （2）利用导数分析函数的单调性，可求函数的最大、最小值. 【小问1详解】 因为函数 的图象过点 ，所以 . 又因为 ，且 在点 处的切线恰好与直线 平行， 所以 ， 由 得： ，所以 . 【小问2详解】 由（1）知： ， 由 ，由 或 . 所以 在上单调递增，在 上单调递减，在 上单调递增， 又 ， ， ， ， 所以 在 上的最大值为4，最小值为 . 16. 已知等差数列 的公差 成等比数列，数列 的前 项和公式为 . （1）求数列 和 的通项公式： （2）设 ，求数列 的前 项和 . 【答案】（1） ， （2） 【解析】 【分析】（1）根据等差数列的通项公式求等差数列的通项公式，根据数列的前 项和，求数列 的通 项公式. （2）利用错位相减求和法求数列的前 项和.【小问1详解】 由题意： ， ， ， 因为 成等比数列， 所以 或 ， 又 ，所以 ，所以 . 所以 . 对数列 ：当 时， ， 当 时， ， ， 两式相减得： ， 所以 是以2为首项，2为公比得等比数列，所以 . 【小问2详解】 由（1）知： ， 所以： ， ， 两式相减得： ， 所以 . 17. 已知函数 为二次函数，有 ，__________，从下列条件中选取一个，补全到 题目中，① ，②函数 为偶函数，③（1）求函数 的解析式； （2）若 ，若对任意的 ，总存在 ，使得 成立，求实数 的取值范围. 【答案】（1） （2） 【解析】 【分析】（1）用待定系数法求函数解析式. （2）分别求函数的值域，根据两个函数值域之间的关系求参数. 【小问1详解】 设 ，由题意： ， 两式相减的： 若选①，则：抛物线的对称轴为： ，即 . 所以 ，所以 ； 若选②，则：抛物线的对称轴为： ，同上； 若选③，则： ，由 ，得： ，所以 . 综上： 【小问2详解】 对 ：当 时，由 ；由 ； 所以 在 上单调递减，在 上单调递增， 所以 时， . 当 时， 恒成立， 所以 在 上恒成立. 观察可知，函数 在 上单调递减，所以 ， 由 . 所以实数 的取值范围是： 18. 已知函数 为 的导函数，记 ，其中 为常数. （1）讨论 的单调性； （2）若函数 有两个极值点 ， ①求 的取值范围； ②求证： . 【答案】（1）见解析 （2）① ；②证明见解析 【解析】 【分析】（1）求出 ，分类讨论，利用 ， 解不等式即可得解； （2）①先分析 不合题意，再求出 时函数 在有两个极值点 的必要条件，再此条件下分析即可得解；②对结论进行转化，只需证 ，换元后利用导数确定函数单调性， 得出函数最值，即可得证. 【小问1详解】 定义域为 . ， ， ， 当 时，g′ (x)>0恒成立， 在 上单调递增， 当 时，令 ，则 ，解得 ， 令 ，则 ，解得 ， 在 单调递增，在 单调递减. 综上，当 时， 在 上单调递增； 当 时， 在 单调递增，在 单调递减. 【小问2详解】 由（1）知， 时， 最多一个根，不符合题意，故 ， 函数 有两个极值点 ， ( 1 ) 1 在 有两个不同零点的必要条件是g =ln >0， 2a 2a 解得 ，当 ， 在 单调递增，在 单调递减， ( 1 ) 1 (1) 2a g =ln >0,g =− <0,x→+∞,g(x)→−∞， 2a 2a e e 由零点存在性定理得： 在 ， 各有1个零点， 的取值范围是 . ② 函数 有两个极值点 ， ① ② ① ②得： ， 2(x −x ) 要证 ，即证x +x > 1 2 ，即证 ， 1 2 lnx −lnx 1 2 即证 ， 令 ，则 ， 1 4 (t−1) 2 令 ，则R′(t)= − = >0， t (t+1) 2 t(t+1) 2 在 上单调递增， ， 在 上成立，，得证. 【点睛】关键点点睛：要证明不等式 ，关键点之一在于消去 后对结论进行恰当变形，转化为 证明 成立，其次关键点在于令 换元，转化为证明 成立. 19. 若在数列的每相邻两项之间插入此两项的和，形成新的数列，再把所得数列按照同样的方法不断构造 出新的数列.现对数列1，3进行构造，第一次得到数列1，4，3：第二次得到数列 ：依次构造， 第 次得到的数列的所有项之和记为 ，如 . （1）求 ； （2）求 的通项公式； . （3）证明： 【答案】（1） （2） （3）证明见解析 【解析】 【分析】（1）求出第三次得到数列再求和即可； （2）设出第 次构造后得到的数列求出 ，则得到第 次构造后得到的数列求出 ，可得 与 关系，再利用构造法求通项即可； （3）利用放缩法求等比数列和可得答案. 【小问1详解】 因为第二次得到数列 ，所以第三次得到数列所以 ； 【小问2详解】 设第 次构造后得的数列为 ，则 ， 则第 次构造后得到的数列为 ， 则 ， ，可得 ， ， 所以 是以 为公比， 为首项的等比数列， 所以 ，即 ； 【小问3详解】 由（2）得 ， 所以当 时， ， 当 时，所以 ， 综上所述， . 【点睛】关键点点睛：（2）问中解题关键点是已知相邻两项关系构造等比数列，进而得到数列的通项公 式；（3）问中根据的通项公式，应用放缩变成等比数列的前项和，应用公式计算即可.