文档内容
2024年新高考新结构2月数学选填压轴好题汇编
一、单选题
1 (2024·广东深圳·高三深圳中学开学考试)已知函数fx
1
满足fx+y =fx +fy -2,f1 =4
且当x>0时,fx >2,若存在x∈1,2 ,使得fax2-4x +f2x =1,则a的取值范围是 ( )
1 A. 0,
2
B. 1 , 5
2 8
C. 5 , 2
8 3
D. 1 , 2
2 3
【答案】D
【解析】任取x 1 ,x 2 ,且x 1 0,而当x>0时,fx >2,于是f(x -x)>2, 2 1
又fx+y =fx +fy -2,因此f(x )=f[x+(x -x)]=f(x)+f(x -x)-2>f(x), 2 1 2 1 1 2 1 1
则函数f(x)是增函数,而f(ax2-4x)+f(2x)=f[(ax2-4x)+2x]+2=f(ax2-2x)+2=1,
于是f(ax2-2x)=-1,令x=y=0,得f(0)=2,令x=1,y=-1,得f(-1)=0,
令x=-1,y=-1,得f(-2)=-2,令x=-2,y=-1,得f(-3)=-4,
3 3
令x=y=- ,得f-
2 2
3
=-1,即有f(ax2-2x)=f-
2
3
,因此ax2-2x=- ,
2
4x-3 原问题即2a= 在1,2
x2
有解,令t= 1 ∈ 1 ,1
x 2
,
2 则2a=-3t2+4t=-3t-
3
2 + 4 在t∈ 1 ,1
3 2
时有解,从而2a∈ 1, 4
3
,a∈ 1 , 2
2 3
,
所以a的取值范围是 1 , 2
2 3
.
故选:D
x2 y2
2 (2024·广东深圳·高三深圳中学开学考试)在椭圆 + =1(a>b>0)中,F,F 分别是左,右焦
a2 b2 1 2
点,P为椭圆上一点(非顶点),I为△PFF 内切圆圆心,若 S △IF1F2 = 1 ,则椭圆的离心率e为 ( )
1 2 S 3
△PF1F2
1 1 3 3
A. B. C. D.
3 2 3 2
【答案】B
x2 y2
【解析】椭圆 + =1(a>b>0)中,F,F 分别是左,右焦点,P为椭圆上一点(非顶点),
a2 b2 1 2
I为△PFF 内切圆圆心,设△PFF 的内切圆半径为r,
1 2 1 2
1
则S △PF1F2 = 2 r× PF 1 +PF 2 +F 1 F 2 =a+c
1
r,S △IF1F2 = 2 F 1 F 2 r=cr,
由 S △IF1F2 = c = 1 ,得a+c=3c,即a=2c,
S a+c 3
△PF1F2
c 1
∴椭圆的离心率为e= = .
a 2
故选:B.
3 (2024·广东中山·高三中山纪念中学开学考试)已知fx =lnx-ax3,gx
3
=xex-lnx-x- ,若不
4
fx
等式
gx
>0的解集中只含有两个正整数,则a的取值范围为 ( )
A. ln3 , ln2
27 8
ln3 ln2 B. ,
27 8
C. ln2 , ln3
32 27
ln2 ln3 D. ,
32 27
【答案】C【解析】gx
2
3
=xex-lnx-x- 定义域为0,+∞
4
,
g x
1 x+1
=ex+xex- -1=
x
xex-1
,
x
令hx =xex-1,再x>0上h x =ex x+1 >0,
∴hx 再x>0上单调递增,
x从+∞趋向于0时,xex趋向于0,则hx
=xex-1趋向于-1,
设hx 0 =x ex0-1=0,即x ex0=1,x =-lnx , 0 0 0 0
则在x∈0,x 0 上hx ∈-1,0 ,在x∈x 0 ,+∞ 上hx ∈0,+∞ ,
∴在x∈0,x 0 上g x <0,在x∈x 0 ,+∞ 上g x >0,
∴gx 在0,x 0 上单调递减,在x 0 ,+∞ 上单调递增,
∴gx min =gx 0
3 3 1
=x ex0-lnx -x - =1+x -x - = >0, 0 0 0 4 0 0 4 4
fx
则
gx
>0等价于fx >0,
fx =lnx-ax3,定义域为0,+∞ ,
则fx
lnx
>0,即lnx-ax3>0,等价于a< ,
x3
令jx
lnx
= ,则j x
x3
x2-3x2lnx
=
x3
x2 1-3lnx
=
2
x3
,
2
1 1
1-3lnx<0,解得x>e3,1-3lnx>0,解得00,当x∈e3,+∞ 时,j x <0,
则jx
lnx 1
= 在0,e3
x3
1
上单调递增,在e3,+∞ 上单调递减,
即jx
1
的最大值在x=e3处取得,
令jx
lnx
= =0,解得x=1,即函数与x轴交于点1,0
x3
,
函数jx
lnx
= 当x由+∞→0时,lnx→-∞,x3→0,则jx
x3
lnx
= →-∞,
x3
当x由+∞→0时,lnx→+∞,x3→+∞,但x3的增长要远远大于lnx,则jx
lnx
= →0,
x3
作jx
lnx
= 图象如下:
x3
lnx
∴要使a< 解集中只含有两个正整数,只能是2,3,
x3
∴j4 ≤a0,则△ABC是锐角三角形 B.若λμ>0,则△ABC是钝角三角形
C.若λμ<0,则△ABC是锐角三角形 D.若λμ<0,则△ABC是钝角三角形
【答案】D
【解析】因为AB⋅AC=λBA⋅BC=μCA⋅CB,
即AB
⋅AC
cosA=λBA
⋅BC
cosB=μCA
⋅CB cosC,
又λμ≠0时,三角形一定不是直角三角形,
AC
则有λ=
cosA
BC
AB
,μ=
cosB
cosA
CB
,
cosC
AC
λμ=
4
AB cos2A
BC
,
2cosBcosC
若λμ>0,则cosBcosC>0,B,C为锐角,但是不能判断A的大小,
故A,B错误;
当λμ<0时,则cosBcosC<0,B,C中必有一个钝角,
故此时△ABC是钝角三角形,C错误,D正确,
故选:D.
6 (2024·湖南长沙·高三雅礼中学校考阶段练习)已知对任意实数x都有f(x)=2ex+f(x),f(0)=-1,
若不等式f(x)0⇒x>- ,f(x)<0⇒x<-
2 2
1
∴f(x)在区间-∞,-
2
1
上单调递减,在区间- ,+∞
2
上单调递增
令h(x)=a(x-1),由于h(x)过定点(1,0),则函数f(x)和h(x)图像如下图所示
要使得f(x)0,f
e
1 1 1
=ee+2ln -1=ee-3,
e
1 1 1 1
由于lnee-ln3= -ln3<0,即有ee<3,所以f
e e
1
=ee-3<0.
1
故f
e
f1 <0,即fx
1
的零点所在区间为 ,1
e
.
故选:C.
9 (2024·湖北襄阳·高三襄阳五中校考开学考试)已知在锐角△ABC中,角A,B,C所对的边分别为
π 3
a,b,c,C= ,c2= ,则c的取值范围为 ( )
3 sinAsinB
A. 0,3 B. 2, 6 C. 1,3 D. 3,3 【答案】B
3 3
【解析】因为c2= =
sinAsinB sinB+C
6
3
=
sinB sin π +B
3
3
=
sinB 3cosBsinB+ 1sin2B
2 2
3 3
= =
3sin2B- 1cos2B+ 1 1sin2B- π
4 4 4 2 6
,
+ 1
4
π π 2π π π π
在锐角△ABC中,因为00,
所以c∈2, 6 ,
故选:B.
x2 y2
10 (2024·湖北襄阳·高三襄阳五中校考开学考试)已知双曲线C: - =1a>0,b>0
a2 b2
的左、右顶
点分别为A,A ,F为C的右焦点,C的离心率为2,若P为C右支上一点,PF⊥FA ,记∠APA =
1 2 2 1 2
π
θ0<θ<
2
,则tanθ= ( )
1
A. B.1 C. 3 D.2
2
【答案】A
【解析】设C的焦距为2c,点Px 0 ,y 0 ,由C的离心率为2可知c=2a,b= 3a,
因为PF⊥FA 2 ,所以x 0 =c,将Pc,y 0
c2 y2
代入C的方程得 a2 - b2 0 =1,即y 0 = 3b,
3b 3b
所以tan∠PA F= =3,tan∠PAF=
2 c-a 1 c--a
=1,
故tanθ=tan∠PA 2 F-∠PA 1 F
3-1 1
= = . 1+3×1 2
故选:A.
11 (2024·山东·高三山东省实验中学校联考开学考试)已知函数f(x)=mx2-xlnx存在极小值点x ,
0
且f(x )<-e3,则实数m的取值范围为 ( )
0
1
A. 0,
e2
2
B. 0,
e2
1
C. 0,
e3
2
D. 0,
e3
【答案】D
【解析】函数f(x)=mx2-xlnx的定义域为(0,+∞),求导得f(x)=2mx-1-lnx,
当m≤0时,函数f(x)在(0,+∞)上单调递减,f(1)=2m-1<0,
f(e2m-1)=2me2m-1-1-(2m-1)=2m(e2m-1-1)>0,则存在x∈(0,1),使得f(x)=0,
1 1
当x∈(0,x)时,f(x)>0,f(x)递增,当x∈(x,+∞)时,f(x)<0,f(x)递减,
1 1
函数f(x)在x=x 取得极大值,无极小值,不符合题意;
1
1
当m>0时,令g(x)=f(x)=2mx-1-lnx,求导得g(x)=2m- ,显然g(x)在(0,+∞)上单调递增,
x1
当x∈0,
2m
7
1
时,g(x)<0,函数f(x)递减,当x∈ ,+∞
2m
时,g(x)>0,函数f(x)递增,
1
于是f(x) =f
min 2m
=ln2m,
1
当2m≥1,即m≥ 时,f(x)≥0,函数f(x)在(0,+∞)上单调递增,函数f(x)无极值,
2
1 1
当00,
e e e
1
存在x ∈0,
2 2m
,使得f(x )=0,当x∈(0,x )时,f(x)>0,函数f(x)递增,
2 2
1
当x∈x ,
2 2m
时,f(x)<0,函数f(x)递减,函数f(x)在x=x 取得极大值,
2
1
又f
m2
2 2 1 2 2
= -1+2lnm,令h(x)= -1+2lnx,0h
2
1
=3-2ln2>0,则f
m2
>0,
1
存在x ∈ ,+∞
3 2m
1
,使得f(x )=0,当x∈ ,x
3 2m 3
时,f(x)<0,函数f(x)递减,
当x∈(x ,+∞)时,f(x)>0,函数f(x)递增,函数f(x)在x=x 取得极小值,因此x =x ,
3 3 3 0
1+lnx x -x lnx
由f(x )=0,得mx = 0,f(x )=mx2-x lnx = 0 0 0 <-e3,
0 0 2 0 0 0 0 2
即有x -x lnx +2e-3<0,令φ(x)=x-xlnx+2e3,x>1,求导得φ(x)=-lnx<0,
0 0 0
函数φ(x)在(1,+∞)上单调递减,而φ(e3)=0,即有φ(x )<φ(e3),于是x >e3,
0 0
1+lnx 1+lnx -lnx
显然m= 0,令u(x)= ,x>e3,求导得u(x)= <0,即函数u(x)在(e3,+∞)上单调递
2x 2x 2x2
0
减
2 2 2 1 2
因此u(x)2b C.acb2
【答案】B
【解析】由题设a>0,则b>1,且a=lnb,c=eb,则a+c=lnb+eb,
1
令f(x)=lnx+ex-2x且x>1,故f(x)= +ex-2,
x
1 1
令g(x)= +ex-2,则g(x)=ex- 在(1,+∞)上递增,故g(x)>g(1)=e-1>0,
x x2
所以g(x)=f(x)在(1,+∞)上递增,故f(x)>f(1)=e-1>0,
所以f(x)在(1,+∞)上递增,故f(x)>f(1)=e-2>0,
即lnx+ex>2x在(1,+∞)上恒成立,故a+c>2b,A错,B对;
对于ac,b2的大小关系,令h(x)=exlnx-x2且x>1,而h(1)=-1<0,h(e)=ee-e2>0,
显然h(x)在(1,+∞)上函数符号有正有负,故exlnx,x2的大小在x∈(1,+∞)上不确定,
即ac,b2的大小在b∈(1,+∞)上不确定,所以C、D错.
故选:B
x2 y2
14 (2024·福建·高三校联考开学考试)已知椭圆C: + =1a>b>0 a2 b2 的左、右焦点分别F,F,椭 1 2
圆的长轴长为2 2,短轴长为2,P为直线x=2b上的任意一点,则∠FPF 的最大值为 ( )
1 2
π π π π
A. B. C. D.
2 4 3 6
【答案】D
【解析】由题意有a= 2,b=1,c=1,
设直线x=2与x轴的交点为Q,
设PQ
PQ
=t,有tan∠PFQ= 1
F 1 Q
t PQ
= ,tan∠PFQ= 3 2
F 2 Q =t,
可得tan∠F 1 PF 2 =tan∠PF 2 Q-∠PF 1 Q
t- t
= 3 = 2t = 2 ≤ 2t = 3 , 1+ t2 t2+3 t+ 3 2 3t 3
3 t
π
当且仅当t= 3时取等号,可得∠FPF 的最大值为 .
1 2 6
故选:D.15 (2024·浙江·高三浙江金华第一中学校考开学考试)已知直线BC垂直单位圆O所在的平面,且直
线BC交单位圆于点A,AB=BC=1,P为单位圆上除A外的任意一点,l为过点P的单位圆O的切线,
则 ( )
A.有且仅有一点P使二面角B-l-C取得最小值
B.有且仅有两点P使二面角B-l-C取得最小值
C.有且仅有一点P使二面角B-l-C取得最大值
D.有且仅有两点P使二面角B-l-C取得最大值
【答案】D
【解析】过A作AM⊥l于M,连接MB、MC,如图所示,
因为直线BC垂直单位圆O所在的平面,直线l在平面内,且直线BC交单位圆于点A,
所以AC⊥l,AM,AC⊂平面AMC,AM∩AC=A,所以l⊥平面AMC,
MC,MB⊂平面AMC,所以l⊥MC,l⊥MB,
所以∠BMC是二面角B-l-C的平面角,
设∠BMC=θ,∠AMC=α,∠AMB=β,AM=t,则θ=α-β,
由已知得t∈0,2
9
,AB=BC=1,
2 1 tanα= ,tanβ= ,tanθ=tanα-β
t t
= tanα-tanβ = 2 t - 1 t = t ,
1+tanα⋅tanβ 1+ 2 ⋅ 1 t2+2
t t
令ft
t
= ,则f t
t2+2
1⋅t2+2
=
-t2t
t2+2
2+t
=
2
2-t
t2+2
,
2
当t∈0, 2 时,f t >0,ft 单调递增,当t∈ 2,2 时,f t <0,ft 单调递减,
f2
1
= >f0
3
=0
所以t∈0,2 ,当t= 2时,ft 取最大值,没有最小值,
即当t= 2时tanθ取最大值,从而θ取最大值,
由对称性知当t= 2时,对应P点有且仅有两个点,
所以有且仅有两点P使二面角B-l-C取得最大值.故选:D.
16 (2024·浙江·高三浙江金华第一中学校考开学考试)在平面直角坐标系xOy中,圆C的方程为
x-3
10
2+y2=1,且圆C与x轴交于M,N两点,设直线l的方程为y=kxk>0 ,直线l与圆C相交于A,B
两点,直线AM与直线BN相交于点P,直线AM、直线BN、直线OP的斜率分别为k,k ,k ,则 ( )
1 2 3
A.k+k =2k B.2k+k =k C.k+2k =k D.k+k =k
1 2 3 1 2 3 1 2 3 1 2 3
【答案】A
【解析】如图,由题意得l
AM
:y=k 1x-2 ,与圆C:x-3 2+y2=1联立,
消y整理得x-2 1+k2 1 x-2k2 1 +4 =0,
2k2+4
∴x =2,x = 1 ,
M A 1+k2
1
2k2+4 2k
∴A 1 , 1
1+k2 1+k2
1 1
4k2+2 -2k
,同理可得B 2 , 2
1+k2 1+k2
2 2
.
∵k =k ,
OA OB
2k -2k
1 2
1+k2 1+k2
∴ 2k2+4 1 = 4k2+2 2 ,即1+k 1 k 2
1 2
1+k2 1+k2
1 2
k 1 +2k 2 =0.
1
∵kk ≠-1,∴k =- k ,
1 2 2 2 1
设Px 0 ,y 0 ,∴ y 0 =k 1x 0 -2 , y 0 =k 2x 0 -4 ,
2k-4k
x = 1 2,
∴ 0 k 1 -k 2 ∴P 2k 1 -4k 2, -2k 1 k 2
y 0 = - k 2 - k 1 k k 2, k 1 -k 2 k 1 -k 2
1 2
8 2k ,即P , 1
3 3
,
2k
1
∴k = 3 = 1 k ,
3 8 4 1
3
1
∴k+k = k=2k ,
1 2 2 1 3
故选:A.
17 (2024·江苏镇江·高三扬中市第二高级中学开学考试)已知斜率为kk>0 的直线过抛物线C:y2=
4x的焦点F且与抛物线C相交于A,B两点,过A,B分别作该抛物线准线的垂线,垂足分别为A ,B ,若
1 1
△ABB 与△ABA 的面积之比为2,则k的值为 ( )
1 1
1 2
A. 2 B. C. D.2 2
2 2
【答案】D
【解析】如图所示:
由抛物线C:y2=4x,得F1,0 ,
设直线AB:y=kx-1 ,Ax 1 ,y 1 ,Bx 2 ,y 2 ,
y2=4x,
由
y=kx-1
得k2x2-2k2+4 x+k2=0,
2k2+4
所以xx =1,x+x = ,
1 2 1 2 k2由已知和抛物线定义知: S △ABB1 = 2 1 BB 1
S △ABA1
11
A 1 B 1
2 1 AA 1 A 1 B 1
= BB 1
AA 1
BF =
AF
=2,
则有x 2 +1=2x 1 +1 ,即x =2x+1, 2 1
x 2 =2x 1 +1,
所以 x 1 x 2 =1,
x+x = 2k2+4,
1 2 k2
1
解得x= ,x =2,k=2 2.
1 2 2
故选:D
18 (2024·江苏镇江·高三扬中市第二高级中学开学考试)已知函数fx 的定义域为R,且fx +x2为
奇函数,fx -2x为偶函数.令函数gx fx = ,x≥0, -fx ,x<0. 若存在唯一的整数x 0 ,使得不等式 gx 0 2
+a⋅gx 0 <0成立,则实数a的取值范围为 ( )
A. -8,-3 ∪1,3 B. -3,-1 ∪3,8 C. -3,0 ∪3,8 D. -8,-3 ∪0,3
【答案】B
【解析】∵fx +x2为奇函数,fx -2x为偶函数,
∴f-x +-x 2=-fx -x2,f-x +2x=fx -2x,
两式相减整理得fx =2x-x2,
∴gx
2x-x2,x≥0,
=
x2-2x,x<0.
gx 的图象如图所示:
∵存在唯一的整数x 0 ,使得不等式 gx 0 2+a⋅gx 0 <0成立,
即存在唯一的整数x 0 ,使得不等式gx 0 gx 0 +a <0成立,
当a=0时,gx 0 2<0,显然不成立;
当a<0时,需满足gx 0 ∈0,-a 只有一个整数解,
∵g1 =1,g-1 =3,则1<-a≤3,即-3≤a<-1;
当a>0时,需满足gx 0 ∈-a,0 只有一个整数解,
∵g2 =0,g3 =-3,g4 =-8,则-8≤-a<-3,即3
4 6
0,得00时,φ x >0,
所以φx 在-∞,0 上单调递减,在0,+∞ 上单调递增,φ(x) min =φ0 =0,
∴φx =ex-x-1≥0,即ex≥x+1,当且仅当x=0时,等号成立.
故fx >1,故B正确.
由fa n+1 = fa n -1 a ,得fa n+1
n+1
= ean+1-1 = fa n a
n+1
-1 , a
n+1
即ean+1=fa n ,所以ean+1=
ean-1
, a
n
a n ean+1=ean-1≥a n +1 -1=a n ,即a nean+1-1 ≥0,
因为函数fx 定义域为0,+∞ ,
所以a >0,有ean+1-1≥0,即a ≥0,
n n+1
下证数列a
n
单调递减,即证ean+10时,g x <0,所以gx 在0,+∞ 上单调递减.
因为a n >0,ga n a ,故C错误,D正确.
n 1 2023 2024
故选:ABD.
23 (2024·湖南长沙·高三长郡中学校考阶段练习)若fx 是定义在R上的偶函数,其图象关于直线x
=1对称,且对任意x,x ∈ 0, 1
1 2 2
,都有f(x+x )=f(x)f(x ),则下列说法正确的是 ( )
1 2 1 2
A. f1 一定为正数 B.2是fx 的一个周期
C.若f1 2023 =1,则f
4
=1 D.若fx 在 0, 1
2
1 上单调递增,则f(1)≠
2024
【答案】BCD
【解析】因为fx =0符合条件,故A错误;
因为偶函数fx 的图像关于直线x=1对称,所以fx+2 =f-x =fx ,故B正确;
因为对任意x ,x ∈ 0, 1 1 2 2 ,都有f(x 1 +x 2 )=f(x 1 )f(x 2 ),所以对任意x∈0,1 x ,取x=x = 得f(x)= 1 2 2x f
2
16
2 ≥0;
若f1 1 =1,即f(1)= f
2
2 1 = f
4
4 1 =1,故f
4
=1,
由2是fx
2023
的周期得f
4
1
=f506-
4
1
=f-
4
1
=f
4
=1,故C正确;
1 1 假设f(1)= ,由f(1)= f
2024 2
2 1 = f
4
4 1 = 及fx
2024
≥0,x∈0,1 1 ,得f
2
1 1 = ,f
2024 4
1
= ,
42024
1 故f
4
1 >f
2
,这与fx 在 0, 1
2
上单调递增矛盾,故D正确.
故选:BCD
24 (2024·湖南长沙·高三长郡中学校考阶段练习)已知 A,C 两点位于直线 l 两侧,B,D 是直线 l
1 1
上两点,且 △ABD 的面积是 △CBD 的面积的 2 倍,若 AC= - -sinx
2 x
AB+ 1+fx
AD,
下列说法正确的是 ( )
A. fx 为奇函数 B. fx
π
在 ,π
2
单调递减
C. fx 在 0,2π 有且仅有两个零点 D. fx 是周期函数
【答案】ABC
【解析】设AC与直线l交于E,由题可得AE=2EC,
1 1
又AC= - -sinx
2 x
AB+ 1+fx
AD,
2 2 1 1
∴AE= AC= - -sinx
3 3 2 x
2
AB+ 1+fx
3
AD,
2 1 1
∴ - -sinx
3 2 x
2
+ 1+fx
3
=1,
∴fx
1
= +sinx,函数的定义域为-∞,0
x
∪0,+∞ ,
又f-x
1
=- -sinx=-fx
x
,
∴函数fx 为奇函数,故A正确;
1 π
因为函数y= ,y=sinx在 ,π
x 2
上为减函数,
所以fx
π
在 ,π
2
上单调递减,故B正确;
由fx
1 1
= +sinx=0,可得sinx=- ,
x x
所以函数fx 在 0,2π
1
的零点数即为y=sinx与y=- 的交点数,
x1
结合函数y=sinx,y=- 的图象可得fx
x
17
在 0,2π 有且仅有两个零点,故C正确;
因为fx
1 1
= +sinx,函数sinx为周期函数,而函数 不是周期函数,故fx
x x
不是周期函数,故D错误.
故选:ABC.
25 (2024·湖南邵阳·高三邵阳市第二中学校考开学考试)已知函数fx ,gx 的定义域均为R,它们的
导函数分别为f x ,g x ,且fx +g2-x =5,gx -fx-4 =3,若gx+2 是偶函数,则下列正确
的是( ).
A. g 2 =0 B. fx 的最小正周期为4
C. fx+1 是奇函数 D. g2
2024
=5,则 fk
k=1
=2024
【答案】ABD
【解析】A选项,gx+2 为偶函数,故g-x+2 =gx+2 ,
两边求导得,-g -x+2 =g x+2 ,
令x=0得-g 2 =g 2 ,解得g 2 =0,A正确;
B选项,因为fx +g2-x =5,g-x+2 =gx+2 ,
所以fx +gx+2 =5①,
因为gx -fx-4 =3,所以gx+2 -fx-2 =3②,
则①②相减得,fx +fx-2 =2③,
又fx-2 +fx-4 =2④,
则③④相减得fx -fx-4 =0,即fx =fx-4 ,
又fx ≠fx-2 ,故fx 的最小正周期为4,B正确;
C选项,假如fx+1 为奇函数,则f-x+1 +fx+1 =0,
当x=1时,可得f0 +f2 =0,
但fx +fx-2 =2,当x=2可得f2 +f0 =2,
显然不满足要求,故fx+1 不是奇函数,C错误;
D选项,因为fx +g2-x =5,所以f0 +g2 =5,
又g2 =5,故f0 =0,
由B选项得fx +fx-2 =2,故f2 +f0 =2,解得f2 =2,
且f3 +f1 =2,
由B选项知fx 的一个周期为4,故f4 =f0 =0,
所以f1 +f2 +f3 +f4 =4,2024
则 fk
k=1
18
=506 f1 +f2 +f3 +f4 =506×4=2024,D正确.
故选:ABD
26 (2024·湖南长沙·高三雅礼中学校考阶段练习)如图,在直四棱柱ABCD-ABCD 中,底面
1 1 1 1
ABCD为菱形,∠BAD=60°,AB=AA=2,P为CC 的中点,点Q满足DQ=λDC+
1 1
μDD λ∈ 0,1 ,μ∈ 1 0,1 ,则下列结论正确的是 ( )
1
A.若λ+μ= ,则四面体ABPQ的体积为定值
3 1
B.若△ABQ的外心为O,则AB⋅AO为定值2
1 1 1
2π
C.若AQ= 5,则点Q的轨迹长度为
1 4
1
D.若λ=1且μ= ,则存在点E∈AB,使得AE+EQ的最小值为 9+2 10
2 1
【答案】ACD
1 1
【解析】A选项,在CD,DD 上分别取F,W,使得DF= DC,DW= DD ,
1 3 3 1
因为DQ=λDC+μDD ,所以DQ=3λDF+3μDW,
1
1
因为λ+μ= ,所以3λ+3μ=1,即DQ=3λDF+1-3λ
3
DW,
故DQ-DW =3λDF-3λDW,即WQ=3λWF,
所以W,Q,F三点共线,
因为WF⎳CD ,AB⎳CD ,所以WF⎳AB ,
1 1 1 1
故WF⎳平面PAB,故点Q为平面PAB的距离为定值,
1 1
又S 为定值,故四面体ABPQ的体积为定值,A正确;
△PA1B 1
B选项,取AB的中点T,因为△ABQ的外心为O,所以OT⊥AB,
1 1 1
又题意得AB= AA2+AB2=2 2,
1 1
则AB⋅AO=AB
1 1 1
⋅AT
1
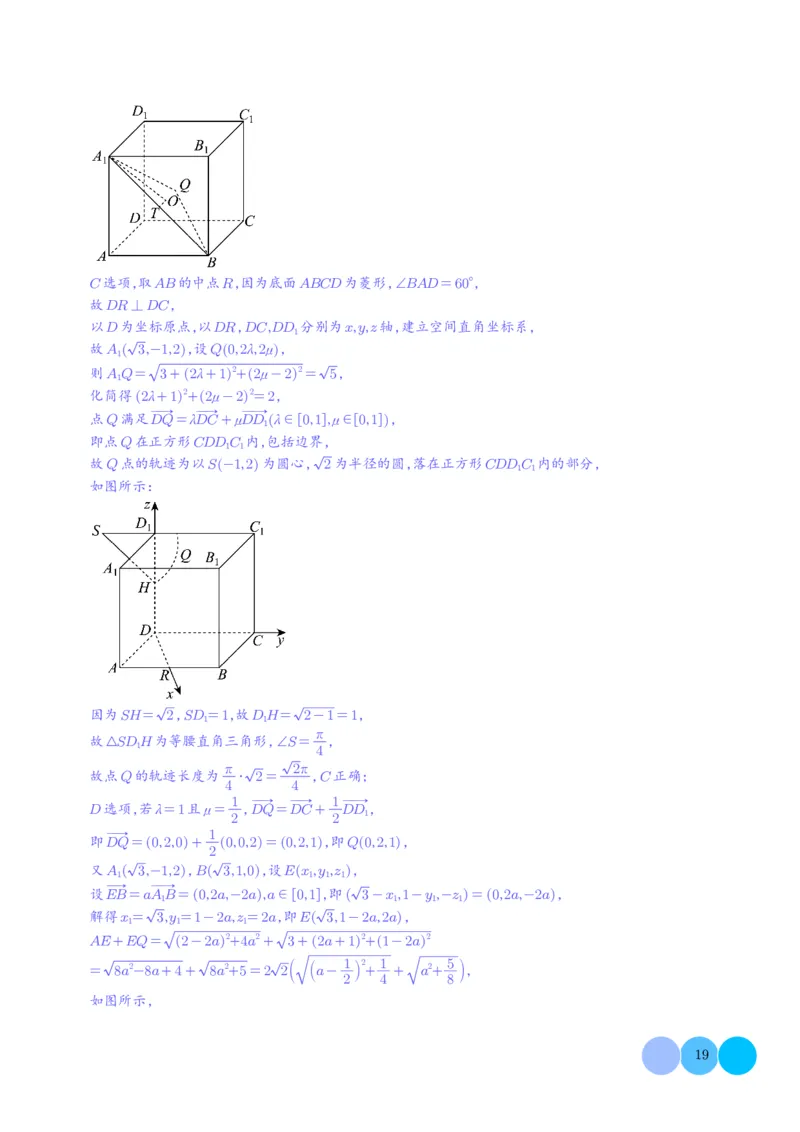
=2 2× 2=4,B错误;C选项,取AB的中点R,因为底面ABCD为菱形,∠BAD=60°,
故DR⊥DC,
以D为坐标原点,以DR,DC,DD 分别为x,y,z轴,建立空间直角坐标系,
1
故A 1 3,-1,2
19
,设Q0,2λ,2μ ,
则A 1 Q= 3+2λ+1 2+2μ-2 2= 5,
化简得2λ+1 2+2μ-2 2=2,
点Q满足DQ=λDC+μDD λ∈ 0,1 ,μ∈ 1 0,1 ,
即点Q在正方形CDDC 内,包括边界,
1 1
故Q点的轨迹为以S-1,2 为圆心, 2为半径的圆,落在正方形CDDC 内的部分, 1 1
如图所示:
因为SH= 2,SD=1,故DH= 2-1=1,
1 1
π
故△SDH为等腰直角三角形,∠S= ,
1 4
π 2π
故点Q的轨迹长度为 ⋅ 2= ,C正确;
4 4
1 1
D选项,若λ=1且μ= ,DQ=DC+ DD ,
2 2 1
即DQ=0,2,0
1
+ 0,0,2
2
=0,2,1 ,即Q0,2,1 ,
又A 1 3,-1,2 ,B 3,1,0 ,设Ex 1 ,y 1 ,z 1 ,
设EB=aA 1 B=0,2a,-2a ,a∈0,1 ,即 3-x 1 ,1-y 1 ,-z 1 =0,2a,-2a ,
解得x 1 = 3,y 1 =1-2a,z 1 =2a,即E 3,1-2a,2a ,
AE+EQ= 2-2a 2+4a2+ 3+2a+1 2+1-2a 2
1
= 8a2-8a+4+ 8a2+5=2 2 a-
2
2 1 5
+ + a2+
4 8
,
如图所示,1 10 1
设KJ= ,GV= ,JG= ,且KJ⊥JG,JG⊥GV,
2 4 2
1
在线段JG上取一点L,设GL=a,则LJ= -a,
2
1
故KL+VL= a-
2
20
2 1 5
+ + a2+ ,
4 8
显然,直接连接KV,此时KL+VL取得最小值,最小值即为KV,
1 10
由勾股定理得KV= +
2 4
2 1 9 10
+ = + ,
4 8 4
1
故AE+EQ=2 2 a-
2
2 1 5
+ + a2+
4 8
9 10
的最小值为2 2 + = 9+2 10,
8 4
D正确.
故选:ACD
27 (2024·湖北武汉·高三武钢三中校考开学考试)已知函数fx ,gx 的定义域为R,g x 为gx 的
导函数,且fx +g x -8=0,fx-2 -g 6-x -8=0,若gx 为偶函数,则下列一定成立的有
( )
A. g 4 =0 B. f1 +f3 =16 C. f2023
20
=8 D. ∑fn
n-1
=160
【答案】ABD
【解析】由gx 是偶函数,则g-x =gx ,两边求导得-g -x =g x ,
所以g x 是奇函数,故g 0 =0.
对于A,由fx +g x -8=0⇒fx-2 +g x-2 -8=0⇒fx-2 =8-g x-2 ,
代入fx-2 -g 6-x -8=0,得8-g x-2 -g 6-x -8=0,
又g x 是奇函数,
则g x-2 =-g 6-x =g x-6 ⇒g x+6-2 =g x+6-6 ⇒g x+4 =g x ,
所以g x 是周期函数,且周期为4,g 0 =g 4 =0,故A正确;
对选项B,令x=1得,f1 +g 1 -8=0,令x=5得,f3 -g 1 -8=0,
故f1 +f3 =16,故B正确;
对于C:令x=2023得f2023 +g 2023 -8=0⇒f2023 +g 4×505+3 -8=0,
即f2023 +g 3 -8=0,
若f2023 =8,则g 3 =0,g 3 =g -1+4 =g -1 =0
但g -1 不一定为0,故C错误;
对于D:令x=4,得f4 +g 4 -8=f4 +g 0 -8=0,
故f4 =8,g 2 =g 2-4 =g -2 =-g 2 ,所以g 2 =0,令x=2,得f2
21
+g 2 -8=0,则f2 =8
则f1 +f3 =16,由g x 是以4为周期得fx +g x -8=0,
20
所以∑fn
n=1
=5 f1 +f2 +f3 +f4 =5×8+16+8 =160,故D正确.
故选:ABD.
28 (2024·湖北襄阳·高三襄阳五中校考开学考试)已知函数fx ,gx 的定义域为R,g x 是gx 的
导函数,且fx +g x -8=0,fx -g 4-x -8=0,若gx 为偶函数,则 ( )
A. f1 +f3 =16 B. f4 =8 C. f-1 =f-3
2023
D. g k
k=1
=0
【答案】ABD
【解析】因为fx +g x -8=0,令x=1,则f1 +g 1 -8=0①,
fx -g 4-x -8=0,令x=3,则f3 -g 1 -8=0②,
联立①②可得f1 +f3 =16,故A正确;
由题可知g x =-g 4-x ,又因为gx 是偶函数,所以g x 是奇函数,
由g x =-g -x =-g 4-x 可得g x =g x+4 ,
所以g x 的周期为4,
又∵g 0 =-g 0 ,故g 0 =g 4 =0,
fx =8-g x ,故f4 =8-g 4 =8,故B正确;
因为g -1 =-g 1 ,由g x =g x+4 得g -3 =g 1 ,
故g -3 =-g -1 ,又f-3 =8-g -3 ,f-1 =8-g -1 ,
若f-3 =f-1 ,则g -3 =g -1 ,
可得-g -1 =g -1 ,即g -1 =0,而g -1 不一定等于0,故C错误;
因为g 1 =-g 3 ,得g 1 +g 3 =0,
在g x =-g 4-x 中,令x=2,可得g 2 =0,又g 4 =0,
故g 1 +g 2 +g 3 +g 4 =0,又g x 的周期为4,
2023
所以 g k
k=1
=505×0+g 1 +g 2 +g 3 =0,故D正确.
故选:ABD.
29 (2024·山东·高三山东省实验中学校联考开学考试)在四棱锥S-ABCD中,ABCD是矩形,AD⊥
SD,∠SDC=120°,SD=CD=2BC=2,P为棱SB上一点,则下列结论正确的是 ( )
A.点C到平面SAD的距离为 3
3
B.若SP=PB,则过点A,D,P的平面α截此四棱锥所得截面的面积为
2
C.四棱锥S-ABCD外接球的表面积为17π
3
D.直线AP与平面SCD所成角的正切值的最大值为
3
【答案】ACD
【解析】如图,对于A,因为AD⊥SD,AD⊥DC,又SD∩DC=D,SD,DC⊂面SDC,
所以AD⊥面SDC,
所以点A到平面SDC的距离为AD=BC=1,
又因为∠SDC=120°,SD=CD=2,
3
所以点C到平面SAD的距离为 ×2= 3,故A正确;
2
对于B,因为SP=PB,所以点P为棱SB的中点,
取SC中点为Q,连接PQ,DQ,可得平面APQD即平面α截此四棱锥所得截面,
且由于Q是SC的中点,点P为棱SB的中点,
1 1
所以在△SBC中,PQ是△SBC的中位线,则PQ= BC= ,PQ⎳BC,
2 2
又因为四边形ABCD是矩形,则BC⎳AD,所以PQ/AD,
因为AD⊥面SDC,
AD⊄面SDC,QC⊂面SDC,
所以四边形APQD是以AD为下底、PQ为上底,DQ为高的直角梯形,
因为SD=CD=2,在等腰三角形SCD中,QD⊥BC,且QD平分∠ADC,
1 1
则QD=CD⋅cos ∠SDC=2× =1,
2 2
1 1
则平面α截此四棱锥所得截面的面积为 ×1+
2 2
22
3
×1= ,故B错误;
4
对于C,又因为∠SDC=120°,SD=CD=2,所以SC=2cos30°+2cos30°=2 3,
SC 2 3
所以2r= = =4,即r=2,其中r为△SCD外接圆半径,
sin∠SDC 3
2
因为AD⊥面SDC,
CD
所以四棱锥S-ABCD外接球的半径为R= r2+
2
2 1
= 22+
2
2 17
= ,
2
所以四棱锥S-ABCD外接球的表面积为17π,故C正确;
对于D,因为AD⊥面SDC,所以直线AP与平面SCD所成角为∠APD,
所以当点P与点B重合时,∠APD最大,积tan∠APD
3
= ,故D正确.
max 3
故选:ACD.
30 (2024·福建泉州·高三福建省安溪第一中学校联考开学考试)学校食堂每天中午都会提供A,B两种
2
套餐供学生选择(学生只能选择其中的一种),经过统计分析发现:学生第一天选择A套餐的概率为 ,选
3
1 1
择B套餐的概率为 .而前一天选择了A套餐的学生第二天选择A套餐的概率为 ,选择B套餐的概率
3 4
3 1 1
为 ;前一天选择B套餐的学生第二天选择A套餐的概率为 ,选择B套餐的概率也是 ,如此反复.记
4 2 2
某同学第n天选择A套餐的概率为A ,选择B套餐的概率为B .一个月(30天)后,记甲、乙、丙三位同学选
n n
择B套餐的人数为X,则下列说法中正确的是 ( )2
A.A +B =1 B.数列A -
n n n 5
23
是等比数列
C. EX =1.5 D.PX=1
36
=
125
【答案】AB
【解析】由于每人每次只能选择A,B两种套餐中的一种,所以A +B =1,所以A正确,
n n
1
依题意,A n+1 =A n × 4 +1-A n
1 2 1 2
× ,则A - =- A - 2 n+1 5 4 n 5 n≥1,n∈N ,
2 2 2 4
又n=1时,A- = - = ,
1 5 3 5 15
2
所以数列A -
n 5
4 1
是以 为首项,以- 为公比的等比数列,
15 4
2 4 1
所以A - = ×-
n 5 15 4
n-1 2 16 1
,A = - ×-
n 5 15 4
n 3 16 1
,B =1-A = + ×-
n n 5 15 4
n
,
3 16 1
当n>30时,B = + ×-
n 5 15 4
n
,
3 16 1
所以X∼B 3, + ×-
5 15 4
n
,PX=1
36
≠ ,EX
125
9
≠ ,
5
所以AB正确,CD错误,
故选:AB.
31 (2024·福建·高三校联考开学考试)如图,在棱长为1的正方体ABCD-ABCD 中,E是线段DD
1 1 1 1 1
上的动点(不包括端点),过A,B ,E三点的平面将正方体截为两个部分,则下列说法正确的是 ( )
1
A.正方体的外接球的表面积是正方体内切球的表面积的3倍
B.存在一点E,使得点A 和点C到平面AEB 的距离相等
1 1
C.正方体被平面AEB 所截得的截面的面积随着D E的增大而增大
1 1
1
D.当正方体被平面AEB 所截得的上部分的几何体的体积为 时,E是DD 的中点
1 3 1
【答案】AC
3 1
【解析】对于A,正方体外接球的半径为 ,内切球的半径为 ,可得正方体的外接球的表面积是正方体
2 2
3
2
内切球的表面积的
2
1
2
=3倍,故A正确;
2
对于B,由点A 和点B到平面AEB 的距离相等,若点A 和点C到平面AEB 的距离相等,
1 1 1 1
必有BC⎳平面AEB ,又由BC∥AD,可得AD⎳平面AEB ,与AD∩平面AEB=A矛盾,
1 1 1
故B错误;
对于C,如图,在C 1 D 1 上取一点F,使得EF∥C 1 D,连接B 1 F,设D 1 E=a00.
可得函数fa 单调递增,可得正方体被平面AEB 所截得的截面面积随着D E的增大而增大, 1 1
故C正确;
1 1 1 1 1 对于D选项,V = × ×1×1×1= ,V = ×a× 1×1- ×1×1-a
E-AA1B1 3 2 6 E-A1B1FD1 3 2
=
1
a2+a
6
,
1
被平面AEB 1 所截得的上部分的几何体的体积为 6 a2+a
1 1
+ = ,整理为a2+a-1=0, 6 3
5-1
解得a= ,故D错误.
2
故选:AC
x2
32 (2024·福建·高三校联考开学考试)在平面直角坐标系xOy中,已知双曲线C: -y2=1的右顶点
3
为A,直线l与以O为圆心,OA 为半径的圆相切,切点为P.则 ( )
2 3
A.双曲线C的离心离为
3
B.当直线OP与双曲线C的一条渐近线重合时,直线l过双曲线C的一个焦点
C.当直线l与双曲线C的一条渐近线平行吋,若直线l与双曲线C的交点为Q,则OQ = 5
D.若直线l与双曲线C的两条渐近线分别交于D,E两点,与双曲线C分别交于M,N两点,则DM =
EN
【答案】ABD
2 2 3
【解析】对于A选项.由a= 3,b=1,c=2,可得双曲线C的离心率为e= = ,故A选项正确;
3 33
对于B选项,双曲线C的渐近线方程为y=± x.
3
3
由对称性,不妨设直线l与渐近线y=- x重合,点P位于第四象限,
3
3 5π π
记直线l与x轴的交点为T,由直线y=- x的倾斜角为 ,有∠POT= ,
3 6 6
又由OP
25
= 3,可得OT =2.又由OF =2,故直线l过双曲线C的一个焦点,故B选项正确;
对于C选项,当直线l与双曲线C的一条渐近线平行时,由对称性,
3 m
不妨设直线l的方程为y= x+m(其中m<0),有
3
= 3,可得m=-2,
1+ 1
3
3
x
3
-y2=1,
5 3 3
直线l的方程为y= x-2,联立方程 解方程组可得点Q的坐标为 ,-
3 y= 3x-2, 4 4
3
.
可得OQ
75 9 21
= + = ,故C选项错误;
16 16 2
对于D选项,设点P的坐标为s,t ,可得直线l的方程为sx+ty=3.其中s2+t2=3.
y= 3x, 3 3 y=- 3x, 3 3
联立方程 3 解得x= ,联立方程 3 解得x= ,
sx+ty=3, 3s+t sx+ty=3. 3s-t
1 3 3 3 3
可得线段DE的中点的横坐标为 +
2 3s+t 3s-t
9s x2 -y2=1,
= ,联立方程 3 ,
3s2-t2 sx+ty=3,
消去y后整理为3s2-t2 x2-18sx+3t2+27 =0,
1 18s 9s
可得线段MN的中点的横坐标为 × = ,
2 3s2-t2 3s2-t
可得线段DE和MN的中点相同,故有DM =EN ,故D选项正确.
故选:ABD.33 (2024·浙江·高三浙江金华第一中学校考开学考试)在平面直角坐标系中,将函数f(x)的图象绕坐
标原点逆时针旋转α(0<α≤90°)后,所得曲线仍然是某个函数的图象,则称f(x)为“α旋转函数”.那么
( )
A.存在90°旋转函数 B.80°旋转函数一定是70°旋转函数
1 bx
C.若g(x)=ax+ 为45°旋转函数,则a=1 D.若h(x)= 为45°旋转函数,则-e2≤b≤0
x ex
【答案】ACD
【解析】对A,如y=x满足条件,故A正确;
对B,如倾斜角为20°的直线是80°旋转函数,不是70°旋转函数,故B错误;
1 1
对C,若g(x)=ax+ 为45°旋转函数,则根据函数的性质可得,g(x)=ax+ 逆时针旋转45°后,不存在
x x
1
与x轴垂直的直线,使得直线与函数有1个以上的交点.故不存在倾斜角为45°的直线与g(x)=ax+ 的
x
函数图象有两个交点.即y=x+bb∈R
26
1 y=ax+ 1
与g(x)=ax+ 至多1个交点.联立 x 可得
x y=x+b
a-1 x2-bx+1=0.
当a=1时,-bx+1=0最多1个解,满足题意;
当a≠1时,a-1 x2-bx+1=0的判别式Δ=b2-4a-1 ,对任意的a,都存在b使得判别式大于0,不满
足题意,故a=1.故C正确;
bx
对D,同C,h(x)= 与y=x+aa∈R
ex
bx
的交点个数小于等于1,即对任意的a,a= -x至多1个解,
ex
故gx
bx
= -x为单调函数,即g x
ex
b1-x
=
-1为非正或非负函数.
ex
又g 1
b1-x
=-1,故
-1≤0,即ex≥-bx-1
ex
恒成立.
即y=ex图象在y=-bx-1 上方,故-b≥0,即b≤0.
当y=ex与y=-bx-1 相切时,可设切点x 0 ,ex0 ,对y=ex求导有y=ex,故
ex0
=ex0,解得x =2,此 x -1 0
0
时b=-ex0=-e2,故-e2≤b≤0.故D正确.
故选:ACD
34 (2024·浙江·高三浙江金华第一中学校考开学考试)已知函数fx ,gx 的定义域均为R,且fx +
g2-x =5,gx -fx-4 =7.若x=2是gx 的对称轴,且g2 =4,则下列结论正确的是 ( )
A. fx 是奇函数 B. 3,6 是gx 的对称中心
C.2是fx
22
的周期 D.gk
k=1
=130
【答案】BD【解析】对于A,因为x=2是gx
27
的对称轴,所以g(2-x)=g(x+2),
又因为fx +g2-x =5,所以f-x +g2+x =5,故fx =f-x ,
即fx 为偶函数,故A错误;
对于B,因为g(x)-f(x-4)=7,所以g(x+4)-f(x)=7,
又因为f(x)+g(2-x)=5,联立得g(2-x)+g(x+4)=12,
所以y=g(x)的图像关于点(3,6)中心对称,故B正确;
对于C,因为fx +g2-x =5,g2 =4,则f0 +4=5,即f0 =1;
因为gx -fx-4 =7,则4-f-2 =7,即f-2 =-3,则f2 =-f-2 =3;
显然f2 ≠f0 ,所以2不是fx 的周期,故C错误;
对于D,因为x=2是gx 的对称轴,所以g(6-x)=g(x-2),
又因为g(2-x)+g(x+4)=12,即gx +g6-x =12,
则gx +gx-2 =12,所以gx+2 +gx =12,
所以gx+2 =gx-2 ,即gx =gx+4 ,所以gx 周期为4,
因为gx 周期为4,对称中心为3,6 ,所以g3 =6,
当x=4时,代入gx -fx-4 =7,即g4 -f0 =7,所以g4 =8,
所以g4 =g0 =8,又x=2是gx 的对称轴,所以g1 =g3 =6,
22
所以gk
k=1
=5×6+4+6+8 +6+4=130,故D正确,
故选:BD.
35 (2024·江苏镇江·高三扬中市第二高级中学开学考试)已知在伯努利试验中,事件A发生的概率为
p01),△ABC是以点B(0,1)为直
a2
角顶点的等腰直角三角形,直角边BA,BC与椭圆分别交于另外两点A,C.若这样的△ABC有且仅有一
个,则该椭圆的离心率的取值范围是 .
6
【答案】0,
3
1
【解析】不妨设直线BA:y=kx+1(k>0),则直线BC:y=- x+1,
k
y=kx+1
联立方程得x2 +y2=1 ,得1+a2k2
a2
x2+2a2kx=0,
2a2k 1 2a2k
∴x =- ,用- 代替k得x = ,
A 1+a2k2 k c a2+k2∴BA
31
= 1+k2 x
A
2a2k 1+k2
= ,BC
1+a2k2
1
= 1+ x
k2 C
2a2 1+k2
= .
a2+k2
由BA =BC ,得k-1 k2+1-a2 k+1 =0,
该方程关于k已有一解k=1,由于符合条件的△ABC有且仅有一个,
∴关于k的方程k2+1-a2 k+1=0无实数解或有两个相等的实数解k=1.
a>1
当方程无实数解时,
Δ=1-a2
2-4<0
,解得11
当方程有两个相等的实数解k=1时,
1-a2=-2
,解得a= 3,
∴10在 ,+∞
2
上
恒成立,则实数m的取值范围是 .
【答案】-∞,2 e+ln2
1
【解析】因为关于x的不等式2ex-2xlnx-m>0在 ,+∞
2
上恒成立,
m 1
即 0,
1
所以存在x ∈ ,1 0 2 ,使得g x 0
1
=0,即ex0- =0, x
0
则x =-lnx ,
0 0
1
所以当x∈ ,x 2 0 时,g x 0 <0,gx
1
在 ,x 2 0 上单调递减,
当x∈x 0 ,+∞ 时,g x 0 >0,gx 在x 0 ,+∞ 上单调递增,
故g(x) min =gx 0
1
=ex0-lnx -1= +x -1>2-1=1>0, 0 x 0
0
所以f x
1
>0在 ,+∞
2
上恒成立,
所以fx
1
在区间 ,+∞
2
上单调递增,
m 1
所以 ≤f
2 2
1 1 1
= e- ln = e+ ln2,
2 2 2
所以m≤2 e+ln2,即实数m的取值范围是-∞,2 e+ln2 .
故答案为:-∞,2 e+ln2
39 (2024·广东中山·高三中山纪念中学开学考试)已知0a,
2
令g x
a+b
>0得x> 或x0,解得x> ,
4
故Wx
a+3b
在-∞,
4
a+3b
上单调递减,在 ,+∞
4
上单调递增,
且Wx 在-∞,a
a+b
和 ,+∞
2
a+b
内下凹,在a,
2
内上凸,
f x
k
的几何意义是点 k,Wk 和点 x,Wx 连线的斜率,
当Wk 在k,+∞ 内下凹时,可满足y=f x
k
都是区间k,+∞ 上严格递增,
因此当k≥1时,f x
k
严格递增,
而当k≤0时,唯一可能使f x
k
不严格递增的区间可能在 a, a+3b
4
,
曲线CA须在直线BA下方,曲线AD须在直线BA上方,
故需使点 0,W0 , -1,W-1
a+b
,⋯都在x= 处的切线上或切线上方即可,
2
从图象可知,只需 0,W0
a+b
在x= 处的切线上或切线上方即可,
2
a+b
W
2
a+b
= -a
2
3 a+b
-b
2
a-b
=-
2
4 a+b
,W
2
a-b
=
2
2
a-b
a-b
=
3
,
4
a+b a-b
故曲线在x= 处的切线方程为y+
2 2
4 a-b
=
3 a+b
x-
4 2
,
1
令x=0,化简得y=- a-b
16
3 3a+b ,
W0
1
=a3b,因此- a-b
16
3 3a+b
b
≥a3b,即 -1
a
3 b
+3
a
b
≤16⋅ ,
ab
令t= >1,则t-1
a
33
3 t+3 ≤16t,即t-1
3
3≤161-
t+3
,
其中3-1
3
3=161-
3+3
=8,画出y=t-1
3
3及y=161-
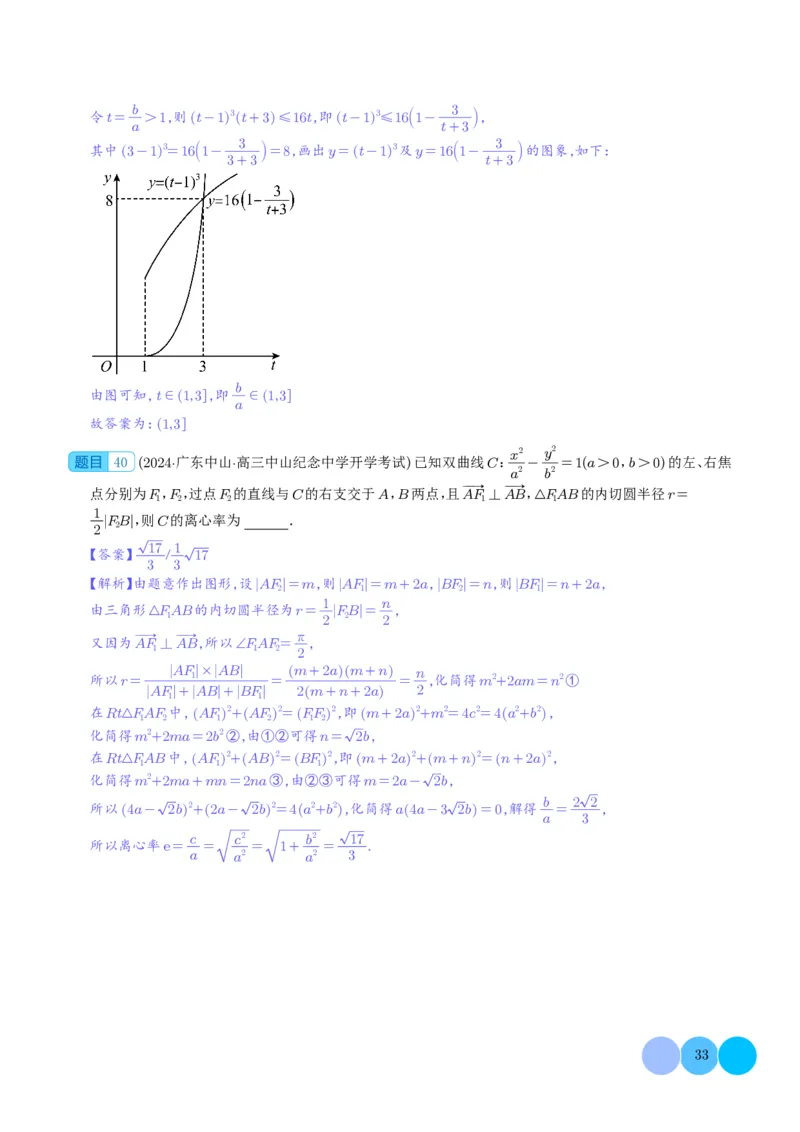
t+3
的图象,如下:
由图可知,t∈1,3
b
,即 ∈1,3
a
故答案为:1,3
x2 y2
40 (2024·广东中山·高三中山纪念中学开学考试)已知双曲线C: - =1(a>0,b>0)的左、右焦
a2 b2
点分别为F,F,过点F 的直线与C的右支交于A,B两点,且AF ⊥AB,△FAB的内切圆半径r=
1 2 2 1 1
1
2 F 2 B ,则C的离心率为 .
17 1
【答案】 / 17
3 3
【解析】由题意作出图形,设AF 2 =m,则AF 1 =m+2a,BF 2 =n,则BF 1 =n+2a,
1
由三角形△F 1 AB的内切圆半径为r= 2 F 2 B
n
= , 2
π
又因为AF ⊥AB,所以∠FAF= ,
1 1 2 2
所以r= AF 1 ×AB
AF 1 +AB +BF 1
m+2a = m+n
2m+n+2a
n = ,化简得m2+2am=n2①
2
在Rt△F 1 AF 2 中,AF 1 2+AF 2 2=F 1 F 2 2,即m+2a 2+m2=4c2=4a2+b2 ,
化简得m2+2ma=2b2②,由①②可得n= 2b,
在Rt△F 1 AB中,AF 1 2+AB 2=BF 1 2,即m+2a 2+m+n 2=n+2a 2,
化简得m2+2ma+mn=2na③,由②③可得m=2a- 2b,
所以4a- 2b 2+2a- 2b 2=4a2+b2 ,化简得a4a-3 2b
b 2 2
=0,解得 = ,
a 3
c c2 b2 17
所以离心率e= = = 1+ = .
a a2 a2 3x2 y2
41 (2024·湖南长沙·高三长郡中学校考阶段练习)已知椭圆C: + =1(a>b>0)的右焦点为F,
a2 b2
π PF
过点F作倾斜角为 的直线交椭圆C于A、B两点,弦AB的垂直平分线交x轴于点P,若
4 AB
34
1
= ,则
4
椭圆C的离心率e= .
1
【答案】 /0.5
2
π
【解析】因为倾斜角为 的直线过点F,
4
设直线l的方程为: y=x-c, Ax 1 ,y 1 ,Bx 2 ,y 2 ,
线段AB的中点Qx 0 ,y 0 ,
y=x-c
联立 x2
+
y2
=1
,化为a2+b2
a2 b2
x2-2a2cx+a2c2-a2b2=0,
2a2c a2c2-a2b2
∴x+x = ,xx = ,
1 2 a2+b2 1 2 a2+b2
∴AB = 1+12⋅ x 1 +x 2
4ab2 x+x a2c
2-4xx = ,x = 1 2 = . 1 2 a2+b2 0 2 a2+b2
b2c
∴y =x -c=-
0 0 a2+b2
b2c a2c
∴AB的垂直平分线为:y+ =-x-
a2+b2 a2+b2
,
c3 c3
令 y=0, 解得 x = ,∴P ,0
P a2+b2 a2+b2
.
2b2c
∴|PF|=c-x = ,
P a2+b2
|PF| c 1 c 1
∴ = = ,则 = ,
|AB| 2a 4 a 2
1
∴ 椭圆C的离心率为 ,
2
1
故答案为: .
2
x2 y2
42 (2024·湖南邵阳·高三邵阳市第二中学校考开学考试)如图,已知双曲线C: - =1(a,b>0)的
a2 b2
左、右焦点分别为F,F,过F的直线与C分别在第一、二象限交于A,B两点,△ABF 内切圆半径为r,若
1 2 1 2
BF 1 =r=a,则C的离心率为 .85
【答案】
5
【解析】设AB
35
=x,内切圆圆心为I,内切圆在BF,AF,AB上的切点分别为U,V,W, 2 2
则BU =BW ,AV =AW ,F 2 U =F 2 V ,
由BF 1 =a及双曲线的定义可知,
BF 2 =3a,AF 2 =x-a,F 2 U =F 2 V
1
= 2 BF 2 +AF 2 -AB =a=r,
故四边形IUFV是正方形,
2
得AF 2 ⊥BF 2 ,于是BF 2 2+AF 2 2=|AB|2,
故x2=9a2+(x-a)2,所以x=5a,
于cos∠F 1 BF 2 =cosπ-∠ABF 2
3
=- ,在△FBF 中, 5 1 2
由余弦定理可得F 1 F 2 2=BF 1 2+BF 2 2-2BF 1 ⋅BF 2
68
⋅cos∠FBF= a2, 1 2 5
68 c 85
从而4c2= a2,所以e= = .
5 a 5
85
故答案为:
5
x2 y2
43 (2024·湖南长沙·高三雅礼中学校考阶段练习)已知双曲线C: - =1a>0,b>0
a2 b2
,F为右焦
点,过点F作FA⊥x轴交双曲线于第一象限内的点A,点B与点A关于原点对称,连接AB,BF,当
∠ABF取得最大值时,双曲线的离心率为 .
6+ 2
【答案】
2
【解析】如图,根据题意Fc,0
36
b2
,Ac,
a
b2
,B-c,-
a
,
b2 b2
∴k=k = ,k =k = =2k ,
1 BF 2ac 2 BA ac 1
设直线BA,BF的倾斜角为α,β,
∴tan∠ABF=tanα-β
tanα-tanβ 2k-k 1 2
= = 1 1 = ≤ ,
1-tanαtanβ 1+2k2 2k+ 1 4
1 1 k
1
b2 2
当且仅当k= = 时等号成立,
1 2ac 2
即b2= 2ac,c2-a2= 2ac,e2- 2e-1=0,又e>1
6+ 2
∴e= ,
2
6+ 2
故答案为: .
2
44 (2024·湖北襄阳·高三襄阳五中校考开学考试)在首项为1的数列a
n
1
中a -a =-
n+1 n 2
n
,若存在
n∈N*,使得不等式m-a n m+a n+3 >0成立,则m的取值范围为 .
1 5
【答案】mm> 或m<-
2 8
.
【解析】结合题意:a n =a 1 +a 2 -a 1 +a 3 -a 2 +⋯+a n -a n-1
1 =1+-
2
1 1 +-
2
2 1 +⋯+-
2
1--1
n-1 2 =
n
1--1
2
2 1 = 1--
3 2
n
,
所以m-a n m+a n+3 >0,解得m>a 或m<-a , n n+3
2 1 当n为偶数时,a = 1-
n 3 2
n
,递增,可得a 的最小值为a = 1 ,则a ∈ 1 , 2
n 2 2 n 2 3
,
2 1 -a =- 1+
n+3 3 2
n+3
<- 2 ,递增,可得-a 的最小值为-a =- 11 ,则-a ∈ - 11 ,- 2
3 n+3 5 16 n+3 16 3
,
2 1 当n为奇数时,a = 1+
n 3 2
n
2 ,递减,可得a 的最大值为a=1,a ∈ ,1
n 1 n 3
,
2 1 -a =- 1-
n+3 3 2
n+3
5 2 5 ,递减,可得-a 的最大值为-a =- ,-a ∈- ,-
n+3 4 8 n+3 3 8
,
综上所述:要使得存在n∈N*,使得不等式m-a n m+a n+3 >0成立,
只需m>a n
1
min = 2 或m<-a n+3
5
=- , max 8
1 5
所以m的取值范围为mm> 或m<-
2 8
.
1 5
故答案为:mm> 或m<-
2 8
.
45 (2024·山东·高三山东省实验中学校联考开学考试)已知抛物线y2=4x的焦点为F,准线为l,过点
F的直线交抛物线于A,B两点,点A,B在直线l上的射影分别为A,B 两点,以线段AB 为直径的圆C与
1 1 1 1y轴交于M,N两点,且MN
37
4
= AB
5
,则直线AB的斜率为 .
【答案】±2
【解析】由题意可知:F1,0 ,l:x=-1,且直线AB与抛物线y2=4x必相交,
设AB:x=my+1,Ax 1 ,y 1 ,Bx 2 y 2 ,则A 1-1,y 1 ,B 1-1,y 2 ,
x=my+1
联立方程
y2=4x
,消去x可得y2-4my-4=0,
则y 1 +y 2 =4m,y 1 y 2 =-4,可得y 1 -y 2 = 16m2+16=4 m2+1,
可知AB = 1+m2 y 1 -y 2 =4m2+1 ,圆C的圆心C-1,2m
1
,半径r= 2 y 1 -y 2 =2 m2+1,
可得MN =2 r2-1=2 4m2+3,
因为MN
4
= AB
5
4
,即2 4m2+3= ×4m2+1
5
1 11
,解得m2= 或m2=- (舍去),
4 16
1 1
即m=± ,所以直线AB的斜率为 =±2.
2 m
故答案为:±2.
46 (2024·福建泉州·高三福建省安溪第一中学校联考开学考试)若过点1,0 可以作曲线y=
lnx+a 的两条切线,则实数a的取值范围为 .
【答案】-1,0
1
【解析】由题意y= x+a ,设切点为 x 0 ,lnx 0 +a ,x 0 >-a ,
则切线斜率满足 lnx 0 +a -0 1 = ,
x -1 x +a
0 0
整理得x 0 +a lnx 0 +a -x 0 +1=0,由题意该方程在-a,+∞ 有两个根,
所以函数gx =x+a lnx+a -x+1在-a,+∞ 有两个零点,
g x =lnx+a +1-1=lnx+a ,令g x =0得x=1-a,
当-a1-a时,g x >0,gx 单调递增,
所以首先有gx =g1-a
min
=-1-a +1=a<0(否则gx 不可能有零点,矛盾),
其次当x→+∞时,gx →+∞,所以gx 在1-a,+∞ 上,有且仅有一个零点,
所以还需保证gx 在-a,1-a 上有1个零点,
现在来说明x趋于-a(x>-a)时,gx →a+1, gx -a)时,t→+∞,
t
所以gx =x+a lnx+a
lnt 1
-x+1=- - -a
t t
+1→a+1,
所以只需保证a+1>0,解得a>-1,综上所述,实数a的取值范围为-1,0
38
.
故答案为:-1,0 .
47 (2024·福建·高三校联考开学考试)方程cos2x=3cosx-2的最小的29个非负实数解之和为
.
811π
【答案】
3
【解析】方程cos2x=3cosx-2可化为2cos2x-3cosx+1=0,
因式分解为cosx-1
1
cosx-
2
1
=0,解得cosx=1或cosx= ,
2
当cosx=1时,x=2kπ,k∈Z,
1 1
1 π 5π
当cosx= 时,x= +2k π,k ∈Z,或x= +2k π,k ∈Z,
2 3 2 2 3 3 3
通过列举,可得方程的最小的29个非负实数解中,
10×9
有10个是以0为首项,2π为公差的等差数列.其和为10×0+ ×2π=90π;
2
π π 10×9 280π
有10个是以 为首项,2π为公差的等差数列,其和为10× + ×2π= ;
3 3 2 3
5π 5π 8×9
有9个是以 为首项,2π为公差的等差数列,其和为9× + ×2π=87π.
3 3 2
280π 811π
可得方程的最小的29个非负实数解之和为90π+ +87π= .
3 3
811π
故答案为:
3
48 (2024·浙江·高三浙江金华第一中学校考开学考试)设严格递增的整数数列a ,a ,⋯,a 满足a=
1 2 20 1
1,a =40.设f为a+a ,a +a ,⋯,a +a 这19个数中被3整除的项的个数,则f的最大值为 ,使
20 1 2 2 3 19 20
得f取到最大值的数列a
n
的个数为 .
【答案】 18 25270
【解析】第一个空,设某个数除以a余数为b,则称该数模a余b(a,b均为整数,且b1,
由题意,得At,2 t ,Bt,-2 t ,即AB =4 t
2 t
所以直线AD的方程为y= x-1
t-1
,
y= 2 t x-1
联立 t-1
,化简得tx2-t2+1
y2=4x
x+t=0,
t2+1
∴x 1 +x 2 = t ,因为At,2 t
t2+1 1
,可得点D的横坐标为 -t= , t t
2
代入抛物线方程可得,y=± ,所以DE
t
4
= ,
t
1
∴S = ×4 t×t-1
△ABF 2
=2 t⋅t-1
1 4 1
,S = × ×1-
△DEF 2 t t
2t-1
=
t⋅ t
S 2 t⋅t-1
∴ △ABF =
S △DEF
2t-1
=t2=4,又t>1,所以t=2.
t⋅ t
故答案为:2
50 (2024·江苏镇江·高三扬中市第二高级中学开学考试)已知非零数列a
n
,b =a⋅a ⋅a ⋯a ,点
n 1 2 3 n
a n ,b n x a 在函数y= 的图象上,则数列 n 2x-2 b n -1 ⋅2n 的前2024项和为 .
1
【答案】2-
2025×22023
【解析】由已知条件b =a⋅a ⋅a ⋯a ,可得b =a⋅a ⋅a ⋯a ,n≥2,
n 1 2 3 n n-1 1 2 3 n-1b
所以 n =a ①,n≥2,
b n
n-1
因为点a n ,b n
40
x
在函数y= 的图象上, 2x-2
b
n
所以b = a n ,将①代入可得,b = b n-1 ,
n 2a -2 n b
n 2 n -2
b
n-1
1
化简得,b -b = ,n≥2,
n n-1 2
b 3
当n=1时,由a=b ,则b= 1 ,得b= ,
1 1 1 2b-2 1 2
1
所以数列b
n
3 1
是以 为首项, 为公差的等差数列,
2 2
所以b = 3 + 1 (n-1)=1+ n ,a = b n = 1+ n 2 = 2+n ,
n 2 2 2 n b n-1 1+ n-1 1+n
2
a
因为 n
b n -1
2+n 1 1
= = -
⋅2n n(n+1)⋅2n-1 n⋅2n-2 n+1
,
⋅2n-1
1 1 1 1 1 1 1
所以 - + - +⋯+ - =2- ,
1×2-1 2×20 2×20 3×21 2024×22022 2025×22023 2025×22023
1
故答案为: 2- .
2025×22023
51 (2024·江苏镇江·高三扬中市第二高级中学开学考试)已知点Px 0 ,ex0 是函数y=ex图像上任意一
点,点Q是曲线x-e4-2 2+y2=1上一点,则P、Q两点之间距离的最小值是 .
【答案】e2 e4+1-1
【解析】曲线x-e4-2 2+y2=1表示圆心为De4+2,0 ,半径r=1的圆,
则PD = x 0 -e4-2 2+e2x0,
令fx =x-e4-2 2+e2x,则f x =2x-e4-2 +2e2x,
令gx =f x =2x-e4-2 +2e2x,则g x =2+4e2x>0,
所以gx 单调递增,又g2 =0,
所以当x<2时gx <0,即f x <0,即fx 在-∞,2 上单调递减,
当x>2时gx >0,即f x >0,即fx 在2,+∞ 上单调递增,
所以fx 在x=2处取得极小值即最小值,即fx =f2
min
=e8+e4,
所以PD = x 0 -e4-2 2+e2x0≥ e8+e4=e2 e4+1,
所以PQ =PD
min
-r=e2 e4+1-1.
min
故答案为:e2 e4+1-1