文档内容
2024年新高考新结构题型数学选填压轴好题汇编 02
一、单选题
1 (2024·广东·一模)已知函数hx
1
的定义域为R,且满足hx+1 +hx-1 =2,h2-x 是偶函数,
h2
103
=0,若n∈Z,则 h(n)= ( )
n=-103
A.202 B.204 C.206 D.208
【答案】C
【解析】因为hx+1 +hx-1 =2,所以hx+2 +hx =2①,即有hx+4 +hx+2 =2②,
由①②得到hx+4 =hx ,所以函数hx 的周期为4,
又h2-x 是偶函数,所以h2+x =h(2-x),得到h(x)=h(4-x)=h(-x),即函数hx 为偶函数,
又由hx+2 +hx =2,得到h1 +h3 =2,h2 +h4 =2,h0 +h2 =2,
又h2 =0,所以h0
103 103
=2,故 h(n)=2h(n)+h(0)=2×25×4+h(0)+2(h(1)+h(2)+h(3))=
n=-103 n=1
206,
故选:C.
2 (2024·高三·湖南·阶段练习)设方程2x⋅log 2 x =1的两根为x 1 ,x 2x 1 2 B.x> C.03
1 2 1 x 1 2 1 2
2
【答案】C
【解析】由题意得,00 ,则f1
1
=- <0,f2 2
1 3 1
=1- = >0,f 4 4 2
1
=1- >0, 2
1
由f 2 ⋅f1 <0,f1 ⋅f2
1
<0得x∈ ,1 1 2 ,x 2 ∈1,2 ,故A错;
由log 2 x 2
1
- 2
x2=log
2 x 1
1
- 2
x1=0,得log
2 x 2 -log 2 x 1
1
= 2
x2- 1
2
x1,
1
由x∈ ,1 1 2 ,x 2 ∈1,2
1
,得log x +log x= 2 2 2 1 2
x2- 1
2
x1<0,
即log xx <0,所以0b>0)与双曲线 - =1(m>0,n>0)有共同的
a2 b2 m2 n2π
焦点F,F,且在第一象限内相交于点P,椭圆与双曲线的离心率分别为e ,e .若∠FPF= ,则e⋅e 的
1 2 1 2 1 2 3 1 2
最小值是
1 2 3 3
A. B. C. D.
2 2 2 2
【答案】C
【解析】设共同的焦点为(-c,0),(c,0),设PF 1
2
=s,PF 2 =t,运用椭圆和双曲线的定义,以及三角形的余
弦定理和基本不等式,即可得到所求最小值.设共同的焦点为(-c,0),(c,0),
设PF 1 =s,PF 2 =t,
由椭圆和双曲线的定义可得s+t=2a,s-t=2m,
解得s=a+m,t=a-m,
π
在ΔPFF 中,∠FPF= ,
1 2 1 2 3
可得F 1 F 2 2=PF 1 2+PF 2 2-2PF 1 ⋅PF 2 ⋅cos∠FPF, 1 2
即为4c2=(a+m)2+(a-m)2-(a+m)(a-m)=a2+3m2,
a2 3m2
即有 + =4,
c2 c2
1 3
即为 + =4,
e2 e2
1 2
1 3 3
由 + ≥2 ,
e2 e2 e2e2
1 2 1 2
3 3
可得e⋅e ≥ ,当且仅当e = 3e 时,取得最小值 ,
1 2 2 2 1 2
故选C.
2cos40°+cos80°
4 (2024·高三·湖南长沙·阶段练习)求值: = ( )
sin80°
3 3
A. 3 B. C.- 3 D.-
3 3
【答案】A
2cos40°+cos80° 2cos120°-80°
【解析】 =
sin80°
+cos80°
sin80°
2cos120°cos80°+sin120°sin80°
=
+cos80° 3sin80°
= = 3.
sin80° sin80°
故选:A.
5 (2024·陕西安康·二模)宋代理学家周敦颐的《太极图》和《太极图说》是象数和义理结合的表达.《朱
子语类》卷七五:“太极只是一个混沦底道理,里面包含阴阳、刚柔、奇偶,无所不有”.太极图(如下图)将平
衡美、对称美体现的淋漓尽致.定义:对于函数fx ,若存在圆C,使得fx 的图象能将圆C的周长和面积
同时平分,则称fx 是圆C的太极函数.下列说法正确的是 ( )
①对于任意一个圆,其太极函数有无数个②fx
3
=log 2x+1
1
2
1
+ x是x2+y+1
2
2=1的太极函数
③太极函数的图象必是中心对称图形
④存在一个圆C,fx =sinx+cosx是它的太极函数
A.①④ B.③④ C.①③ D.②③
【答案】A
【解析】对于①:过圆心的直线都可以将圆的周长和面积平分,
所以对于任意一个圆,太极函数有无数个,故①正确
对于②:f-x =log 2-x+1
1
2
1 1+2x
- x=log
2
2
1 2x
1
- x,
2
fx -f-x
2x+1
=log
1
2
+x=-x+x=0,所以fx
2x+1
2x
关于y轴对称,不是太极函数,故②错误;
对于③:中心对称图形必定是太极函数,对称点即为圆心.
但太极函数只需平分圆的周长和面积,不一定是中心对称图形,故③错误;
对于④:曲线fx
π
=sinx+cosx= 2sinx+
4
存在对称中心,
所以必是某圆的太极函数,故④正确.
故选:A.
6 已知定义在[0,1]上的函数f(x)满足:
①f(0)=f(1)=0;
②对所有x,y∈[0,1],且x≠y,有f(x)-f(y)
1
< x-y
2
.
若对所有x,y∈[0,1],f(x)-f(y) 时,fx
2
-fy = fx -f0 - fy -f1
≤ fx -f1 + fy -f0
1
< x-1
2
1
+ y-0
2
1
= 1-x
2
1 1 1
+ y= + y-x
2 2 2
1
< ,
41
故k≤
4
考点:1.抽象函数问题;2.绝对值不等式.
π
7 (2024·高三·浙江杭州·专题练习)已知三棱锥S-ABC中,∠SAB=∠ABC= ,SB=4,AB=2,
2
π
BC= 3,SA和BC所成的角为 ,则该三棱锥外接球的表面积是 ( )
3
A.12π B.16π C.24π D.32π
【答案】B
【解析】将三棱锥S-ABC放入长方体ABCD-EFGH中,S在棱EH上面,
并以A为原点,AB,AD,AE所在直线分别为x,y,z轴建立如图所示的空间直角坐标系:
π
由题意∠SAB=∠ABC= ,SB=4,AB=2,BC= 3,
2
所以SA= 16-4=2 3,
π
因为SA和BC所成的角为 ,AD⎳BC,
3
π π
所以AE=2 3sin =3,ES=2 3cos = 3,
3 3
而底面三角形外接圆圆心为AC中点O ,设球心O到平面ABC的距离为h,
1
则A0,0,0
4
,B2,0,0 ,C2, 3,0 ,S0, 3,3
3
,O 1, ,0 1 2
3
,O1, ,h 2 ,
3
所以OA=-1,- ,-h
2
3
,OS=-1, ,3-h
2
,
则由OA
=OS
3 3
=R⇒R2= +1+h2= +1+3-h
4 4
2,
3
解得h= ,R2=4,从而S=4πR2=16π,
2
即该三棱锥外接球的表面积是16π.
故选:B.
8 已知等差数列a
n
a +1
中,a +a =2 记b = n ,n∈N*,则数列b
4 5 n a -1 n
n
的前8项和为 ( )
A.0 B.4 C.8 D.16
【答案】C
【解析】由等差数列性质得a +a =a +a
n 9-n 4 5
a +1 a -1+2 2
b = n = n =1+ ,
n a -1 a -1 a -1
n n n
2
设c = ,当1≤n≤8,n∈N*时,
n a -1
n
2 2 a +a -2
c +c = + =2⋅ n 9-n
n 9-n a n -1 a 9-n -1 a n -1 a 9-n -1
a +a -2
=2⋅ 4 5
a n -1 a 9-n -1
=0,
故b+b +b +⋯+b
1 2 3 8
2 2 2
=1+ +1+ +⋯+1+ =8+c+c +⋯+c
a-1 a -1 a -1 1 2 8
1 2 8
=8+c 1 +c 8 +c 2 +c 7 +c 3 +c 6 +c 4 +c 5 =8
故选:C
π
9 (2024·高三·浙江·阶段练习)若3sinθ+cosθ= 10,则tanθ+
8
1
-
tanθ+ π
8
的值为 ( )1 2
A.-7 B.-14 C. D.
7 7
【答案】B
【解析】一方面由题意3sinθ+cosθ= 10,且注意到sin2θ+cos2θ=1,
3 10 10
联立得10sin2θ-6 10sinθ+9=0,解得sinθ= ,cosθ= ,
10 10
sinθ
所以tanθ= =3,
cosθ
2tanπ
另一方面不妨设x=tan π >0,且tan π =1= 8 ,
8 4 1-tan2π
8
π
所以有x2+2x-1=0,解得x=-1+ 2或x=-1- 2(舍去),即x=tan =-1+ 2,
8
π
由两角和的正切公式有tanθ+
8
5
tanθ+x 3+-1+ 2
= =
1-x⋅tanθ
1-3-1+ 2
2+ 2
=
×4+3 2
4-3 2 ×4+3 2
=
-7+5 2 ,
π
所以tanθ+
8
1
-
tanθ+ π
8
=-7+5 2
1
+
7+5 2
=-7+5 2
7-5 2
+
7+5 2 ×7-5 2
=-7-5 2+5 2-7=-14.
故选:B.
x2 y2
10 (2024·高三·江苏镇江·开学考试)已知过坐标原点O且异于坐标轴的直线交椭圆 + =1(a>
a2 b2
b>0)于P,M两点,Q为OP中点,过Q作x轴垂线,垂足为B,直线MB交椭圆于另一点N,直线PM,PN
1
的斜率分别为k,k ,若kk =- ,则椭圆离心率为 ( )
1 2 1 2 2
1 3 3 6
A. B. C. D.
2 3 2 3
【答案】D
【解析】如图所示:
设Pm,n ,则M-m,-n
m n
,Q ,
2 2
m
,B ,0
2
,
而k ⋅k = y N +n ⋅ y N -n = y2 N -n2 = a b2 2 a2-x2 N
MN PN x +m x -m x2-m2
N N N
- b2 a2-m2 a2 b2 =- ,
x2-m2 a2
N
1
又因为k ⋅k =- ,
PM PN 2
n
所以 k PM = m = 3 = a2 ,解得 b2 = 1 ,
k n 2 2b2 a2 3
MN
m+m
2
c b2 6
所以椭圆离心率为e= = 1- = .
a a2 3
故选:D.
1 x2 y2
11 (2024·高三·江苏南京·开学考试)斜率为 的直线l经过双曲线 - =1(a>0,b>0)的左焦
2 a2 b2
点F,与双曲线左,右两支分别交于A,B两点,以双曲线右焦点F 为圆心的圆经过A,B,则该双曲线的离
1 2
心率为 ( )15
A. 2 B. 3 C. 5 D.
3
【答案】D
【解析】取AB的中点M,连接MF,
2
由题意可知:AF 2
6
=BF 2 ,则MF⊥AB, 2
设AF 1 =m>0,则AF 2 -AF 1 =2a,即BF 2 =AF 2 =m+2a,
因为BF 1 -BF 2 =2a,则BF 1 =BF 2 +2a=m+4a,
可得AM
1
= AB 2 =2a,MF 1 =AF 2 =m+2a,
1 1
又因为直线AB的斜率为 ,即tan∠AFF= ,且∠AFF为锐角,
2 1 2 2 2 1
则 c s o in s ∠ ∠ A A F F 1 1 F F 2 2 = 2 1 ,可得 sin∠AF 1 F 2 = 5 5 或 sin∠AF 1 F 2 =- 5 5 (舍去),
sin2∠AFF+cos2∠AFF=1 cos∠AFF= 2 5 cos∠AFF=-2 5
1 2 1 2 1 2 5 1 2 5
则MF 2 =F 1 F 2
2 5c
sin∠AF 1 F 2 = 5 ,MF 1 =F 1 F 2
4 5c
cos∠AFF= , 1 2 5
且MF 2 2+AM 2=AF 2
2 5c
2,即4a2+ 5
2 4 5c
= 5
2 5
,整理得c2= a2, 3
c2 15
所以双曲线的离心率e= = .
a2 3
故选:D.
1.焦点三角形的作用
在焦点三角形中,可以将圆锥曲线的定义,三角形中边角关系,如正余弦定理、勾股定理结合起来.
x2 y2
12 (2024·高三·湖南长沙·阶段练习)双曲线C: - =1的右支上一点P在第一象限,F,F 分别为
9 16 1 2
双曲线C的左、右焦点,I为△PFF 的内心,若内切圆I的半径为1,则△PFF 的面积等于 ( )
1 2 1 2
32 16
A.24 B.12 C. D.
3 3
【答案】C
x2 y2
【解析】由双曲线C: - =1的a=3,b=4,c=5,
9 16
设圆与三角形三边相切于点M,N,Q,
则PF 1 -PF 2 =PM +MF 1 -QF 2 -PQ =MF 1 -QF 2 =NF 1 -NF 2 =2a,
又NF 1 +NF 2 =2c,
所以NF 1 =a+c=8,NF 2 =c-a=2,
因此IN⊥x轴,因此NF 1 =a+c=8,NF 2 =c-a=2,IN =1,I(3,1),
IN
tan∠IFN=
1
NF 1
1 IN
= ,tan∠IFN=
8 2
NF 2
1
= ,
2
1 π 所以tan ∠FPF=tan -∠IFN-∠IFN
2 2 1 2 1 2
sin π -∠IFN-∠IFN
2 1 2 =
cos π -∠IFN-∠IFN 2 1 2
1 =
tan∠IF 1 N+∠IF 2 N
=
1- 2 1 × 8 1 3 IM
= = 1 + 1 2
2 8
PM PM
2
= 3 ,∴PF 1
2 26
= +8= , 3 3
因此PF 2 =PF 1
8 1
-2a= 3 ,故三角形的面积为 2 PF 1 +PF 2 +F 1 F 2
32
×1= . 3
故选:C13 (2024·高三·江苏无锡·开学考试)已知函数fx
7
x-1
=
, x<2
2x-3
,若方程f fx
2-1, x≥2
1
= 的实
2
根个数为 ( )
A.4 B.8 C.10 D.12
【答案】C
【解析】因为fx
x-1
=
, x<2
2x-3
1
,则f
2-1, x≥2 2
1 3
= ,f
2 2
1
= ,f2
2
=1,f4 =1,
2x-3
令
2-1= 1 3 3
2 ,解得x=3- 或x=3+ ,
x≥2 2 2
又在同一平面直角坐标系中画出y=fx
1
与y= 的图象,
2
由图象观察可知y=fx
1
与y= 有4个交点,不妨设为x,x ,x ,x 且xb>c B.c>a>b C.a>c>b D.b>c>a
【答案】B
【解析】构建fx
x
= ,x>e,则f x
lnx
lnx-1
=
lnx
>0在e,+∞
2
内恒成立,
可知fx 在e,+∞ 内单调递增,
π π 2 4
因为a= = ,c= = ,
2ln π lnπ ln2 ln4
可知f4 >fπ >fe =e,即c>a>e;
构建gx =x-sinx,x>0,则g x =1-cosx≥0在0,+∞ 内恒成立,
可知gx 在0,+∞ 内单调递增,则gx >g0 =0,即x>sinx,x>0,
1 1 1
可得 >sin ,且e>0,则e>e2⋅sin ,即e>b;
e e e
综上所述:c>a>b.
故选:B.
20 (2024·高三·重庆·阶段练习)将分别标有数字1,2,3,4,5的五个小球放入A,B,C三个盒子,每个
小球只能放入一个盒子,每个盒子至少放一个小球.若标有数字1和2的小球放入同一个盒子,且A盒子中
只放一个小球,则不同的放法数为 ( )
A.28 B.24 C.18 D.12【答案】C
【解析】第一种情况,将五个小球按1,1,3分为三组,则安排的方法有C1C1A2=12种;
3 2 2
第二种情况,将五个小球按1,2,2分为三组,则安排的方法有C1C1=6种.
3 2
不同的放法数为18.
故选:C.
二、多选题
21 (2024·高三·广东·阶段练习)已知O为坐标原点,点F为抛物线C:y2=4x的焦点,点P4,4
11
,直线l:
x=my+1交抛物线C于A,B两点(不与P点重合),则以下说法正确的是 ( )
A. FA
π
≥1 B.存在实数m,使得∠AOB<
2
2
C.若AF=2BF,则m=± D.若直线PA与PB的倾斜角互补,则m=-2
4
【答案】CD
【解析】由题意可知,抛物线焦点为F(1,0),准线方程为x=-1,
直线x=my+1恒过F(1,0),如下图所示:
设A(x,y),B(x ,y ),作AA 垂直于准线x=-1,垂足为A ,
1 1 2 2 1 1
根据抛物线定义可知,FA =AA 1 =x 1 +1,易知x 1 ≥0,所以FA =x+1≥1, 1
但当FA =1时,此时A与坐标原点重合,直线与抛物线仅有一个交点,因此FA ≠1,
所以FA >1,即A错误;
联立直线x=my+1和抛物线C:y2=4x方程得y2-4my-4=0;
y2 y2
所以yy =-4,xx = 1 ⋅ 2 =1,
1 2 1 2 4 4
此时OA∙OB=OA
OB
π
cos∠AOB=xx +yy =-3<0,所以cos∠AOB<0,即∠AOB> ,
1 2 1 2 2
π
所以不存在实数m,使得∠AOB< ,故B错误;
2
1
若AF=2FB,由几何关系可得y=-2y ,结合yy =-4,可得y = 2或y =- 2,即B , 2
1 2 1 2 2 2 2
或
1
B ,- 2
2
,
2
将B点坐标代入直线方程可得m=± ,所以C正确;
4
若直线PA与PB的倾斜角互补,则k +k =0,
PA PB
y-4 y -4
即 1 + 2 =0,整理得2myy -(4m+3)(y+y )+24=0,
x-4 x -4 1 2 1 2
1 2
3
代入yy =-4,y+y =4m解得m=-2或m= ,
1 2 1 2 43
当m= 时,直线过点P4,4
4
12
,A与P点重合,不符合题意,所以m=-2;即D正确.
故选:CD
22 (2024·广东·一模)将圆柱OO 的下底面圆O 置于球O的一个水平截面内,恰好使得O 与水平截
1 2 1 1
面圆的圆心重合,圆柱OO 的上底面圆O 的圆周始终与球O的内壁相接(球心O在圆柱OO 内部).已
1 2 2 1 2
3
知球O的半径为3,OO= .若R为上底面圆O 的圆周上任意一点,设RO与圆柱OO 的下底面所成
1 2 2 1 2
的角为α,圆柱OO 的体积为V,则 ( )
1 2
π
A.α可以取到0,
2
27π
中的任意一个值 B.V= cos2α1+2sinα
2
81π
C.V的值可以是任意小的正数 D.V =
max 4
【答案】BD
【解析】
过R作圆柱OO 的轴截面PQRS,过O作MN⊥OO 交圆柱轴截面的边于M,N,
1 2 1 2
由RO与圆柱的下底面所成的角为α,则OM=3cosα,MR=3sinα,所以V=π⋅OM2⋅QR=π⋅(3cosα)2
OO 1 +3sinα
27π
= cos2α(1+2sinα), 2
27π 27π
即V= cos2α(1+2sinα)= 1-sin2α
2 2
⋅(1+2sinα),故B正确;
3 π
当点P,Q均在球面上时,角α取得最小值,此时OO=OO = ,所以α= ,
1 2 2 6
所以a∈ π , π
6 2
,故A错误;
令sina=t∈ 1 ,1
2
27π ,所以V= 1-t2
2
27π (1+2t)= -2t3-t2+2t+1
2
,
27π
所以V= -6t2-2t+2
2
,另-6t2-2t+2=0,
-1- 13 -1+ 13
解得两根t= ,t = ,
1 2 2 2
27π 27π 1 所以V= -6t2-2t+2)≤ × -6×
2 2 2
2 -2× 1 +2
2
27π =- <0,
4
27π 所以V= -2t3-t2+2t+1
2
在t∈ 1 ,1
2
时单调递减,
27π 1 所以V = × -2⋅
max 2 2
3 1 -
2
2 1 +2×
2
+1
81π = ,故D正确,C错误;
4
故选:BD.
23 (2024·高三·湖南·阶段练习)已知体积为2的四棱锥P-ABCD,底面ABCD是菱形,AB=2,PA
=3,则下列说法正确的是 ( )π
A.若PA⊥平面ABCD,则∠BAD为
6
B.过点P作PO⊥平面ABCD,若AO⊥BD,则BD⊥PC
π
C.PA与底面ABCD所成角的最小值为
6
D.若点P仅在平面ABCD的一侧,且AB⊥AD,则P点轨迹长度为3 3π
【答案】BCD
【解析】设P到底面的距离为h,
1 1 4
V = S ⋅h= AB⋅ADsin∠BAD⋅h= hsin∠BAD=2,
P-ABCD 3 ABCD 3 3
1 π 5π
则当PA⊥平面ABCD时,h=PA=3,则sin∠BAD= ,即∠BAD为 或 ,A错误;
2 6 6
如图1,若PO⊥平面ABCD,BD⊂平面ABCD,则PO⊥BD,又AO⊥BD,
PO∩AO=O,PO,AO⊂平面PAO,
则BD⊥平面PAO,PA⊂平面PAO,故BD⊥PA,又BD⊥AC,
PA∩AC=A,PA,AC⊂平面PAC,
所以BD⊥平面PAC,PC⊂平面PAC,BD⊥PC,B正确;
1 1
设PA与底面ABCD所成角为θ,又V = S h= S PAsinθ=2,
P-ABCD 3 ABCD 3 ABCD
2 1
则sinθ= ,因为S =4sin∠BAD≤4,则sinθ≥ ,
S ABCD 2
ABCD
π 由于θ∈0,
2
13
,所以θ∈ π , π
6 2
π
则PA与底面ABCD所成角的最小值为 ,C正确;
6
1 3 3
如图2,当AB⊥AD,根据V = S h=2,得h= ,即P点到底面ABCD的距离为 ,过A点作
P-ABCD 3 ABCD 2 2
3
底面ABCD的垂线为l,过点P作PO⊥l交l于点O,则PO= AP2-AO2= 32-
2
2 3 3
= ,点P的
2
3 3
轨迹是以O为圆心, 为半径的圆,轨迹长度为3 3π,D正确.
2
故选:BCD
24 (2024·高三·湖南长沙·阶段练习)已知函数fx =x+1 ex-x-1 ,则下列说法正确的有
A. fx 有唯一零点 B. fx 无最大值
C. fx 在区间1,+∞ 上单调递增 D.x=0为fx 的一个极小值点【答案】BCD
【解析】对于A,依题意,f-1
14
=f0 =0,即x=-1和x=0是函数fx =x+1 ex-x-1 的零点,A错
误;
对于B,当x>0时,令ux =ex-x-1,求导得u x =ex-1>0,函数ux 在0,+∞ 上递增,当x≥2
时,ux ≥e2-3>1,
而y=x+1在0,+∞ 上递增,值域为1,+∞ ,
因此当x≥2时,fx >x+1,则fx 无最大值,B正确;
对于C,f x =x+2 ex-2x-2,
令gx =x+2 ex-2x-2,求导得g x =x+3 ex-2,
当x>0时,令hx =x+3 ex-2,则h x =x+4 ex>0,即g x =hx 在0,+∞ 上递增,
g x >g 0 =1>0,则f x =gx 在0,+∞ 上递增,f x >f 0 =0,
因此fx 在0,+∞ 上递增,即fx 在1,+∞ 上单调递增,C正确;
对于D,当-10,则存在x 0 ∈-1,0 ,使得φ x 0 =0,
当x∈x 0 ,0 时,φ x >0,函数φx 在x 0 ,0 上单调递增,则φx <φ0 =0,
即当x∈x 0 ,0
2x+2
时,ex< ,则f x x+2 =x+2 ex-2x-2<0,又f 0 =0,
因此x=0为fx 的一个极小值点,D正确.
故选:BCD
25 (2024·高三·山东济南·期末)已知函数fx 的定义域为R,且fx+y =fx +fy +1,f1 =0,
则 ( )
A. f0 =-1 B. fx 有最小值 C. f2024 =2023 D. fx +1是奇函数
【答案】ACD
【解析】对于A中,令x=y=0,可得f0 =-1,所以A正确;
对于B中,令x=x 1 ,y=x 2 -x 1 ,且x 1 0时,fx >-1时,fx 2 -fx 1 >0,此时函数fx 为单调递增函数;
若x>0时,fx <-1时,fx 2 -fx 1 <0,此时函数fx 为单调递减函数,
所以函数fx 不一定有最小值,所以B错误;
对于C中,令y=1,可得fx+1 =fx +f1 +1=fx +1,
即fx+1 -fx =1,
所以f2 -f1 =1,f3 -f2 =1,⋯ ,f2024 -f2023 =1,
各式相加得f2024 -f1 =2023,所以f2024 =f1 +2023=2023,所以C正确;
对于D中,令y=-x,可得f0 =fx +f-x +1,可得fx +1+f-x +1=0,
即f-x +1=- fx +1 ,所以函数fx +1是奇函数,所以D正确;
故选:ACD.
26 (2024·高三·山东德州·期末)双曲线具有以下光学性质:从双曲线的一个焦点发出的光线,经双曲线
反射后,反射光线的反向延长线经过双曲线的另一个焦点.由此可得,过双曲线上任意一点的切线平分该
x2
点与两焦点连线的夹角.已知F,F 分别为双曲线C: -y2=1的左,右焦点,过C右支上一点
1 2 3Ax 0 ,y 0
15
x 0 > 3 作双曲线的切线交x轴于点M,交y轴于点N,则 ( )
A.平面上点B4,1 ,AF 2 +AB 的最小值为 37-2 3
B.直线MN的方程为xx -3yy =3
0 0
C.过点F 1 作F 1 H⊥AM,垂足为H,则OH =2(O为坐标原点)
D.四边形AFNF 面积的最小值为4
1 2
【答案】ABD
【解析】对于A,由双曲线定义得AF 1 -AF 2 =2a=2 3,且F 1-2,0 ,
则AF 2 +AB =AF 1 +AB -2 3≥BF 1 -2 3= 4--2 2+1-2 3= 37-2 3,
所以AF 2 +AB 的最小值为 37-2 3.故A正确;
对于B,设直线MN的方程为y-y 0 =kx-x 0
3
,k≠± , 3
联立方程组 y-y 0 =kx-x 0 x2-3y2=3 ,消去y整理得,1-3k2 x2+6k2x 0 -6ky 0 x-3k2x2+6kx y -3y2-3=0, 0 0 0 0
x
∴Δ=0,化简整理得9y2k2-6x y k+x2=0,解得k= 0 ,
0 0 0 0 3y
0
x
可得直线MN的方程为y-y 0 = 3y 0 x-x 0
0
,即x x-3y y=3,故B正确; 0 0
对于C,由双曲线的光学性质可知,AM平分∠FAF,延长FH与AF 的延长线交于点E,
1 2 1 2
则AH垂直平分F 1 E,即AF 1 =AE ,H为FE的中点, 1
又O是F 1 F 2 中点,所以OH
1
= 2 F 2 E
1
= AE 2 -AF 2
1
= 2 AF 1 -AF 2 =a= 3,故C错误;
1 1
对于D,由直线MN的方程为x x-3y y=3,令x=0,得y=- ,则N0,-
0 0 y y
0 0
,
1
S AF1NF2 =S △AF1F2 +S △NF1F2 = 2 ×F 1 F 2 × y 0
1
+ y 0
1
≥ 2 ×4×2 y 0
1
⋅ y 0 =4,
当且仅当y 0
1
=
y 0
,即y =±1时等号成立, 0
所以四边形AFNF 面积的最小值为4,故D项正确.
1 2
故选:ABD.
27 (2024·高三·浙江杭州·专题练习)数列a n
1
满足a n+1 = 4 a n -6 3+6(n=1,2,3⋯),则 ( )
A.当a=3时,a
1 n
为递减数列,且存在M∈R,使a >M恒成立
n
B.当a=5时,a
1 n
为递增数列,且存在M≤6,使a M恒成立
n
D.当a=9时,a
1 n
递增数列,且存在M∈R,使a M恒成立,故C正确;
n n
3
D:当a=9时,a -6=2×
1 n 2
3n-1
,则a
n
为递增数列,无边界,故D错误;
故选:BC.
28 (2024·高三·吉林·阶段练习)在《九章算术》中,底面是直角三角形的直三棱柱被称为“堑堵”.如图,
在堑堵ABC-ABC 中,P是BB 的中点,AA=AC=BC=2,若平面α过点P,且与AC 平行,则
1 1 1 1 1 1
( )
10
A.异面直线AC 与CP所成角的余弦值为
1 10
1
B.三棱锥C-ACP的体积是该“堑堵”体积的
1 3
3 3
C.当平面α截棱柱的截面图形为等腰梯形时,该图形的面积等于
2
D.当平面α截棱柱的截面图形为直角梯形时,该图形的面积等于2 2
【答案】ABC
【解析】对于A,由题可知AC,CB,CC 两两垂直,如图建立空间直角坐标系,则
1
A2,0,0 ,C 10,0,2 ,C0,0,0 ,P0,2,1 ,
所以AC 1 =-2,0,2
,CP=0,2,1 ,
所以cosAC,CP
1
17
AC ⋅CP
= 1
AC
1
⋅CP
2 10
= = ,
8⋅ 5 10
10
所以异面直线AC 与CP所成角的余弦值为 ,故A正确;
1 10
1 4 1
对于B,V =V = S ×2= ,V = ×2×2×2=4,所以B正确;
C1-ACP P-C1CA 3 △C1CA 3 ABC-A1B1C1 2
对于C,如图,E,F,G分别为AA,AC,CB 的中点,
1 1 1 1 1
1
则EF⎳AC ,FG⎳AB,FG= AB ,AB⎳PE,AB=PE,EF=FG=GP= 2,PE=2 2,
1 1 1 2 1 1 1 1 1 1
1
所以FG⎳PE,FG= PE,P,E,F,G共面,又EF⎳AC ,AC⊄平面PEFG,EF⊂平面PEFG,
2 1 1
所以AC⎳平面PEFG,
1
则四边形PEFG为平面α截棱柱的截面图形,
6
所以四边形PEFG是等腰梯形,且高为 ,
2
当E不是AA 中点时,PE不平行平面ABC ,
1 1 1 1
1
则四边形不是梯形,等腰梯形有且仅有一个,S = × 2+2 2
PEFG 2
6 3 3
× = ,所以C正确;
2 2
对于D,如图,Q,R,S分别为AB,AC,CC 的中点,
1
1
则RS⎳AC ,QR⎳BC,QR= BC,BC⎳PS,BC=PS,QR=1,RS= 2,PS=2,
1 2
1
所以QR⎳PS,QR= PS,
2
同理可得四边形PQRS为平面α截棱柱的截面图形,
由题可知CB⊥AC,CB⊥CC,AC∩CC=C,AC⊂平面ACCA ,CC⊂平面ACCA ,
1 1 1 1 1 1 1
所以BC⊥平面ACCA ,所以PS⊥平面ACCA ,又RS⊂平面ACCA ,
1 1 1 1 1 1
所以PS⊥RS,
故四边形PQRS是直角梯形,当S不是CC 中点时,PS不平行平面ABC,
1
1
则四边形不是梯形,直角梯形有且仅有一个,其面积为S= ×1+2
2
3
× 2= 2,故D错误.
2故选:ABC.
29 (2024·高三·湖南株洲·期末)已知点A(-2,0),B(2,0),N(0,- 2)动点M满足直线AM和BM的斜
1
率之积为- ,记点M的轨迹为曲线C,过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x
2
轴,垂足为E,连接QE并延长交C于点G,则 ( )
x2 y2
A.曲线C的方程为: + =1 B.△PQG为直角三角形
4 2
16
C.△PAN面积最大值为2 D.△PQG面积最大值为
9
【答案】BD
y y 1 x2 y2
【解析】对A:设M(x,y),则 ⋅ =- ,化简得: + =1(x≠±2),故A错误;
x+2 x-2 2 4 2
对B:设Px 0 ,y 0
18
,Gx 1 ,y 1 ,Q-x 0 ,-y 0 ,Ex 0 ,0
y y k y+y
,则k = 0 =k>0,k = 0 = ,k k = 1 0 ⋅ PQ x QE 2x 2 QG GP x+x
0 0 1 0
y-y y2-y2
1 0 = 1 0 ,
x-x x2-x2
1 0 1 0
x2 x2
x2 y2 x2 y2 2- 2 1 -2- 2 0
∵ 1 + 1 =1, 0 + 0 =1,∴k k =
4 2 4 2 QG GP
1 k 1
=- = k ,则k =- ,则k ⋅k =-1,
x2-x2 2 2 GP GP k GP PQ
1 0
∠QPG=90°,故B 正确;
2
对C:与直线AN平行且与曲线C相切且切点在第一象限的切线方程为y=- x+mm>0
2
,
y=- 2x+m
联立 2 得x2- 2mx+m2-2=0,由Δ=2m2-4m2-2
x2
+
y2
=1
4 2
=0得m=2,
2 2 2+4
∴切线为y=- x+2,两平行直线的距离为d=
2
2
(2+ 2) 6
= ,
2+22 3
1 (2+ 2) 6
此时△PAN面积最大,最大值为 × 6× =2+ 2,故C错误;
2 3
x = 2
对D:设直线PQ得方程为y=kx(k>0), y x2 = +2 k y x 2=4 ,解得 y 0 = 2 2 k k 2+1 ,
0 2k2+1
1
则直线PG:y=- k x-x 0
1 k2+1
+y =- x+ x , 0 k k 0
联立直线PG与曲线C的方程可得2+k2 x2-4x 0k2+1 x+2x2 0k2+1 2-4=0,则x +x =
4x 0k2+1
0 G
, k2+2
1 S △PQG = 2 y 0 x 0 +x G 8k2+1 = k k2+2 2k2+1 8k+ 1 k = k+ 2
k
2k+ 1
k
8k+ 1 k = 2k+ 1
k
, 2+1
1 8t 8 2 令t=k+ ≥2,则S = = ,∵y=2t+ 在2t∈ 2,+∞
k ΔPQG 2t2+1 2t+ 2 2t
2t
,即t∈ 2 ,+∞
2
上单调
2 2 9
递增,故y=2t+ ≥4+ = ,
2t 4 2
8 16
即S = ≤ ,当且仅当k=1时等号成立,故D正确,
ΔPQG 2t+ 2 9
2t
故选:BD
30 (2024·高三·江苏镇江·开学考试)正方体ABCD-ABCD的8个顶点中的4个不共面顶点可以确
1 1 1 1
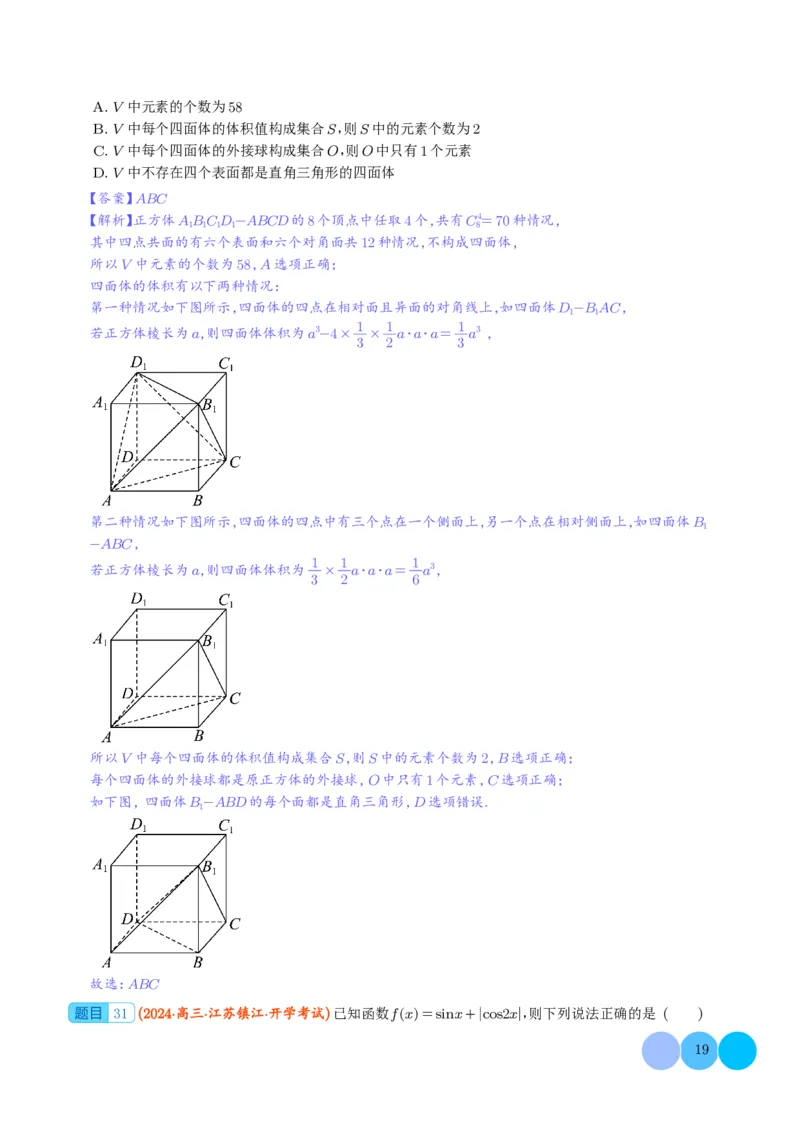
定一个四面体,所有这些四面体构成集合V,则 ( )A.V中元素的个数为58
B.V中每个四面体的体积值构成集合S,则S中的元素个数为2
C.V中每个四面体的外接球构成集合O,则O中只有1个元素
D.V中不存在四个表面都是直角三角形的四面体
【答案】ABC
【解析】正方体ABCD-ABCD的8个顶点中任取4个,共有C4=70种情况,
1 1 1 1 8
其中四点共面的有六个表面和六个对角面共12种情况,不构成四面体,
所以V中元素的个数为58,A选项正确;
四面体的体积有以下两种情况:
第一种情况如下图所示,四面体的四点在相对面且异面的对角线上,如四面体D-BAC,
1 1
1 1 1
若正方体棱长为a,则四面体体积为a3-4× × a⋅a⋅a= a3 ,
3 2 3
第二种情况如下图所示,四面体的四点中有三个点在一个侧面上,另一个点在相对侧面上,如四面体B
1
-ABC,
1 1 1
若正方体棱长为a,则四面体体积为 × a⋅a⋅a= a3,
3 2 6
所以V中每个四面体的体积值构成集合S,则S中的元素个数为2,B选项正确;
每个四面体的外接球都是原正方体的外接球,O中只有1个元素,C选项正确;
如下图,四面体B-ABD的每个面都是直角三角形,D选项错误.
1
故选:ABC
31 (2024·高三·江苏镇江·开学考试)已知函数fx
19
=sinx+cos2x ,则下列说法正确的是 ( )A.2π是fx
20
的一个周期
B. fx 的最小值是-2
C.存在唯一实数a∈0,2 ,使得fx+a 是偶函数
D. fx 在0,π 上有3个极大值点
【答案】ACD
【解析】对于A,fx+2π =sinx+2π + cos2x+2π =sinx+cos2x =fx ,所以2π是fx 的一个
周期;
对于B,fx =sinx+cos2x ≥sinx≥-1>-2,故B错误;
对于C,若fa+x =fa-x ,
π
则fa+
2
π
=fa-
2
,即cosa+cos2a =-cosa+cos2a ,
所以cosa=0,又a∈0,2
π
,所以a= ,经检验符合题意,故C正确;
2
对于D,设px =sinx+cos2x,qx =sinx-cos2x,
则p x =cosx-2sin2x,q x =cosx+2sin2x,
令mx =p x ,nx =q x ,
则m x
π
=-sinx-4cos2x在0,
4
3π
, ,π
4
上的函数值小于0,
n x
π 3π
=-sinx+4cos2x在 ,
4 4
上的函数值小于0,
故所有上面的极值点都是极大值点,
同时,p 0
2 π
=1>0> -2=p
2 4
π
,q
4
2 2 3π
=2+ >0>- -2=q
2 2 4
,
3π
p
4
2
=- +2>0>-1=p π
2
,
所以fx
π
在0,
4
π 3π
, ,
4 4
3π
, ,π
4
上各有一个极大值点,从而有三个极大值点,故D正确.
故选:ACD.
32 (2024·高三·江苏南京·开学考试)如图,该几何体是由正方形ABCD沿直线AB旋转90°得到的,已
知点G是圆弧CE的中点,点H是圆弧DF上的动点(含端点),则下列结论正确的是 ( )
A.不存在点H,使得CH⊥平面BDG
B.存在点H,使得平面AHE⎳平面BDG
7
C.存在点H,使得直线EH与平面BDG的所成角的余弦值为
3
1
D.不存在点H,使得平面BDG与平面CEH的夹角的余弦值为
3
【答案】BCD
【解析】由题意,可将几何体补全为一个正方体ADMF-BCNE,建立空间直角坐标系,如图所示,设正方体棱长为2,则A(0,0,0),B0,0,2
21
,C2,0,2 ,D2,0,0 ,
G 2, 2,2 ,E0,2,2 ,F0,2,0 ,设H2cosα,2sinα,0
π
0≤α≤
2
.
对于A选项,假设存在点H,使得CH⊥平面BDG,
因为CH=2cosα-2,2sinα,-2
,DB=-2,0,2
,BG= 2, 2,0 ,
CH⋅DB=4-4cosα-4=0 则
CH⋅BG=2 2cosα-1
,可得 sinα=1 ,
+2 2sinα=0 cosα=0
π π
因为0≤α≤ ,则α= ,
2 2
即当点H与点F重合时,CH⊥平面BDG,故A选项错误;
对于B选项,由A选项可知,平面BDG的一个法向量为FC=2,-2,2 ,
假设存在点H,使得平面AHE⎳平面BDG,则FC⊥AH,FC⊥AE,
AH=2cosα,2sinα,0
,AE=0,2,2
FC⋅AH=4cosα-4sinα=0
,则 ,可得tanα=1,
FC⋅AE=-4+4=0
π π
又因为0≤α≤ ,解得α= ,即当点H为DF的中点时,平面AHE⎳平面BDG,故B选项正确;
2 4
7
对于C选项,若存在点H,使得直线EH与平面BDG所成角的余弦值为 ,
3
7
则直线EH与平面BDG所成角的正弦值为 1-
3
2 2
= ,EH=2cosα,2sinα-2,-2
3
,
所以cosEH,FC
EH⋅FC
=
EH
⋅FC
4cosα-4sinα
=
2 3× 4cos2α+4sinα-1
cosα-sinα
=
2+4
2
= ,
3 3-2sinα 3
整理可得3sin2α-4sinα+3=0,
因为函数fα =3sin2α-4sinα+3在α∈ 0, π
2
时的图象是连续的,
且f0
π
=3>0,f 2
π
=-4+3=-1<0,所以存在α ∈0, 0 2 ,使得fα =0,
7
所以,存在点H,使得直线EH与平面BDG所成角的余弦值为 ,C选项正确;
3
对于D选项,设平面CEH的法向量为n=x,y,z
,CE=-2,2,0
,CH=2cosα-2,2sinα,-2 ,
n⋅CE=-2x+2y=0
则
n⋅CH=2xcosα-1
,取x=1,则y=1,z=sinα+cosα-1,可得n=
+2ysinα-2z=0
1,1,sinα+cosα-1 ,
1
假设存在点H,使得平面BDG与平面CEH的夹角的余弦值为 ,则cosn,FC 3
n⋅FC
=
n
⋅FC
=
2sinα+cosα-1 1
= ,
2+(sinα+cosα-1)2×2 3 3
可得sinα+cosα-1 2=1,即sinα+cosα-1=±1可得sinα+cosα=0或sinα+cosα=2,
因为α∈ 0, π
2
π π 3π 2 π ,则 ≤α+ ≤ 则 ≤sinα+
4 4 4 2 4
π ≤1,所以sinα+cosα= 2sinα+
4
∈
1, 2 ,
故当α∈ 0, π
2
时,方程sinα+cosα=0和sinα+cosα=2均无解,
1
综上所述,不存在点H,使得平面BDG与平面CEH的夹角的余弦值为 ,故D选项正确.
3
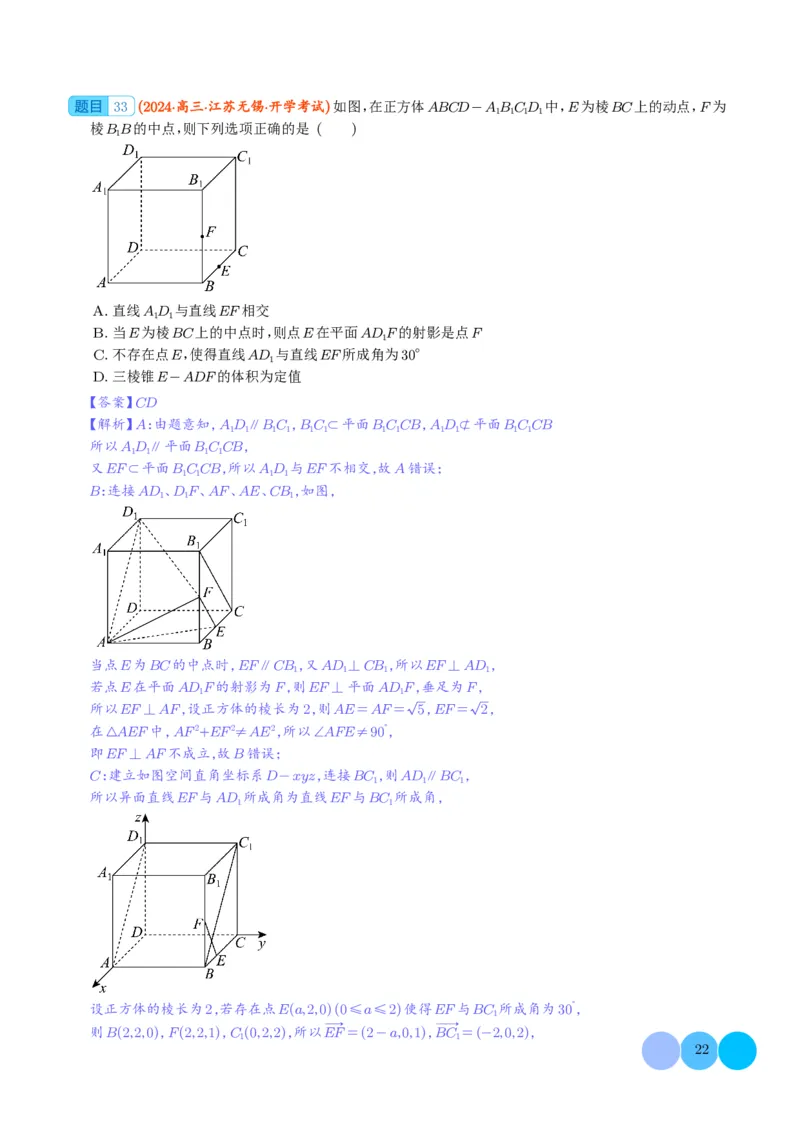
故选:BCD33 (2024·高三·江苏无锡·开学考试)如图,在正方体ABCD-ABCD 中,E为棱BC上的动点,F为
1 1 1 1
棱BB的中点,则下列选项正确的是 ( )
1
A.直线AD 与直线EF相交
1 1
B.当E为棱BC上的中点时,则点E在平面ADF的射影是点F
1
C.不存在点E,使得直线AD 与直线EF所成角为30°
1
D.三棱锥E-ADF的体积为定值
【答案】CD
【解析】A:由题意知,AD⎳BC ,BC⊂平面BCCB,AD⊄平面BCCB
1 1 1 1 1 1 1 1 1 1 1 1
所以AD⎳平面BCCB,
1 1 1 1
又EF⊂平面BCCB,所以AD 与EF不相交,故A错误;
1 1 1 1
B:连接AD 、DF、AF、AE、CB ,如图,
1 1 1
当点E为BC的中点时,EF⎳CB ,又AD⊥CB ,所以EF⊥AD ,
1 1 1 1
若点E在平面ADF的射影为F,则EF⊥平面ADF,垂足为F,
1 1
所以EF⊥AF,设正方体的棱长为2,则AE=AF= 5,EF= 2,
在△AEF中,AF2+EF2≠AE2,所以∠AFE≠90°,
即EF⊥AF不成立,故B错误;
C:建立如图空间直角坐标系D-xyz,连接BC ,则AD⎳BC ,
1 1 1
所以异面直线EF与AD 所成角为直线EF与BC 所成角,
1 1
设正方体的棱长为2,若存在点E(a,2,0)(0≤a≤2)使得EF与BC 所成角为30°,
1
则B(2,2,0),F(2,2,1),C(0,2,2),所以EF=(2-a,0,1),BC =(-2,0,2),
1 1
22
所以EF⋅BC =2a-2,又EF⋅BC
1 1
23
=EF
BC
1
cos30°,
得2a-2
3
=2 2× (2-a)2+1× ,解得a=4± 3,
2
不符合题意,故不存在点E使得EF与AD 所成角为30°,故C正确;
1
D:如图,
由等体积法可知V =V ,
E-ADF F-ADE
1 1 1
又V = S ⋅BF= × ×AD×AB×BF,
F-ADE 3 △ADE 3 2
AD、AB、BF为定值,所以V 为定值,
F-ADE
所以三棱锥E-ADF的体积为定值,故D正确.
故选:CD.
1
34 (2024·全国·一模)设a为常数,f(0)= ,f(x+y)=f(x)f(a-y)+f(y)f(a-x),则( ).
2
1 1
A. f(a)= B. f(x)= 成立
2 2
C. f(x+y)=2f(x)f(y) D.满足条件的f(x)不止一个
【答案】ABC
1
【解析】f(0)= ,f(x+y)=f(x)f(a-y)+f(y)f(a-x)
2
1 1
对A:对原式令x=y=0,则 = fa
2 2
1
+ fa
2
=fa ,即fa
1
= ,故A正确;
2
对B:对原式令y=0,则fx =fx fa +f0 fa-x
1
= fx
2
1
+ fa-x
2
,故fx =fa-x ,
对原式令x=y,则f2x =fx fy +fy fx =2fx fy =2f2 x ≥0,故fx 非负;
对原式令y=a-x,则fa =f2 x +f2 a-x =2f2 x
1
= ,解得fx
2
1
=± ,
2
又fx 非负,故可得fx
1
= ,故B正确;
2
对C:由B分析可得:fx+y =2fx fy ,故C正确;
对D:由B分析可得:满足条件的fx 只有一个,故D错误.
故选:ABC.
35 (2024·高三·河北保定·开学考试)如图,在三棱锥P-ABC中,∠ACD=60°,2AC=BC=PB=
PC,平面PBC⊥平面ABC,D是BC的中点,PD=4 3,则 ( )
32 3 π
A.三棱锥P-ABC的体积为 B.PA与底面ABC所成的角为
3 4
208π
C.PA=8 D.三棱锥P-ACD的外接球的表面积为
3
【答案】CD
【解析】因为BC=PB=PC,则三角形△PBC为等边三角形,
又D是BC的中点,PD=4 3,所以BC=PB=PC=8,
所以AC=4,
在△ACD中,AC=CD=4,∠ACD=60°,则三角形△ACD为等边三角形,
对于A:因为平面PBC⊥平面ABC,
且PD⊥BC,平面PBC∩平面ABC=BC,PD⊂面PBC,
所以PD⊥平面ABC,
1 1 3
则V = ×4 3× ×4×4× ×2=32,A错误;
P-ABC 3 2 2
对于B:因为PD⊥平面ABC,所以∠PAD为PA与底面ABC所成的角,
PD 4 3 π
则tan∠PAD= = = 3,所以∠PAD= ,B错误;
AD 4 3
对于C:PA= PD2+DA2= 4 3
24
2+42=8,C正确;
对于D:设三棱锥P-ACD的外接球半径为R,△ACD的外接圆半径为r,
4 4 8 4
则2r= = = ,所以r= ,
sin60° 3 3 3
2
PD
则R2=r2+
2
2 4
=
3
2
+2 3
52
2= ,
3
208
则外接球表面积为4πR2= π,D正确.
3
故选:CD.
36 (2024·高三·河北保定·开学考试)已知fx+1 是奇函数,fx 的图象关于直线x=-1对称,则下
列结论正确的为 ( )
A. fx 是周期为4的周期函数 B. fx-5 为偶函数
C. fx 的图象关于点-3,0 对称 D. f5 =0
【答案】BCD
【解析】由题知fx+1 为奇函数,所以有fx+1 +f-x+1 =0,
所以fx 关于1,0 对称,即有f-x +f2+x =0①,
因为fx 的图象关于直线x=-1对称,
所以f-x =f-2+x ②,
将②带入①可得f-2+x +f2+x =0,
将x换为2+x带入上式有:fx +fx+4 =0③,
再将x换为x+4带入上式有:fx+4 +fx+8 =0④,
④·③可得:fx =fx+8 ,
所以fx 是周期为8的函数,
同时,由③知fx+4 =-fx ,故选项A错误;
关于选项B,由A知fx 关于x=-1对称且周期为8,
所以fx-5 =f-x+3 =f-x-5 ,
所以fx-5 为偶函数,故选项B正确;
关于C,fx-3 =f-x+1 =-fx+1 =-f-x-3 ,
所以fx 的图象关于点-3,0 对称,故选项C正确;
因为fx+1 +f-x+1 =0,取x=0可得f1 =0,
所以f5 =f-3 =f1 =0,故选项D正确.
故选:BCD.
37 (2024·高三·山西晋城·开学考试)设函数fx 的定义域为R,且满足fx+2 +fx =0,f-x +
fx =0,当x∈0,1 时,fx =xlnx,则 ( )A. fx
25
是周期为4的函数
B. f2024 =0
C. fx 的取值范围为 - 2 , 2
e e
D. efx =1在区间 0, 2023
2
内恰有1011个实数解
【答案】ABD
【解析】因为fx+2 +fx =0,所以fx+4 +fx+2 =0,
所以fx+4 =fx ,故fx 是周期为4的函数,故A正确.
故f2024 =f4×506 =f(0),
而f-x +fx =0,故fx 为R上的奇函数,故f0 =0,
故f2024 =0,故B正确.
当x∈0,1 时,fx =xlnx,则f x =1+lnx,
1
当x∈0,
e
时,f x
1
<0;当x∈ ,1
e
时,f x >0,
故fx 1 在0,
e
1 上为减函数,在 ,1
e
上为增函数,
而x→0时,fx
1
→0,f
e
1
=- ,f1
e
=0,
故fx 在0,1 上的值域为 - 1 ,0
e
,
而fx+2 +fx =0,即fx+2 =f-x ,故fx 的图象关于x=1对称,
故fx 在1,2 的值域为 - 1 ,0
e
,而f2 +f0 =0,故f2 =0,
故fx 在0,2 的值域为 - 1 ,0
e
,
根据fx 为奇函数可得fx 在-2,2 的值域为 - 1 , 1
e e
,
故fx 在R上的值域为 - 1 , 1
e e
,故C错误.
令gx = fx ,故gx+2 = fx+2 = -fx = fx ,
故 fx 为周期函数且周期为2.
当x∈0,1 时,fx =xlnx =-xlnx,
1 1 1
此时0≤-xlnx≤ ,当且仅当x= 时,-xlnx= 即 fx
e e e
1
= ,
e
故当x∈1,2 时,x-1∈0,1 ,
故 fx = f2-x =(2-x)ln(2-x) =-(2-x)ln(2-x),
此时0≤-2-x ln2-x
1
≤ ,
e
1
当且仅当x=2- 时,-2-x
e
ln2-x
1
= 即 fx
e
1
= ,
e
因 f0 = f2 =0,故在0,2 上,fx
1 1 1
= 有且只有2个不同的实数解 ,2- ,
e e e
且这两个实数解在0,2 内,
故在0,1010 上共有1010个不同的实数解,且它们在0,1010 内,
3 考虑0,
2
上 fx 1 1 3 = 的解的个数,因为 ∈0,
e e 2
1 3 ,2- ∉0,
e 2
,
结合 fx 的周期可得 fx 1 2023 = 在1010,
e 2
上有且只有两个不同的实数解,故 efx
26
=1在 0, 2023
2
上共有1011个不同的实数解,故D正确.
故选:ABD.
38 (2024·高三·山西晋城·开学考试)已知函数fx
x-1
=
ex+k
,其导函数为f x
x
,且f1 =1,记
gx =xfx ,则下列说法正确的是 ( )
A. f x >0恒成立
B.函数gx 的极小值为0
C.若函数y=gx -m在其定义域内有两个不同的零点,则实数m的取值范围是0,1
D.对任意的x 1 ,x 2 ∈2,+∞ x+x ,都有f 1 2 2 ≤ fx 1 +fx 2 2
【答案】CD
【解析】由函数fx
x-1
=
ex+k
,因为f1
x
=1,可得k=1,所以fx
x-1
=
ex+1
,
x
对于A中,由f x
x2-x+1
=
ex-1
,因为f -2
x2
7e-2-1
= <0,,
4
所以f x >0不恒成立,所以A不正确;
对于B中,由gx =xfx =x-1 ex+1,x≠0,可得g x =xex,x≠0,
其中g0 无意义,所以gx 的极小值一定不为0,所以B错误;
对于C中,由g x =xex,x≠0,
当x<0时,可得g x <0;当x>0时,可得g x >0,
所以函数gx 在(-∞,0)上单调递减,在在(0,+∞)上单调递增,
且当x→-∞时,gx →1,当x→0时,gx →0,当x→∞时,gx →+∞,
函数gx 的图象,如图所示,
结合图象得,当00,x>2,
x2
设hx =f x
x2-x+1
=
ex-1
,x>2,可得h x
x2
ex(x-1)x+2
=
+2
>0,
x3
所以h x >0,hx 单调递增,即f x 单调递增,
所以fx 为单调递增函数,且f x 单调递增函数,且f2
e2+1
= ,
2
所以函数fx 的图像,如图所示,函数图象为凸函数,
x+x 所以f 1 2
2
≤ fx 1 +fx 2 ,当且仅当x=x 时,等号成立,所以D正确.
2 1 2
故选:CD
39 (2024·高三·山西·阶段练习)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠DAB
=60°,侧面PAD为正三角形,且平面PAD⊥平面ABCD,则 ( )A.AD⊥PB
B.在棱PB上存在点M,使得AM⊥平面PBC
C.平面PAD与平面PBC的交线平行于平面ABCD
15
D.C到平面PBD的距离为
5
【答案】AC
【解析】对A,如图所示,取AD中点H,连接PH,BH,
因为底面ABCD是菱形,∠DAB=60°,则△ABD为三角形,又因为侧面PAD为正三角形,
则BA=BD,PA=PD,则AD⊥PH,AD⊥BH,
又PH∩BH=H,PH,BH⊂平面PBH,所以AD⊥平面PBH,
因为PB⊂平面PBH,所以AD⊥PB,故A正确;
对B,假设在棱PB上存在点M,使得AM⊥平面PBC,因为PB⊂平面PBC,则AM⊥PB,
因为PA=AB,所以M为PB的中点,
连接HM,因为AD⊥平面PBH,HM⊂平面PBH,则HM⊥AD,
所以∠HAM为锐角,AM与AD不垂直,因为AD⎳BC,
则AM与BC不垂直,因为BC⊂平面PBC,这与AM⊥平面PBC矛盾,
所以不存在这样的点M,使得AM⊥平面PBC,故B错误;
对C,因为底面ABCD为菱形,所以AD⎳BC,又BC⊂平面PBC,AD⊄平面PBC,
所以AD⎳平面PBC.设平面PAD与平面PBC的交线为l,
因为AD⊂平面PAD,AD⎳平面PBC,平面PAD∩平面PBC=l,所以AD⎳l.
又因为l⊄平面ABCD,AD⊂平面ABCD,所以l⎳平面ABCD,故C正确;
因为平面PAD⊥平面ABCD,PH⊥AD,平面PAD∩平面ABCD=AD,PH⊂平面ABCD,
所以PH⊥平面ABCD,所以PH为三棱锥P-BCD的高,
因为△ABD和△PAD为等边三角形,则BD=2,BH=PH= 3,
因为PH⊥平面ABCD,BH⊂平面ABCD,则PH⊥BH,则PB= 6,
1 6
所以S = × 6× 22-
△PBD 2 2
27
2 15
= ,
2
设C到平面PBD的距离为d,
1 1 1 15 2 15
则由V =V 得 × ×2× 3× 3= × ×d,解得d= ,故D错误.
P-BCD C-PBD 3 2 3 2 5
故选:AC.40 (2024·高三·山西·阶段练习)已知定义域为R的函数fx
28
的导函数为f x ,若函数f4x+1 和f
x+2 均为偶函数,且f 2 =-1,f1 =1,则 ( )
2023
A. f i
i=1
2024
=-1 B. f i
i=1
2023
=0 C. fi
i=1
2024
=2023 D. fi
i=1
=0
【答案】AB
【解析】因为f4x+1 为偶函数,则f4x+1 =f-4x+1 ,
即fx+1 =f-x+1 ,可知fx 关于x=1对称,
又因为f x+2 为偶函数,则f x+2 =f -x+2 ,可知f x 关于x=2对称,
且fx+1 =f-x+1 ,则f x+1 =-f -x+1 ,即f x =-f -x+2 ,
可得f x 关于点1,0 对称,且f x =-f x+2 ,
则f x =-f x+2 =- -f x+4 =f x+4 ,可知4为f x 的周期,
由f x =-f -x+2 ,可得f 1 =-f 1 ,即f 1 =0,
则f 1 =-f 3 =0,f 2 =-f 4 =-1,
即f 1 +f 2 +f 3 +f 4 =0,
2023
所以 f i
i=1
=f 1 +f 2 +f 3
2024
=-1, f i
i=1
=0,故AB正确;
因为f x =f x+4 ,则fx +c=fx+4 +c,即fx =fx+4 ,
可知4为fx 的周期,
又因为f x+2 =f -x+2 ,则fx+2 =-f-x+2 +2c,
即fx+2 +f-x+2 =2c,可知fx 关于点2,c 对称,
但没有充分条件求f2 ,故无法求CD选项的值,故CD错误;
故选:AB.
x2 y2
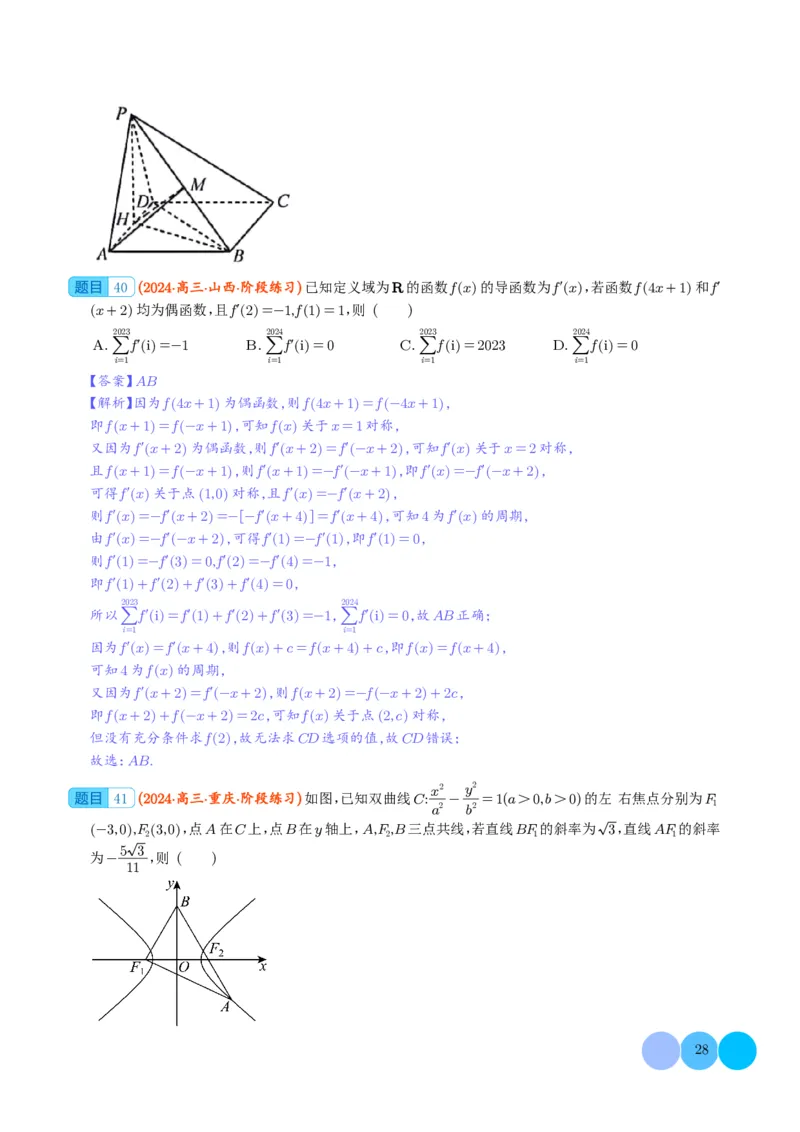
41 (2024·高三·重庆·阶段练习)如图,已知双曲线C: - =1(a>0,b>0)的左、右焦点分别为F
a2 b2 1
-3,0 ,F 23,0 ,点A在C上,点B在y轴上,A,F,B三点共线,若直线BF的斜率为 3,直线AF的斜率 2 1 1
5 3
为- ,则 ( )
113
A.C的渐近线方程为y=±2x B.C的离心率为
2
C. AB
29
=16 D.△ABF的面积为16 3 1
【答案】BC
π
【解析】依题意,直线BF 1 的斜率为 3,所以∠BF 1 F 2 = 3 ,又BF 1 =BF 2 ,所以△BFF 为等边三角形,故 1 2
BF 1 =BF 2 =F 1 F 2
π
=2c=6,∠BFF= . 2 1 3
5 3 5 3 11
在△AFF 中,tan∠FFA= >0,∠FFA为锐角,∴sin∠FFA= ,cos∠FFA=
1 2 2 1 11 2 1 2 1 14 2 1 14
2π
所以sinA=sin +∠FFA
3 2 1
3 3
= ,根据正弦定理可得
14
F 1 F 2 = AF 1 sinA = AF 2 sin∠FFA
1 2
sin∠FFA ,解得AF 1
2 1
=14,AF 2 =10,
所以2a=4,即a=2,b= c2-a2= 5,
5 c 3
所以C的渐近线方程为y=± x,C的离心率为 = ,AB 2 a 2 =BF 2 +AF 2 =16,
1
△ABF 1 的面积为 2 F 1 F 2 BF 2
π 1
sin 3 + 2 F 1 F 2 AF 2
π 1
sin 3 = 2 F 1 F 2 BA
π 1 π
sin = ×6×16×sin =24 3 3 2 3
故选:BC.
三、填空题
42 (2024·浙江·模拟预测)已知平面向量a、b、c、e,满足a⊥b,a
=2b
,c=a+b,e =1,若a
2
-6a
⋅
e
+8=0,则c
⋅e
-
1
c
2的最大值是
.
3
3 10-7
【答案】
6
【解析】因为a
2
-6a
⋅e
+8=0,即a
2
-6a
⋅e
+9e
2
=1,可得a
-3e
=1,
设e=1,0
,a=x,y
,则a-3e=x-3,y ,则x-3 2+y2=1,
设 x=3+cosθ ,则a =3+cosθ,sinθ
y=sinθ
,
因为a⊥b,a
=2b
sinθ 3+cosθ
,则b=- ,
2 2
sinθ 3+cosθ
或b= ,-
2 2
,
sinθ 3 cosθ
因为c=a+b,则c=3+cosθ- , +sinθ+
2 2 2
或c=
sinθ 3 cosθ
3+cosθ+ ,- +sinθ-
2 2 2
,
令c=m,n ,则m-3
3
2+n-
2
2 5
= 或m-3
4
3
2+n+
2
2 5
= ,
4
根据对称性,可只考虑m-3
3
2+n-
2
2 5
= ,
4
由c ⋅e - 1 c 2 =m- 1 m2+n2
3 3
1 3 =- m-
3 2
2 +n2
3 + ,
4
3
记点A3,
2
3
、B ,0
2
、Pm,n ,则AB
3
= 3-
2
2 3
+
2
2 3 2
= ,PA
2
=1,
所以,PB
=PA+AB
≥ PA
-AB
3 2- 5
= ,
2
当且仅当点M为线段AB与圆x-3
3
2+y-
2
2 5
= 的交点时,等号成立,
4
所以,c ⋅e - 1 c 2 =- 1 m- 3
3 3 2
2 +n2
3 1 + =- PB
4 3
3 1 3 2- 5 2+ ≤- ×
4 3 2
2 3 +
43 10-7
= .
6
3 10-7
故答案为: .
6
43 (2024·高三·山东菏泽·开学考试)已知cosα+β
30
1 α-β α+β
=- ,cosα+cosβ=1,则cos cos =
3 2 2
sinα+β
,
= .
sinα+sinβ
1 2
【答案】 /0.5
2 3
【解析】由cosα+β
1 α+β 1 α+β 1
=- 得2cos2 -1=- ,则cos2 = ,
3 2 3 2 3
因为cosx+y =cosxcosy-sinxsiny,cosx-y =cosxcosy+sinxsiny,
所以cosx+y +cosx-y =2cosxcosy,
α+β α-β
令x+y=α,x-y=β,则x= ,y= ,
2 2
α-β α+β
所以cosα+cosβ=2cos cos =1,
2 2
α-β α+β 1
则cos cos = ,
2 2 2
α-β 3 α+β
所以cos = cos ,
2 2 2
因为sinx+y =sinxcosy+cosxsiny,sinx-y =sinxcosy-cosxsiny,,
所以sinx+y +sinx-y =2sinxcosy,
α+β α-β
令x+y=α,x-y=β,则x= ,y= ,
2 2
α+β α-β
所以sinα+sinβ=2sin cos ,
2 2
又因为sinα+β
α+β α+β
=2sin cos ,
2 2
sinα+β
α+β α+β α+β
2sin cos cos 2 2 2 2
= = = .
sinα+sinβ α+β α-β α-β 3
2sin cos cos
2 2 2
1 2
故答案为: ; .
2 3
44 某同学在学习和探索三角形相关知识时,发现了一个有趣的性质:将锐角三角形三条边所对的外接
圆的三条圆弧(劣弧)沿着三角形的边进行翻折,则三条圆弧交于该三角形内部一点,且此交点为该三角形
的垂心(即三角形三条高线的交点).如图,已知锐角△ABC外接圆的半径为2,且三条圆弧沿△ABC三边
翻折后交于点P.若AB=3,则sin∠PAC= ;若AC:AB:BC=6:5:4,则PA+PB+PC的值为
.7 23
【答案】 /5.75
4 4
【解析】设外接圆半径为R,则R=2,
AB 3
由正弦定理,可知 = =2R=4,
sin∠ACB sin∠ACB
3 7
即sin∠ACB= ,由于∠ACB是锐角,故cos∠ACB= ,
4 4
π
又由题意可知P为三角形ABC的垂心,即AP⊥BC,故∠PAC= -∠ACB,
2
7
所以sin∠PAC=cos∠ACB= ;
4
设∠CAB=θ,∠CBA=α,∠ACB=β,
π π π
则∠PAC= -β,∠PBA= -θ,∠PAB= -α,
2 2 2
由于AC:AB:BC=6:5:4,不妨假设AC=6,AB=5,BC=4,
62+52-42 3 42+52-62 1 42+62-52 9
由余弦定理知cosθ= = ,cosα= = ,cosβ= = ,
2×6×5 4 2×4×5 8 2×4×6 16
π π
设AD,CE,BF为三角形的三条高,由于∠ECB+∠EBC= ,∠PCD+∠CPD= ,
2 2
故∠EBC=∠CPD ,
则得∠APC=π-∠CPD=π-∠EBC=π-∠ABC,
PC
所以
sin π -β
2
31
PA
=
sin π -θ
2
AC AC
= = =2R=4,
sin∠APC sin∠ABC
PB
同理可得
sin π -α
2
AB AB
= = =2R=4,
sin∠APB sin∠ACB
所以PA+PB+PC=4cosθ+cosα+cosβ
3 1 9
=4 + +
4 8 16
23
= ,
4
7 23
故答案为: ;
4 4
45 (2024·高三·上海宝山·期中)如图,画一个正三角形,不画第三边;接着画正方形,对这个正方形,不
画第四边,接着画正五边形;对这个正五边形不画第五边,接着画正六边形;⋯⋯,这样无限画下去,形成一
条无穷伸展的等边折线.设第n条线段与第n+1条线段所夹的角为θ n n∈N*,θ n ∈0,π ,则θ = 2022
.
【答案】174.46°
【解析】第一条线段与第二条线段所夹的角θ=60°,由此类推,θ =90° ,θ =90°,
1 2 3
θ =108°,θ =108°,θ =108°,θ =120°,θ =120°,θ =120°,θ =120°,⋯⋯
4 5 6 7 8 9 9
观察规律,三角形会有1个相等的角,并且角的度数恰好是其内角的度数,
正方形有2个90°,正五边形有3个108°,正六边形有4个120°,⋯⋯
180° n-2
∴n多边形有n-2个
n
又观察图形得:正三角形画2条线段,正方形画2条线段,正五边形画3条线段,正六边形画4条线段,⋯⋯,正n边形画n-2条线段;
∴画到正n多边形时,画线段的条数为m=2+2+3+4+⋯+n-2
32
nn-3
=2+
,
2
当n=65时,m=2017;当n=66时,m=2081
180°×63
∴第2022条线段应在正65边形中,∴θ = ≈174.46°
2022 65
故答案为:174.46°.
46 (2024·全国·模拟预测)已知圆锥SO的母线SA=5,侧面积为15π,则圆锥SO的内切球半径为
;若正四面体A-BCD 能在圆锥SO内任意转动,则正四面体A-BCD 的最大棱长为 .
1 1 1 1 1 1 1 1
3
【答案】 6
2
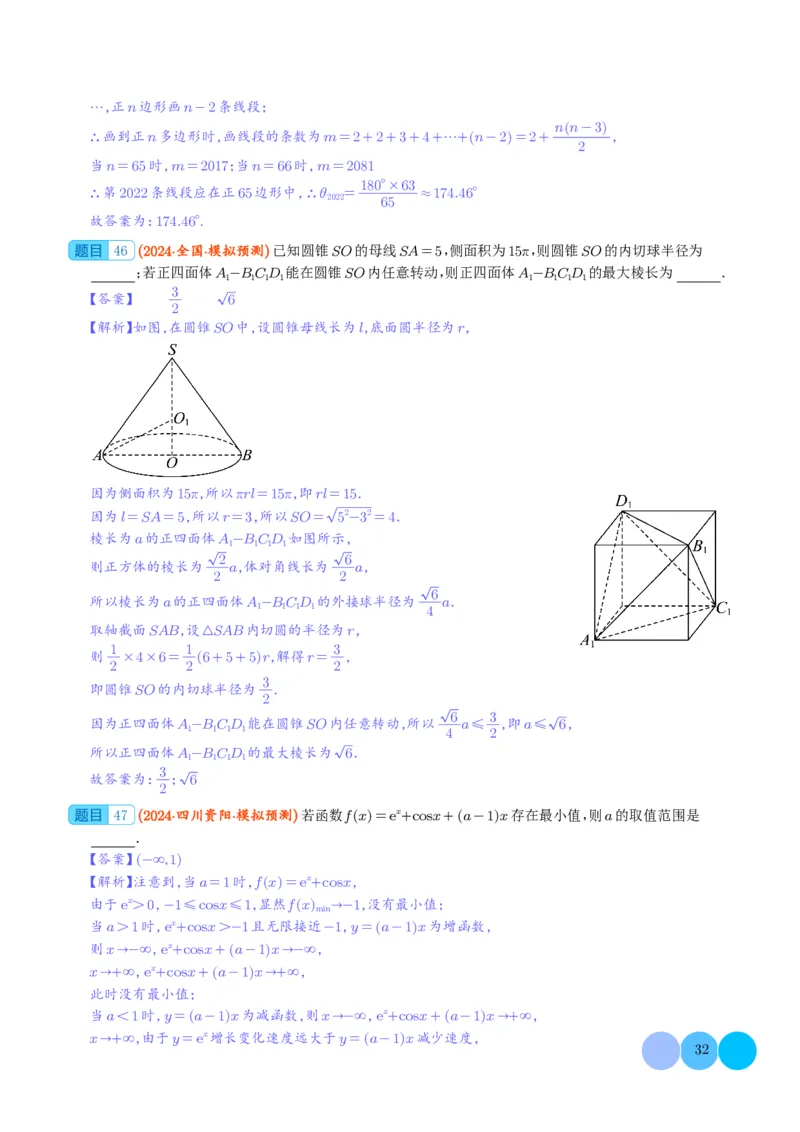
【解析】如图,在圆锥SO中,设圆锥母线长为l,底面圆半径为r,
因为侧面积为15π,所以πrl=15π,即rl=15.
因为l=SA=5,所以r=3,所以SO= 52-32=4.
棱长为a的正四面体A-BCD 如图所示,
1 1 1 1
2 6
则正方体的棱长为 a,体对角线长为 a,
2 2
6
所以棱长为a的正四面体A-BCD 的外接球半径为 a.
1 1 1 1 4
取轴截面SAB,设△SAB内切圆的半径为r,
1 1
则 ×4×6= 6+5+5
2 2
3
r,解得r= ,
2
3
即圆锥SO的内切球半径为 .
2
6 3
因为正四面体A-BCD 能在圆锥SO内任意转动,所以 a≤ ,即a≤ 6,
1 1 1 1 4 2
所以正四面体A-BCD 的最大棱长为 6.
1 1 1 1
3
故答案为: ; 6
2
47 (2024·四川资阳·模拟预测)若函数fx =ex+cosx+a-1 x存在最小值,则a的取值范围是
.
【答案】-∞,1
【解析】注意到,当a=1时,fx =ex+cosx,
由于ex>0,-1≤cosx≤1,显然fx →-1,没有最小值;
min
当a>1时,ex+cosx>-1且无限接近-1,y=a-1 x为增函数,
则x→-∞,ex+cosx+a-1 x→-∞,
x→+∞,ex+cosx+a-1 x→+∞,
此时没有最小值;
当a<1时,y=a-1 x为减函数,则x→-∞,ex+cosx+a-1 x→+∞,
x→+∞,由于y=ex增长变化速度远大于y=a-1 x减少速度,此时ex+cosx+a-1
33
x→+∞,由于函数定义域为R,函数连续不断,所以fx =ex+cosx+a-1 x存在
最小值.
故答案为:-∞,1
48 (2024·高三·山东青岛·期中)已知四边形ABCD,Fn∈N*
n
为边BC边上一点,连接AF 交BD于
n
E n∈N* n ,点E n 满足21+a n
E n F n -E n C=a n+1 -2
E B,其中a n n
是首项为1的正项数列,BC=λ ⋅ n
BF,则λ
n n
的前n项T= .
n
【答案】2n+3-4n-8
【解析】因为21+a n
E n F n -E n C=a n+1 -2
E B, n
所以E n C=21+a n
E n F n +2-a n+1
E B, n
因为B,F,C三点共线,所以2(1+a )+(2-a )=1,
n n n+1
所以a +3=2(a +3),
n+1 n
因为a+3=4,所以a +3
1 n
是以4为首项,2为公比的等比数列,
所以a +3=4×2n-1=2n+1,所以a =2n+1-3,
n n
因为BC=λ ⋅BF,所以E C-E B=λ ⋅(E F -E B),
n n n n n n n n
所以E C=λ ⋅E F +(1-λ )E B,
n n n n n n
因为E n C=21+a n
E n F n +2-a n+1
E B, n
λ =2(1+a )
所以 n n
1-λ =2-a
n n+1
因为a =2n+1-3,所以λ =2(1+2n+1-3)=2n+2-4,
n n
8(1-2n)
所以T=23+24+⋅⋅⋅+2n+2-4n= -4n=2n+3-4n-8,
n 1-2
故答案为:2n+3-4n-8
49 (2024·高三·江苏苏州·阶段练习)过抛物线y2=6x的焦点F的直线交抛物线于A,B两点,C在抛物
线的准线上,则∠ACB的最大值为 ;若△ACB为等边三角形,则其边长为 .
【答案】 90° 18
3
【解析】抛物线y2=6x的准线为:x=- ,
2
3
令点A,B到直线x=- 的距离分别为d ,d ,
2 A B
3
弦AB中点M到直线x=- 的距离为d,
2
d +d |AF|+|BF| 1
由抛物线定义知,d= A B = = |AB|,
2 2 2
因此,以AB为直径的圆与准线相切于点N,
3
即直线x=- 上除点N外,其余各点都在以AB为直径的圆外,
2
由圆的性质知,当点C与点N重合时,∠ACB是直角,
当点C与点N不重合时,∠ACB是锐角,
所以∠ACB的最大值是90°;
3
若△ABC为正三角形,F ,0
2
3
,设直线AB:x=ky+ ,
2点A(x,y),B(x ,y ),弦AB中点M(x ,y ),
1 1 2 2 0 0
x=ky+ 3
由 2 消去x并整理得:y2-6ky-9=0,
y2=6x
则y 1 +y 2 =6k,y 1 y 2 =-9,x 1 +x 2 =ky 1 +y 2
34
+3=6k2+3,
y+y x+x 3
其中y = 1 2 =3k,x = 1 2 =3k2+ ,
0 2 0 2 2
AB =x+x +p=6k2+6, 1 2
3
显然,k≠0,直线CM:y-3k=-kx-3k2-
2
,
3 3
且准线为x=- ,得点C- ,6k+3k3
2 2
,
由CM
3
= AB
2
,得3k2+3 2+3k+3k3
3
2= 6k2+6
4
2,
解得k2=2,则AB =18,
所以正三角形边长为18.
故答案为:90°;18.
50 (2024·高三·江苏镇江·开学考试)如果函数fx 在区间a,b 上为增函数,则记为f(x)a,b ,函数
fx 在区间a,b 上为减函数,则记为f(x)
a,b
4 .已知x+
x
m,3 ,则实数m的最小值为 ;函数
fx =2x3-3ax2+12x+1,且f(x)
1,2
,f(x)2,3 ,则实数a= .
【答案】 2 3
【解析】对于第一空:由题意gx
4
=x+ 在m,3
x
上单调递增,首先有00时,gx
4
=x+ 的单调递增区间为2,+∞
x
,
所以2≤m<3,即实数m的最小值为2;
对于第二空:fx 显然可导,f x =6x2-6ax+12,
由题意fx 在1,2 上单调递减,在2,3 上单调递增,即x=2是函数fx 的极值点,
所以f 2 =64-2a+2 =0,解得a=3,经检验a=3满足题意.
故答案为:2,3.
51 (2024·高三·江苏镇江·开学考试)已知AB是圆锥PO的底面直径,C是底面圆周上的一点,PC=
AB=2,AC= 3,则二面角A-PB-C的余弦值为 .
5 1
【答案】 / 5
5 5
【解析】如图,以点O为坐标原点,OB,OP分别为y,z轴,过点O垂直AB为x轴,建立空间直角坐标系,
点C为底面圆周上一点,则∠ACB=90o,又AC= 3,AB=PC=2,
∴BC=1,PO= 3,
∴A0,-1,0 ,B0,1,0 ,P0,0, 3
3 1
,C , ,0
2 2
,
PB=0,1,- 3
3 1
,PC= , ,- 3
2 2
,
设平面CPB的一个法向量为m=x,y,z
m⋅PB=0
,则 ,
m⋅PC=0
y- 3z=0
即 3x+ 1y- 3z=0 ,令z=1,得x=1,y= 3,∴m=1, 3,1
2 2
,
又易知平面APB的一个法向量为n=1,0,0
35
,
m⋅n
∴cosm,n=
m n
1 1 5
= = = ,
1+3+1×1 5 5
5
如图,锐二面角A-PB-C的余弦值为 .
5
5
故答案为: .
5
n+lnn=3
52 (2024·高三·江苏南京·开学考试)已知实数m,n满足
1+lnm=e2-lnm
,则mn= .
【答案】e2
【解析】由1+lnm=e2-lnm可得1+lnm=e3-1+lnm ,
由n+lnn=3得n=e3-n,
记gx =x-e3-x,因为y=et,在R上单调递增,t=3-x在R上单调递减,
根据复合函数性质知y=e3-x在R上在单调递减,所以gx
=x-e3-x在R上单调递增,
由n=e3-n可得gn =n-e3-n=0,又g1+lnm =1+lnm-e3-1+lnm =0,
因此1+lnm=n,由n+lnn=3可得lnn=3-n,
所以lnn+lnm=3-n +n-1 =2,可得mn=e2,
故答案为:e2
53 (2024·高三·江苏无锡·开学考试)“曼哈顿距离”是人脸识别中的一种重要测距方式,其定义如下:设
Ax 1 ,y 1 ,Bx 2 ,y 2 ,则A,B两点间的曼哈顿距离dA,B = x 1 -x 2+ y 1 -y 2 .已知M4,6 ,点N在圆C:x2
+y2+6x+4y=0上运动,若点P满足dM,P =2,则PN 的最大值为 .
【答案】 149+ 13/ 13+ 149
【解析】由题意得,圆C:(x+3)2+(y+2)2=13,圆心C-3,-2 ,半径r= 13,
设点Px 0 ,y 0 ,则 x 0 -4+ y 0 -6 =2,
故点P的轨迹为如下所示的正方形,其中A4,8 ,B6,6 ,
则AC = 4+3 2+8+2 2= 149,BC = 6+3 2+6+2 2= 145,
则PN ≤AC +r= 149+ 13,即PN 的最大值为 149+ 13.
故答案为: 149+ 13.
54 (2024·高三·河北保定·开学考试)对于函数fx
1
,若在定义域内存在实数x,满足f
x
=-fx ,则
称fx 为“局部反比例对称函数”.若fx
1 1
= x3- mx2+m2-3
3 2
x+5的导函数f x 是定义在区间
2,+∞ 上的“局部反比例对称函数”,则实数m的最大值与最小值之差为 .
9
【答案】
4
【解析】f x =x2-mx+m2-3 ,因为fx
36
的导函数f x 是定义在区间2,+∞ 上的“局部反比例对称函数”,
所以存在x∈2,+∞
1
,f
x
=-f x
1 1
,即 -m +m2-3
x2 x
=-x2+mx-m2-3 ,
1
所以 +x
x
2 1
-m +x
x
+2m2-8=0,在x∈2,+∞ 上有解,
令t=hx
1
= x +x,设x 1 >x 2 ≥2,则hx 1 -hx 2
1 1
= x +x 1 - x -x 2 =x 1 -x 2
1 2
xx -1
1 2 xx
1 2
,
因为x 1 >x 2 ≥2,所以hx 1 -hx 2 >0,所以hx 在2,+∞ 上单调递增,
所以x∈2,+∞ 时,t∈ 5 ,+∞
2
,
设gt =t2-mt+2m2-8,所以t∈ 5 ,+∞
2
时gt =t2-mt+2m2-8=0有解,
m 5 当 ≤ 即m≤5时,gt
2 2
=t2-mt+2m2-8在t∈ 5 ,+∞
2
5 上单调递增,所以g
2
5 =
2
2 5 - m+
2
1 7
2m2-8≤0,解得- ≤m≤ ;
2 4
m 5 当 > 即m>5时,gt
2 2
=t2-mt+2m2-8在t∈ 5 , m
2 2
上单调递减,在t∈ m ,+∞
2
上单调递增,
m
所以g
2
m
=
2
2 1 4 14 4 14
- m2+2m2-8≤0,解得- 5,所以不存在符合条件的m.
2 7 7
1 7 7 1
综上可得- ≤m≤ ,所以实数m的最大值与最小值之差为 --
2 4 4 2
9
= .
4
9
故答案为:
4
55 (2024·高三·河北保定·开学考试)已知平面向量a,b是非零向量,2a-b
⊥2a+b
,向量b在向
a⋅b
量a方向上的投影向量为-a,则 = ;向量a,b的夹角为 .
|a|2
2π
【答案】 -1
3
【解析】因为2a-b
⊥2a+b ,
所以2a-b ⋅2a+b =4a 2 - b 2 =0,即 b =2a ,
a⋅b
又向量b在向量a方向上的投影向量为
a
a
⋅
a
a
=
⋅2a
cosa,b
a
a
⋅
a
=2cosa,b
⋅a=-a,
所以cosa,b
1
=- ,又a,b
2
∈0,π ,
所以a,b
2π
= ,
3
a⋅b
所以
a
a
=
2
⋅2a
cosa,b
a
1
=2×-
2 2
=-1.
2π
故答案为:-1; .
3
56 (2024·全国·高考真题)如图在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值
范围是 .【答案】( 6- 2, 6+ 2)
【解析】如图所示,延长BA,CD交于E,平移AD,当A与D重合与E点时,AB最长,在△BCE中,∠B=
BC BE 2 BE
∠C=75°,∠E=30°,BC=2,由正弦定理可得 = ,即 = ,解得BE= 6+
sin∠E sin∠C sin30o sin75o
2,平移AD ,当D与C重合时,AB最短,此时与AB交于F,在△BCF中,∠B=∠BFC=75°,∠FCB=
BF BC BF 2
30°,由正弦定理知, = ,即 = ,解得BF= 6- 2,所以AB的取值范
sin∠FCB sin∠BFC sin30o sin75o
围为( 6- 2, 6+ 2).
考点:正余弦定理;数形结合思想
57 (2024·高三·山西·阶段练习)锐角△ABC的内角A的对边为a,若△ABC的面积是a2,则
sinA
的最小值是 .
cosBcosC
【答案】8
1
【解析】作AD⊥BC于D,则 a⋅AD=a2,所以AD=2a.
2
设BD=xa,则DC=a-xa,因为△ABC是锐角三角形,
00,
00
,gx
x
=x2+2x+1-2λ,λ∈R,若关于
x的方程f gx =λ有6个解,则λ的取值范围为 .
1 2
【答案】 ,
2 e
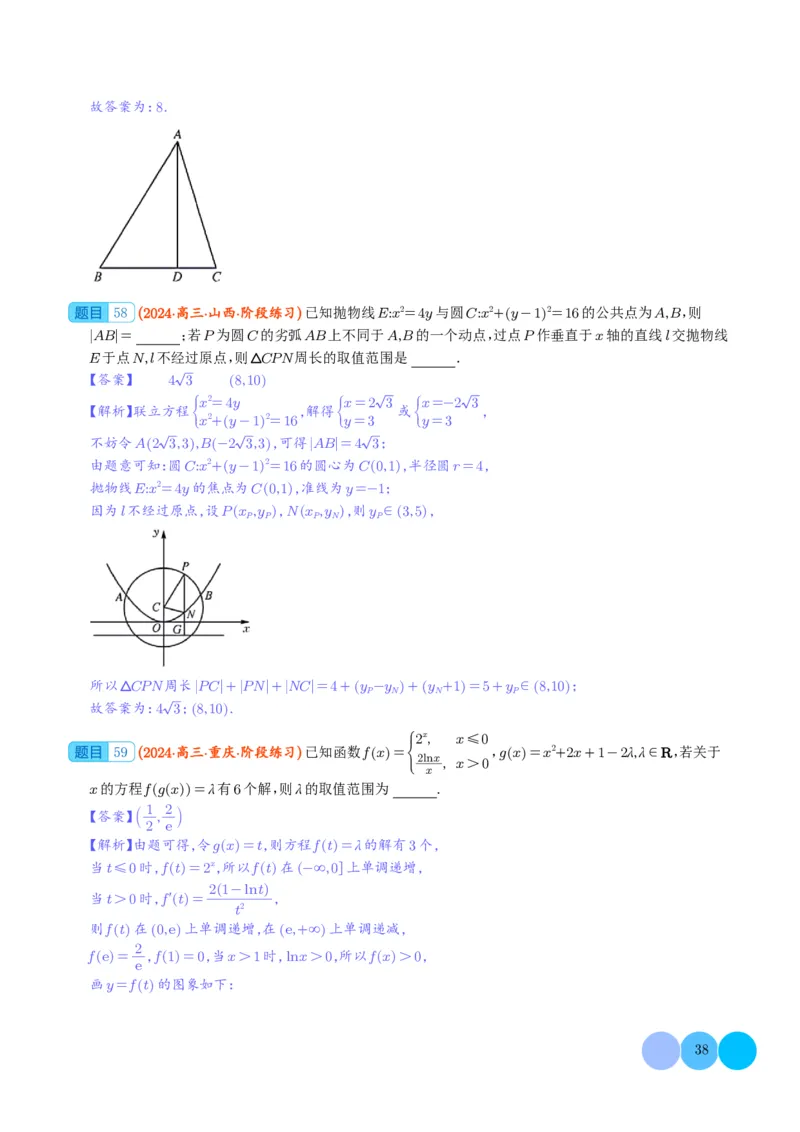
【解析】由题可得,令gx =t,则方程ft =λ的解有3个,
当t≤0时,ft =2x,所以ft 在-∞,0 上单调递增,
当t>0时,f t
21-lnt
=
,
t2
则ft 在0,e 上单调递增,在e,+∞ 上单调递减,
fe
2
= ,f1
e
=0,当x>1时,lnx>0,所以fx >0,
画y=ft 的图象如下:2
由图象可得0<λ< ,
e
且方程ft
39
=λ的三个解分别为t,t ,t ,不妨设t-2λ,即2λ+log λ>0,
2 2
令hλ =2λ+log 2 λ,λ>0 ,所以h λ
1
=2+ >0, λln2
所以hλ 在0,+∞ 上单调递增,
1
又h
2
1
=0,所以2λ+log λ>0的解集为 ,+∞
2 2
,
1 2
综上,λ的取值范围为 ,
2 e
。
1 2
故答案为: ,
2 e