THUSSAT2023年3月诊断性测试数学答案_2024年2月_01每日更新_16号_2023届THUSSAT中学生标准学术能力高三下学期3月月诊断性测试_THUSSAT2023年3月诊断性测试数学试卷及答案

中学生标准学术能力诊断性测试 2023 年 3 月测试
数学参考答案
一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一
项是符合题目要求的．
1 2 3 4 5 6 7 8
A D B D C C A B
二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项
符合题目要求．全部选对的得5分，部分选对但不全的得2分，有错选的得0分．
9 10 11 12
AC BCD ABD AD
三、填空题：本题共4小题，每小题5分，共20分．
13．
第1页 共7页
5 − 2 14． ( −  , − 1 )
15．108 16．1
四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．
17．（10分）
（1） ( 3 n + 9 )  ( n + 1 ) 2 a
n + 1
= ( n + 2 ) 3 a
n

3 ( n
( n
+
+
3 )
2
a
2 )
n + 1 =
( n
( n
+
+
2
1
) a
2 )
n
即
( n
(
+
n
3
+
)
2
a
)
n2 + 1 =
1
3

( n
( n
+
+
2
1
) a
2 )
n ····································································· 2分
又
( 1
(
+
1 +
2
1
)
)
a
2
1 =
1
3
  (n+2)a  
，所以数列 n 是首项为

(n+1)2

1
3
，公比为
1
3
的等比数列
从而
( n
( n
+
+
2
1
) a
2 )
n =
 1
3
 n (n+1)2
，则a = ·················································· 5分
n (n+2)3n
（2） a
n
=
(
(
n
n
+
+
2
1
)
)

2
3 n
=
n
n
+
+
1
2

n
3
+
n
1

n
3
+
n
1
··························································· 6分
 S
n

2
3 1
+
3
3 2
+ +
n
3
+
n
1
2 3 n+1 1 2 3 n+1
设T = + + + ，则 T = + + +
n 31 32 3n 3 n 32 33 3n+1两式相减得：
1 1 n−1
1−   
2 2 1 1 n+1 2 9 3  n+1
T = + + + − = + −
3 n 31 32 3n 3n+1 3 1 3n+1
1−
3
第2页 共7页
=
2
3
+
1
6

1 −
 1
3
 n − 1 
−
n
3
+
n +
1
1
=
5
6
−
2
2
n
 3
+
n
5
+ 1
················································ 9分
5 2n+5 5 2n+5
从而T = − ，故S  − ····················································· 10分
n 4 43n n 4 43n
18．（12分）
（1）由已知及正弦定理得：2sinBcosA−sinA=2sinC
又在  A B C 中， s i n C = s i n ( A + B ) = s i n A c o s B + c o s A s i n B ························· 2分
 2 s i n B c o s A − s i n A = 2 s i n A c o s B + 2 c o s A s i n B
即2sinAcosB=−sinA
又 s i n A  0 ，  c o s B = −
1
2
········································································ 4分
又 0 B    ， B =
2
3

 ，即角 B 的大小为
2
3

·············································· 5分
（2） S
 A B C
=
1
2
a c s i n B =
4
3
a c ····································································· 6分
B D 是  A B C 的角平分线，而 S
 A B C
= S
 A B D
+ S
 B C D
3 1 1
 ac= ABBDsin60+ BDBCsin60
4 2 2
3 3
即 ac= BD(a+c)，
4 4
 B D =
a
a
+
c
c
················································· 8分
B D = 2
，ac=2(a+c)
a + c  2 a c ，ac4 ac ，即ac16 ··············································· 10分
当且仅当 a = c = 4
1 3
时取等号，则S = acsinB 16=4 3
ABC 2 4
即ABC的面积的最小值为4 3 ······························································· 12分19．（12分）
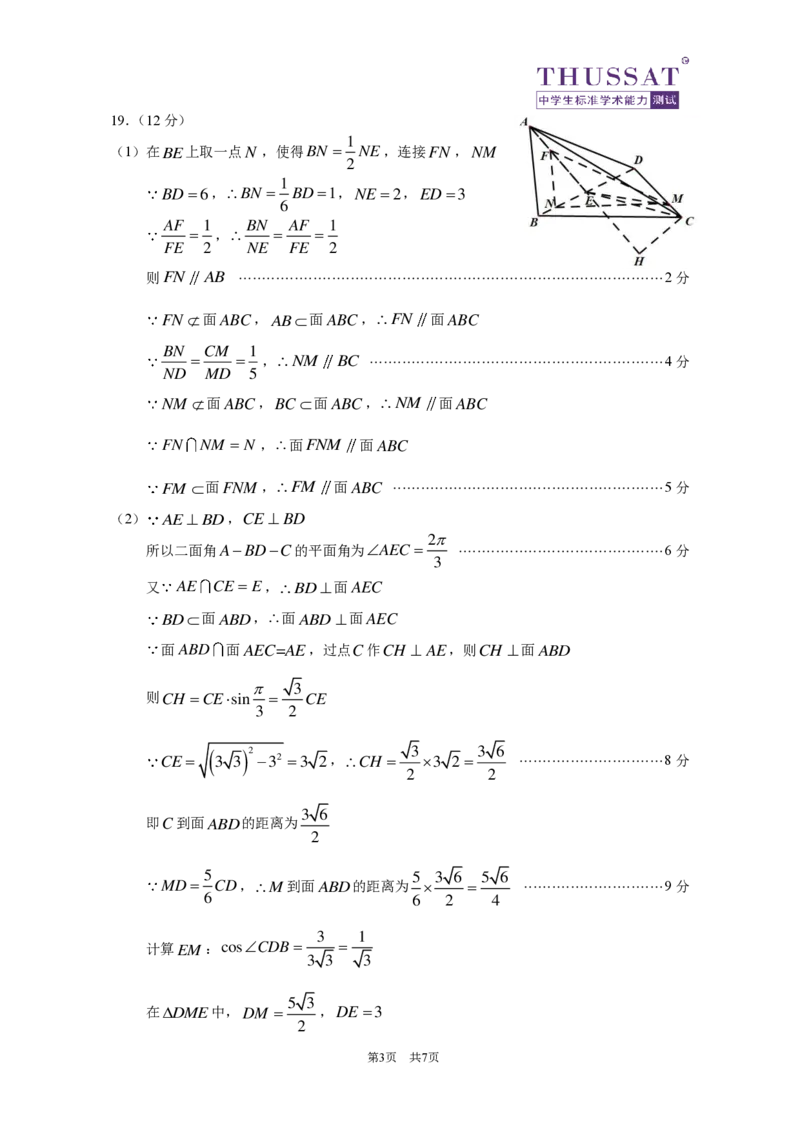
（1）在
第3页 共7页
B E 上取一点 N ，使得 B N =
1
2
N E ，连接 F N ， N M
B D = 6 ，  B N =
1
6
B D = 1 ， N E = 2 ， E D = 3
AF 1 BN AF 1
= ， = =
FE 2 NE FE 2
则FN AB ··························································································· 2分
F N  面 A B C ， A B  面 A B C ，  F N 面 A B C
B
N
N
D
=
C
M
M
D
=
1
5
，  N M B C ······························································· 4分
N M  面 A B C ， B C  面 A B C ，  N M 面 A B C
F N N M = N ，  面 F N M 面 A B C
F M  面 F N M ，  F M 面 A B C ·························································· 5分
（2） A E ⊥ B D ，CE ⊥BD
2
所以二面角A−BD−C的平面角为AEC = ············································ 6分
3
又 AE CE = E，BD⊥面 A E C
B D  面 A B D ，  面 A B D ⊥ 面 A E C
面ABD 面 A E C = A E ，过点C作 C H ⊥ A E ，则 C H ⊥ 面 A B D
则 C H C E s i n
3 2
3
C E

=  =
C E =
(
3 3
) 2
− 3 2 = 3 2
3 3 6
，CH = 3 2 = ······························· 8分
2 2
即 C 到面 A B D 的距离为
3
2
6
M D =
5
6
C D
5 3 6 5 6
，M到面ABD的距离为  = ······························ 9分
6 2 4
计算EM： c o s  C D B =
3
3
3
=
1
3
5 3
在DME中，DM = ，DE =3
2第4页 共7页

1
3
=
 5
2
3
2


2
5
+
2
3
3
2 −

E
3
M 2
 E M =
5
2
1
··············································· 11分
 E M 与面 A B D 所成角的正弦值为
5
45
2
6
1
=
5
3
3
4
4
········································· 12分
（其他方法酌情给分）
20．（12分）
（1）列联表如下：
感兴趣 不感兴趣 合计
男生 12 4 16
女生 9 5 14
合计 21 9 30
·········································· 2分
K 2 =
3 0 
1
(
6
1

2
1

4
5

−
2
4
1 

9
9 ) 2
 0 . 4 0 8 2  2 . 0 7 2
所以没有85%的把握认为学生对“数学建模”选修课的兴趣度与性别有关 ············ 5分
（2）由题意可知X 的取值可能为0，1，2，3
C3 5
则P(X =0)= 5 = ··········································································· 6分
C3 42
9
P ( X = 1 ) =
C 14
C
C
39
25
=
1
2
0
1
············································································ 7分
C2C1 5
P(X =2)= 4 5 = ············································································ 8分
C3 14
9
C3 1
P(X =3)= 4 = ················································································ 9分
C3 21
9
故X 的分布列为
X 0 1 2 3
5 10 5 1
P
42 21 14 21第5页 共7页
E ( X ) = 0 
5
4 2
+ 1 
1
2
0
1
+ 2 
1
5
4
+ 3 
1
2 1
=
4
3
··············································· 12分
21．（12分）
（1）因为双曲线C以2x 5y =0为渐近线
设双曲线方程为
(
2 x 5 y
) (
2 x 5 y
)
 + − = ，即 4 x 2 5 y 2  − = ························· 1分
F ( 0 , 3 ) ， 0    ，即：
y 2
5
x 2
4
1
 
−
−
−
=
 
− − =9，
5 4
9
2 0
9

 − = ，即 2 0  = − ····················································· 3分
所以双曲线 C 的方程为：
y
4
2
−
x
5
2
= 1 ··························································· 4分
（2）设直线 l : y = k x + 3 ， P ( x
1
, y
1
) ， Q ( x
2
, y
2
)
 5
y
y
=
2 −
k x
4
+
x 2
3
= 2 0
 5 ( k x + 3 ) 2 − 4 x 2 = 2 0
化简得： ( 5 k 2 − 4 ) x 2 + 3 0 k x + 2 5 = 0 ··························································· 6分
此方程的两根为 x
1
, x
2
 30k
x +x =−
  1 2 5k2 −4
，则
25

x x =
 1 2 5k2 −4
900k2 100 9k2 − ( 5k2 −4 )
 PQ = 1+k2  − =10 1+k2 
( 5k2 −4 )2 5k2 −4 ( 5k2 −4 )2
4k2 +4 20 ( k2 +1 )
=10 1+k2  =
·············································· 8分
( 5k2 −4 )2 5k2 −4
 15k −12 
PQ中点M 坐标为 − ,  ······················································· 9分
 5k2 −4 5k2 −4
 P Q
12 1 15k 
中垂线方程为：y+ =−

x+

5k2 −4 k 5k2 −4
−27  −27 
令x=0，y= ，T  0, 
5k2 −4  5k2 −4则
第6页 共7页
T F = 3 +
5 k
2
2
7
− 4
=
1 5
5
k
k
2
2
+
−
1
4
5
···························································· 11分

T
P
F
Q
=
1
2
5
5
0
5
k
k(
k
2
2
k
2
+
−
2
−
1
4
+
4
5
1 )
=
3
4 ········································································ 12分
22．（12分）
（1）令
f  ( x ) =
e x
(
−
e x
x
)
e
2
x
=
1 −
e x
x
 0
··································································· 1分
 x  1 ，即函数 f ( x ) 的单调递增区间为 ( −  , 1 ) ，函数 f ( x ) 的单调递减区间为 ( 1 , +  )
·········································· 2分
当 x = 1
2
时， f  1
2
 =
1
2
e
12
=
2
1
e
，  切点为  1
2
,
2
1
e

1
又 f 1 = 2 = 1 ，
 
2 1 2 e
e2
 f ( x ) 在 x = 1
2
处的切线方程为：
y −
2
1
e
=
2
1
e

x −
1
2

 y =
2
1
e
x +
4
1
e
················································· 4分
（2）
e x
e
2
x
 k  ( l n x + 1 ) ，
x
e x
 k 
l n x
e x
+ 1
= k 
l n
e
x
ln
+
x + 1
1
x(1,+) ，  l n
e
x
ln
+
x + 1
1  0 ，  k 
l n
e
x
x ex
+
ln x + 1
1
··············································· 6分
由（1）可知 f ( x ) =
x
e x
在 (1,+) 上单调递减，下证： x  l n x + 1
即证：x−lnx1在x(1,+)
恒成立
令 g ( x ) = x − l n x ，则 g  ( x ) = 1 −
1
x
=
x −
x
1
 0
g(x)
在
(1,+)
上单调递增
又
x1，g(x)g(1)=1−ln1=1
························································ 9分
xlnx+11第7页 共7页
f ( x ) 在 x  ( 1 , +  ) 上单调递减
 f ( x )  f ( l n x + 1 ) ，即 x
e x
 l n
e
x
ln
+
x + 1
1 ， 
l n
e
x
x ex
+
ln x + 1
1
 1 ································· 11分
 k  1 ·································································································· 12分