文档内容
更多全科试卷,请关注公众号:高中试卷君
2024 届高三二轮复习“8+3+3”小题强化训练(12)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.小李同学参加了高三以来进行的 6次数学测试,6次成绩依次为: 90分、100分、120分、115
分、130分、125分.则这组成绩数据的上四分位数为( )
A. 120 B. 122.5 C. 125 D. 130
【答案】C
【解析】将6次成绩分数从小到大排列依次为: ,
由于 ,故这组成绩数据的上四分位数为第5个数125,
故选:C
2.已知集合 , ,则 ( )
A. B. C. D.
【答案】B
【解析】由 ,得 ,解得 ,
所以 ,
因为 ,
所以以 ,
所以 ,
所以 .
故选:B.
3.已知数列 满足 ,若 ,则 ( )
A. 2 B. C. D.
【答案】D
【解析】因为 , ,
所以 , , ,
所以数列 的周期为3.
所以 .
故选:D.
4.设 是两条异面直线,下列命题中正确 是的( )
A. 过 且与 平行的平面有且只有一个
B. 过 且与 垂直的平面有且只有一个
C. 过空间一点 与 均相交的直线有且只有一条
D. 过空间一点 与 均平行的平面有且只有一个
【答案】A更多全科试卷,请关注公众号:高中试卷君
【解析】
对于A,过 上一点 作 的平行直线 ,则 与 确定一平面 ,由 平面 ,
平面 ,所以 平面 ,故A正确;
对于B,设过 的平面为 ,若 平面 ,则 ,故若 与 不垂直,则不存在过 的平面
与 垂直,故B错误;
对于C,当点 与 确定一个平面 ,且与 平行时,如图,则过空间一点 与 均相交的直线不
存在,故C错误;
对于D,当点 与 中一条确定的平面与另一条直线平行时,满足条件的平面就不存在,故D错误.
故选:A.
5.2023 年11月30日,重庆市轨道交通新开通 6 个站点,包括5号线中段忠恕沱、红岩村、歇台子
3个站点和10号线南湖、万寿路、兰花路3个站点,为广大市民的出行提供了更多便利.某同学从中随
机选择4个站点实地考察周边情况,则在红岩村被选中的条件下,10号线不少于2个站点的概率为(
)
A. B. C. D.
【答案】B
【解析】在红岩村被选中的条件下,还需从其它5个站点中选择3个,共有 种选法,
其中10号线不少于2个站点的选法有 种,
故在红岩村被选中的条件下,10号线不少于2个站点的概率为 ,
故选:B
6.公元 年,唐代李淳风注《九章》时提到祖暅的“开立圆术”.祖暅在求球的体积时,使用一个
原理:“幂势既同,则积不容异”.“幂”是截面积,“势”是立体的高,意思是两个同高的立体,如
在等高处的截面积相等,则体积相等.更详细点说就是,介于两个平行平面之间的两个立体,被任一平
行于这两个平面的平面所截,如果两个截面的面积相等,则这两个立体的体积相等.上述原理在中国被
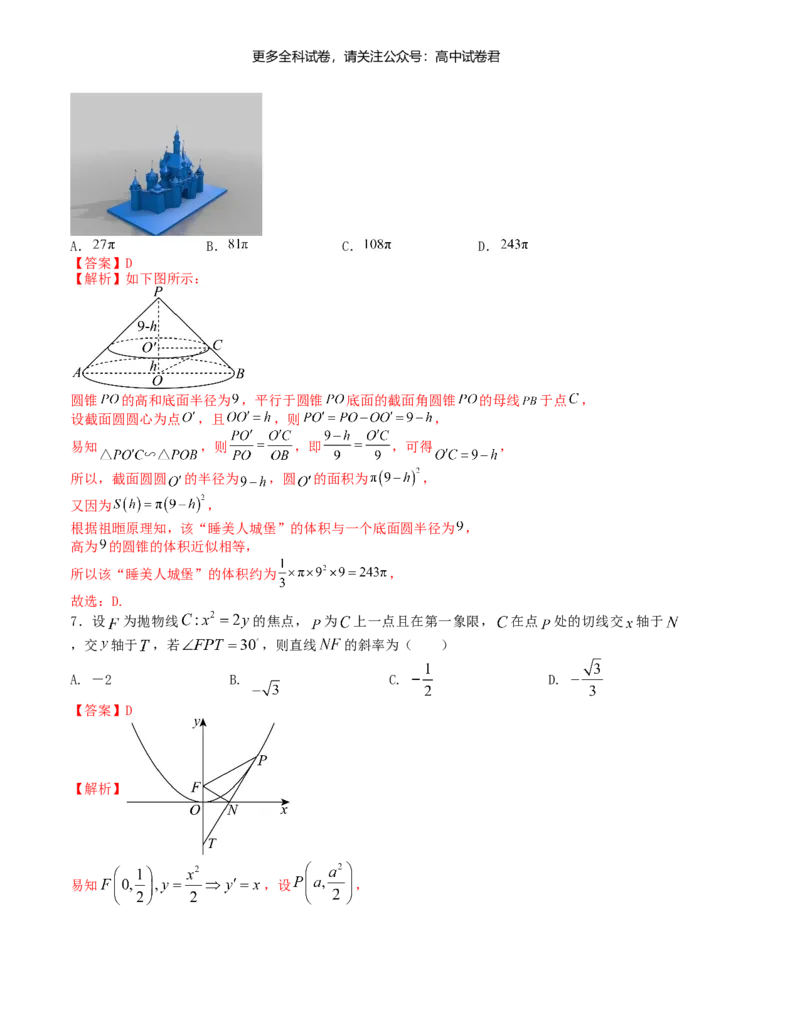
称为“祖暅原理”. 打印技术发展至今,已经能够满足少量个性化的打印需求,现在用 打印技术
打印了一个“睡美人城堡”.如图,其在高度为 的水平截面的面积 可以近似用函数
, 拟合,则该“睡美人城堡”的体积约为( )更多全科试卷,请关注公众号:高中试卷君
A. B. C. D.
【答案】D
【解析】如下图所示:
圆锥 的高和底面半径为 ,平行于圆锥 底面的截面角圆锥 的母线 于点 ,
设截面圆圆心为点 ,且 ,则 ,
易知 ,则 ,即 ,可得 ,
所以,截面圆圆 的半径为 ,圆 的面积为 ,
又因为 ,
根据祖暅原理知,该“睡美人城堡”的体积与一个底面圆半径为 ,
高为 的圆锥的体积近似相等,
所以该“睡美人城堡”的体积约为 ,
故选:D.
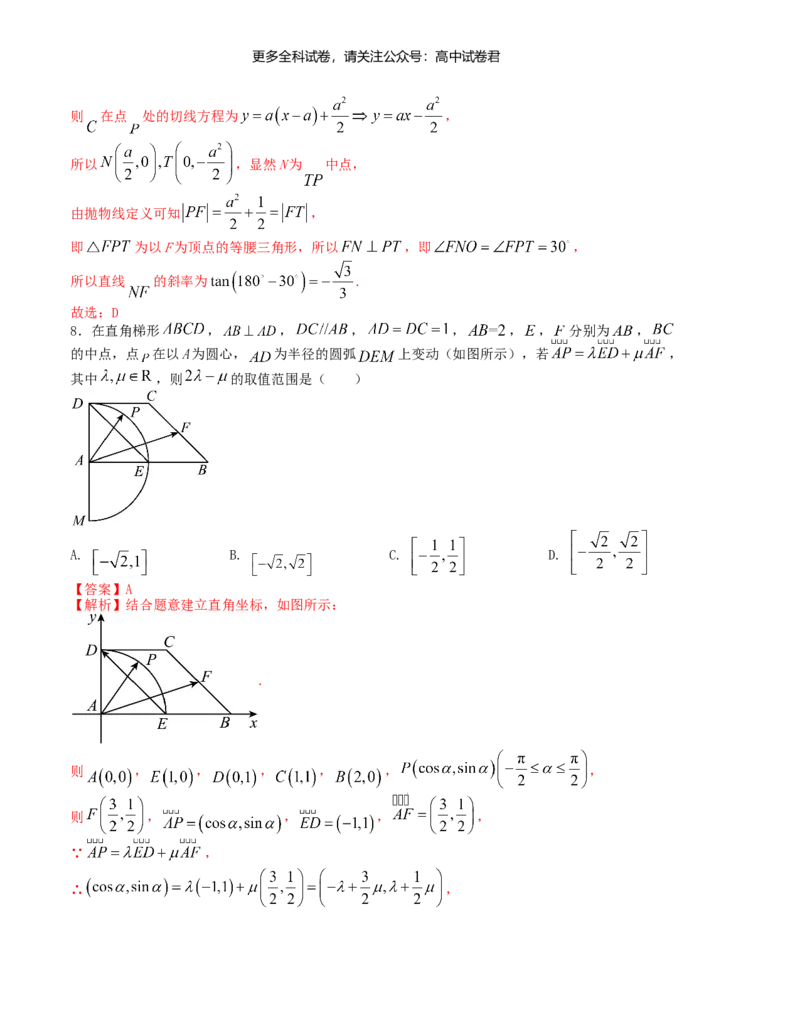
7.设 为抛物线 的焦点, 为 上一点且在第一象限, 在点 处的切线交 轴于
,交 轴于 ,若 ,则直线 的斜率为( )
A. -2 B. C. D.
【答案】D
【解析】
易知 ,设 ,更多全科试卷,请关注公众号:高中试卷君
则 在点 处的切线方程为 ,
所以 ,显然N为 中点,
由抛物线定义可知 ,
即 为以F为顶点的等腰三角形,所以 ,即 ,
所以直线 的斜率为 .
故选:D
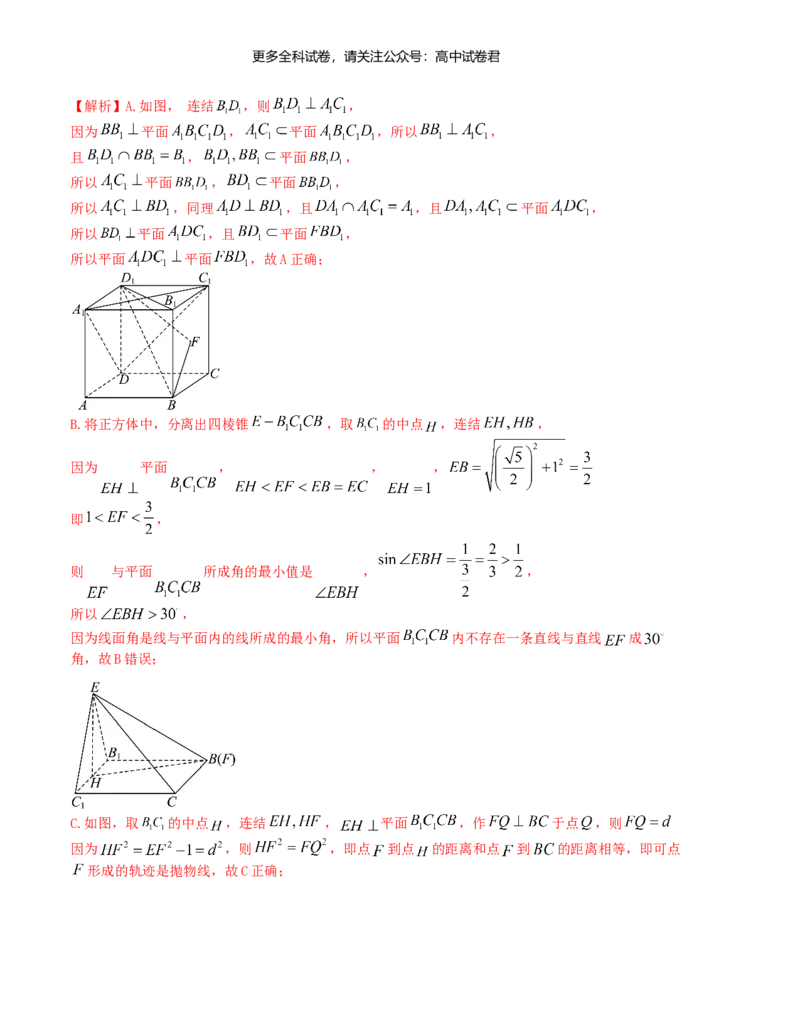
8.在直角梯形 , , , , , , 分别为 ,
的中点,点 在以A为圆心, 为半径的圆弧 上变动(如图所示),若 ,
其中 ,则 的取值范围是( )
A. B. C. D.
【答案】A
【解析】结合题意建立直角坐标,如图所示:
.
则 , , , , , ,
则 , , , ,
∵ ,
∴ ,更多全科试卷,请关注公众号:高中试卷君
∴ , ,
∴ , ,
∴ ,
∵ ,∴ ,∴ ,
∴ ,故 ,即 .
故选:A.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列函数中最小值为2的是( )
A. B.
C. D.
【答案】AB
【解析】由题意,
A项, ,故A正确;
B项,在 中, ,所以 ,当且仅当
时,等号成立,故B正确;
C项, , ,故 ,当且仅当 即
时等号成立,C错误;
D项, , ,只有当 时才有 ,当且仅当
即 时等号成立,故D错误.
故选:AB
10.已知点 在圆 上,点 , ,则( )
A. 存在点 ,使得 B.
C. 存在点 ,使得 D.
【答案】ABD更多全科试卷,请关注公众号:高中试卷君
【解析】圆 即 ,圆心 ,半径 ,又 ,
所以 ,因为点 在圆 上,所以 ,
所以存在点 ,使得 ,故A对.
因为 ,所以点 在圆外,又 ,点 在圆内,
所以当 与圆 相切时, 取最大值,
此时 ,所以 ,故B对.
对于D,设 ,若
,
又点 在圆 上, 一定成立,故D对,C错.
故选:ABD.
11.在正方体 中, , 为 的中点, 是正方形 内部一点(不
含边界),则下列说法正确的是( )
A. 平面 平面
B. 平面 内存在一条直线与直线 成 角
C. 若 到 边距离为 ,且 ,则点 的轨迹为抛物线的一部分
D. 以 的边 所在直线为旋转轴将 旋转一周,则在旋转过程中, 到平面 的
距离的取值范围是
【答案】ACD更多全科试卷,请关注公众号:高中试卷君
【解析】A.如图, 连结 ,则 ,
因为 平面 , 平面 ,所以 ,
且 , 平面 ,
所以 平面 , 平面 ,
所以 ,同理 ,且 ,且 平面 ,
所以 平面 ,且 平面 ,
所以平面 平面 ,故A正确;
B.将正方体中,分离出四棱锥 ,取 的中点 ,连结 ,
因为 平面 , , ,
即 ,
则 与平面 所成角的最小值是 , ,
所以 ,
因为线面角是线与平面内的线所成的最小角,所以平面 内不存在一条直线与直线 成
角,故B错误;
C.如图,取 的中点 ,连结 , 平面 ,作 于点 ,则
因为 ,则 ,即点 到点 的距离和点 到 的距离相等,即可点
形成的轨迹是抛物线,故C正确;更多全科试卷,请关注公众号:高中试卷君
D.连结 交 于点 ,取 的中点 ,连结 ,
则点 的运动轨迹是平面 内以 为圆心, 为半径的圆,
易知 ,由 ,知 , ,且 平面 ,
所以 平面 , 平面 ,
所以平面 平面 ,
,
如图, 与圆的交点分别为 ,
当点 位于点 时,点 到平面 的距离分别取得最大值和最小值,
且距离的最大值为 ,
距离的最小值为 ,
所以点 到平面 的距离的取值范围是 ,故D正确.
故选:ACD
三、填空题:本题共3小题,每小题5分,共15分.
12.已知双曲线 的一条渐近线为 ,则该双曲线的离心率为__________.
【答案】2更多全科试卷,请关注公众号:高中试卷君
【解析】由题意得 ,易知双曲线 ,即 的渐近线方程为
得
所以该双曲线的离心率
故答案为: .
13.已知函数 ,若 的最小值为 ,则
________.
【答案】
【解析】 , , 或
,
.
故答案为: .
14.已知函数 ( , )且 ),若 恒成立,则 的最小值为
______.
【答案】
【解析】函数 的定义域为 ,
当 时,可得 在 上单调递增, ,不合题意;
当 时, ,令 ,解得 ,
当 时, , 单调递减,
当 时, , 单调递增,
所以当 时, 有极小值,也是最小值,
又因为 且 ,所以 ,
则 ,得 ,所以 ,更多全科试卷,请关注公众号:高中试卷君
设 , ,令 ,得 ,
当 , ,
当 , ,
所以 在区间 单调递减, 单调递增,
所以 ,即 的最小值为 .
故答案为: .