文档内容
5.1 导数的概念及意义
【题组一 平均速率】
1.函数f(x)=x2在x 到x+Δx之间的平均变化率为k,在x-Δx到x 之间的平均变化率为k,则k,k 的
0 0 1 0 0 2 1 2
大小关系是( )
A.k<k B.k>k
1 2 1 2
C.k=k D.无法确定
1 2
【答案】D
【解析】∵k= =2x+Δx,k= =2x-Δx,
1 0 2 0
又Δx可正可负且不为零,∴k,k 的大小关系不确定.选D.
1 2
2.(2020·全国高二课时练习)若函数f(x)=-x2+10的图象上一点 及邻近一点
,则 =( )
A.3 B.-3
C.-3- D.- -3
【答案】D
【解析】 , .故选:D.
3.(2020·临海市白云高级中学高二月考)已知函数y=f(x)=x2+1,则在x=2,Δx=0.1时,Δy的值为(
)
A.0.40 B.0.41 C.0.43 D.0.44
【答案】B
【解析】 故选B.
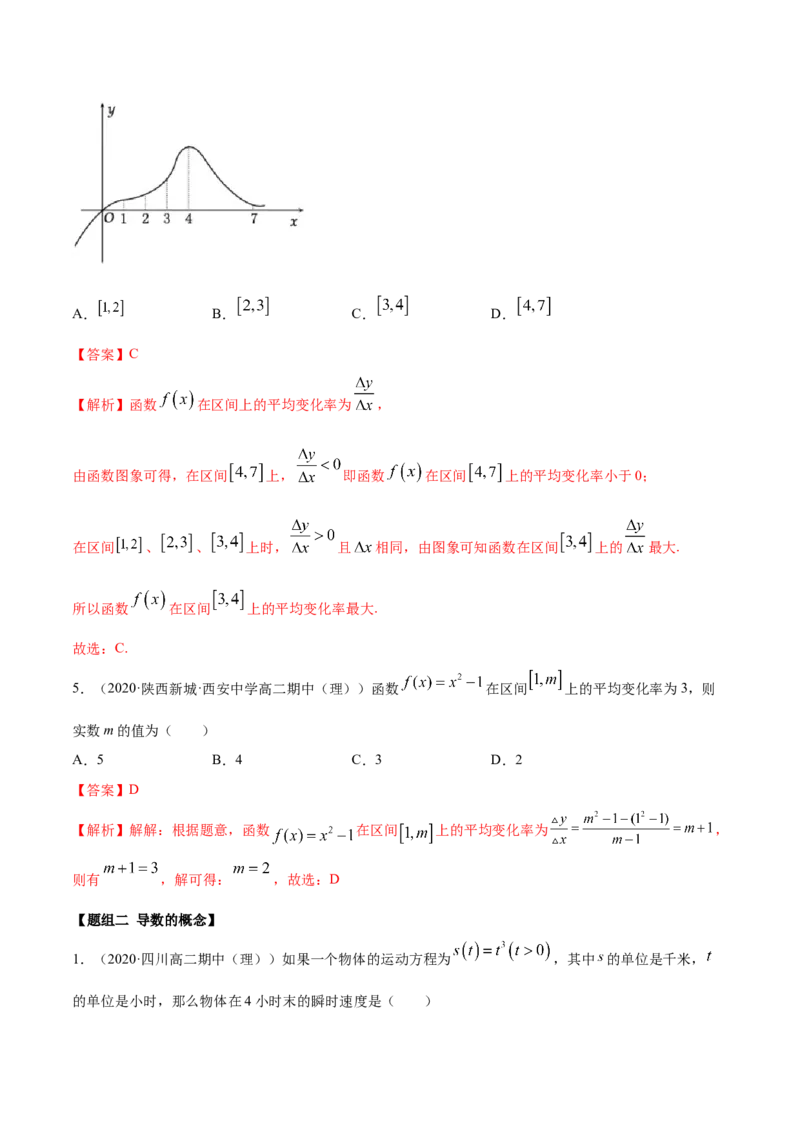
4.(2020·河南洛阳·高二期中(理))函数 的图象如下图,则函数 在下列区间上平均变化率
最大的是( )A. B. C. D.
【答案】C
【解析】函数 在区间上的平均变化率为 ,
由函数图象可得,在区间 上, 即函数 在区间 上的平均变化率小于0;
在区间 、 、 上时, 且 相同,由图象可知函数在区间 上的 最大.
所以函数 在区间 上的平均变化率最大.
故选:C.
5.(2020·陕西新城·西安中学高二期中(理))函数 在区间 上的平均变化率为3,则
实数m的值为( )
A.5 B.4 C.3 D.2
【答案】D
【解析】解解:根据题意,函数 在区间 上的平均变化率为 ,
则有 ,解可得: ,故选:D
【题组二 导数的概念】
1.(2020·四川高二期中(理))如果一个物体的运动方程为 ,其中 的单位是千米,
的单位是小时,那么物体在4小时末的瞬时速度是( )A.12千米/小时 B.24千米/小时 C.48千米/小时 D.64千米/小时
【答案】C
【解析】由 ,则当 , 故选:C.
2.(2020·广东宝安·高三开学考试)设函数 则 ( )
A. B. C. D.
【答案】B
【解析】 .故选:B.
3.(2020·全国高二单元测试)已知 ,则 ( )
A. B.1 C.3 D.9
【答案】D
【解析】 .故选:D.
4.(2020·伊美区第二中学高二期末(文))设 在 处可导,则 (
)
A. B. C. D.
【答案】A
【解析】因为 在 处可导,
所以,由导数的定义可得: .
故选:A5.(2020·陕西蓝田·高二期末(理))设函数f(x)在x=1处存在导数为2,则 =(
)
A.2 B.1 C. D.6
【答案】C
【解析】∵函数f(x)在x=1处存在导数,
∴ f′(1)= .故选C.
6.(2020·贵州威宁·高二期末(理))已知 是 的导函数,且 ,则
( )
A.4 B.8 C.-8 D.-2
【答案】C
【解析】因为 , , 故选:C
7.(2020·青海西宁·高二期末(文))若 ,则 ( )
A.e B. C.1 D.0
【答案】D
【解析】 , ,则 ,
∴ ,故选:D.
8.(2020·辽宁葫芦岛·高二期末)设函数 在 处可导,且 ,则 等于( )
A. B. C.1 D.-1
【答案】A
【解析】由题意知 ,
所以 ,故选:A.
9.(2020·宜城市第二高级中学高二期中)已知函数 可导,则 等于(
)
A. B.不存在
C. D.以上都不对
【答案】A
【解析】因为 ,所以 ,
所以 .故选:A
10.(2020·江苏广陵·扬州中学高二月考(文))已知某物体的运动方程是 ,则当 时的瞬
时速度是( )
A. B. C. D.
【答案】C【解析】当 时的瞬时速度是为 导函数在 的值,因为 ,所以 ,因此当
时的瞬时速度是 ,选C.
11.(2020·陕西咸阳·高二期末(理))设 是可导函数,且 ,则
( )
A.2 B.-1 C.1 D.-2
【答案】A
【解析】 .故选:A.
12.(2020·广东清远·高二期末)将原油精炼为汽油、柴油、塑胶等各种不同产品时,需要对原油进行冷
却和加热.如果第xh时,原油的温度(单位:℃)为y=f(x)=x2﹣7x+15(0≤x≤<8),则第4h时,原油温
度的瞬时变化率为( )
A.﹣1 B.1 C.3 D.5
【答案】B
【解析】根据题意,第4h时,原油温度的瞬时变化率为 ;
又 ,故可得 ,则 .故选: .
13.(2020·陕西省商丹高新学校高二期中(理))如图所示的是 的图象,则 与
的大小关系是( )
A. B.C. D.不能确定
【答案】B
【解析】由函数图像可知函数在A处的切点斜率比在B处的切线斜率要小,由导数的几何意义可知
成立
14.(2020·陕西咸阳·高二期末(文))已知 是可导函数,且 ,则
( )
A.2 B. C.1 D.
【答案】A
【解析】根据题意, ;故 ;故选: .
15.(2019·安徽马鞍山二中高二期中(理))有一机器人的运动方程为 (t是时间,s是位移),
则该机器人在时刻 时的瞬时速度为( )
A. B. C. D.
【答案】D
【解析】因为 ,所以 ,则 ,
所以机器人在时刻 时的瞬时速度为 ,故选D.
【题组三 导数的计算】
1.(2020·陕西省丹凤中学高三一模(理))点P在曲线 上移动,设点P处切线的倾斜角为
,则角 的范围是( )A. B. C. D.
【答案】D
【解析】由 ,则 ,
则 ,又 ,所以 ,故选:D.
2.(2020·广东汕尾·高二期末)已知曲线 ,P为曲线C上任意一点,设曲线C在点P处的
切线的倾斜角为α,则α的取值范围是( )
A. B. C. D.
【答案】D
【解析】由题意可知, ,
曲线C在点 处的切线斜率为 ,
当且仅当 ,即 ,即 时,等号成立,
∴ ,即 ,∴ .
故选:D.
3.(2020·江西省奉新县第一中学高三月考(理))曲线 在点 处的切线的
斜率为( )A. B.
C. D.
【答案】C
【解析】 ,故选C.
4.(2020·全国高三月考)已知函数 ,则在曲线 的所有切线中,斜
率的最大值为______.
【答案】
【解析】因为 ,所以 ,
因为当 时 取得最大值为 ,
所以根据导数的几何意义可知,曲线 的切线中斜率的最大值为 .
故答案为: .
5.(2019·广东湛江·高二期末(文))函数 在 处的切线的斜率为_________.
【答案】1
【解析】由 ,得 ,则 ,
所以 在 处的切线的斜率为1故答案为:1
6.(2020·河南高三月考(文))曲线 的一条切线的斜率为 ,则该切线的方程为
_______.
【答案】【解析】设切点坐标为 ,其中 ,
对函数 求导得 ,所以切线的斜率 ,
因为 ,解得 ,则 ,切点为 ,
则该切线的方程为 ,即所求切线方程为 .
故答案为: .