文档内容
5.3.2 第一课时 函数的极值
[A级 基础巩固]
1.已知函数f(x)=2x3+ax2+36x-24在x=2处有极值,则该函数的一个递增区间是( )
A.(2,3) B.(3,+∞)
C.(2,+∞) D.(-∞,3)
2.已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围是( )
A.(-1,2) B.(-3,6)
C.(-∞,-3)∪(6,+∞) D.(-∞,-1)∪(2,+∞)
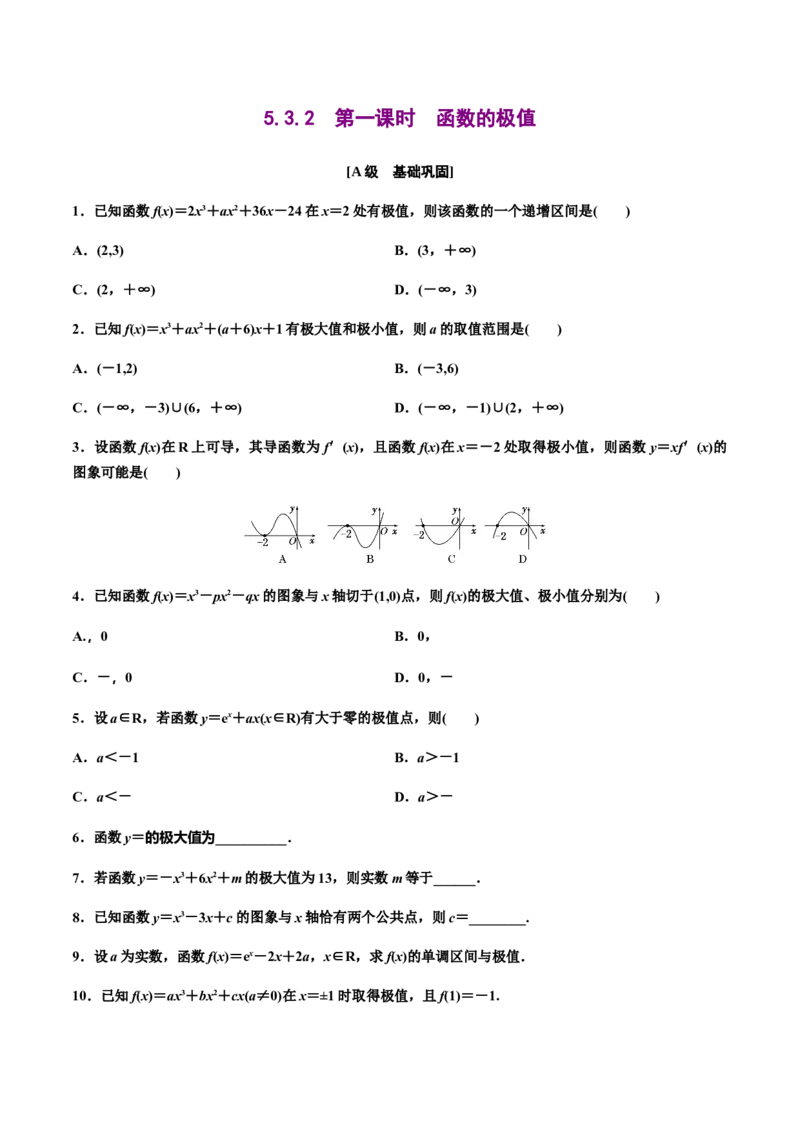
3.设函数f(x)在R上可导,其导函数为f′(x),且函数f(x)在x=-2处取得极小值,则函数y=xf′(x)的
图象可能是( )
4.已知函数f(x)=x3-px2-qx的图象与x轴切于(1,0)点,则f(x)的极大值、极小值分别为( )
A.,0 B.0,
C.-,0 D.0,-
5.设a∈R,若函数y=ex+ax(x∈R)有大于零的极值点,则( )
A.a<-1 B.a>-1
C.a<- D.a>-
6.函数y=的极大值为__________.
7.若函数y=-x3+6x2+m的极大值为13,则实数m等于______.
8.已知函数y=x3-3x+c的图象与x轴恰有两个公共点,则c=________.
9.设a为实数,函数f(x)=ex-2x+2a,x∈R,求f(x)的单调区间与极值.
10.已知f(x)=ax3+bx2+cx(a≠0)在x=±1时取得极值,且f(1)=-1.(1)试求常数a,b,c 的值;
(2)试判断x=±1时函数取得极小值还是极大值,并说明理由.
[B级 综合运用]
11.(多选)已知函数f(x)=ax3+bx2+cx,其导函数y=f′(x)的图象经过点(1,0),(2,0).如图,则下列说法中
正确的是( )
A.当x=时,函数f(x)取得极小值
B.f(x)有两个极值点
C.当x=2时函数取得极小值
D.当x=1时函数取得极大值
12.已知函数f(x)=ex(sin x-cos x),x∈(0,2 021π),则函数f(x)的极大值之和为( )
A. B.
C. D.
13.若函数f(x)=x3+x2-ax-4在区间(-1,1)上恰有一个极值点,则实数a的取值范围为______.
14.已知函数f(x)=ex(ax+b)-x2-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4.
(1)求a,b的值;
(2)讨论f(x)的单调性,并求f(x)的极大值.
[C级 拓展探究]
15.已知函数f(x)=(a∈R,a≠0).
(1)当a=-1时,求函数f(x)的极值;
(2)若函数F(x)=f(x)+1没有零点,求实数a的取值范围.