文档内容
111公式章 1 节 1课时同步练
5.3.2 函数的极值与导数
一、单选题
1.函数 有( )
A.极大值 ,极小值3 B.极大值6,极小值3
C.极大值6,极小值 D.极大值 ,极小值
【答案】C
【解析】根据题意, ,故当 时, ;
当 时, ;当 时, .故 在 处取得极大值
;在 处取得极小值 ,
故选C.
2.函数 的极值点所在的区间为( )
A. B. C. D.
【答案】A
【解析】∵ ,
∴ ,且函数 单调递增.
又 ,
∴函数 在区间 内存在唯一的零点,
即函数 的极值点在区间 内.
故选A.3.函数 ,则( )
A. 为函数 的极大值点 B. 为函数 的极小值点
C. 为函数 的极大值点 D. 为函数 的极小值点
【答案】A
【解析】 ,故当 时函数单调递增,
当 时,函数单调递减,故 为函数的极大值点.
故选A
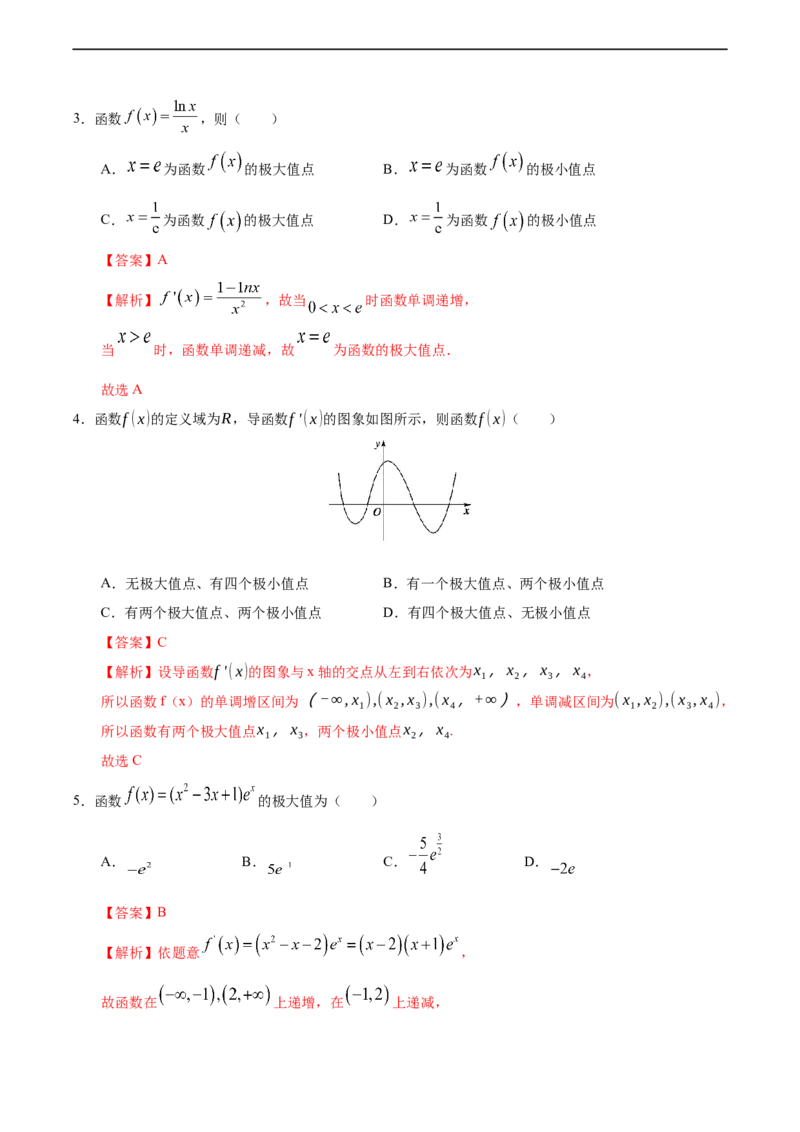
4.函数f (x)的定义域为R,导函数f '(x)的图象如图所示,则函数f (x)( )
A.无极大值点、有四个极小值点 B.有一个极大值点、两个极小值点
C.有两个极大值点、两个极小值点 D.有四个极大值点、无极小值点
【答案】C
【解析】设导函数f '(x)的图象与x轴的交点从左到右依次为x ,x ,x ,x ,
1 2 3 4
所以函数f(x)的单调增区间为(-∞,x ),(x ,x ),(x ,+∞),单调减区间为(x ,x ),(x ,x ),
1 2 3 4 1 2 3 4
所以函数有两个极大值点x ,x ,两个极小值点x ,x .
1 3 2 4
故选C
5.函数 的极大值为( )
A. B. C. D.
【答案】B
【解析】依题意 ,
故函数在 上递增,在 上递减,所以函数在 处取得极大值为 .
故选B.
6.函数 上的极小值点为( )
A.0 B. C. D.
【答案】C
【解析】y′=1﹣2sinx=0,得x 或x ,
故y=x+2cosx在区间[0, ]上是增函数,在区间[ , ]上是减函数,在[ ,π]是增函数.
∴x 是函数的极小值点,
故选C.
7.函数 的图像如图所示,则关于函数 的说法正确的是( )
A.函数 有3个极值点
B.函数 在区间 上是增加的
C.函数 在区间 上是增加的
D.当 时,函数 取得极大值
【答案】C
【解析】函数有两个极值点: 和 ,但 不是函数的极值点,所以A错误;
函数在 和 上单调递增,在 上单调递减,所以B错误,C正确;不是函数的极值点,所以D错误.
故选C.
8.已知函数 在 处取得极小值 ,则 的值分别为( )
A.-4,4 B.4,-4 C.4,4 D.-4,-4
【答案】A
【解析】 ,
,
因为函数 在 处取得极小值 ,
即 解得
故选
9.设函数 满足 , ,则 时, ( )
A.有极大值,无极小值 B.有极小值,无极大值
C.既有极大值又有极小值 D.既无极大值也无极小值
【答案】B
【解析】由 ,即 ,
结合 ,可知 ,
,
可知此函数仅有一个极值点,是极小值点,没有极大值.
故选B
10.若函数 仅在 处有极值,则 的取值范围为( )A. B. C. D.
【答案】A
【解析】由题意,
要保证函数 仅在x=0处有极值,必须满足 在x=0两侧异号,
所以要 恒成立,
由判别式有: ,∴
∴ ,
∴a的取值范围是
故选A.
11.若函数 在 内无极值,则实数 的取值范围是( )
A. B. C. D.
【答案】D
【解析】由函数的解析式可得: ,
函数 在 内无极值,则 在区间 内没有实数根,
当 时, 恒成立,函数 无极值,满足题意,
当 时,由 可得 ,故: ,解得: ,
综上可得:实数 的取值范围是 .
故选D.
12.已知函数 在 上有两个极值点,且 在 上单调递增,则实数 的取值范围是( )
A. B. C. D.
【答案】C
【解析】由题意,函数 ,
可得 ,
又由函数 在 上有两个极值点,
则 ,即 在 上有两解,
即 在在 上有不等于2的解,
令 ,则 ,
所以函数 在 为单调递增函数,
所以 且 ,
又由 在 上单调递增,则 在 上恒成立,
即 在 上恒成立,即 在 上恒成立,
即 在 上恒成立,
又由函数 在 为单调递增函数,所以 ,
综上所述,可得实数 的取值范围是 ,即 ,
故选C.
二、填空题13.函数 共有________个极值.
【答案】0
【解析】由题知 的导函数 ,
,
恒成立.
函数 在 上是单调递增函数,
函数没有极值.
故填 .
14.已知 是函数 的极值点,则实数 的值为______.
【答案】2
【解析】函数 ,
所以 ,
因为 是 的极值点,
所以 ,即
所以 .
故填2.
15.正项等差数列 中的 , 是函数 的极值点,则 ______.
【答案】4
【解析】因为 ,所以 ,
又 , 是函数 的极值点,所以 , 是方程 的两实根,因此 ,
因为数列 是正项等差数列,所以 ,解得 ,
因此 .
故填 .
16.已知 是函数 的一个极值点,则曲线 在点 处的切线斜率为
__________.
【答案】
【解析】由题意,函数 ,则 ,
又由 是函数 的一个极值点,
所以 ,解得 ,即 ,
所以 ,所以函数 在点 处切线的斜率为 .
故填
17.若函数 有唯一一个极值点,则实数a的取值范围是________.
【答案】
【解析】 ,定义域为 ,
令 ,令 ,可得 ,
令 ,
在 上只有一个极值点,
在 上只有一个根且不是重根.所以 ,解得 .
实数 的取值值范围是: ,
故填
18.已知函数 ,若 是函数 的唯一一个极值点,则实数 的取值范围为
_________
【答案】
【解析】由题可得
因为 是函数 的唯一一个极值点,
所以 是导函数 的唯一根
所以 在 上无变号零点.
设 ,则
当 时, , 在 上单调递减
当 时, , 在 上单调递增
所以 ,
结合 与 的图像可知,若 是函数 的唯一极值点,则
故实数 的取值范围为 .故填
三、解答题
19.已知函数 .
(1)求曲线 在点 处的切线的方程;
(2)求曲线 的极大值,极小值.
【解析】(1)∵ ,
∴ 在点 处的切线的斜率为 .
∴切线的方程为 .
(2)令 ,解得 或 .
当 变化时, , 的变化情况如下表:
极大值 极小值
由上表,知 , .
20.已知 为函数 的导函数,且 .
(1)求 的值;
(2)求 的单调区间与极值.
【解析】(1)解:(1)由 ,得 .因为 ,所以 ,解得 .
(2)因为 ,则 .
当 时, ,则函数 的单调递减区间为 ;
当 时, ,则函数 的单调递增区间为 .
故 在 处取得极小值,极小值为 ,无极大值.
21.已知函数 .
(1)当 时,求 的单调区间;
(2)是否存在实数a,使 的极大值为3;若存在,求出a的值,若不存在,请说明理由.
【解析】(1)当 时, ,所以 ,
令 ,得 或 ,
所以当 或 时, ;当 时, ,
所以 在 和 上单调递增,在 上单调递减;
(2)存在, ,理由如下:
,令 ,得 或 ,
因为 所以
所以当 时, 恒成立,所以 在R上单调递增,此时函数 不存在极值,所以
;
当 时, ,所以当 或 时, ;当 时, ,所以 在 和 上单调递增,在 上单调递减,
所以函数 在 时,取得极大值,所以 ,即 ,解得
,
所以存在, ,使 的极大值为3.
22.已知函数 .
(1)当a=2时,求曲线 在点 处的切线方程;
(2)设函数 ,讨论 的单调性并判断有无极值,有极值时求
出极值.
【解析】(1)由题意 ,
所以,当 时, , ,
所以 ,
因此,曲线 在点 处的切线方程是 ,
即 .
(2)因为 ,
所以 ,
,
令 ,
则 ,所以 在 上单调递增,
因为 ,
所以,当 时, ;当 时, .
①当 时, ,
当 时, , , 单调递增;
当 时, , , 单调递减;
当 时, , , 单调递增.
所以当 时 取到极大值,极大值是 ,
当 时 取到极小值,极小值是 .
②当 时, ,
当 时, , 单调递增;
所以 在 上单调递增, 无极大值也无极小值.
③当 时, ,
当 时, , , 单调递增;
当 时, , , 单调递减;
当 时, , , 单调递增.
所以当 时 取到极大值,极大值是 ;
当 时 取到极小值,极小值是 .
综上所述:当 时,函数 在 和 上单调递增,在 上单调递减,函数既有极大值,又有
极小值,极大值是 ,极小值是 ;
当 时,函数 在 上单调递增,无极值;
当 时,函数 在 和 上单调递增,在 上单调递减,函数既有极大值,又
有极小值,极大值是 ,极小值是 .