文档内容
专题03 空间向量的应用
一、单选题
1.(2020·贵州省铜仁第一中学高二开学考试)已知两个异面直线的方向向量分别为 , ,且| |=| |
=1, • ,则两直线的夹角为( )
A. B.
C. D.
2.(2019·穆棱市第一中学高二期末)若平面 的法向量分别为 ,则(
)
A. B. 与 相交但不垂直
C. D. 或 与 重合
3.(2020·北京高二期末)已知直线 的方向向量为 ,平面 的法向量为 ,则“ ”是“ ∥ ”
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.(2019·山东省济南一中高二期中)在平面ABCD中, , , ,若
,且 为平面ABCD的法向量,则 等于( )
A.2 B.0 C.1 D.无意义
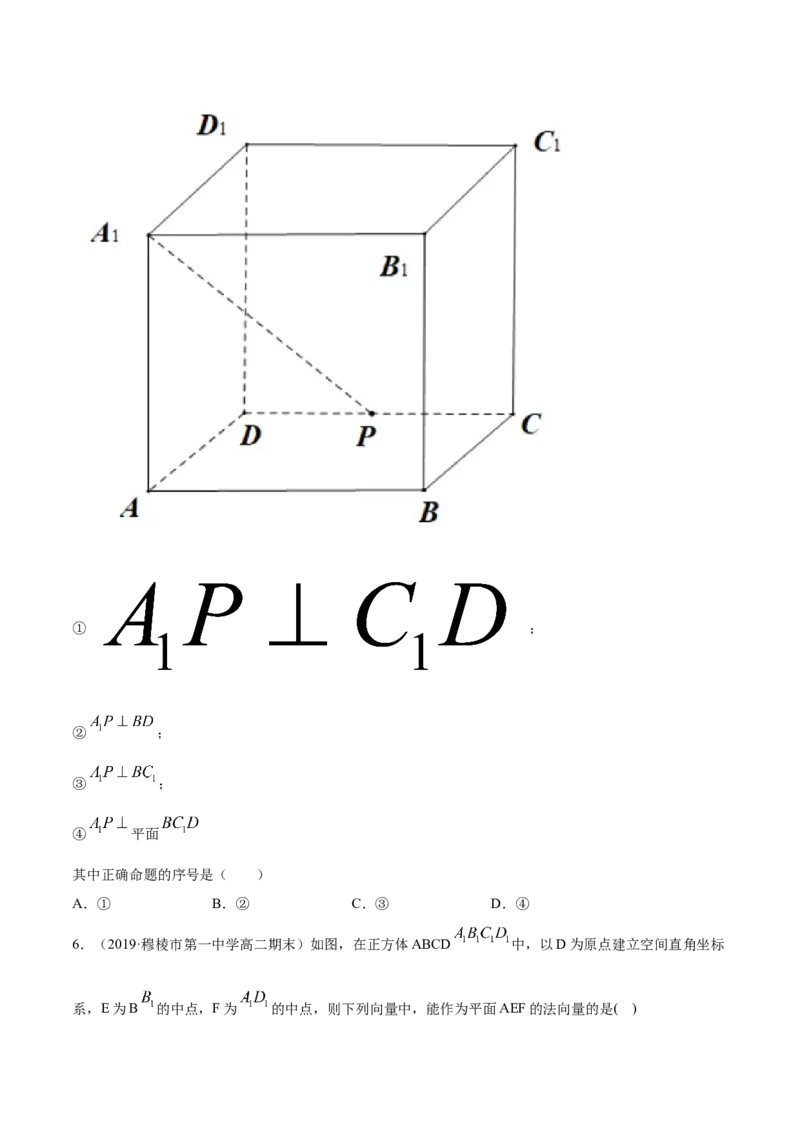
5.(2019·四川省双流中学高三月考)已知点 是正方体 的棱 的中点,给出以下结
论:① ;
② ;
③ ;
④ 平面
其中正确命题的序号是( )
A.① B.② C.③ D.④
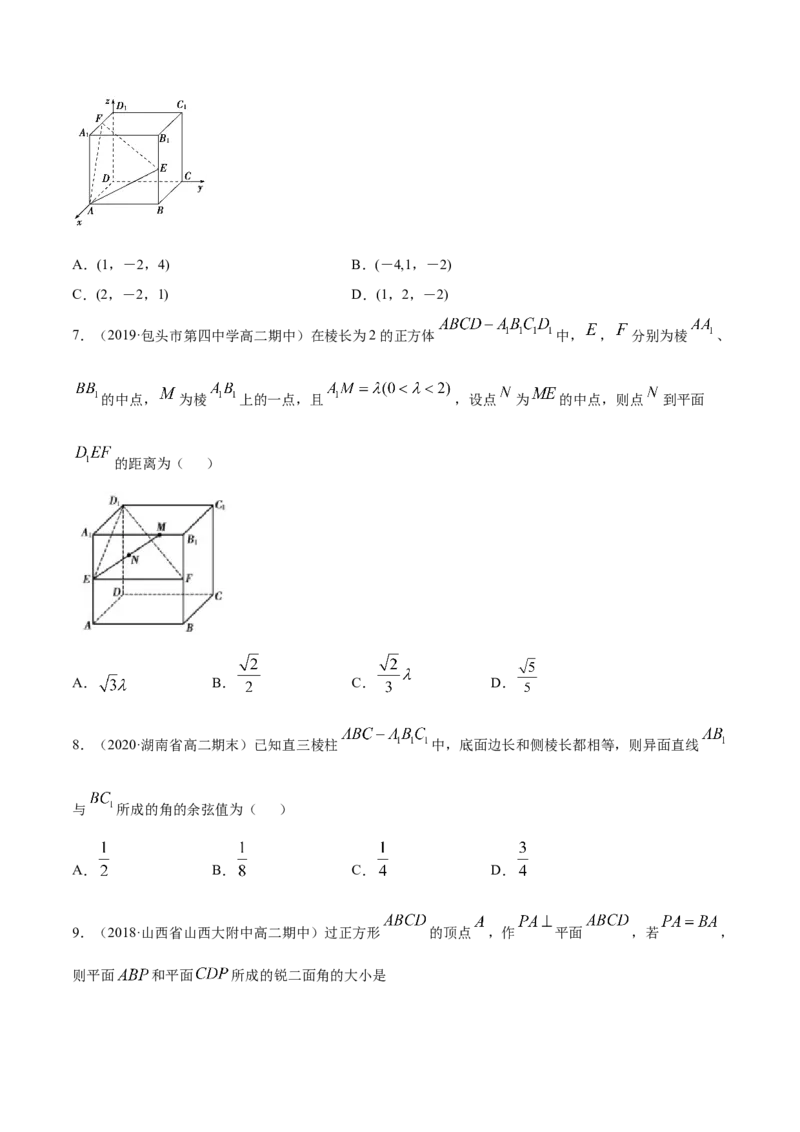
6.(2019·穆棱市第一中学高二期末)如图,在正方体ABCD 中,以D为原点建立空间直角坐标
系,E为B 的中点,F为 的中点,则下列向量中,能作为平面AEF的法向量的是( )A.(1,-2,4) B.(-4,1,-2)
C.(2,-2,1) D.(1,2,-2)
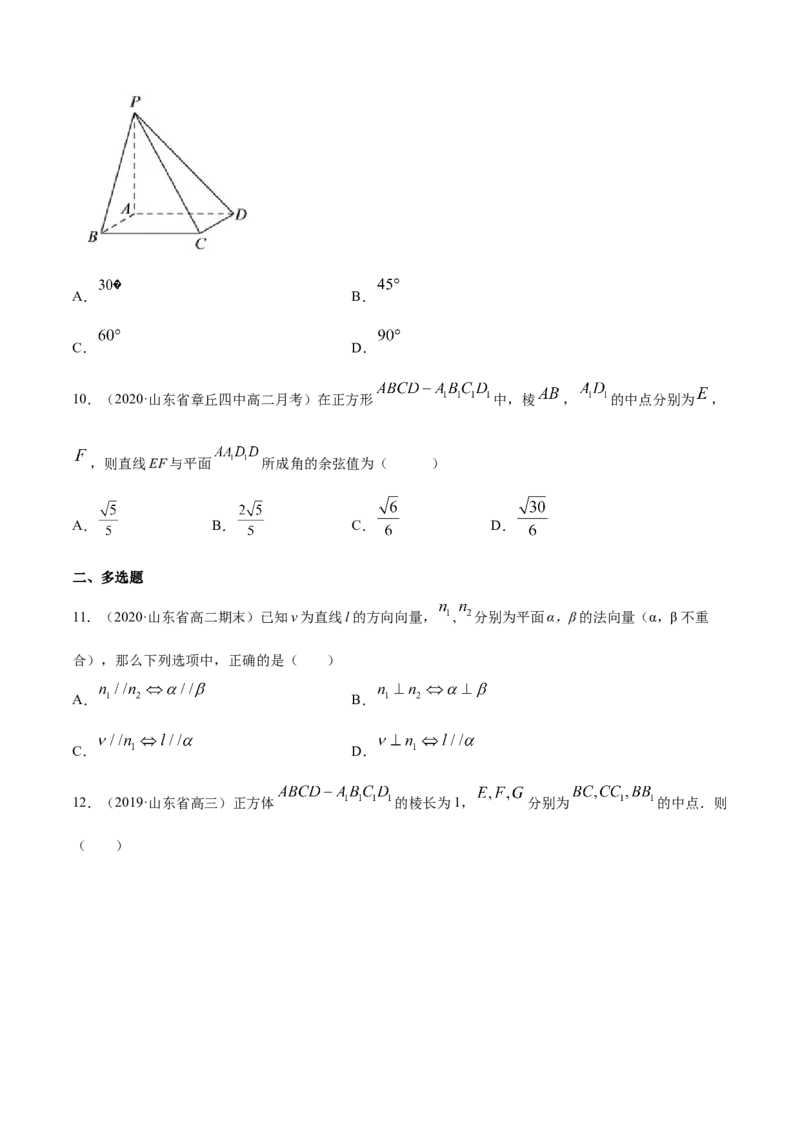
7.(2019·包头市第四中学高二期中)在棱长为2的正方体 中, , 分别为棱 、
的中点, 为棱 上的一点,且 ,设点 为 的中点,则点 到平面
的距离为( )
A. B. C. D.
8.(2020·湖南省高二期末)已知直三棱柱 中,底面边长和侧棱长都相等,则异面直线
与 所成的角的余弦值为( )
A. B. C. D.
9.(2018·山西省山西大附中高二期中)过正方形 的顶点 ,作 平面 ,若 ,
则平面 和平面 所成的锐二面角的大小是A. B.
C. D.
10.(2020·山东省章丘四中高二月考)在正方形 中,棱 , 的中点分别为 ,
,则直线EF与平面 所成角的余弦值为( )
A. B. C. D.
二、多选题
11.(2020·山东省高二期末)已知ν为直线l的方向向量, , 分别为平面α,β的法向量(α,β不重
合),那么下列选项中,正确的是( )
A. B.
C. D.
12.(2019·山东省高三)正方体 的棱长为1, 分别为 的中点.则
( )A.直线 与直线 垂直 B.直线 与平面 平行
C.平面 截正方体所得的截面面积为 D.点 和点 到平面 的距离相等
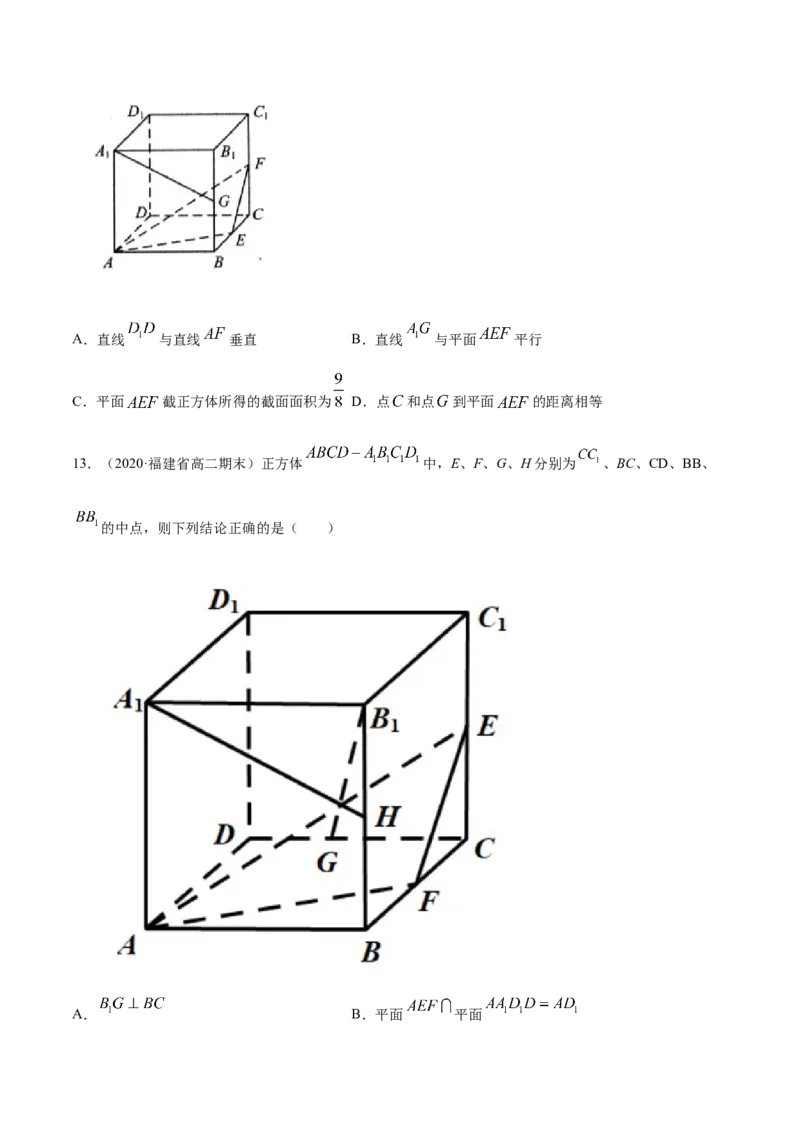
13.(2020·福建省高二期末)正方体 中,E、F、G、H分别为 、BC、CD、BB、
的中点,则下列结论正确的是( )
A. B.平面 平面C. 面AEF D.二面角 的大小为
三、填空题
14.(2019·山东省济南一中高二期中)若平面 的一个法向量为 ,直线l的一个方向向量
为 ,则l与 所成角的正弦值为________.
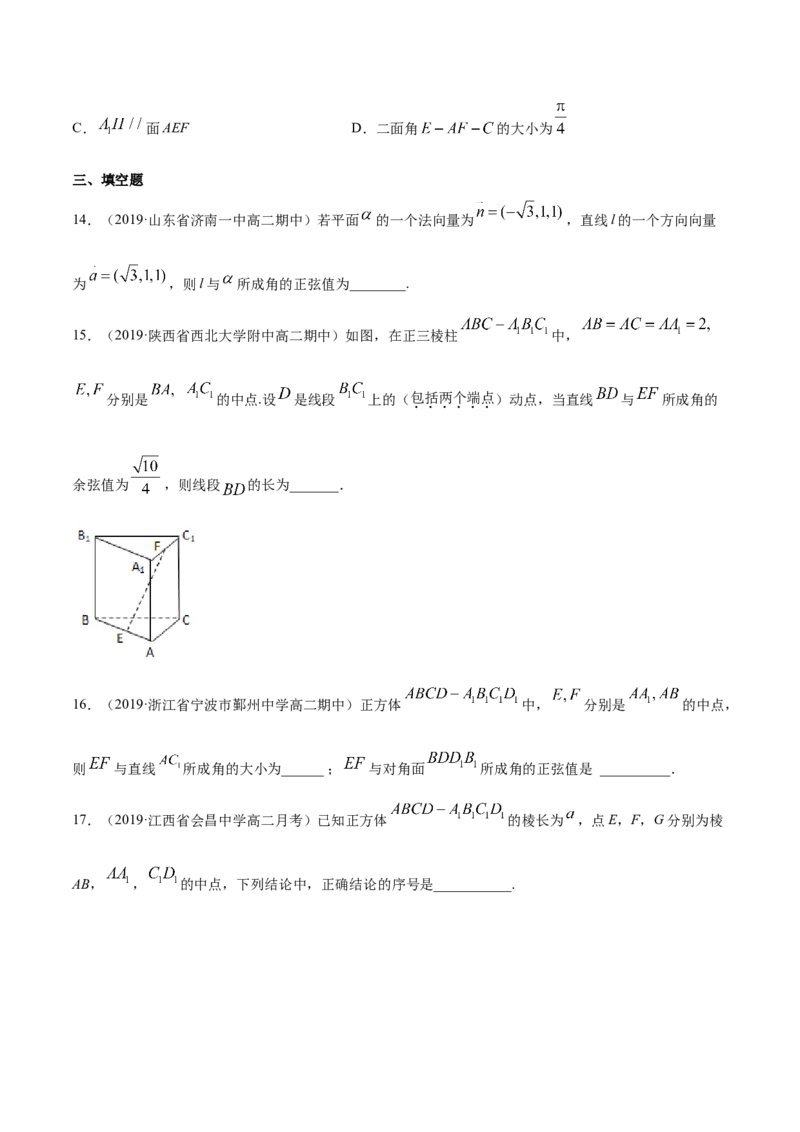
15.(2019·陕西省西北大学附中高二期中)如图,在正三棱柱 中,
分别是 的中点.设 是线段 上的(包括两个端点)动点,当直线 与 所成角的
余弦值为 ,则线段 的长为_______.
16.(2019·浙江省宁波市鄞州中学高二期中)正方体 中, 分别是 的中点,
则 与直线 所成角的大小为______ ; 与对角面 所成角的正弦值是 __________.
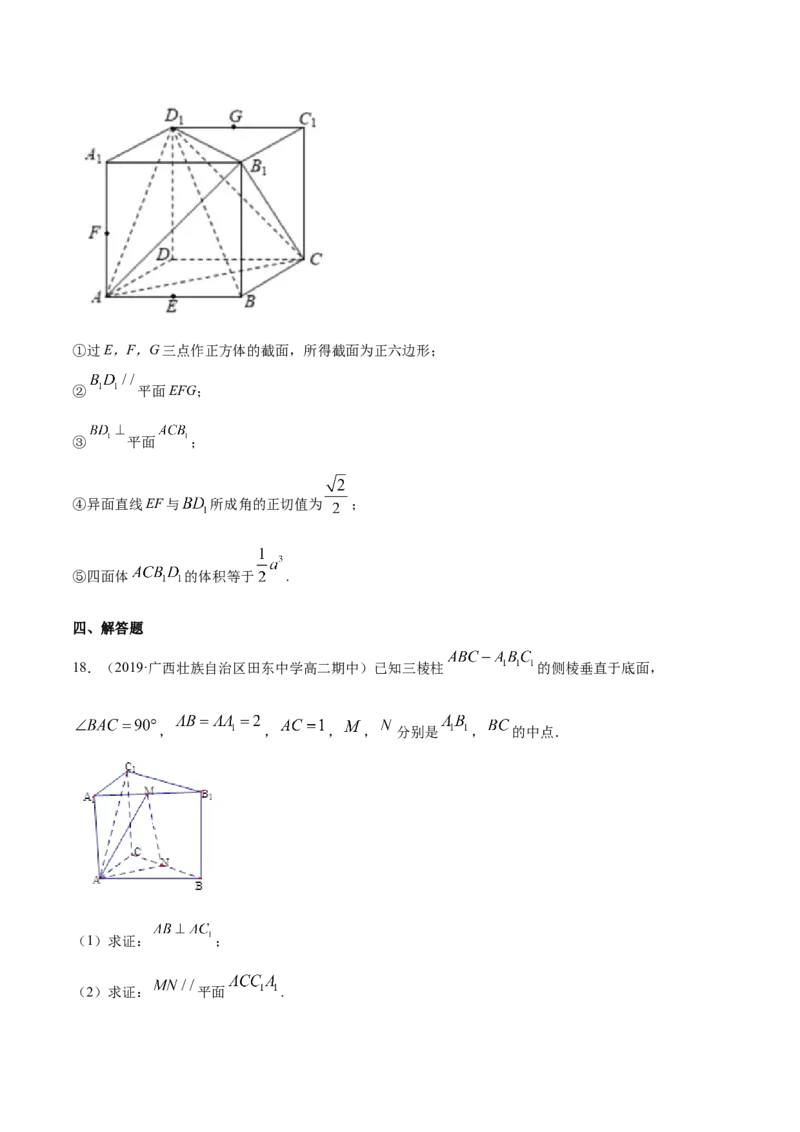
17.(2019·江西省会昌中学高二月考)已知正方体 的棱长为 ,点E,F,G分别为棱
AB, , 的中点,下列结论中,正确结论的序号是___________.①过E,F,G三点作正方体的截面,所得截面为正六边形;
② 平面EFG;
③ 平面 ;
④异面直线EF与 所成角的正切值为 ;
⑤四面体 的体积等于 .
四、解答题
18.(2019·广西壮族自治区田东中学高二期中)已知三棱柱 的侧棱垂直于底面,
, , , , 分别是 , 的中点.
(1)求证: ;
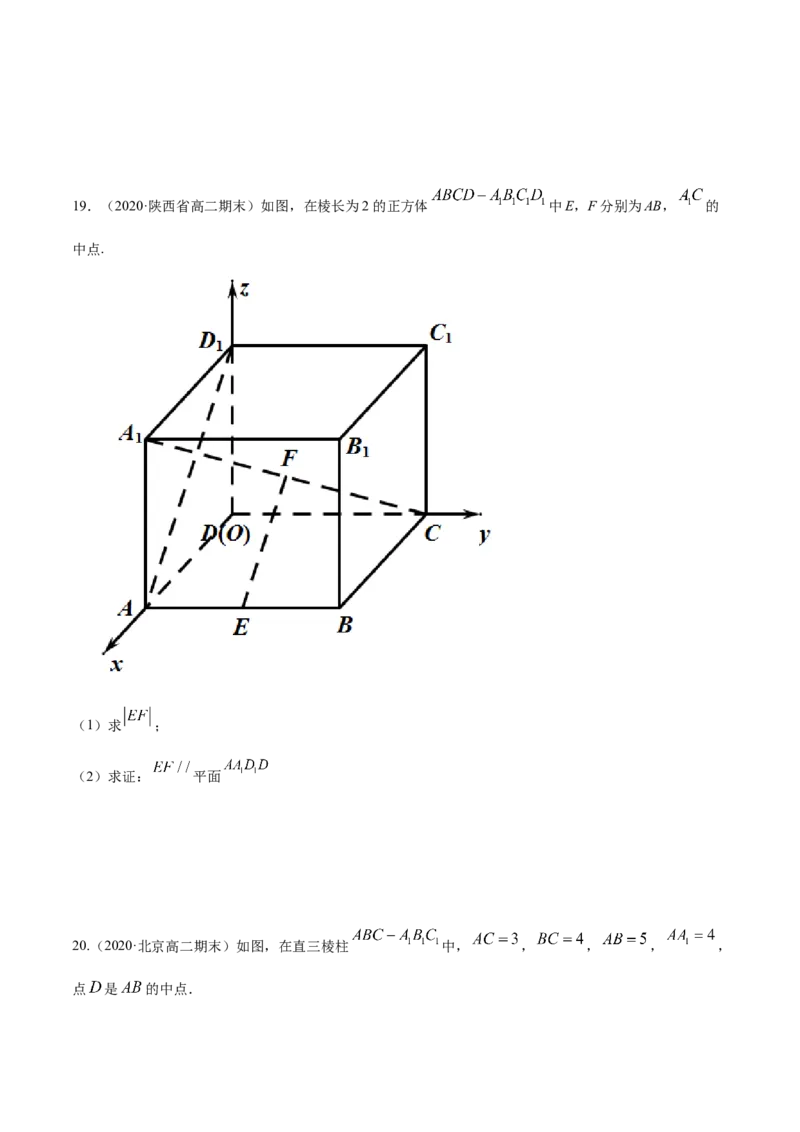
(2)求证: 平面 .19.(2020·陕西省高二期末)如图,在棱长为2的正方体 中E,F分别为AB, 的
中点.
(1)求 ;
(2)求证: 平面
20.(2020·北京高二期末)如图,在直三棱柱 中, , , , ,
点 是 的中点.(1)求异面直线 与 所成的角;
(2)求证: 平面 .
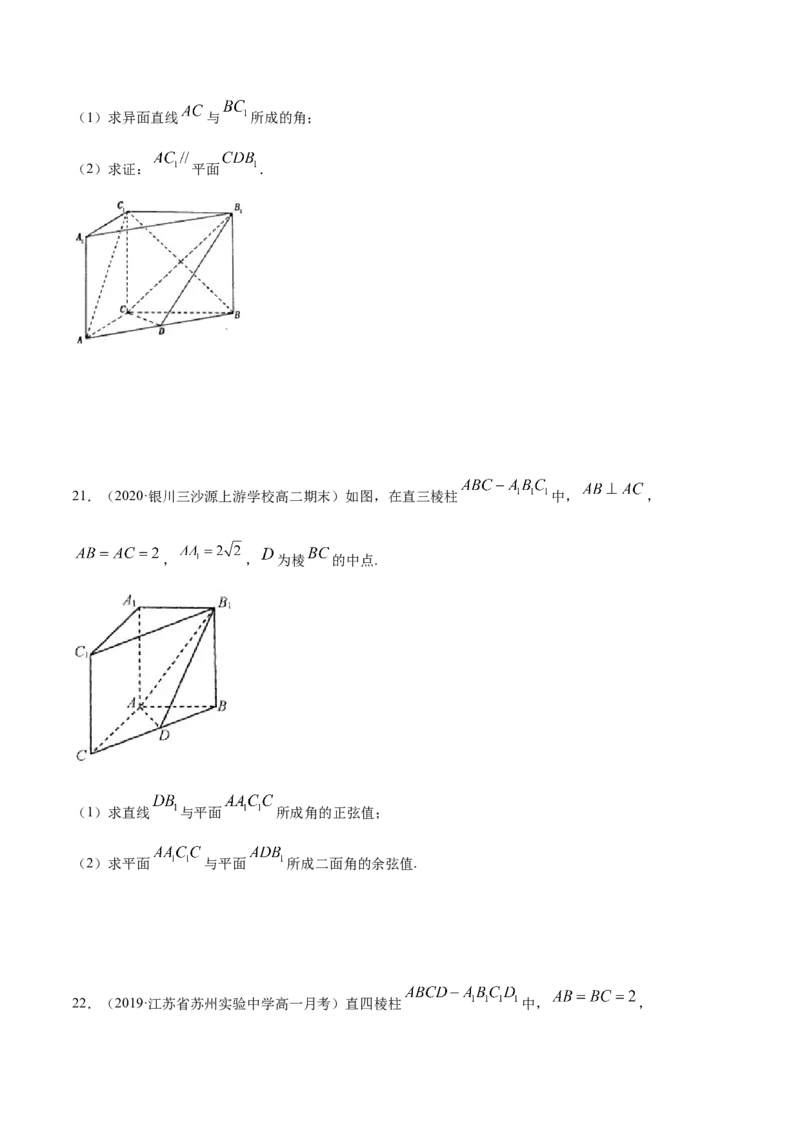
21.(2020·银川三沙源上游学校高二期末)如图,在直三棱柱 中, ,
, , 为棱 的中点.
(1)求直线 与平面 所成角的正弦值;
(2)求平面 与平面 所成二面角的余弦值.
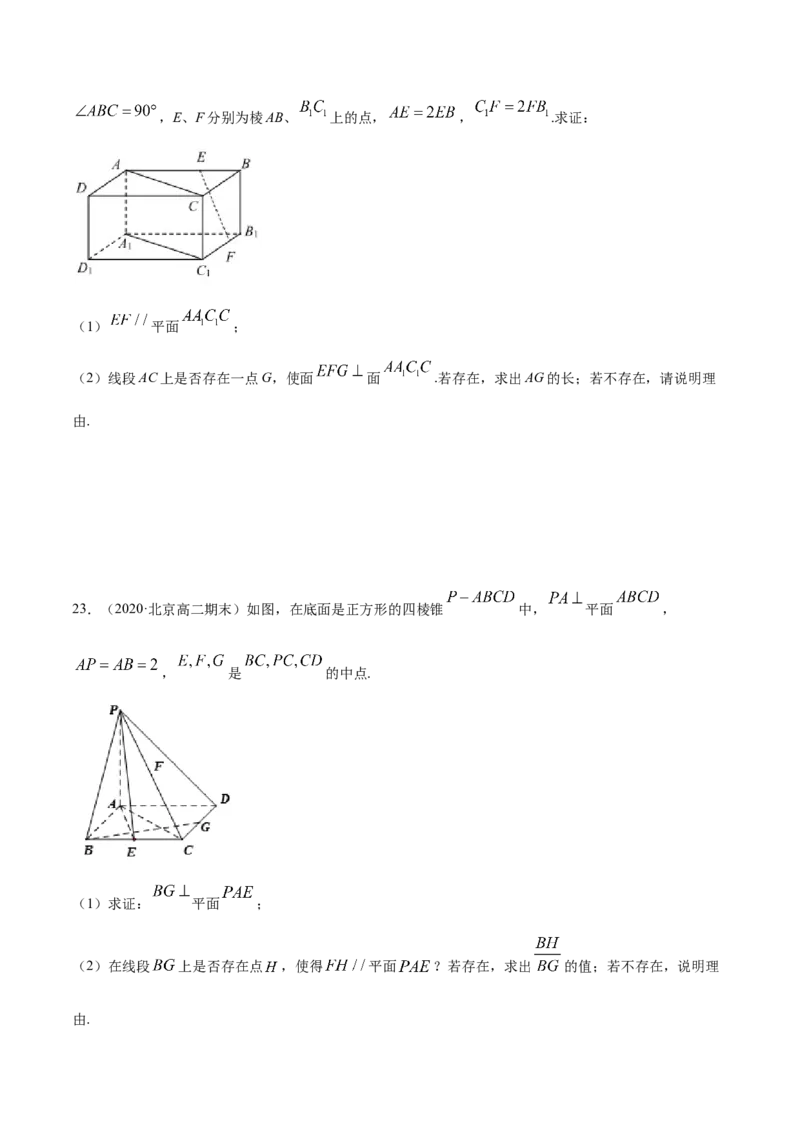
22.(2019·江苏省苏州实验中学高一月考)直四棱柱 中, ,,E、F分别为棱AB、 上的点, , .求证:
(1) 平面 ;
(2)线段AC上是否存在一点G,使面 面 .若存在,求出AG的长;若不存在,请说明理
由.
23.(2020·北京高二期末)如图,在底面是正方形的四棱锥 中, 平面 ,
, 是 的中点.
(1)求证: 平面 ;
(2)在线段 上是否存在点 ,使得 平面 ?若存在,求出 的值;若不存在,说明理
由.