文档内容
专题04 《空间向量与立体几何》单元测试卷
一、单选题
1.(2020·山东省微山县第二中学高二月考)空间直角坐标中A(1,2,3),B(-1,0,5),C(3,0,4),
D(4,1,3),则直线AB与CD的位置关系是( )
A.平行 B.垂直
C.相交但不垂直 D.无法确定
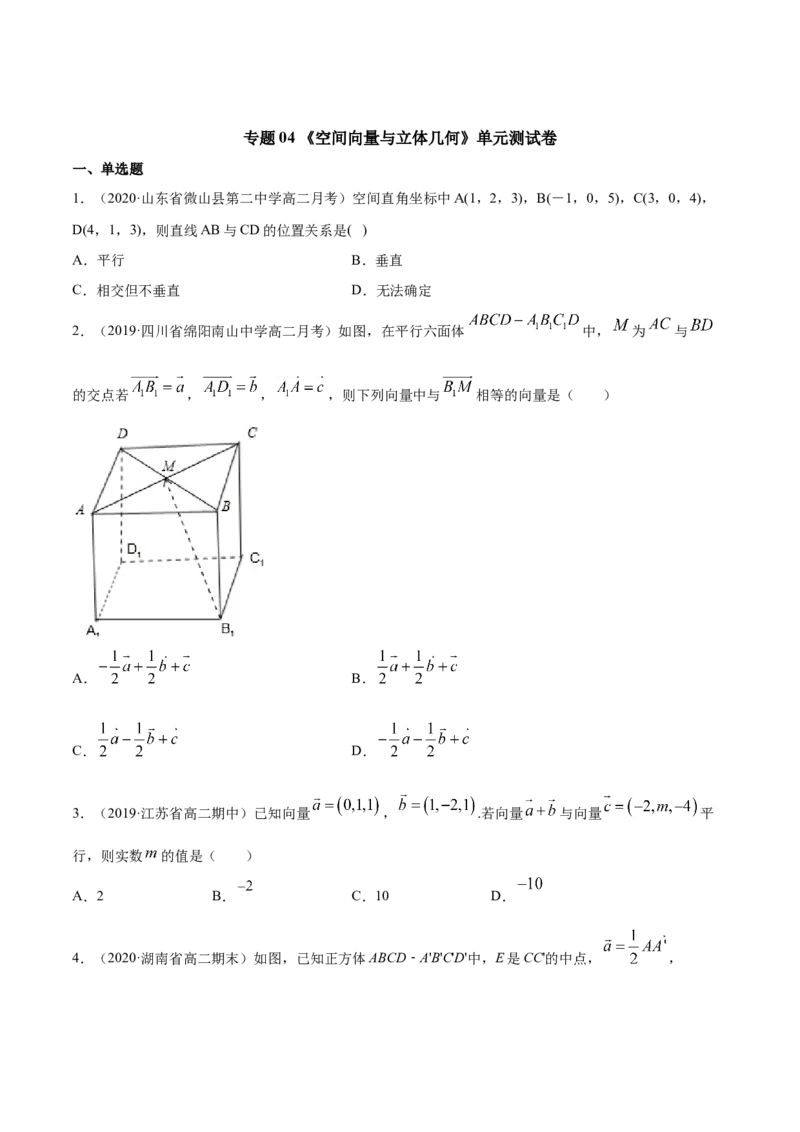
2.(2019·四川省绵阳南山中学高二月考)如图,在平行六面体 中, 为 与
的交点若 , , ,则下列向量中与 相等的向量是( )
A. B.
C. D.
3.(2019·江苏省高二期中)已知向量 , .若向量 与向量 平
行,则实数 的值是( )
A.2 B. C.10 D.
4.(2020·湖南省高二期末)如图,已知正方体ABCD﹣A'B'C'D'中,E是CC'的中点, ,, , x y z ,则( )
A.x=1,y=2,z=3 B.x ,y=1,z=1
C.x=1,y=2,z=2 D.x ,y=1,z
5.(2020·四川省双流中学高二月考)正方体不在同一侧面上的两顶点 , ,则正方体
外接球体积是( )
A. B. C. D.
6.(2019·江苏省苏州实验中学高二月考)已知 ,若点D是
AC中点,则 ( )
A.2 B. C.-3 D.6
7.(2019·江苏省苏州实验中学高二月考)平行六面体 中,
,则实数x,y,z的值分别为( )
A. B. C. D.
8.(2020·银川唐徕回民中学高二月考)三棱柱 中,底面边长和侧棱长都相等,,则异面直线 与 所成角的余弦值为( )
A. B. C. D.
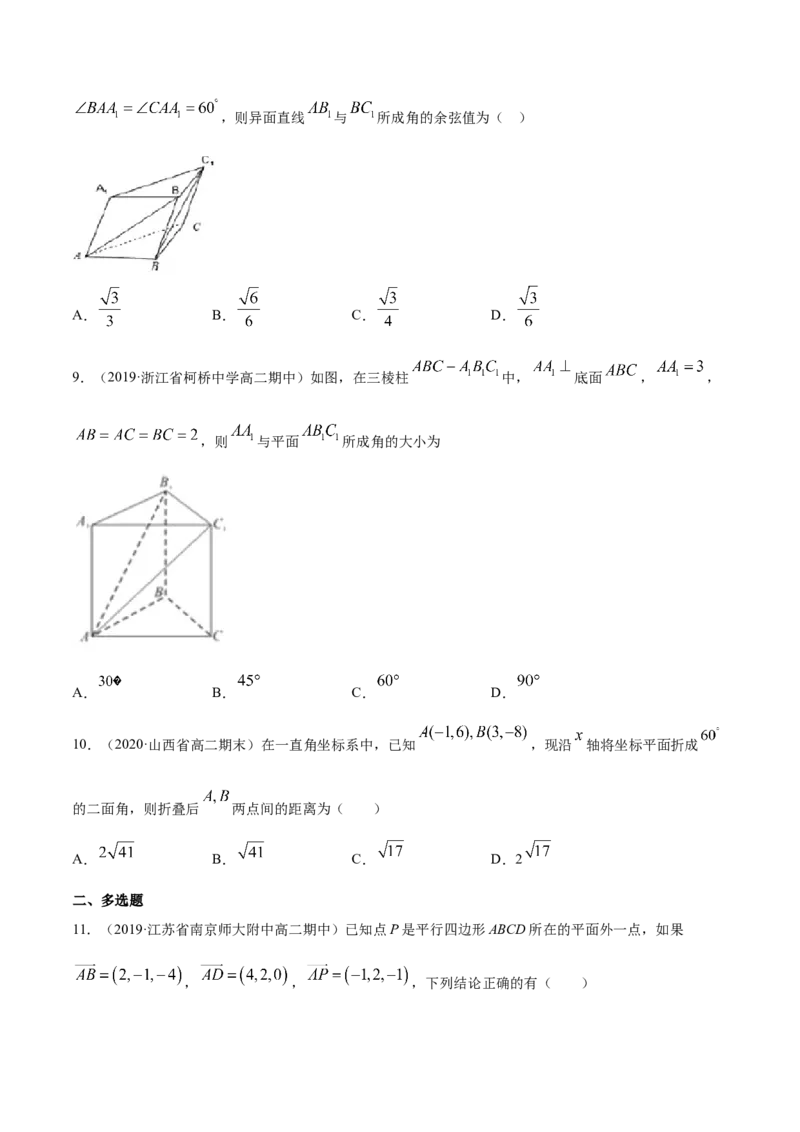
9.(2019·浙江省柯桥中学高二期中)如图,在三棱柱 中, 底面 , ,
,则 与平面 所成角的大小为
A. B. C. D.
10.(2020·山西省高二期末)在一直角坐标系中,已知 ,现沿 轴将坐标平面折成
的二面角,则折叠后 两点间的距离为( )
A. B. C. D.2
二、多选题
11.(2019·江苏省南京师大附中高二期中)已知点P是平行四边形ABCD所在的平面外一点,如果
, , ,下列结论正确的有( )A. B.
C. 是平面ABCD的一个法向量 D.
12.(2020·福建省高二期末)在正方体 中, , 分别是 和 的中点,则下
列结论正确的是( )
A. 平面 B. 平面
C. D.点 与点 到平面 的距离相等
13.(2020·江苏省启东中学高二开学考试)在正三棱柱 中,所有棱长为1,又 与
交于点 ,则( )
A. = B.
C.三棱锥 的体积为 D. 与平面BB′C′C所成的角为
三、填空题
14.(2020·山东省微山县第二中学高二月考)已知向量 2, , x, ,且 ,则
x的值为______.
15.(2020·河南省高二期末)若向量 , ,且 与 的夹角为钝角,则实数
的取值范围为________.
16.(2019·山东省济南一中高二期中)如图所示,在正方体 中,M为棱 的中点,
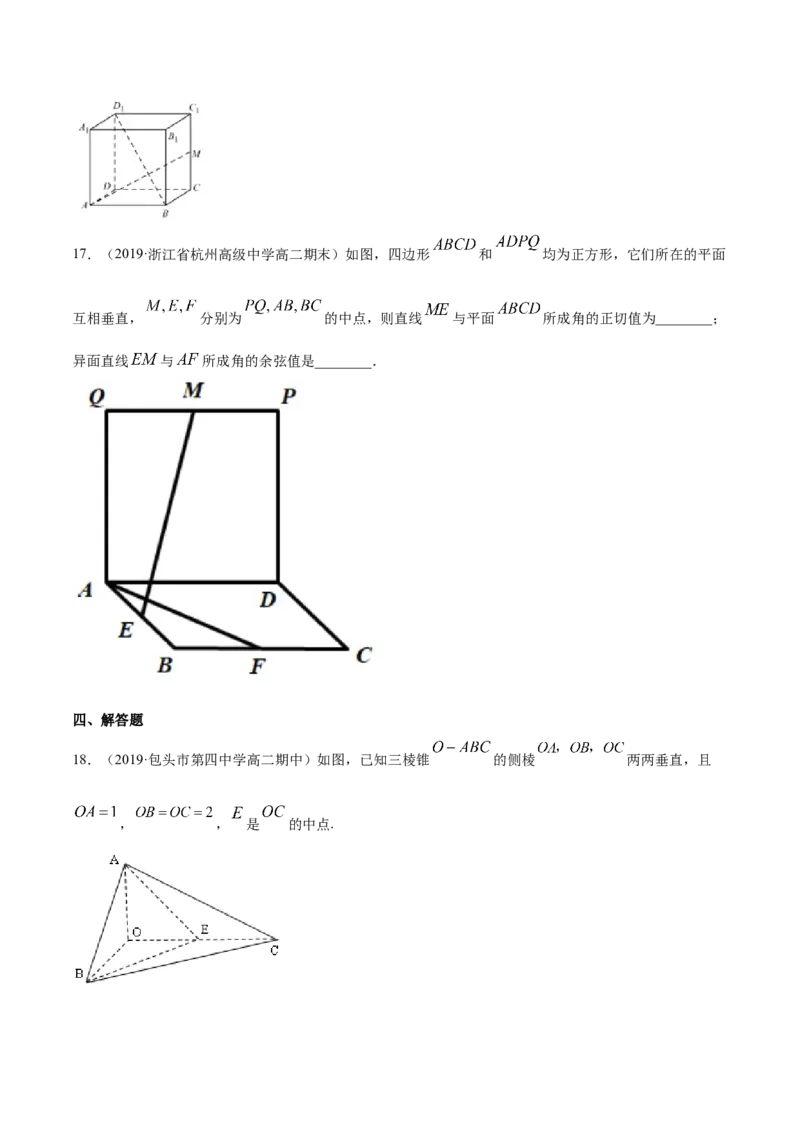
则异面线 与AM所成角的余弦值为________.17.(2019·浙江省杭州高级中学高二期末)如图,四边形 和 均为正方形,它们所在的平面
互相垂直, 分别为 的中点,则直线 与平面 所成角的正切值为________;
异面直线 与 所成角的余弦值是________.
四、解答题
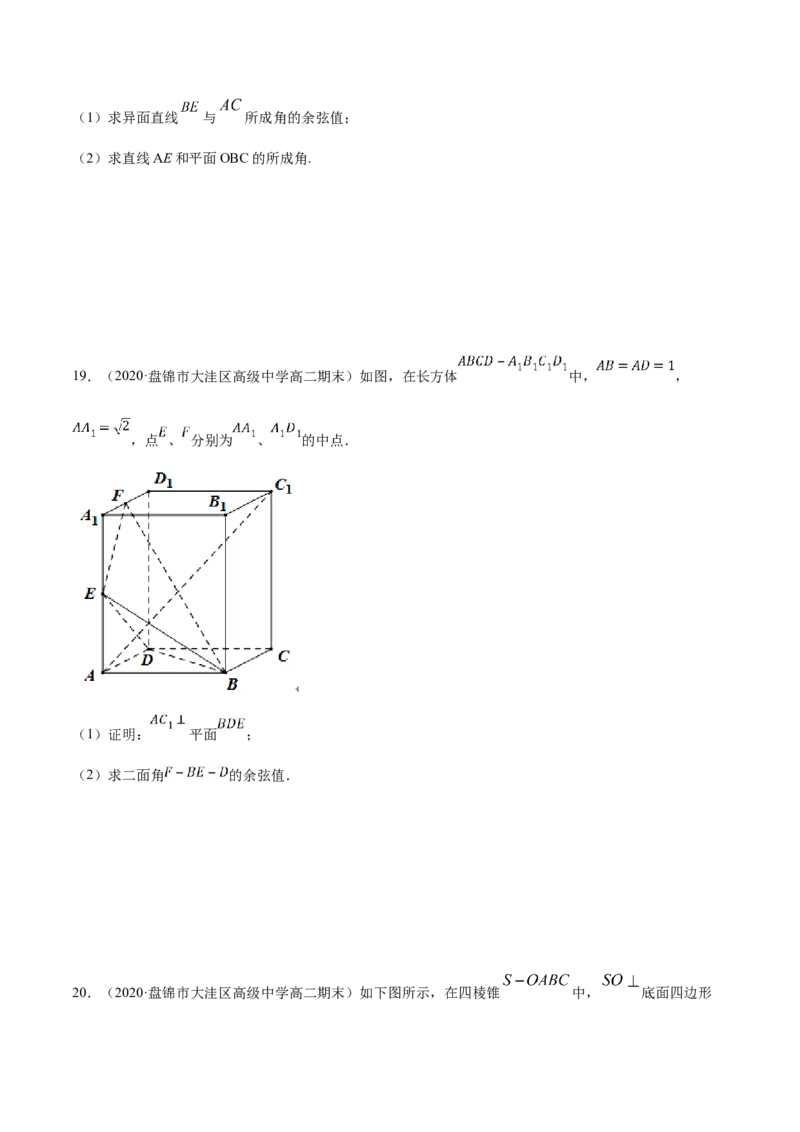
18.(2019·包头市第四中学高二期中)如图,已知三棱锥 的侧棱 两两垂直,且
, , 是 的中点.(1)求异面直线 与 所成角的余弦值;
(2)求直线AE和平面OBC的所成角.
19.(2020·盘锦市大洼区高级中学高二期末)如图,在长方体 中, ,
,点 、 分别为 、 的中点.
(1)证明: 平面 ;
(2)求二面角 的余弦值.
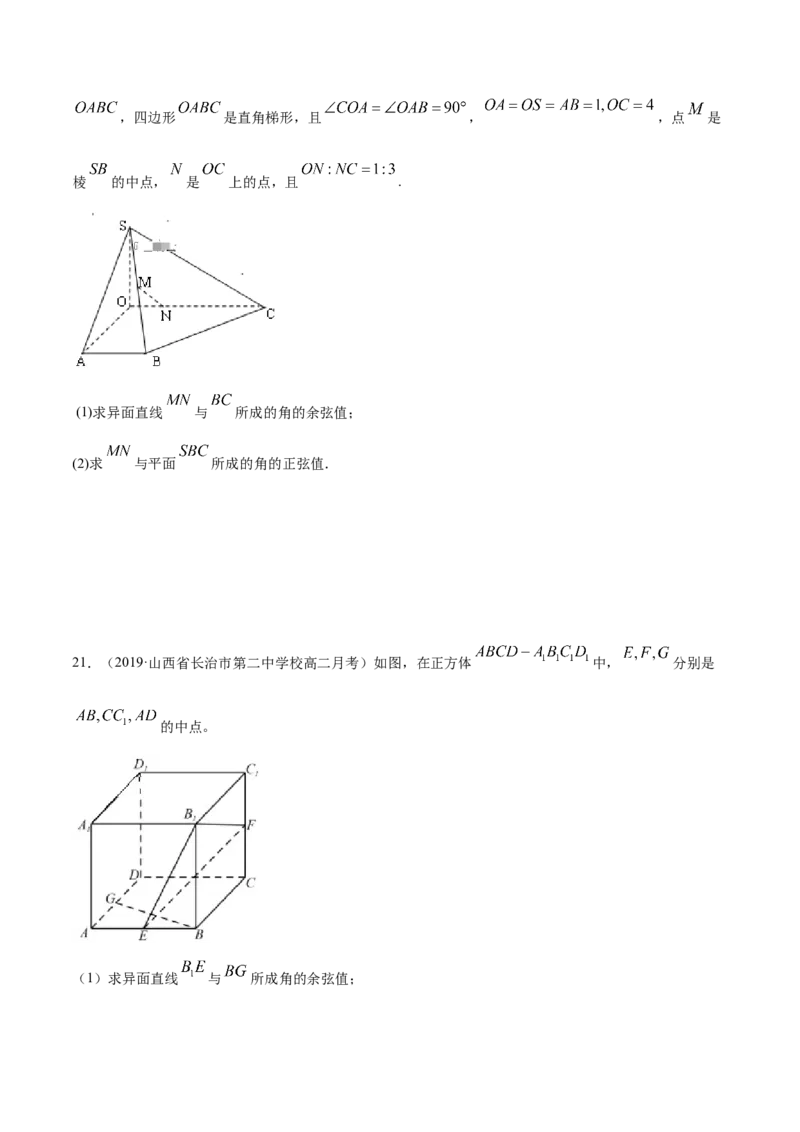
20.(2020·盘锦市大洼区高级中学高二期末)如下图所示,在四棱锥 中, 底面四边形,四边形 是直角梯形,且 , ,点 是
棱 的中点, 是 上的点,且 .
(1)求异面直线 与 所成的角的余弦值;
(2)求 与平面 所成的角的正弦值.
21.(2019·山西省长治市第二中学校高二月考)如图,在正方体 中, 分别是
的中点。
(1)求异面直线 与 所成角的余弦值;(2)棱 上是否存在点 ,使得 平面 ?请证明你的结论。
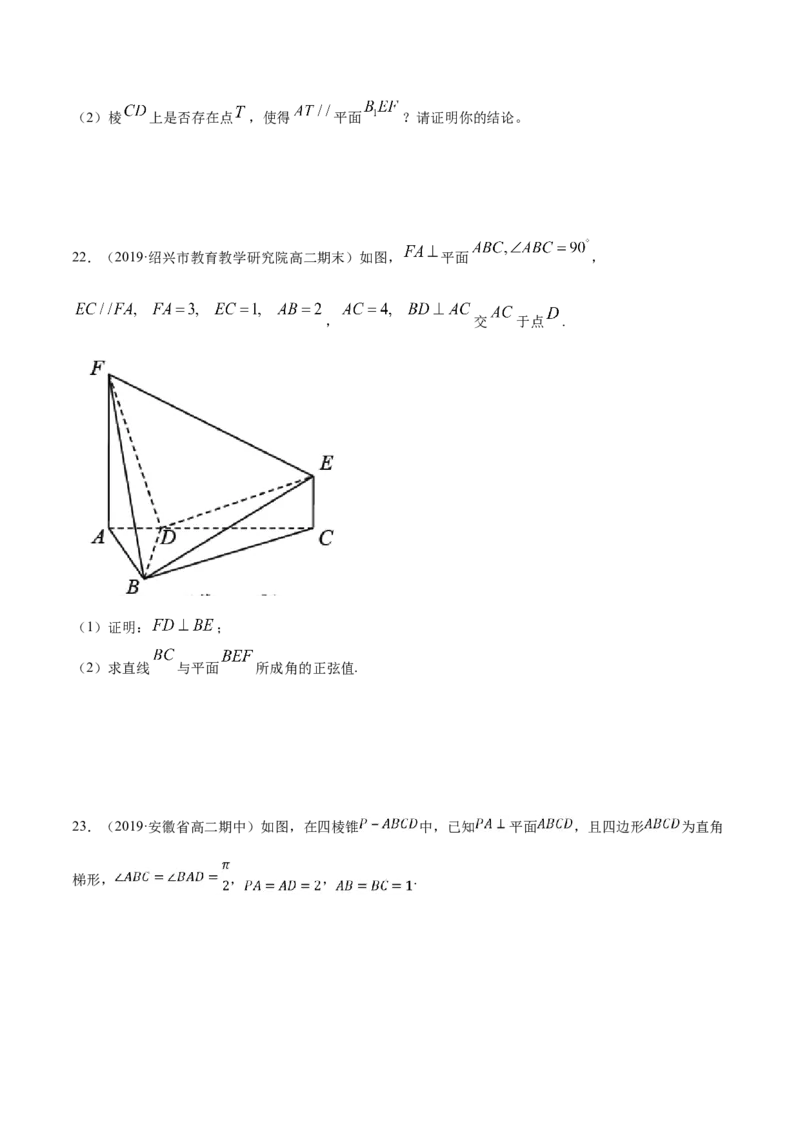
22.(2019·绍兴市教育教学研究院高二期末)如图, 平面 ,
, 交 于点 .
(1)证明: ;
(2)求直线 与平面 所成角的正弦值.
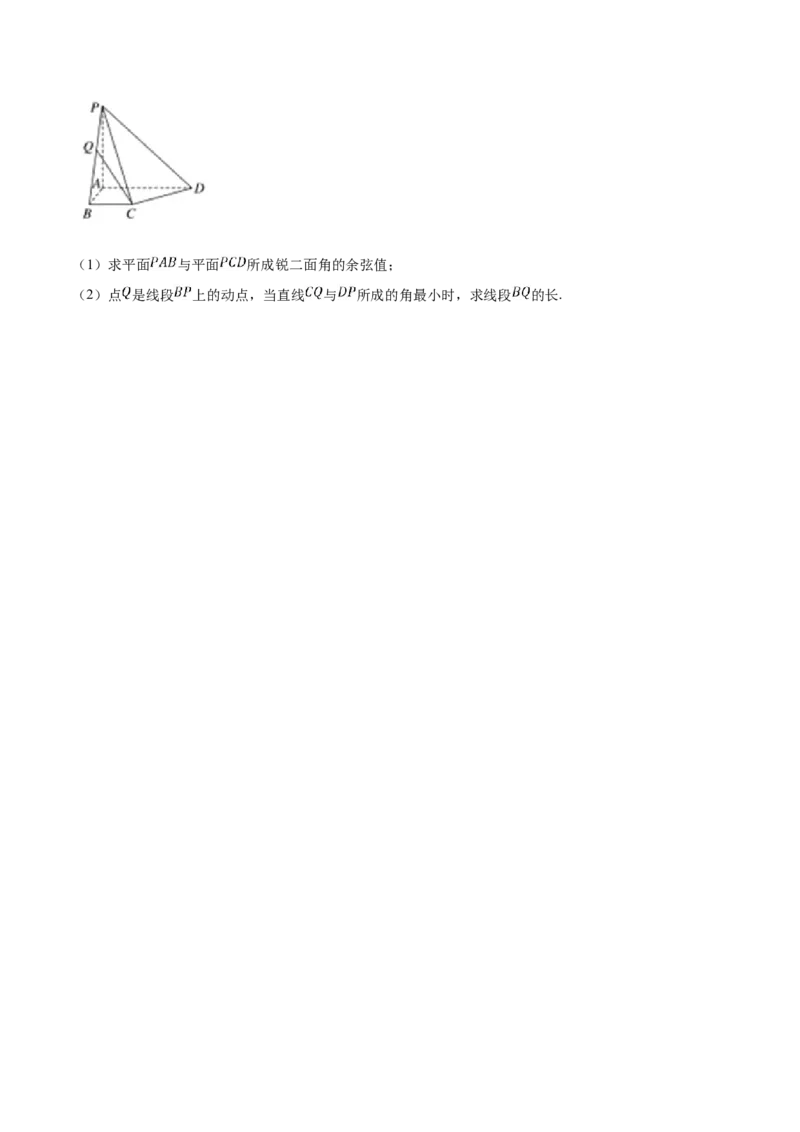
23.(2019·安徽省高二期中)如图,在四棱锥 中,已知 平面 ,且四边形 为直角
梯形, , , .(1)求平面 与平面 所成锐二面角的余弦值;
(2)点 是线段 上的动点,当直线 与 所成的角最小时,求线段 的长.