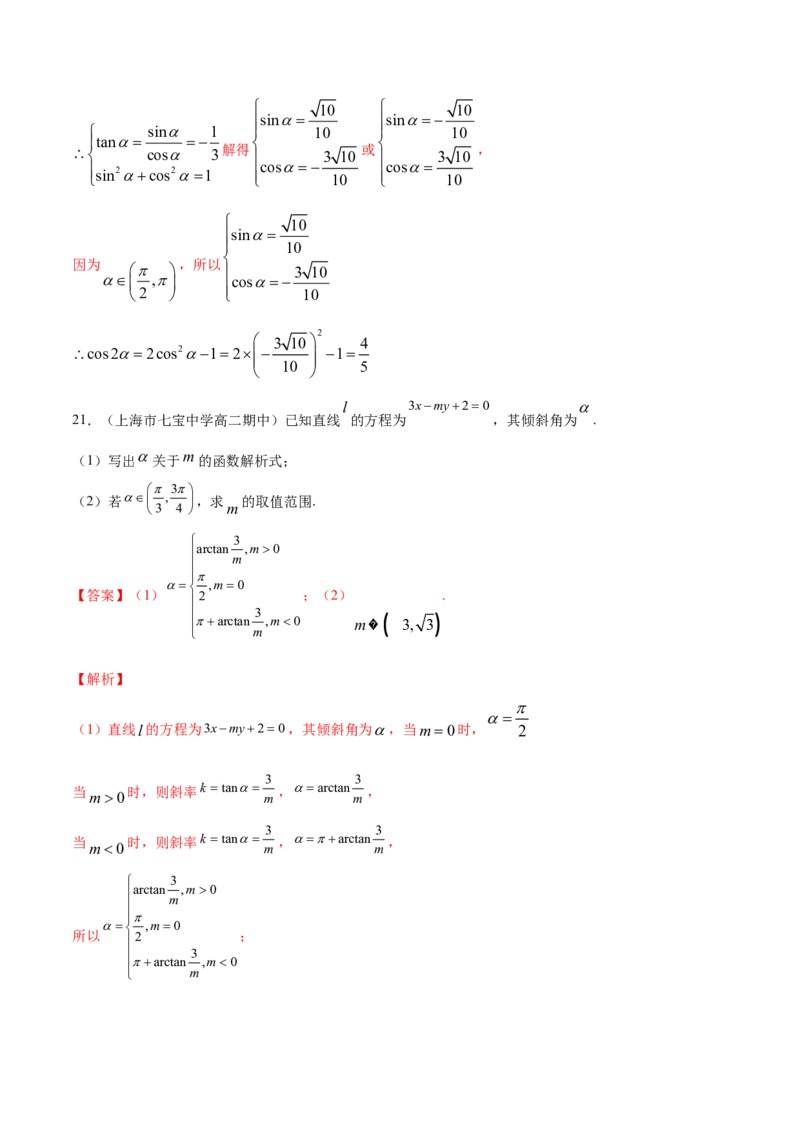专题05直线的倾斜角与斜率（解析版）_E015高中全科试卷_数学试题_选修1_06.专项练习_专题05直线的倾斜角与斜率-高中数学新教材人教A版选择性必修配套提升训练

专题05 直线的倾斜角与斜率 一、单选题 x 3 1．（2020·四川省高二期末（理））直线 的倾斜角为( ) 30 45 60 90 A． B． C． D． 【答案】D 【解析】 x 3  90 直线 的斜率不存在， 其倾斜角为 . 故选：D. x1   2．（2019·四川省仁寿一中高二期中（文））若直线 的倾斜角为 ，则 （ ）   A．0 B． 3 C． 2 D． 【答案】C 【解析】  直线x1与x轴垂直，故倾斜角为 2 . 故选：C. x y10 3．（2020·江苏省丹徒高中高一开学考试）直线 的倾斜角为（ ）  3 5  A．4 B． 4 C． 4 D． 2 【答案】B 【解析】 x y10 k 1 由题意，直线 的斜率为 3 k tan1 故 4故选:B A3,1 B2,k C8,11 k 4．（2019·江苏省扬州中学高一期中）如果 、 、 在同一直线上，那么 的值是( ) A．-6 B．-7 C．-8 D．-9 【答案】D 【解析】 A(3,1) B(2,k) C(8,11)  、 、 三点在同一条直线上， 直线AB和直线AC 的斜率相等， k1 111  ，解得 ．  23 83 k 9 故选：D． (2,4) (1,4 3) 5．（2019·山东省高二期中）若直线过点 ， ，则此直线的倾斜角是（ ） 30 60 120 150 A． B． C． D． 【答案】C 【解析】 k  3 由题意知，直线的斜率 ，  tan 3 即直线的倾斜角 满足 ， 0 180 120  又 ， ， 故选：C 6．（2019·浙江省高三期中）以下哪个点在倾斜角为45°且过点（1，2）的直线上（ ） A．（﹣2，3） B．（0，1） C．（3，3） D．（3，2） 【答案】B 【解析】 k tan45 1 由直线的倾斜角为45°，则直线的斜率为 ，32 1 2,3   2,3 则过点 与点（1，2）的直线的斜率为21 3，显然点 不满足题意； 12 0,1 1 0,1 过点 与点（1，2）的直线的斜率为01 ，显然点 满足题意； 32 1 3,3  3,3 过点 与点（1，2）的直线的斜率为 31 2，显然点 不满足题意； 22  0 3,2 2,3 过点 与点（1，2）的直线的斜率为 31 ，显然点 不满足题意； 0,1 即点 在倾斜角为45°且过点（1，2）的直线上， 故选：B. A(2,4) B(a,5) 7．（2020·四川省高二期末（理））已知一直线经过两点 ， ，且倾斜角为135°，则a的值 为（ ） A．-1 B．-2 C．2 D．1 【答案】D 【解析】 k tan135 1 由直线斜率的定义知, AB , 54 k  由直线的斜率公式可得, AB a2 ， 54 1 所以a2 ,解得a1. 故选:D 8．（2019·浙江省高二期中）直线xsinα＋y＋2＝0的倾斜角的取值范围是( )  3 [0, ][ ,) A．[0，π) B． 4 4    [0, ] [0, ][ ,) C． 4 D． 4 2【答案】B 【解析】 直线xsinα+y+2＝0的斜率为k＝﹣sinα， ∵﹣1≤sinα≤1，∴﹣1≤k≤1  3 ∴倾斜角的取值范围是[0， 4 ]∪[4 π，π） 故选：B．   tan   3   9．（2019·内蒙古自治区高二期末（文））已知直线l的倾斜角为，若  3  ，则 （ ）  5 A．0 B． 2 C． 6 D． 【答案】A 【解析】   tan 3 tan    3    3  1 3tan ，解得 tan0 ， 0 0  ， . 故选:A    2   , U  ,  10．（2019·浙江省镇海中学高一期末）已知直线倾斜角的范围是 3 2  2 3 ，则此直线的斜 率的取值范围是（ ）    3, 3 , 3U  3, A．  B．    3 3  3  3   ,  , U  , C． D．  3 3 3 3       【答案】B 【解析】   2    2   , U  ,    , U  ,  因为直线倾斜角的范围是 3 2  2 3 ,又直线的斜率k tan, 3 2  2 3 .故  2 tantan  3 tantan  3 3 或 3 .   k , 3U  3, 故   . 故选：B 二、多选题 11．（2020·吴江汾湖高级中学高一月考）下列说法中正确的是( )  l 0 180 A．若 是直线 的倾斜角，则 k l kR B．若 是直线 的斜率，则 C．任意一条直线都有倾斜角，但不一定有斜率 D．任意一条直线都有斜率，但不一定有倾斜角 【答案】ABC 【解析】  l 0 180 A. 若 是直线 的倾斜角，则 ,是正确的； k l k tanR B. 若 是直线 的斜率，则 ，是正确的； C. 任意一条直线都有倾斜角，但不一定有斜率，倾斜角为90°的直线没有斜率，是正确的； D. 任意一条直线都有斜率，但不一定有倾斜角，是错误的，倾斜角为90°的直线没有斜率. 故选：ABC 12．（2020·江苏省苏州实验中学高一月考）有下列命题：其中错误的是（ ） A．若直线的斜率存在，则必有倾斜角与之对应； B．若直线的倾斜角存在，则必有斜率与之对应； C．坐标平面上所有的直线都有倾斜角； D．坐标平面上所有的直线都有斜率． 【答案】BD 【解析】任何一条直线都有倾斜角，但不是任何一条直线都有斜率 当倾斜角为90时，斜率不存在 故选：BD l :x y10 l :(k1)xkyk 0(kR) 13．（2018·全国单元测试）已知直线 1 ，动直线 2 ，则下列结 论错误的是（ ） l l l k k A．不存在 ，使得 2的倾斜角为90° B．对任意的 ， 1与 2都有公共点 l l l l k k C．对任意的 ， 1与 2都不重合 D．对任意的 ， 1与 2都不垂直 【答案】AC 【解析】 逐一考查所给的选项： l k 0 x0 A.存在 ，使得 2的方程为 ，其倾斜角为90°，故选项不正确． l :x y10 0,1 l :k1xkyk 0kRkx y1x0 B直线 1 过定点 ，直线 2 过定 0,1 点 ，故B是正确的． 1 1 1 1 x x y 0 C.当 2 时，直线 l 2 的方程为2 2 2 ，即x y10， l 1 与 l 2 都重合，选项C错误； 1k11k 0 l l k D.两直线重合，则： ，方程无解，故对任意的 ， 1与 2都不垂直，选项D正确． 故选：AC. 三、填空题 3 14．（2019·银川唐徕回民中学高三月考（理））已知点P(－ ，1)，点Q在y轴上，直线PQ的倾斜角 为120°，则点Q的坐标为_____． 【答案】(0，－2) 【解析】 Q y Q 0,y 因为 在 轴上，所以可设 点坐标为 ，tan120  3 又因为 ， y1  3 则0 3 ，解得y 2， Q0,2 0,2 因此 ，故答案为 . 15．（2020·浙江省温州中学高三月考）平面直角坐标系中，直线倾斜角的范围为______，一条直线可能经 过______个象限. [0,p) 【答案】 0，2，3 【解析】 0, 平面直角坐标系中，直线倾斜角的范围为 ， 一条直线可能经过2个象限，如过原点，或平行于坐标轴； 也可能经过3个象限，如与坐标轴不平行且不过原点时； 也可能不经过任何象限，如坐标轴； 所以一条直线可能经过0或2或3个象限． 0, 故答案为： ，0或2或3． 16．（2019·浙江省效实中学高一期中）若直线斜率k∈(－1,1)，则直线倾斜角α∈________. 【答案】[0°，45°)∪(135°，180°) 【解析】 直线的斜率为负时，斜率也随着倾斜角的增大而增大 由于斜率有正也有负，且直线的斜率为正时，斜率随着倾斜角的增大而增大，故α∈(0°，45°)；又直线的 斜率为负时，斜率也随着倾斜角的增大而增大，故α∈(135°，180°)；斜率为0时，α＝0°.所以α∈[0°， 45°)∪(135°，180°) 故答案为[0°，45°)∪(135°，180°) P1,0 A2,1 B3,2 17．（2018·山西省山西大附中高二期中（文））已知直线l经过点 且与以 ， 为端 l AB 点的线段 有公共点，则直线 的倾斜角的取值范围为____． 3 [0, ] [ ,)  【答案】 4 4 【解析】 l l  当直线 过B时，设直线 的倾斜角为 ，则 3 tan1 4 l l  当直线 过A时，设直线 的倾斜角为 ，则  tan1 4 P1,0 A2,1 B3,2 l 综合：直线l经过点 且与以 ， 为端点的线段AB有公共点时，直线 的倾斜角的   3  0,  ,   取值范围为 4 4  四、解答题 A1,2 120 18．（2019·全国高一课时练习）已知点 ，在y轴上求一点P，使直线AP的倾斜角为 ．   P 0,2 3 【答案】 【解析】 y2 y2 k  设P(0,y)，  PA 01 ，tan120＝ 01 ，y 2 3， (0,2 3) P点坐标为 . y1 19．（2019·全国高一课时练习）点M(x,y)在函数y 2x8的图像上，当x[2,5]时，求 x1的取 值范围.  1 5  ,   【答案】 6 3【解析】 y1 y(1)  x1 x(1) 的几何意义是过M(x,y),N(1,1)两点的直线的斜率，点M在线段 y 2x8,x[2,5] x2 y 4 M(2,4) N(1,1) 上运动，易知当 时， ，此时 与 两项连线的斜率最大， 5 为3； 1 1 y1 5   剟 当x5时，y 2，此时M(5,2)与N(1,1)两点连线的斜率最小，为 6 . 6 x1 3,即HF  1 5  ,   的取值范围为 6 3 l x3y20  20．（2020·广东省恒大足球学校高三期末）已知直线 ： 的倾斜角为角 . （1）求tan； sin cos2 （2）求 ， 的值. 1 10 4  【答案】（1） 3；（2） 10 ；5 【解析】 1  （1）因为直线x3y20的斜率为 3，且直线的倾斜角为角， 1 tan 所以 3 1 tan （2）由（1）知 3， 10  10 sin sin  sin 1  10  10 tan     cos 3 解得  3 10 或  3 10 ， cos cos  sin2cos21   10   10  10 sin  10  因为 ，所以    3 10   ,  cos  2    10 2  3 10  4 cos22cos212  1   10 5   l 3xmy20  21．（上海市七宝中学高二期中）已知直线 的方程为 ，其倾斜角为 .  m （1）写出 关于 的函数解析式；  3 （2）若 , ，求 的取值范围. 3 4  m  3 arctan ,m0  m    ,m0 【答案】（1） 2 ；（2） .   3  arctan ,m0 m� ( 3, 3 )  m 【解析】   （1）直线l的方程为3xmy20，其倾斜角为，当m0时， 2 3 3 当 时，则斜率k tan ，arctan ， m0 m m 3 3 当 时，则斜率k tan ，arctan ， m0 m m  3 arctan ,m0  m    ,m0 所以 2 ；   3 arctan ,m0   m骣  3 �琪 琪 , k = � ( 3,ノ ) ,m ( 0, 3 ) （2）当 琪桫3 2 时， m ，   当 2 时，m0， 骣 3 3 �琪 琪 , k = �(� � , 1),m ( 3,0) 当 琪桫2 4 时， m ， ( ) m� 3, 3 综上所述： . P(0,1) A(1,2)、B(2,1) 22．（2019·全国高一课时练习）经过点 作直线l，若直线l与连接 的线段总有公 共点. 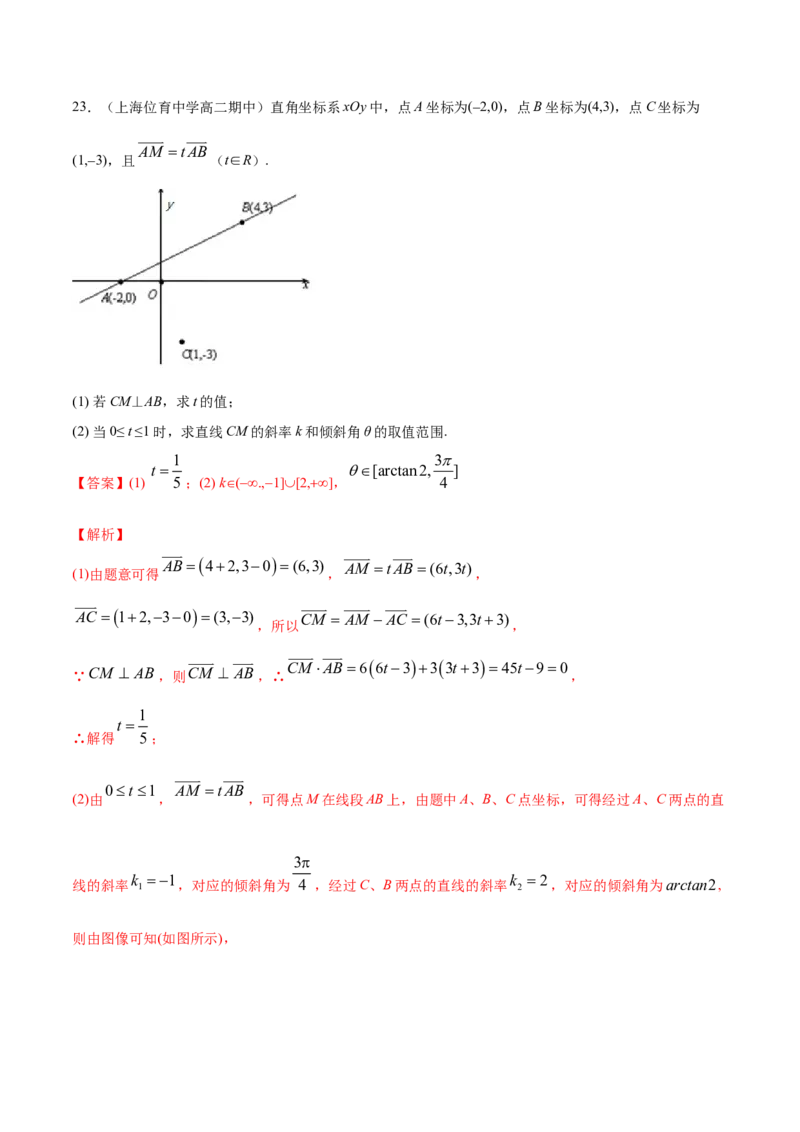（1）求直线l斜率k的范围；  （2）直线l倾斜角 的范围；  3 0 或  【答案】（1）1k 1（2） 4 4 【解析】 2(1) k  1 （1） pA 10 1(1) k  1 pB 20 l  与线段AB相交 k k k pA pB 1k 1 0tan1或1tan0 （2）由（1）知    y tanx在  0,  ( ,0) 由于  2 及 2 均为减函数  3 0 或  4 423．（上海位育中学高二期中）直角坐标系xOy中，点A坐标为(2,0)，点B坐标为(4,3)，点C坐标为   AM tAB (1,3)，且 （t∈R）. (1) 若CM⊥AB，求t的值； (2) 当0≤ t ≤1时，求直线CM的斜率k和倾斜角θ的取值范围. 1 3 t  [arctan2, ] 【答案】(1) 5；(2) k(.,1][2,]， 4 【解析】  A  B  42,30(6,3)  A  M  t  A  B  (6t,3t) (1)由题意可得 ， ，  A  C  12,30(3,3) C  M    A  M    A  C  (6t3,3t3) ，所以 ，     CM AB 66t333t345t90 ∵CM  AB，则CM  AB，∴ ， 1 t  ∴解得 5；   0t 1 AM tAB (2)由 ， ，可得点M在线段AB上，由题中A、B、C点坐标，可得经过A、C两点的直 3 线的斜率 k 1 ，对应的倾斜角为 4 ，经过C、B两点的直线的斜率 k 2 ，对应的倾斜角为arctan2, 1 2 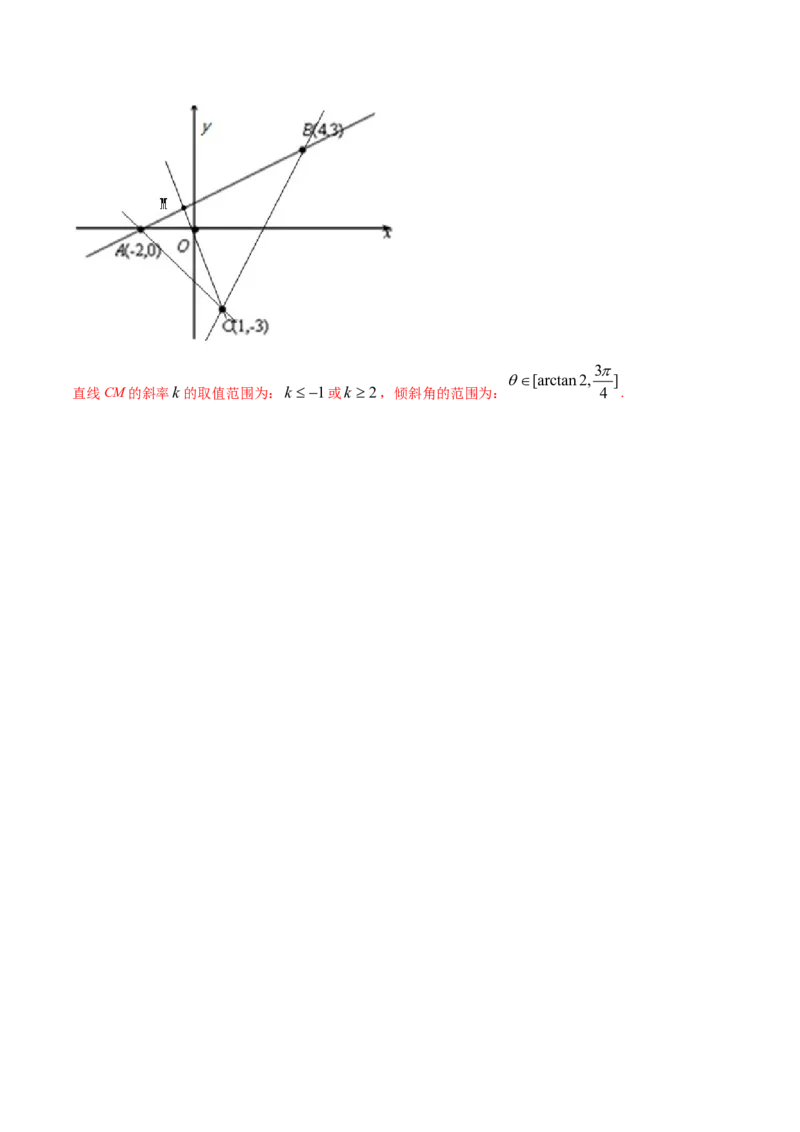则由图像可知(如图所示)，3 [arctan2, ] 直线CM的斜率k的取值范围为：k 1或k 2，倾斜角的范围为： 4 .