文档内容
专题 3.2 函数的基本性质
知识点一:函数的单调性
1.增函数、减函数的概念
一般地,设函数 的定义域为A,区间
如果对于 内的任意两个自变量的值 、 ,当 时,都有 ,
那么就说 在区间 上是增函数.
如果对于 内的任意两个自变量的值 、 ,当 时,都有 ,
那么就说 在区间 上是减函数.
知识点诠释:
(1)属于定义域A内某个区间上;
(2)任意两个自变量 且 ;
(3)都有 ;
(4)图象特征:在单调区间上增函数的图象从左向右是上升的,减函数的图象从左
向右是下降的.
2.单调性与单调区间
(1)单调区间的定义
如果函数f(x)在区间 上是增函数或减函数,那么就说函数 在区间 上具有
单调性, 称为函数f(x)的单调区间.
函数的单调性是函数在某个区间上的性质.
知识点诠释:
①单调区间与定义域的关系:单调区间可以是整个定义域,也可以是定义域的真
子集;
②单调性是通过函数值变化与自变量的变化方向是否一致来描述函数性质的;
③不能随意合并两个单调区间;
④有的函数不具有单调性.(2)已知解析式,如何判断一个函数在所给区间上的单调性?
3.证明函数单调性的步骤
(1)取值.设 是 定义域内一个区间上的任意两个量,且 ;
(2)变形.作差变形(变形方法:因式分解、配方、有理化等)或作商变形;
(3)定号.判断差的正负或商与1的大小关系;
(4)得出结论.
4.函数单调性的判断方法
(1)定义法:根据增函数、减函数的定义,按照“取值—变形—判断符号—下结
论”进行判断。
(2)图象法:就是画出函数的图象,根据图象的上升或下降趋势,判断函数的单调
性。
(3)直接法:就是对我们所熟悉的函数,如一次函数、二次函数、反比例函数等,
直接写出它们的单调区间。
(4)记住几条常用的结论
f(x) f(x)
①若 是增函数,则 为减函数;若 是减函数,则 为增函数;
f(x)
②若 和 均为增(或减)函数,则在 和 的公共定义域上
为增(或减)函数;
f(x)
③若 且 为增函数,则函数 为增函数, 为减函数;若
且 为减函数,则函数 为减函数, 为增函数.
5.复合函数单调性的判断
讨论复合函数 的单调性时要注意:既要把握复合过程,又要掌握基本
函数的单调性。一般需要先求定义域,再把复杂的函数正确地分解为两个简单的初等
函数的复合,然后分别判断它们的单调性,再用复合法则,复合法则如下:
(1)若 在所讨论的区间上都是增函数或都是减函数,则为增函数;
(2)若 在所讨论的区间上一个是增函数,另一个是减函数,则
为减函数。
列表如下:
增 增 增
增 减 减
减 增 减
减 减 增
复合函数单调性可简记为“同增异减”,即内外函数的单性相同时递增;单性相
异时递减。
因此判断复合函数的单调性可按下列步骤操作:
(1)将复合函数分解成基本初等函数: , ;
(2)分别确定各个函数的定义域;
(3)分别确定分解成的两个基本初等函数的单调区间。
若两个基本初等函数在对应的区间上的单调性是同增或同减,则 为增
函数;若为一增一减或一减一增,则 为减函数。
知识点诠释:
(1)单调区间必须在定义域内;
(2)要确定内层函数 的值域,否则就无法确定 的单调性。
( 3 ) 若 , 且 在 定 义 域 上 是 增 函 数 , 则
都是增函数。
6.利用函数单调性求函数最值时应先判断函数的单调性,再求最值。常用到下面
的结论:
(1)如果函数 在区间 上是增函数,在区间 上是减函数,则函数 在 处有最大值 。
(2)如果函数 在区间 上是减函数,在区间 上是增函数,则函
数 在 处有最小值 。
若函数 在 上是严格单调函数,则函数 在 上一定有最大、
最小值。
(3)若函数 在区间 上是单调递增函数,则 的最大值是
,最小值是 。
(4)若函数 在区间 上是单调递减函数,则 的最大值是
,最小值是 。
7.利用函数单调性求参数的范围
若已知函数的单调性,求参数 的取值范围问题,可利用函数单调性,先列出关
于参数 的不等式,利用下面的结论求解。
(1) 在 上恒成立 在 上的最大值。
(2) 在 上恒成立 在 上的最小值。
实际上将含参数问题转化成为恒成立问题,进而转化为求函数在其定义域上的最
大值和最小值问题。
知识点二:基本初等函数的单调性
1.正比例函数
当k>0时,函数 在定义域R是增函数;当k<0时,函数 在定义域R是
减函数.
2.一次函数
当k>0时,函数 在定义域R是增函数;当k<0时,函数 在定义
域R是减函数.3.反比例函数
当 时,函数 的单调递减区间是 ,不存在单调增区间;
当 时,函数 的单调递增区间是 ,不存在单调减区间.
4.二次函数
若a>0,在区间 ,函数是减函数;在区间 ,函数是增函数;
若a<0,在区间 ,函数是增函数;在区间 ,函数是减函数.
知识点三:函数的最大值
(1)定义:一般地,设函数 的定义域为I,如果存在实数M满足:
① ,都有 ;
② ,使得 .
那么,称M是函数 的最大值.
(2)几何意义:函数 的最大值是图象最高点的纵坐标.
知识点四:函数的最小值
(1)定义:一般地,设函数 的定义域为I,如果存在实数M满足:
① ,都有 ;
② ,使得 .
那么,称M是函数 的最小值.
(2)几何意义:函数 的最小值是图象最低点的纵坐标.
知识点五:函数的奇偶性概念及判断步骤
1.函数奇偶性的概念
偶函数:若对于定义域内的任意一个 ,都有 ,那么 称为偶函
数.
奇函数:若对于定义域内的任意一个 ,都有 ,那么 称为奇
函数.
知识点诠释:
(1)奇偶性是整体性质;
(2) 在定义域中,那么 在定义域中吗?----具有奇偶性的函数,其定义域必定是关于原点对称的;
(3) 的等价形式为: ,
的等价形式为: ;
(4)由定义不难得出若一个函数是奇函数且在原点有定义,则必有 ;
(5)若 既是奇函数又是偶函数,则必有 .
2.奇偶函数的图象与性质
(1)如果一个函数是奇函数,则这个函数的图象是以坐标原点为对称中心的中心
对称图形;反之,如果一个函数的图象是以坐标原点为对称中心的中心对称图形,则
这个函数是奇函数.
(2)如果一个函数为偶函数,则它的图象关于 轴对称;反之,如果一个函数的
图像关于 轴对称,则这个函数是偶函数.
3.用定义判断函数奇偶性的步骤
(1)求函数 的定义域,判断函数的定义域是否关于原点对称,若不关于原
点对称,则该函数既不是奇函数,也不是偶函数,若关于原点对称,则进行下一步;
(2)结合函数 的定义域,化简函数 的解析式;
(3)求 ,可根据 与 之间的关系,判断函数 的奇偶性.
若 =- ,则 是奇函数;
若 = ,则 是偶函数;
若 ,则 既不是奇函数,也不是偶函数;
若 且 ,则 既是奇函数,又是偶函数
知识点六:判断函数奇偶性的常用方法
(1)定义法:若函数的定义域不是关于原点对称,则立即可判断该函数既不是奇
函数也不是偶函数;若函数的定义域是关于原点对称的,再判断 与 之一是否相等.
(2)验证法:在判断 与 的关系时,只需验证 =0 及
是否成立即可.
(3)图象法:奇(偶)函数等价于它的图象关于原点( 轴)对称.
(4)性质法:两个奇函数的和仍为奇函数;两个偶函数的和仍为偶函数;两个奇
函数的积是偶函数;两个偶函数的积是偶函数;一个奇函数与一个偶函数的积是奇函
数.
(5)分段函数奇偶性的判断
判断分段函数的奇偶性时,通常利用定义法判断.在函数定义域内,对自变量 的
不同取值范围,有着不同的对应关系,这样的函数叫做分段函数.分段函数不是几个函
数,而是一个函数.因此其判断方法也是先考查函数的定义域是否关于原点对称,然后
判断 与 的关系.首先要特别注意 与 的范围,然后将它代入相应段的函数
表达式中, 与 对应不同的表达式,而它们的结果按奇偶函数的定义进行比
较.
知识点七:关于函数奇偶性的常见结论
奇函数在其对称区间 和 上具有相同的单调性,即已知 是奇函数,
它在区间 上是增函数(减函数),则 在区间 上也是增函数(减函
数);偶函数在其对称区间 和 上具有相反的单调性,即已知 是偶函
数且在区间 上是增函数(减函数),则 在区间 上也是减函数(增函
数).题型一:函数单调区间的确定
1.函数 的单调递减区间是( )
A. B. C. D.
【答案】A
【解析】解:因为 定义域为 ,函数在 和 上单调
递减,故函数的单调递减区间为 和 ;故选:A
2.已知函数 在 上是增函数,则实数 的取值范围为( )
A. B. C. D.
【答案】D
【解析】函数 的单调递增区间是 ,依题意, ,
所以 ,即实数 的取值范围是 .故选:D
3.已知函数 对于任意两个不相等实数 ,都有
成立,则实数 的取值范围是( )
A. B. C. D.
【来源】山东省潍坊市2021-2022学年高一上学期期末数学试题
【答案】B
【解析】由题可得,函数 为单调递减函数,
当 时,若 单减,则对称轴 ,得: ,
当 时,若 单减,则 ,在分界点处,应满足 ,即 ,
综上: 故选:B4.已知 是定义在 上的函数,若对于任意 ,都有
,则实数a的取值范围是( )
A. B. C. D.
【来源】四川省凉山州2021-2022学年高一上学期期末考试数学试题
【答案】C【解析】因为 ,所以由
,
构造函数 ,由 ,
因为 ,所以函数 是 上的增函数,
当 时,函数 是 上的增函数,符合题意;
当 时,函数 的对称轴为: ,
当 时,显然函数 是 上的增函数,符合题意;
当 时,要想函数 是 上的增函数,只需 ,而
,所以 ,
综上所述:实数a的取值范围是 ,故选:C
5.已知函数 ,则满足不等式 的 的取值范围是
( )
A. B. C. D.
【来源】陕西省西安高新第一中学2021-2022学年高一下学期月考2数学试题
【答案】C画出 的图象如图所示,要使不等式 成立,必有 或
,由 可得 ;由 可得 ,综上可得
.故选:C.
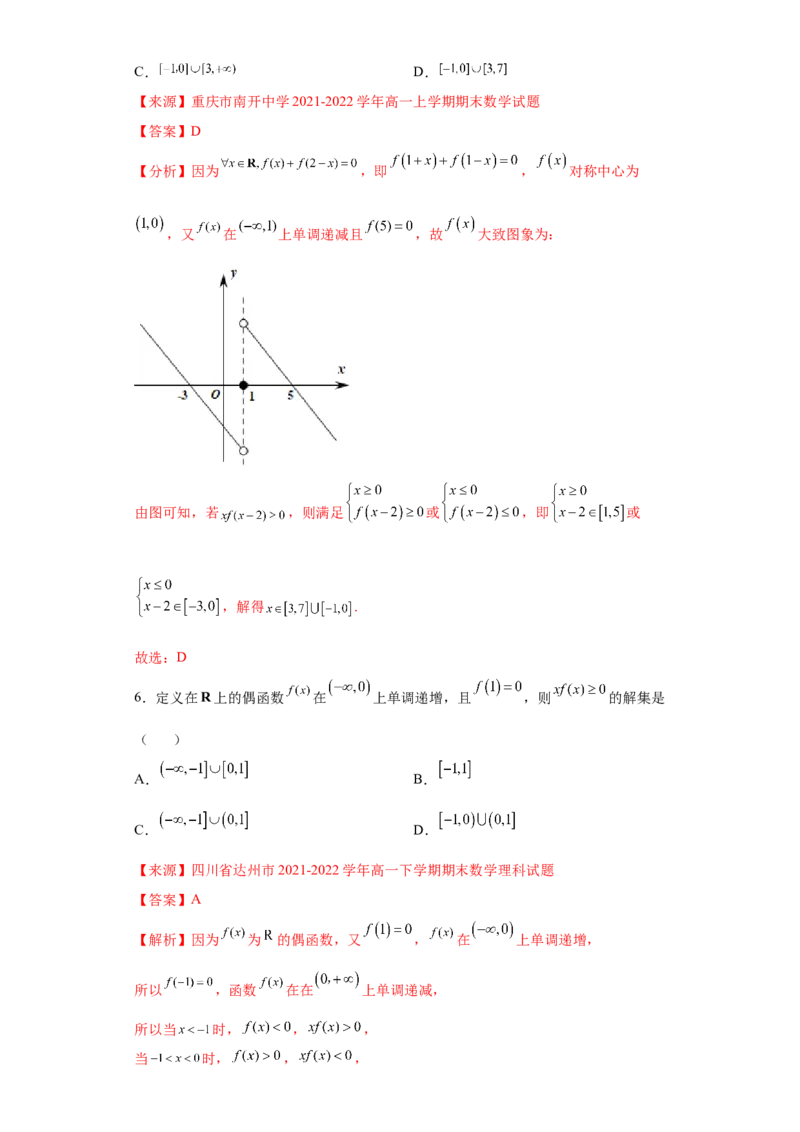
6.若函数 在 上是减函数,则实数m的取值范围是( )
A. B. C. D.
【来源】陕西省咸阳市2021-2022学年高一下学期期末数学试题
【答案】B
【解析】函数 的对称轴为 ,
由于 在 上是减函数,所以 .
故选:B
7.(2022·山西运城·高二阶段练习)已知函数
.
(1)若函数 的值域为 ,求a的取值集合;
(2)若对于任意的 ,总存在 ,使得 成立,求实数a的
取值范围.
【答案】(1) (2)【解析】(1)∵函数 的值域为 ,∴ ,
解得 ;
(2)由题意可知
对于函数 在 上是减函数,∴ ,
函数 图象开口向上,对称轴为直线 .
①当 时,函数 在 上为增函数,
,
∴ 此时 ;
②当 时,函数 在区间 上为减函数,在 上为增函数,
,
∴ 此时 ;
③当 时,函数 在区间 上为减函数,在 上为增函数,
,
∴ 此时 ;
④当 时,函数 在 上是减函数,∴
,
∴ 此时 ;综上所述,实数a的取值范围是 .
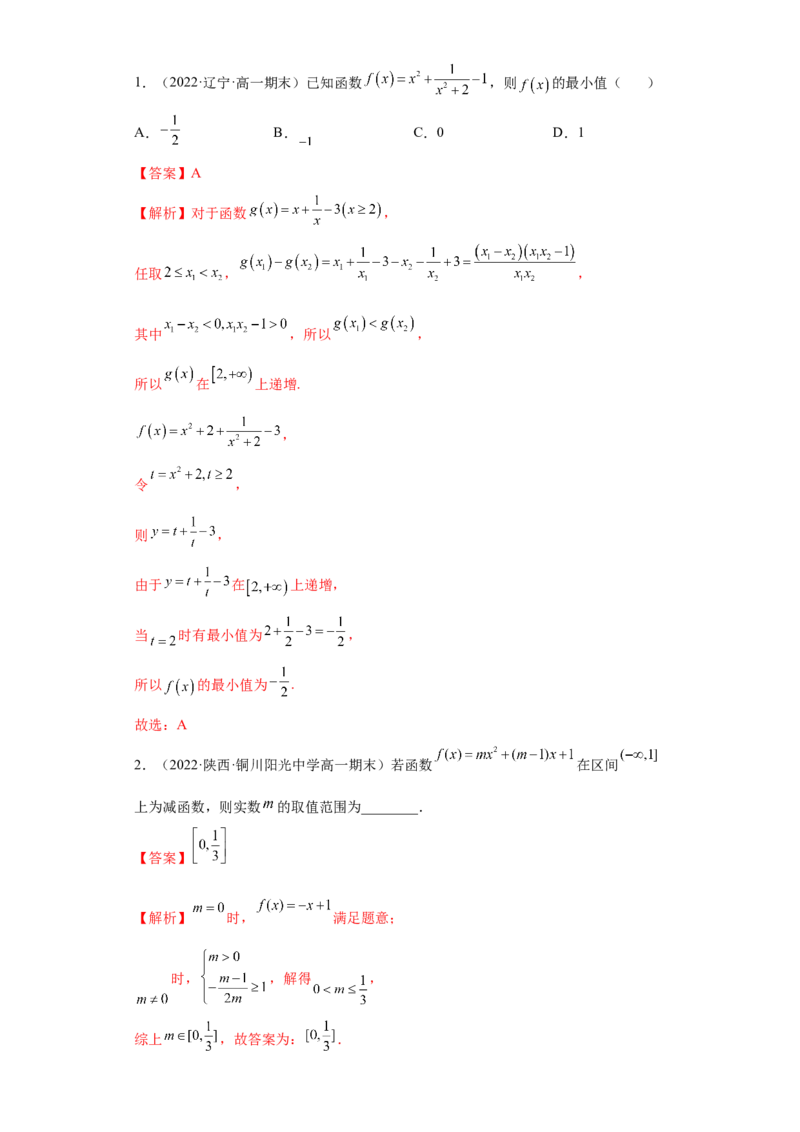
题型二:利用函数单调性求最值、求参数1.(2022·辽宁·高一期末)已知函数 ,则 的最小值( )
A. B. C.0 D.1
【答案】A
【解析】对于函数 ,
任取 , ,
其中 ,所以 ,
所以 在 上递增.
,
令 ,
则 ,
由于 在 上递增,
当 时有最小值为 ,
所以 的最小值为 .
故选:A
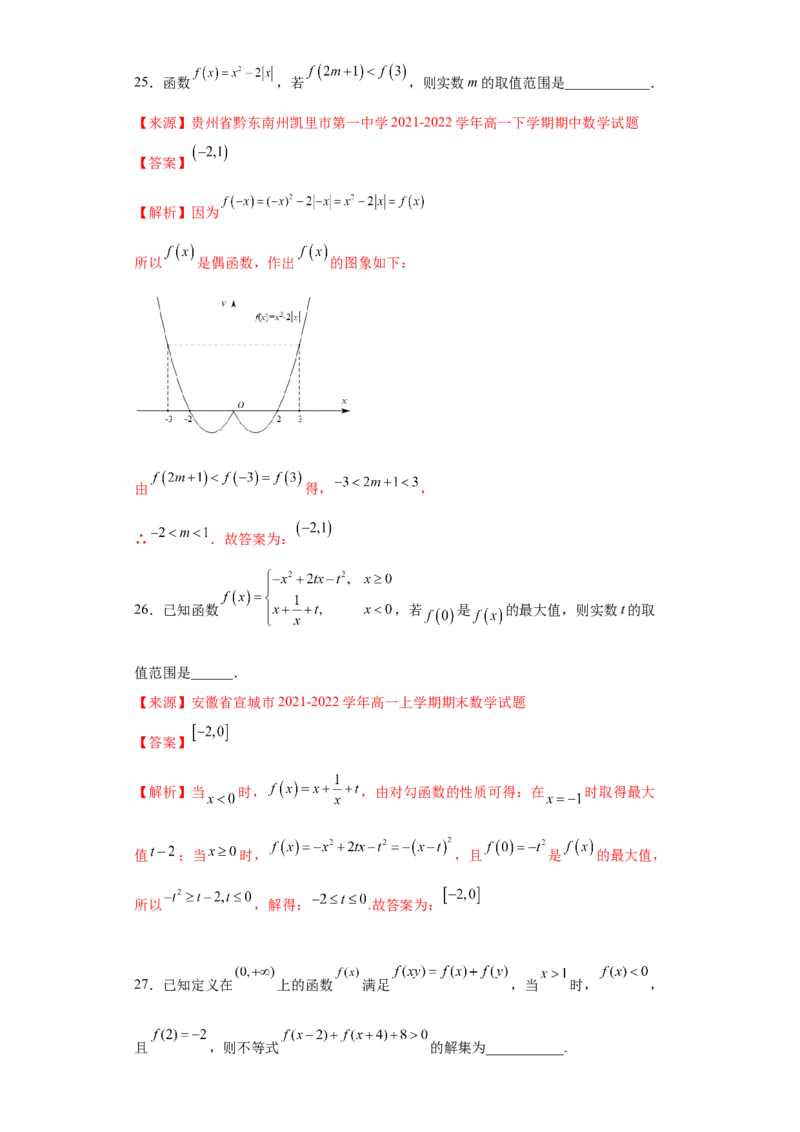
2.(2022·陕西·铜川阳光中学高一期末)若函数 在区间
上为减函数,则实数 的取值范围为________.
【答案】
【解析】 时, 满足题意;
时, ,解得 ,
综上 ,故答案为: .3.(2022·浙江浙江·高一期中)若函数 在区间 上是单调函
数,则实数t的取值范围是__________.
【答案】
【解析】 ,
时, 时, ,满足题意,
时, 时, , 单调,则
, ,
时, 时, , 单调,则
, ,
时, ,
,因此 在 是单调递增,
要使得 在 上单调,则 在 上是增函数,
因此 ,即 ,无解,
综上, 的范围是 .
故答案为: .
4.(2022·湖北·黄石一中高一期中)已知函数 在区间 上单调递减,
则实数 的取值范围为___________.
【答案】
【解析】当 时, 在 上单调递增,故在区间 上单调递增,不
合题意;当 时, 在区间 上单调递减,在区间 上单调
递增,若 在区间 上单调递减,则 , ;当 时, 在区间 上单调递减,在区间 上单调递增,
若 在区间 上单调递减,则 , ;
综上,实数 的取值范围为 .故答案为: .
5.(2022·湖北·武汉东湖新技术开发区教育发展研究院高一期末)若函数
在区间 上单调递增,则实数 的取值范围是__________.
【答案】
【解析】当 时,函数 在R上单调递增,即 在 上递增,则
,
当 时,函数 是二次函数,又 在 上单调递增,由二次函数性质知,
,
则有 ,解得 ,
所以实数 的取值范围是 .
故答案为:
6.(2022·重庆·高一期末)设函数 ,其中 .
(1)当 时,求函数 的零点;
(2)若 ,求函数 的最大值.
【答案】(1)1和 (2)答案见解析
【解析】(1)当 时,
当 时,由 得 ;
当 时,由 得 ( 舍去)当 时,函数 的零点为1和
(2)①当 时, , ,
由二次函数的单调性可知 在 上单调递减
②当 即 时, , ,
由二次函数的单调性可知 在 上单调递增
③当 时,
在 上递增, 在 上的最大值为
当 时 在 递增,在 上递减,
在 上的最大值为
, 当 时
当 时 在 上递增,
在 上的最大值为
,当 时
综上所述:
当 时,
当 时,
当 时,当 时,
7.(2022·江西·临川一中高一阶段练习)已知函数 , .
(1)若 的值域为 ,求a的值.
(2)证明:对任意 ,总存在 ,使得 成立.
【答案】(1)2(2)证明见解析
【解析】(1)解:因为 的值域为 ,所以
,解得 .
(2)证明:由题意,根据对勾函数的单调性可得 在 上单调递增,所以
.
设 在 上的值域为M,
当 ,即 时, 在 上单调递增,因为 ,
,所以 ;
当 ,即 时, 在 上单调递减,因为 ,
,所以 ;
当 ,即 时, ,
,所以 ;
综上, 恒成立,即 在 上的值域是 在 上值域的子集恒成
立,
所以对任意 总存在 ,使得 成立.题型三:利用函数奇偶性求值、求表达式、求参数
1.(江苏省徐州市第三十六中学2021-2022学年高一上学期期中数学试题)设 为
奇函数,且当 时, ,则当 时, ( )
A. B.
C. D.
【答案】B
【解析】设 ,则 ,所以 ,
又 为奇函数,所以 ,
所以当 时, .故选:B.
2.(陕西省宝鸡市渭滨区2019-2020学年高二下学期期末数学(文)试题)已知
是 上的奇函数,且当 时, ,则当 时, ( )
A. B.
C. D.
【答案】B
【解析】
【分析】由题意,设 ,则 ,则 ,
因为函数 为 上的奇函数,则 ,
得 ,
即当 时, .
故选:B.3.(河南省林州市2021-2022学年高一上学期期末考试理科数学试题)已知 是定
义在R上的奇函数,当 时, ,则当 时, ______.
【答案】
【解析】 时, , 是奇函数,此时
故答案为:
4.(四川省攀枝花市第七高级中学校2021-2022学年高一上学期第一次月考数学试
题)已知函数 是定义在 上的函数, 恒成立,且
(1)确定函数 的解析式;
(2)用定义证明 在 上是增函数;
(3)解不等式 .
【答案】(1) (2)证明见解析(3)
【解析】(1)
解:因为函数 , 恒成立,
所以 ,则 ,
此时 ,所以 ,
解得 ,所以 ;
(2)证明:设 ,
则 ,
,,且 ,则 ,
则 ,即 ,
所以函数 是增函数.
(3) , , 是定义在 上的增函数,
,得 ,所以不等式的解集为 .
题型四:函数单调性与奇偶性的综合问题
经典例题:
1.下列说法正确的是( )
A.若一个函数的定义域关于坐标原点对称,则这个函数为奇函数
B.若一个函数为偶函数,则它的定义域关于坐标原点对称
C.若一个函数的定义域关于坐标原点对称,则这个函数为偶函数
D.若函数f(x)的定义域为 ,且 ,则 是奇函数
【来源】2.4.4 函数的奇偶性 (分层练习)-2022年初升高数学无忧衔接
【答案】B
【解析】
奇偶函数的定义域一定关于原点对称,B正确;
定义域关于原点对称的函数不一定具有奇偶性,如R上的函数 既不是奇函数,
也不是偶函数,A,C都错误,
如函数 的定义域是R,且有 ,但 不是奇函数,D错误.
故选:B
2.下列函数既是奇函数,又是增函数的是( )
A. B. C. D.
【答案】B
【解析】解:由题意得:对于选项A:函数 是偶函数,故不符合题意;
对于选项B:函数 是奇函数,且是单调递增函数,故符合题意;
对于选项C:函数 是非奇非偶函数,故不符合题意;
对于选项D:根据幂函数的性质可知函数 是奇函数,但不是单调递增函数,故
不符合题意;
故选:B
3.已知函数 是偶函数, 的图象关于直线l对称,则直线l的方程为
( )
A. B. C. D.
【来源】陕西省西安地区八校2022届高三下学期5月联考理科数学试题
【答案】A
【解析】因为函数 是偶函数,所以 的图象关于直线 对称,
向左平移两个单位可得 的图象关于直线 对称.
故选:A
4.若偶函数 在 上是减函数,则( )
A. B.
C. D.
【答案】B
【解析】 为偶函数, ;
在 上是减函数, ,
即 .
故选:B.
5.设 是R上的任意函数,则下列叙述正确的是( )A. 是奇函数 B. 是奇函数
C. 是奇函数 D. 是奇函数
【答案】C
【解析】A选项:设 , ,则
为偶函数,A错误;
B选项:设 ,则 , 与 关系不定,
即不确定 的奇偶性,B错误;
C选项:设 ,则 ,则
为奇函数,C正确;
D选项:设 ,则 ,则
为偶函数,D错误.
故选:C.
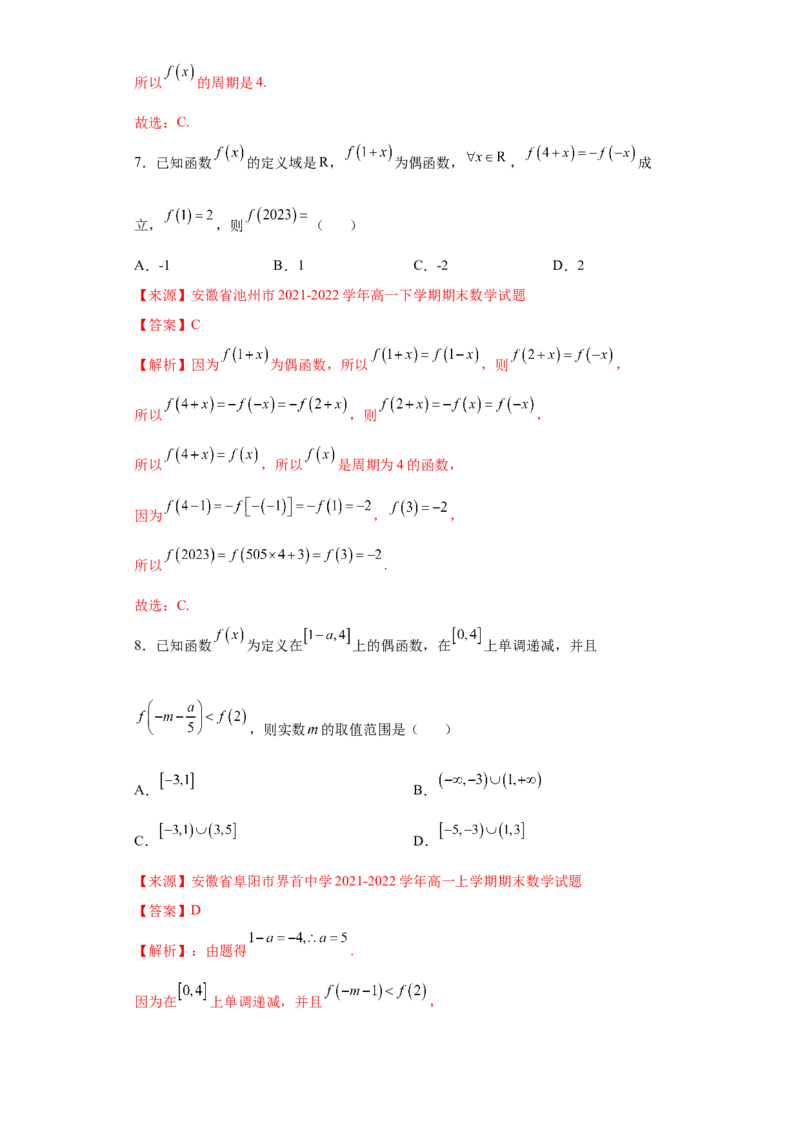
6.已知函数 的定义域为 , 为奇函数, 为偶函数,则函数
的周期是( )
A. B. C. D.
【来源】陕西省西安市长安区第一中学2021-2022学年高一下学期期末数学试题
【答案】C
【解析】因为 为奇函数,所以 ,
因为 为偶函数,所以 ,则 ,
则 ,即 ,
所以 ,即 ,则 ,所以 的周期是4.
故选:C.
7.已知函数 的定义域是R, 为偶函数, , 成
立, ,则 ( )
A.-1 B.1 C.-2 D.2
【来源】安徽省池州市2021-2022学年高一下学期期末数学试题
【答案】C
【解析】因为 为偶函数,所以 ,则 ,
所以 ,则 ,
所以 ,所以 是周期为4的函数,
因为 , ,
所以 .
故选:C.
8.已知函数 为定义在 上的偶函数,在 上单调递减,并且
,则实数 的取值范围是( )
A. B.
C. D.
【来源】安徽省阜阳市界首中学2021-2022学年高一上学期期末数学试题
【答案】D
【解析】:由题得 .
因为在 上单调递减,并且 ,所以 ,所以 或 .
故选:D
9.已知偶函数 的定义域为 ,当 时, ,若 ,则
的解集为( )
A. B. C. D.
【来源】河北省秦皇岛市2021-2022学年高一上学期期末数学试题
【答案】D
【解析】因为 为偶函数,所以 ,解得 .
在 上单调递减,且 .
因为 ,所以 ,解得 或 .
故选:D
10.设奇函数 在 上是增函数, .若函数 对所有
的 都成立,则当 时,t的取值范围是( )
A. B.
C. ,或 ,或 D. ,或 ,或
【来源】陕西省西安市长安区第一中学2021-2022学年高一下学期期中数学试题
【答案】C
【解析】因奇函数 在 上是增函数, ,则
,依题意, , 恒成立,
则有 ,解得 或 或 ,
所以t的取值范围是 或 或 .
故选:C
11.已知函数 是定义在 上的奇函数,且 ,若对于任意
两个实数 , 且 ,不等式 恒成立,则不等式
的解集是( )
A. B.
C. D.
【来源】湖北省新高考联考协作体2021-2022学年高一下学期期末数学试题
【答案】D
【解析】:由题可知, 在区间 上单调递减,
又 为奇函数,则 ,且 ,故 ,
设 ,则 ,故 为偶函数,
又 在区间 上单调递增,在区间 上单调递减,
又 ,所以 的解集为 ,
即 的解集为 .
故选:D.
12.设函数 的定义域为R, 为奇函数, 为偶函数,当 时,
.若 ,则 ( )A. B. C. D.
【来源】北京一零一中学2021-2022 学年高一下学期期末考试数学模拟试题(一)
【答案】D
【解析】因为 是奇函数,所以 ①;
因为 是偶函数,所以 ②.
令 ,由①得: ,由②得: ,
因为 ,所以 ,
令 ,由①得: ,所以 .
思路一:从定义入手.
所以 .
思路二:从周期性入手
由两个对称性可知,函数 的周期 .
所以 .
故选:D.
二、多选题
13.已知函数 是定义在 上的偶函数,当 时, ,则( )
A. 的最小值为 B. 在 上单调递减
C. 的解集为 D.存在实数 满足
【来源】广东省深圳市2021-2022学年高一下学期期末数学试题【答案】ACD
【解析】:函数 是定义在 上的偶函数,当 时, ,
设 ,则 ,所以 ,因为 是偶函数,所以 ,
所以 ,所以 ,
函数图象如下所示:
可得 时, 在 时取得最小值 ,由偶函数的图象关于 轴对称,可得
在 上取得最小值 ,故A正确;
在 上单调递减,在 上单调递增,故B错误;
由 或 ,解得 或 ,综上可得 的解集为
,故C正确;
由 , ,即存在实数 满足 ,故D正确;
故选:ACD.
14.已知函数 为 上的奇函数, 为偶函数,下列说法正确的有
( )
A. 图象关于直线 对称 B.
C. 的最小正周期为4 D.对任意 都有
【来源】湖南省邵阳市第二中学2021-2022学年高一下学期期末数学试题
【答案】ABD【解析】由 的对称中心为 ,对称轴为 ,
则 也关于直线 对称且 ,A、D正确,
由A分析知: ,故 ,
所以 ,
所以 的周期为4,则 ,B正确;
但不能说明 最小正周期为4,C错误;
故选:ABD
四、解答题
15.已知函数 对任意 ,都有 ,且当 时,
.
(1)求证: 在 上是增函数;
(2)若关于a的方程 的一个实根是1,求 的值;
(3)在(2)的条件下,已知 ,解关于x的不等式 .
【来源】辽宁省大连市大连育明高级中学2021-2022学年高一上学期期末数学试题
【答案】(1)证明见解析(2) (3)详见解析
【解析】(1)依题意 ,且 时, ,
令 ,则 ,
,
任取 ,
,
由于 ,所以 ,
所以 ,所以 在 上递增.
(2)由(1)知, 在 上递增,
,
.
(3)
依题意 , 在 上递增, .
, ,
,
当 时,不等式的解集为空集.
当 时,不等式的解集为 .
当 时,不等式的解集为 .
16.已知函数 , ( ).
(1)当 时,求不等式 的解集;
(2)若对任意 ,不等式 恒成立,求 的取值范围;
(3)若对任意 ,存在 ,使得 ,求 的取值范围.
【来源】北京市朝阳区2021-2022学年高一上学期期末数学试题
【答案】(1) 或 (2) (3)
(1)当 时,由 得 ,
即 ,解得 或 .
所以不等式 的解集为 或 .
(2)由 得 ,
即不等式 的解集是 .所以 ,解得 .
所以 的取值范围是 .
(3)当 时, .
又 .
①当 ,即 时,
对任意 , .
所以 ,此时不等式组无解,
②当 ,即 时,
对任意 , .
2