文档内容
专题 4.4 对数函数
1 对数函数
(1)对数函数的概念
函数y=log x(a>0 , a ≠1)叫做对数函数,其中x是自变量,定义域是(0,+∞).
a
解释
函数y=log x中系数为1,底数是不为1正实数的常数,真数为变量x.
a
(2)图像与性质
a>1 00,且
a
a≠1)的函数称为对数型函数.
4 反函数
指数函数y=ax (a>0,且a≠1)与对数函数y=log x(a>0 , a ≠1)互为反函数.
a
它们的图象关于直线y=x对称,定义域与值域相反.
比如 y=2x与y=log x互为反函数.
2一、单选题
1.函数 的单调递减区间是
A. B. C. D.
【来源】宁夏石嘴山市平罗中学2021-2022学年高一上学期期末考试数学试题
【答案】A
【解析】∵x2+2x﹣3>0,
∴x>1或x<﹣3;
又∵y=x2+2x﹣3在(﹣∞,﹣1]上是减函数,在[﹣1,+∞)上是增函数;
且y=log x在(0,+∞)上是增函数;
2
∴函数y=log (x2+2x﹣3)的单调递减区间为(﹣∞,﹣3);故选A.
2
2.已知 , , ,则 的大小关系为( )
A. B.
C. D.
【来源】贵州省黔西南州2021-2022学年高一下学期期末质量检测数学试题
【答案】C
【解析】 , .故选:C.
3.设函数 ,则使得 成立的 的取值范围为
( )
A. B.C. D.
【答案】D
【解析】方法一 :
由 得 ,
则 ,解得 或 .
方法二 :根据题意,函数 ,其定义域为 ,
有 ,即函数 为偶函数,
设 ,则 ,
在区间 上, 为增函数且 , 在区间 上为增函数,
则 在 上为增函数,
,
解得 或 ,故选:D.
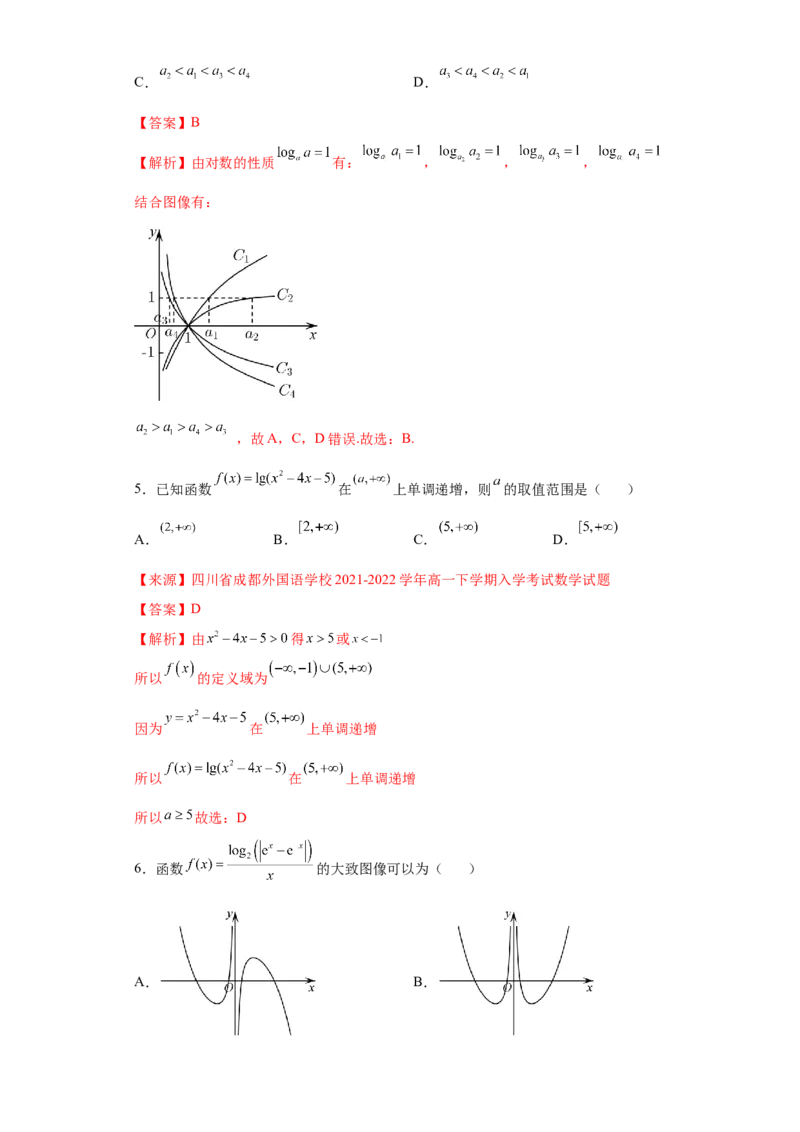
4.已知图中曲线 分别是函数 , , ,
的图像,则 的大小关系是( )
A. B.C. D.
【答案】B
【解析】由对数的性质 有: , , ,
结合图像有:
,故A,C,D错误.故选:B.
5.已知函数 在 上单调递增,则 的取值范围是( )
A. B. C. D.
【来源】四川省成都外国语学校2021-2022学年高一下学期入学考试数学试题
【答案】D
【解析】由 得 或
所以 的定义域为
因为 在 上单调递增
所以 在 上单调递增
所以 故选:D
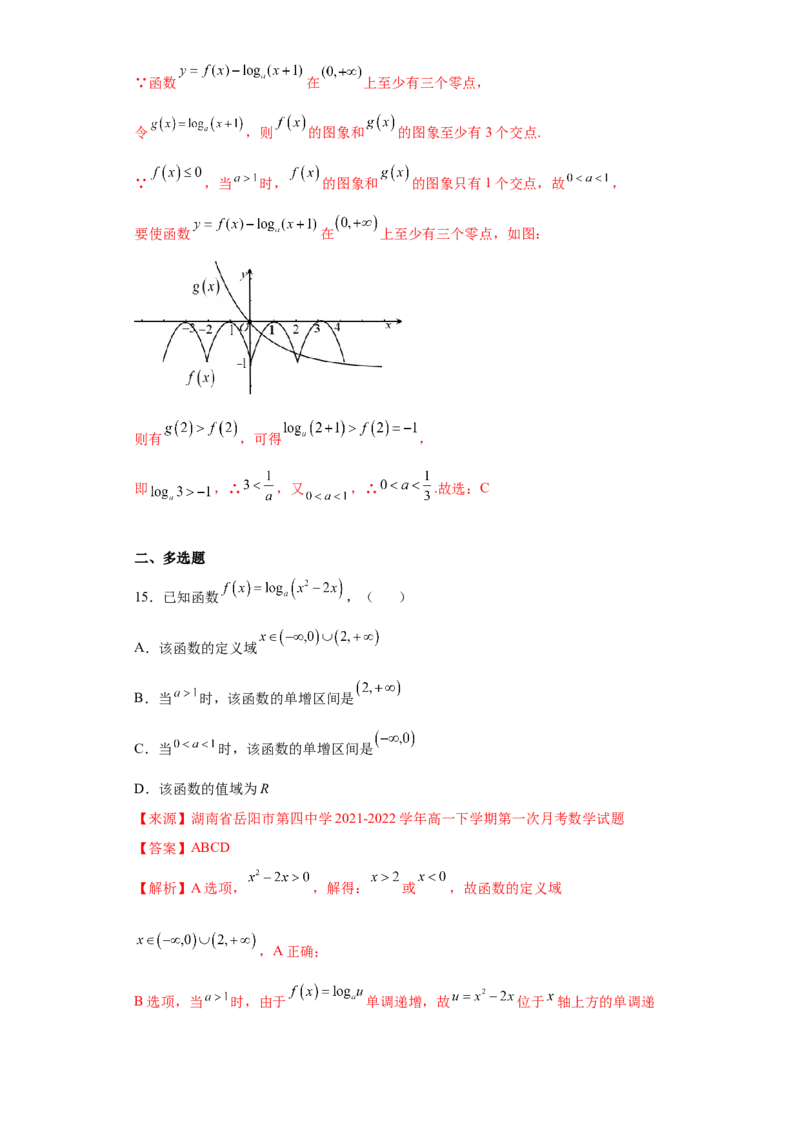
6.函数 的大致图像可以为( )
A. B.C. D.
【来源】云南省曲靖市第二中学2021-2022学年高一下学期期末考试数学试题
【答案】C
【解析】依题意,函数 的定义域为 , ,
即 为奇函数,选项B,D不满足;
当 时, 单调递增,即 ,恒有 ,选项A不满足,
C满足.故选:C
7.已知函数 ,若 ,则( )
A. B.
C. D.以上选项均有可能
【来源】辽宁省县级重点高中协作体2021-2022学年高一下学期期末考试数学试题
【答案】C
【解析】作出函数 的图象,如图:
由题意可知, ,且由图象可知, ,
所以即 ,
所以 ,即 , ,即 ,
故选:C
8.已知函数 是定义在R上的偶函数,且在区间 上单调递减.若实数 满足
,则 的取值范围是( )
A. B. C. D.
【来源】江西省抚州市临川第一中学暨临川第一中学实验学校2021-2022学年高一上
学期期末数学试题
【答案】D
【解析】∵ 是定义域为 上的偶函数,且在区间 上单调递减
∴函数 在区间 上是单调递增函数,
∴不等式 ,
可化为 ,即 ,
则 ,又函数在区间 上是单调递增函数,
∴ ,即 ,
解得 .故选:D
9.已知函数 , ,对于任意 ,存在
有 ,则实数 的取值范围是( )
A. B.C. D.
【来源】江西省景德镇市第一中学2021-2022学年高一上学期期末数学试题
【答案】B
【解析】对于任意 ,存在 有 等价于
.
由 ,函数 单调递增,可得
, ,对称轴为 ,
时, ,
,解得 .故选:B
10.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足
,其中星等为mk的星的亮度为Ek(k=1,2).已知太阳的星等是–
26.7,天狼星的星等是–1.45,则太阳与天狼星的亮度的比值为
A.1010.1 B.10.1 C.lg10.1 D.
【来源】第11讲 对数-【暑假自学课】2022年新高一数学暑假精品课(苏教版2019
必修第一册)
【答案】A两颗星的星等与亮度满足 ,令 ,
.故选A.
11.函数 是定义在R上的偶函数,且在 单调递增,若 , ,,则( )
A. B.
C. D.
【来源】四川省巴中市2021-2022学年高一下学期期末数学试(文)题
【答案】C
【解析】由偶函数知 ,又 ,
, ,
显然 ,又在 单调递增,则 .
故选:C.
12.已知函数 ,若不等式 恒成立,则实数a的
取值范围为( )
A. B. C. D.
【答案】B【解析】因为函数 满足 ,且定义域为R,
所以函数 为偶函数,且当 时,函数 单调递增,
故 可以变为 ,即 ,
当 时, ;
当 时,可得 .
又 ,当且仅当 时取等号,
所以 ,解得 .故选:B.
13.已知函数 若 存在最小值,则实数a的取值范围是( )A. B.
C. D.
【来源】贵州省威宁县2021-2022学年高一上学期高中素质教育期末测试数学试题
【答案】D
【解析】∵函数
∴当 时, 的范围是 ;当 时, ,
,
由题意 存在最小值,则 ,
解得 .
故选:D.
14.定义在R上的偶函数 满足对任意 ,有 ,且当
时, ,若函数 在 上至少有3个零
点,则实数 的取值范围是( )
A. B. C. D.
【来源】福建省龙岩第一中学2021-2022学年高一上学期第三次月考数学试题
【答案】C
【解析】∵ ,且 是定义域为 的偶函数,
令 可得 ,
又 ,∴ ,则有 ,
∴ 是最小正周期为2的偶函数.
当 时, ,开口向下,顶点为 的抛物线.∵函数 在 上至少有三个零点,
令 ,则 的图象和 的图象至少有3个交点.
∵ ,当 时, 的图象和 的图象只有1个交点,故 ,
要使函数 在 上至少有三个零点,如图:
则有 ,可得 ,
即 ,∴ ,又 ,∴ .故选:C
二、多选题
15.已知函数 ,( )
A.该函数的定义域
B.当 时,该函数的单增区间是
C.当 时,该函数的单增区间是
D.该函数的值域为R
【来源】湖南省岳阳市第四中学2021-2022学年高一下学期第一次月考数学试题
【答案】ABCD
【解析】A选项, ,解得: 或 ,故函数的定义域
,A正确;
B选项,当 时,由于 单调递增,故 位于 轴上方的单调递增区间即为该函数的单增区间,故该函数的单增区间是 ,B正确;
C选项,当 时,由于 单调递减,故 位于 轴上方的单调
递减区间即为该函数的单增区间,故该函数的单增区间是 ,C正确;
D选项, 能取到 的任何值,故该函数的值域为R,D正确.
故选:ABCD
16.已知 ,则下列结论正确的是( )
A.
B.函数 单调递增区间为
C.当 时,方程 有三个不等实根
D.当且仅当 时,方程 有两个不等实根
【来源】广东省汕尾市2021-2022学年高一上学期期末数学试题
【答案】AC
【解析】A: ,所以 ,故A正确;
B:作出函数 的图象,如图,由图象可知,函数 在 和 上单调递增,
但不连续,所以不能用“ ”的符号,故B错误;
C:由图象可知,当 时,函数 与 的图象有3个交点,方程
有3个不等的实根,故C正确;
D:由图象可知,当 或 时,函数 与 的图象有2个交点,方
程 有2个不等的实根,故D错误;
故选:AC.17.已知函数 , ,则下列说法正确的是( )
A.若函数 的定义域为 ,则实数 的取值范围是
B.若函数 的值域为 ,则实数
C.若函数 在区间 上为增函数,则实数 的取值范围是
D.若 ,则不等式 的解集为
【来源】重庆市第八中学2021-2022学年高一上学期期末数学试题
【答案】ABC
【解析】A选项:因为 的定义域为 ,所以 恒成立,则
,解得: ,故正确;
B选项:因为 的值域为 ,所以 ,所以 ,
解得 ,故正确;
C选项:因为函数 在区间 上为增函数,由复合函数的单调性可知:
,解得 ,故正确;D选项:当 时, ,由 ,可得 ,解
得: ,故错误;
故选:ABC.
18.已知函数 ,则下列四个命题中正确命题的个数是( )
A.在 上单调递减 B. 上单调递减
C. 的图象关于直线 对称 D. 的值域为
【来源】江西省宜春市铜鼓中学2021-2022学年高一下学期开学考数学试题
【答案】BC
【解析】对于函数 ,有 ,解得 ,
所以,函数 的定义域为 ,且 .
对于AB选项,内层函数 在 上单调递增,在 上单调递减,
由于外层函数 为增函数,故函数 在 上单调递增,在 上单调递减,
A错B对;
对于C选项, ,
所以,函数 的图象关于直线 对称,C对;
对于D选项,当 时, ,故
,D错.故选:BC.
19.中国传统文化中很多内容体现了数学的“对称美”,如图所示的太极图是由黑白
两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相对统一的和谐
美,定义:圆O的圆心在原点,若函数的图像将圆O的周长和面积同时等分成两部分,则这个函数称为圆O的一个“太极函数”,则( )
A.对于圆O,其“太极函数”有1个
B.函数 是圆O的一个“太极函数”
C.函数 不是圆O的“太极函数”
D.函数 是圆O的一个“太极函数”
【来源】山东省东营市广饶县第一中学2021-2022学年高一下学期开学考试数学试题
【答案】BD
【解析】:对于A选项,圆O,其“太极函数”不止1个,故错误;
对于B选项,由于函数 ,当 时, ,
当 时, ,故 为奇函数,故根据对称
性可知函数 为圆O的一个“太极函数”,故正确;
对于C选项,函数定义域为 , ,也是奇函数,故为圆O的
一个“太极函数”,故错误;
对于D选项, 函数定义域为 ,
,故为奇函数,故
函数 是圆O的一个“太极函数”,故正确.故选:BD
三、填空题
20.函数 ( 且 )的图象恒过定点_________
【来源】山西省长治市第四中学校2021-2022学年高一上学期期末数学试题
【答案】
【解析】解:因为函数 ( 且 ),
令 ,解得 ,所以 ,即函数 恒过点 ;
故答案为:
21.函数 的定义域是__________.
【来源】云南省昆明市2021-2022学年高一下学期期末质量检测数学试题
【答案】
【解析】对于函数 ,由 ,即 ,解得
.因此,函数 的定义域为 .故答案为: .
22.函数 的值域为 ,则实数 的取值范围为______.
【来源】中原名校2021-2022学年高一上学期12月第三次大联考数学试题
【答案】
【解析】解:由题可知,函数 的值域为 ,
令 ,由题意可知 为函数 的值域的子集.
①当 时, ,此时 ,
函数 的值域为 ,合乎题意;
②当 时,若 为函数 的值域的子集,
则 ,解得 .综上所述,实数 的取值范围是 .
故答案为: .
23.设函数 ,则 的单调递增区间为_________.
【来源】河北省唐县第一中学2021-2022学年高一下学期5月月考数学试题
【答案】
【解析】记 ,
因为 为减函数,所以当 单调递增时, 单调递减,
由 得 或 ,
又当 时, 单调递减.
故 .
故答案为: .
24.若不等式 在 上恒成立,则实数a的取值范围为____.
【来源】甘肃省张掖市2021-2022学年高一上学期期末数学试题
【答案】
【解析】: 变形为: ,即
在 上恒成立.
令 ,
若 ,此时 在 上单调递减,
,而当 时, ,显然不合题
意;当 时,画出两个函数的图象,
要想满足 在 上恒成立,只需 ,即
,解得: .
综上:实数a的取值范围是 .故答案为:
25.已知 为奇函数, ,若对 、 ,
恒成立,则b的取值范围为___________.
【来源】河南省信阳市信阳高级中学2021-2022学年高一下学期第一次月考数学(文
科)试题
【答案】
【解析】 的定义域为 , 为奇函数,所以 ,
所以 ,
, ,
所以 的值域为 .对于函数 , 的定义域为 ,所以 恒成立,
所以 恒成立,所以 ,此时 , ,
所以 的值域为 ,由于对 、 , 恒成立,
所以 ,所以 的取值范围是 . 故答案为:四、解答题
26.已知函数 .
(1)判断函数 的奇偶性,并进行证明;
(2)若实数 满足 ,求实数 的取值范围.
【来源】云南省德宏州2021-2022学年高一上学期期末统一监测数学试题
【答案】(1) 为奇函数,证明见解析(2)
【解析】(1) 为奇函数,证明如下:
定义域为 , ,
为定义在 上的奇函数.
(2) ,
又 在 上单调递增, 在 上单调递增;
由(1)知: ,
, ,
,即 ,
,解得: ,即实数 的取值范围为 .
27.已知函数 .
(1)求函数f(x)的值域;(2)若 ,且 ,求实数m的取值范围.
【来源】云南省保山市2021-2022学年高一下学期期末质量监测数学试题
【答案】(1) (2)
【解析】(1)因为 定义域为 ,
则
设 ,
令 ,
所以 值域为
(2)设 , 因为 所以
即 ,即 ,所以
则 的两根为
整理得
因为 解得 再由韦达定理可得:
则
解得 综上,
28.已知函数 是 上的偶函数,且当 时, .
(1)求 的值;
(2)求函数 的表达式,并直接写出其单调区间(不需要证明);
(3)若 ,求实数 的取值范围.
【来源】云南省寻甸一中、昆明西联学校阳宗海学校2021-2022学年高一上学期期末联考数学试题
【答案】(1) (2)答案见解析(3)
【解析】(1)因为 是 上的偶函数,所以 .
(2)当 时,则 ,则 ,
故当 时, ,
故 ,
故 的单调递增区间为 ,单调递减区间为 .
(3)若 ,即 ,即
因为 在 单调递减,所以 ,
故 或 ,解得: 或 ,即 .
29.已知函数 的图象关于原点对称,其中 为常数.
(1)求 的值;
(2)当 时, 恒成立,求实数 的取值范围.
【答案】(1) (2)
【解析】(1)函数 的图象关于原点对称,则函数 为奇
函数,有 ,
即 ,解得 ,当 时,不满足题意,所以 ;
(2)由 ,得 ,即 ,
令 ,易知 在 上单调递减,则 的最大值为 .又因为当 时, 恒成立,
即 在 恒成立,所以 .
30.已知函数
(1)若m=1,求函数f(x)的定义域;
(2)若函数f(x)在区间 上是增函数,求实数m的取值范围.
【答案】(1) (2)
【解析】(1)若m=1,则
要使函数有意义,需 ,解得x∈
∴若m=1,函数f(x)的定义域为 .
(2)若函数 在区间 上是增函数,
则 在区间 上是减函数且 在区间 上
恒成立,∴ ,且 ,即 且 .
31.已知函数 ),当点M(x,y)在函数g(x)的图象上运动
时,对应的点 在f(x)的图象上运动,则称g(x)是f(x)的相关函数.
(1)解关于x的不等式 ;
(2)若对任意的 ,f(x)的图象总在其相关函数图象的下方,求a的取值范围;(3)设函数 , ,当 时,求|F(x)|的最大值.
【来源】湖北省恩施州高中教育联盟2021-2022学年高一下学期期中数学试题
【答案】(1) (2)(0,1](3)
【解析】(1)解:依题意得
则 ,
所以 ,
所以原不等式的解集为 .
(2)由题意得 ,所以 ,
所以f(x)的相关函数为 .
依题意,对任意的 ,f(x)的图象总在其相关函数图象的下方,
即当 时, 恒成立①.
由 ,对任意的 总成立, ,结合题设条件有 ,
在此条件下,①等价于当 时, 恒成立,
即 ,即 .
设 ,
要使当 时, 恒成立,
只需 ,即 成立,
解得 ,即a的取值范围是(0,1].
(3)由(2)可得当 时,在区间(0,1)上, ,即 .
设 ,则 .
令 ,则 ,
所以 ,
因为 (当且仅当 时,等号成立),
可得 ,当 时,等号成立,
满足 ,则t的最大值为 ,
所以|F(x)|的最大值是 .