专题4.6《数列》单元测试卷（B卷提升篇）解析版_E015高中全科试卷_数学试题_选修2_01.同步练习_同步练习（第四套）_专题4.6《数列》单元测试卷（B卷提升篇）

专题4. 6《数列》单元测试卷（B 卷提升篇）（人教A版第二册,浙江专 用） 参考答案与试题解析 第Ⅰ卷（选择题） 一．选择题（共10小题，满分50分，每小题5分） {a } S a S 1．（2020·贵州毕节市·贵阳一中高三月考（理））已知等差数列 n 的前n项和为 n， 3=5，则 5=（ ） A．5 B．25 C．35 D．50 【答案】B 【解析】 {a } 由题意可知， n 为等差数列， 5(a a ) 52a 525 所以S  1 5  3  25 5 2 2 2 故选：B 2．（2020·全国高二课时练习）设数列 a n  nN 是等差数列， S n是其前n项和，且 S 5 S 6， S S S 6 7 8，则下列结论中错误的是（ ） d 0 a 0 S S S S S A． B． 7 C． 9 6 D． 6与 7均为 n的最大值 【答案】C 【解析】 S S S S S S S a 0 S S a 0 S S a 0 由于 5 6， 6 7 8，所以 6 5 6 ， 7 6 7 ， 8 7 8 ， d 0,a 0 S S S S S a a a 3a 0 S S 所以 7 ， 6与 7均为 n的最大值．而 9 6 7 8 9 8 ，所以 9 6， 所以C选项结论错误． 故选:C． a  a 9 a 1 T aa …a (n1,2,…) 3．（2021·山东高三专题练习）在等差数列 n 中， 1 ， 5 .记 n 1 2 n ，则T  数列 n （ ） A．有最大项，有最小项 B．有最大项，无最小项 C．无最大项，有最小项 D． 无最大项，无最小项 【答案】B 【解析】 a a 19 d  5 1  2 由题意可知，等差数列的公差 51 51 ， a a n1d 9n122n11 则其通项公式为： n 1 ， a a a a a 0a 1a  注意到 1 2 3 4 5 6 7  ， T 0 T 0i6,iN 且由 5 可知 i ， T i a 1i7,iN 由T i 可知数列 T  不存在最小项， i1 n a 9,a 7,a 5,a 3,a 1,a 1 由于 1 2 3 4 5 6 ， T  T 63 T 6315945 故数列 n 中的正项只有有限项： 2 ， 4 . T  T 故数列 n 中存在最大项，且最大项为 4. 故选：B. 1a a  n 4．（2020·河南高二月考（文））在数列 a  中，a 2， n1 1a ，则a （ ） n 1 n 2021 1 1   A．2 B． 3 C． 2 D．3 【答案】A 【解析】 1a 1 1 a  n a   a  ∵a 2， n1 1a ，∴ 2 3， 3 2 ，a 3，a 2. 1 n 4 5 T 4 ∴该数列是周期数列，周期 .202150541 a a 2 又 ，∴ 2021 1 ， 故选：A. 5．（2020·贵州毕节市·贵阳一中高三月考（理））古代数学著作《九章算术》有如下问题：“今有女子善 织，日自倍，五日五尺，问日织几何?”意思是：“女子善于织布，每天织的布都是前一天的2倍，已知她5 天共织布5尺，问这名女子每天分别织布多少?”某数学兴趣小组依托某制造厂用织布机完全模拟上述情景， 则从第一天开始，要使织布机织布的总尺数为165尺，则所需的天数为（ ） A．7 B．8 C．9 D．10 【答案】D 【解析】 x(125) 5 5 x  设该女子第一天织布x尺，则5天共织布 12 ，解得 31尺，在情境模拟下，设需要n天织布 5 (12n) 总尺数达到165尺，则有 31 165，整理得 ，解得 .故选：D． 12 2n 1024 n10 1 1 6．（2020·四川师范大学附属中学高二期中（文））已知等比数列 a n  中， a 2  4 ,a 5  32 ，则数列 log a  10 2 n 的前 项之和是（ ） 45 35 55 55 A． B． C． D． 【答案】D 【解析】 a  q 设等比数列 n 的公比为 ， 1 1 1 1 1 a  ,a  a q3  q3  q  由 2 4 5 32 ，可得 2 4 32 ，解得 2 ， n 1 1 1 1 又由 a 1 q a 1  2  4 ，解得 a 1  2 ，所以 a n   2   ， 1 log a log ( )n n 则 2 n 2 2 ，10[(1)(10)] 数列 log 2 a n  的前10项之和为 S 10  2 55 . 故选：D. a  a 15 3a 3a 2  nN* 7．（2021·全国高二课时练习）数列 n 中， 1 ， n1 n ，则该数列中相邻两项的 乘积是负数的是（ ） a ,a a ,a a ,a a ,a A． 21 22 B． 22 23 C． 23 24 D． 24 25 【答案】C 【解析】 2  2 472n a a  a 15(n1)     n1 n 3 ，则 n  3 3 ． (452n)(472n) 45 47 0 n 要使 a a 0 ，即 9 ，可得 2 2 ，nN*， n1 n a a ∴n=23．则该数列中相邻两项的乘积为负数的项是 23和 24， 故选：C 1a b  n 8．（2020·浙江高三月考）已知数列 a n  是首项为a，公差为1的等差数列，数列 b n  满足 n a n .若 nN* b b a 对任意的 ，都有 n 5成立，则实数 的取值范围是（ ） 6,5 6,5 5,4 5,4 A． B． C． D． 【答案】D 【解析】 1a 1 b  n  1 由已知 n a a n n 1 1 1 1 1 1  对nN*都有b b 成立，即a a ，即a a  n 5 n 5 n 5 a  又数列 n 是首项为 a ，公差为1的等差数列，1 0 a n an1且数列 a n  是单调递增数列，当n时，a n ， 5a10  所以a 0，a 0，即 6a10，解得 5a4 . 5 6 5,4 即实数a的取值范围是 故选：D 9．（2020·成都市·四川电子科大实验中学高一期中）设数列 a n  满足 a 1 1 ， a n1 a n  2 1 n  nN* ， a  则数列 n 的通项公式为（ ）． a 2  1 2  nN* a 2  1 1  nN*     A． n  2n  B． n  2n  a 1 1  nN* a 2 1  nN* C． n 2n1 D． n 2n 【答案】B 【解析】 1 a a   n1 n 2n ， 1 1 1 a a  a a  a a  所以当n2时， n n1 2n1 ， n1 n2 2n2 ， ， 2 1 21 ，  1 1 1 a a    将上式累加得： n 1 21 22 2n1 ， 1 1 n1 1    2  2  a 1 n1，即 n1 ， n 1 1 1 1 1   a 2   2 2 n 2 (n2) a 1 n1 又 时， 1 也适合，1  1  a 2 2  1  n 2n1  2n ． 故选：B． a  b  2a a 3n1 10．（2020·成都市实验外国语学校（西区）高一期中）已知数列 n ， n 中满足 n1 n ， 1 a 1 10 ， b n a n 1 ，若 b n  前n项之和为 S n ，则满足不等式 S n 6  170 的最小整数n是（ ）. A．8 B．9 C．11 D．10 【答案】D 【解析】 2a a 3 由题意可知： n1 n ， 1 3 a  a  即 n1 2 n 2 ， 1 a 1 a 1 即 n1 2 n ， Qa 10 又 1 ， a 19 1 ， 1  a 1 即数列 n 是以首项为9，公比为 2 的等比数列， n1  1 a 19  n   2   ， n1  1 a 19  即 n   2   ， n1  1 b a 19  n n   2   ，  1 n 11       2   1 n S b b b 9 66    ， n 1 2 n  1  2 1     2 1 1 S 6 3  则 n 2n1 170， n1 1 1  即  ， 2 510 9 1 1  又  ， 2 512 1 S 6  满足不等式 n 170 的最小整数n19， n10 即 . 故选：D. 第Ⅱ卷（非选择题） 二．填空题（共7小题，单空每小题4分，两空每小题6分，共36分） 11．（2019·四川省大竹中学高二期中（文））已知等比数列 的公比 ，且 ，则 _______________________. 【答案】 【解析】 等比数列 的公比 且 .故答案为： . 12．（2020·浙江高一期末）在《九章算术》中有一个古典名题“两鼠穿墙”问题：今有垣厚若千尺，两鼠对 穿，大鼠日一尺，小鼠也日一尺，大鼠日自倍，小鼠日自半，大意是有两只老鼠从墙的两边分别打洞穿墙， 大老鼠第一天进一尺，以后每天加倍，小老鼠第一天也进一尺，以后每天减半，若垣厚33尺，则两鼠 ______日可相逢. 【答案】6 【解析】 大老鼠打洞构成首项为1，公比为2的等比数列， 小老鼠打洞构成首项为1，公比为 的等比数列， 设相遇时是第n天， 则 ， 即 ， 即 ， 令 ，在 上是增函数， 又 ， 所以相遇时是第6天， 故答案为：6 13．（2020·成都市·四川电子科大实验中学高一期中）朱载堉（1536-1611）是中国明代一位杰出的音乐家、 数学家和天文历算家，他的著作《律学新说》中制作了最早的“十二平均律”．十二平均律是目前世界上通 用的把一组音（八度）分成十二个半音音程的律制，各相邻两律之间的频率之比完全相等，亦称“十二等 程律”，即一个八度13个音，相邻两个音之间的频率之比相等，且最后一个音是最初那个音的频率的2倍． 设第三个音的频率为 ，第七个音的频率为 ，则 ______． 【答案】【解析】 由题知：一个八度13个音，且相邻两个音之间的频率之比相等， 可以将每个音的频率看作等比数列 ，一共13项，且 ， 最后一个音是最初那个音的频率的2倍， ， ， ， ． 故答案为： 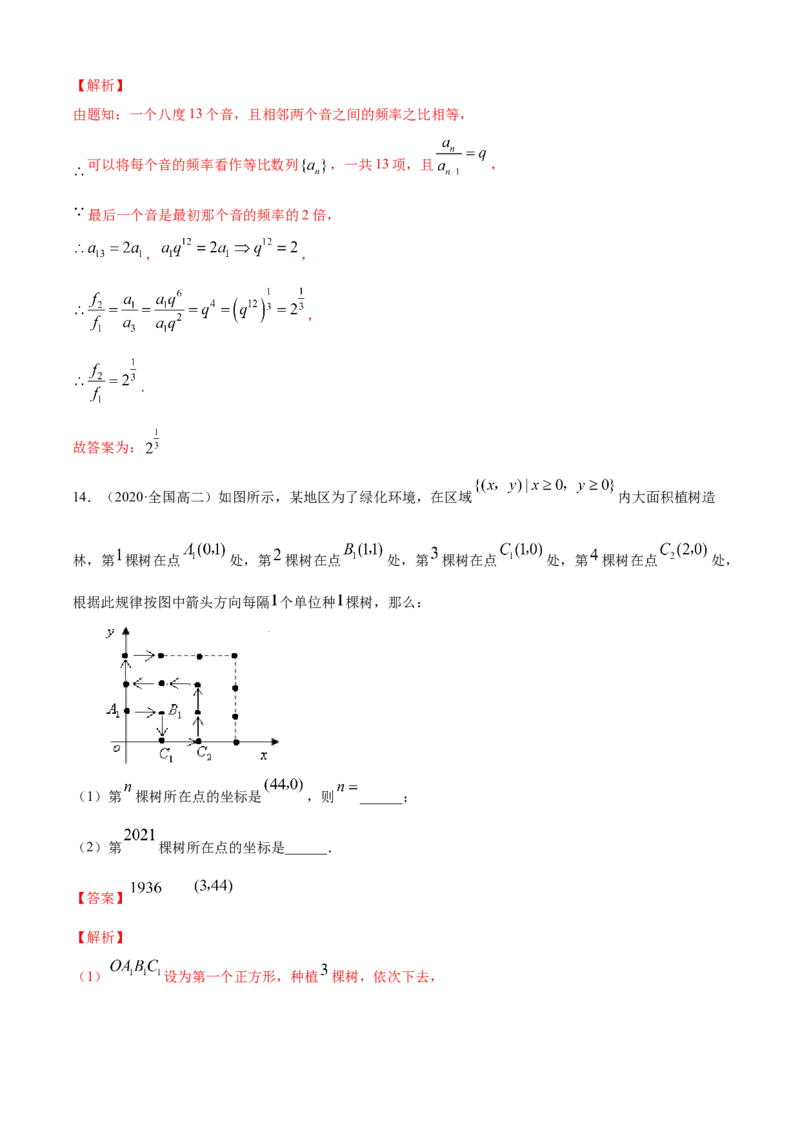14．（2020·全国高二）如图所示，某地区为了绿化环境，在区域 内大面积植树造 林，第 棵树在点 处，第 棵树在点 处，第 棵树在点 处，第 棵树在点 处， 根据此规律按图中箭头方向每隔 个单位种 棵树，那么： （1）第 棵树所在点的坐标是 ，则 ______； （2）第 棵树所在点的坐标是______． 【答案】 【解析】 （1） 设为第一个正方形，种植 棵树，依次下去，第二个正方形种植 棵树，第三个正方形种植 棵树， 构成公差为 的等差数列， 个正方形有 棵树， 由第 棵树所在点坐标是 ，则 ； （2）由（1）可知正方形种植的树，它们构成一个等差数列，公差为 ， 故前 个正方形共有 棵树， 又 ， ， ，因此第 棵树在 点处． 15．（2020·浙江高一期末）若对任意 ，都有 ， （n为正整数），则 _______. ______. 【答案】 【解析】 因为对任意 ，都有 ，（n为正整数）， 所以当 时， ， ， 所以 ，解得 ， 所以 或 ， 所以 是以1为首项，以2为公比的等比数列， 所以 ， 所以 是以1为首项，以-1为公比的等比数列， 所以 ， 两式联立得： ， 故答案为：0， 16．（2020·全国高二课时练习）在数列 中， ，且 ． （1） 的通项公式为__________； （2）在 这2019项中，被10除余2的项数为__________． 【答案】 403 【解析】 （1） ，且 ， ∴数列 是以1为首项，2为公差的等差数列， ， ．（2）被10除且余数为2的整数可表示为 ， 令 ，可得 ， ，且 奇数， ∴n为10的倍数或 为5的奇数倍且n为偶数． 当n为10的倍数时，n的取值有10、20、30、…、2010，共201个； 当 为5的奇数倍且n为偶数时，n的取值有8、18、28…、2018，共202个． 综上所述，在 这2019项中，被10除余2的项数为201+202=403． 故答案为： ；403 17．（2020·苏州市相城区陆慕高级中学高二期中）大衍数列来源于《乾坤谱》中对易传“大衍之数五十”的 推论，主要用于解释中国传统文化中的太极衍生原理．大衍数列中的每一项，都代表太极衍生过程中，曾 经经历过的两仪数量总和，是中国传统文化中隐藏着的世界数学史上第一道数列题，其前10项依次是0， 2，4， 8，12， 18， 24， 32， 40， 50， 则此数列第19项的值为____．此数列的通项公式 ______． 【答案】 【解析】 观察前10项可得， ， ， ， ， ， 即当 为奇数时， ，所以 ； 又 ， ， ， ， ，即当 为偶数时， ；所以 . 故答案为： ； . 三．解答题（共5小题，满分64分，18--20每小题12分，21,22每小题14分） 18．（2020·河南高二月考（文））已知公差不为零的等差数列 的前3项和为3，且 ， ， 成等 比数列. （1）求 的通项公式； （2）设 ，求数列 的前 项和 . 【答案】（1） ；（2） . 【解析】 （1）设 的公差为 ， 因为等差数列 的前3项和为3，且 ， ， 成等比数列， 所以 解得 ∴ . （2）∵ ， ∴ ， ，∴数列 是首项为 ，公比为9的等比数列， ∴ . 19．（2020·山西高三期中（理））已知正项数列 的前n项和为 ，满足 （ ， ）， ． （1）求数列 的通项公式； （2）设 ，求数列 的前 项和 的表达式． 【答案】（1） ；（2） ． 【解析】 （1）正项数列 的前n项和为 ，满足 （ ， ）， 所以 ， 整理得： ， 由于数列为正项数列，所以 （常数）， 所以 是以1为首项，1为公差的等差数列， 所以 ， 所以 ，易见 也适合该式． 由于 ，， 当n为奇数时， ，n为偶数时， ， 所以 ， ， ， ， 所以 ． 20．（2020·全国高二（文））已知数列 和 都是等差数列， ． （1）求数列 的通项公式； （2）设 ，数列 的前 项和为 ，求证： ． 【答案】（1） ；（2）证明见解析． 【解析】 （1）设等差数列 的公差为 ，∵ ，∴ ， ， 则 ， ， ，又数列 是等差数列，∴ ， 化简得 ，解得 ， 则 ； （2）由（1）可知 ， 当 时， ， ，符合， 当 时， ， ， 综上，当 时， ． 21．（2020·四川省都江堰中学高一期中）已知数列 满足 ， . （1）证明：数列 为等差数列，并求数列 的通项公式. （2）若记 为满足不等式 的正整数 的个数，数列 的前 项和为 ， 求关于 的不等式 的最大正整数解. 【答案】（1）证明见解析； ；（2）8. 【解析】（1）由 取倒数得 ，即 ，所以 为公差为 的等差数列， . （2）当 时， ， 所以这样 有 个 ， ， ， ， 两式相减得： ， 所以 为递增数列. ， ， ， 所以最大正整数解为8. 22．（2020·四川省成都市盐道街中学高一期中）已知 ． （1）设 ， ，求 ． （2）设 ， ，且 ，问是否存在最小正整数 ，使得对任意 ，都有 成立．若存在，请求出 的值；若不存在，请说 明理由． 【答案】（1） ；（2）存在， ． 【解析】 （1）由 得： ，则 ， 故 是以 为首项， 为公差的等差数列， ，由 可得 ， 故 ． （2） ， ， ， 由题干对任意 ，都有 成立得 ，由 得 ， ，解得： ， 又 为正整数， ， 综上，存在 ，使得对任意 ，都有 成立．