文档内容
专题 5.2 三角函数概念
知识点一.任意角的三角函数的定义
(1)单位圆
在直角坐标系中,我们称以原点为圆心,以__单位长度__为半径的圆为单位圆.
(2)三角函数的定义
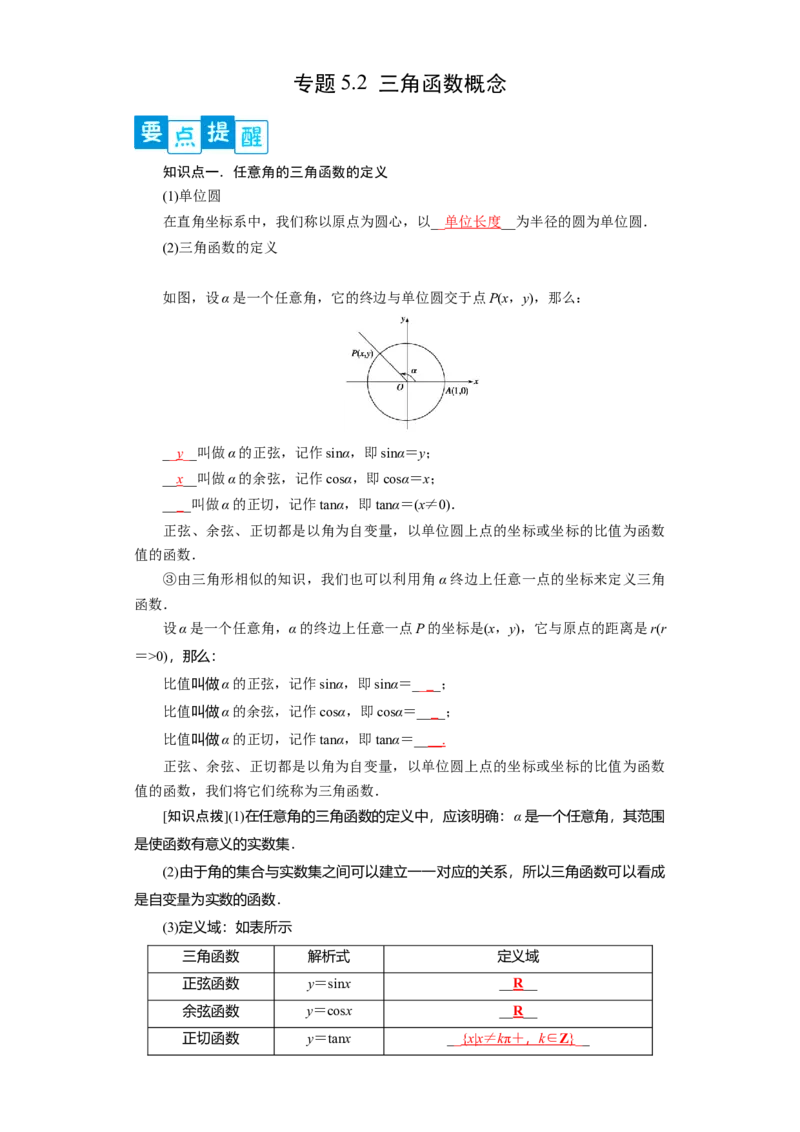
如图,设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:
__y__叫做α的正弦,记作sinα,即sinα=y;
__x__叫做α的余弦,记作cosα,即cosα=x;
____叫做α的正切,记作tanα,即tanα=(x≠0).
正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数
值的函数.
③由三角形相似的知识,我们也可以利用角 α终边上任意一点的坐标来定义三角
函数.
设α是一个任意角,α的终边上任意一点P的坐标是(x,y),它与原点的距离是r(r
=>0),那么:
比值叫做α的正弦,记作sinα,即sinα=____;
比值叫做α的余弦,记作cosα,即cosα=____;
比值叫做α的正切,记作tanα,即tanα=____.
正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数
值的函数,我们将它们统称为三角函数.
[知识点拨](1)在任意角的三角函数的定义中,应该明确:α是一个任意角,其范围
是使函数有意义的实数集.
(2)由于角的集合与实数集之间可以建立一一对应的关系,所以三角函数可以看成
是自变量为实数的函数.
(3)定义域:如表所示
三角函数 解析式 定义域
正弦函数 y=sinx __R__
余弦函数 y=cosx __R__
正切函数 y=tanx __ { x | x ≠ k π + , k ∈ Z } __2.三角函数值的符号
sinα、cosα、tanα在各个象限的符号如下:
[知识点拨]正弦、余弦和正切函数在各象限的符号可用以下口诀记忆:
“一全正,二正弦,三正切,四余弦”.
其含义是在第一象限各三角函数值全为正,在第二象限只有正弦值为正,在第三
象限只有正切值为正,在第四象限只有余弦值为正.
3.公式一(k∈Z)
sin(α+2kπ)=__ sin α __,
cos(α+2kπ)=__ cos α __,
tan(α+2kπ)=__ tan α __.
知识点二:同角三角函数的基本关系式
1.公式
(1)平方关系:__ sin 2 α + cos 2 α = 1 .__
(2)商数关系:__ = tan α .__α≠kπ+(k∈Z)
[知识点拨]对同角三角函数基本关系式的理解
(1)注意“同角”,这里“同角”有两层含义,一是“角相同”,二是对“任意”
一个角(在使函数有意义的前提下)关系式都成立,即与角的表达形式无关,如sin23α+
cos23α=1成立,但是sin2α+cos2β=1就不一定成立.
(2)sin2α是(sinα)2的简写,读作“sinα的平方”,不能将sin2α写成sinα2,前者是α
的正弦的平方,后者是α2的正弦,两者是不同的,要弄清它们的区别,并能正确书写.
(3)同角三角函数的基本关系式是针对使三角函数有意义的角而言的,sin2α+cos2α
=1对一切α∈R恒成立,而tanα=仅对α≠+kπ(k∈Z)成立.
3.常用的等价变形
sin2α+cos2α=1⇒
tanα=⇒
[拓展]变形公式的应用要注意哪些方面?
(1)使用变形公式sinα=±,cosα=±时,“±”号是由α的终边所在的象限确定的,
而对于其他形式的变形公式就不必考虑符号问题.
(2)对这些关系式不仅要牢牢掌握,还要能灵活运用(正用、逆用、变形应用).
一、单选题1.在平面直角坐标系 中,角 以 为始边,它的终边经过点 ,则
( )
A. B. C. D.
【来源】北京市石景山区2021-2022学年高一下学期期末数学试题
【答案】D
【解析】根据正弦函数的定义可得 .故选:D.
2.已知角 的终边过点 ,则 的值为( )
A. B. C. D.
【来源】西藏林芝市第二高级中学2021-2022学年高一下学期第二学段考试(期末)
数学试题
【答案】D
【解析】角 的终边经过点 ,则 ,
由三角函数的定义可得: .故选:D.
3.已知角 的终边经过点 ,则 ( )
A. B. C. D.-2
【来源】陕西省渭南市白水县2021-2022学年高一下学期期末数学试题
【答案】A
【解析】:因为角 的终边经过点 ,
所以 .故选:A.
4.已知角 的终边经过点 ,且 ,则 ( )
A. B.1 C.2 D.【来源】陕西省渭南市华阴市2021-2022学年高一下学期期末数学试题
【答案】C
【解析】由题意 ,解得 .故选:C.
5.在平面直角坐标系xOy中,角 与 均以Ox为始边,它们的终边关于y轴对称,
若 ,则 ( )
A. B. C. D.
【来源】陕西省榆林市第一中学2021-2022学年高一下学期期中文科数学试题
【答案】A
【解析】设角a与β的终边分别与单位圆交于点 、 ,
因为它们的终边关于y轴对称,
所以 且 ,
因为 ,所以 ,
所以 .故选:A.
6.已知 是第一象限角,若 ,那么 是( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
【来源】陕西省西安市鄠邑区第二中学2021-2022学年高一下学期第一次月考数学试
题
【答案】C
【解析】由 是第一象限角知 , ,
当 为奇数时, 在第三象限,当 为偶数时, 在第一象限,
又 ,可知 在第三象限.故选:C.7.已知角 的顶点与原点重合,始边与 轴的正半轴重合,终边在直线 上,
则 ( )
A. B. C. D.
【来源】北京市昌平区2021-2022学年高一下学期期末质量抽测数学试题
【答案】D
【解析】因为角 的顶点与原点重合,始边与 轴的正半轴重合,终边在直线
上,
所以 ,故选:D
8.平面直角坐标系 中,角 的顶点在坐标原点 ,始边是 轴的非负半轴,终边
经过点 ,若 ,则 ( )
A.-2 B. C. D.2
【来源】辽宁省丹东市2021-2022学年高一下学期期末数学试题
【答案】B
【解析】由题意, ,解得 ,
故选:B.
9.已知 是角 终边上一点,且 ,则 的值是( )
A. B. C. D.
【来源】陕西省渭南市富平县2021-2022学年高一下学期期末数学试题
【答案】D
【解析】:因为 是角 终边上一点, ,故点 位于第二
象限,所以 , ,
整理得: ,因为 ,所以 .故选:D.
10.若 ,则 的值为
A. B. C. D.
【来源】内蒙古自治区赤峰市赤峰红旗中学2021-2022学年高一上学期期末数学文科
试题
【答案】C
【解析】由 ,整理得 ,
所以 ,
又由三角函数的基本关系式,可得由
解得 ,所以 .故选C.
11.若 ,则 ( )
A. B. C. 或 D. 或
【来源】山西省怀仁市2021-2022学年高一上学期期末数学试题
【答案】C由题意可得 ,解得 或 ,
因此, 或 .故选:C.
12.已知 ,且 ,则 ( )A. B. C. D.
【答案】B
【解析】∵ ,∴ ,
∵ ,
∴ ,
又∵ ,
∴ ,即 .故选:B.
13.已知角 的终边在第三象限,且 ,则 ( )
A. B.1 C. D.
【来源】北京市第二中学2021-2022学年高一下学期第四学段考试数学试题
【答案】C
【解析】由角 的终边在第三象限,则
由题设知 ,解得 ,
所以 故选:C
14.已知角 , ,则 ( )
A.2 B. C.1 D.-1
【来源】浙江省浙南名校联盟2021-2022学年高一下学期返校考数学试题
【答案】A
【解析】由 ,解得 或 ,
因为 ,故 .故选:A
15.若 ,且 ,则 是( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
【来源】陕西省汉中市镇巴县2021-2022学年高一下学期期中数学试题
【答案】D
【解析】解:因为 , ,所以 ,且 ,
故a是第四象限角.故选:D
16.已知 中,若 ,则 ( )
A. B. C. 或 D. 或
【来源】辽宁省大连市第二十四中学2021-2022学年高一下学期期中考试数学试题
【答案】A
【解析】 ,
或 ,
或 ,
,故选:A.
17.若 ,且满足 ,则 ( )
A. B. C. D.
【来源】贵州省黔东南州凯里市第一中学2021-2022学年高一下学期期中数学试题【答案】A
【解析】:由 得 ,∴ 或 ,
因为 , ,所以 .
由 及 得 ,∴ ,
所以 .故选:A
18.已知函数 ( 且 )的图像经过定点 ,且点 在角 的终
边上,则 ( )
A. B.0 C.7 D.
【答案】D
【解析】:令 得 ,故定点 为 ,
所以由三角函数定义得 ,
所以 故选:D
19.已知角 的终边经过点 ,且 ,则实数的a值是( )
A. B. C. 或 D.1
【来源】江苏省镇江市扬中市第二高级中学2021-2022学年高一下学期3月第一次阶段
检测数学试题
【答案】B【解析】由题设, 且 ,即 ,
∴ ,则 ,解得 或 ,
综上, .故选:B.
20.已知 ,若 ,则 的值为( )
A. B. C. D.
【来源】北京市第一六一中学2021-2022学年高一下学期期中阶段练习数学试题
【答案】A
【解析】因为 ,所以 ,
所以 ,
因此 ,故选:A
二、解答题
21.已知 .
(1)若 ,求 的值;
(2)若 ,且 ,求实数 的值.
【来源】河北省保定市2021-2022学年高一上学期期末数学试题
【答案】(1) (2)
【解析】(1)由 ,可得
所以 ,即 ,所以
(2)由 ,可得 ,
解得 或 ,
而 ,所以 ,解得 ,
所以 .
22.已知 .
(1)求 的值;
(2)求 的值.
【来源】江西省南昌市第二中学2021—2022学年高一下学期第一次月考数学试题
【答案】(1) (2)
【解析】(1)解:
,
解得:
(2)解:
23.已知 是第二象限角,
(1)求 的值;(2)若 ,求tan .
【来源】广西钦州市2021-2022学年高一下学期教学质量监测(期末)数学试题
【答案】(1)0(2)
【解析】(1)因为 是第二象限角,所以 ,故
(2) 是第二象限角, ,由 ,故 ,因此
24.已知 , .
(1)求 的值.
(2)求 的值.
(3)求 的值.
【来源】辽宁省大连市第二十四中学2021-2022学年高一下学期期中考试数学试题
【答案】(1) (2) (3)
【解析】(1)解:因为 ,
所以 ,
所以 ;
(2)解:因为 , ,
所以 ,
所以 ;
(3)解:由(2)得 ,则
.
25.(1)已知 ,求 的值;
(2)已知 ,且 ,求 的值.
【来源】宁夏银川市第二中学2021-2022学年高一下学期期末考试数学试题
【答案】(1) ;(2) .
【解析】(1)由 知
原式=
(2)
又
原式= = =