专题5.3导数在研究函数中的应用（2）（A卷基础篇）解析版_E015高中全科试卷_数学试题_选修2_01.同步练习_同步练习（第四套）_专题5.3导数在研究函数中的应用（2）（A卷基础篇）

专题5. 3导数在研究函数中的应用（2）（A卷基础篇） （新教材人教A版,浙江专用） 参考答案与试题解析 第Ⅰ卷（选择题） 一．选择题（共10小题，满分50分，每小题5分） f(x) [a,b] (a,b) 1．（2020·全国高二课时练习）设 是区间 上的连续函数，且在 内可导，则下列结论中正 确的是（ ） f(x) A． 的极值点一定是最值点 f(x) B． 的最值点一定是极值点 f(x) [a,b] C． 在区间 上可能没有极值点 f(x) [a,b] D． 在区间 上可能没有最值点 【答案】C 【解析】 f(x) f(x) 根据函数的极值与最值的概念知， 的极值点不一定是最值点， 的最值点不一定是极值点．可能 f(x) 是区间的端点，连续可导函数在闭区间上一定有最值，所以选项A，B，D都不正确，若函数 在区间 [a,b] f(x) [a,b] 上单调，则函数 在区间 上没有极值点，所以C正确． 故选：C. 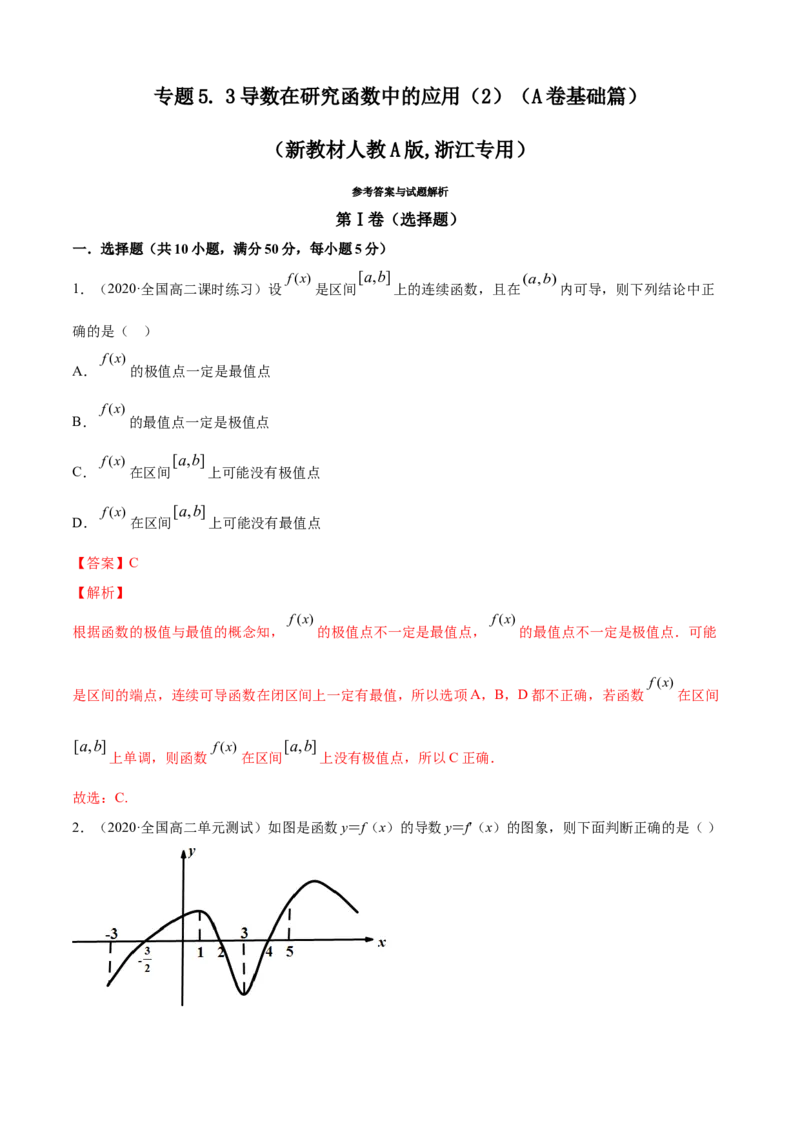2．（2020·全国高二单元测试）如图是函数y＝f（x）的导数y＝f'（x）的图象，则下面判断正确的是（ ）A．在（﹣3，1）内f（x）是增函数 B．在x＝1时，f（x）取得极大值 C．在（4，5）内f（x）是增函数 D．在x＝2时，f（x）取得极小值 【答案】C 【解析】 根据题意，依次分析选项： 3  对于A，在（﹣3， 2 ）上，f′（x）＜0，f（x）为减函数，A错误； 3  对于B，在（ 2 ，2）上，f′（x）＞0，f（x）为增函数，x＝1不是f（x）的极大值点，B错误； 对于C，在（4，5）上，f′（x）＞0，f（x）为增函数，C正确； 3  对于D，在（ 2 ，2）上，f′（x）＞0，f（x）为增函数，在（2，4）上，f′（x）＜0，f（x）为减函数， 则在x＝2时f（x）取得极大值，D错误； 故选：C． f(x)lnxax x2 a 3．（2020·横峰中学高三月考（文））已知函数 在 处取得极值，则 （ ） 1 A．1 B．2 C． D．-2 2 【答案】C 【解析】 1 1 1 f 'x a f '20 a 0,a  x ，依题意 ，即2 2 . 1 1 2x f 'x   x0 f x 0,2 2, 此时 x 2 2x ，所以 在区间 上递增，在区间 上递减，所以 f x x2 在 处取得极大值，符合题意. 1 a  所以 2.故选：C f xax3bx1 1,ab1 4．（2020·霍邱县第二中学高二月考（文））已知函数 的图象在点 处的切 f x 6 x2 ab 线斜率为 ，且函数 在 处取得极值，则 （ ） 26 22 26  A． 3 B．7 C． 3 D． 3 【答案】C 【解析】 f 'x3ax2 b 由题可知： ， 3ab6, 2  a  则 12ab0,解得 3 ， b8 . 2 a  f x 经检验，当 3，b8时， 在x2处取得极大值， 22 ab 所以 3 . 故选：C 1 f(x) x34x f x 5．（2020·北京高二期末）已知函数 3 ，则 ）的极大值点为（ ） x4 x4 x2 x2 A． B． C． D． 【答案】C 【解析】 1 f(x) x34x 由 3 ， fx x2 4 得： . fx x2 40 由 ，得： x2 ，或x2. fx x2 40 2 x2 由 ，得： .f x ,2,2, f x 2,2 所以函数 的增区间为 .函数 的减区间为 . x2 x2 所以， 是函数的极大值点， 是函数的极小值点. 故选：C. 1 f x x2 cosx f x 6．（2020·河南信阳市·高二期末（文））设 2 ，则函数 （ ） A．有且仅有一个极小值 B．有且仅有一个极大值 C．有无数个极值 D．没有极值 【答案】A 【解析】 fx xsinx fx1cosx0 ， ， f x f00 ∴ 单调递增且 ， fx0 f x x0 ∴当 时， ，函数 单调递减， fx0 f x x0 当 时， ，函数 单调递增， f x 故 有唯一的极小值点. 故选：A. 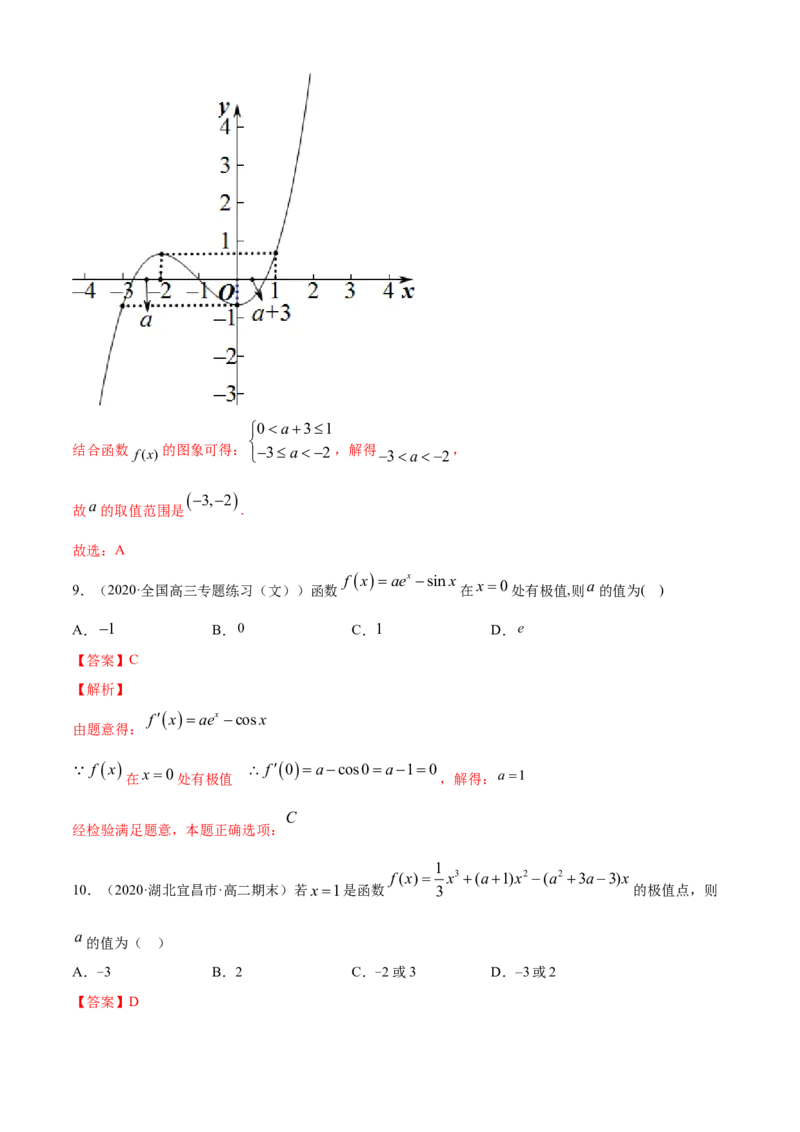f x x3 3axa 0,1 7．（2020·绵阳市·四川省绵阳江油中学高二月考（理））函数 在 内有最小值， 则a的取值范围为( ) 0a1 0a1 A． B． 1 C． D．0a 1a1 2 【答案】B 【解析】 ∵函数f（x）=x3﹣3ax﹣a在（0，1）内有最小值， ∴f′（x）=3x2﹣3a=3（x2﹣a）， ①若a≤0，可得f′（x）≥0，f（x）在（0，1）上单调递增，f（x）在x=0处取得最小值，显然不可能，a ②若a＞0，f′（x）=0解得x=± ， a a a 当x＞ ，f（x）为增函数，0＜x＜ 为减函数，f（x）在x= 处取得极小值，也是最小值， 所以极小值点应该在（0，1）内，符合要求． 综上所述，a的取值范围为（0，1） 故答案为B 1 2 f x x3 x2  a,a3 8．（2020·佳木斯市第二中学高二期末（文））若函数 3 3 在区间 内既存在最 大值也存在最小值，则a的取值范围是（ ） 3,2 3,1 2,1 2,0 A． B． C． D． 【答案】A 【解析】 fx x2 2x x(x2)0 x2 x0 由 得 或 ， 2 2 f x f 0 f 2 可以判断 在x0处取得极小值 3 ，在x2处取得极大值 3. 2 2 f x f x 令 3，得x3或x0，令 3 ，得x2或x1， a,a3 f(x) x2 x0 由题意知函数 在开区间 内的最大、最小值只能在 和 处取得，0a31  结合函数 f(x) 的图象可得： 3a2，解得 3a2 ， 3,2 a 故 的取值范围是 . 故选：A f xaex sinx x0 a 9．（2020·全国高三专题练习（文））函数 在 处有极值,则 的值为( ) A．1 B．0 C．1 D．e 【答案】C 【解析】 fxaex cosx 由题意得： f x  f0acos0a10  在 x0 处有极值 ，解得：a1 C 经检验满足题意，本题正确选项： 1 f(x) x3(a1)x2 (a2 3a3)x 10．（2020·湖北宜昌市·高二期末）若x1是函数 3 的极值点，则 a 的值为（ ） A．-3 B．2 C．-2或3 D．–3或2 【答案】D【解析】 f(x) x2 2(a1)x(a2 3a3) f(1)0 由题意，知： 且 ， a2 a60 a 3 a2 ∴ ，解得： 或 . a 3 f(x) x2 4x3(x1)(x3) x1 f(0)30 当 时， ，即在 的左侧 ，右侧 f(2)10 x1 ，所以 是极值点，而非拐点； a2 f(x) x2 6x7(x1)(x7) x1 f(0)70 f(2)90 当 时， ，即在 的左侧 ，右侧 ， x1 所以 是极值点，而非拐点； 故选：D 第Ⅱ卷（非选择题） 二．填空题（共7小题，单空每小题4分，两空每小题6分，共36分） 11．（2020·四川成都市·高三开学考试（文））已知函数 ，则 在 上的最小 值是_______________. 【答案】 【解析】 在 上，有 ，知： 单调递减， ∴ ， 故答案为： . 12．（2020·昆明呈贡新区中学（云南大学附属中学呈贡校区）高三月考（理））若x＝2是f(x)＝ax3-3x的 一个极值点，则a＝________ .【答案】 【解析】 因为 ，所以 ， 因为x＝2是f(x)＝ax3-3x的一个极值点， 所以 ，故 ， 经验证当 时， 是 的一个极值点. 所以 . 故答案为： 13．（2019·浙江高三专题练习）若函数 在 ，则函数的最小值是 _______ ；最大值 是_________. 【答案】 0 【解析】 由题得 ， 令 得x=2（舍去）或0， 因为 ， 所以函数的最小值是 ，最大值为0.故答案为 14．（2020·东台创新高级中学高二月考）已知函数 ，则 的极小值为______． 【答案】 【解析】 因为 ，所以 ， 由 得 ；由 得 ； 所以函数 在 上单调递减，在 上单调递增， 所以 的极小值为 . 故答案为： . 15．（2019·西藏拉萨市·拉萨那曲第二高级中学高二月考（文））函数 的极值是： ________和________. 【答案】-54 54 【解析】 由函数 有 令 解得 或 . 令 解得 所以函数 在 上单调递增，在 上单调递减，在 上单调递增. 所以当 时，函数 有极大值 ，当 时，函数 有极小值 . 故答案为： ， 54. 16．（2019·浙江绍兴市·高二期末）函数 （其中 …是自然对数的底数）的 极值点是________；极大值 ________. 【答案】1或－2 【解析】 由已知得 ， ，令 ，可得 或 ， 当 时 ，即函数 在 上单调递增； 当 时， ，即函数 在区间 上单调递减； 当 时， ，即函数 在区间 上单调递增． 故 的极值点为 或 ，且极大值为 ． 故答案为(1). 1或－2 (2). ． 17．（2020·全国高三专题练习）设 是奇函数 的导函数， ，且对任意 都有 ，则 _________，使得 成立的x的取值范围是_________．【答案】3 【解析】 ∵ 是奇函数，∴ ， 设 ，则 ， ， ∴ 在 上单调递减， 由 得 ，即 ， ∴ ，得 ， 故答案为：3； ． 三．解答题（共5小题，满分64分，18--20每小题12分，21,22每小题14分） 18．（2020·全国高三（文））已知函数 . （1）求 的单调区间； （2）求函数的极值；(要列表). 【答案】（1）增区间为 ，减区间为 ；（2）极大值为 ，极小值为 . 【解析】 （1） ， ， 设 可得 或 . ①当 时， 或 ； ②当 时， ， 所以 的单调增区间为 ，单调减区间为： . （2）由（1）可得，当 变化时， ， 的变化情况如下表：当 时， 有极大值，并且极大值为 当 时， 有极小值，并且极小值为 . 19.（2020·海南省直辖县级行政单位·临高二中高二月考）若 ， ，求： （1） 的单调增区间； （2） 在 上的最小值和最大值. 【答案】(1) 增区间为 ;(2) . 【解析】 （1） ， 由 解得 ， 的增区间为 ； （2） ， （舍）或 ， , , ， 20.（2020·北京通州区·高二期末）已知函数 .（1）求曲线 在点 ， 处的切线方程； （2）求 在 ， 上的最大值和最小值. 【答案】（1） ；（2）最大值 (2) ，最小值 (1) . 【解析】 （1）由 得， ， 所以 ， ， 所以曲线 在点 ， 处的切线方程 即 ； （2）令 可得 或 ，此时函数单调递增，令 可得 ，此时函数单调递 减， 故函数 在 ， 上单调递增， 所以 的最大值 （2） ，最小值 （1） . 21．（2020·江苏宿迁市·宿豫中学高二月考）已知函数 , （1）计算函数 的导数 的表达式; （2）求函数 的值域. 【答案】（1） ;（2） . 【解析】 （1）因为 ,所以 . 故函数 的导数 ; （2） , , 函数 在 上是单调增函数, 所以 , 所以 ; 故函数 的值域为 . 22．（2020·哈尔滨市第十二中学校高二期末（文））已知函数 ， 是 的一个极值点． （1）求 的单调递增区间； （2）若当 时， 恒成立，求实数 的取值范围． 【答案】(1) 的单调递增区间为 ， (2) 【解析】 （Ⅰ） . ∵ 是 的一个极值点，∴ 是方程 的一个根，解得 . 令 ，则 ，解得 或 . ∴函数 的单调递增区间为 ， . （Ⅱ）∵当 时 ， 时 ， ∴ 在（1，2）上单调递减， 在（2，3）上单调递增. ∴ 是 在区间[1，3]上的最小值，且 . 若当 时，要使 恒成立，只需 ， 即 ，解得 .