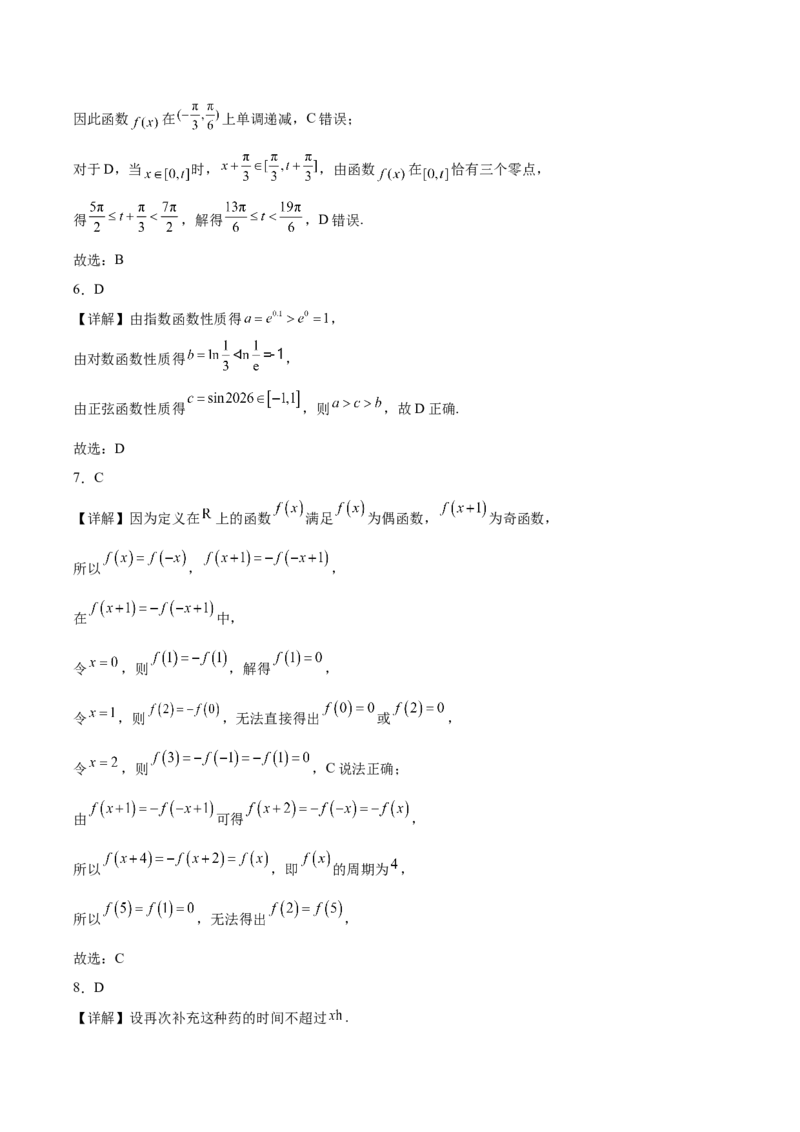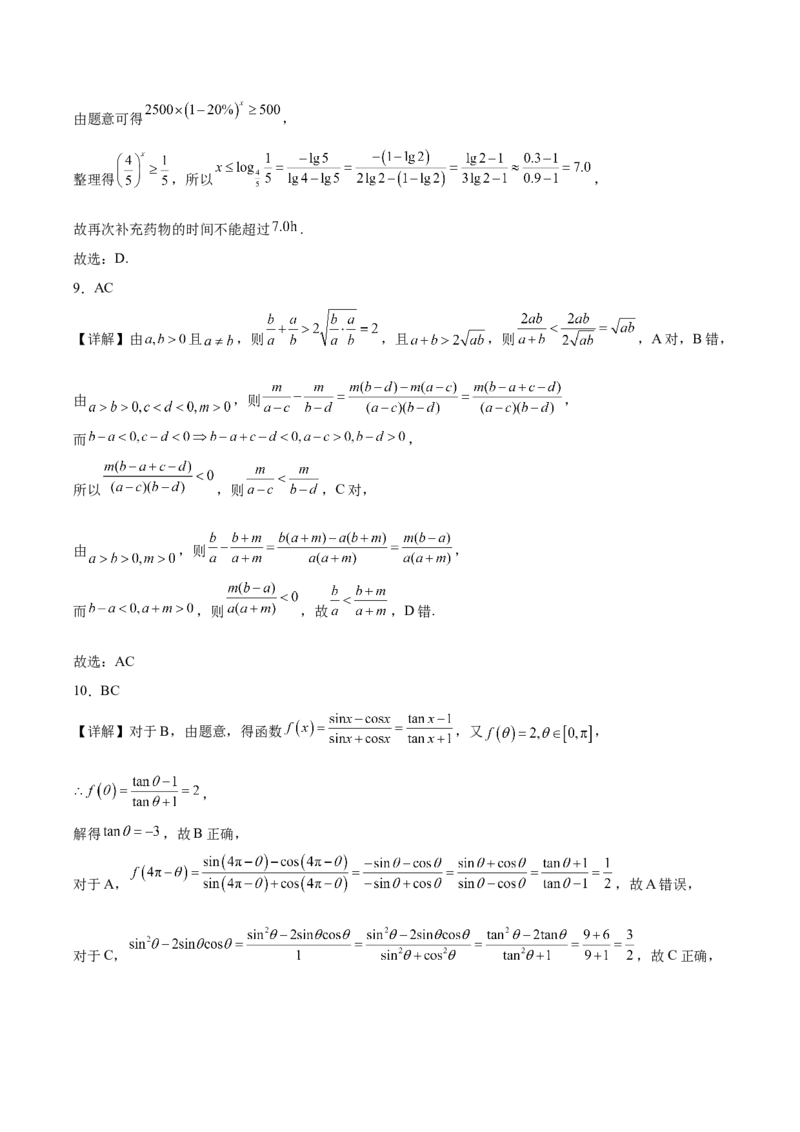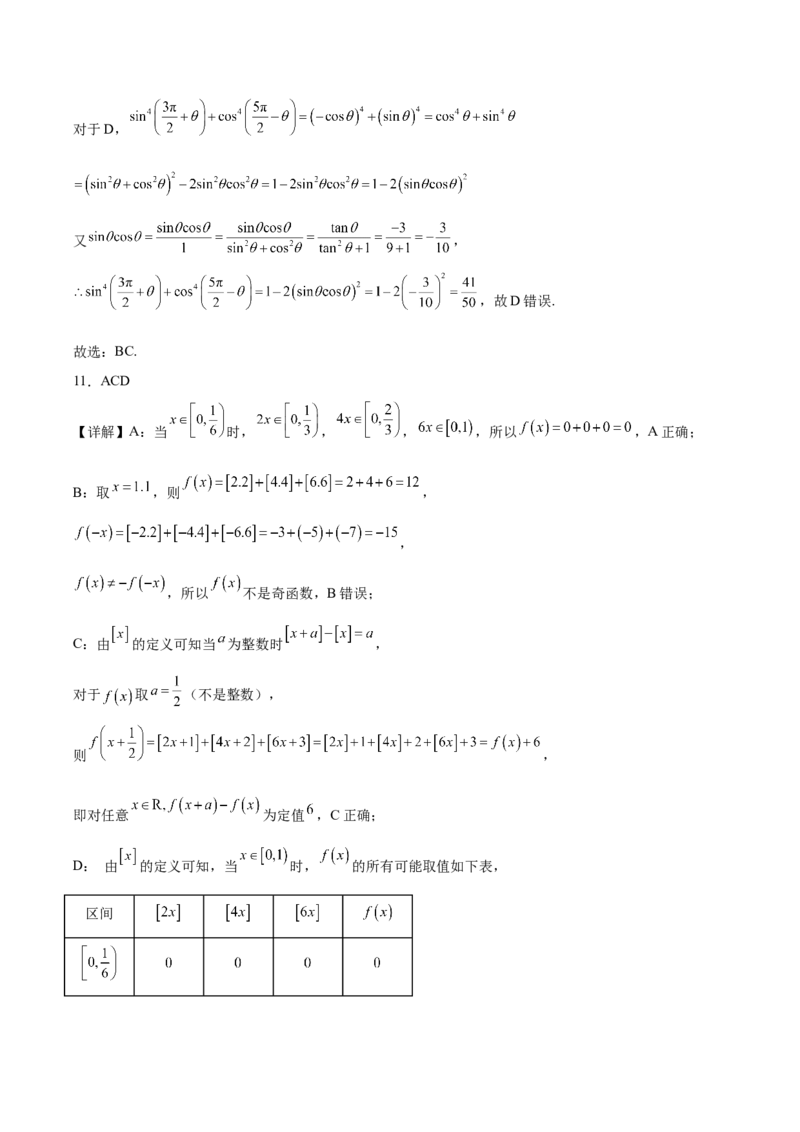文档内容
四川省内江市2025-2026学年高一上学期末数学试题
一、单选题
1.命题“ ”的否定是( )
A. B.
C. D.
2.若角 的终边与单位圆的交点为 ,则 ( )
A. B. C. D.
3.下列函数既是偶函数,又在 上单调递减的是( )
A. B.
C. D.
4.已知 是第三象限角,则 ( )
A. B. C. D.
5.设函数 ,则下列结论正确的是( )
A. 的一个周期为
B. 图象的一个对称中心点为
C. 在 单调递增
D.若 在 恰有三个零点,则
6.已知 ,则 的大小关系是( )A. B. C. D.
7.定义在 上的函数 满足 为偶函数, 为奇函数,则下列说法一定成立的是( )
A. B.
C. D.
8.某药在病人血液中的量低于 时病人就有危险.现给某病人的静脉注射了这种药 ,如果药在
血液中以每小时 的比例衰减,那么再次向病人补充这种药的时间间隔不能超过( ) .(精确到 ,
参考数据: )
A. B. C. D.
二、多选题
9.下列命题正确的是( )
A.若 都是正数,且 ,则
B.若 都是正数,且 ,则
C.若 ,则
D.若 ,则
10.已知函数 ,且 ,则( )
A.
B.
C.
D.11.(多选)已知函数 ,它的值域为集合 .其中 表示不超过 的最大整
数,如 ,则下列说法正确的是( )
A.当 时,
B. 为奇函数
C.存在一个不是整数的数 ,对任意 为定值
D.若集合 ,则集合 的元素个数为1351
三、填空题
12.已知函数 是定义域为 的奇函数,当 时, ,则 .
13.已知弧长为 的弧所对的圆心角为 ,则该弧所在的扇形面积为 .
14.函数 与 的图象关于点 中心对称,且 恰有一个零点,则
的最小值为 .
四、解答题
15.已知集合 , 或 ,命题 ,命题 .
(1)当 时,求 ;
(2)若 是 的充分条件,求实数 的取值范围.
16.已知函数 .
(1)求函数 的对称轴及单调递增区间;(2)求 在 的最大值和最小值.
17.设函数 ,其中 .
(1)若不等式 的解集为 ,求 的值;
(2)若 ,求不等式 的解集.
18.已知定义域为 的函数 是奇函数.
(1)求实数 的值;
(2)判断函数 的单调性,并利用定义法证明;
(3)若不等式 在 恒成立,求 的取值范围.
19.若函数 存在两个不同零点 满足: (其中 为常数),则定义 关于 为零
点近似函数.
(1)若函数 ,证明: 关于2为零点近似函数;
(2)若函数 ,若对任意实数 均关于 为零点近似函数,求 的最小值;
(3)若函数 关于1为零点近似函数,求 的取值范围.
参考答案
1.C
【详解】根据命题否定的原则,
该命题“ ”的否定是 ,
故选:C.
2.D【详解】角 的终边与单位圆的交点为 ,
根据正弦函数的定义, .
故选:D
3.C
【详解】由 为偶函数,且在 上单调递增,A不符;
由 为非奇非偶函数,B不符;
由 的定义域为R,且 ,即函数为偶函数,
当 ,则 ,故函数在 上单调递减,C符合;
由 为奇函数,D不符.
故选:C
4.A
【详解】 是第三象限角,
,
,
.
故选:A.
5.B
【详解】对于A,函数 的最小正周期为 ,A错误;
对于B, ,则 是 图象的对称中心,B正确;
对于C,当 时, ,而余弦函数 在 上单调递减,因此函数 在 上单调递减,C错误;
对于D,当 时, ,由函数 在 恰有三个零点,
得 ,解得 ,D错误.
故选:B
6.D
【详解】由指数函数性质得 ,
由对数函数性质得 ,
由正弦函数性质得 ,则 ,故D正确.
故选:D
7.C
【详解】因为定义在 上的函数 满足 为偶函数, 为奇函数,
所以 , ,
在 中,
令 ,则 ,解得 ,
令 ,则 ,无法直接得出 或 ,
令 ,则 ,C说法正确;
由 可得 ,
所以 ,即 的周期为 ,
所以 ,无法得出 ,
故选:C
8.D
【详解】设再次补充这种药的时间不超过 .由题意可得 ,
整理得 ,所以 ,
故再次补充药物的时间不能超过 .
故选:D.
9.AC
【详解】由 且 ,则 ,且 ,则 ,A对,B错,
由 ,则 ,
而 ,
所以 ,则 ,C对,
由 ,则 ,
而 ,则 ,故 ,D错.
故选:AC
10.BC
【详解】对于B,由题意,得函数 ,又 ,
,
解得 ,故B正确,
对于A, ,故A错误,
对于C, ,故C正确,对于D,
又 ,
,故D错误.
故选:BC.
11.ACD
【详解】A:当 时, , , ,所以 ,A正确;
B:取 ,则 ,
,
,所以 不是奇函数,B错误;
C:由 的定义可知当 为整数时 ,
对于 取 (不是整数),
则 ,
即对任意 为定值 ,C正确;
D: 由 的定义可知,当 时, 的所有可能取值如下表,
区间所以在 时, 的可能取值为 ,
因为对于任意 ( 为整数),
,
即 ,
所以 的值域 ,
因为 ,
当 时,由 可知 ,
又因为 , ,
所以集合 的元素个数为 ,D正确;
故选:ACD
12.
【详解】由题意可得 ,因为函数 为奇函数,故 .故答案为: .
13.
【详解】设扇形的半径为 ,弧长为 的弧所对的圆心角为 ,所以 ,所以 ,
则该弧所在的扇形面积为 .
故答案为: .
14.3
【详解】函数 与 的图象关于点 中心对称,则对 上任意一点 ,其对称点
在 的图象上,
,即 ,
又 , ,
,
令 ,
又 恰有一个零点,
当 时, , ,此时 有无数零点,不满足题意;
当 时, 为一个二次函数,则 ,
即 , ,
,令 ,则 ,对称轴为 ,
,
综上所述, 的最小值为3.
故答案为: .
15.(1) , 或 ,
(2)
【详解】(1)当 时, , .
因为 或 ,
所以 ,
或 ,
(2)因为 是 的充分条件,
所以 ,于是有 ,
所以实数 的取值范围为 .
16.(1)对称轴为 ,递增区间为 ;
(2)最大值和最小值分别为1和 .
【详解】(1)函数 ,由 ,得 ,
所以函数 的对称轴为 ;
由 ,得 ,
所以函数 的单调递增区间为 .(2)当 时, ,则当 ,即 时, ;
当 ,即 时, ,
所以 在 的最大值和最小值分别为1和 .
17.(1)
(2)答案见解析
【详解】(1)由题意,不等式 的解集为 ,
则 和 是方程 的两个根,
得 解得 ,
所以 ;
(2)若 ,则 ,即 ,
因为 ,所以 , 是方程 的两个实数根,
①当 时, ,不等式的解集为 ;
②当 时, ,不等式的解集为 ;
③当 时,解集为 ;
④当 时, ,不等式的解集为 ;
综上所述,当 时,解集为 ;当 时,解集为 ;
当 时,解集为 ;当 时,解集为 .18.(1)
(2)函数 是实数集上的减函数,证明见解析
(3)
【详解】(1)因为定义域为 的函数 是奇函数,
所以
.
(2)函数 是实数集上的减函数,证明如下:
由(1)可知 ,
设 是任意两个实数,且 ,
,
因为 ,
所以 ,
所以 ,
所以函数 是实数集上的减函数.
(3)因为函数 是实数集上的奇函数,
所以由不等式
,由(2)可知:函数 是实数集上的减函数,
所以由
,
因为 ,所以 ,
所以由 ,
所以原问题转化为 在 时恒成立,
设 , ,
,
当 时,函数 是增函数,且 ,
由复合函数单调性的性质可知函数 也是增函数,
所以函数 也是增函数, ,即 ,
所以要想 在 时恒成立,
只需 ,所以 的取值范围为 .
19.(1)证明见解析
(2)1
(3)
【详解】(1)设 ,则 单调递增,
,则存在 ,使得 ,
令 ,即 或 ,
则 ,
则 ,
则 关于2为零点近似函数.
(2)设 ,则对于方程 ,
, , ,
则 ,
则 的两根为 ,
则 ,
,
设 ,则 ,
解得 ,
则 ,
则 的最小值为1.
(3) ,
设 ,则 ,对于方程 ,即 ,
设 , ,
由对勾函数性质可得,当 时, 单调递减,
当 时, 单调递增,
则 ,
则当 时该方程有根,
设该方程其中1根为 ,
由于 ,
则 有两个相反的根,设为 ,
①若 ,则 ,则 ,
此时 符合题意;
②当 时, , 只有1解, 只有1个零点,不符合题意;
③当 时,由于 ,则 有且仅有1 解,
且 ,由①知不符合题意;
④当 时, 有且仅有1 解,且 ,由①知不符合题意;
⑤当 时, 有两解 ,设 ,
由于 ,则 ,设 , ,
由于 ,
则 ,
则 符合题意;
综上 .