文档内容
2024-2025 学年安徽省合肥市普通高中六校联盟高一下学期 4 月期中联
考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知z=−1+i,则z在复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.设⃗
a
, ⃗b 是向量,则“ (⃗a+⃗b)⋅(⃗a−⃗b)=0 ”是“ ⃗a=−⃗b 或 ⃗a=⃗b ”的( )
A. 必要不充分条件 B. 充分不必要条件
C. 充要条件 D. 既不充分也不必要条件
3.记△ABC的内角A,B,C的对边分别为a,b,c,a=3,b=4,C=60∘,则c的值为( )
A. 13 B. √13 C. 19 D. √19
4.若向量 ⃗a=(2,1) , ⃗b=(1,0) ,则向量 ⃗b 在向量⃗
a
上的投影向量为( )
2√5 4√5 2√5 4 2
A. B. (4,2) C. ( , ) D. ( , )
5 5 5 5 5
5.已知向量⃗
a
, ⃗b 满足 |⃗a|=5 , |⃗b|=6 ,⃗
a⋅
⃗
b=6
,则 cos<⃗a ,⃗
a−
⃗
b>=
( )
31 19 17 19
A. − B. − C. D.
35 35 35 35
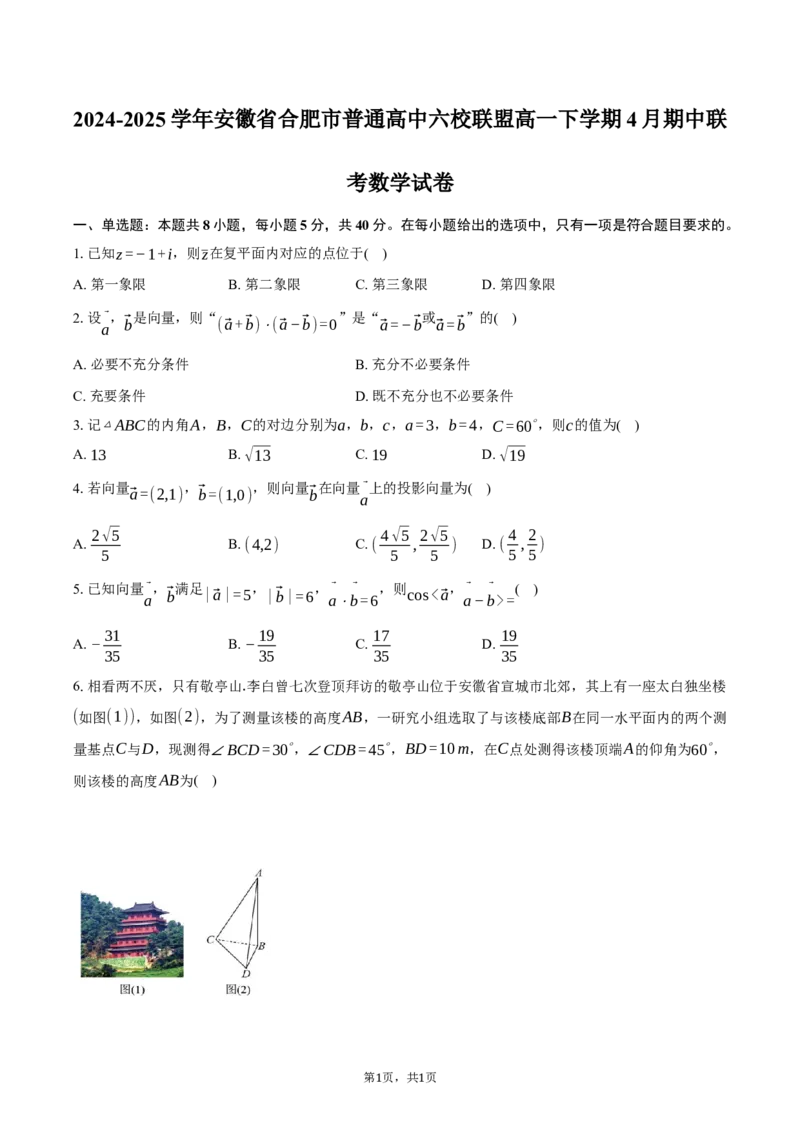
6.相看两不厌,只有敬亭山.李白曾七次登顶拜访的敬亭山位于安徽省宣城市北郊,其上有一座太白独坐楼
(如图(1)),如图(2),为了测量该楼的高度AB,一研究小组选取了与该楼底部B在同一水平面内的两个测
量基点C与D,现测得∠BCD=30∘,∠CDB=45∘,BD=10m,在C点处测得该楼顶端A的仰角为60∘,
则该楼的高度AB为( )
第 页,共 页
1 1A. 10√6(m) B. 10√2(m) C. 10√3(m) D. 20√3(m)
7.某水平放置的平面图形的斜二侧直观图是等腰梯形(如图所示),将该平面图形绕其直角腰AB边旋转一周
1
得到一个圆台,已知∠ABC=45∘,AD=AB= BC=1,则该圆台的体积为( )
2
7 14
A. π B. 7π C. π D. 14π
3 3
8.已知⊙O的半径为1,直线PA与⊙O相切于点A,直线PB与⊙O交于B,C两点,D为BC的中点,若
|PO|=√2 ,则 ⃗ ⃗ 的最大值为( )
PA⋅PD
1+√2 1+2√2
A. B. C. 1+√2 D. 2+√2
2 2
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.在下列各组向量中,可以作为基底的是( )
A. , B. ,
⃗a=(−3,2) ⃗b=(6,−4) ⃗a=(2,3) ⃗b=(3,2)
C. ⃗a=(1,−2) ,⃗
b=(7,14)
D. ⃗a=(−2,3) ,⃗
b=(4,6)
10.下列命题正确的是( )
A. 复数2−2i的虚部为−2i
B. 若z ,z 是复数,则|z ⋅z |=|z |⋅|z |
1 2 1 2 1 2
C. 若z ,z 是复数,|z +z |=|z −z |,则z ⋅z =0
1 2 1 2 1 2 1 2
D. 复平面内满足条件|z+i|≤2的复数z所对应的点Z的集合是以点(0,−1)为圆心,2为半径的圆面.
11.下列命题错误的是( )
A. 用平面去截一个棱锥,则截面与底面之间的部分为棱台.
3
B. 若向量⃗a=(x,3),⃗b=(2,−1)的夹角为钝角,则x< .
2
第 页,共 页
2 1π
C. 若B= ,BC=2√3且△ABC有两解,则AC的取值范围是(3,2√3).
3
D. 设点O是△ABC所在平面内一点,若⃗OA+2⃗OB+3⃗OC=0⃗,则△AOC与△ABC的面积之比为1:3.
三、填空题:本题共3小题,每小题5分,共15分。
12.已知长方体的长宽高分别为3,4,5,则该长方体的外接球的表面积是 .
⃗ 1 ⃗ ⃗
13.已知正方形ABCD的边长为1,点P满足AP= (AB+AC),则
|P
⃗
D|=
.
2
AC
14.已知▵ABC中,点D在边BC上,∠ADB=120∘,AD=2,CD=2BD.当 取得最小值时,BD=
AB
.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
已知向量 ⃗a=(1,k) ,⃗
b=(2,k−2)
,
若 ⃗ ⃗ ⃗,求实数
(1) (a+b)//a k;
若 ,求实数 .
(2) (⃗a−2⃗b)⊥⃗a k
16.(本小题15分)
已知复数z =3+4i,z =1−ai(a∈R,i是虚数单位).
1 2
若z 是纯虚数,求
(1) 2 |z |;
z 2
1
(2)若z 是实系数一元二次方程x2−px+3=0的根,求实数a和p的值.
2
17.(本小题15分)
如图,一个几何体是由一个正三棱柱内挖去一个倒圆锥组成,该三棱柱的底面边长为2,高为3.圆锥的底
第 页,共 页
3 1面内切于该三棱柱的上底面,顶点在三棱柱下底面的中心处.
(1)求该几何体的体积;
(2)求该几何体的表面积.
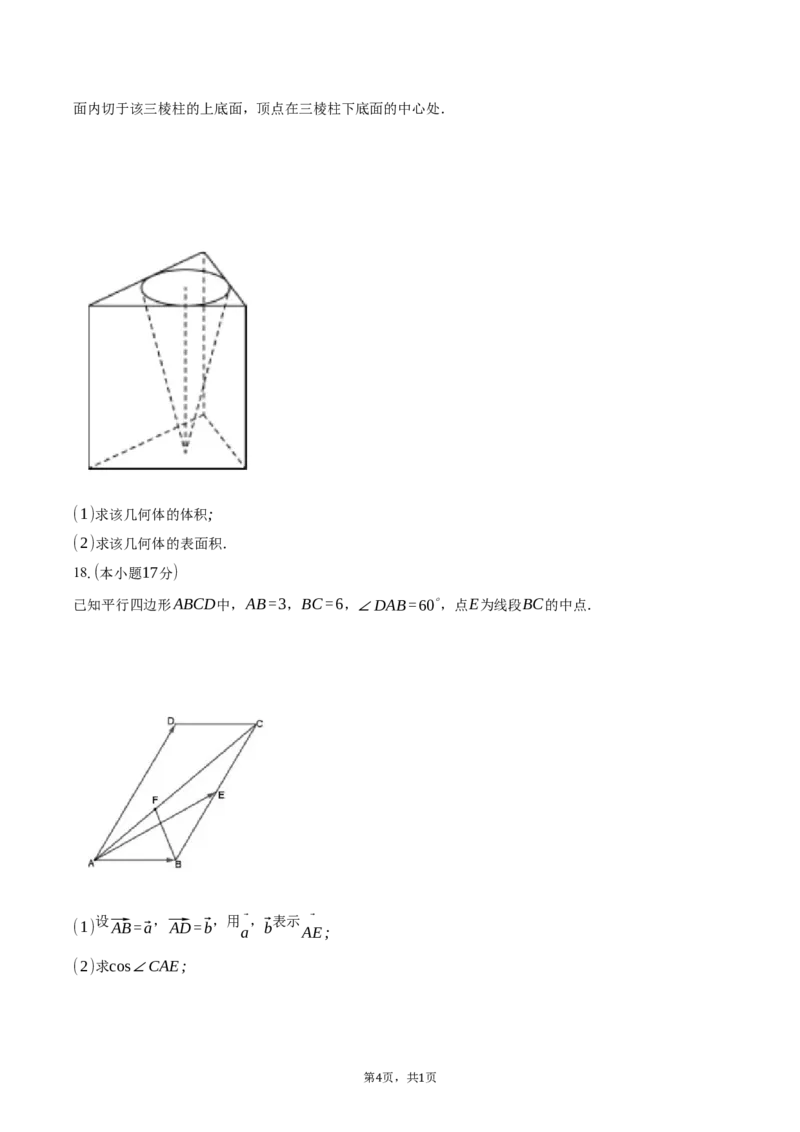
18.(本小题17分)
已知平行四边形ABCD中,AB=3,BC=6,∠DAB=60∘,点E为线段BC的中点.
设 , ,用⃗, 表示 ⃗
(1) ⃗AB=⃗a ⃗AD=⃗b
a
⃗b
AE;
(2)求cos∠CAE;
第 页,共 页
4 1⃗
|AF|
⃗ ⃗
(3)点F在线段AC上, ,求 的值.
BF⊥AE
⃗
|AC|
19.(本小题17分)
记△ABC的内角A,B,C的对边分别为a,b,c,√3c+bsin A=√3acosB.
(1)求A;
(2)点D在边BC上.
(ⅰ)若AD为中线且长为√3,AB=2,求△ABC的面积;
(ⅱ)若AD平分∠BAC,且AD=2,求△ABC面积的最小值.
第 页,共 页
5 1参考答案
1.C
2.A
3.B
4.D
5.D
6.A
7.C
8.A
9.BCD
10.BD
11.AB
12.50π
√5
13.
2
14.√3−1
15.解: ⃗ ⃗ ,
(1)a+b=(3,2k−2)
由 ⃗ ⃗ ⃗,
(a+b)//a
得(2k−2)−3k=0,
解得k=−2;
⃗ ⃗ ,
(2)a−2b=(−3,−k+4)
由 ,
(⃗a−2⃗b)⊥⃗a
得 ⃗ ⃗ ⃗ ,
(a−2b)·a=0
所以−3+k(−k+4)=0,
解得k=1或3.
第 页,共 页
6 116.解:(1)因为z =3+4i,z =1−ai,
1 2
所以z 1−ai (1−ai)(3−4i) (3−4a)−(4+3a)i,
2= = =
z 3+4i (3+4i)(3−4i) 25
1
z 是纯虚数,
∵ 2
z
1
3−4a −(4+3a) 3
∴ =0,且 ≠0,解得a= ,
25 25 4
√ 3 5
所以|z |= 12+(− ) 2= ;
2 4 4
依题意, ,即 ,
(2) (1−ai) 2−p(1−ai)+3=0 (4−a2−p)+a(p−2)i=0
即 且 ,
(4−a2−p)=0 a(p−2)=0
即{a=0或{a=±√2.
p=4 p=2
1
17.解:(1)因为正三棱柱的底面积为 ×22×sin60∘=√3,
2
所以正三棱柱的体积为√3×3=3√3,
设正三角形的内切圆半径为r,
1 √3
所以 ×r×(2+2+2)=√3,解得r= ,
2 3
1 √3 π π
所以圆锥的体积为 π( ) 2×3= ,故该几何体的体积为3√3− ;
3 3 3 3
(2)因为正三棱柱的表面积为2√3+2×3×3=2√3+18,
倒圆锥的底面圆面积为 √3 π,倒圆锥的母线长为√ √3 2√21,
π×( ) 2= 32+( ) 2=
3 3 3 3
第 页,共 页
7 1√3 2√21 2√7π
倒圆锥的侧面积为π × = ,
3 3 3
(2√7−1)π
所以该几何体的表面积为2√3+18+ .
3
⃗ ⃗ ⃗ ⃗ 1 ⃗ ⃗ 1 ⃗ ⃗ 1⃗
18.解:(1)AE=AB+BE=AB+ BC=AB+ AD=a+ b
2 2 2
⃗ ⃗ ⃗ ⃗ ⃗
(2)AC=AB+AD=a+b
⃗ ⃗ ⃗ ⃗ ⃗ 1⃗ ⃗ 3⃗ ⃗ 1⃗ 81
AC⋅AE=(a+b)⋅(a+ b)=a2+ a⋅b+ b2=
2 2 2 2
⃗ √(⃗ ⃗) 2 √⃗ ⃗ ⃗ ,
|AC|= a+b = a2+2a⋅b+b2=3√7
|A ⃗ E|= √ (⃗ a+ 1⃗ b ) 2 = √⃗ a2+ ⃗ a⋅ ⃗ b+ 1⃗ b2=3√3
2 4
⃗ ⃗
AC·AE 3√21
cos∠CAE= =
| ⃗ || ⃗ | 14
AC AE
设 ⃗ ⃗ ⃗ ⃗
(3) AF=λAC=λ(a+b)
⃗ ⃗ ⃗ ⃗ ⃗
BF=AF−AB=(λ−1)a+λb
⃗ ⃗ ⃗ λ⃗ 3 1 ⃗ ⃗ 81 27
AE⋅BF=(λ−1)a2+ b2+( λ− )a⋅b= λ− =0,
2 2 2 2 2
⃗
1 |AF| 1
解得λ= , =
3 ⃗ 3
|AC|
a b c
19.解:(1)因为√3c+bsin A=√3acosB, = = ,
sin A sinB sinC
所以√3sinC+sinBsin A=√3sin AcosB,
所以√3sin(A+B)+sinBsin A=√3sin AcosB,
第 页,共 页
8 1所以sinB(√3cosA+sin A)=0.
因为sinB≠0,所以√3cosA+sin A=0,即tan A=−√3.
2π
因为A∈(0,π),所以A= .
3
⃗ 1 ⃗ ⃗ , ⃗ 1 ⃗ ⃗ 1√ ⃗ ⃗ 1√ ⃗ ⃗ ⃗ ⃗ ,
(2)AD= (AB+AC) |AD|= |AB+AC|= (AB2+AC) 2= AB2+2AB⋅AC+AC2=√3
2 2 2 2
解得AC=4,
1
S = AB×ACsin A=2√3
ΔABC 2
π
(3)因为AD平分∠BAC,所以∠DAB=∠DAC= ,
3
1 1 1
因为S =S +S ,所以 bcsin∠BAC= c⋅AD⋅sin∠DAB+ b⋅AD⋅sin∠DAC,
△ABC △ABD △ACD 2 2 2
即bc=2(b+c).
因为b+c≥2√bc,所以bc=2(b+c)≥4√bc,
所以bc≥16(当且仅当b=c=4时等号成立).
1 2π 1 √3
所以S = bcsin ≥ ×16× =4√3,所以△ABC面积的最小值为4√3.
△ABC 2 3 2 2
第 页,共 页
9 1