文档内容
第七章 随机变量及其分布(A卷基础卷)
考试时间:100分钟;
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 总分
得分
评卷人 得 分
一.选择题(共8小题)
1.(2020春•郑州期末)随机变量X的分布列如下:
X ﹣1 0 1
P a b c
其中a,b,c成等差数列,则P(|X|=1)=( )
A. B. C. D.
2.(2019春•来宾期末)随机变量X~B(100,p),且EX=20,则D(2X﹣1)=( )
A.64 B.128 C.256 D.32
3.(2020•柳州模拟)袋中装有形状和大小完全相同的 4个黑球,3个白球,从中不放回地依次随机摸取
两球,在第一次摸到了黑球的条件下,第二次摸到白球的概率是( )
A. B. C. D.
4.(2020•江西模拟)新冠肺炎病毒可以通过飞沫传染,佩戴口罩可以预防新冠肺炎病毒传染,已知 A,
B,C三人与新冠肺炎病人甲近距离接触,由于A,B,C三人都佩戴了某种类型的口罩,若佩戴了该种
类型的口罩,近距离接触病人被感染的概率为 ,记A,B,C三人中被感染的人数为X,则X的数学期
望EX=( )
A. B. C. D.
5.(2020•长春四模)田径比赛跳高项目中,在横杆高度设定后,运动员有三次试跳机会,只要有一次试跳成功即完成本轮比赛.在某学校运动会跳高决赛中,某跳高运动员成功越过现有高度即可成为本次比
赛的冠军,结合平时训练数据,每次试跳他能成功越过这个高度的概率为 0.8(每次试跳之间互不影
响),则本次比赛他获得冠军的概率是( )
A.0.832 B.0.920 C.0.960 D.0.992
6.(2020•安阳二模)2020年2月,受新冠肺炎的影响,医卫市场上出现了“一罩难求”的现象.在政府
部门的牵头下,部分工厂转业生产口罩,已知某工厂生产口罩的质量指标ξ~N(15,0.0025),单位为
g,该厂每天生产的质量在(14.9g,15.05g)的口罩数量为818600件,则可以估计该厂每天生产的质量
在15.15g以上的口罩数量为( )
参考数据:若ξ~N(μ,σ2),则P(μ﹣σ<ξ<μ+σ)=0.6827,P(μ﹣2σ<ξ<μ+2σ)=0.9545,P(μ
﹣3σ<ξ<μ+3σ)=0.9973.
A.158 700 B.22 750 C.2 700 D.1 350
7.(2020•温州模拟)已知随机变量ξ的分布列如表:
ξ x x x
1 2 3
P P P P
1 2 3
其中x ﹣x =x ﹣x >0.若E(ξ)>x ,则( )
2 1 3 2 2
A.P >P B.P <P C.P >P D.P <P
1 2 2 3 2 3 1 3
8.(2020•葫芦岛一模)从标有数字1,2,3,4,5的五张卡片中,依次抽出2张(取后不放回),则在
第一次抽到卡片是偶数的情况下,第二次抽到卡片是奇数的概率为( )
A. B. C. D.
评卷人 得 分
二.多选题(共4小题)
9.(2020春•亭湖区校级期中)若随机变量 X服从两点分布,其中 ,E(X)、D(X)分别
为随机变量X均值与方差,则下列结论正确的是( )
A.P(X=1)=E(X) B.E(3X+2)=4
C.D(3X+2)=4 D.10.(2020春•皇姑区校级期中)如图所示的电路中,5只箱子表示保险匣分别为A,B,C,D,E.箱中
所示数值表示通电时保险丝被切断的概率,下列结论正确的是( )
A.AB所在线路畅通的概率为
B.ABC所在线路畅通的概率为
C.DE所在线路畅通的概率为
D.当开关合上时,整个电路畅通的概率为
11.(2019秋•崂山区校级月考)已知随机变量X服从正态分布N(100,102),则下列选项正确的是(
)
(参考数值:随机变量ξ服从正态分布N(μ,σ2),则P(μ﹣σ<ξ<μ+σ)=0.6826),P(μ﹣2σ<ξ
<μ+2σ)=0.9544,P(μ﹣3σ<ξ<μ+3σ)=0.9974)
A.E(X)=100 B.D(X)=100
C.P(X≥90)=0.8413 D.P(X≤120)=0.9987
12.(2020•山东模拟)甲、乙两人练习射击,命中目标的概率分别为 和 ,甲、乙两人各射击一次,下
列说法正确的是( )
A.目标恰好被命中一次的概率为
B.目标恰好被命中两次的概率为C.目标被命中的概率为
D.目标被命中的概率为1
评卷人 得 分
三.填空题(共4小题)
13.(2020•全国三模)随着国内疫情形势好转,暂停的中国正在重启,为了尽快提升经济、吸引顾客,哈
西某商场举办购物抽奖活动,凡当日购物满1000元的顾客,可参加抽奖,规则如下:盒中有大小质地
均相同5个球,其中2个红球和3个白球,不放回地依次摸出2个球,若在第一次和第二次均摸到红球
则获得特等奖,否则获得纪念奖,则顾客获得特等奖的概率是 .
14.(2020•厦门模拟)排球比赛实行“五局三胜制”,某次比赛中,中国女排和M国女排相遇,统计以
往数据可知,每局比赛中国女排获胜的概率为 ,M国女排获胜的概率为 ,则中国女排在先输一局的
情况下最终获胜的概率为 .
15.(2020春•桃城区校级月考)世卫组织就新型冠状病毒感染的肺炎疫情称,新型病毒可能造成“持续
人传人”.通俗点说就是存在A传B,B又传C,C又传D,这就是“持续人传人”.那么A、B、C就
会被称为第一代、第二代、第三代传播者.假设一个身体健康的人被被第一代、第二代、第三代传播者
感染的概率分别为0.95,0.9,0.85,健康的小明参加了一次多人宴会,事后知道,参加宴会的人有5名
第一代传播者,3名第二代传播者,2名第三代传播者,试计算,小明参加聚会,仅和感染的10个人其
中一个接触,感染的概率有多大 .
16.(2020•吉林模拟)在人类与大自然的较量中,经常面对影响人类生存、反复无常的天气变化.人类对
天气变化经历了漫长的认识过程,积累了丰富的气象经验,三国时期,孙刘联军运用气象观测经验,预
报出会有一场大雾出现,并在大雾的掩护下,演出了一场“草船借箭”的好戏,令世人惊叹.小明计划
8月份去上海游览,受台风“利马奇”的影响,上海市8月份一天中发生雷雨天气的概率上升为0.8,那
么小明在上海游览的3天中,只有1天不发生雷雨天气的概率约为
评卷人 得 分四.解答题(共5小题)
17.(2020春•南阳期中)某校从学生文艺部6名成员(4男2女)中,挑选2人参加学校举办的文艺汇演
活动.
(1)求男生甲被选中的概率;
(2)在已知男生甲被选中的条件下,女生乙被选中的概率;
(3)在要求被选中的两人中必须一男一女的条件下,求女生乙被选中的概率.
18.(2019春•抚顺期末)唐代饼茶的制作一直延续至今,它的制作由“炙”、“碾”、“罗”三道工序
组成:根据分析甲、乙、丙三位学徒通过“炙”这道工序的概率分别是 0.5,0.6,0.5;能通过“碾”这
道工序的概率分别是0.8,0.5,0.4;由于他们平时学习刻苦,都能通过“罗”这道工序;若这三道工序
之间通过与否没有影响,
(Ⅰ)求甲、乙、丙三位同学中恰好有一人通过“炙”这道工序的概率;
(Ⅱ)设只要通过三道工序就可以制成饼茶,求甲、乙、丙三位同学中制成饼茶人数X的分布列.
19.(2019秋•密云区期末)甲、乙两位运动员一起参加赛前培训.现分别从他们在培训期间参加的若干
次测试成绩中随机抽取8次,记录如下:
甲:82 81 79 78 95 88 93 84
乙:86 85 79 86 84 84 85 91
(Ⅰ)请你运用茎叶图表示这两组数据;
(Ⅱ)若用甲8次成绩中高于85分的频率估计概率,对甲同学在今后的3次测试成绩进行预测,记这3
次成绩中高于85分的次数为ξ,求ξ的分布列及数学期望Eξ;
(Ⅲ)现要从中选派一人参加正式比赛,依据所抽取的两组数据分析,你认为选派哪位选手参加较为合
适?并说明理由.
20.(2018秋•黔西县期末)某企业有甲、乙两个研发小组,他们研发新产品成功的概率分别为 和 .现
安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
(I)求至少有一种新产品研发成功的概率;
(Ⅱ)若新产品A研发成功,预计企业可获利润120万元;若新产品B研发成功,预计企业可获利润
100万元,该企业可获利润有哪几种可能,其利润及概率各为多少?
21.(2020•香坊区校级二模)新型冠状病毒最近在全国蔓延,具有很强的人与人之间的传染性,该病毒在
进入人体后一般有14天的潜伏期,在这14天的潜伏期内患者无任何症状,为病毒传播的最佳时间.假
设每位病毒携带者在潜伏期内每天有n位密切接触者,接触病毒携带者后被感染的概率为p,每位密切接触者不用再接触其他病毒携带者.
(1)求一位病毒携带者一天内感染的人数X的均值;
(2)若n=3, 时,从被感染的第一天算起,试计算某一位病毒携带者在 14天潜伏期内,被他平
均累计感染的人数(用数字作答);
(3)3月16日20时18分,由我国军事科学院军事科学研究院陈薇院士领衔的科学团队,研制重组新
型冠状病毒疫苗获批进入临床状态,新疫苗的使用,可以极大减少感染新型冠状病毒的人数,为保证安
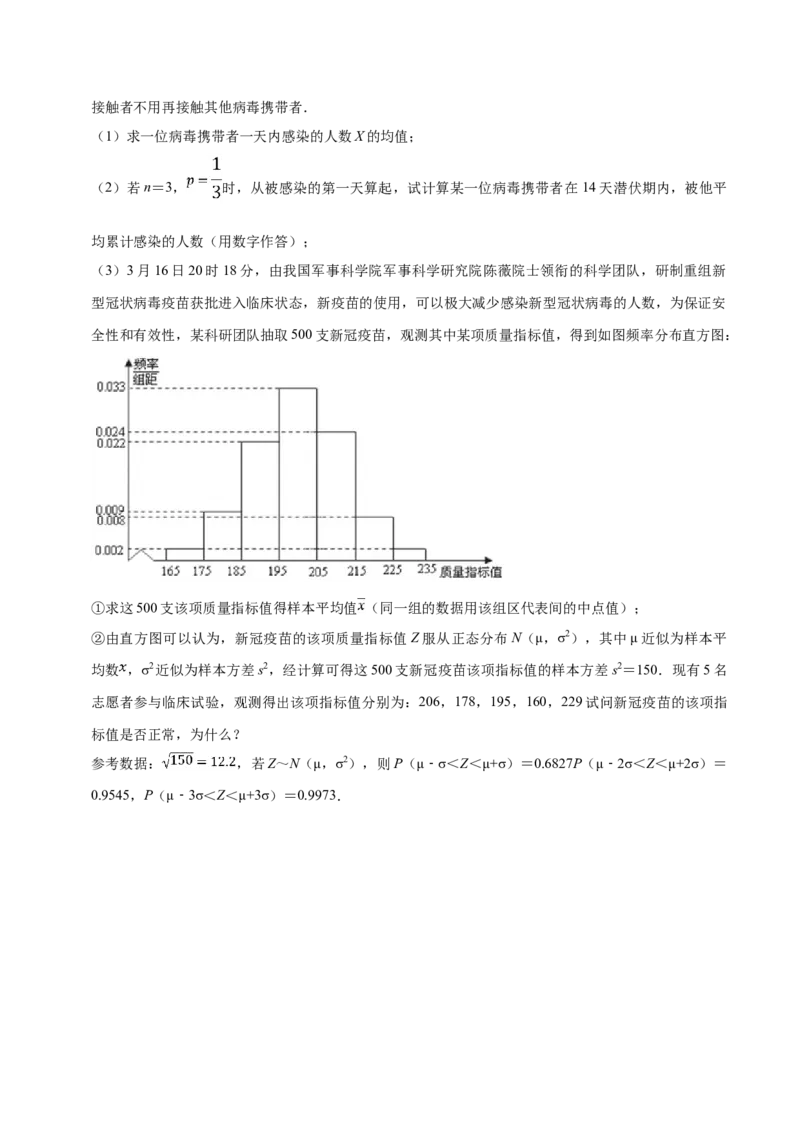
全性和有效性,某科研团队抽取500支新冠疫苗,观测其中某项质量指标值,得到如图频率分布直方图:
①求这500支该项质量指标值得样本平均值 (同一组的数据用该组区代表间的中点值);
②由直方图可以认为,新冠疫苗的该项质量指标值 Z服从正态分布N(μ,σ2),其中μ近似为样本平
均数 ,σ2近似为样本方差s2,经计算可得这500支新冠疫苗该项指标值的样本方差s2=150.现有5名
志愿者参与临床试验,观测得出该项指标值分别为:206,178,195,160,229试问新冠疫苗的该项指
标值是否正常,为什么?
参考数据: ,若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)=0.6827P(μ﹣2σ<Z<μ+2σ)=
0.9545,P(μ﹣3σ<Z<μ+3σ)=0.9973.