文档内容
第七章 随机变量及其分布(B 卷提高卷)
参考答案与试题解析
一.选择题(共8小题)
1.(2019春•福州期末)抛掷甲、乙两颗骰子,若事件A:“甲骰子的点数大于3”;事件B:“甲、乙两
骰子的点数之和等于7”,则P(B|A)的值等于( )
A. B. C. D.
【解答】解:由题意可得:事件A:“甲骰子的点数大于3”包含点数为4,5,6三种情况,
所以为P(A) ,
又事件B:“甲、乙两骰子的点数之和等于7”,
所以,事件A与事件B都发生所包含的情况有(4,3),(5,2),(6,1),共3个基本事件;而抛
掷甲、乙两颗骰子,共有36种情况,
所以事件A与事件B都发生的概率为P(AB) ,
故P(B|A) .
故选:B.
2.(2019秋•浙江月考)设 ,随机变量X的分布列是:
X ﹣1 0 1
P a
则当a在 内增大时( )
A.D(X)增大 B.D(X)减小
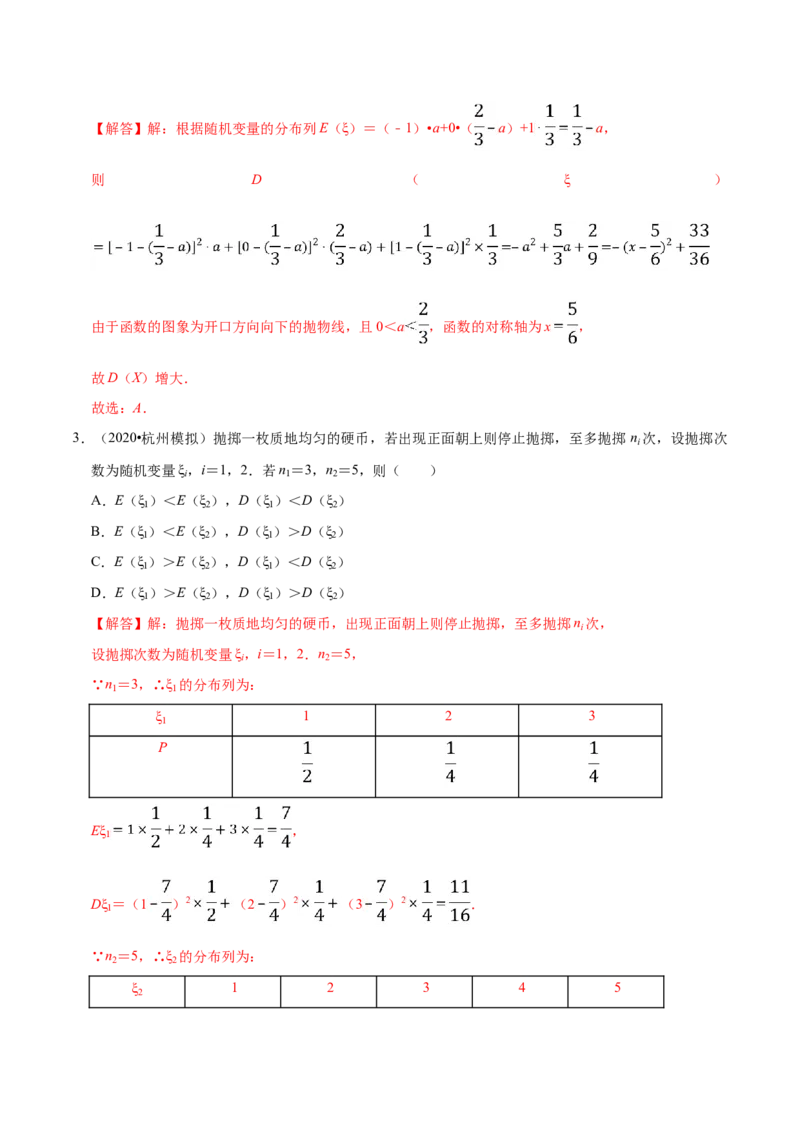
C.D(X)先增大后减小 D.D(X)先减小后增大【解答】解:根据随机变量的分布列E(ξ)=(﹣1)•a+0•( a)+1 a,
则 D ( ξ )
由于函数的图象为开口方向向下的抛物线,且0<a ,函数的对称轴为x ,
故D(X)增大.
故选:A.
3.(2020•杭州模拟)抛掷一枚质地均匀的硬币,若出现正面朝上则停止抛掷,至多抛掷 n 次,设抛掷次
i
数为随机变量ξ,i=1,2.若n =3,n =5,则( )
i 1 2
A.E(ξ )<E(ξ ),D(ξ )<D(ξ )
1 2 1 2
B.E(ξ )<E(ξ ),D(ξ )>D(ξ )
1 2 1 2
C.E(ξ )>E(ξ ),D(ξ )<D(ξ )
1 2 1 2
D.E(ξ )>E(ξ ),D(ξ )>D(ξ )
1 2 1 2
【解答】解:抛掷一枚质地均匀的硬币,出现正面朝上则停止抛掷,至多抛掷n 次,
i
设抛掷次数为随机变量ξ,i=1,2.n =5,
i 2
∵n =3,∴ξ 的分布列为:
1 1
ξ 1 2 3
1
P
Eξ ,
1
Dξ =(1 )2 (2 )2 (3 )2 .
1
∵n =5,∴ξ 的分布列为:
2 2
ξ 1 2 3 4 5
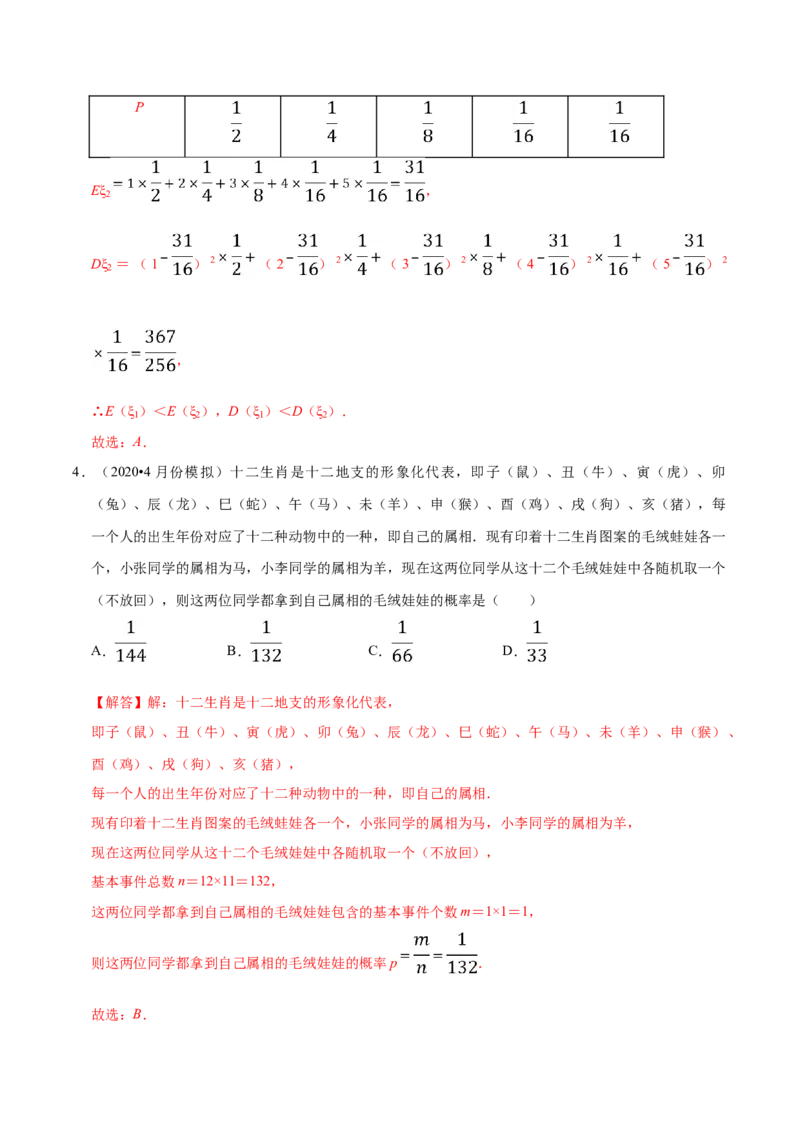
2P
Eξ ,
2
Dξ =(1 )2 (2 )2 (3 )2 (4 )2 (5 )2
2
,
∴E(ξ )<E(ξ ),D(ξ )<D(ξ ).
1 2 1 2
故选:A.
4.(2020•4月份模拟)十二生肖是十二地支的形象化代表,即子(鼠)、丑(牛)、寅(虎)、卯
(兔)、辰(龙)、巳(蛇)、午(马)、未(羊)、申(猴)、酉(鸡)、戌(狗)、亥(猪),每
一个人的出生年份对应了十二种动物中的一种,即自己的属相.现有印着十二生肖图案的毛绒蛙娃各一
个,小张同学的属相为马,小李同学的属相为羊,现在这两位同学从这十二个毛绒娃娃中各随机取一个
(不放回),则这两位同学都拿到自己属相的毛绒娃娃的概率是( )
A. B. C. D.
【解答】解:十二生肖是十二地支的形象化代表,
即子(鼠)、丑(牛)、寅(虎)、卯(兔)、辰(龙)、巳(蛇)、午(马)、未(羊)、申(猴)、
酉(鸡)、戌(狗)、亥(猪),
每一个人的出生年份对应了十二种动物中的一种,即自己的属相.
现有印着十二生肖图案的毛绒蛙娃各一个,小张同学的属相为马,小李同学的属相为羊,
现在这两位同学从这十二个毛绒娃娃中各随机取一个(不放回),
基本事件总数n=12×11=132,
这两位同学都拿到自己属相的毛绒娃娃包含的基本事件个数m=1×1=1,
则这两位同学都拿到自己属相的毛绒娃娃的概率p .
故选:B.5.(2020•濮阳模拟)设一个正三棱柱ABC﹣DEF,每条棱长都相等,一只蚂蚁从上底面ABC的某顶点出
发,每次只沿着棱爬行并爬到另一个顶点,算一次爬行,若它选择三个方向爬行的概率相等,若蚂蚁爬
行10次,仍然在上底面的概率为P ,则P 为( )
10 10
A. B.
C. D.
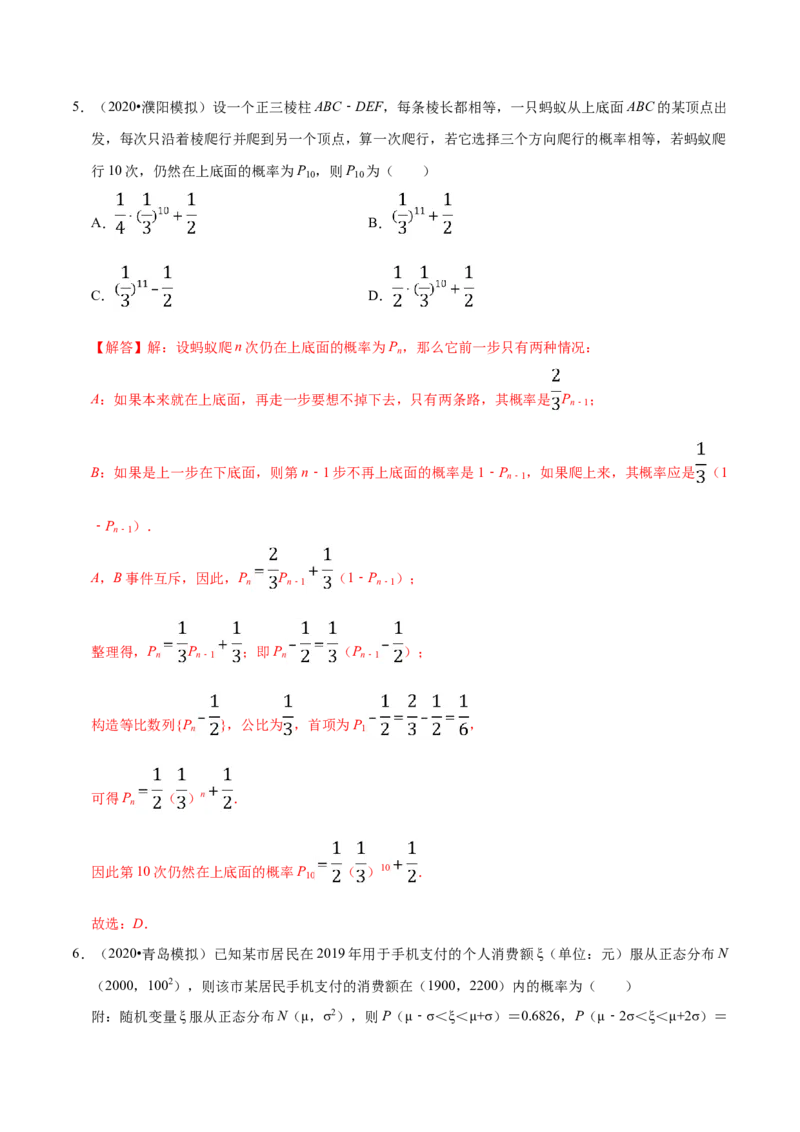
【解答】解:设蚂蚁爬n次仍在上底面的概率为P ,那么它前一步只有两种情况:
n
A:如果本来就在上底面,再走一步要想不掉下去,只有两条路,其概率是 P ;
n﹣1
B:如果是上一步在下底面,则第n﹣1步不再上底面的概率是1﹣P ,如果爬上来,其概率应是 (1
n﹣1
﹣P ).
n﹣1
A,B事件互斥,因此,P P (1﹣P );
n n﹣1 n﹣1
整理得,P P ;即P (P );
n n﹣1 n n﹣1
构造等比数列{P },公比为 ,首项为P ,
n 1
可得P ( )n .
n
因此第10次仍然在上底面的概率P ( )10 .
10
故选:D.
6.(2020•青岛模拟)已知某市居民在2019年用于手机支付的个人消费额ξ(单位:元)服从正态分布N
(2000,1002),则该市某居民手机支付的消费额在(1900,2200)内的概率为( )
附:随机变量ξ服从正态分布N(μ,σ2),则P(μ﹣σ<ξ<μ+σ)=0.6826,P(μ﹣2σ<ξ<μ+2σ)=0.9544,P(μ﹣3σ<ξ<μ+3σ)=0.9974.
A.0.9759 B.0.84 C.0.8185 D.0.4772
【解答】解:∵ξ服从正态分布N(2000,1002),
∴μ=2000,σ=100,
则P(1900<ξ<2200)=P(μ﹣σ<ξ<μ+σ) [P(μ﹣2σ<ξ<μ+2σ)﹣P(μ﹣σ<ξ<μ+σ)]
=0.6826 (0.9544﹣0.6826)=0.8185.
故选:C.
7.(2019春•越城区校级月考)随机变量ξ有四个不同的取值,且其分布列如下:
ξ 2sinαsinβ 3cosαsinβ 3sinαcosβ cosαcosβ
P t
则E(ξ)的最大值为( )
A.﹣1 B. C. D.1
【解答】解:依题意,t=1 ,
所以E(ξ) (2sinαsinβ+3cosαsinβ+3sinαcosβ) cosαcosβ
(cosαsinβ+sinαcosβ) (sinαsinβ+cosαcosβ)
sin(α+β) cos(α﹣β),
所以当α+β ,α﹣β=2kπ,(k∈z)时,即 (k∈Z)时,E(ξ)取得最大值 1.
故选:D.
8.(2020•九龙坡区校级模拟)2020年初,新冠病毒肺炎(COVID﹣19)疫情在武汉爆发,并以极快的速
度在全国传播开来.因该病毒暂无临床特效药可用,因此防控难度极大.湖北某地防疫防控部门决定进
行全面入户排查4类人员:新冠患者、疑似患者、普通感冒发热者和新冠密切接触者,过程中排查到一
户5口之家被确认为新冠肺炎密切接触者,按要求进一步对该5名成员逐一进行核糖核酸检测,若出现
阳性,则该家庭定义为“感染高危户”,设该家庭每个成员检测呈阳性的概率相同均为 p(0<p<
1),且相互独立,该家庭至少检测了4人才能确定为“感染高危户”的概率为f(p),当p=p 时,f
0
(p)最大,此时p =( )
0
A. B. C. D.
【解答】解:根据相互独立事件同时发生的概率公式得:
f(p)=(1﹣p)3p+(1﹣p)4p,
∴f′(p)=﹣3(1﹣p)2p+(1﹣p)3﹣4(1﹣p)3p+(1﹣p)4=(1﹣p)2(5p2﹣10p+2)
=(1﹣p)(p )(p ),
∵0≤p≤1,当p=p 时,f(p)最大,
0
∴p 1 .
0
故选:A.
二.多选题(共4小题)
9.(2020•山东模拟)甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球.
先从甲罐中随机取出一球放入乙罐,分别以A ,A 和A 表示由甲罐取出的球是红球,白球和黑球的事
1 2 3
件;再从乙罐中随机取出一球,以B表示由乙罐取出的球是红球的事件,则下列结论中正确的是
( )
A.B.
C.事件B与事件A 相互独立
1
D.A ,A ,A 是两两互斥的事件
1 2 3
【 解 答 】 解 : 易 见 A , A , A 是 两 两 互 斥 的 事 件 ,
1 2 3
.
故选:BD.
10.(2020•泰安二模)“杂交水稻之父”袁隆平一生致力于杂交水稻技术的研究、应用与推广,发明了
“三系法”籼型杂交水稻,成功研究出“两系法”杂交水稻,创建了超级杂交稻技术体系,为我国粮食
安全、农业科学发展和世界粮食供给做出了杰出贡献;某杂交水稻种植研究所调查某地水稻的株高,得
出株高(单位:cm)服从正态分布,其密度曲线函数为 ,
则下列说法正确的是( )
A.该地水稻的平均株高为100cm
B.该地水稻株高的方差为10
C.随机测量一株水稻,其株高在120cm以上的概率比株高在70cm以下的概率大
D.随机测量一株水稻,其株高在(80,90)和在(100,110)(单位:cm)的概率一样大
【解答】解:由正态分布密度曲线函数为 ,
得μ=100,σ=10.
∴该地水稻的平均株高为E(X)=100cm,故A正确;
该地水稻株高的标准差σ=10,方差为100,故B错误;
∵P(X>120) [1﹣P(μ﹣2σ<X<μ+2σ)] (1﹣0.9544)=0.0228,P(X<70) [1﹣P(μ﹣3σ<X<μ+3σ)] (1﹣0.9974)=0.0013,
∴随机测量一株水稻,其株高在120cm以上的概率比株高在70cm以下的概率大,故C正确;
P(80<X<90) [P(μ﹣2σ<X<μ+2σ)﹣P(μ﹣σ<X<μ+σ)]
(0.9544﹣0.6826)=0.1359,
P(100<X<110) [P(μ﹣σ<X<μ+σ)] 0.6826=0.3413.
∴随机测量一株水稻,其株高在(80,90)和在(100,110)(单位:cm)的概率不一样大,
故D错误.
故选:AC.
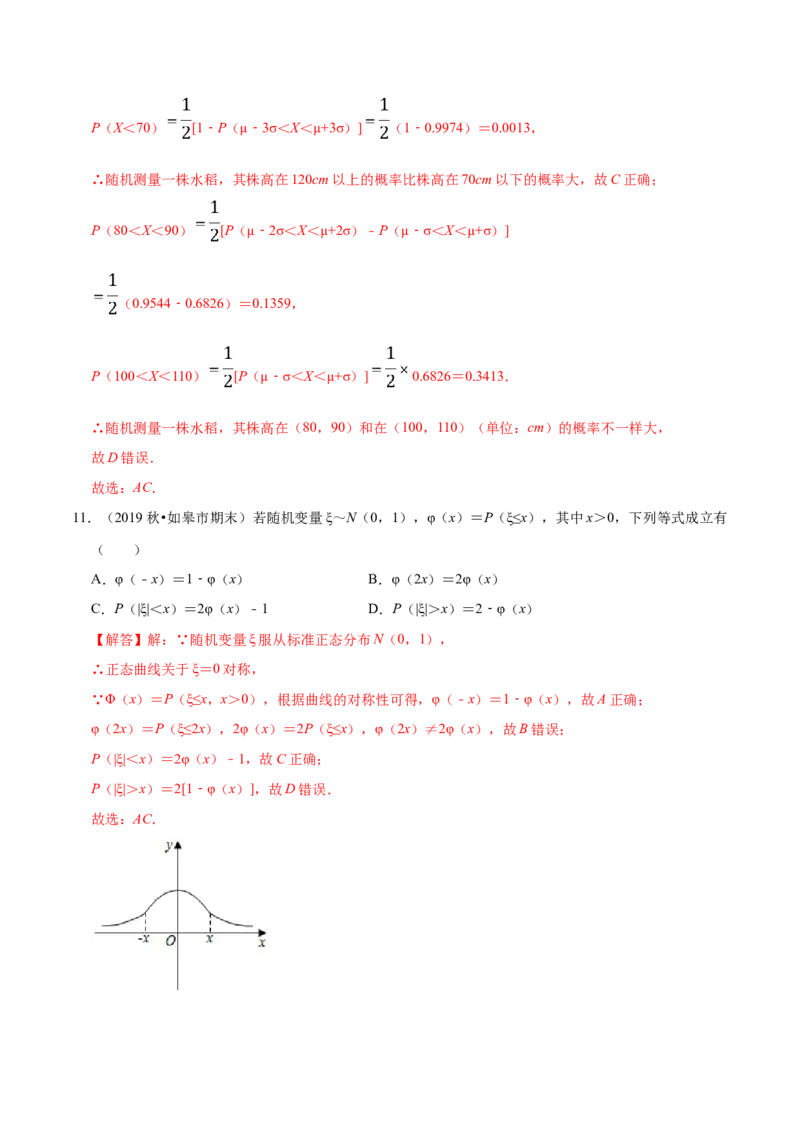
11.(2019秋•如皋市期末)若随机变量ξ~N(0,1),φ(x)=P(ξ≤x),其中x>0,下列等式成立有
( )
A.φ(﹣x)=1﹣φ(x) B.φ(2x)=2φ(x)
C.P(|ξ|<x)=2φ(x)﹣1 D.P(|ξ|>x)=2﹣φ(x)
【解答】解:∵随机变量ξ服从标准正态分布N(0,1),
∴正态曲线关于ξ=0对称,
∵Φ(x)=P(ξ≤x,x>0),根据曲线的对称性可得,φ(﹣x)=1﹣φ(x),故A正确;
φ(2x)=P(ξ≤2x),2φ(x)=2P(ξ≤x),φ(2x)≠2φ(x),故B错误;
P(|ξ|<x)=2φ(x)﹣1,故C正确;
P(|ξ|>x)=2[1﹣φ(x)],故D错误.
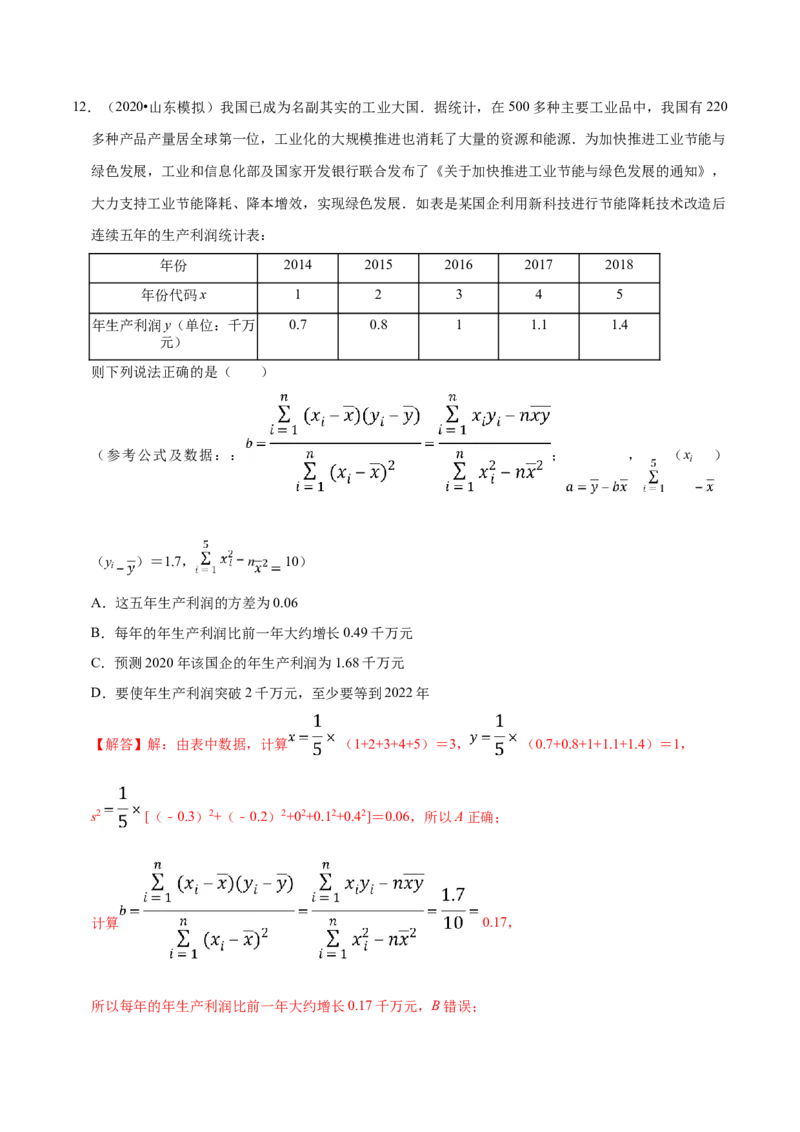
故选:AC.12.(2020•山东模拟)我国已成为名副其实的工业大国.据统计,在500多种主要工业品中,我国有220
多种产品产量居全球第一位,工业化的大规模推进也消耗了大量的资源和能源.为加快推进工业节能与
绿色发展,工业和信息化部及国家开发银行联合发布了《关于加快推进工业节能与绿色发展的通知》,
大力支持工业节能降耗、降本增效,实现绿色发展.如表是某国企利用新科技进行节能降耗技术改造后
连续五年的生产利润统计表:
年份 2014 2015 2016 2017 2018
年份代码x 1 2 3 4 5
年生产利润y(单位:千万 0.7 0.8 1 1.1 1.4
元)
则下列说法正确的是( )
(参考公式及数据:: ; , (x )
i
(y )=1.7, n 10)
i
A.这五年生产利润的方差为0.06
B.每年的年生产利润比前一年大约增长0.49千万元
C.预测2020年该国企的年生产利润为1.68千万元
D.要使年生产利润突破2千万元,至少要等到2022年
【解答】解:由表中数据,计算 (1+2+3+4+5)=3, (0.7+0.8+1+1.1+1.4)=1,
s2 [(﹣0.3)2+(﹣0.2)2+02+0.12+0.42]=0.06,所以A正确;
计算 0.17,
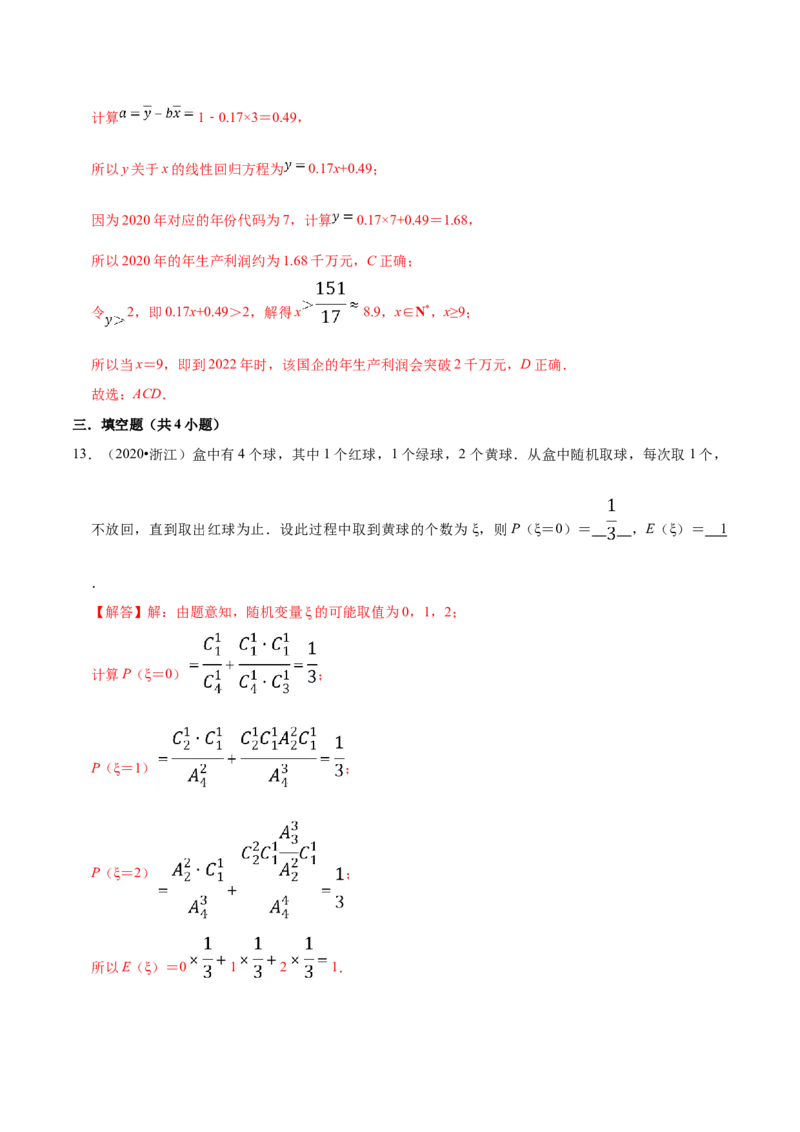
所以每年的年生产利润比前一年大约增长0.17千万元,B错误;计算 1﹣0.17×3=0.49,
所以y关于x的线性回归方程为 0.17x+0.49;
因为2020年对应的年份代码为7,计算 0.17×7+0.49=1.68,
所以2020年的年生产利润约为1.68千万元,C正确;
令 2,即0.17x+0.49>2,解得x 8.9,x∈N*,x≥9;
所以当x=9,即到2022年时,该国企的年生产利润会突破2千万元,D正确.
故选:ACD.
三.填空题(共4小题)
13.(2020•浙江)盒中有4个球,其中1个红球,1个绿球,2 个黄球.从盒中随机取球,每次取1个,
不放回,直到取出红球为止.设此过程中取到黄球的个数为 ξ,则P(ξ=0)= ,E(ξ)= 1
.
【解答】解:由题意知,随机变量ξ的可能取值为0,1,2;
计算P(ξ=0) ;
P(ξ=1) ;
P(ξ=2) ;
所以E(ξ)=0 1 2 1.故答案为: ,1.
14.(2019秋•襄城区校级月考)将4瓶外观相同,品质不同的酒让品酒师品尝,要求按品质优劣将4种
酒排序,经过一段时间后,再让其品尝这4瓶酒,并让他重新按品质优劣将4种酒排序.根据测试中两
次排序的偏离程度评估品酒师的能力.a ,a ,a ,a ,表示第一次排序为1,2,3,4的四种酒分別在
1 2 3 4
第二次排序中的序号,记X=|1﹣a |+|2﹣a |+|3﹣a |+|4﹣a |为其偏离程度,假设a ,a ,a ,a 为1,
1 2 3 4 1 2 3 4
2,3,4的等可能的各种排列,假设每轮测试之间互不影响,p 表示在1轮测试中X≤2的概率,p 表示
1 2
在前3轮测试中恰好有一轮X≤2的概率,则p = .
2
【解答】解:依题意,基本事件的总数为 24,
随机变量X≤2时,4种酒全排对,或者相邻的两种位置互换,包含的基本事件个数为1+3=4,
故在1轮测试中X≤2的概率P ,
依题意,前3轮测试中随机变量X~B(3, ),
所以p ,
2
故答案为: .
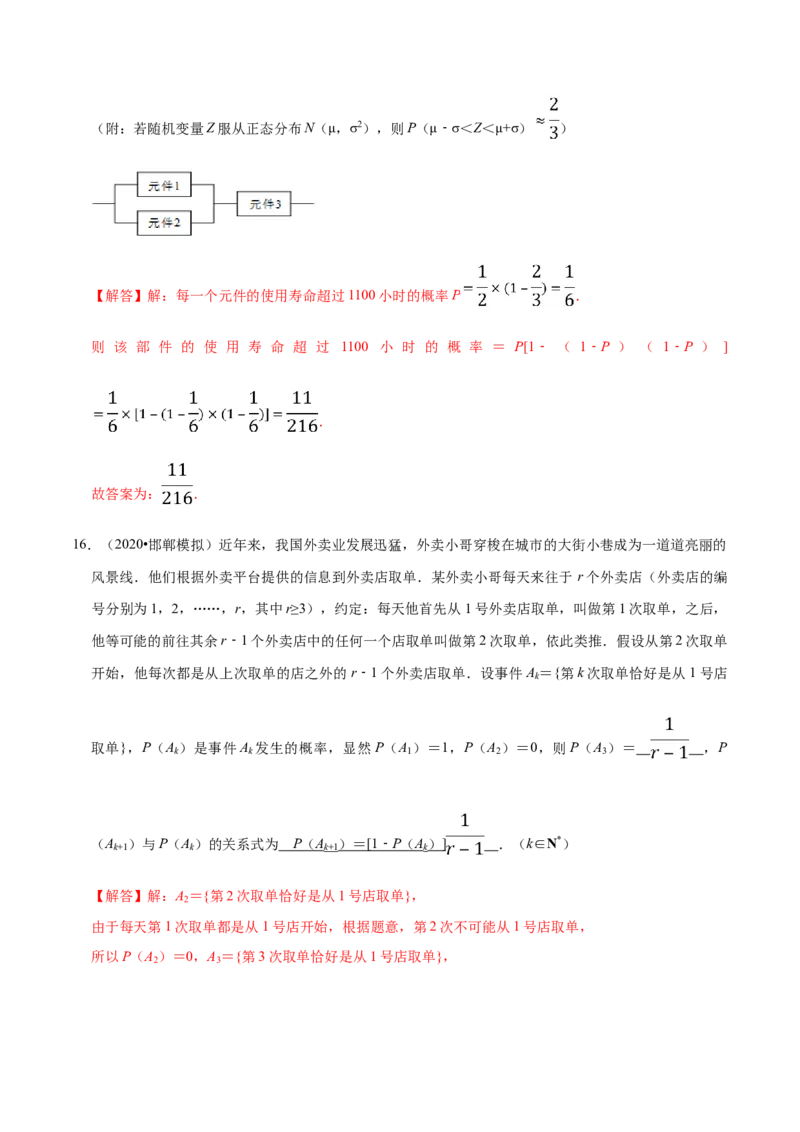
15.(2019春•福清市校级期末)某一部件由三个电子元件按下图方式连接而成,元件 1或元件2正常工
作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)均服从正态分布
N(1000,1002),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1100小时的概率为(附:若随机变量Z服从正态分布N(μ,σ2),则P(μ﹣σ<Z<μ+σ) )
【解答】解:每一个元件的使用寿命超过1100小时的概率P .
则 该 部 件 的 使 用 寿 命 超 过 1100 小 时 的 概 率 = P[1﹣ ( 1﹣P ) ( 1﹣P ) ]
.
故答案为: .
16.(2020•邯郸模拟)近年来,我国外卖业发展迅猛,外卖小哥穿梭在城市的大街小巷成为一道道亮丽的
风景线.他们根据外卖平台提供的信息到外卖店取单.某外卖小哥每天来往于 r个外卖店(外卖店的编
号分别为1,2,……,r,其中r≥3),约定:每天他首先从1号外卖店取单,叫做第1次取单,之后,
他等可能的前往其余r﹣1个外卖店中的任何一个店取单叫做第2次取单,依此类推.假设从第2次取单
开始,他每次都是从上次取单的店之外的r﹣1个外卖店取单.设事件A ={第k次取单恰好是从1号店
k
取单},P(A )是事件A 发生的概率,显然P(A )=1,P(A )=0,则P(A )= ,P
k k 1 2 3
(A )与P(A )的关系式为 P ( A )= [1﹣ P ( A ) ] .(k∈N*)
k+1 k k+1 k
【解答】解:A ={第2次取单恰好是从1号店取单},
2
由于每天第1次取单都是从1号店开始,根据题意,第2次不可能从1号店取单,
所以P(A )=0,A ={第3次取单恰好是从1号店取单},
2 3因此 ,
.
故答案为: ;P(A )=[1﹣P(A )] .
k+1 k
四.解答题(共5小题)
17.(2020•葫芦岛二模)在2019年女排世界杯比赛中,甲队以3:1力克主要竞争对手乙队,取得了一场
关键性的胜利.排球比赛按“五局三胜制的规则进行(即先胜三局的一方获胜,比赛结束),且各局之
间互不影响.根据两队以往的交战成绩分析,乙队在前四局的比赛中每局获胜的概率是 ,但前四局打
成2:2的情况下,在第五局中甲队凭借过硬的心理素质,获胜的概率为 .若甲队与乙队下次在比赛上
相遇.
(1)求甲队以3:1获胜的概率;
(2)设甲的净胜局数(例如:甲队以3:1获胜,则甲队的净胜局数为2,乙队的净胜局数为﹣2)为
ξ,求ξ的分布列及Eξ.
【解答】解:(1)甲队以3:1获胜的概率P .
(2)由题意可知,甲队和乙队的比分有如下六种0:3,1:3,2:3,3:2,3:1,3:0,
则的ξ取值有﹣3,﹣2,﹣1,1,2,3
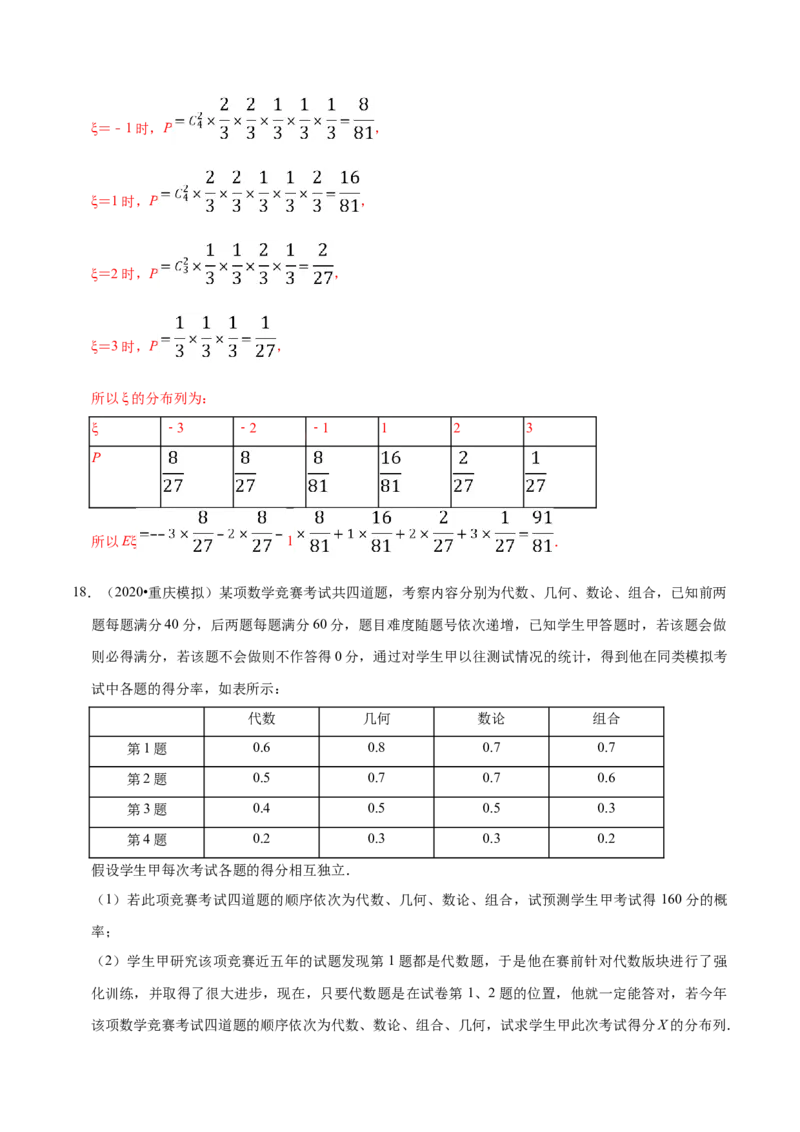
ξ=﹣3时,P ,
ξ=﹣2时,P ,ξ=﹣1时,P ,
ξ=1时,P ,
ξ=2时,P ,
ξ=3时,P ,
所以ξ的分布列为:
ξ ﹣3 ﹣2 ﹣1 1 2 3
P
所以Eξ 1 .
18.(2020•重庆模拟)某项数学竞赛考试共四道题,考察内容分别为代数、几何、数论、组合,已知前两
题每题满分40分,后两题每题满分60分,题目难度随题号依次递增,已知学生甲答题时,若该题会做
则必得满分,若该题不会做则不作答得0分,通过对学生甲以往测试情况的统计,得到他在同类模拟考
试中各题的得分率,如表所示:
代数 几何 数论 组合
第1题 0.6 0.8 0.7 0.7
第2题 0.5 0.7 0.7 0.6
第3题 0.4 0.5 0.5 0.3
第4题 0.2 0.3 0.3 0.2
假设学生甲每次考试各题的得分相互独立.
(1)若此项竞赛考试四道题的顺序依次为代数、几何、数论、组合,试预测学生甲考试得 160分的概
率;
(2)学生甲研究该项竞赛近五年的试题发现第1题都是代数题,于是他在赛前针对代数版块进行了强
化训练,并取得了很大进步,现在,只要代数题是在试卷第 1、2题的位置,他就一定能答对,若今年
该项数学竞赛考试四道题的顺序依次为代数、数论、组合、几何,试求学生甲此次考试得分X的分布列.【解答】解:(1)学生甲得160分,即第1,2题做对一道,第3、4题都做对,
∴P=(0.6×0.3+0.4×0.7)×0.5×0.2=0.046.
(2)由题知学生甲第1题必得40分,只需考虑另三道题的得分情况,
故X的所有可能取值为40,80,100,140,160,200,
P(X=40)=0.3×0.7×0.7=0.147,
P(X=80)=0.7×0.7×0.7=0.343,
P(X=100)=0.3 ,
P(X=140) ,
P(X=160)=0.3×0.3×0.3=0.027,
P(X=200)=0.7×0.3×0.3=0.063.
∴X的分布列为:
X 40 80 100 140 160 200
P 0.147 0.343 0.126 0.294 0.027 0.063
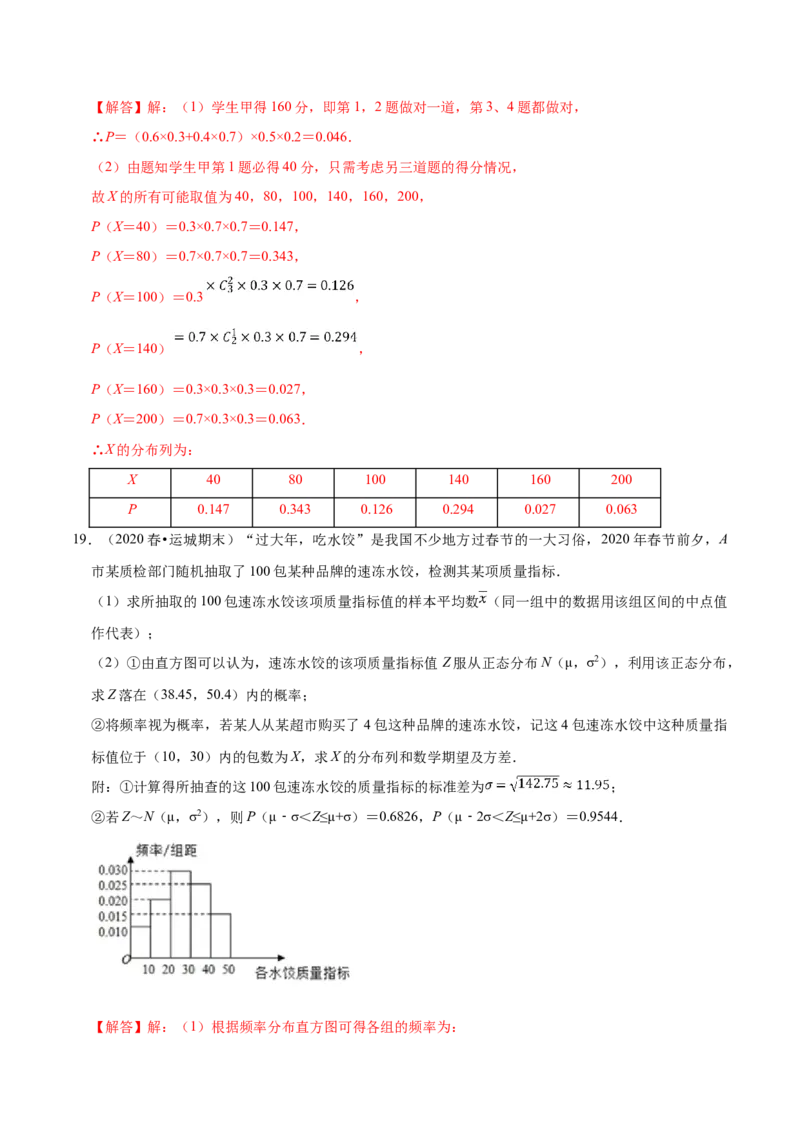
19.(2020春•运城期末)“过大年,吃水饺”是我国不少地方过春节的一大习俗,2020年春节前夕,A
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数 (同一组中的数据用该组区间的中点值
作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值 Z服从正态分布N(μ,σ2),利用该正态分布,
求Z落在(38.45,50.4)内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指
标值位于(10,30)内的包数为X,求X的分布列和数学期望及方差.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为 ;
②若Z~N(μ,σ2),则P(μ﹣σ<Z≤μ+σ)=0.6826,P(μ﹣2σ<Z≤μ+2σ)=0.9544.
【解答】解:(1)根据频率分布直方图可得各组的频率为:(0,10]的频率为:0.010×10=0.1,
(10,20]的频率为:0.020×10=0.2,
(20,30]的频率为:0.030×10=0.3,
(30,40]的频率为:0.025×10=0.25,
(40,50]的频率为:0.015×10=0.15,
所以所抽取的100包速冻水饺该项质量指标值的样本平均数 为:
.
(2)①∵Z服从正态分布N(μ,σ2),且μ=26.5,σ≈11.95,
P(38.45<Z<50.4)
=P(26.5﹣2×11.95<Z<26.5+2×11.95)﹣P(26.5﹣11.95<Z<26.5+11.95)
=(0.9544﹣0.6826)÷2=0.1359
∴Z落在(38.45,50.4)内的概率是0.1359.
②根据题意得每包速冻水饺的质量指标值位于(10,30)内的概率为0.2+0.3=0.5,
∴X~B(4, ),X的可能取值分别为:0,1,2,3,4,
,
,
,
,
,
∴X的分布列为:
X 0 1 2 3 4
P∵X~B(4, ),∴ .,D(X)=4 1.
20.(2020•6月份模拟)时至21世纪.环境污染已经成为世界各国面临的一大难题,其中大气污染是目
前城市急需应对的一项课题.某市号召市民尽量减少开车出行以绿色低碳的出行方式支持节能减排.原
来天天开车上班的王先生积极响应政府号召,准备每天从骑自行车和开小车两种出行方式中随机选择一
种方式出行.从即日起出行方式选择规则如下:第一天选择骑自行车方式上班,随后每天用“一次性抛
掷6枚均匀硬币”的方法确定出行方式,若得到的正面朝上的枚数小于 4,则该天出行方式与前一天相
同,否则选择另一种出行方式.
(1)求王先生前三天骑自行车上班的天数X的分布列;
(2)由条件概率我们可以得到概率论中一个很重要公式﹣﹣全概率公式.其特殊情况如下:如果事件
A A 相互对立并且P(A)>0(i=1,2),则对任一事件B有P(B)=P(B|A )P(A )+P(B|A )
1 2 i 1 1 2
P(A )=P(A B)+P(A B).
2 1 2
设P (n∈N*)表示事件“第n天王先生上班选择的是骑自行车出行方式”的概率.
n
(i)用p 表示p (n≥2);
n﹣1 n
(ii)王先生的这种选择随机选择出行方式有没有积极响应该市政府的号召,请说明理由.
【解答】解:(1)设一把投掷6枚均匀的硬币,得到正面向上的枚数为ξ,则ξ~B(6, ),
故P(ξ<4)=( )6 ( )6 ( )6 ( )6 ,P(ξ≥4)=1 ,
X的可能取值为1,2,3,
P(X=1) • ,P(X=3) ,
P(X=2)=1 ,
∴X的分布列为:
X 1 2 3P
(2)(i)P =P • (1﹣P )• P (n≥2).
n n﹣1 n﹣1 n﹣1
(ii)由(i)可知:P (P ),又P ,
n n﹣1 1
∴{P }是以 为首项,以 为公比的等比数列,
n
∴P •( )n﹣1,即P •( )n﹣1 .
n n
∵P •( )n﹣1 ,
n
∴王先生每天骑自行车的概率总大于开小汽车的概率,
∴王先生的这种选择随机选择出行方式有积极响应该市政府的号召.
21.(2020•山东模拟)某高校的大一学生在军训结束前,需要进行各项过关测试,其中射击过关测试规定:
每位测试的大学生最多有两次射击机会,第一次射击击中靶标,立即停止射击,射击测试过关,得5分;
第一次未击中靶标,继续进行第二次射击,若击中靶标,立即停止射击,射击测试过关,得4分;若未
击中靶标,射击测试未能过关,得2分.现有一个班组的12位大学生进行射击过关测试,假设每位大
学生两次射击击中靶标的概率分别为m,0.5,每位大学生射击测试过关的概率为p.
(1)求p(用m表示);
(2)设该班组中恰有9人通过射击过关测试的概率为f(p),求f(p)取最大值时p和m的值;
(3)在(2)的结果下,求该班组通过射击过关测试所得总分的平均数.
【解答】解:(1)每位大学生射击测试过关的概率:
P=1﹣(1﹣m)(1﹣0.5)=0.5+0.5m.
(2)f(p) ,(0<p<1),
∴f′(p)=3 (1﹣p)2(3﹣4p),0<p<1,
由f′(p)=0,得p=0.75,
由f′(p)>0,得0<p<0.75,
由f′(p)<0,得0.75<p<1,
∴f(p)在(0,0.75)上是增函数,在(0.75,1)上是减函数,
∴p=0.75是f(p)的极大值点,也是f(p)的最大值点,
此时,由0.5+0.5m=0.75,解得m=0.5.
∴f(p)取得最大值时,p,m的值分别为0.75,0.5.
(3)设一位大学生射击过关测试所得分数为随机变量X,
则X的可能取值分别为5,4,2,
则P(X=5)=0.5,
P(X=4)=(1﹣0.5)×0.5=0.25,
P(X=2)=(1﹣0.5)(1﹣0.5)=0.25,
∴一位大学生射击过关测试所得分数的平均数:
E(X)=5×0.5+4×0.25+2×0.25=4,
∴该班组通过射击过关测试所得总分的平均数为:12×4=48.